1. Introduction
Robotic manipulation tasks become highly challenging when a mobile manipulator is required to obtain a feasible plan to solve a given problem under potential uncertainties. Uncertainty shall be viewed in the initial state of the robot environment, e.g., objects may rest in different positions or some object features (like color) could be initially unknown for a robot. Uncertainty, moreover, must be considered in the result of manipulation actions (as nondeterministic effects) since there could be different action outcomes. To deal with such uncertainties, robots generally look for a sequence of actions to satisfy the goal of a task and perform replanning in the case of action execution failure or uncertain situations. This process may be costly while a robot requires repetition of expensive replanning.
To tackle those challenging issues, these problems can rely on contingent task planning which plans in belief space and can generate conditional plans under uncertainty in terms of initial state and action effects. Contingent-based task planners can provide a tree of plans rather than a single sequence of executive actions. Therefore, uncertainty is observed during the plan execution, and the tree of plans is followed according to the binary observation values.
Other challenges are related to some demanding or difficult tasks which are either not performable easily by robots or are out of their reach, but that can be done in collaboration with a human operator. In these cases, the robot can ask the human operator to do some particular difficult actions, to transfer some objects located in the human workspace or to share knowledge that is initially incomplete to the robot. Moreover, there could be some geometric constraints imposed in the environment, e.g., lack of space for placing objects, occlusions, kinematic issues, etc., and the finding of the geometric values for each manipulation action becomes substantial in order to make a manipulation plan feasible. Therefore, the way of combining task and motion planning plays a significant role when the manipulation task is highly constrained in terms of geometric information and there is amount of uncertainty.
In this paper, we are going to deal with manipulation tasks carried out by a mobile manipulator assisted by a human operator. The mobile manipulator will be responsible to execute the main task, while the human operator will be responsible for some difficult actions (like to open some box-like containers which cannot be opened by the robot), to share knowledge with the robot, and to transfer objects to the robot when they are not reachable. Uncertainty in the initial state and in some action effects are considered. Some manipulation and sensing actions are considered in the current proposal, which allow illustration of the approach, and that can be extended to handle a broader set of manipulation tasks. No geometric uncertainty is considered, e.g., in the robot motion or the object poses.
Contributions: To deal with the aforementioned challenges, we propose a contingent-based task and motion planner based on
Contingent-FF [
1] that works under uncertainty and considers human–robot collaboration. The
Contingent-FF includes two main components,
heuristic evaluation and
search space, and results in a tree-shaped set of plans involving sensing actions. Three main contributions extend the basic
Contingent-FF planner:
Robot action reasoning. Two types of geometric reasoning are proposed and integrated with the basic planner: relaxed geometric reasoning and lazy motion evaluation. The former refers to Reachability, Spatial, and Manipulation reasoning. This reasoning process is embedded within the heuristic computation of the planner. Motion paths are lazily evaluated when actions are selected by the state space search. If the reasoning processes fail, geometric constraints are fed back to the planner. This part of the computation is done offline and aims to prune infeasible actions due to geometric constraints and to obtain a feasible set of actions in the tree of plans. As the basic contingent planner considers only symbolic reasoning, this module enables it to incorporate geometric reasoning to deal with practical applications. The reasoning process provides feasible initial and goal configurations for motion planning queries, improving its success rate and thus the overall performance of the planner in the generation of a feasible manipulation plan.
Human–robot collaboration. There are some actions which can be executed by the robot and others that require the collaboration of a human operator. The proposed relaxed geometric reasoning is extended to inform the planner about which actions cannot be executed by the robot, and hand over them to the human operator, allowing the planner to handle those cases where the selection of actions to be performed by a human operator is required. In these cases, the geometric world resulting by these actions is simulated and used in the planning system for further geometric reasoning evaluation. This step makes the basic planner flexible to consider the result of human actions, extending its performance to situations it is not able to be handled autonomously.
State observation. To observe the binary outcomes of actions, two modules are proposed: perception and human knowledge. Perception is used to detect, e.g., the actual locations of the objects or some objects feature like color. The knowledge provided by the operator is required for more difficult observations like determining if a can is filled or empty, or if a glass contains a given drink. Action observation takes place at execution time. The combining of both modules widens the capacity of the planner to identify the current situation of the robot’s world and decide the best course of actions in execution, thus improving the planner performance in finding feasible solutions.
One of the main advantages of the proposed framework is that the offline computation is valid and works despite the actual values of the uncertainty variables or the actual outcomes of the executable actions.
The rest of the paper is structured as follows. First,
Section 2 summarizes some related work and
Section 3 explains a proposal for contingent task and motion planning. Afterwards,
Section 4 presents and illustrates the proposed relaxed geometric reasoning for mobile manipulators,
Section 5 demonstrates contingent heuristic computation using relaxed information,
Section 6 details tree-based planning using search space, and
Section 7 presents manipulation plan execution using sensing and human interaction. Finally,
Section 8 shows some implementation issues as well as empirical results, and
Section 9 sketches the conclusions and future works.
2. Related Work
Manipulation problems of different nature have been tackled in the literature with different strategies, e.g., the manipulation problem of Navigation Among Movable Obstacles (NAMO) has been addressed in [
2,
3] using a backward search algorithm, and dual-arm table-top manipulation problems by combining motion planning and task assignment [
4]. These robotic applications, like many others, must deal with different sources of uncertainty and the use of sensors and perception strategies may be required, e.g., the studies in [
5,
6] have investigated the machine robotic cell scheduling problem for manufacturing systems with or without sensor inspection. The following sections classify more approaches in the field of task and motion planning with and without uncertainty.
2.1. Task and Motion Planning without Uncertainty
Recently, much study has been centered to solve robotics manipulation tasks by combining task and motion planning problems with no consideration on uncertainty. It is assumed that the initial state of the environment is perfectly known, and actions are deterministic, i.e., state of planning is only changed by the selected action. There is a huge number of task planners being able to solve manipulation problems under perfect information [
7].
In principle, two methods of combining task and motion planning have been explored: interleaved or simultaneously. Several studies call first task planning, and then motion planning to determine whether a plan is feasible or not such as [
8,
9,
10,
11,
12]. In the case of failure, geometric constraints are identified and reported to task planning and the procedure continues. This might be costly as a number of times the process could be repeated in order to find a geometrically feasible plan.
On the other hand, other approaches enable task planning to incorporate geometric reasoning within the task planning process [
13,
14,
15,
16,
17,
18]. Hence, in this case, task planning results in a feasible manipulation plan. In this line, we recently proposed a heuristic-based task and motion planner [
19] to deal with constrained table-top problems for bi-manual robots by offering different type of geometric reasoners that can be used in heuristic computation or when an action is selected. Our previous approach does not consider any uncertainty, human actions, and reasoning about mobile manipulation problems which are the subjects of this paper.
The way of integrating task and motion planning information in the current proposal is based on the simultaneous approach in order to generate feasible plans, and is an extension of [
19] that copes with mobile manipulators, uncertainty, and to consider collaborative tasks with human operators.
2.2. Task and Motion Planning under Uncertainty
There are some situations in which a robot has incomplete information about its manipulation environment; therefore, it needs to plan under uncertainty. Task planning under uncertainty is a well-established field in Artificial Intelligence. Conditional-based task planners can provide conditional plan to cope with uncertain information when either the initial state is not completely known, or the result of actions are nondeterministic. There are various classes of planning in this field like conformant, contingent, or probabilistic planning.
Conformant planning looks for plans under given uncertainty concerning the start state and the effects of symbolic actions, assuming no sensing capabilities during the execution of the plan. The plan should be successful regardless of which is the start state. Contingent planning also considers uncertainty regarding the start state and the effects of actions. However, it can provide some sort of observation over a conditional plan in execution. Probabilistic planning does planning under probabilistic uncertainty regarding the start state and the effects of actions.
More details on some approaches following conditional-based task planning are commented next as we are interested in this type of planner due to its feature of providing observation over a conditional plan. Some conditional task planners are
Contingent-FF [
1],
POND [
20], and
PKS [
21]. They plan in the belief space and compute conditional plans in the offline mode, which are guided by the result of sensing actions. On the other hand, there are some conditional task planners like
K-Planner [
22],
SDR [
23], and
HCP [
24] solving conditional plans online. Although these planners can prune some branches by considering online sensing actions, satisfying the goal of task may not be possible and the planners may face with dead-end even if there is a solution.
The concept of contingent-based task and motion planning has also emerged. For instance, the
Planning with Knowledge and Sensing (PKS) planner considers incomplete information and performs contingent planning [
25] in two main scenarios, using
force sensing and
visual sensing. In a similar direction, offline-based hybrid conditional task and motion planning has been proposed [
26], i.e., task planning is foremost performed, and then geometric evaluation is considered by incorporating low-level feasibility checks inside conditional planning (assuming that actuation actions are deterministic). On the contrary, the approach proposed here interweaves simultaneously efficient geometric reasoning inside the task planning process to provide geometrically feasible plans. The approach also copes with collaboration between the mobile robot and a human operator to perform a manipulation task.
3. A Proposal for Contingent Task and Motion Planning
This section first presents a brief overview of the original Contingent-FF task planning, and the modifications introduced in the present proposal to compute geometrically feasible manipulation conditional plans.
3.1. Contingent-FF Overview
The
Contingent-FF task planner [
1] handles uncertainty in the initial state and in the result of actions. The task planner has two main components which are heuristic computation and search space. For the heuristic computation, the planner uses a modified version of the
Relaxed Planning Graph (RPG) used in the
Fast-Forward (FF) planner [
27]. The relaxed plan including a number of relaxed actions is computed from the
RPG, and the heuristic value is the length of this relaxed plan. Also, promising actions (called helpful actions in
FF) are extracted from the relaxed plan as a pruning technique in the search space, as discussed in
FF. The
Contingent-FF planner extends the
RPG process, called
CRPG, by adding unknown facts in an additional layer in the heuristic phase. Known facts are basically those which do not have uncertainty and unknown facts are the ones which could be the result of nondeterministic actions or uncertain in the initial state. It introduces reasoning about unknown facts that allows such facts to become known in the
RPG process. Once
CRPG is successfully built, the relaxed plan is extracted.
In Contingent-FF, belief states including known and unknown facts are considered. The search space starts from the initial belief state and applies an And-Or search. The search space progress is guided by the heuristic value and helpful actions. The result of planning provides conditional plans that may involve a variety of sensing actions whose outcome causes different plan branches.
3.2. Planning Formulation
Our planning system domain is a tuple where is the action space, is the sensing action space, is a set of literals, is a workspace involving a mobile manipulator (described by the pose of the base along the arm configuration ) and a number of objects , and, is a set of grasping poses described for objects. Objects are denoted as: (pos,fe) ... (pos,fe), (pos,fe) (pos,fe)}, where j and k are the number of Movable and Fixed objects respectively, whose initial position and orientation are denoted by , and whose features are denoted by .
An action is a tuple 〈name(a), pre(a), effect(a), coneffect(a), geom(a), , where name(a) is the action symbolic name, pre(a) is a propositional formula which must hold for the action to be applied, geom(a) is the numerical counterpart of an action containing geometric information, effect(a) represents the negative and positive effects of a on the state it is applied to, and is a query function to the motion planner which computes a motion between two robot configurations and stores the solution if any. A relaxed action (where is the relaxed action space) is similar to the action despite it does not consider any negative effects. Actions refer to executable actions, i.e., requiring motion, and can be done by either the robot or a person. The following actions types are considered to deal with some examples of mobile robot manipulation:
Transit: an action done by the robot to travel from one configuration to another one without an attached object.
Transfer: an action done by the robot to move an attached object from one pose to another one.
Push: an action done by the robot to push an object from one pose to another one.
Open: an action done by the robot to open a box-like container (articulated cap with prismatic joint is assumed with two positions corresponding to fully closed and fully opened, the state being stored in the containers objects features).
HumanTransfer: an action done by a person to transfer/push an object to the robot workspace.
HumanOpen: an action done by a person to open a box-like container.
Each sensing action is a tuple , where is a literal with uncertainty. These are actions not involving motion, devoted to observing the value of . The observation is done in run-time. Some sample sensing actions are considered in the proposed planning system. They are the following:
SenseColor: a sensing action is done by a perception module to determine the color of an object.
SensePose: a sensing action is done by a perception module to determine the pose of an object.
CheckContainer: a sensing action is done by a person to evaluate whether a container is open or not.
CheckCan: a sensing action is done by a person to evaluate whether can-like objects are filled or not.
A belief state S is a tuple where includes a set of known literals which hold in that state and a set of uncertain literals which may hold or not in the state, and represents a full geometric description of the scene, i.e., configurations of robots and poses of objects corresponding to certain and uncertain literals. An executable action from a state results in a new world state using the state transition functions and . A sensing action splits a belief state and introduces two branches into the plan marked with , and .
The planning problem is expressed by a tuple where is a domain, consists of a set of literals representing the initial symbolic state such that along their geometric assignments regarding the initial state of the world , and is the set of symbolic goal conditions. The solution of a Combined Task and Motion Planning (TAMP) problem under uncertainty, which we denote by , is a tree-shaped conditional plan, i.e., a sequence of symbolic actions achieving , along with a feasible motion for each action.
3.3. Geometric Constraint Predicates
Basically, three general predicates, evaluated by geometric reasoning, are allocated that set constraints to the task states: isCrit(, , ), infeasByRob(, , ), and assist(Human, , ). The first predicate indicates that there is a blocking object which is located towards the target object placed in the pose . The second one shows that the target object cannot be manipulated by the robot in the corresponding pose . The last predicate shows the manipulation action with the target object and the corresponding must be done by a human operator Human.
The proposed predicates are interleaved inside the pre- and post-conditions of the actions. Concerning the actions done by the robot, the predicates ∼isCrit and ∼infeasByRob are inserted within the preconditions of the actions Transit, Open, Transfer, and Push in order to avoid moving the robot to any unreachable or infeasible configuration. Referring to the post-conditions, the last two actions may include the negation of the predicate isCrit if they are moving a blocking object to a placement where the obstruction does no longer hold. With respect to the actions performed by a human, the preconditions of the actions HumanTransfer and HumanOpen may include the predicate assist in order to indicate the requirement of a human operator.
To illustrate the use of these predicates, the actions Transit and HumanOpen are described next. The action template Transit(, , Surface, ) is designed to move the robot (arm and base), without holding any object, towards a grasp configuration of a manipulatable object located on a surface Surface at pose . In the final configuration, the robot holds the target object. The action is applicable if the following preconditions hold: the object is located on a surface, top of the object is clear, the robot arm is empty, it can reach the grasp configuration if there is no movable objects blocking its way to . The last precondition is represented by fact isCrit(, , ); objects that make this fact to hold are called Critical Objects which are the objects blocking the way of reaching the object. As a result of the action, the robot holds an object.
Transit(, , Surface, ):
Pre: onSurface(, Surface, ), armEmpty(), clear(), ∼infeasByRob(, , ),∀∼isCrit(, , )
Effect: holding(, , ), ∼clear(), ∼armEmpty(), ∼onSurface(, Surface, )
The action template HumanOpen(Human, , , Closed, Open) is used to open a box-like container when it is closed. The action is applicable if the robot needs the assistance from a human operator, represented by the assist predicate, and its status is closed, shown by the predicate status. These conditions are introduced in the action preconditions. As a result of the action, the corresponding container will be open.
HumanOpen(Human, , , Closed, Open):
Pre: assist(Human, , ), status(, Closed)
Effect: status(, Open), ∼status(, Closed)
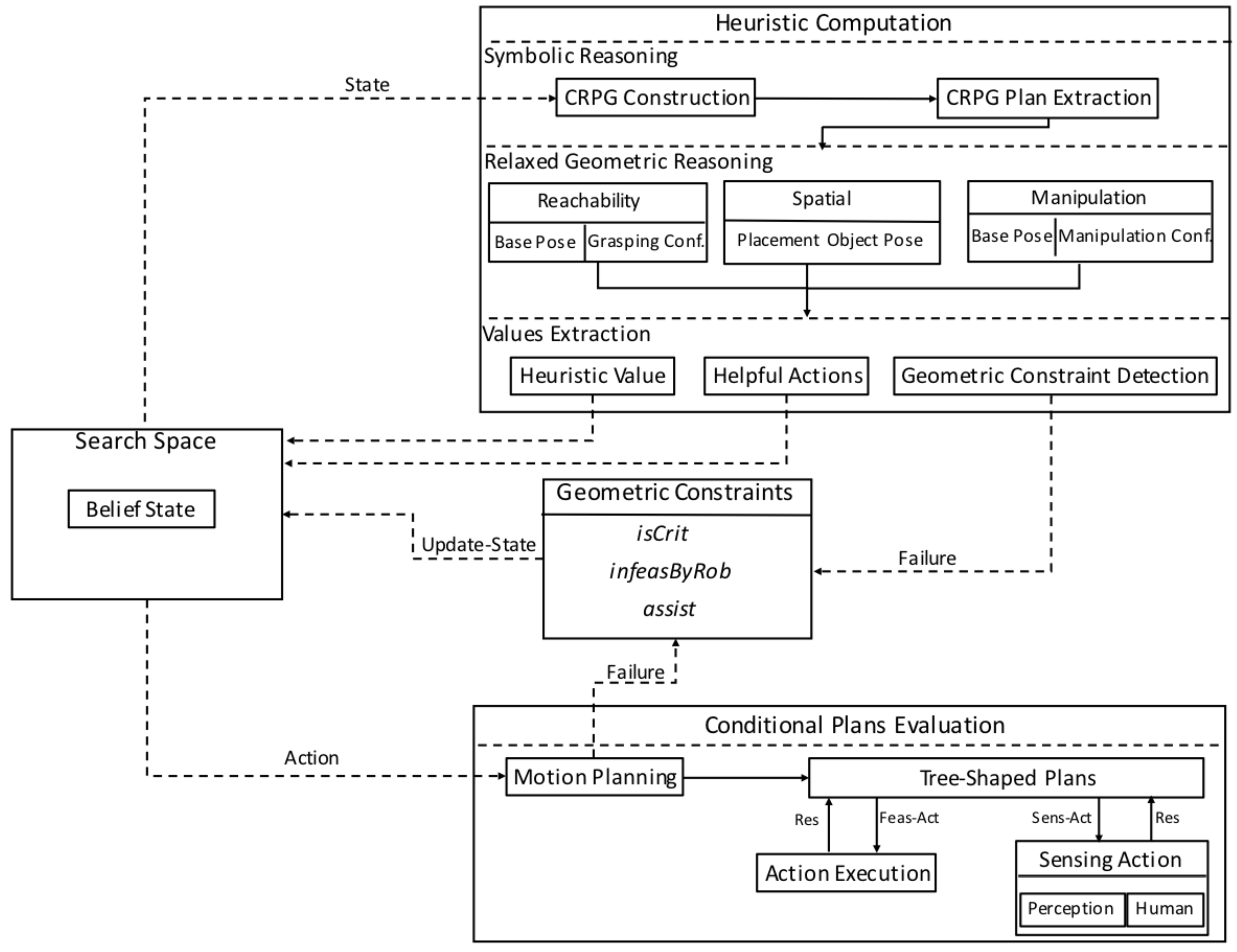
3.4. The Proposed Framework
The proposed framework for task and motion planning under uncertainty extends the basic
Contingent-FF planner, aiming to incorporate different geometric reasoning procedures, observations on sensing actions, as well as human–robot collaboration within planning. The overview of the system is sketched in
Figure 1. It involves three main parts:
Heuristic Computation, Space Search, and
Conditional Plans Evaluation.
Heuristic Computation basically provides a value which is distance to goal and promising actions for each belief state. The basic CRPG is initially computed and the associated relaxed plan is obtained. This plan is forwarded to the relaxed geometric reasoner determining the feasibility of actions in terms of reachability, collisions, manipulation constraints, and graspability. The heuristic value is returned along with helpful actions if such constraints are met. If a constraint is violated, the associated belief state is updated with facts describing the cause of failure, and an alternative relaxed plan is looked for. Hence, the heuristic function is informative both in terms of symbolic and geometric constraints.
Space Search maintains the basic algorithm of the Contingent-FF planner that is based on the And-Or search strategy. From each belief state, the action resulting in the state with lowest heuristic value is selected and is a candidate to be added to the conditional plans. The only difference is that the heuristic value now accounts for geometric constraints.
Conditional Plans Evaluation tries to solve motion planning for an action if possible. It considers sensing procedure to evaluate sensing actions and may assign actions, which are infeasible for robots, to operators.
If motion planning fails, the current belief state is updated with the cause of failure and the search resumes. In general, the geometric failure could be due to collisionable objects, so the literal isCrit is added to the belief state. If the failure is because of fixed obstacles blocking the way of reaching an object, inverse kinematic problems, or motion planning time-out problem, the literal infeasByRob is added to the state. In such failure, if the type of the evaluated action is either transit or open, the literal assist is also inserted.
Otherwise, when motion planning succeeds, the action is added to the tree-shaped conditional plans at hand. After finding the complete conditional plans, feasible actions are executed by a robot or a human operator in the real world and sensing actions are observed either using a perception module or the information provided by the human operator in run-time. Therefore, the robot plan can determine the correct branch to follow up its plan.
4. Relaxed Geometric Reasoning for Mobile Manipulators
Relaxed geometric reasoning is the evaluation of geometric conditions of actions with no call to motion planning. It indicates that a feasible motion is likely to be obtained for the selected actions if certain task constraints are satisfied. Therefore, the relaxed geometric reasoning process contains three modules:
reachability reasoning,
spatial reasoning, and
manipulation reasoning. This set of reasoning extends our previous relaxed geometric reasoning process [
19] to consider reasoning on mobile manipulation along human actions.
Reachability reasoning (): This reasoning is applied for only transit action. To transit the robot to a target position, a feasible arm configuration and robot base pose must be first obtained. A set of robot poses is considered in the workspace of the robot. From each pose, an Inverse Kinematic (IK) solver is called for each candidate grasping pose, and moreover the result of IK is determined whether it is collision-free or not. The first collision-free IK solution along the corresponding grasping pose is reported if possible. Otherwise, failure is reported if there is neither IK solution nor collision-free configuration among a set of robot poses. Accordingly, the reasoner returns the collisionable objects.
Spatial reasoning (): This reasoning is applied for the transfer, push, open, humanOpen, and humanTransfer actions. This is considered to find a valid placement for an object within a given region with no consideration of the robot. A pose is sampled, i.e., an object lies in the target region and the initial stable posture is maintained. The feasibility of the sampled pose is also determined through a collision-checking procedure to verify whether there are any collisions with other objects in the robot environment or not. If it is valid, the sampled pose is stored in the geometry details of the action which transfers the object. Otherwise, another sample will be attempted. In the case that all tried samples are not valid, failure occurs and the collisionable objects are reported. Moreover, some constraints are taken into consideration while the sample placement is accomplished. For example, in the case of the push action, the sample is considered in the direction in which the object is being pushed. In the case of humanOpen and Open, the valid object placement is extracted from the object feature (the box cap is assumed to have a single full-open position).
Manipulation reasoning (): This reasoning is considered to evaluate the compatibility of the grasp poses to move an object from the initial position to the final one (using ). The process applies reasoning to return on of the feasible ways to transfer an object from initial to final position in terms of collision-free IK solution. In the case that there is no possible solution meeting these conditions because of collisions, then the collisionable objects are returned. In this way, it can obtain the valid robot pose and grasping configuration when the robot manipulates an object.
Algorithm 1 describes the relaxed geometric function when applying the actions. Algorithm is detailed below:
Reasoning about the robot actions [lines 5–15]: The transit action calls the reachability reasoning by the function [line 6]. The transfer, push and open actions call the spatial reasoning by the function [line 11], and then call the function [line 13]. If the reasoning processes are successfully done, the corresponding response is set to feasible and geometric details are appended to the evaluated action [line 8] and [line 15]. On the contrary, if the failure is due to manipulatable objects, the response is set to infeasible-criticalObjects and the collisionable objects are stored in . In other cases of failure, the response is set to infeasible-infeasByRob that could be because of collisions with fixed obstacles or because the IK module is not able to find a configuration.
Reasoning and finding the geometric values of the human actions [lines 16–23]: The humanTransfer action calls the spatial reasoning by the function [line 17]. This function is responsible to find the pose of the object placement for the human action and inserts it to the action [line 19]. For the humanOpen action, the pose of the container object being opened is extracted from the object feature by the spatial reasoner function [line 21] and is stored into the action details [line 23].
| Algorithm 1: |
![Applsci 10 01665 i001 Applsci 10 01665 i001]() |
5. Contingent Heuristic Computation using Relaxed Information
Heuristic computation returns the heuristic value as well as helpful actions using relaxed symbolic along geometric reasoning from each state. Algorithm 2 explains the modified version of Contingent-FF heuristic computation for a given belief state S and goal by taking into account geometric information. This involves three steps: computing the CRPG and the relaxed plan , determining , and computing the heuristic value and the helpful actions, as follows.
Computing the CRPG and [lines 1–2]: The CRPG graph involving state layers and action layers is built by the function CRPGConst [line 1]. The function CRPGPlan extracts from that graph [line 2]. The process is performed in a similar way to the standard Contingent-FF.
Evaluating [lines 3–13]: Actions in
are sent to the relaxed geometric reasoning for the feasibility evaluation [line 5]. Basically, this process tries to figure out whether there is any feasible world to meet the action conditions or not as we proposed in [
19]. Upon failure, the function MaxUp [line 9] determines whether a predefined maximum number of trials is reached or not to update the belief state and find another relaxed plan. If updating the state is required, the feedback of the geometric reasoner is evaluated. In the case of failure because of
infeasible-criticalObjects, the literal
isCrit(, , ) with critical objects is added to the current belief state. Otherwise, the failure is because of
infeasible-infeasByRob and the literal
infeasByRob(, , ) is added to the state. In this case, if the type of action is either transit or open, the literal
assist(Human, , ) is also added to the state.
Computing the heuristic value and with helpful actions [lines 14–15]: In the case that the relaxed plan is geometrically feasible with respect to the geometric reasoning evaluation, the heuristic value along the helpful actions are achieved. The function HValue extracts the heuristic value
[line 14] and the function HelpAct reports helpful actions
[line 15] as the generic
Contingent-FF.
| Algorithm 2: |
![Applsci 10 01665 i002 Applsci 10 01665 i002]() |
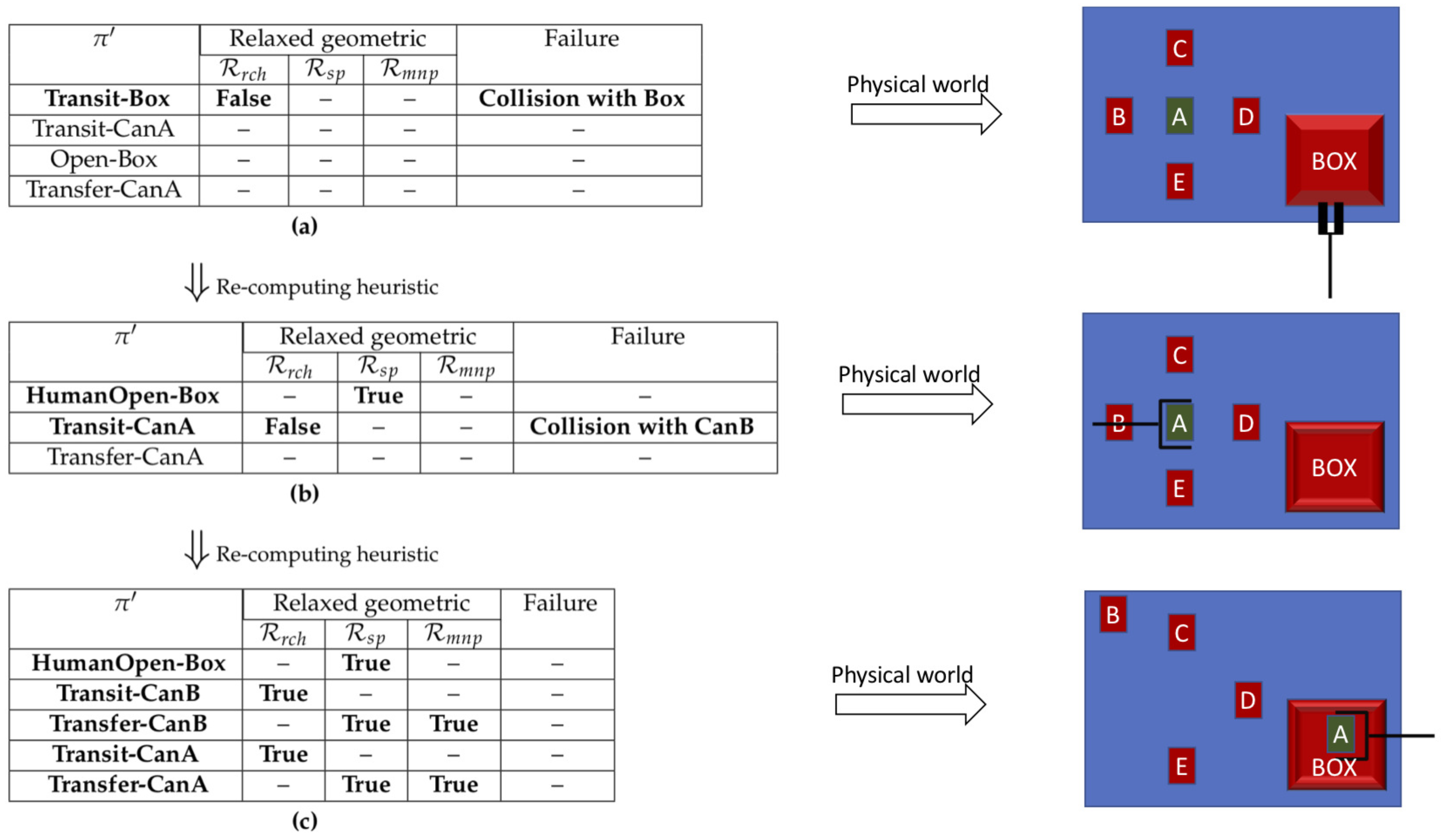
An example is considered to show how geometric constraints are captured and handled during the heuristic computation. The initial scene of the example is shown in
Figure 2 where the robot is required to move
Can A inside
Box. To make the problem challenging, it is assumed that top grasps are not allowed and some side grasping poses are considered for each can. Several task constraints are imposed, e.g., there is no direct collision-free motion to reach
Can A, and also the robot is not able to open
Box and needs an operator assistant.
The computation of the heuristic process in terms of geometric feasibility is represented in
Figure 3. The corresponding physical world for each relaxed plan has been shown also.
Figure 3a shows the initial relaxed plan extracted. When the first action is forwarded for the relaxed geometric reasoning, the reachability reasoner fails. This is because when the inverse kinematic module checks side grasping poses considered for the box cap, all retrieved joint configurations have collisions with the box object. The geometric reasoning process is done by the proposed function RelaxGeomReas in Algorithm 2 that is added to the basic planner.
To handle this task constraint, the predicates
infeasByRob(tiago, box, posBox) and
assist(person, box, posBox) are asserted to the planning state by the associated reasoning process. The updating sate step is done by the proposed function UpState as it lets the planner know the detected constraints of the environment.
Figure 3b shows the next heuristic computation taking into account the task constraint. In this case, the spatial reasoner module successfully finds the geometric state of
Box after applying the action
humanOpen. However, the reachability reasoner reports a failure for evaluating the
transit action for the object
Can A due to collision between the robot arm and
Can B. This object is marked as a critical object, so the state is updated with the predicate
isCrit(can B, can A, pos A). The heuristic computation is again repeated, and finally the reasoning processes can correctly find feasible geometric details for the actions. This process results in geometrically feasible heuristic computation.
6. Tree-Based Planning using Search Space
The And-Or search procedure as considered in the Contingent-FF planner is used to result in a feasible manipulation plan. The heuristic computation has been modified to incorporate geometric check and, moreover, selected actions must be evaluated using motion planning. The process is represented in Algorithm 3.
The algorithm gets as input and outputs if possible. First, the trials counter is set [line 1] and the state is the initial belief state [line 4]. The function Search performs the standard search mechanism as Contingent-FF does [line 6]: it provides the next state using the transit function to visit along the promising applicable action(s) with . This step is done with the modified CRPG function (see Algorithm 2), by taking geometric constraints into account.
In the case that
does not exist [line 7], the algorithm performs another search from the beginning. Until the maximum number of iterations is not reached [line 9], the process is repeated with the initial state updated by the function UpdateInitState [line 11]. If the maximum number of trials is reached, the process returns failure [line 14].
| Algorithm 3: The Proposed Planning Algorithm |
![Applsci 10 01665 i003 Applsci 10 01665 i003]() |
For those actions that either do not belong to the set of sensing actions and are not assigned to human, the MotionPlanner function is used to compute a collision-free path for the currently selected action(s) [line 17]. If a path is found, is set to feasible and the path is returned. Afterwards, is appended with the sensing, human, or normal action(s) [line 19]. In the case of failure due to infeasible-criticalObjects, the literal isCrit(, , ) with critical objects is added to the current belief state. Otherwise, the failure is because of motion planning time-out problem or collisionable fixed obstacles, the type of failure is infeasible-infeasByRob and the literal infeasByRob(, , ) is added to the state. In this case, if the type of action is either transit or open, the literal assist(Human, , ) is also added to the state.
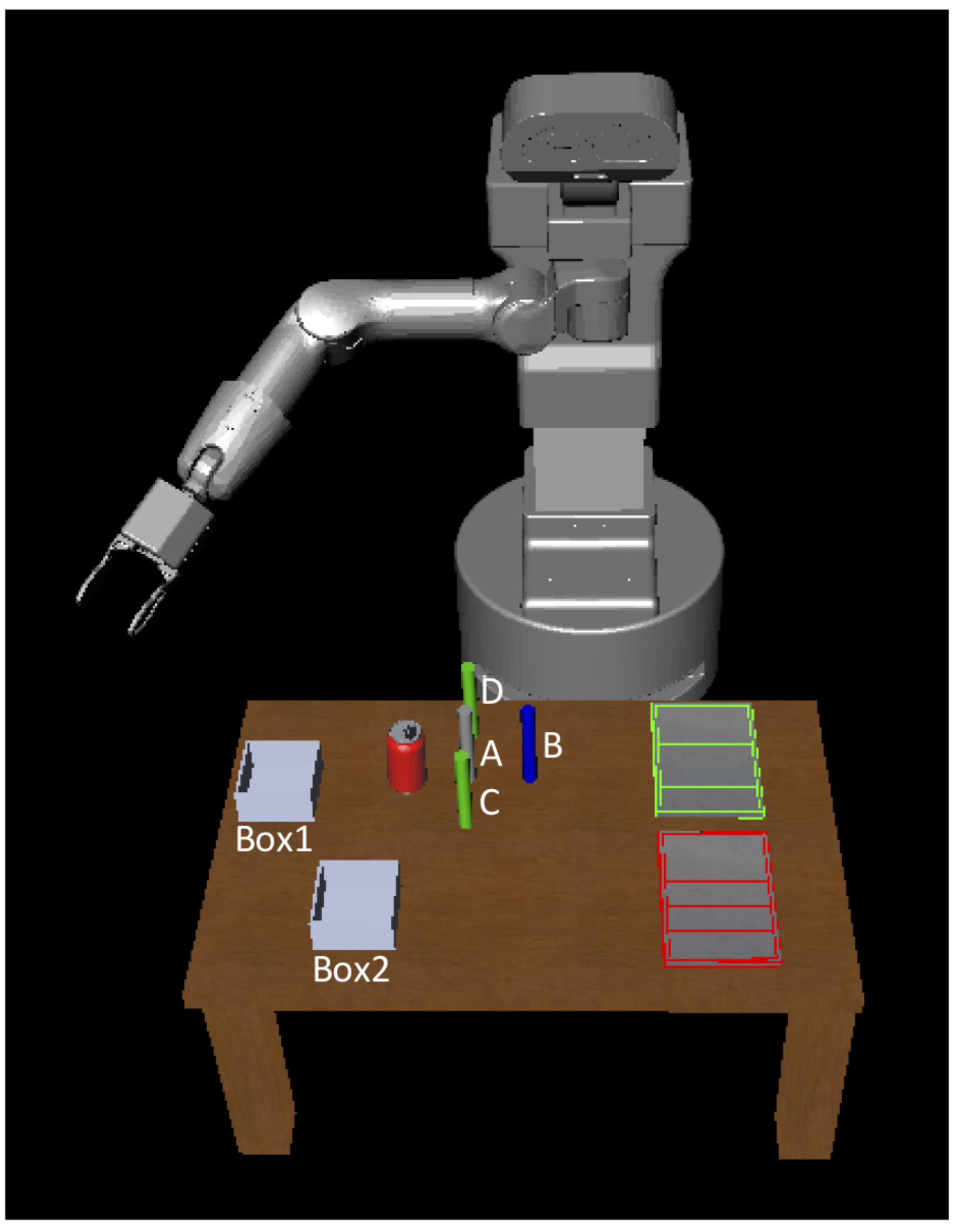
An example is considered to illustrate how the geometrically feasible conditional plan is obtained offline under belief information of the initial state. The scene depicted in
Figure 4 shows the initial belief state of the mobile manipulation problem, where the color of the gray cylinder is uncertain (it could be red or green), it is not known whether the can is filled or not, nor if the containers are open or closed. The goal is to transfer the cylinder A to either the red or the green tray. Some particular placements regions allocated for the manipulatable objects if required:
The green cylinders must be placed on the green tray.
The red cylinders must be placed over the red tray.
The blue cylinders must be placed within the containers.
The can objects may be optionally placed anywhere over the table.
The complete conditional plan is represented in
Figure 5 that is obtained by Algorithm 3. It is briefly discussed how this geometrically feasible plan is obtained. While the planning process is taking place, there are several challenges in terms of geometric constraints which are captured and handled by the proposed geometry reasoner. These steps are mainly done using the Search function which internally calls Algorithm 2. To reach the target object, the reachability reasoning process, place in the function RelaxGeomReas, detects cylinder B and reports that the object is blocking the way of reaching object A in the heuristic computation. Therefore, the predicate
isCrit(cylinderB, cylinderA, posA) is inserted to the initial belief state of the planner using the function updating the belief state. This predicate says that cylinder B blocks the way of reaching cylinder A.
Furthermore, when the robot attempts to find a feasible configuration for opening box 1 in the case that the box is closed, the reachability reasoner fails due to colliding with the box. Here, it is the case that robot needs to ask a human operator for collaboration. Accordingly, the reasoner appends the predicates infeasByRob(tiago, box1, posBox1) and assist(person, box1, posBox1) to the corresponding state. The humanOpen action then appears.
7. Manipulation Plan Execution using Sensing and Human Interaction
When the manipulation conditional plan is achieved, it will be forwarded to for the execution module. Algorithm 4 outlines the process of actions execution performed by the robot or human, and calls to the sensing actions. The conditional plan is initialized from its root [line 1]. For each action of the plan, its type first identified whether it is execution or sensing one. In the case of execution action, if it has to be executed by human, the function executeByHuman asks a person to do the corresponding action [line 5] and an operator then sends a command to the robot that the action has been done successfully. Otherwise, the action is executed by the robot [line 7].
On the other hand, if the type of action becomes sensing, the function senseAct determines the binary value of the sensing action which is
True or
False. This is done using the perception module allocated for the robot. Depending on the type of uncertainty, the function may request to human or activate a sensing module to observe the action value. Regarding the
CheckCan or
CheckOpen sensing actions, human information is used, while a sensing module is used for the
SensePose and
SenseColor sensing actions.
| Algorithm 4: Manipulation Plan Execution |
![Applsci 10 01665 i004 Applsci 10 01665 i004]() |
8. Empirical Results and Discussion
This section describes some manipulation problem solved using the proposed framework, and the implementation issues. The mobile robot considered is TIAGo. It has 7 degrees of freedom arm, equipped with a gripper, mounted on a mobile platform through a lift torso.
The executive simulated result of the manipulation problem represented in
Figure 4, called
Problem-1, is shown in
Figure 6. For the domain of the problem, a number of actions is considered for the robot being
transit, transfer, open, and
push along with some actions for an operator that are
humanTransfer and
humanOpen. Actions are selected according to the planning mechanism in terms of symbolic and geometric reasoning. We assume that the values of the uncertainty information are provided in run-time in simulation. Therefore, the executive plan is provided below:
Executive Plan: { Transit-B, CheckContainer-Box1-Open (False), HumanOpen-Box1, Transfer-B-Box1, Transit-A, SenseColor-A-Red (True), Transfer-A-RedTray }
The states represented in the figure are classified as follows:
- (a)
is the initial belief state of the robot and environment.
- (b)
is the state where the robot applies transit action to reach cylinder B.
- (c)
is the state where the sensing action CheckContainer-Box1-Open showed that Box 1 is currently closed.
- (d)
is the state where the HumanOpen action is executed as the robot is not capable enough to open the box.
- (e)
is the state where the robot places cylinder B within box 1.
- (f)
is the state where the robot transits to cylinder A.
- (g)
is the state where the sensing action SenseColor-A-Red showed that the cylinder is actually red.
- (h)
is the state where the robot moves its base and the arm configuration to place cylinder A over the red tray.
In addition, the proposal has been evaluated for other cluttered problems where the robot needs to sort objects according to the colors. Regarding the action domain, Robot actions are
transit and
transfer, and the action template
humanTransfer is considered for an operator. The problem represented in
Figure 7, called
Problem-2, shows the initial and goal states of manipulation where the green and red objects must be located on the green and red regions respectively. The red object is not initially located on the table. The pink region is considered on the robot workspace where an operator can transfer objects. The planning uncertainties are the color of the green object which could be actually green or red and the location of the red object which could be on the robot table or in the human workspace. Therefore, the
humanTransfer action is applied to transfer the object to the robot workspace as the robot is not allowed to move to the human workspace. The final executable plan would be to transfer the green object to the target placement region by the robot. It then looks for the red object and figures out the object is not located on the table and asks an operator to transfer the object. The
humanTransfer action is selected in the conditional plan, so the requested object is transferred to the robot workspace. The operator updates the robot knowledge through the robot system terminal. The robot is aware that the human action has been successfully performed, and afterwards it travels to grasp the object. Eventually, the robot transfers the object to the target region.
The proposed approach has been tested for similar problems by increasing the number of objects and varying color and/or location uncertainties. The problems performance are represented in
Table 1 in terms of conditional and executive plan length, and moreover planning time.
Problems-3 includes a cluttered problem where there are nine objects and three of them need to be sorted. Similar uncertainty of
Problem-2 is considered regarding the color and location of objects.
Problem-4 is the one where 12 objects exist and four of them must be sorted. In this case, the uncertainty information like the objects color and locations are considered for more objects.
Concerning the implementation framework, four components are considered: task planning, relaxed geometric reasoning, motion planning, and executive module. Task planning is developed using a modified version of the
Contingent-FF planner coded in C++. All the action templates are described using
PDDL by considering
ADL (Action Description Language, ref. [
28]) enabling us to define operators in a more compact way, using quantifiers and conditional effects. There is not any pre-processing step to compute geometric details of actions and they are computed and assigned during the manipulation planning process.
We use
The Kautham Project [
29], a C++-based open-source tool for motion planning that enables planning under geometric and kinodynamic constraints for relaxed geometric reasoning and motion planning. It uses the
Open Motion Planning Library (OMPL) [
30] as a core set of sampling-based planning algorithms. In this work, the
RRT-Connect [
31] motion planner is used for motion planning. This planner is one of the most efficient motion planners, but it does not guarantee optimal motions.
The Kautham Project involves different collision checking modules to detect robot-object and object-object collisions, and features a placement sampling mechanism to find feasible object poses in the workspace. Relaxed geometric reasoning uses these modules to find feasible sample geometric instances for symbolic actions. The executive module uses a sensing module which uses the 3D camera mounted inside the
TIAGo robot, and also some components provided by
PAL Robotics to send a motion path to the robot. The communication between task, relaxed geometric reasoning, motion planning, and executive modules is done via
Robotic Operating System (ROS) [
32].
9. Conclusions
This paper has proposed a contingent-based task and motion planning approach able to cope with high-dimension mobile manipulation problems in the presence of high-level uncertainty and human interactions (referred to the sharing of knowledge and to collaborative actions which are out of the robot capabilities). For this purpose, the basic Contingent-FF planner has been modified to include robot action reasoning, human–robot collaboration, and state observation. A set of geometric reasoning processes has been offered to the planning process to capture the task constraints imposed in the robot environment and to update belief state while task planning is done. Moreover, some modules linked with the human knowledge along with the perception system, have been also designed to observe the binary outcomes of actions. It is worth noting that the proposed approach results in a tree-shaped conditional plan which is geometrically feasible regardless of the values of sensing actions.
To evaluate the proposed approach, several manipulation tasks have been executed in simulation and real environments to show the way of tackling human–robot interactions, and identifying and handling both geometric constraints and high-level uncertainty. Problems performance has been reported in terms of the length of the manipulation plan and planning time, considering an increasing number of objects. In all the cases, the robot in collaboration with the human operator has been able to solve the tasks despite the uncertainty and the constraints.
Future work will concentrate on manipulation tasks also subject to low-level geometric uncertainty, its effects in sensing and how it is transferred to task planning.