Robust Estimation of Arrival Time of Complex Noisy Partial Discharge Pulse in Power Cables Based on Adaptive Variational Mode Decomposition
Abstract
1. Introduction
2. Methods
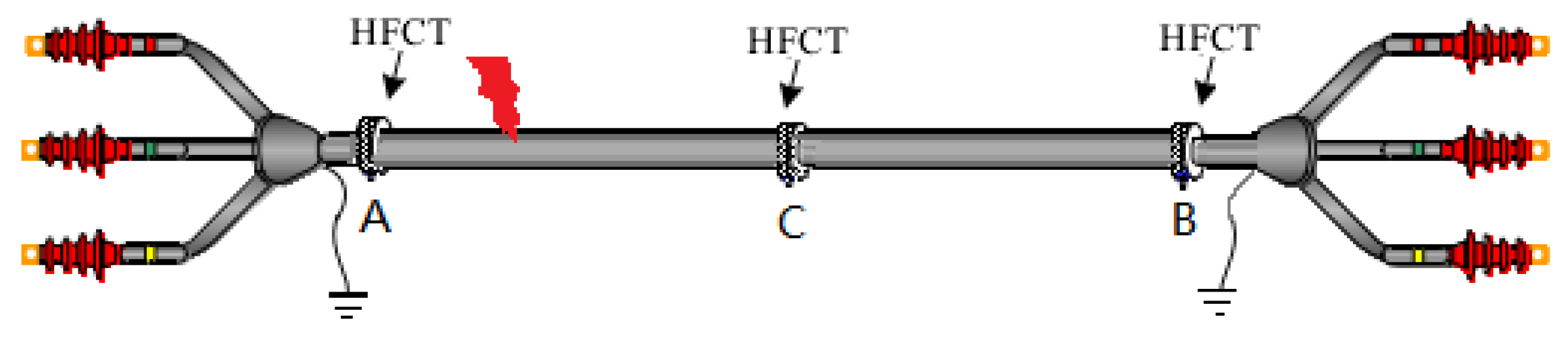
2.1. Multi-Sensor Travelling Wave Based Localization Problem
2.2. The Principle of Improved VMD Algorithm
2.2.1. Construction and Solution of Variational Problem
2.2.2. Improvements of VMD
2.3. Scale Adaptive Wavelet Packet Transform
2.3.1. Basic Principles of Wavelet Packet Transform
2.3.2. Selection of Wavelet Base and Scale
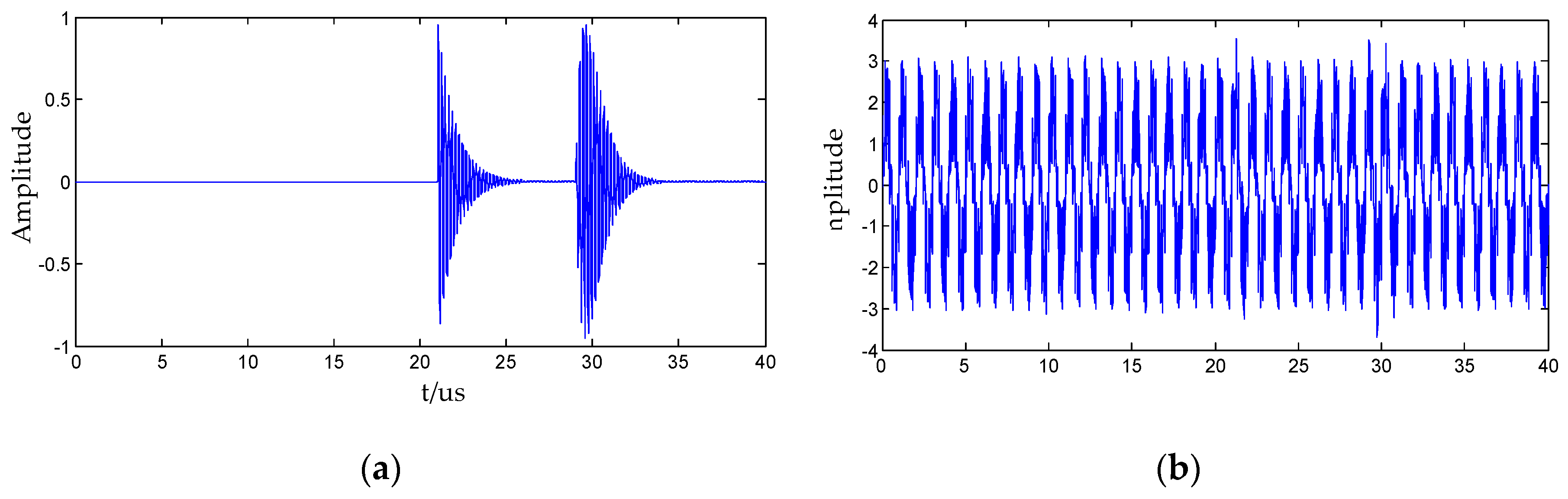
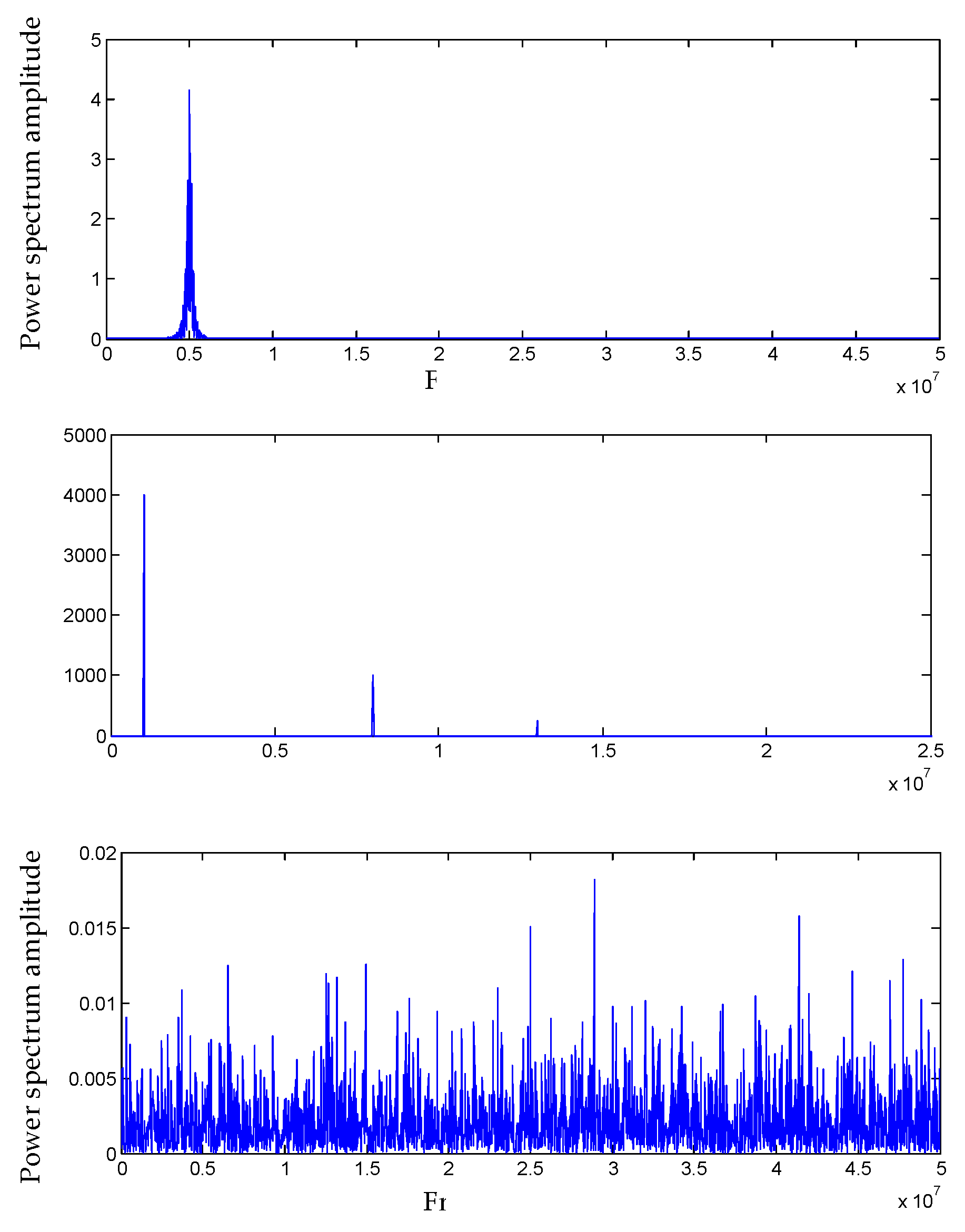
2.3.3. Performance Analysis of Adaptive Wavelet Packet Decomposition for Noisy PD Signal
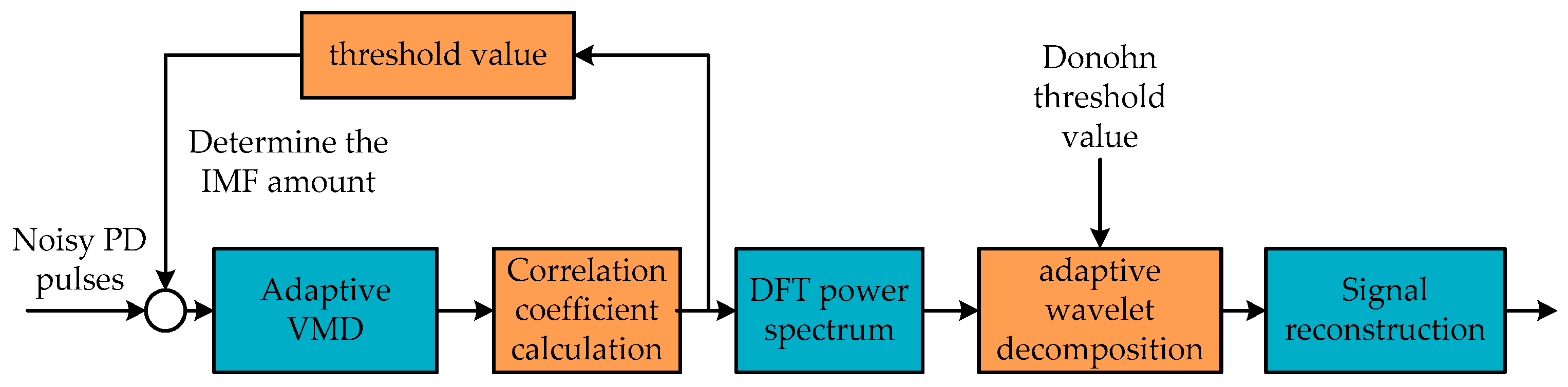
2.4. Proposed De-Noising Method for Complex Noisy PD Signal
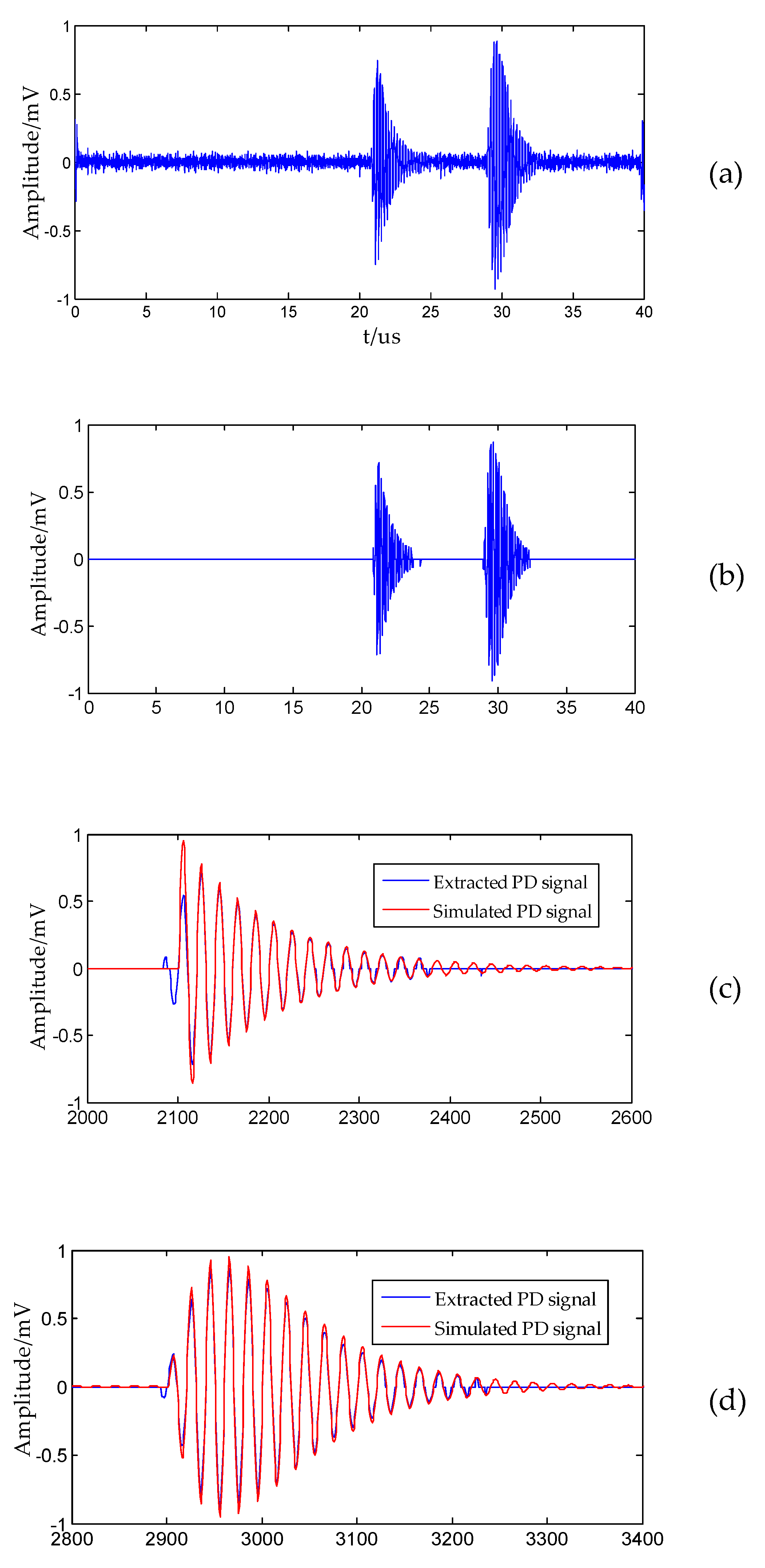
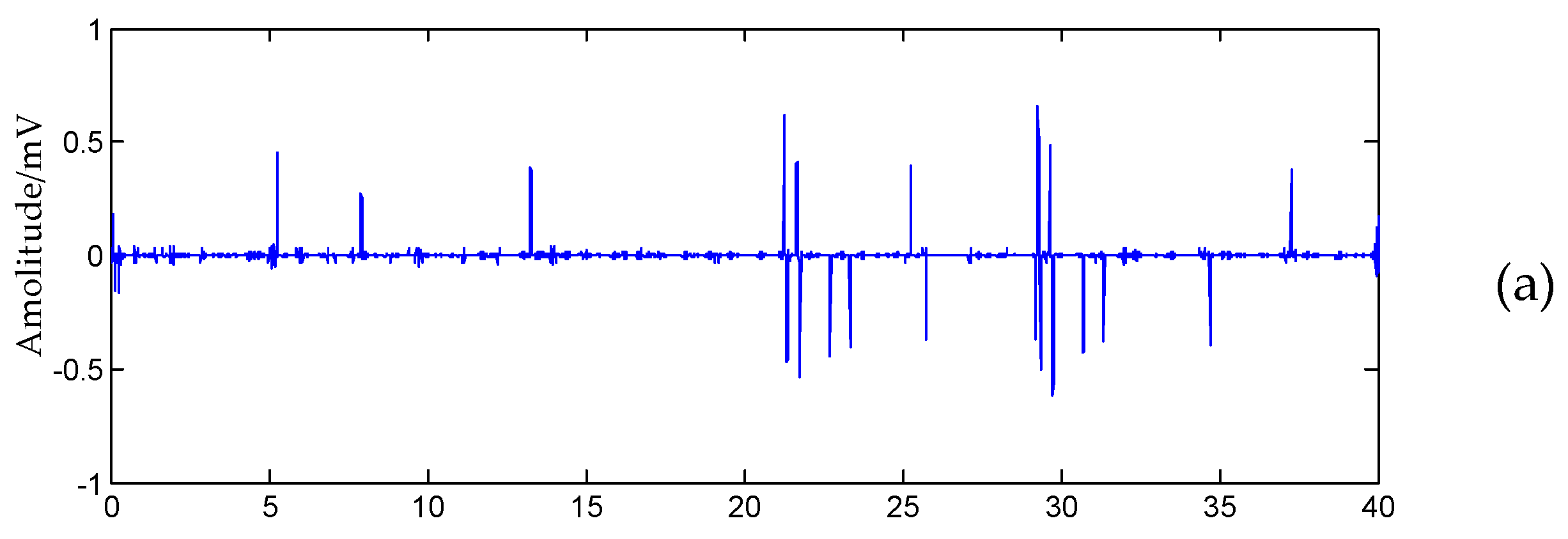
3. Results and Discussion
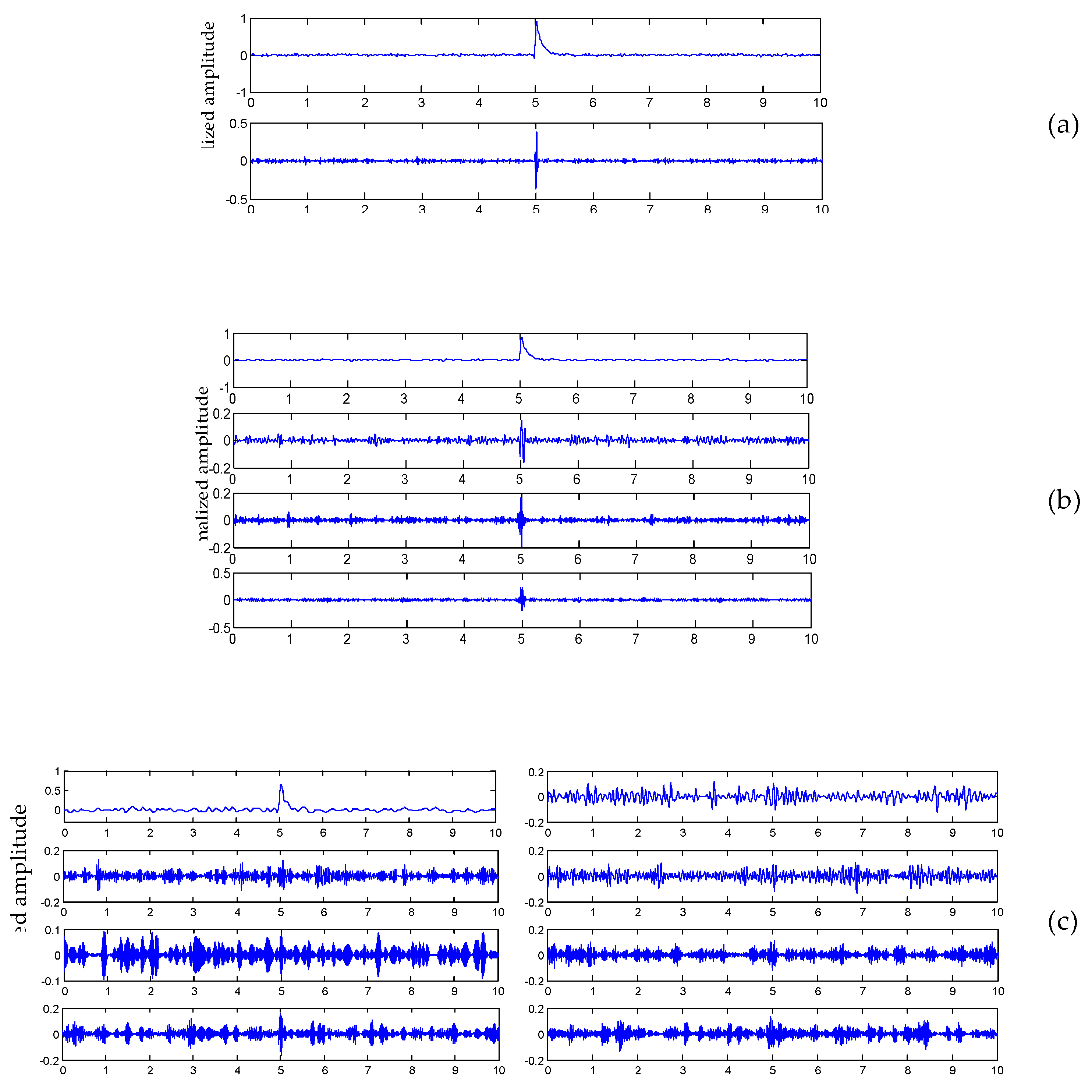
3.1. Comparison of De-Noising Results
3.2. Robust Estimation of Arrival Time of PD Pulse
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Orton, H. Power cable technology review. High Voltage Eng. 2015, 41, 1057–1067. [Google Scholar]
- Gargari, S.M.; Wouters, P.A.A.F.; Wielen, P.C.J.M.; Steennis, E.F. Partial discharge parameters to evaluate the insulation condition of on-line located defects in medium voltage cable networks. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 868–877. [Google Scholar] [CrossRef]
- Wu, R.N.; Chang, C.K. The use of partial discharges as an online monitoring system for underground cable joints. IEEE Trans. Power Del. 2011, 26, 1585–1591. [Google Scholar] [CrossRef]
- Li, J.H.; Han, X.T.; Liu, Z.H.; Yanming, L. Review on partial discharge measurement technology of electrical equipment. High Voltage Eng. 2015, 41, 2583–2601. [Google Scholar]
- Babaee, A.; Shahrtash, S.M. On-line partial discharge defected phase selection and localization in cross-bonded single core cables. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2995–3006. [Google Scholar] [CrossRef]
- Álvarez, F.; Garnacho, F.; Ortego, J.; Sánchez-Urán, M.Á. Application of HFCT and UHF sensors in on-line partial discharge measurements for insulation diagnosis of high voltage equipment. Sensors. 2015, 15, 7360–7387. [Google Scholar] [CrossRef]
- Xu, Y.; Gu, X.; Liu, B.; Hui, B.; Ren, Z.; Meng, S. Special requirements of high frequency current transformers in the on-line detection of partial discharges in power cables. IEEE Elect. Insul. Mag. 2016, 32, 8–19. [Google Scholar] [CrossRef]
- Hu, X.; Siew, W.H.; Judd, M.D.; Peng, X. Transfer function characterization for HFCTs used in partial discharge detection. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1088–1096. [Google Scholar] [CrossRef]
- Mohamed, F.P.; Siew, W.H.; Soraghan, J.J.; Strachan, S.M.; McWilliam, J. Partial discharge location in power cables using a double ended method based on time triggering with GPS. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 2212–2221. [Google Scholar] [CrossRef]
- Choi, W.; Kim, J.; Seo, I.; Hwang, J.; Koo, J. Development of a partial discharge detection algorithm and verification test for extra-high-voltage cable system. IET Sci. Meas. Technol. 2016, 10, 111–119. [Google Scholar] [CrossRef]
- Sun, K.; Guo, J.; Yang, Y. On Line Partial Discharge Detection and Localization Based on AIC Criterion and Time-Window Energy Ratio. Chin. J. Sens. Actuators 2017, 30, 1209–1214. [Google Scholar]
- Herold, C.; Leibfried, T. Advanced signal processing and modeling for partial discharge diagnosis on mixed power cable systems. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 791–800. [Google Scholar] [CrossRef]
- Jian, X.U.; Cheng-Jun, H. Research on improved fast Fourier transform algorithm applied in suppression of discrete spectral interference in partial discharge signals. Power Syst. Technol. 2004, 28, 80–83. [Google Scholar]
- Lu, Y.; Han, Z.; Chen, Y. FFT narrowband filtering method based on energy-ratio pretreatment. J. Southeast Univ. 2010, 40, 948–951. [Google Scholar]
- Zhou, X.; Zhou, C.; Kemp, I.J. An improved methodology for application of wavelet transform to partial discharge measurement denoising. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 586–594. [Google Scholar] [CrossRef]
- Mohammadi, F.; Zheng, C.; Su, R. Fault Diagnosis in Smart Grid Based on Data-Driven Computational Methods. In Proceedings of the 5th International Conference on Applied Research in Electrical, Mechanical, and Mechatronics Engineering, Tehran, Iran, 24 January 2019. [Google Scholar]
- Strela, V.; Heller, P.N.; Strang, G. The application of multi-wavelet filter banks to image processing. IEEE Trans. Image Proc. 2009, 8, 548–563. [Google Scholar] [CrossRef]
- Li, Y.; Wei, H.; Billings, S.A. Identification of Time-Varying Systems Using Multi-Wavelet Basis Functions. IEEE Trans. Control Syst. Technol. 2011, 19, 656–663. [Google Scholar] [CrossRef]
- Zhang, Y.; Duan, W.; Li, T. A Reverse Separation Method of Suppressing Periodic Narrowband Noise in Partial Discharge Signal. Trans China Electrotech. Soc. 2015, 30, 232–239. [Google Scholar]
- Wu, Z.; Huang, N. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adaptive Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yuan, N.; Zhu, Y.L.; Liang, H.Q. EEMD denoising method using rectangular window. Proc. CSU-EPSA 2015, 27, 54–58. [Google Scholar]
- Sun, K.; Zhang, J.; Shi, W.; Guo, J. Extraction of Partial Discharge Pulses from the Complex Noisy Signals of Power Cables Based on CEEMDAN and Wavelet Packet. Energies 2019, 12, 3242. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Proc. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Liu, C.; Wu, Y.; Zhen, C. Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy C means clustering. Proc. CSEE 2015, 35, 3358–3365. [Google Scholar]
- Zhu, Y.; Jia, Y.; Wang, L. Feature extraction and classification on partial discharge signals of power transformers based on improved variational mode decomposition and Hilbert transform. Trans. China Electrotech. Soc. 2017, 32, 221–235. [Google Scholar]
- Pan, Y.; Zhang, X.; Zhang, Y. Denoising Method for Transformer Partial Discharge Signals Based on Complete Ensemble Empirical Mode Decomposition. Guangdong Electr. Power 2017, 30, 93–98. [Google Scholar]
- Jiao, S.; Shi, W.; Liu, Q. Self-adaptive partial discharge denoising based on variational mode decomposition and wavelet packet transform. In Proceedings of the 2017 Chinese Automation Congress (CAC2017), Jinan, China, 20 October 2017; pp. 7301–7306. [Google Scholar]
- Mohammadi, F.; Zheng, C. A Precise SVM Classification Model for Predictions with Missing Data. In Proceedings of the 4th National Conference on Applied Research in Electrical, Mechanical Computer and IT Engineering, Tehran, Iran, 4 October 2018; pp. 3594–3606. [Google Scholar]



| J | NCC | SNR | D (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| J = 1 | 0.794 | 0.608 | 0.6744 | −0.1 dB | 10.0 | ||||
| J = 2 | 0.672 | 0.424 | 0.414 | 0.446 | 0.7741 | 2.6 dB | 16.7 | ||
| J = 3 | 0.446 | 0.251 | 0.251 | 0.230 | 0.210 | 0.238 | 0.8294 | 4.6 dB | 23.3 |
| J = 4 | −2.5 × 10−4 | −0.006 | 1.8 × 10−4 | −6.2 × 10−4 | 0.002 | 0.066 | 0.8229 | 4.8 dB | 43.3 |
| Parameter | Signal1 | Signal2 | Signal3 |
|---|---|---|---|
| SNR of noisy signal (dB) | 0.0 | −2.5 | −13.0 |
| NCC | 0.9507 | 0.9397 | 0.8294 |
| SNR of de-noised signal (dB) | 10.2 | 9.4 | 4.6 |
| Signal | NCC | SNR | VTP |
|---|---|---|---|
| Pulse 1 | 0.9816 | 13.39 dB | 1.0886 |
| Pulse2 | 0.9970 | 19.44 dB | 1.0879 |
| Total | 0.9886 | 15.51 dB | 1.1166 |
| Method | Evaluation Parameter | Pulse 1 | Pulse 2 | Total |
|---|---|---|---|---|
| CEEMD | NCC | 0.3847 | 0.4387 | 0.3908 |
| SNR(dB) | 0.6752 | 0.8935 | 0.7166 | |
| VMD wavelet threshold method | NCC | 0.6677 | 0.8100 | 0.5509 |
| SNR(dB) | −0.2551 | 3.0568 | 3.0239 | |
| Proposed method | NCC | 0.9816 | 0.9970 | 0.9886 |
| SNR(dB) | 13.3906 | 19.4398 | 15.5064 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, K.; Wu, T.; Li, X.; Zhang, J. Robust Estimation of Arrival Time of Complex Noisy Partial Discharge Pulse in Power Cables Based on Adaptive Variational Mode Decomposition. Appl. Sci. 2020, 10, 1641. https://doi.org/10.3390/app10051641
Sun K, Wu T, Li X, Zhang J. Robust Estimation of Arrival Time of Complex Noisy Partial Discharge Pulse in Power Cables Based on Adaptive Variational Mode Decomposition. Applied Sciences. 2020; 10(5):1641. https://doi.org/10.3390/app10051641
Chicago/Turabian StyleSun, Kang, Tong Wu, Xinwei Li, and Jing Zhang. 2020. "Robust Estimation of Arrival Time of Complex Noisy Partial Discharge Pulse in Power Cables Based on Adaptive Variational Mode Decomposition" Applied Sciences 10, no. 5: 1641. https://doi.org/10.3390/app10051641
APA StyleSun, K., Wu, T., Li, X., & Zhang, J. (2020). Robust Estimation of Arrival Time of Complex Noisy Partial Discharge Pulse in Power Cables Based on Adaptive Variational Mode Decomposition. Applied Sciences, 10(5), 1641. https://doi.org/10.3390/app10051641




