Railway Polygonized Wheel Detection Based on Numerical Time-Frequency Analysis of Axle-Box Acceleration
Abstract
1. Introduction
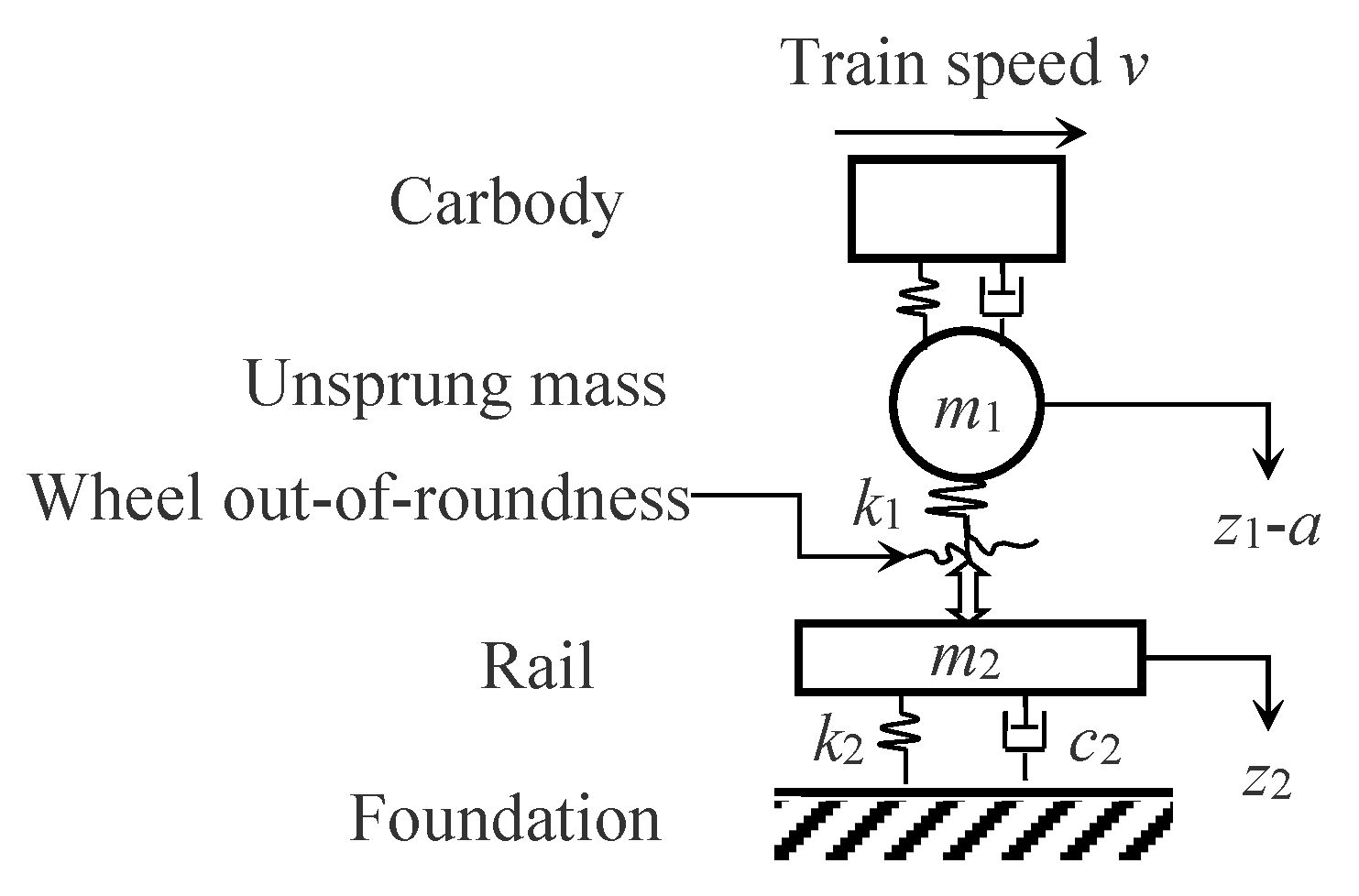
2. Theoretical Analysis
3. Modeling and Signal Analysis Method
3.1. Vehicle-Track Rigid-Flexible Coupling Dynamics Model
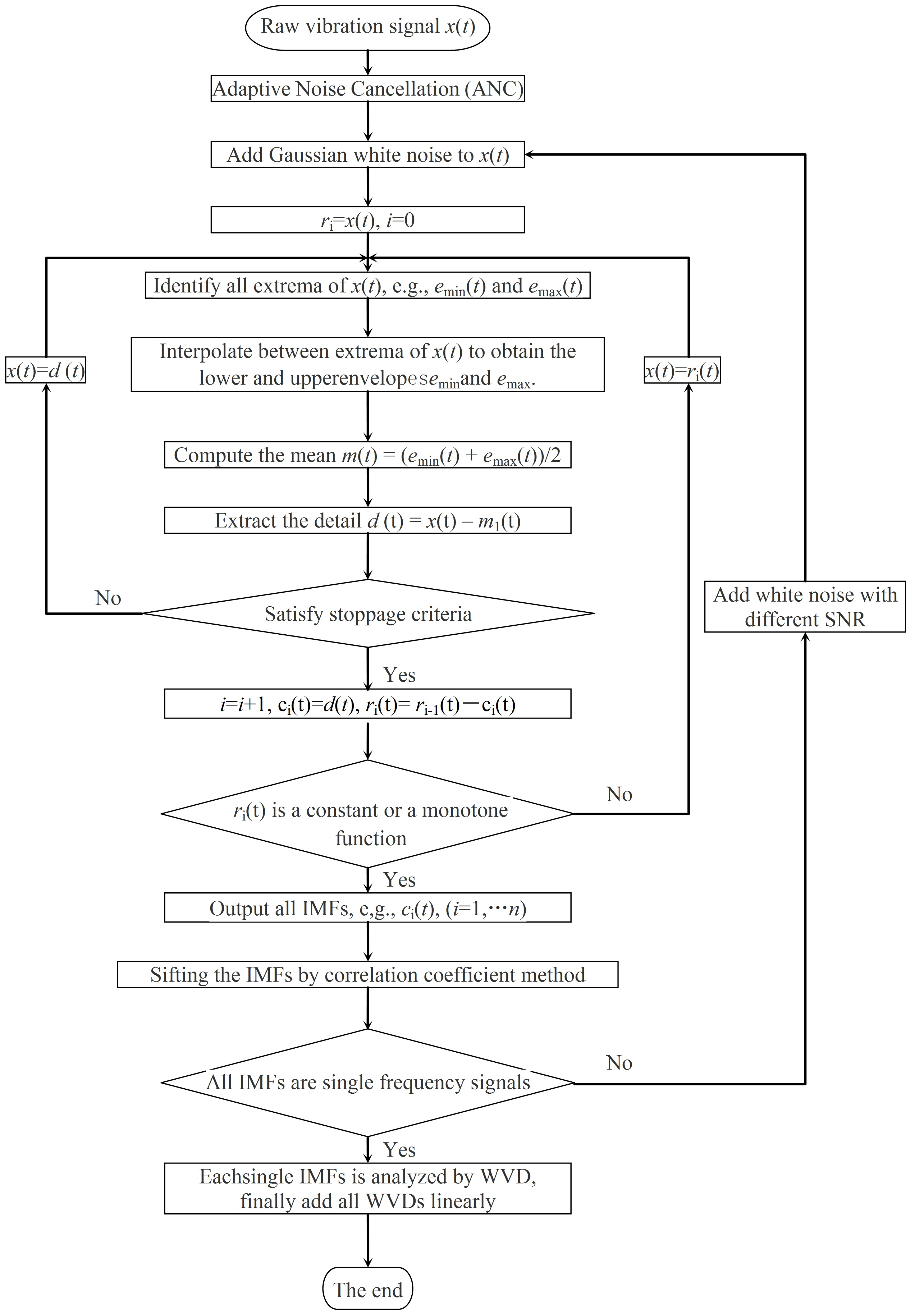
3.2. Joint Time-Frequency Method based on EEMD and WVD
4. Results and Discussions
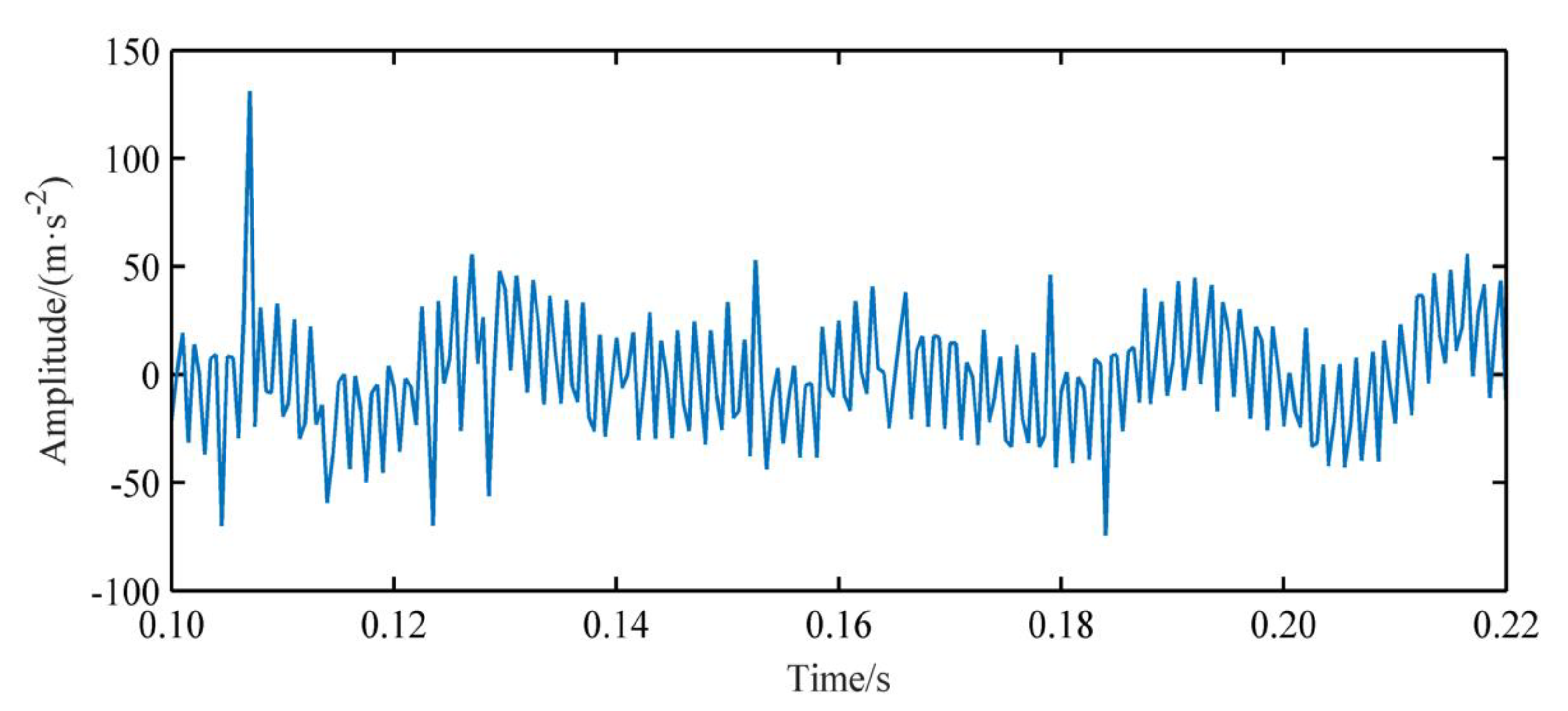
4.1. Results of Axle-Box Vibration Acceleration Caused by Wheel Polygons in Time-Domain
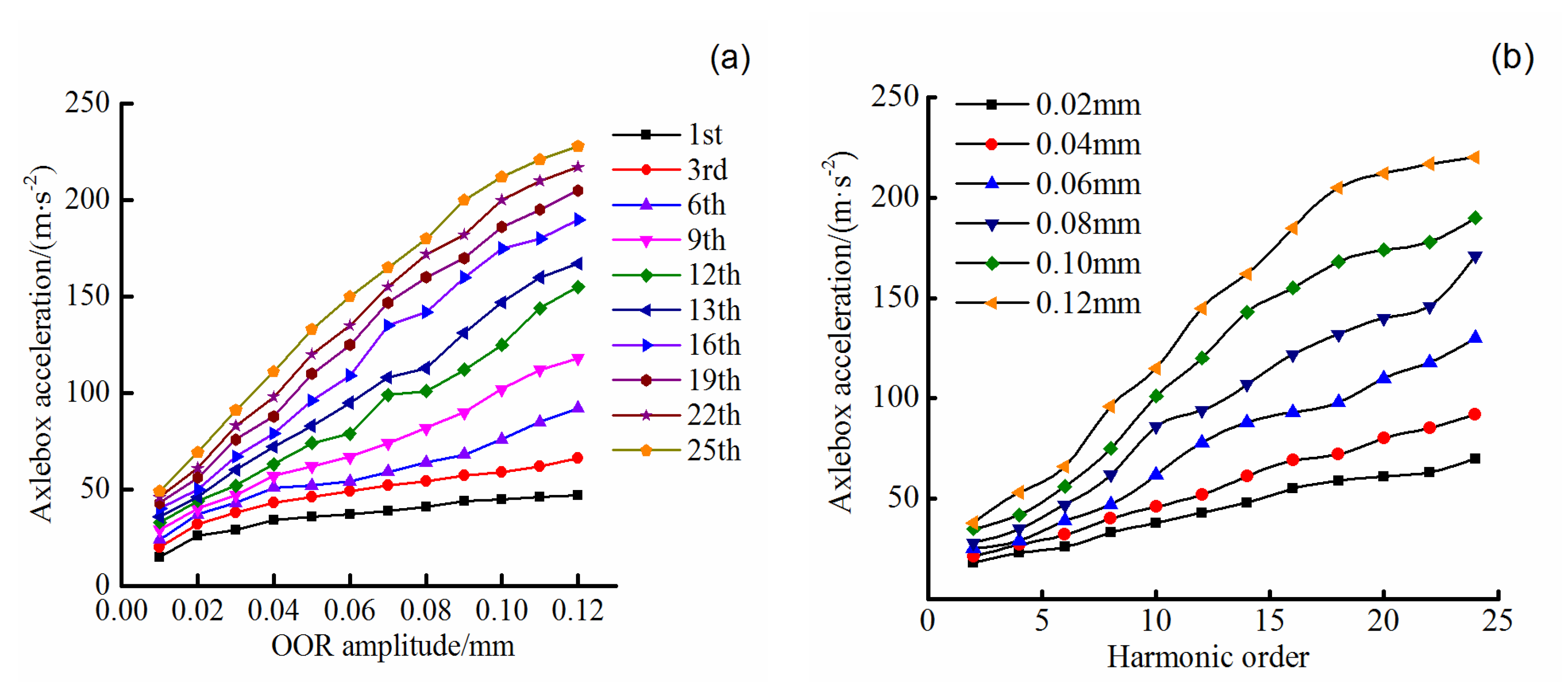
4.1.1. Effect of Wheel Polygon
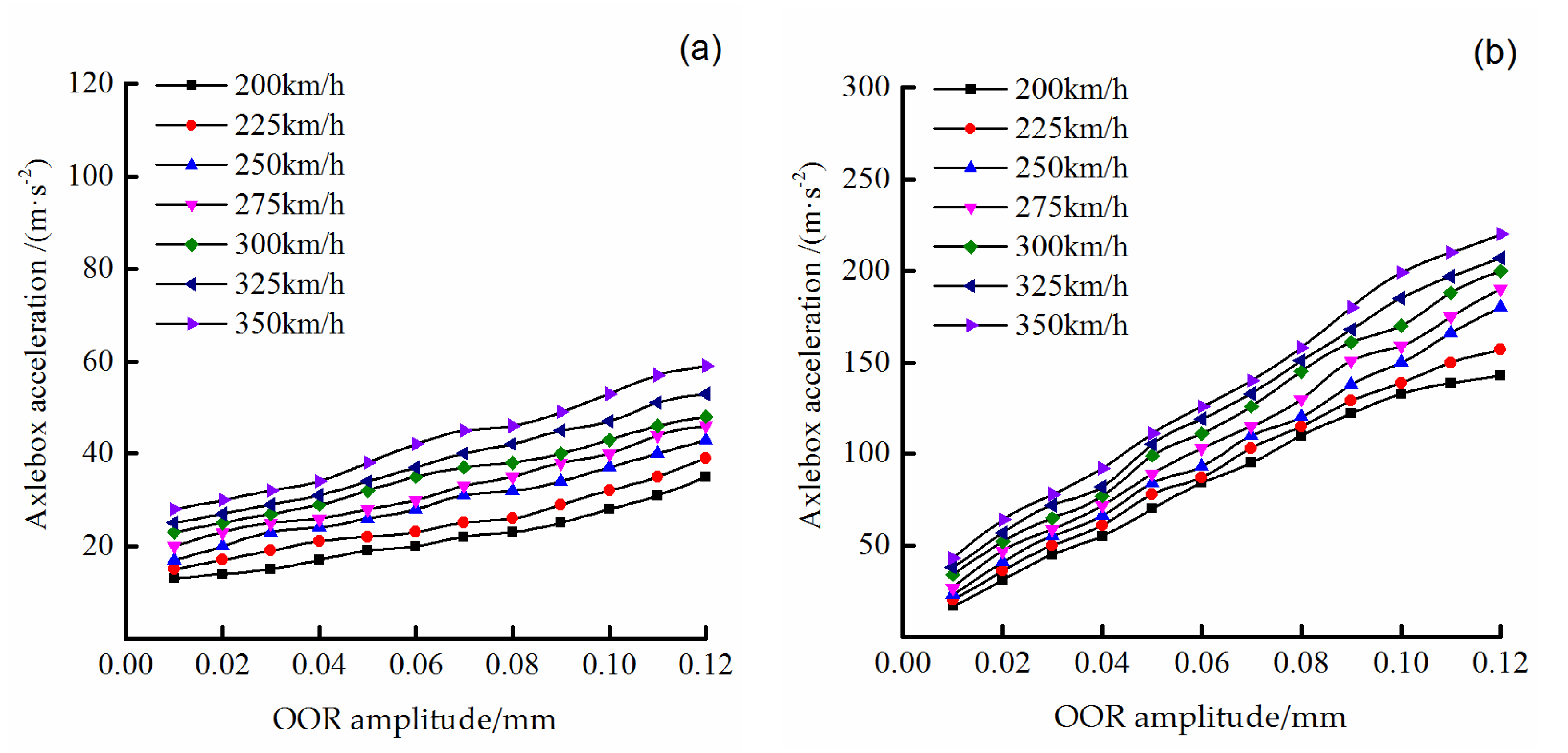
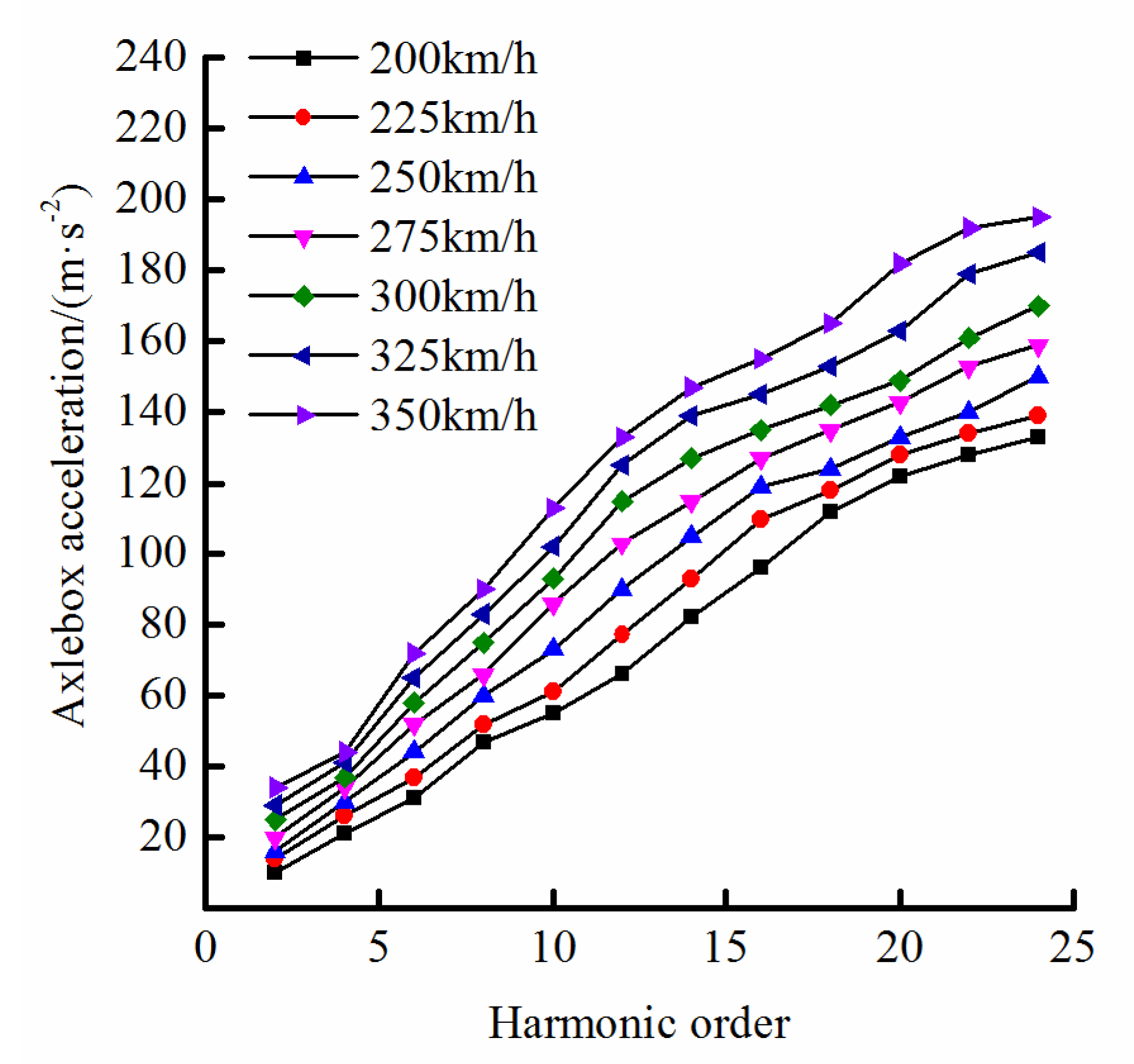
4.1.2. Effect of Vehicle Speed
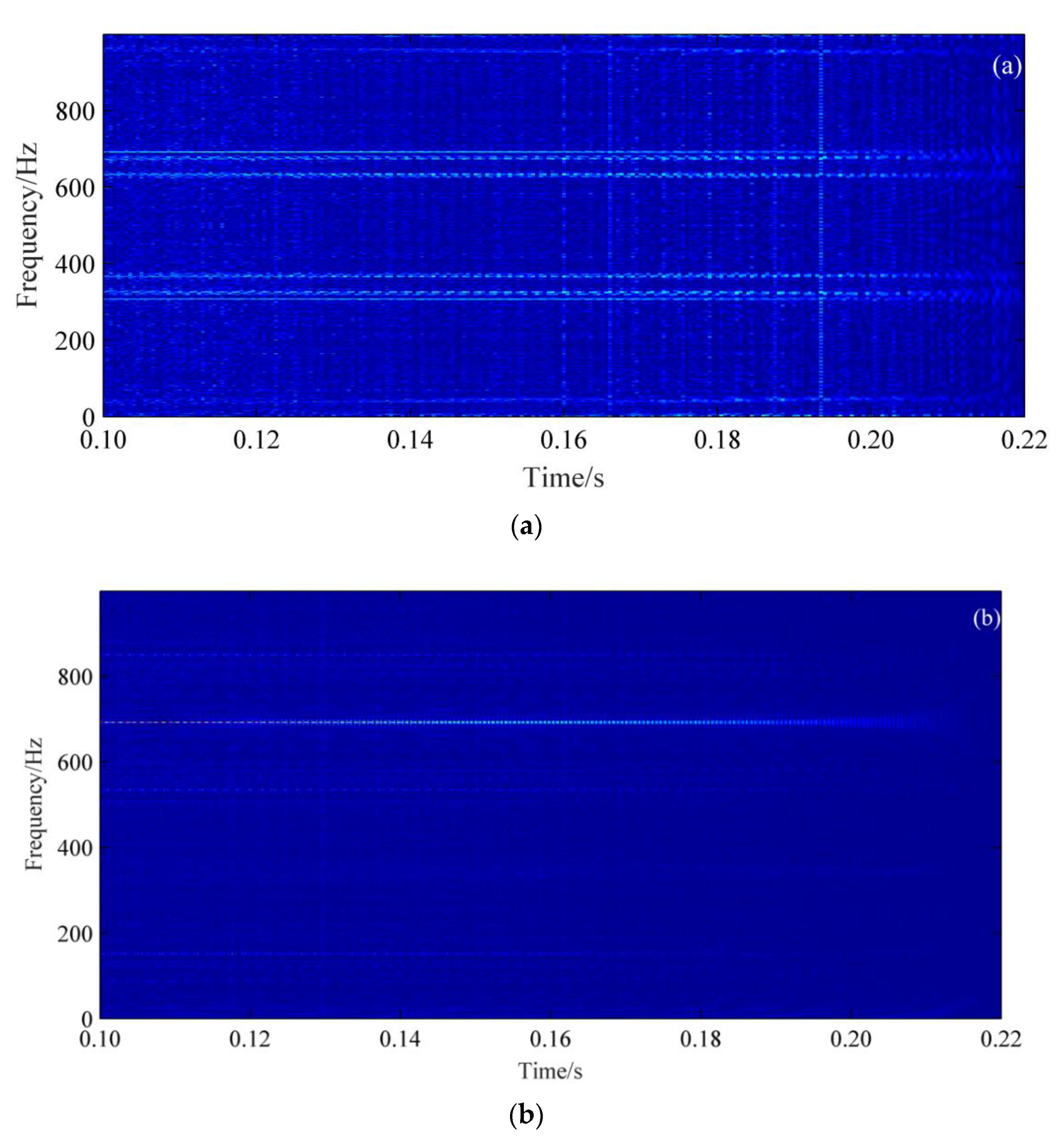
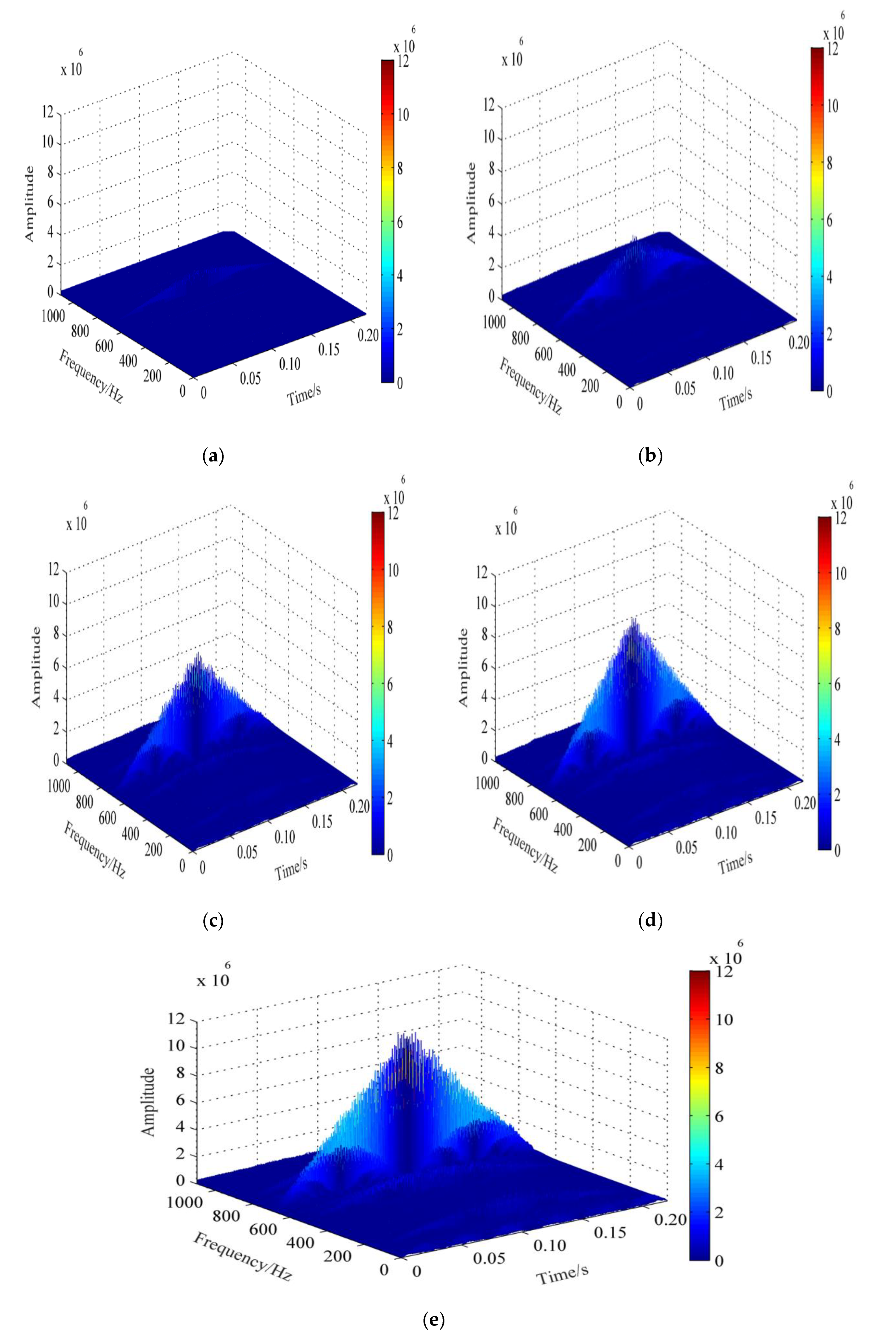
4.2. Time-Frequency Analysis of Axle-Box Accelerations based on EEMD and WVD
4.3. Comparision with Other Author Results
4.4. Limitation and Futherwork
5. Conclusions
- (1)
- The quantitative relationship between the characteristics of axle-box acceleration and wheel polygon defects is determined based on a parameter-lumped simple wheel-track model that accounts for wheel out-of-roundness. The frequency of the axle-box acceleration coincides with the characteristic frequency of polygonized wheels, which underpins the detection of wheel polygon defects based on axle-box vibration.
- (2)
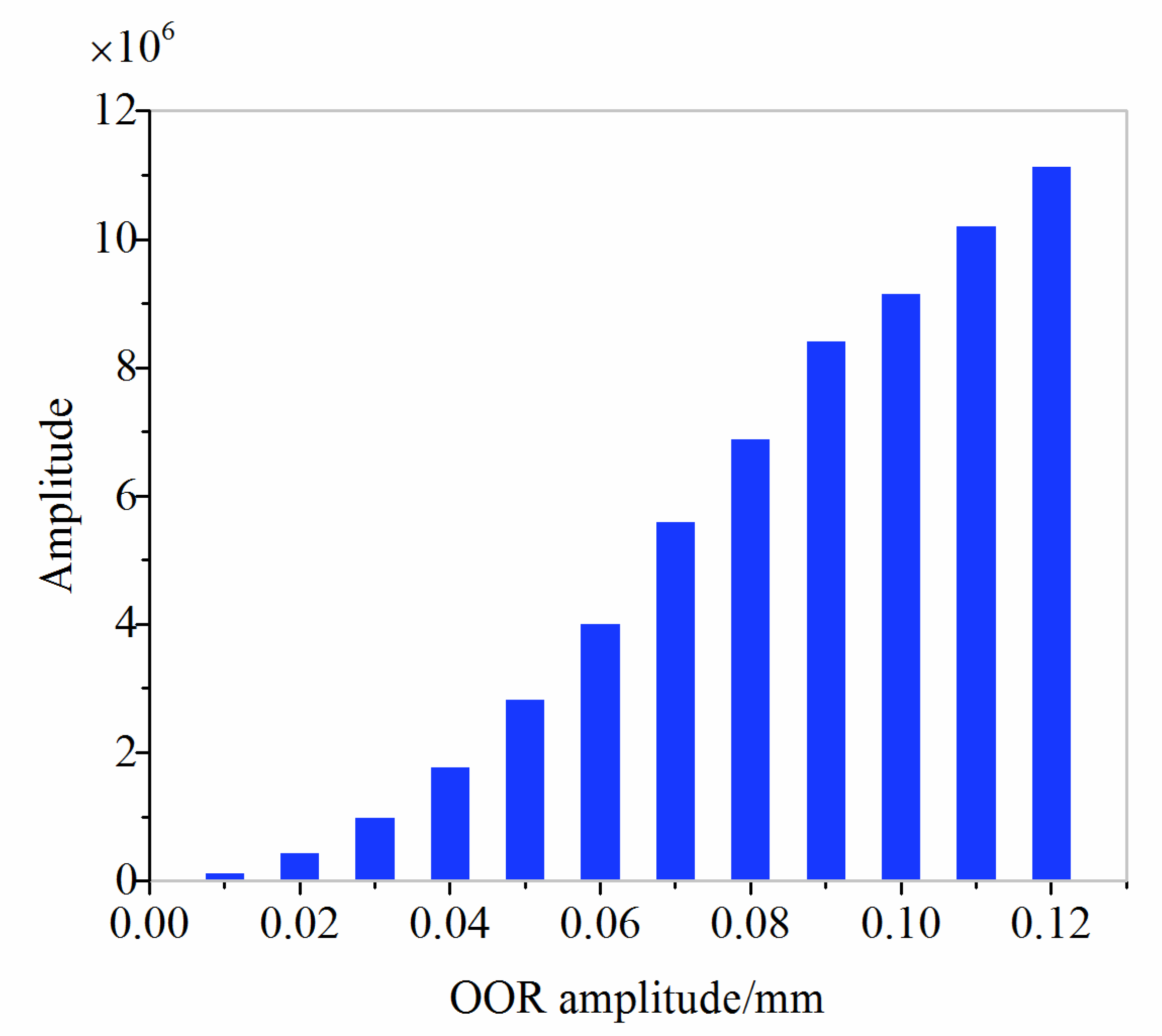
- A dynamic model of a vehicle-track coupled system with flexible wheelsets and tracks is presented to determine the relationship between wheel polygon defects and axle-box acceleration. The results indicate that the maximum amplitude of the vertical axle-box acceleration is linear in both the harmonic order and in OOR amplitude of the polygonal wheel. Furthermore, the growth rate of acceleration increases monotonically with vehicle speed.
- (3)
- The EEMD-WVD combined method is used to make a time-frequency analysis of the axle-box acceleration. The frequency and corresponding amplitude of axle-box acceleration are quantitatively related to wheel polygon defects. It’s concluded that EEMD-WVD can be applied for wheel polygons detection and severity assessment.
- (4)
- The analysis shows that axle-box acceleration measurements can be used to detect and assess polygon wheels. When the characteristic frequency f1 ofaxle-box acceleration and the maxima magnitude aaxlebox at a given train speed v1 are determined, the wheel polygonal defects can be detected, provided f1 does not coincide with the axle-box vibration frequency f2 excited by round wheels. If f1≠ f2, the harmonic order n of the polygon wheel can be determined by comparing f1 with the characteristic frequencies corresponding to the first 25 harmonics of a polygon wheel at the train speed v1.Based on the peak amplitude and the frequency of axle-box acceleration from the joint time-frequency analysis, the degradation due to wheel polygon defects can be evaluated.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ahlbeck, D.R. A study of dynamic impact load effects due to railroad wheel profile roughness. Veh. Syst. Dyn. 1988, 17, 13–16. [Google Scholar] [CrossRef]
- Liu, J.; Han, J.; Xiao, X.B.; Liu, X.L.; Jin, X.S.; Wang, P. Influence of wheel non-circular wear on axle box cover abnormal vibration in high–speed train. Chin. J. Mech. Eng. 2017, 53, 98–105. [Google Scholar] [CrossRef]
- Zhang, F.B.; Wu, P.B.; Wu, X.W. Effects of wheel polygonalization on axle box for high speed train. Zhendong Ceshi Yu Zhenduan 2018, 38, 1063–1068. [Google Scholar]
- Johansson, A.; Andersson, C. Out–of–round railway wheels—A study of wheel polygonalization through simulation of three–dimensional wheel–rail interaction and wear. Veh. Syst. Dyn. 2005, 43, 539–559. [Google Scholar] [CrossRef]
- Lutzenberge, S.; Wu, Q.L. Condition based maintenance of railway wheel treads and identification of the relevant mechanism with monitoring. In Proceedings of the 18th International Wheelset Congress, Chengdu, China, 7–10 November 2016. [Google Scholar]
- Remington, P.; Webb, J. Estimation of wheel/rail interaction forces in the contact area due to roughness. J. Sound Vib. 1996, 1, 83–102. [Google Scholar] [CrossRef]
- Attivissimo, F.; Danese, A.; Giaquinto, N.; Sforza, P. A railway measurement system to evaluate the wheel–rail interaction quality. IEEE Trans. Instru. Meas. 2007, 5, 1583–1589. [Google Scholar] [CrossRef]
- Stratman, B.; Liu, Y.; Mahadevan, S. Structural health monitoring of railroad wheels using wheel impact load detectors. J. Fail. Anal. Prev. 2007, 3, 218–225. [Google Scholar] [CrossRef]
- Lee, M.L.; Chiu, W.K. A comparative study on impact force prediction on a railway track–like structure. Struct. Health. Monit. 2005, 4, 355–376. [Google Scholar] [CrossRef]
- Wei, C.; Xin, Q.; Chung, W.H.; Liu, S.-Y.; Tam, H.-Y.; Ho, S.L. Real–time train wheel condition monitoring by Fiber Bragg Grating sensors. Int. J. Distrib. Sens. Netw. 2011, 8, 409048. [Google Scholar] [CrossRef]
- Papaelias, M.; Huang, Z.; Amini, A.; Vallely, P.; Day, N.; Sharma, R.; Kerkyras, Y.; Kerkyras, S. Advanced wayside condition monitoring of rolling stock wheelsets. In Proceedings of the 11th ECNDT, Prague, Czech, 6–10 October 2014. [Google Scholar]
- Guagliano, M.; Pau, M. An experimental–numerical approach for the analysis of internally cracked railway wheels. Wear 2008, 9–10, 1387–1395. [Google Scholar] [CrossRef]
- Yang, K.; Gao, X.R.; Dai, L.X. Research on the principle of railway wheel out-of-roundness on-line dynamic detecting system based on laser measurement. In Proceedings of the 2014 IEEE 11th Far East Forum on Nondestructive Evaluation/Testing: New Technology and Application, Chengdu, China, 20–23 June 2014. [Google Scholar]
- Coudert, F.; Sunaga, Y.; Takegami, K. Use of axle box acceleration to detect track and rail irregularities. WCRR 1999, 7, 1–7. [Google Scholar]
- Tanaka, H.; Furukawa, A. The estimation method of wheel load and lateral force using the axlebox acceleration. In Proceedings of the World Congress of Rail Research, Seoul, Korea, 22 May 2008. [Google Scholar]
- Molodova, M.; Li, Z.; Dollevoet, R. Axle box acceleration: Measurement and simulation for detection of short track defects. Wear 2011, 271, 349–356. [Google Scholar] [CrossRef]
- Salvador, P.; Naranjo, V.; Insa, R.; Teixeira, P. Axlebox accelerations: Their acquisition and time–frequency characterisation for railway track monitoring purposes. Meas. J. Int. Meas. Confed. 2016, 82, 301–312. [Google Scholar] [CrossRef]
- Li, Y.F.; Liu, J.X.; Li, Z.J. The fault diagnosis method of railway out-of-round wheels using Hilbert–Huang transform. ZhendongCeshi Yu Zhenduan 2016, 36, 734–739. [Google Scholar]
- Caprioli, A.; Cigada, A.; Raveglia, D. Rail inspection in track maintenance: A benchmark between the wavelet approach and the more conventional Fourier analysis. Mech. Syst. Signal Process. 2007, 2, 631–652. [Google Scholar] [CrossRef]
- Jia, S.; Dhanasekar, M. Detection of rail wheel flats using wavelet approaches. Struct. Health Monit. 2007, 2, 121–131. [Google Scholar] [CrossRef]
- Shin, Y.S.; Jeon, J.J. Pseudo Wigner–Ville time-frequency distribution and its application to machinery condition monitoring. Shock Vib. 1993, 1, 65–76. [Google Scholar] [CrossRef]
- Liang, B.; Iwnicki, S.; Ball, A.; Young, A.E. Adaptive noise cancelling and time–frequency techniques for rail surface defect detection. Mech. Syst. Signal Process. 2015, 54, 41–51. [Google Scholar] [CrossRef]
- Wang, X.L. Detection of Out–Of–Roundness Wheels of Urban Rail Train Based on Improved Wigner–Ville Distribution. Master’s Thesis, Nanjing University of Science & Technology, Nanjing, China, 2017. [Google Scholar]
- Xu, P.; Cai, C.B. Dynamic analysis of longitudinally connected ballastless track on earth subgrade. J. SouthwestJiaotong Univ. 2011, 46, 189–194. [Google Scholar]
- Ripke, B.; Knothe, K. Simulation of high frequency vehicle—Track interactions. Veh. Syst. Dyn. 1995, 24, 72–85. [Google Scholar] [CrossRef]
- Song, Y.; Du, Y.; Zhang, X.; Sun, B. Evaluating the effect of wheel polygons on dynamic track performance in high–speed railway systems using co–simulation analysis. Appl. Sci. 2019, 9, 4165. [Google Scholar] [CrossRef]
- Chen, M.; Zhai, W.M.; Ge, X.; Sun, Y. Analysis of wheel-rail dynamic characteristics due to polygonal wheel passing through rail weld zone in high-speedrailways. Chin. Sci. Bull. 2019, 64, 2573–2582. (In Chinese) [Google Scholar] [CrossRef]


| Component | Parameter | Value |
|---|---|---|
| Carbody | Mass (kg) | 4.0× 104 |
| Moments of pitch inertia (kg·m2) | 2.0× 106 | |
| Moments of roll inertia (kg·m2) | 1.0× 105 | |
| Moments of yaw inertia (kg·m2) | 2.0× 106 | |
| Bogie | Mass (kg) | 2.0× 103 |
| Moments of pitch inertia (kg·m2) | 2.5× 103 | |
| Moments of roll inertia (kg·m2) | 1.5× 103 | |
| Moments of yaw inertia (kg·m2) | 3.5× 103 | |
| Wheelset | Mass (kg) | 1.5× 103 |
| Moments of pitch inertia (kg·m2) | 120 | |
| Moments of roll inertia (kg·m2) | 800 | |
| Moments of yaw inertia (kg·m2) | 800 | |
| nominal rolling radius (m) | 0.46 | |
| Axlebox | Mass (kg) | 50.0 |
| Moments of pitch inertia (kg·m2) | 5.0 | |
| Moments of roll inertia (kg·m2) | 1.0 | |
| Moments of yaw inertia (kg·m2) | 5.0 | |
| CHN60 rail | Elastic modulus (N·m−2) | 2.1 × 1011 |
| Poisson ratio | 0.3 | |
| Density(kg·m−3) | 7800 | |
| Rail fastenings | Elastic stiffness(MN·m−1) | 50 |
| Damping coefficient (kN·s·m−1) | 60 | |
| Longitudinal spacing(m) | 0.65 | |
| Concrete slab layer | Elastic modulus(N·m−2) | 3.9×1010 |
| Poisson ratio | 0.2 | |
| Length × width × thickness (m) | 6.45 × 2.55 × 0.20 | |
| Density(kg·m−3) | 2500 | |
| CA mortar layer | Elastic modulus(N·m−2) | 7.0×109 |
| Poisson ratio | 0.167 | |
| Thickness(m) | 0.03 | |
| Density(kg·m−3) | 2590 | |
| Foundation | Elastic modulus(N·m−2) | 5.0×109 |
| Poisson ratio | 0.2 | |
| Width × thickness(m) | 3.25 × 0.3 | |
| Density(kg·m−3) | 2500 |
| Train Speed(km·h−1) | |||||||
|---|---|---|---|---|---|---|---|
| 200 | 225 | 250 | 275 | 300 | 325 | 350 | |
| Harmonic Order | Growth Rate (m·s−2·mm−1) | ||||||
| 1 | 108 | 122 | 156 | 170 | 192 | 233 | 242 |
| 2 | 123 | 155 | 171 | 184 | 224 | 248 | 261 |
| 3 | 173 | 199 | 214 | 225 | 246 | 255 | 275 |
| 4 | 198 | 206 | 216 | 229 | 234 | 267 | 285 |
| 5 | 205 | 221 | 242 | 256. | 268 | 294 | 327 |
| 6 | 213 | 222 | 266 | 301 | 315 | 336 | 415 |
| 7 | 251 | 258 | 298 | 336 | 355 | 389 | 452 |
| 8 | 295 | 310 | 316 | 378 | 406 | 446 | 510 |
| 9 | 324 | 337 | 340 | 434 | 446 | 480 | 542 |
| 10 | 349 | 398 | 394 | 471 | 465 | 556 | 642 |
| 11 | 374 | 438 | 456 | 519 | 599 | 675 | 757 |
| 12 | 426 | 472 | 493 | 651 | 749 | 788 | 936 |
| 13 | 472 | 519 | 583 | 708 | 872 | 936 | 1100 |
| 14 | 491 | 566 | 635 | 804 | 958 | 1091 | 1257 |
| 15 | 520 | 645 | 793 | 904 | 1009 | 1215 | 1447 |
| 16 | 553 | 672 | 883 | 940 | 1020 | 1264 | 1452 |
| 17 | 580 | 698 | 898 | 1063 | 1090 | 1289 | 1475 |
| 18 | 626 | 755 | 938 | 1196 | 1211 | 1345 | 1602 |
| 19 | 744 | 870 | 1071 | 1296 | 1302 | 1468 | 1699 |
| 20 | 829 | 1012 | 1240 | 1450 | 1483 | 1619 | 1832 |
| 21 | 996 | 1180 | 1350 | 1498 | 1511 | 1692 | 1899 |
| 22 | 1023 | 1354 | 1467 | 1611 | 1685 | 1721 | 1975 |
| 23 | 1155 | 1413 | 1556 | 1756 | 1792 | 1821 | 2034 |
| 24 | 1302 | 1522 | 1621 | 1796 | 1803 | 1875 | 2089 |
| 25 | 1421 | 1611 | 1743 | 1882 | 1901 | 1968 | 2115 |
| Speed(km·h−1) | |||||||
|---|---|---|---|---|---|---|---|
| 200 | 225 | 250 | 275 | 300 | 325 | 350 | |
| OOR Amplitude (mm) | Growth Rate (m·s−2) | ||||||
| 0.01 | 0.38 | 0.45 | 0.62 | 0.75 | 0.97 | 0.99 | 1.05 |
| 0.02 | 0.63 | 1.15 | 1.31 | 1.45 | 1.58 | 1.64 | 1.97 |
| 0.03 | 1.51 | 1.75 | 1.82 | 1.97 | 2.17 | 2.64 | 3.73 |
| 0.04 | 2.01 | 2.43 | 2.55 | 2.75 | 3.12 | 3.20 | 4.14 |
| 0.05 | 2.94 | 3.12 | 3.52 | 3.78 | 4.40 | 4.98 | 5.28 |
| 0.06 | 3.22 | 3.67 | 4.49 | 5.28 | 5.80 | 5.89 | 6.24 |
| 0.07 | 4.06 | 4.38 | 4.87 | 5.58 | 6.34 | 6.92 | 7.13 |
| 0.08 | 4.43 | 4.58 | 5.25 | 5.90 | 6.60 | 7.05 | 7.78 |
| 0.09 | 5.01 | 5.73 | 6.29 | 7.08 | 7.84 | 8.20 | 8.68 |
| 0.10 | 5.45 | 6.25 | 6.98 | 7.55 | 8.11 | 8.86 | 9.35 |
| 0.11 | 5.84 | 6.77 | 7.11 | 7.89 | 8.76 | 9.13 | 9.87 |
| 0.12 | 6.12 | 7.31 | 7.94 | 8.34 | 9.15 | 9.94 | 10.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Liang, L.; Du, Y.; Sun, B. Railway Polygonized Wheel Detection Based on Numerical Time-Frequency Analysis of Axle-Box Acceleration. Appl. Sci. 2020, 10, 1613. https://doi.org/10.3390/app10051613
Song Y, Liang L, Du Y, Sun B. Railway Polygonized Wheel Detection Based on Numerical Time-Frequency Analysis of Axle-Box Acceleration. Applied Sciences. 2020; 10(5):1613. https://doi.org/10.3390/app10051613
Chicago/Turabian StyleSong, Ying, Lei Liang, Yanliang Du, and Baochen Sun. 2020. "Railway Polygonized Wheel Detection Based on Numerical Time-Frequency Analysis of Axle-Box Acceleration" Applied Sciences 10, no. 5: 1613. https://doi.org/10.3390/app10051613
APA StyleSong, Y., Liang, L., Du, Y., & Sun, B. (2020). Railway Polygonized Wheel Detection Based on Numerical Time-Frequency Analysis of Axle-Box Acceleration. Applied Sciences, 10(5), 1613. https://doi.org/10.3390/app10051613






