Wave Propagation in Periodic Metallic Structures with Equilateral Triangular Holes
Abstract
1. Introduction
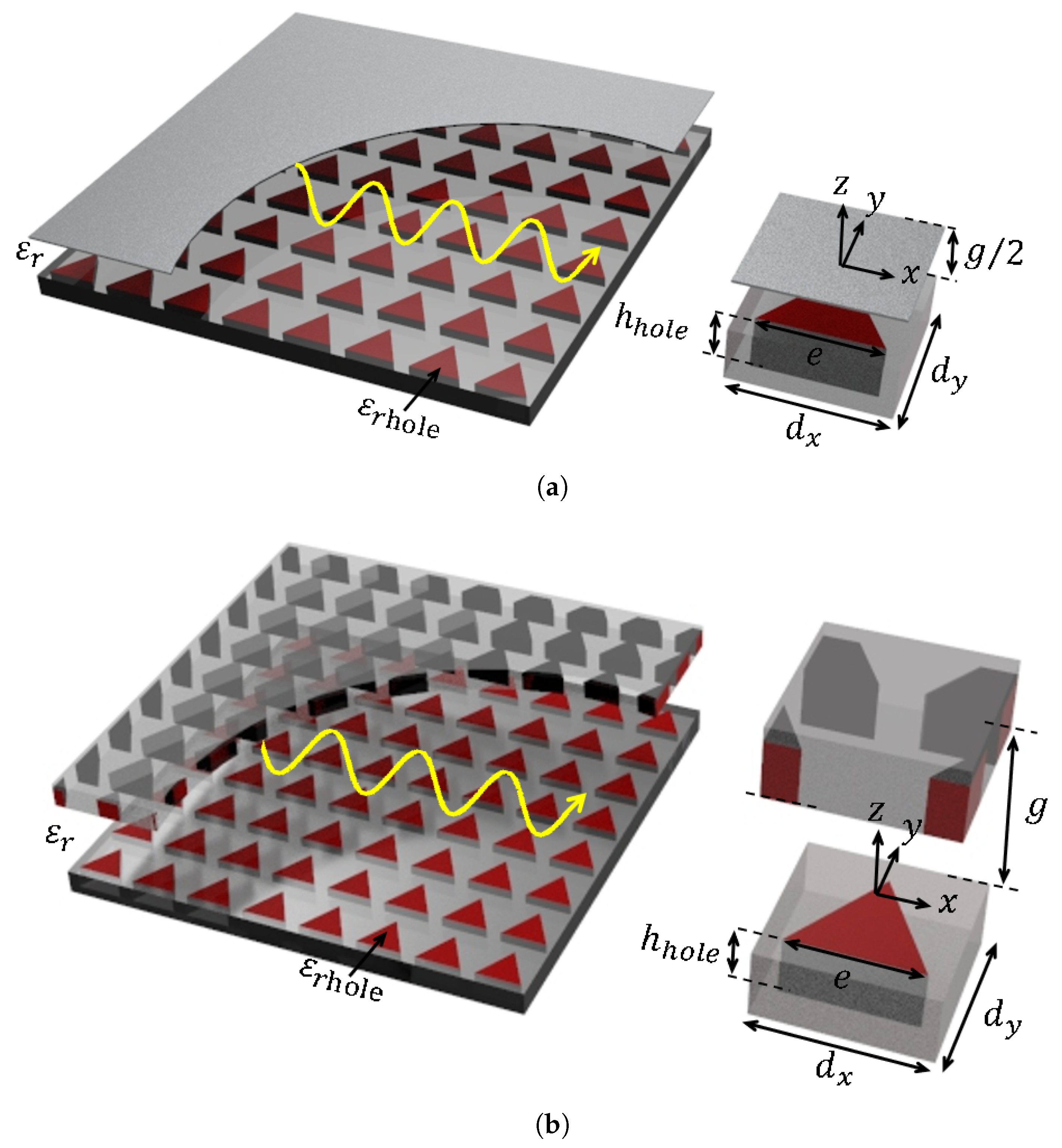
2. Formulation
2.1. Mode Matching
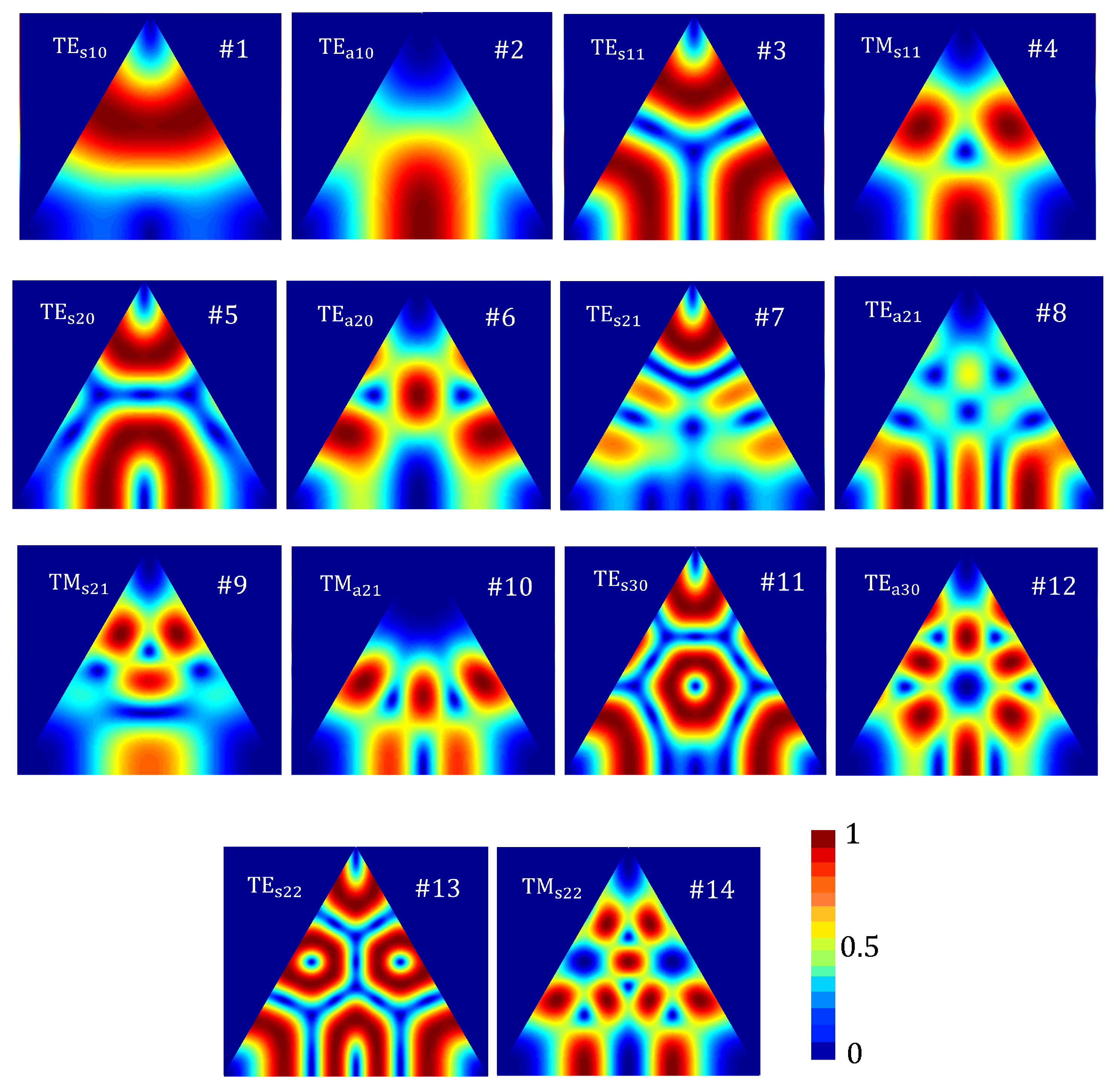
2.2. Modal Functions
3. Results
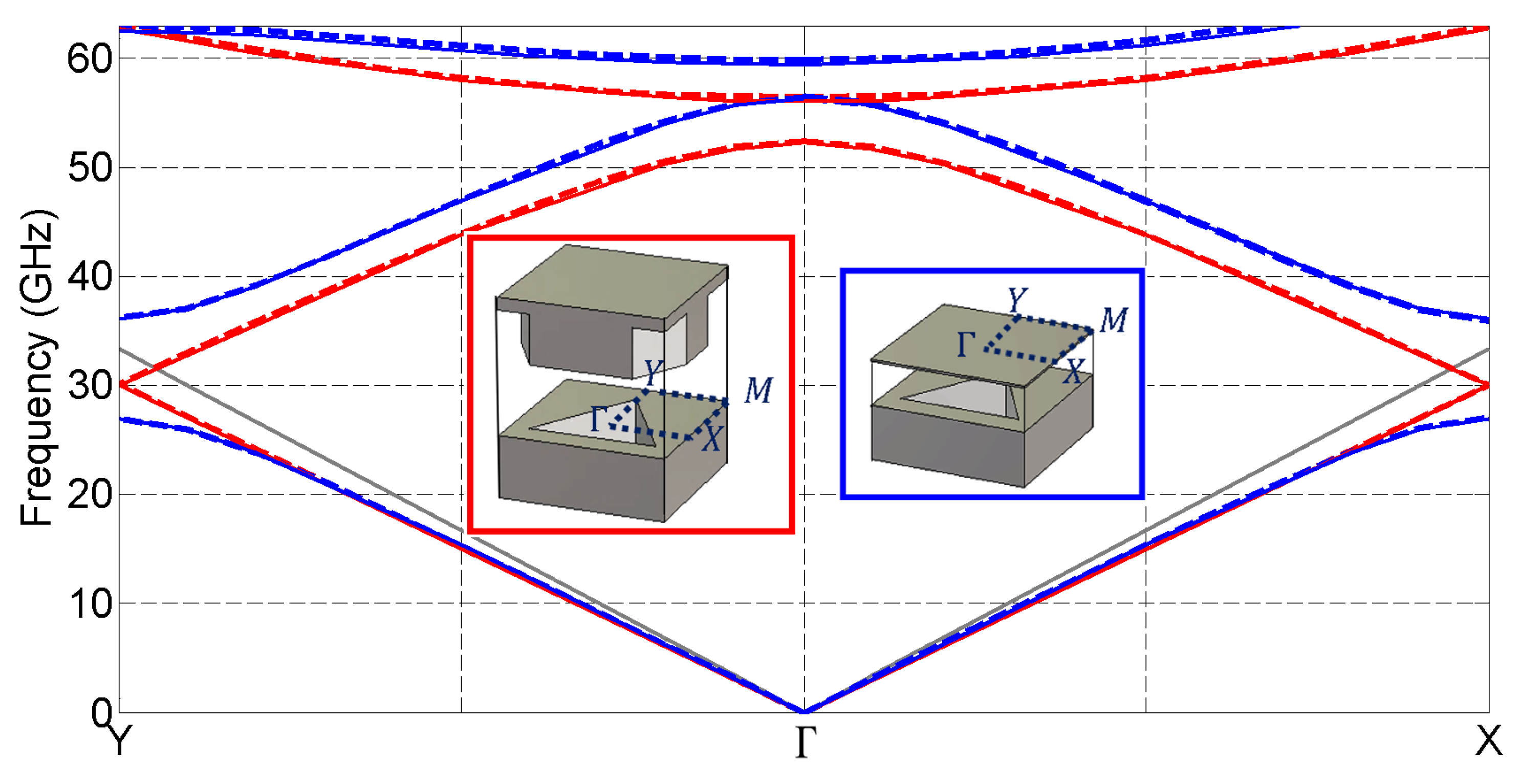
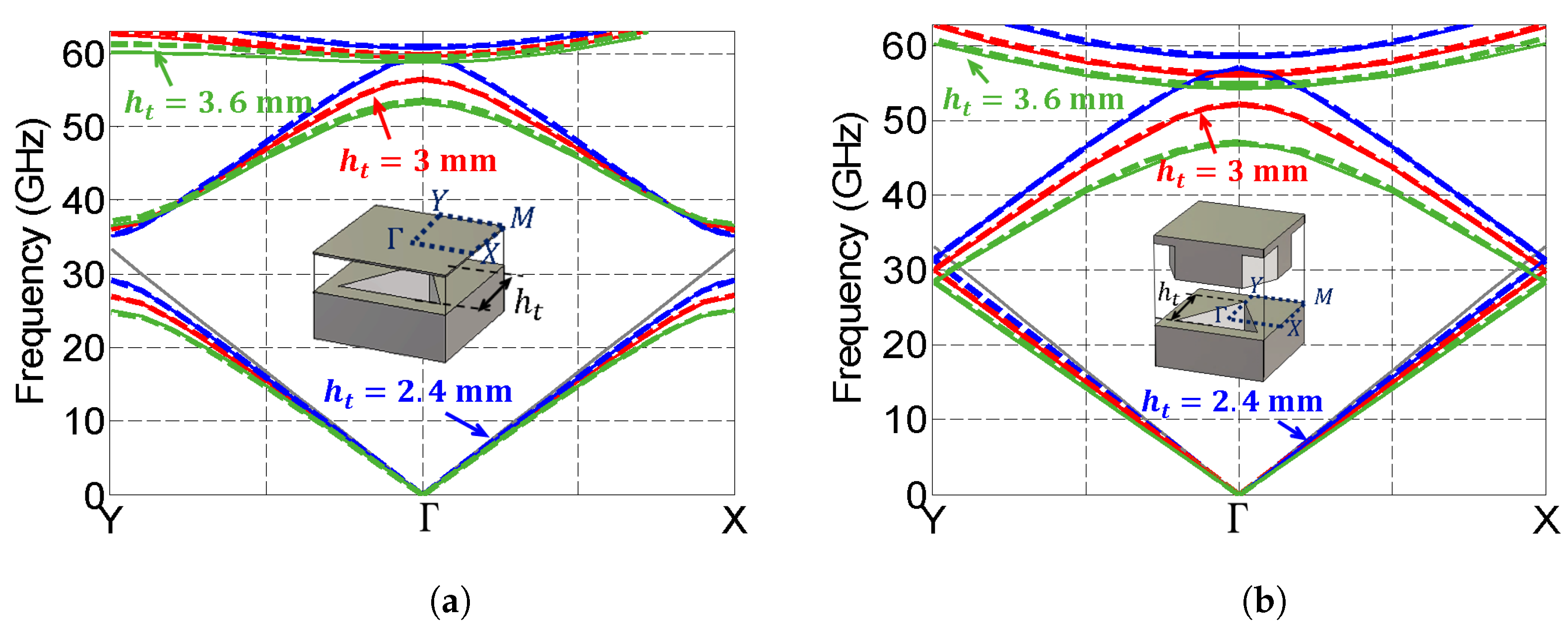
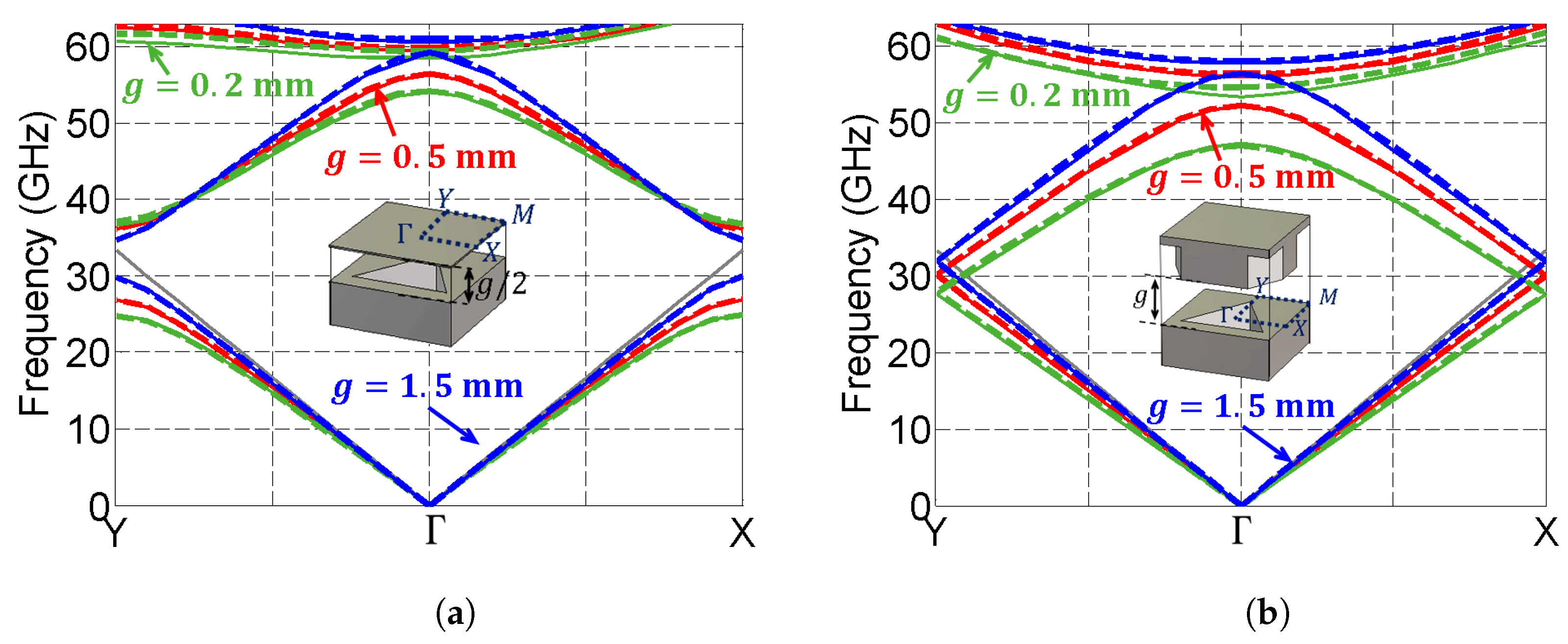
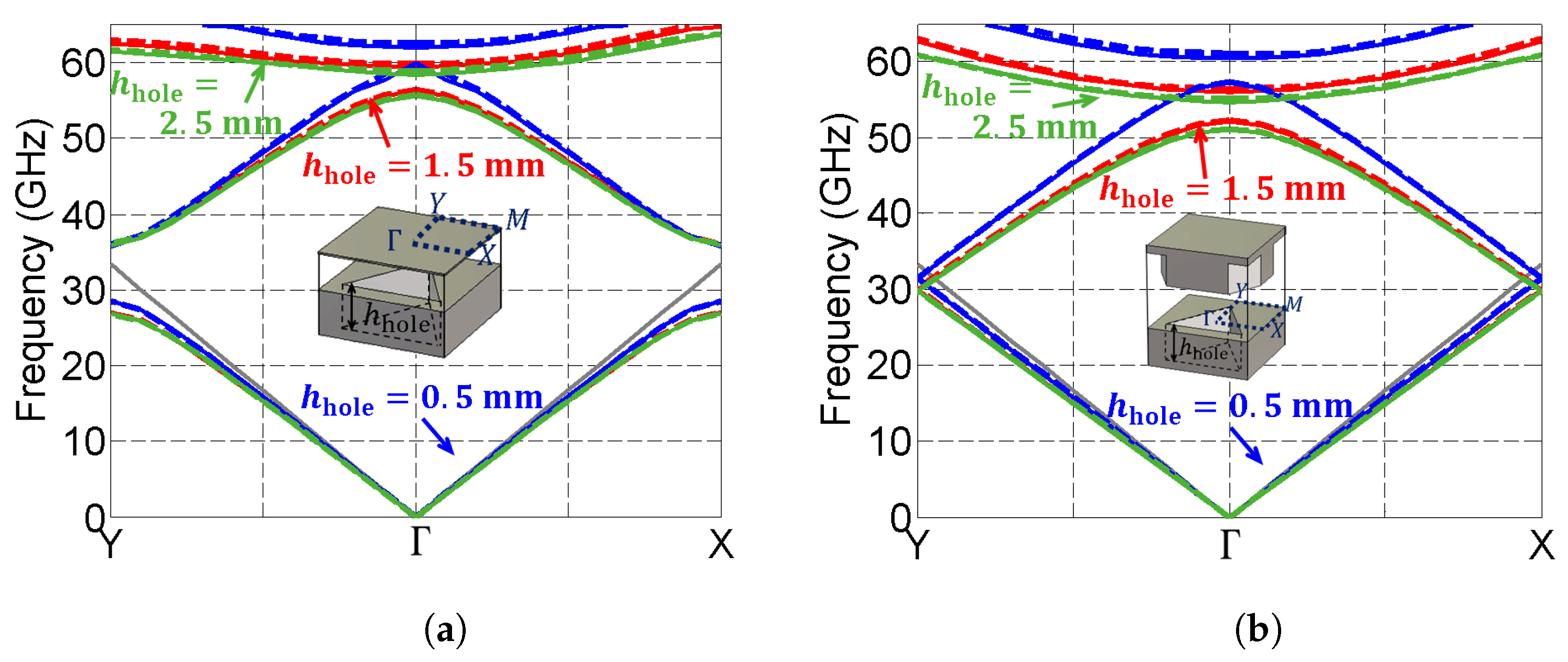
3.1. Dispersion Diagram
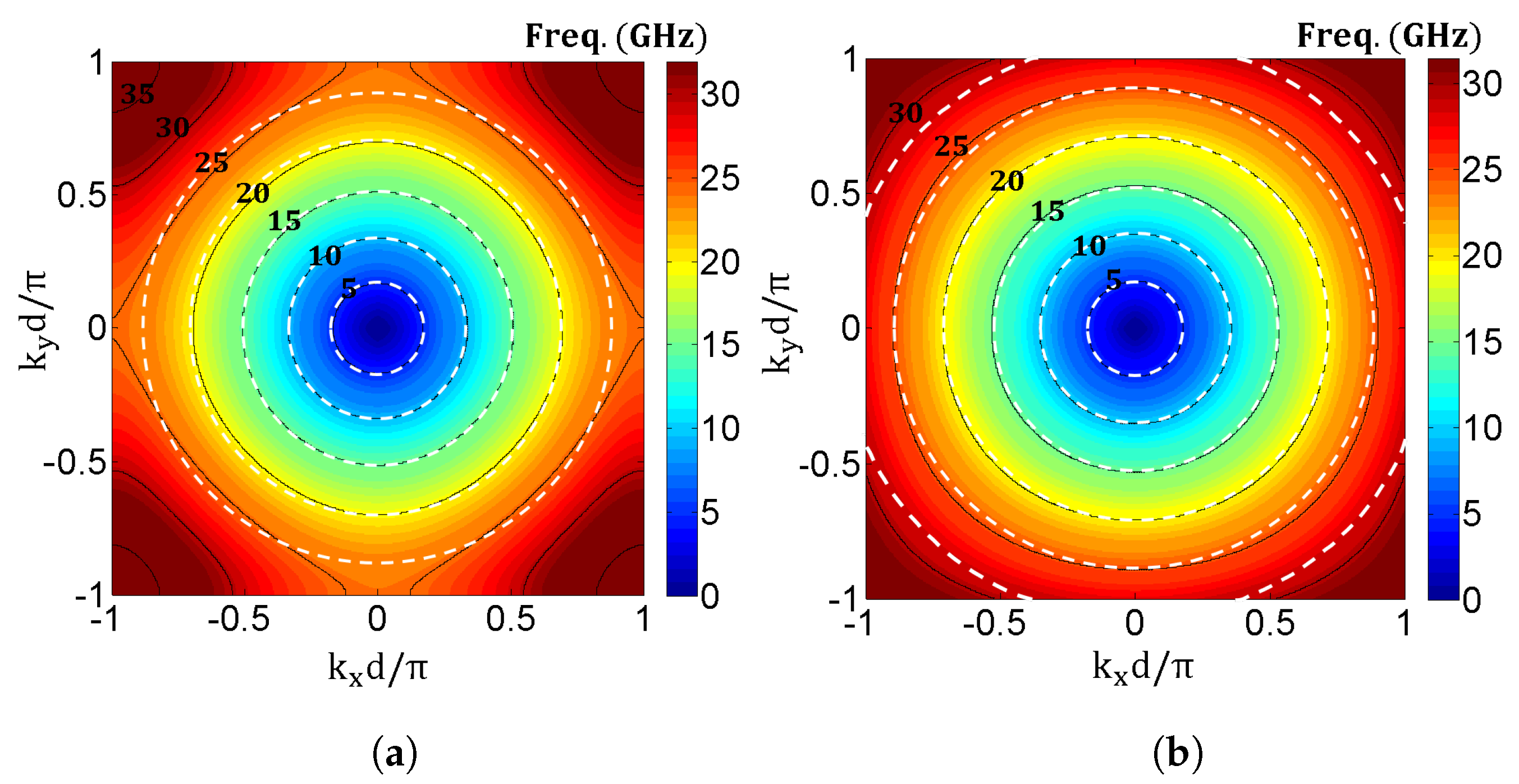
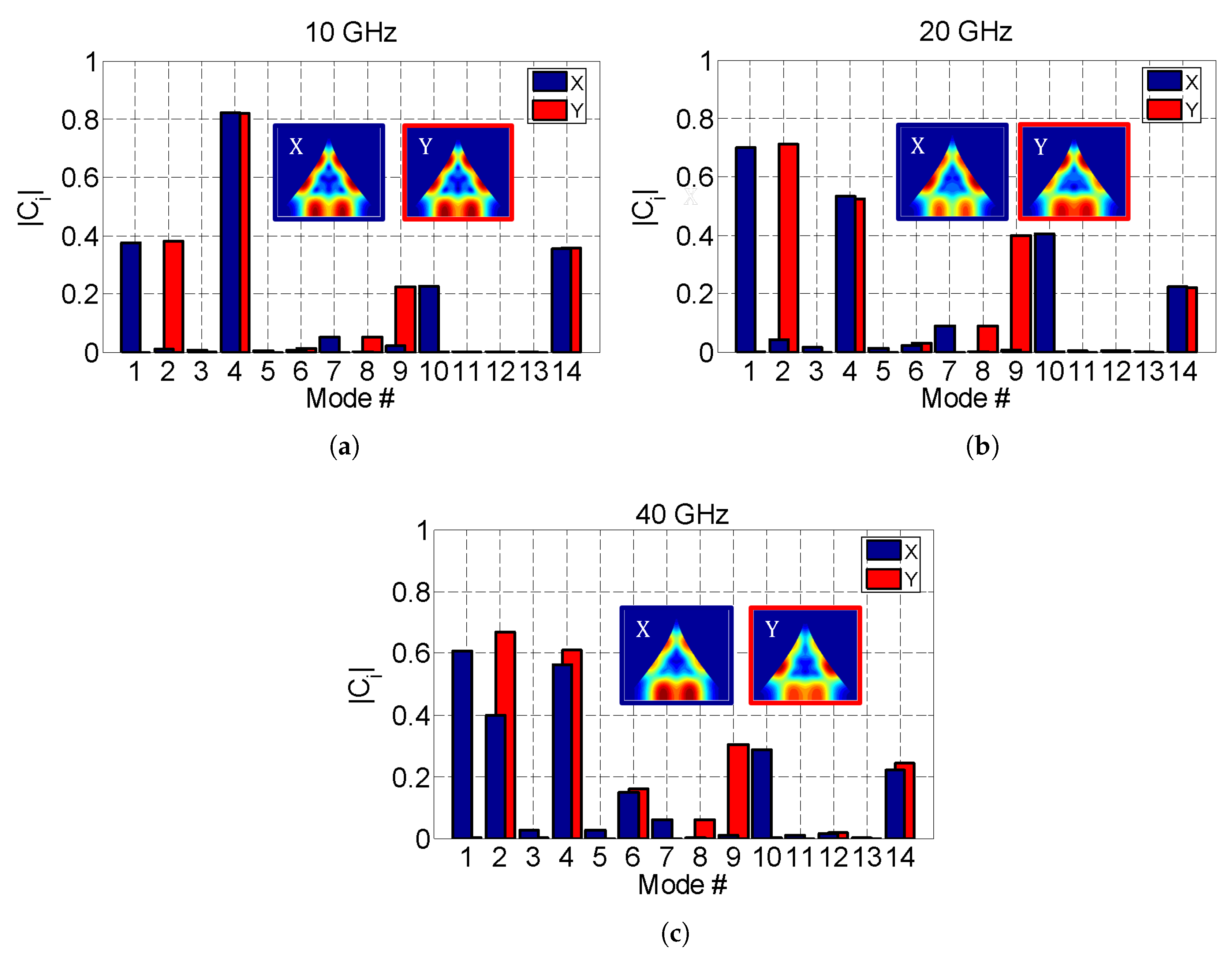
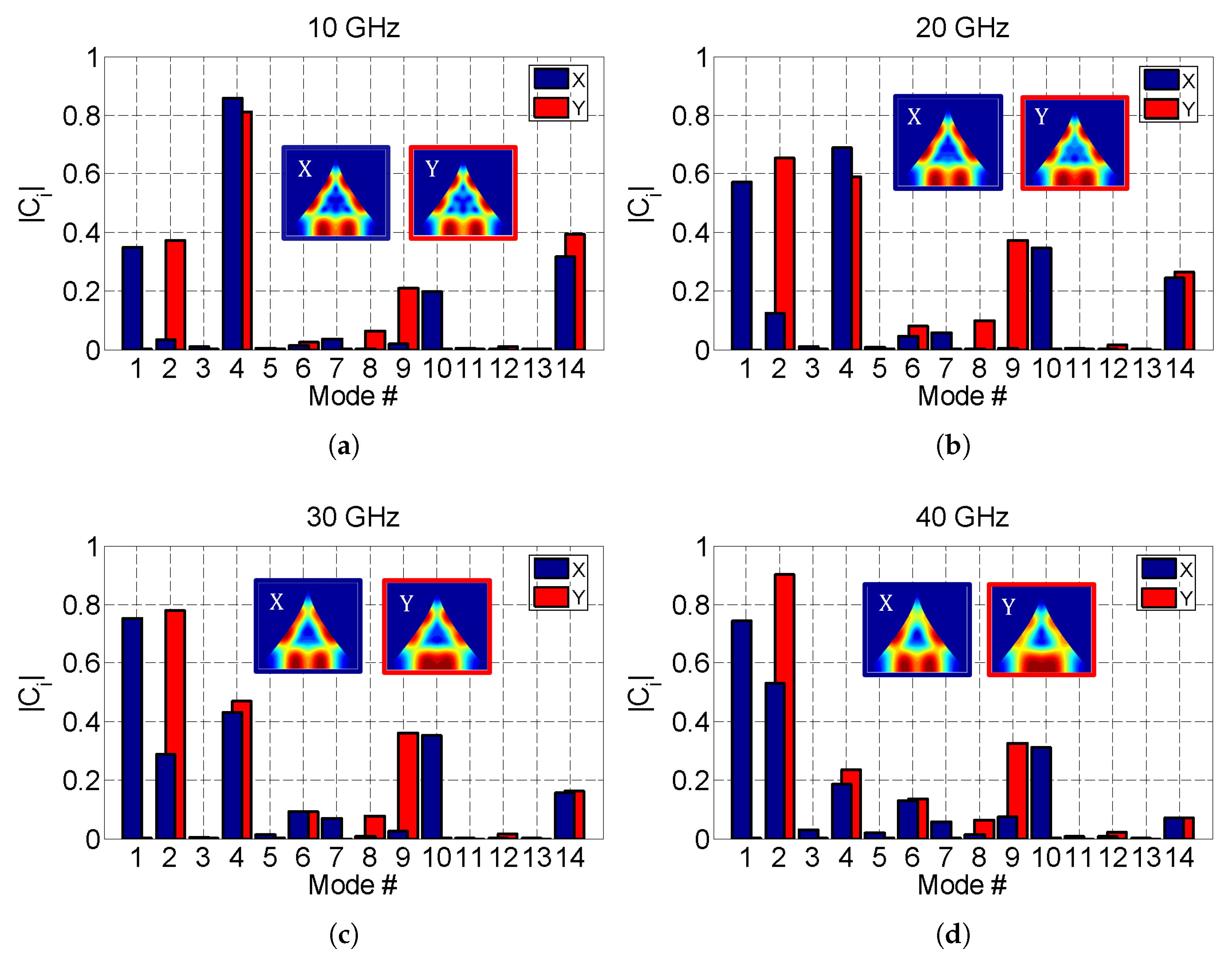
3.2. Isotropic Behavior
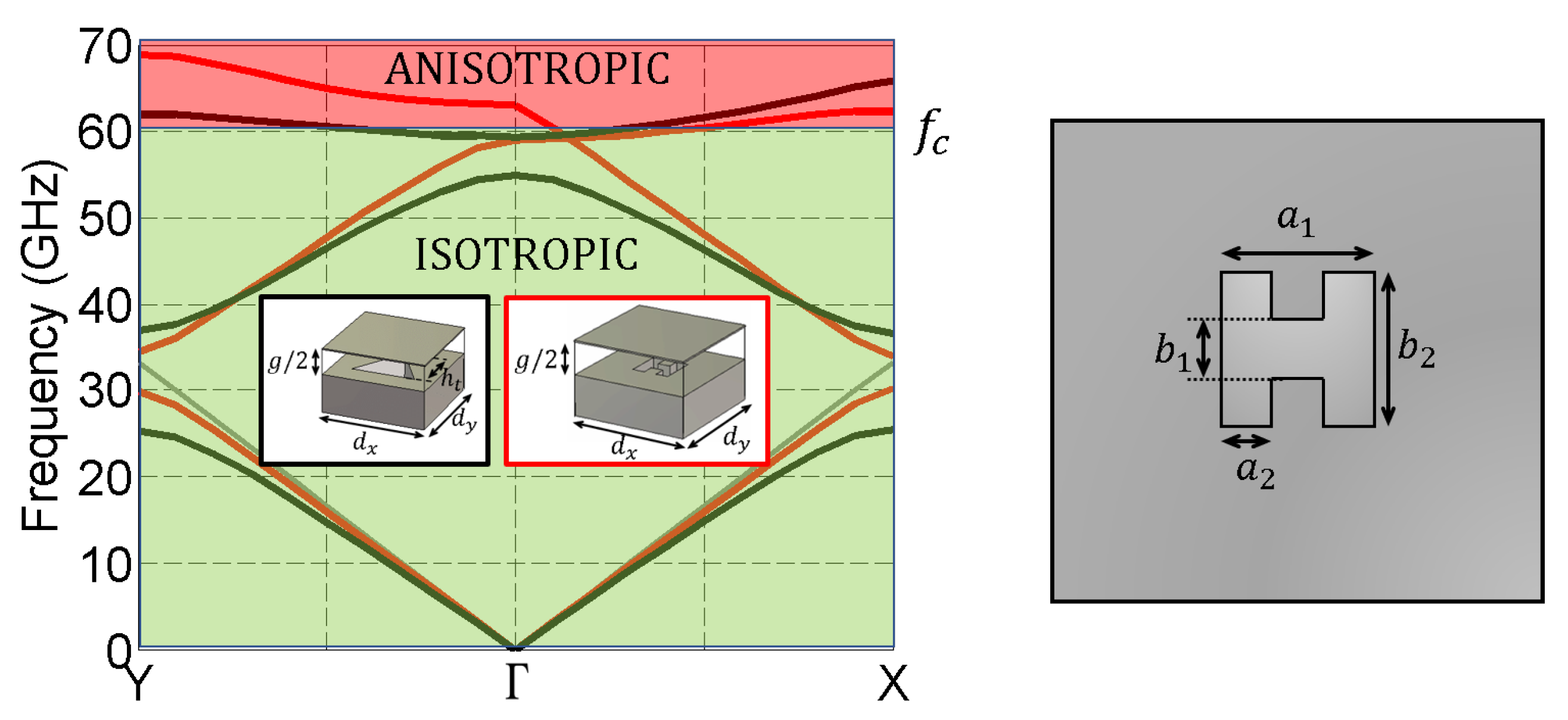
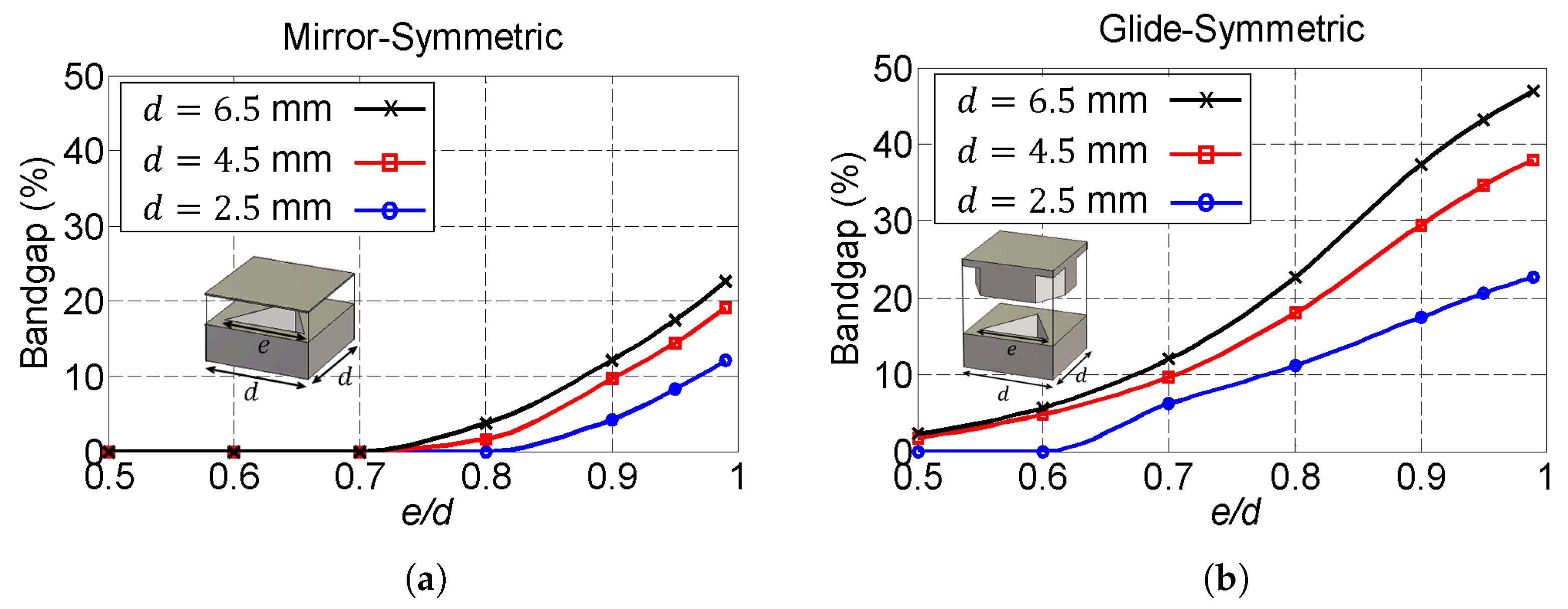
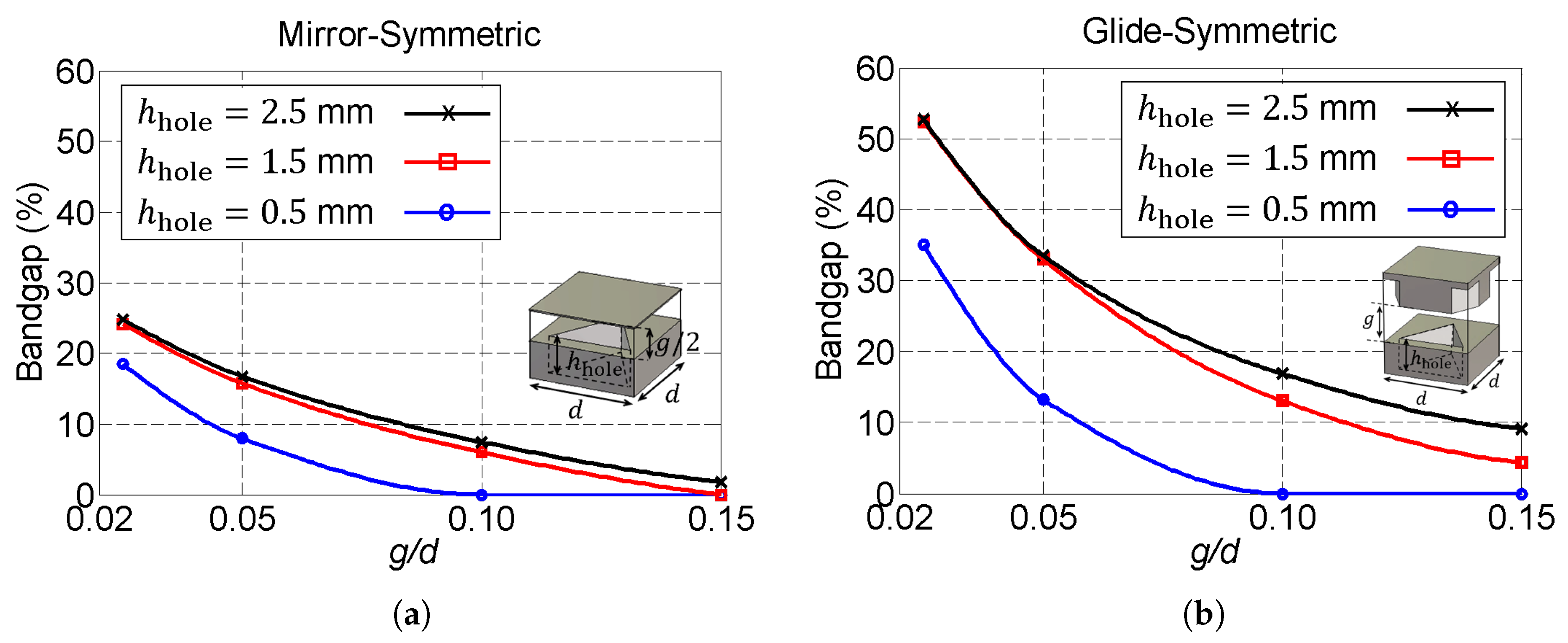
3.3. Bandgaps
3.4. Applications
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pendry, J.B.; Martin-Moreno, L.; García-Vidal, F.J. Mimicking Surface Plasmons with Structured Surfaces. Science 2004, 305, 847–848. [Google Scholar] [CrossRef] [PubMed]
- Quesada, R.; Martín-Cano, D.; García-Vidal, F.J.; Bravo-Abad, J. Deep-subwavelength negative-index waveguiding enabled by coupled conformal surface plasmons. Opt. Lett. 2014, 39, 2990–2993. [Google Scholar] [CrossRef] [PubMed]
- Collin, R.E. Field Theory of Guided Waves, 2nd ed.; IEEE Press: New York, NY, USA, 1990. [Google Scholar]
- Ishimaru, A. Electromagnetic Wave Propagation, Radiation, and Scattering; Prentice Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Tang, W.X.; Zhang, H.C.; Ma, H.F.; Jiang, W.X.; Cui, T.J. Concept, Theory, Design, and Applications of Spoof Surface Plasmon Polaritons at Microwave Frequencies. Adv. Opt. Mater. 2019, 7, 1800421. [Google Scholar] [CrossRef]
- Meng, W.; Ma, H.F.; Tang, W.X.; Sun, S.; Cui, T.J. Leaky-Wave Radiations with Arbitrarily Customizable Polarizations Based on Spoof Surface Plasmon Polaritons. Phys. Rev. Appl. 2019, 12, 11. [Google Scholar]
- Quevedo-Teruel, O.; Ebrahimpouri, M.; Ng Mou Kehn, M. Ultrawideband metasurface lenses based on off-shifted opposite layers. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 484–487. [Google Scholar] [CrossRef]
- Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O. Dispersion analysis of 2D glide-symmetric corrugated metasurfaces using mode-matching technique. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 1–3. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Quevedo-Teruel, O.; Rajo-Iglesias, E. Design Guidelines for Gap Waveguide Technology Based on Glide-Symmetric Holey Structures. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 542–544. [Google Scholar] [CrossRef]
- Monje-Real, A.; Fonseca, N.J.G.; Zetterstrom, O.; Pucci, E.; Quevedo-Teruel, O. Holey glide-symmetric filters for 5G at millimeter-wave frequencies. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 31–34. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Quevedo-Teruel, O. Ultrawideband anisotropic glide-symmetric metasurfaces. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1547–1551. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Herran, L.F.; Quevedo-Teruel, O. Wide angle impedance matching using glide-symmetric metasurfaces. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 8–11. [Google Scholar] [CrossRef]
- Palomares-Caballero, A.; Padilla, P.; Alex-Amor, A.; Valenzuela-Valdés, J.; Quevedo-Teruel, O. Twist and glide symmetries for helix antenna design and miniaturization. Symmetry 2019, 11, 349. [Google Scholar] [CrossRef]
- Palomares-Caballero, A.; Alex-Amor, A.; Padilla, P.; Luna, F.; Valenzuela-Valdés, J. Compact and Low-Loss V-band Waveguide Phase Shifter Based on Glide-Symmetric Pin Configuration. IEEE Access 2019, 7, 31297–31304. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Miao, J.; Mattsson, M.; Algaba-Brazalez, A.; Johansson, M.; Manholm, L. Glide-symmetric fully metallic Luneburg lens for 5G communications at Ka-band. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1588–1592. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Rajo-Iglesias, E.; Sipus, Z.; Quevedo-Teruel, O. Cost-effective gap waveguide technology based on glide-symmetric holey EBG structures. IEEE Trans. Microw. Theory Technol. 2018, 66, 927–934. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Brazalez, A.A.; Manholm, L.; Quevedo-Teruel, O. Using glide-symmetric holes to reduce leakage between waveguide flanges. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 473–475. [Google Scholar] [CrossRef]
- Rajo-Iglesias, E.; Ebrahimpouri, M.; Quevedo-Teruel, O. Wideband phase shifter in groove gap waveguide technology implemented with glide-symmetric holey EBG. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 476–478. [Google Scholar] [CrossRef]
- Padilla, P.; Palomares-Caballero, A.; Alex-Amor, A.; Valenzuela-Valdés, J.; Fernández-González, J.M.; Quevedo-Teruel, O. Broken glide-symmetric holey structures for bandgap selection in gap-waveguide technology. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 327–329. [Google Scholar] [CrossRef]
- Liao, Q.; Rajo-Iglesias, E.; Quevedo-Teruel, O. Ka-band fully metallic TE40 slot array antenna with glide-symmetric gap waveguide technology. IEEE Trans. Antennas Propag. 2019, 67, 6410–6418. [Google Scholar] [CrossRef]
- Valerio, G.; Ghasemifard, F.; Sipus, Z.; Quevedo-Teruel, O. Glide-Symmetric All-Metal Holey Metasurfaces for Low-Dispersive Artificial Materials: Modeling and Properties. IEEE Trans. Microw. Theory Technol. 2018, 66, 3210–3223. [Google Scholar] [CrossRef]
- Ghasemifard, F. Periodic Structures with Higher Symmetries: Analysis and Applications. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O.; Valerio, G. Analyzing Glide-Symmetric Holey Metasurfaces Using a Generalized Floquet Theorem. IEEE Access 2018, 6, 71743–71750. [Google Scholar] [CrossRef]
- Alex-Amor, A.; Ghasemifard, F.; Valerio, G.; Ebrahimpouri, M.; Padilla, P.; Fernández-González, J.M.; Quevedo-Teruel, O. Glide-Symmetric Metallic Structures with Elliptical Holes for Lens Compression. IEEE Trans. Microw. Theory Technol. 2019. submitted. [Google Scholar]
- Valerio, G.; Sipus, Z.; Grbic, A.; Quevedo-Teruel, O. Non-resonant modes in plasmonic holey metasurfaces for the design of artificial flat lenses. Opt. Lett. 2017, 42, 2026–2029. [Google Scholar] [CrossRef] [PubMed]
- Morán-López, A.; Córcoles, J.; Ruiz-Cruz, J.A.; Montejo-Garai, J.R.; Rebollar, J.M. Electromagnetic Scattering at the Waveguide Step between Equilateral Triangular Waveguides. Adv. Math. Phys. 2016, 2016, 2974675. [Google Scholar] [CrossRef]
- Schelkunoff, S.A. Electromagnetic Waves; D. Van Nostrand Company: New York, NY, USA, 1943. [Google Scholar]
- Wang, C.Y. Exact solution of equilateral triangular waveguide. Electron. Lett. 2010, 46, 925–927. [Google Scholar] [CrossRef]
- Milton, K.A.; Schwinger, J. Rectangular and Triangular Waveguides. In Electromagnetic Radiation: Variational Methods, Waveguides and Accelerators; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Morán-López, A.; Córcoles, J.; Ruiz-Cruz, J.A.; Montejo-Garai, J.R.; Rebollar, J.M. Dual-mode filters in equilateral triangular waveguides with wide spurious-free response. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA, 4–9 June 2017; pp. 1192–1195. [Google Scholar]
- Tamayo-Domínguez, A.; Fernández-González, J.M.; Quevedo-Teruel, O. One-Plane Glide-Symmetric Holey Structures for Stop-Band and Refraction Index Reconfiguration. Symmetry 2019, 11, 495. [Google Scholar] [CrossRef]
| HOLE SHAPE | Anisotropy (<5%) | Refr. Index (@10 GHz) | Dispersion (<5%) | Bandgap (%) |
|---|---|---|---|---|
| Triangular | 16.20 GHz | 1.31 | 25.71 GHz | 39.50 |
| Circular | 28.86 GHz | 1.17 | 46.04 GHz | 0 |
| Square | 22.98 GHz | 1.21 | 32.10 GHz | 6.81 |
| HOLE SHAPE | Min. Iso. Range | Max. Refr. Index (@10 GHz) | Min. Low-Disp. Range | Max. Bandgap (%) |
|---|---|---|---|---|
| Triangular | 16.20 GHz | 1.31 | 25.71 GHz | 39.50 |
| Circular | 24.76 GHz | 1.23 | 34.41 GHz | 22.55 |
| Square | 19.85 GHz | 1.34 | 21.76 GHz | 48.66 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alex-Amor, A.; Valerio, G.; Ghasemifard, F.; Mesa, F.; Padilla, P.; Fernández-González, J.M.; Quevedo-Teruel, O. Wave Propagation in Periodic Metallic Structures with Equilateral Triangular Holes. Appl. Sci. 2020, 10, 1600. https://doi.org/10.3390/app10051600
Alex-Amor A, Valerio G, Ghasemifard F, Mesa F, Padilla P, Fernández-González JM, Quevedo-Teruel O. Wave Propagation in Periodic Metallic Structures with Equilateral Triangular Holes. Applied Sciences. 2020; 10(5):1600. https://doi.org/10.3390/app10051600
Chicago/Turabian StyleAlex-Amor, Antonio, Guido Valerio, Fatemeh Ghasemifard, Francisco Mesa, Pablo Padilla, José M. Fernández-González, and Oscar Quevedo-Teruel. 2020. "Wave Propagation in Periodic Metallic Structures with Equilateral Triangular Holes" Applied Sciences 10, no. 5: 1600. https://doi.org/10.3390/app10051600
APA StyleAlex-Amor, A., Valerio, G., Ghasemifard, F., Mesa, F., Padilla, P., Fernández-González, J. M., & Quevedo-Teruel, O. (2020). Wave Propagation in Periodic Metallic Structures with Equilateral Triangular Holes. Applied Sciences, 10(5), 1600. https://doi.org/10.3390/app10051600








