Edge Couplers in Silicon Photonic Integrated Circuits: A Review
Abstract
1. Introduction
2. Operation Mechanism and Design Principles of Edge Couplers
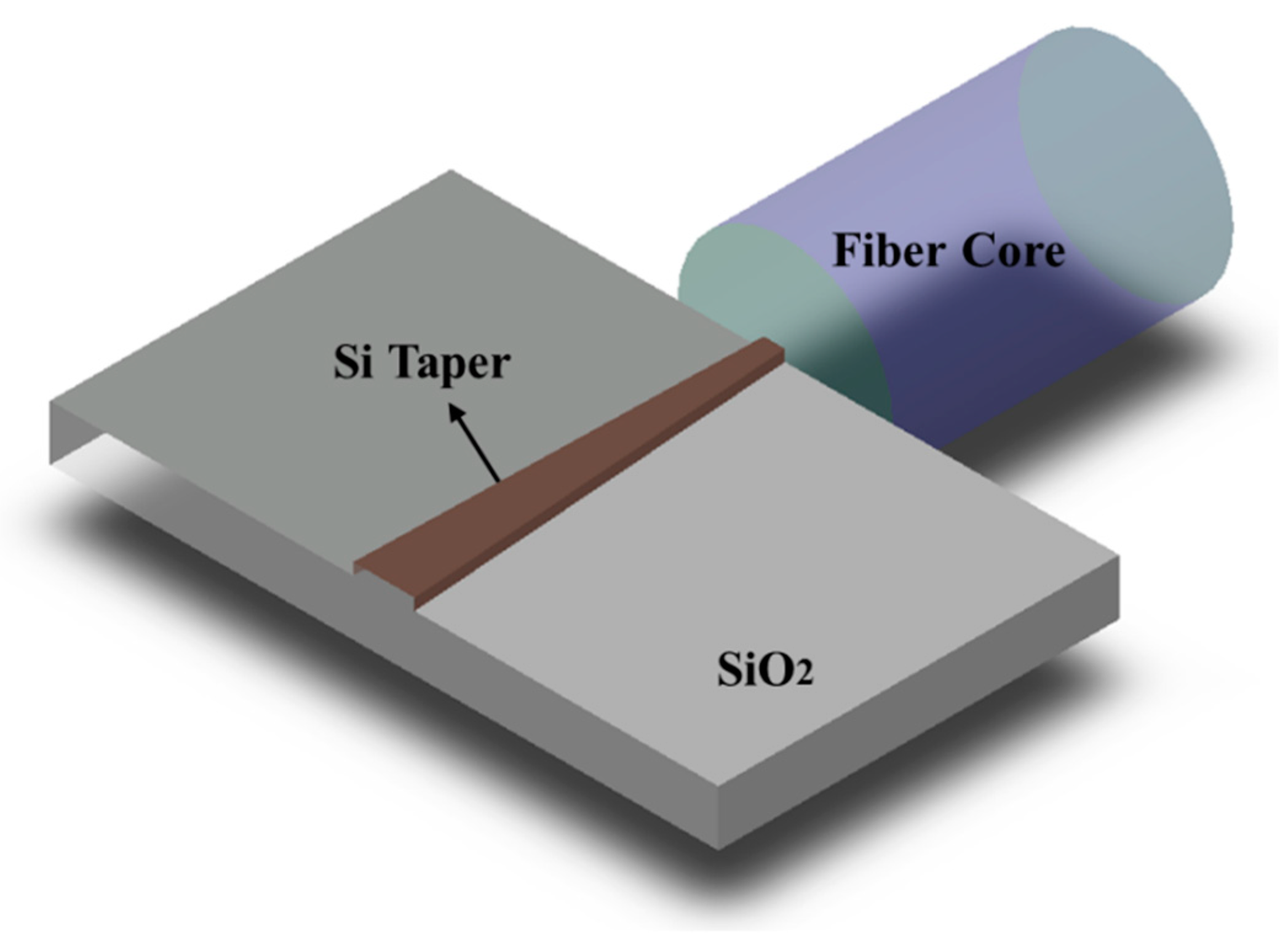
2.1. General Operation Mechanism of Edge Couplers
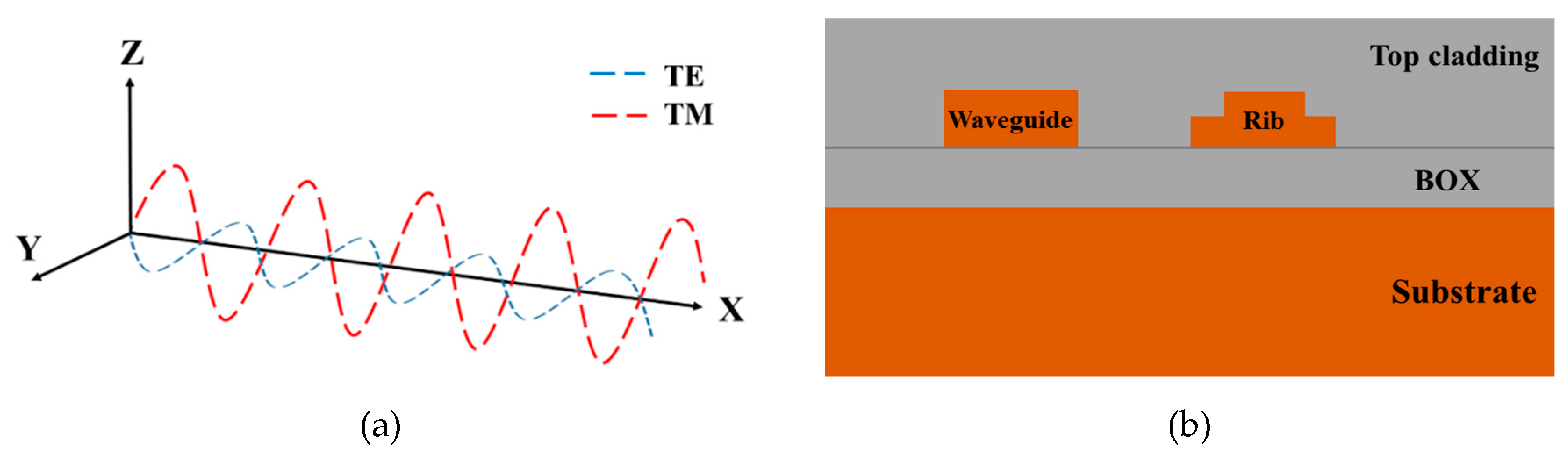
2.2. Performance Metric Parameters and Design Principles of Edge Couplers
3. Structural Transformations of Edge Couplers in Horizontal Direction
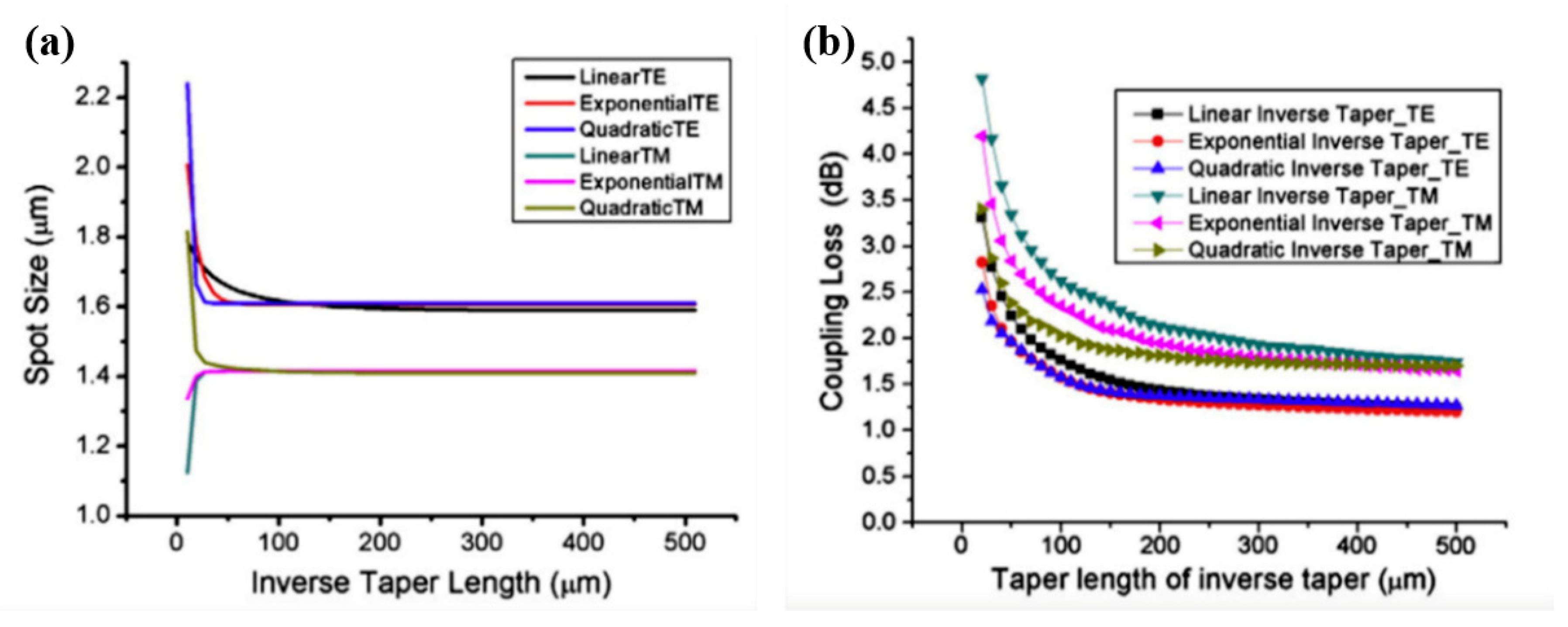
3.1. Edge Couplers Based on Inverse Taper with Nonlinear Profile
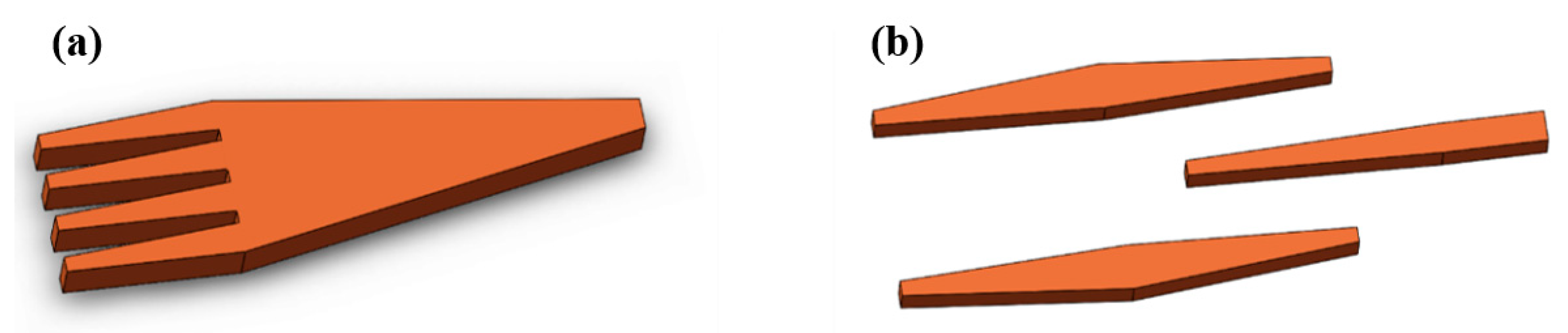
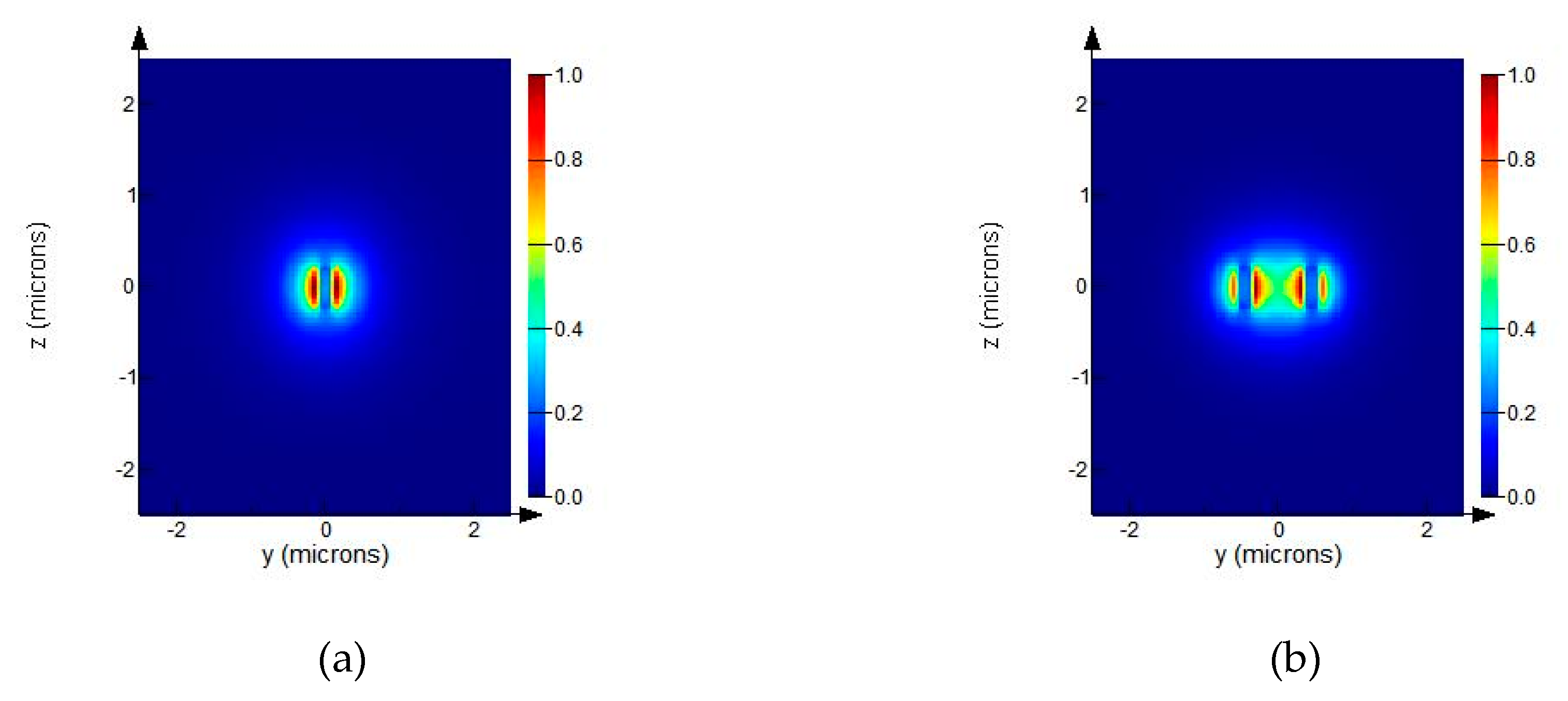
3.2. Edge Couplers Based on a Multi-Tip Taper
3.3. Edge Couplers Based on Multiple Tapers
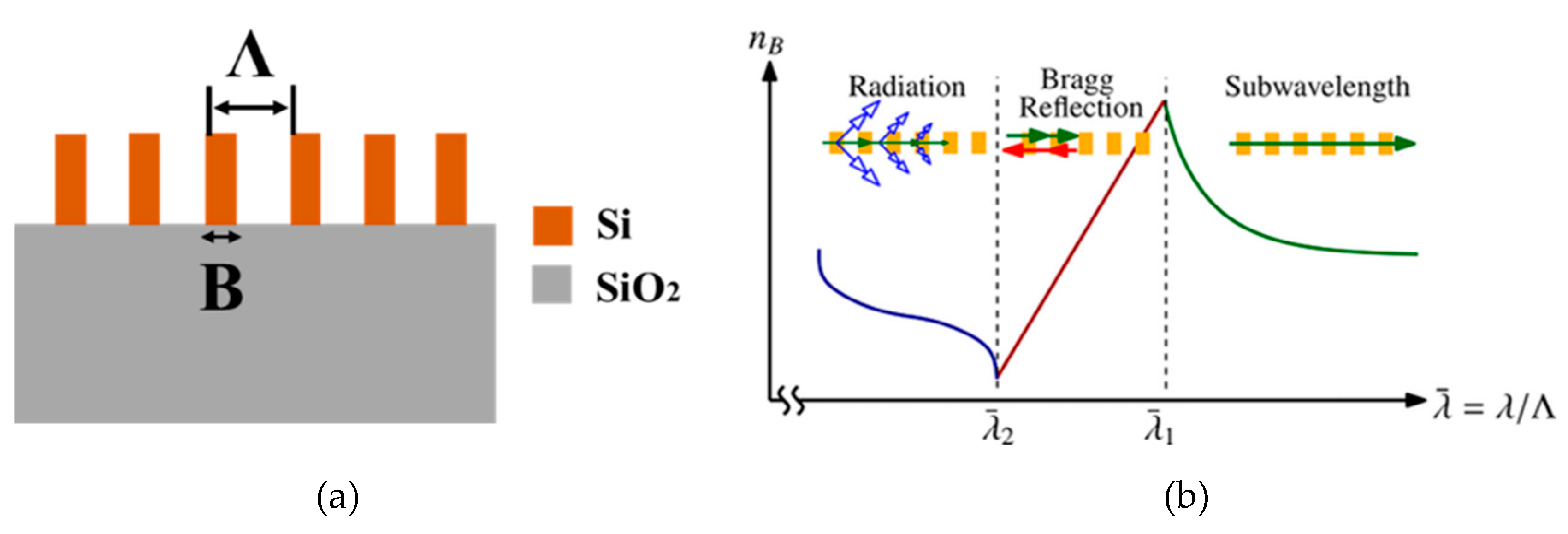
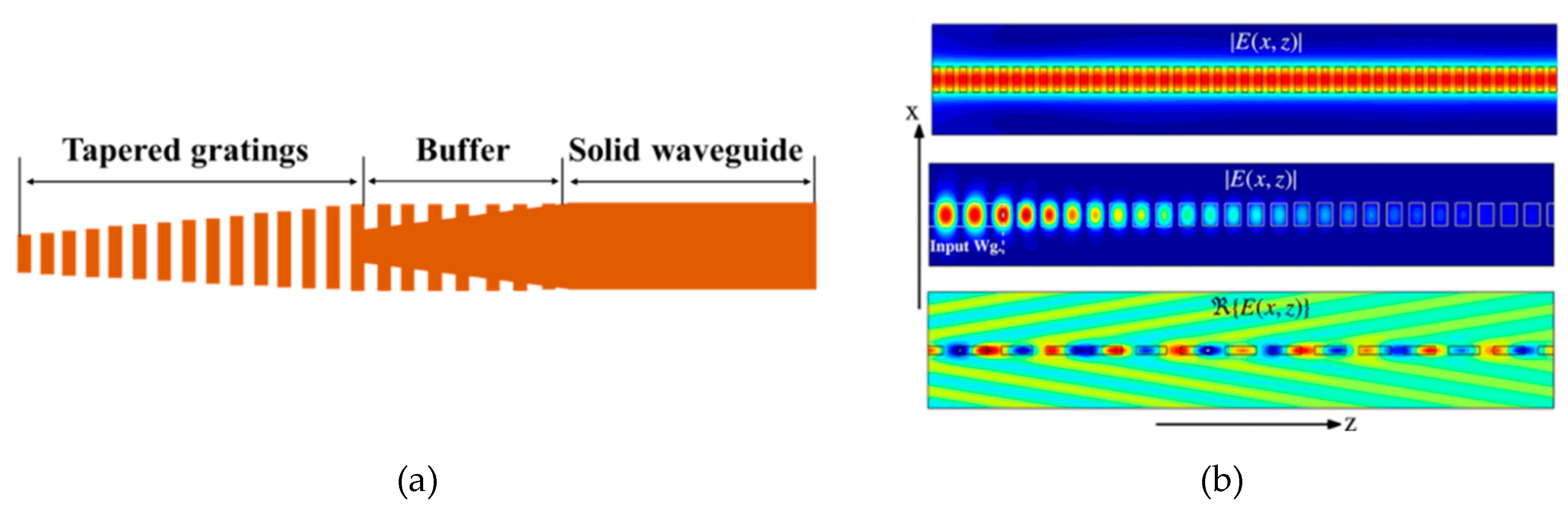
3.4. Edge Couplers Based on Subwavelength Gratings Structure
4. Structural Transformations of Edge Couplers in Vertical Direction
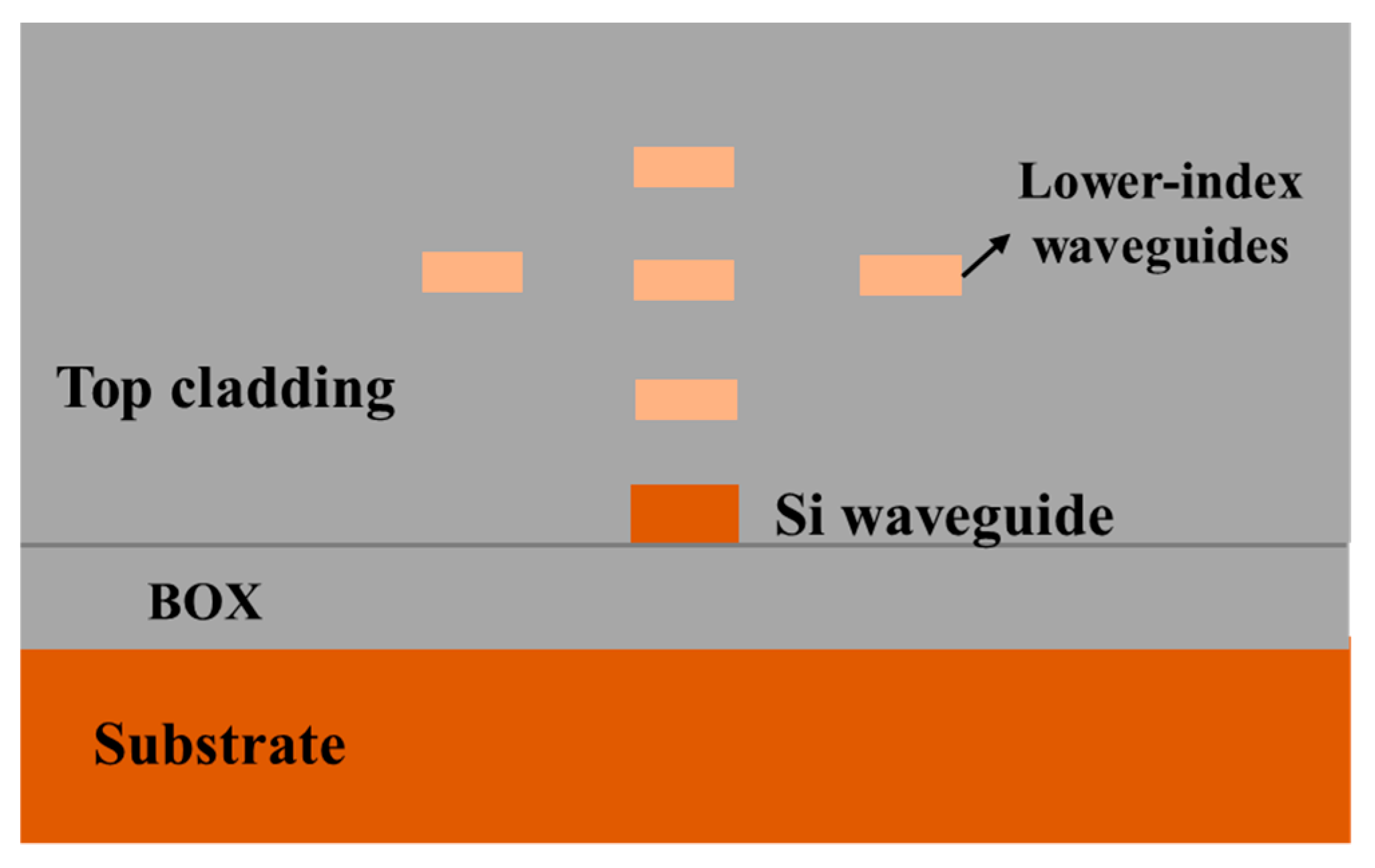
4.1. Edge Couplers Assisted with Multiple Upper Waveguides
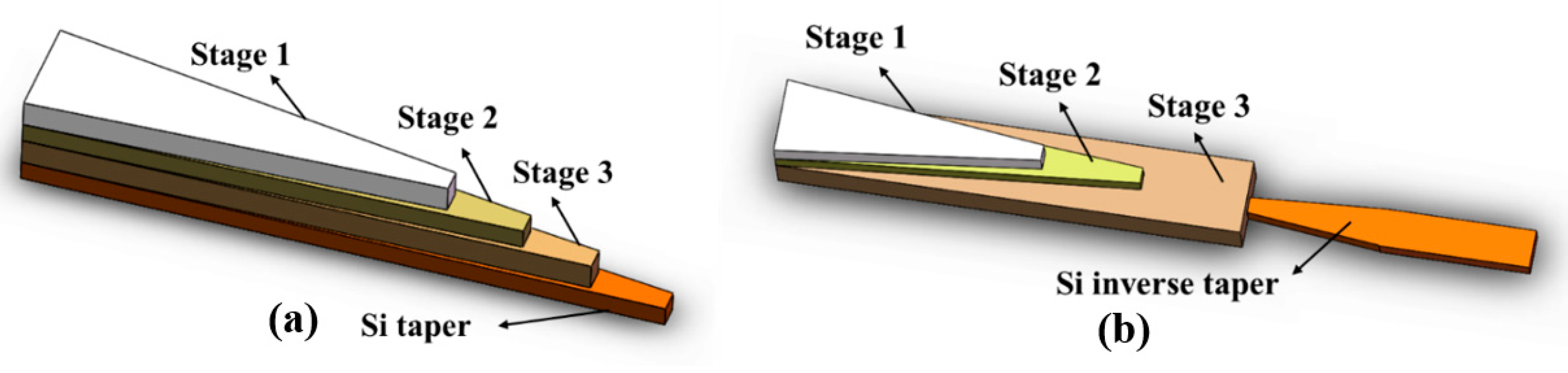
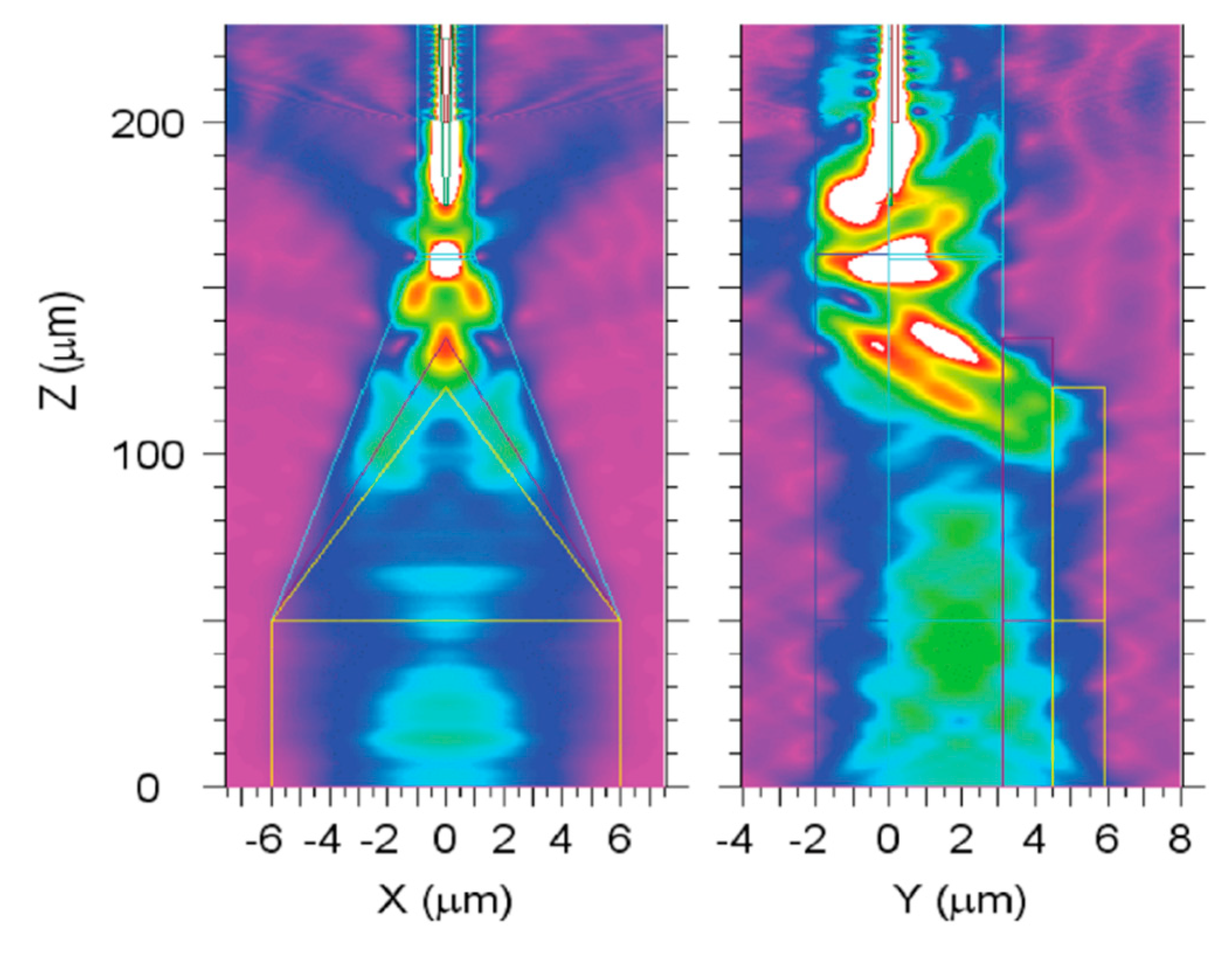
4.2. Edge Couplers Based on Cascaded Multi-Stage Tapers
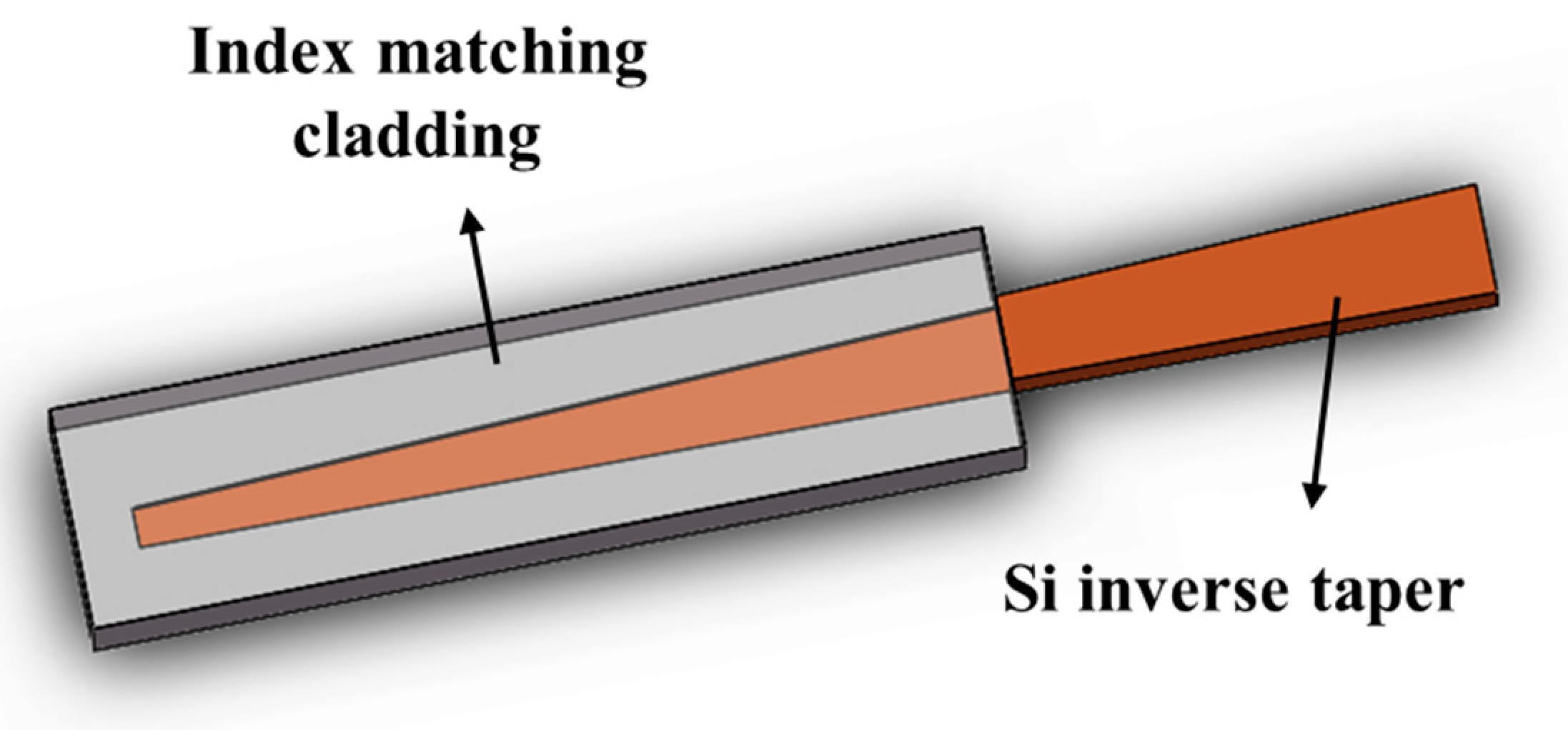
4.3. Edge Couplers with Index-Matching Cladding
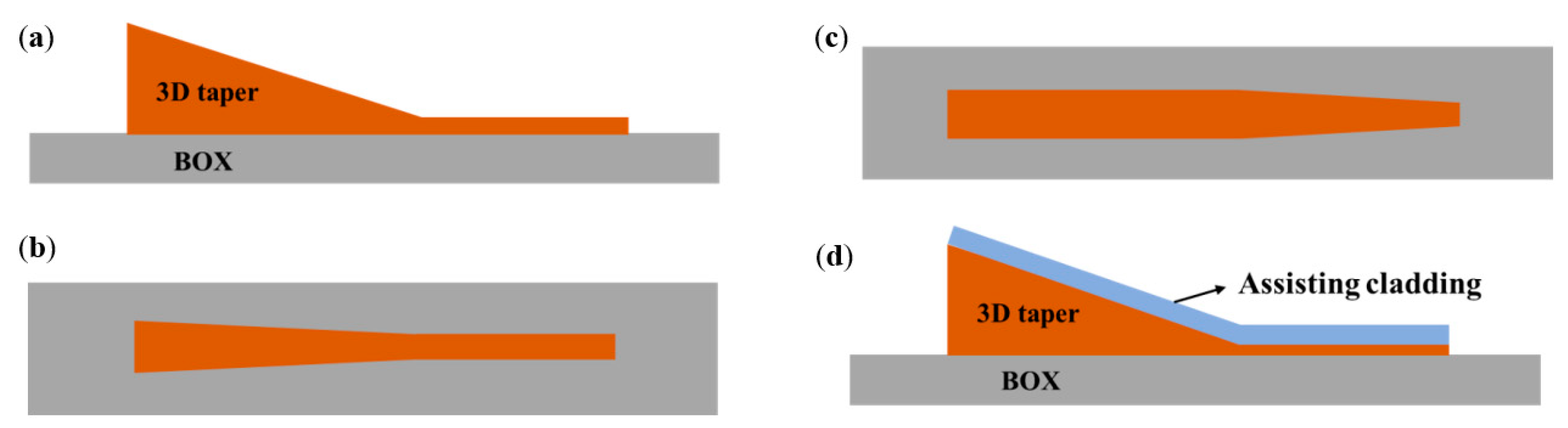
4.4. Edge Couplers Based on Three-Dimensional Taper
4.5. Edge Couplers Based on Cantilever Structure
5. Discussions and Perspectives
5.1. An Overall Overview of Edge Coupler Performance
5.2. A Brief Comparison between Edge Couplers and Vertical Couplers
5.3. Packaging Issue of Optical Couplers
5.4. Future Trends of Silicon Photonic Edge Couplers
5.4.1. Polarization and Mode (de)Multiplexing Technology
5.4.2. Multilayer Silicon Nitride-on-Silicon Photonic Integrated Platform
5.4.3. Inverse Design Method for Nanophotonics
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jalali, B.; Fathpour, S. Silicon photonics. J. Lightwave Technol. 2006, 24, 4600–4615. [Google Scholar] [CrossRef]
- Soref, R. The past, present, and future of silicon photonics. IEEE J. Sel. Top. Quant. 2006, 12, 1678–1687. [Google Scholar] [CrossRef]
- Xu, D.X.; Schimid, J.H.; Reed, G.T.; Mashanovich, G.Z.; Thomson, D.J.; Nedeljkovic, M.; Chen, X.; Thourhout, D.V.; Keyvaninia, S.; Selvaraja, S.K. Silicon photonic integration platform—Have we found the sweet spot? IEEE J. Sel. Top. Quant. 2014, 20, 189–205. [Google Scholar]
- Thomson, D.; Zilkie, A.; Bowers, J.E.; Komljenovic, T.; Reed, G.T.; Vivien, L.; Marris-Morini, D.; Cassan, E.; Virot, L.; Fédéli, J.-M.; et al. Roadmap on silicon photonics. J. Opt. 2016, 18, 073003. [Google Scholar] [CrossRef]
- Chen, X.; Milosevic, M.M.; Stankovic, S.; Reynolds, S.; Bucio, T.D.; Li, K.; Thomson, D.J.; Gardes, F.; Reed, G.T. The emergence of silicon photonics as a flexible technology platform. Proc. IEEE 2018, 106, 2101–2116. [Google Scholar] [CrossRef]
- Xiao, X.; Li, Z.; Chu, T.; Xu, H.; Li, X.; Nemkova, A.; Kang, X.; Yu, Y.; Yu, J. Development of silicon photonic devices for optical interconnects. Sci. China Technol. Sci. 2013, 56, 586–593. [Google Scholar] [CrossRef]
- Chen, X.; Li, C.; Tsang, H.K. Device engineering for silicon photonics. NPG Asia Mater. 2011, 3, 34–40. [Google Scholar] [CrossRef]
- Subbaraman, H.; Xu, X.; Hosseini, A.; Zhang, X.; Zhang, Y.; Kwong, D.; Chen, R.T. Recent advances in silicon-based passive and active optical interconnects. Opt. Express 2015, 23, 2487–2510. [Google Scholar] [CrossRef]
- Son, G.; Han, S.; Park, J.; Kwon, K.; Yu, K. High-efficiency broadband light coupling between optical fibers and photonic integrated circuits. Nanophotonics 2018, 7, 1845–1864. [Google Scholar] [CrossRef]
- Vermeulen, D.; Poulton, C.V. Optical interfaces for silicon photonic circuits. Proc. IEEE 2018, 106, 2270–2280. [Google Scholar] [CrossRef]
- Sunak, H.R.D. Single-mode fiber measurements. IEEE Insrtu. Meas. 1988, 37, 557–560. [Google Scholar] [CrossRef]
- Dutta, H.S.; Goyal, A.K.; Srivastava, V.; Pal, S. Coupling light in photonic crystal waveguides: A review. Photonic. Nanostruct. 2016, 20, 41–58. [Google Scholar] [CrossRef]
- Marchetti, R.; Lacava, C.; Carroll, L.; Gradkowski, K.; Minzioni, P. Coupling strategies for silicon photonics integrated chips. Photonics Res. 2019, 7, 201–239. [Google Scholar] [CrossRef]
- Feng, J.; Zhou, Z. Polarization beam splitter using a binary blazed grating coupler. Opt. Lett. 2017, 32, 1662–1664. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.; Luan, F.; Liow, T.Y.; Zhang, J.; Shum, P. Design for broadband high-efficiency grating couplers. Opt. Lett. 2012, 37, 530–532. [Google Scholar] [CrossRef] [PubMed]
- Qin, K.; Gao, D.; Bao, C.; Zhao, Z.; Zhou, X.; Lu, T.; Chen, L. High efficiency and broadband two-dimensional blazed grating coupler with fully etched triangular holes. J. Lightwave Technol. 2012, 30, 2363–2366. [Google Scholar] [CrossRef]
- Xu, D.X.; Cheben, P.; Dalacu, D.; Delâge, A.; Janz, S.; Lamontagne, B.; Picard, M.J.; Ye, W.N. Eliminating the birefringence in silicon-on-insulator ridge waveguides by use of cladding stress. Opt. Lett. 2004, 29, 2384–2386. [Google Scholar] [CrossRef]
- Bozzola, A.; Carroll, L.; Gerace, D.; Cristiani, I.; Andreani, L.C. Optimising apodized grating couplers in a pure SOI platform to -0.5 dB coupling efficiency. Opt. Express 2015, 23, 16289–16304. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J.; Lu, H.; Wu, W.; Huang, J.; Chang, S. Polarization-independent grating coupler based on silicon-on-insulator. Chin. Opt. Lett. 2015, 13, 091301–091305. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, W.; Wang, X.; Lu, Z.; Caverley, M.; Bojko, R.; Chrostowski, L.; Jaeger, N.A. Design of broadband subwavelength grating couplers with low back reflection. Opt. Lett. 2015, 40, 4647–4650. [Google Scholar] [CrossRef]
- Watanabe, T.; Ayata, M.; Koch, U.; Fedoryshyn, Y.; Leuthold, J. Perpendicular grating coupler based on a blazed antiback-reflection structure. J. Lightwave Technol. 2017, 35, 4663–4669. [Google Scholar] [CrossRef]
- Wang, Y.; Yun, H.; Lu, Z.; Bojko, R.; Shi, W.; Wang, X.; Flueckiger, J.; Zhang, F.; Caverley, M.; Jaeger, N.A.F.; et al. Apodized focusing fully etched subwavelength grating couplers. IEEE Photonics J. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Ho, C.P.; Zhao, Z.; Li, Q.; Takagi, S.; Takenaka, M. Tunable grating coupler by thermal actuation and thermo-optic effect. IEEE Photonic. Tech. L. 2018, 30, 1503–1506. [Google Scholar] [CrossRef]
- Papes, M.; Cheben, P.; Benedikovic, D.; Schmid, J.H.; Pond, J.; Halir, R.; Ortega-Monux, A.; Wanguemert-Perez, G.; Ye, W.N.; Xu, D.X.; et al. Fiber-chip edge coupler with large mode size for silicon photonic wire waveguides. Opt. Express 2016, 24, 5026–5038. [Google Scholar] [CrossRef] [PubMed]
- Romero-Garcia, S.; Marzban, B.; Merget, F.; Shen, B.; Witzens, J. Edge couplers with relaxed alignment tolerance for pick-and-place hybrid integration of III–V lasers with SOI waveguides. IEEE J. Sel. Top. Quant. 2014, 20, 369–379. [Google Scholar] [CrossRef]
- Tao, S.H.; Song, J.; Fang, Q.; Yu, M.B.; Lo, G.Q.; Kwong, D.L. Improving coupling efficiency of fiber-waveguide coupling with a double-tip coupler. Opt. Express 2008, 16, 20803–20808. [Google Scholar] [CrossRef]
- Hatori, N.; Shimizu, T.; Okano, M.; Ishizaka, M.; Yamamoto, T.; Urino, Y.; Mori, M.; Nakamura, T.; Arakawa, Y. A hybrid integrated light source on a silicon platform using a trident spot-size converter. J. Lightwave Technol. 2014, 32, 1329–1336. [Google Scholar] [CrossRef]
- Lai, Y.; Yu, Y.; Fu, S.; Xu, J.; Shum, P.P.; Zhang, X. Efficient spot size converter for higher-order mode fiber-chip coupling. Opt. Lett. 2017, 42, 3702–3705. [Google Scholar] [CrossRef]
- Yasuhara, K.; Yu, F.; Tshigure, T. Polymer waveguide based spot-size converter for low-loss coupling between Si photonics chips and single-mode fibers. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19 March 2017. [Google Scholar]
- Snyder, B.; Lepage, G.; Balakrishnan, S.; Verheyen, P.; Pantouvaki, M.; Absil, P.; Campenhout, J.V. Broadband, polarization-insensitive lensed edge couplers for silicon photonics. In Proceedings of the 2018 IEEE 68th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 29 May 2018. [Google Scholar]
- Jia, L.; Li, C.; Liow, T.-Y.; Lo, G.-Q. Efficient suspended coupler with loss less than −1.4 dB between Si-photonic waveguide and cleaved single mode fiber. J. Lightwave Technol. 2018, 36, 239–244. [Google Scholar] [CrossRef]
- Larrea, R.; Gutierrez, A.M.; Griol, A.; Brimont, A.; Sanchis, P. Fiber-to-chip spot-size converter for coupling to silicon waveguides in the O-band. IEEE Photonic. Tech. L. 2019, 31, 31–34. [Google Scholar] [CrossRef]
- Cardenas, J.; Luke, K.; Luo, L.W.; Poitras, C.B.; Morton, P.A.; Lipson, M. High coupling efficiency etched facet tapers in silicon. In Proceedings of the 2012 Conference on Lasers and Electro-Optics, San Jose, CA, USA, 6 May 2012. [Google Scholar]
- Chuang, S. Physics of Photonic Devices, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 273–279. [Google Scholar]
- Chrostowski, L.; Hochberg, M. Silicon Photonics Design: From Devices to Systems, 1st ed.; Cambridge University Press: Cambridge, UK, 2015; pp. 10–14. [Google Scholar]
- Dong, P.; Preble, S.F.; Robinson, J.T.; Manipatruni, S.; Lipson, M. Inducing photonic transitions between discrete modes in a silicon optical microcavity. Phys. Rev. Lett. 2008, 100, 033904. [Google Scholar] [CrossRef]
- Stern, B.; Zhu, X.; Chen, C.P.; Tzhuang, L.D.; Cardenas, J.; Bergman, K.; Lipsonm, M. On-chip mode-division multiplexing switch. Optica 2015, 2, 530–535. [Google Scholar] [CrossRef]
- He, Y.; Zhang, Y.; Zhu, Q.; An, S.; Cao, R.; Guo, X.; Qiu, C.; Su, Y. Silicon High-Order Mode (De)Multiplexer on Single Polarization. J. Lightwave Technol. 2018, 36, 5746–5753. [Google Scholar] [CrossRef]
- Kopp, C.; Bernabé, S.; Bakir, B.B.; Fedeli, J.M.; Orobtchouk, R.; Schrank, F.; Porte, H.; Zimmermann, L. Silicon photonic circuits: On-CMOS integration, fiber optical coupling, and packaging. IEEE J. Sel. Top. Quant. 2011, 17, 498–509. [Google Scholar] [CrossRef]
- Reed, G.T.; Knights, A.P. Silicon Photonics: An Introduction, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; pp. 1–6. [Google Scholar]
- Ding, Y.; Xu, J.; Da Ros, F.; Huang, B.; Ou, H.; Peucheret, C. On-chip two-mode division multiplexing using tapered directional coupler-based mode multiplexer and demultiplexer. Opt. Express 2013, 21, 10376–10382. [Google Scholar] [CrossRef] [PubMed]
- Yamada, H.; Chu, T.; Ishida, S.; Arakawa, Y. Si photonic wire waveguide devices. IEEE J. Sel. Top. Quant. 2006, 12, 1371–1379. [Google Scholar] [CrossRef]
- Chiang, K.S.; Liu, Q. Formulae for the design of polarization-insensitive multimode interference couplers. IEEE Photonic. Technol. Lett. 2011, 23, 1277–1279. [Google Scholar] [CrossRef]
- Xiao, Z.; Luo, X.; Lim, P.H.; Prabhathan, P.; Silalahi, S.T.; Liow, T.Y.; Zhang, J.; Luan, F. Ultra-compact low loss polarization insensitive silicon waveguide splitter. Opt. Express 2013, 21, 16331–16336. [Google Scholar] [CrossRef]
- Dai, D.; He, S. Optimization of ultracompact polarization-insensitive multimode interference couplers based on Si nanowire waveguides. IEEE Photonic. Technol. Lett. 2006, 18, 2017–2019. [Google Scholar] [CrossRef]
- Ramadan, T.; Osgood, R.M. Adiabatic couplers: Design rules and optimization. J. Lightwave Technol. 1998, 16, 277. [Google Scholar] [CrossRef]
- Guo, D.; Chu, T. Silicon mode (de)multiplexers with parameters optimized using shortcuts to adiabaticity. Opt. Express 2017, 25, 9160–9170. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Sun, W.; Xie, H.; Zhang, N.; Xu, K.; Yao, Y.; Xiao, S.; Song, Q. Adiabatic and ultracompact waveguide tapers based on digital metamaterials. IEEE J. Sel. Top. Quant. 2019, 25, 1–6. [Google Scholar] [CrossRef]
- Fu, Y.; Ye, T.; Tang, W.; Chu, T. Efficient adiabatic silicon-on-insulator waveguide taper. Photonics Res. 2014, 2, 41–44. [Google Scholar] [CrossRef]
- Seok, T.J.; Quack, N.; Han, S.; Muller, R.S.; Wu, M.C. Large-scale broadband digital silicon photonic switches with vertical adiabatic couplers. Optica 2016, 3, 64–70. [Google Scholar] [CrossRef]
- Suchoski, P.; Ramaswamy, R. Design of single-mode step-tapered waveguide sections. IEEE J. Sel. Top. Quant. 1987, 23, 205–211. [Google Scholar] [CrossRef]
- Wang, J.; Qi, M.; Xuan, Y.; Huang, H.; Li, Y.; Li, M.; Chen, X.; Jia, Q.; Sheng, Z.; Wu, A.; et al. Proposal for fabrication-tolerant SOI polarization splitter-rotator based on cascaded MMI couplers and an assisted bi-level taper. Opt. Express 2014, 22, 27869–27879. [Google Scholar] [CrossRef]
- Hettrick, S.J.; Wang, J.; Li, C.; Wilkinson, J.S.; Shepherd, D.P. An experimental comparison of linear and parabolic tapered waveguide lasers and a demonstration of broad-stripe diode pumping. J. Lightwave Technol. 2004, 22, 845–849. [Google Scholar] [CrossRef]
- Ren, G.; Chen, S.; Cheng, Y.; Zhai, Y. Study on inverse taper based mode transformer for low loss coupling between silicon wire waveguide and lensed fiber. Opt. Commun. 2011, 284, 4782–4788. [Google Scholar] [CrossRef]
- Snyder, A.W.; Love, J. Optical Waveguide Theory; Springer Science & Business Media: New York, NY, USA, 2012; pp. 238–280. [Google Scholar]
- Liu, Y.; Yu, J. Low-loss coupler between fiber and waveguide based on silicon-on-insulator slot waveguides. Appl. Opt. 2007, 46, 7858–7861. [Google Scholar] [CrossRef]
- Tu, X.; Fu, H.; Geng, D. Y-branch edge coupler between cleaved single mode fiber and nano-scale waveguide on silicon-on-insulator platform. In Proceedings of the 2014 Asia Communications and Photonics Conference, Shanghai, China, 11 November 2014. [Google Scholar]
- Mu, X.; Wu, S.; Cheng, L.; Tu, X.; Fu, H. High-performance silicon nitride fork-shape edge coupler. In Proceedings of the 2019 Frontiers in Optics, Washington, DC, USA, 15 September 2019. [Google Scholar]
- Tu, Y.C.; Fu, P.H.; Huang, D.W. High-efficiency ultra-broadband multi-tip edge couplers for integration of distributed feedback laser with silicon-on-insulator waveguide. IEEE Photonics J. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Wang, J.; Xuan, Y.; Lee, C.H.; Niu, B.; Liu, L.; Liu, G.N.; Qi, M. Low-loss and misalignment-tolerant fiber-to-chip edge coupler based on double-tip inverse tapers. In Proceedings of the 2016 Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20 March 2016. [Google Scholar]
- Hatori, N.; Urino, Y.; Shimizu, T.; Okano, M.; Yamamoto, T.; Mori, M.; Nakamura, T.; Arakawa, Y. Quantum dot laser for a light source of an athermal silicon optical interposer. Photonics 2015, 2, 355–364. [Google Scholar] [CrossRef]
- Itoh, K.; Kuno, Y.; Hayashi, Y.; Suzuki, J.; Hojo, N.; Amemiya, T.; Nishiyama, N.; Arai, S. Crystalline/amorphous Si integrated optical couplers for 2D/3D interconnection. IEEE J. Sel. Top. Quant. 2016, 22, 255–263. [Google Scholar] [CrossRef]
- Hatori, N.; Shimizu, T.; Okano, M.; Ishizaka, M.; Yamamoto, T.; Urino, Y.; Mori, M.; Nakamura, T.; Arakawa, Y. A novel spot size convertor for hybrid integrated light sources on photonics-electronics convergence system. In Proceedings of the 2012 IEEE 9th International Conference on Group IV Photonics (GFP), San Diego, CA, USA, 29 August 2012. [Google Scholar]
- Tu, X.; Dumain, P.; Li, M.; Goodwill, D.; Fu, H.; Geng, D.; Bernier, E. Low polarization-dependent-loss silicon photonic trident edge coupler fabricated by 248 nm optical lithography. In Proceedings of the 2015 Asia Communications and Photonics Conference, Hongkong, China, 19 November 2015. [Google Scholar]
- Mu, X.; Wu, S.; Cheng, L.; Tu, X.; Fu, H.Y. A compact adiabatic silicon photonic edge coupler based on silicon nitride/silicon trident structure. In Proceedings of the 2019 18th International Conference on Optical Communications and Networks (ICOCN), Huangshan, China, 5 August 2019. [Google Scholar]
- Cheben, P.; Xu, D.X.; Janz, S.; Densmore, A. Subwavelength waveguide grating for mode conversion and light coupling in integrated optics. Opt. Express 2006, 14, 4695–4702. [Google Scholar] [CrossRef] [PubMed]
- Cheben, P.; Bock, P.J.; Schimid, J.H.; Lapointe, J.; Janz, S.; Xu, D.X.; Densmore, A.; Delâge, A.; Lamontagne, B.; Hall, T.J. Refractive index engineering with subwavelength gratings for efficient microphotonic couplers and planar waveguide multiplexers. Opt. Lett. 2010, 35, 2526–2528. [Google Scholar] [CrossRef] [PubMed]
- Bock, P.J.; Cheben, P.; Schmid, J.H.; Lapointe, J.; Delâge, A.; Janz, S.; Aers, G.C.; Xu, D.X.; Densmore, A.; Hall, T.J. Subwavelength grating periodic structures in silicon-on-insulator: A new type of microphotonic waveguide. Opt. Express 2010, 18, 20251–20262. [Google Scholar] [CrossRef]
- Donzella, V.; Sherwali, A.; Flueckiger, J.; Talebi Fard, S.; Grist, S.M.; Chrostowski, L. Sub-wavelength grating components for integrated optics applications on SOI chips. Opt. Express 2014, 22, 21037–21050. [Google Scholar] [CrossRef]
- Cheben, P.; Schmid, J.H.; Wang, S.; Xu, D.X.; Vachon, M.; Janz, S.; Lapointe, J.; Painchaud, Y.; Picard, M.J. Broadband polarization independent nanophotonic coupler for silicon waveguides with ultra-high efficiency. Opt. Express 2015, 23, 22553–22563. [Google Scholar] [CrossRef]
- Halir, R.; Bock, P.J.; Cheben, P.; Ortega-Moñux, A.; Alonso-Ramos, C.; Schmid, J.H.; Lapointe, J.; Xu, D.-X.; Wangüemert-Pérez, J.G.; Molina-Fernández, Í.; et al. Waveguide sub-wavelength structures: A review of principles and applications. Laser Photonics Rev. 2015, 9, 25–49. [Google Scholar] [CrossRef]
- Mu, X.; Wu, S.; Cheng, L.; Tu, X.; Fu, H.Y. Ultra-compact silicon photonic edge coupler based on subwavelength gratings. In Proceedings of the 2019 Asia Communications and Photonics Conference, Chengdu, China, 2 November 2019. [Google Scholar]
- Teng, M.; Hondardoost, A.; Alahmadi, Y.; Polkoo, S.S.; Kojima, K.; Wen, H.; Renshaw, C.K.; LiKanWa, P.; Li, G.; et al. Miniaturized Silicon Photonics Devices for Integrated Optical Signal Processors. J. Lightwave Technol. 2020, 38, 6–17. [Google Scholar] [CrossRef]
- Picard, M.J.; Latrasse, C.; Larouche, C.; Painchaud, Y.; Poulin, M.; Pelletier, F.; Guy, M. CMOS-compatible spot-size converter for optical fiber to sub-um silicon waveguide coupling with low-loss low-wavelength dependence and high tolerance to misalignment. In Proceedings of the SPIE OPTO, San Francisco, CA, USA, 14 March 2016. [Google Scholar]
- Sisto, M.M.; Fisette, B.; Paultre, J.E.; Paquet, A.; Desroches, Y. Novel spot size converter for coupling standard single mode fibers to SOI waveguides. In Proceedings of the SPIE OPTO, San Francisco, CA, USA, 14 March 2016. [Google Scholar]
- Voigt, K.; Brulis, V.; Petermann, K.; Zimmermann, L. Study of backend waveguide arrays for adiabatic coupling to Si waveguides. In Proceedings of the 2017 IEEE 14th International Conference on Group IV Photonics (GFP), Berlin, Germany, 23 August 2017. [Google Scholar]
- Doylend, J.K.; Knights, A.P. Design and simulation of an integrated fiber-to-chip coupler for silicon-on-insulator waveguides. IEEE J. Sel. Top. Quant. 2006, 12, 1363–1370. [Google Scholar] [CrossRef]
- Kruse, K.; Middlebrook, C.T. Polymer taper bridge for silicon waveguide to single mode waveguide coupling. Opt. Commun. 2016, 362, 87–95. [Google Scholar] [CrossRef]
- Dewanjee, A.; Caspers, J.N.; Aitchison, J.S.; Mojahedi, M. Demonstration of a compact bilayer inverse taper coupler for Si-photonics with enhanced polarization insensitivity. Opt. Express 2016, 24, 28194–28203. [Google Scholar] [CrossRef] [PubMed]
- Khilo, A.; Popović, M.A.; Araghchini, A.; Kärtner, F.X. Efficient planar fiber-to-chip coupler based on two-stage adiabatic evolution. Opt. Express 2010, 18, 15790–15806. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Kim, S.; Park, J.; Joo, J.; Kim, G. A fiber-to-chip coupler based on Si/SiON cascaded tapers for Si photonic chips. Opt. Express 2013, 21, 29313–29319. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Song, J.; Luo, X.; Tu, X.; Jia, L.; Yu, M.; Lo, G. Low loss fiber-to-waveguide converter with a 3-D functional taper for silicon photonics. IEEE Photonic. Tech. L. 2016, 28, 2533–2536. [Google Scholar] [CrossRef]
- Hastings, F.D.; Schneider, J.B.; Broschat, S.L. A Monte-Carlo FDTD technique for rough surface scattering. IEEE T. Antenn. Propag. 1995, 43, 1183–1191. [Google Scholar] [CrossRef]
- Teng, M.; Niu, B.; Han, K.; Qi, M. Effect of waveguide surface roughness on the fiber coupling efficiency of inverse tapers. In Proceedings of the 2015 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 22 March 2015. [Google Scholar]
- Lee, K.K.; Lim, D.R.; Kimerling, L.C.; Shin, J.; Cerrina, F. Fabrication of ultralow-loss Si/SiO2 waveguides by roughness reduction. Opt. Lett. 2001, 26, 1888–1890. [Google Scholar] [CrossRef]
- Jaberansary, E.; Masaud, T.M.B.; Milosevic, M.M.; Nedeljkovic, M.; Mashanovich, G.Z.; Chong, H.M.H. Scattering loss estimation using 2-D Fourier analysis and modeling of sidewall roughness on optical waveguides. IEEE Photonics J. 2013, 5, 6601010. [Google Scholar] [CrossRef]
- Fang, Q.; Song, J.F.; Tao, S.H.; Yu, M.B.; Lo, G.Q.; Kwong, D.L. Low loss (~6.45dB/cm) sub-micron polycrystalline silicon waveguide integrated with efficient SiON waveguide coupler. Opt. Express 2008, 16, 6425–6432. [Google Scholar]
- Lee, J.-M.; Kim, D.-J.; Ahn, H.; Park, S.-H.; Kim, G. Temperature dependence of silicon nanophotonic ring resonator with a polymeric overlayer. J. Lightwave Technol. 2007, 25, 2236–2243. [Google Scholar] [CrossRef]
- Pu, M.; Liu, L.; Ou, H.; Yvind, K.; Hvam, J.M. Ultra-low-loss inverted taper coupler for silicon-on-insulator ridge waveguide. Opt. Commun. 2010, 283, 3678–3682. [Google Scholar] [CrossRef]
- Ben Bakir, B.; de Gyves, A.V.; Orobtchouk, R.; Lyan, P.; Porzier, C.; Roman, A.; Fedeli, J.M. Low-loss (<1 dB) and polarization-insensitive edge fiber couplers fabricated on 200-mm silicon-on-insulator wafers. IEEE Photonic. Technol. Lett. 2010, 22, 739–741. [Google Scholar] [CrossRef]
- Raghunathan, V.; Yagüe, J.L.; Xu, J.; Michel, J.; Gleason, K.K.; Kimerling, L.C. Co-polymer clad design for high performance athermal photonic circuits. Opt. Express 2012, 20, 20808–20813. [Google Scholar] [CrossRef] [PubMed]
- Ku, K.-N.; Lee, M.-C.M. Wide-band optical mode converters for coupling between fibers and silicon photonic wires with large misalignment tolerance. J. Lightwave Technol. 2013, 31, 1616–1620. [Google Scholar] [CrossRef]
- Jia, L.; Song, J.; Liow, T.Y.; Luo, X.; Tu, X.; Fang, Q.; Koh, S.C.; Yu, M.; Lo, G. Mode size converter between high-index-contrast waveguide and cleaved single mode fiber using SiON as intermediate material. Opt. Express 2014, 22, 23652–23660. [Google Scholar] [CrossRef]
- Takei, R.; Maegami, Y.; Omoda, E.; Sakakibara, Y.; Mori, M.; Kamei, T. Low-loss and low wavelength-dependence vertical interlayer transition for 3D silicon photonics. Opt. Express 2015, 23, 18602–18610. [Google Scholar] [CrossRef] [PubMed]
- Maegami, Y.; Takei, R.; Omoda, E.; Amano, T.; Okano, M.; Mori, M.; Kamei, T.; Sakakibara, Y. Spot-size converter with a SiO2 spacer layer between tapered Si and SiON waveguides for fiber-to-chip coupling. Opt. Express 2015, 23, 21287–21295. [Google Scholar] [CrossRef]
- Fritze, M.; Knecht, J.; Bozler, C.; Keast, C.; Fijol, J.; Jacobson, S.; Keating, P.; LeBlanc, J.; Fike, E.; Kessler, B.; et al. Fabrication of three-dimensional mode converters for silicon-based integrated optics. J. Vac. Sci. Technol. B 2003, 21, 2897–2902. [Google Scholar] [CrossRef]
- Holly, R.; Hingerl, K.; Merz, R.; Hudek, P. Fabrication of silicon 3D taper structures for optical fibre to chip interface. Microelectron. Eng. 2007, 84, 1248–1251. [Google Scholar] [CrossRef]
- Shiraishi, K.; Yoda, H.; Ohshima, A.; Ikedo, H.; Tsai, C.S. A silicon-based spot-size converter between single-mode fibers and Si-wire waveguides using cascaded tapers. Appl. Phys. Lett. 2007, 91, 141120. [Google Scholar] [CrossRef]
- Takei, R.; Suzuki, M.; Omoda, E.; Manako, S.; Kamei, T.; Mori, M.; Sakakibara, Y. Silicon knife-edge taper waveguide for ultralow-loss spot-size converter fabricated by photolithography. Appl. Phys. Lett. 2013, 102, 101108. [Google Scholar] [CrossRef]
- Harke, A.; Lipka, T.; Amthor, J.; Horn, O.; Krause, M.; Muller, J. Amorphous silicon 3-D tapers for Si photonic wires fabricated with shadow masks. IEEE Photonic. Tech. L. 2008, 20, 1452–1454. [Google Scholar] [CrossRef]
- Lee, M.-C.M.; Chiu, W.-C.; Yang, T.-M.; Chen, C.-H. Monolithically integrated low-loss silicon photonic wires and three-dimensional tapered couplers fabricated by self-profile transformation. Appl. Phys. Lett. 2007, 91, 191114. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Chang, C.J.; Lee, M.C.; Tseng, F.G. SU8 3D prisms with ultra small inclined angle for low-insertion-loss fiber/waveguide interconnection. Opt. Express 2011, 19, 18956–18964. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Liow, T.S.; Song, J.; Tan, C.; Yu, M.; Lo, G.; Kwong, D.L. Suspended optical fiber-to-waveguide mode size converter for Silicon photonics. Opt. Express 2010, 18, 7763–7769. [Google Scholar] [CrossRef]
- Chen, L.; Doerr, C.R.; Chen, Y.-K.; Liow, T.-Y. Low-loss and broadband cantilever couplers between standard cleaved fibers and high-index-contrast Si3N4 or Si Waveguides. IEEE Photonic. Tech. L. 2010, 22, 1744–1746. [Google Scholar] [CrossRef]
- Fang, Q.; Song, J.; Luo, X.; Yu, M.; Lo, G.; Liu, Y. Mode-size converter with high coupling efficiency and broad bandwidth. Opt. Express 2011, 19, 21588–21594. [Google Scholar] [CrossRef]
- Wood, M.; Sun, P.; Reano, R.M. Compact cantilever couplers for low-loss fiber coupling to silicon photonic integrated circuits. Opt. Express 2012, 20, 164–172. [Google Scholar] [CrossRef]
- Jia, L.; Song, J.; Liow, T.S.; Luo, X.; Tu, X.; Fang, Q.; Koh, S.C.; Yu, M.; Lo, G. Low loss/large tolerance mode converter between SiN waveguide and cleaved single mode fiber. In Proceedings of the 2014 Optical Fiber Communications Conference and Exhibition (OFC), San Francisco, CA, USA, 9 March 2014. [Google Scholar]
- Wang, X.; Quan, X.; Liu, M.; Cheng, X. Silicon-nitride-assisted edge coupler interfacing with high numerical aperture fiber. IEEE Photonic. Tech. L. 2019, 31, 349–352. [Google Scholar] [CrossRef]
- He, L.; Liu, Y.; Galland, C.; Lim, A.E.J.; Lo, G.Q.; Baehr-Jones, T.; Hochberg, M. A high-efficiency nonuniform grating coupler realized with 248-nm optical lithography. IEEE Photonic. Tech. L. 2013, 25, 1358–1361. [Google Scholar] [CrossRef]
- Halir, R.; Cheben, P.; Schmid, J.H.; Ma, R.; Bedard, D.; Janz, S.; Xu, D.X.; Densmore, A.; Lapointe, J.; Molina, I. Continuously apodized fiber-to-chip surface grating coupler with refractive index engineered subwavelength structure. Opt. Lett. 2010, 35, 3243–3245. [Google Scholar] [CrossRef] [PubMed]
- Vermeulen, D.; Selvaraja, S.; Verheyen, P.; Lepage, G.; Bogaerts, W.; Absil, P.; Thourhout, D.V.; Roelkens, G. High-efficiency fiber-to-chip grating couplers realized using an advanced CMOS-compatible Silicon-On-Insulator platform. Opt. Express 2010, 18, 18278–18283. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Thomson, D.J.; Crudginton, L.; Khokhar, A.Z.; Reed, G.T. Dual-etch apodised grating couplers for efficient fibre-chip coupling near 1310 nm wavelength. Opt. Express 2017, 25, 17864–17871. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Peucheret, C.; Ou, H.; Yvind, K. Fully etched apodized grating coupler on the SOI platform with -0. 58dB coupling efficiency. Opt. Lett. 2014, 39, 5348–5350. [Google Scholar]
- Xue, Y.; Chen, H.; Bao, Y.; Dong, J.; Zhang, X. Two-dimensional silicon photonic grating coupler with low polarization-dependent loss and high tolerance. Opt. Express 2019, 27, 22268–22274. [Google Scholar] [CrossRef] [PubMed]
- Streshinsky, M.; Shi, R.; Novack, A.; Cher, R.T.P.; Lim, A.E.J.; Lo, P.G.Q.; Baehr-Jones, T.; Hochberg, M. A compact bi-wavelength polarization splitting grating coupler fabricated in a 220 nm SOI platform. Opt. Express 2013, 21, 31019–31028. [Google Scholar] [CrossRef] [PubMed]
- Na, N.; Frish, H.; Hsieh, I.W.; Harel, O.; George, R.; Barkai, A.; Rong, H. Efficient broadband silicon-on-insulator grating coupler with low backreflection. Opt. Lett. 2011, 36, 2101–2103. [Google Scholar] [CrossRef]
- Errando-Herranz, C.; Saharil, F.; Romero, A.M.; Sandstrom, N.; Shafagh, R.Z.; Wijngaart, W.V.D.; Haraldsson, T.; Gylfason, K.B. Integration of microfluidics with grating coupled silicon photonic sensors by one-step combined photopatterning and molding of OSTE. Opt. Express 2013, 21, 21293–21298. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, M.; Ruocco, A.; Geessels, J.; Khan, U.; Bogaerts, W. Compact silicon photonics circuit to extract multiple parameters for process control monitoring. OSA Continuum 2020, 3, 379–390. [Google Scholar] [CrossRef]
- Carroll, L.; Lee, J.S.; Scarcella, C.; Gradkowski, K.; Duperron, M.; Lu, H.; Zhao, Y.; Eason, C.; Morrissey, P.; Rensing, M.; et al. Photonic packaging: Transforming silicon photonic integrated circuits into photonic devices. Appl. Sci. 2016, 6, 426. [Google Scholar] [CrossRef]
- Li, C.; Chee, K.S.; Tao, J.; Zhang, H.; Yu, M.; Lo, G.Q. Silicon photonics packaging with lateral fiber coupling to apodized grating coupler embedded circuit. Opt. Express 2014, 22, 24235–24240. [Google Scholar] [CrossRef] [PubMed]
- Nambiar, S.; Sethi, P.; Selvaraja, S. Grating-assisted fiber to chip coupling for SOI photonic circuits. Appl. Sci. 2018, 8, 1142. [Google Scholar] [CrossRef]
- Vivien, L.; Laval, S.; Cassan, E.; Le Roux, X.; Pascal, D. 2-D taper for low-loss coupling between polarization-insensitive microwaveguides and single-mode optical fibers. J. Lightwave Technol. 2003, 21, 2429–2433. [Google Scholar] [CrossRef]
- Schmid, J.H.; Cheben, P.; Rahim, M.; Wang, S.; Xu, D.X.; Vachon, M.; Janz, S.; Lapointe, J.; Painchaud, Y.; Picard, M.J.; et al. Subwavelength gratings for broadband and polarization independent fiber-chip coupling with −0.4 dB efficiency. In Proceedings of the 2016 Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20 March 2016. [Google Scholar]
- Chen, X.; Xu, K.; Cheng, Z.; Fung, C.K.Y.; Tsang, H.K. Wideband subwavelength gratings for coupling between silicon-on-insulator waveguides and optical fibers. Opt. Lett. 2012, 37, 3483–3485. [Google Scholar] [CrossRef] [PubMed]
- Dai, D.; Bauters, J.; Bowers, J.E. Passive technologies for future large-scale photonic integrated circuits on silicon: Polarization handling, light non-reciprocity and loss reduction. Light-Sci. Appl. 2012, 1, e1. [Google Scholar] [CrossRef]
- Dai, D.; Liu, L.; Gao, S.; Xu, D.-X.; He, S. Polarization management for silicon photonic integrated circuits. Laser Photonics Rev. 2013, 7, 303–328. [Google Scholar] [CrossRef]
- Dai, D.; Mao, M. Mode converter based on an inverse taper for multimode silicon nanophotonic integrated circuits. Opt. Express 2015, 23, 28376–28388. [Google Scholar] [CrossRef]
- Dai, D.; Wang, J.; Chen, S.; Wang, S.; He, S. Monolithically integrated 64-channel silicon hybrid demultiplexer enabling simultaneous wavelength- and mode-division-multiplexing. Laser Photonics Rev. 2015, 9, 339–344. [Google Scholar] [CrossRef]
- Wang, S.; Wu, H.; Tsang, H.K.; Dai, D. Monolithically integrated reconfigurable add-drop multiplexer for mode-division-multiplexing systems. Opt. Lett. 2016, 41, 5298–5301. [Google Scholar] [CrossRef]
- Wang, J.; He, S.; Dai, D. On-chip silicon 8-channel hybrid (de)multiplexer enabling simultaneous mode- and polarization-division-multiplexing. Laser Photonics Rev. 2014, 8, L18–L22. [Google Scholar] [CrossRef]
- Dai, D.; Wang, J.; Shi, Y. Silicon mode (de)multiplexer enabling high capacity photonic networks-on-chip with a single-wavelength-carrier light. Opt. Lett. 2013, 38, 1422–1424. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.W.; Ophir, N.; Chen, C.P.; Gabrielli, L.H.; Poitras, C.B.; Bergmen, K.; Lipson, M. WDM-compatible mode-division multiplexing on a silicon chip. Nat. Commun. 2014, 5, 3069. [Google Scholar] [CrossRef] [PubMed]
- Maegami, Y.; Okano, M.; Cong, G.; Ohno, M.; Yamada, K. Completely CMOS compatible SiN-waveguidebased fiber coupling structure for Si wire waveguides. Opt. Express 2016, 24, 16856–16865. [Google Scholar] [CrossRef]
- Sacher, W.D.; Mikkelsen, J.C.; Huang, Y.; Mak, J.C.C.; Yong, Z.; Luo, X.; Li, Y.; Dumais, P.; Jiang, J.; Goodwill, D.; et al. Monolithically integrated multilayer silicon nitride-on-silicon waveguide platforms for 3-D photonic circuits and devices. Proc. IEEE 2018, 106, 2232–2245. [Google Scholar] [CrossRef]
- Sodagar, M.; Pourabolghasem, R.; Eftekhar, A.A.; Adibi, A. High-efficiency and wideband interlayer grating couplers in multilayer Si/SiO2/SiN platform for 3D integration of optical functionalities. Opt. Express 2014, 22, 16767–16777. [Google Scholar] [CrossRef] [PubMed]
- Sacher, W.D.; Huang, Y.; Ding, L.; Taylor, B.J.F.; Jayatilleka, H.; Lo, G.Q.; Poon, J.K.S. Wide bandwidth and high coupling efficiency Si3N4-on-SOI dual-level grating coupler. Opt. Express 2014, 22, 10938–10947. [Google Scholar] [CrossRef]
- Sacher, W.D.; Huang, Y.; Lo, G.-Q.; Poon, J.K.S. Multilayer silicon nitride-on-silicon integrated photonic platforms and devices. J. Lightwave Technol. 2015, 33, 901–910. [Google Scholar] [CrossRef]
- Sacher, W.D.; Mikkelsen, J.C.; Dumais, P.; Jiang, J.; Goodwill, D.; Luo, X.; Huang, Y.; Yang, Y.; Bois, A.; Lo, P.G.; et al. Tri-layer silicon nitride-on-silicon photonic platform for ultra-low-loss crossings and interlayer transitions. Opt. Express 2017, 25, 30862–30875. [Google Scholar] [CrossRef]
- Huang, Y.; Song, J.; Luo, X.; Liow, T.Y.; Lo, G.Q. CMOS compatible monolithic multi-layer Si3N4-on-SOI platform for low-loss high performance silicon photonics dense integration. Opt. Express 2014, 22, 21859–21865. [Google Scholar] [CrossRef]
- Zhu, S.; Lo, G.-Q. Vertically stacked multilayer photonics on bulk silicon toward three-dimensional integration. J. Lightwave Technol. 2016, 34, 386–392. [Google Scholar] [CrossRef]
- Bauters, J.F.; Davenport, M.L.; Heck, M.J.R.; Doylend, J.K.; Chen, A.; Fang, A.W.; Bowers, J.E. Silicon on ultra-low-loss waveguide photonic integration platform. Opt. Express 2013, 21, 544–555. [Google Scholar] [CrossRef] [PubMed]
- Xiang, C.; Davenport, M.L.; Khurgin, J.B.; Morton, P.A.; Bowers, J.E. Low-loss continuously tunable optical true time delay based on Si3N4 ring resonators. IEEE J. Sel. Top. Quant. 2018, 24, 1–9. [Google Scholar] [CrossRef]
- Goh, J.; Fushman, I.; Englund, D.; Vučković, J. Genetic optimization of photonic bandgap structures. Opt. Express 2007, 15, 8218–8230. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Vučković, J. Objective-first design of high-efficiency, small-footprint couplers between arbitary nanophotonic waveguide modes. Opt. Express 2012, 20, 7221–7236. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Vuckovic, J. Nanophotonic computational design. Opt. Express 2013, 21, 13351–13367. [Google Scholar] [CrossRef] [PubMed]
- Piggott, A.Y.; Lu, J.; Lagoudakis, K.G.; Petykiewicz, J.; Babinec, T.M.; Vučković, J. Inverse design and demonstration of a compact and broadband on-chip wavelength demultiplexer. Nat. Photonics 2015, 9, 374–377. [Google Scholar] [CrossRef]
- Wen, X.; Xu, K.; Song, Q. Design of a barcode-like waveguide nanostructure for efficient chip–fiber coupling. Photonics Res. 2016, 4, 209–213. [Google Scholar] [CrossRef]
- Callewaert, F.; Butun, S.; Li, Z.; Aydin, K. Inverse design of an ultra-compact broadband optical diode based on asymmetric spatial mode conversion. Sci. Rep. 2016, 6, 32577. [Google Scholar] [CrossRef]
- Xie, H.; Liu, Y.; Sun, W.; Wang, Y.; Xu, K.; Du, J.; He, Z.; Song, Q. Inversely designed 1 × 4 power splitter with arbitrary ratios at 2-μm spectral band. IEEE Photonics J. 2018, 10, 1–6. [Google Scholar] [CrossRef]
- Michaels, A.; Yablonovitch, E. Inverse design of near unity efficiency perfectly vertical grating couplers. Opt. Express 2018, 26, 4766–4779. [Google Scholar] [CrossRef]
- Su, L.; Trivedi, R.; Sapra, N.V.; Piggott, A.Y.; Vercruysse, D.; Vuckovic, J. Fully-automated optimization of grating couplers. Opt. Express 2018, 26, 4023–4034. [Google Scholar] [CrossRef] [PubMed]
- Molesky, S.; Lin, Z.; Piggott, A.Y.; Jin, W.; Vucković, J.; Rodriguez, A.W. Inverse design in nanophotonics. Nat. Photonics 2018, 12, 659–670. [Google Scholar] [CrossRef]
- Lebbe, N.; Dapogny, C.; Oudet, E.; Hassan, K.; Gliere, A. Robust shape and topology optimization of nanophotonic devices using the level set method. J. Comput. Phys. 2019, 395, 710–746. [Google Scholar] [CrossRef]


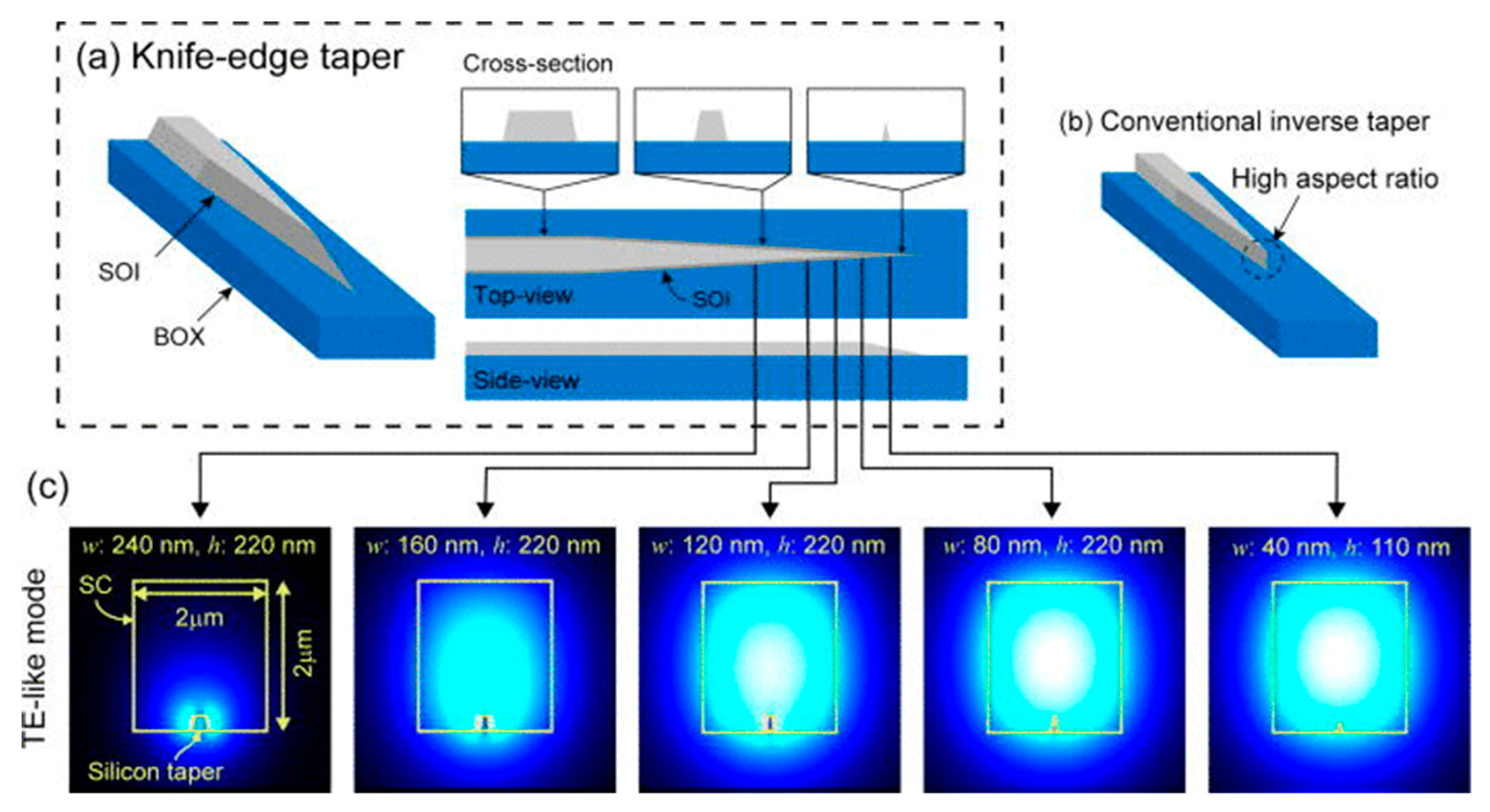
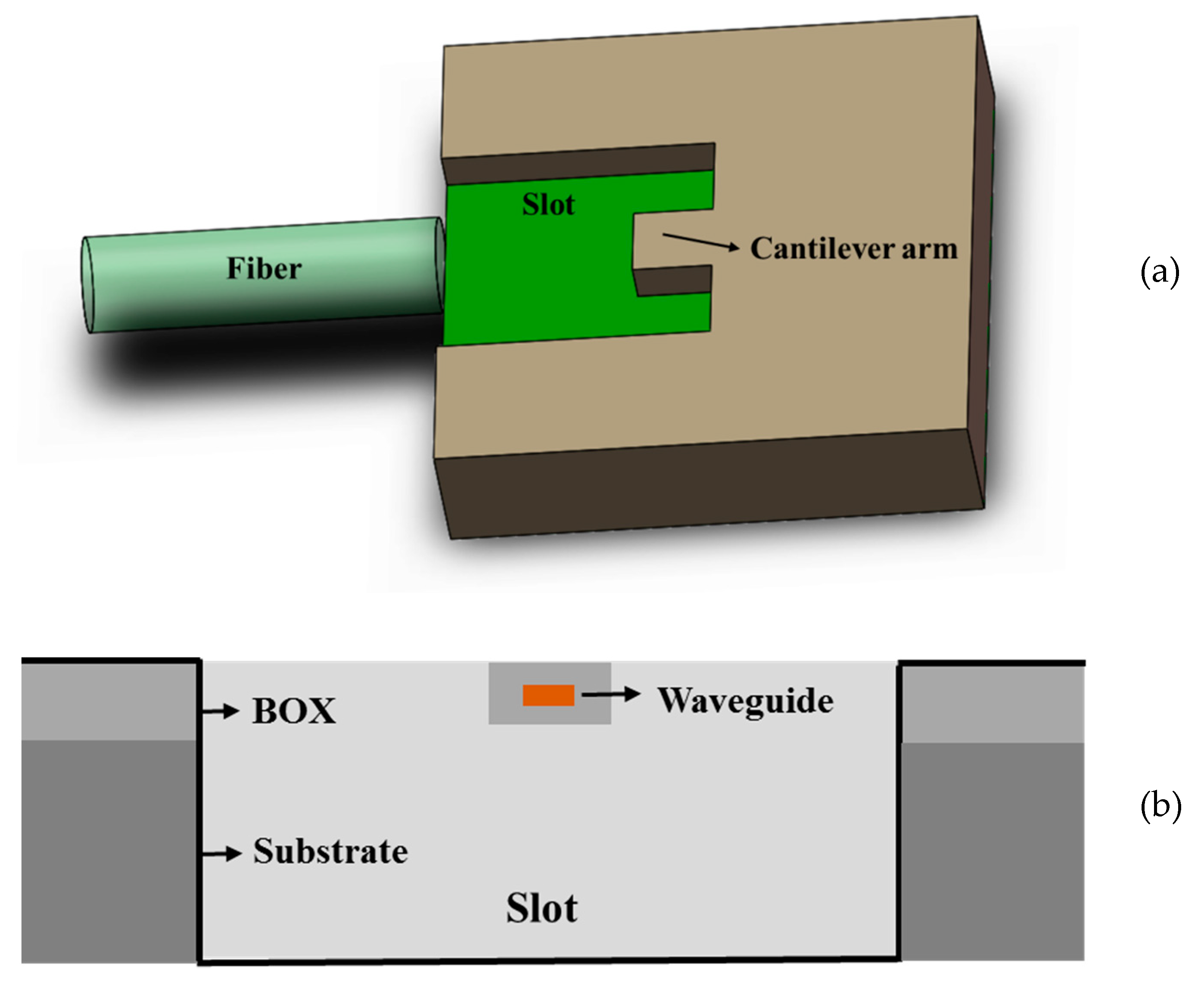
| Edge Coupler Configuration | Coupling Loss (dB) | Polarization | Size (μm) | Comments |
|---|---|---|---|---|
| Edge coupler based on inverse taper with various nonlinear profiles [54] | 1 1.37 | TE | 250 | Comparable efficiency with normal taper in shorter device length, simple and practical fabrication process, and particularly enhanced TM mode performance. |
| 2.13 | TM | 200 | ||
| 2 1.37 | TE | 170 | ||
| 2.12 | TM | 140 | ||
| 3 1.39 | TE | 170 | ||
| 1.87 | TM | 150 | ||
| Edge coupler consisting of double-tip inverse taper [60] | 1.10 | TE | 40 | Lower coupling loss and higher misalignment tolerance than single-tip taper coupler, and ultra-compact for highly integration. |
| 1.52 | TM | |||
| Trident edge coupler [64] | <1.5 | TE | 300 | Lower polarization dependence than normal taper and feasible via lithography process. |
| <1.7 | TM | |||
| SWG edge coupler assisted with SiN layer [24] | 0.75 | TE | 1500 | High coupling efficiency, but complicated fabrication process and large footprint. |
| Si taper under multiple SiN rods and SiON cladding [74] | 0.5 | TE | ~500 | High coupling performance to SMF with low wavelength dependence and PDL, but complex and difficult for mass production. |
| 0.9 | TM | |||
| Mode converter with cascaded upper claddings and cantilever [82] | 1.5 | TE | 240 | Fabricated at IME with comprehensively good performance, but infeasible with overlapped tapers and cantilever structure. |
| 2.1 | TM | |||
| Nano-taper coupler cladded with polymer waveguide [89] | 0.66 | TE | 300 | Single taper and SU-8 polymer applied with electron-beam lithography, straightforward design at the expense of high cost. |
| 0.36 | TM | |||
| Knife-edge shape coupler fabricated using a double-patterning method [99] | 0.35 | TE | ~180 | Excellent performance with i-line stepper photolithography and angled sidewall dry-etching, challenging for fabrication. |
| 0.21 | TM | |||
| A cantilevered mode-size converter [105] | 1.0 | TE | 250 | Excess and complex process on SOI wafer required to prepare the subtle cantilever structure, low feasibility and integrability. |
| 1.5 | TM |
| Description | Coupling Loss (dB) | Bandwidth | Polarization | Comments |
|---|---|---|---|---|
| Shallow etched grating coupler [109] | 3.1 | Approximately 40 nm @ 1 dB | TE | Standard 248 nm DUV plus shallow etch, good coupling efficiency. |
| Subwavelength grating coupler [110] | 3.7 | 60 nm @ 1 dB | TM | 193 nm DUV, good efficiency, wide bandwidth, sensitive to fabrication. |
| Grating coupler with silicon overlay [111] | 1.6 | 80 nm @ 3 dB | TE | 193 nm DUV plus amorphous silicon overlay available at Imec and IME |
| Polarization-splitting grating coupler [114] | 4.2 | / | TE and TM | EBL plus shallow etch, low PDL, fair coupling efficiency. |
| Bi-wavelength grating coupler [115] | 7.1 | 35 nm @ 3 dB | TE and TM | 248 nm DUV plus shallow etch, high loss, dual wavelength bands. |
| Two-tip slot edge coupler [56] | 1.8 | / | TE | Feasible with EBL, low loss, simple structure, hard to align. |
| SWG edge coupler [67] | 0.9 | >200 nm @ 3 dB | TE | EBL, ultra-low loss, ultra-broad bandwidth, high feasibility |
| Description | Coupling Loss (dB) | Bandwidth | Polarization | Comments |
|---|---|---|---|---|
| Shallow etched SOI grating coupler [109] | 3.1 | Approximately 40 nm @1 dB | TE | Feasible one-step shallow etch with lithography, standard fabrication, and good performance. |
| Tri-level SiN-on-SOI grating coupler [134] | 5.6 | Approximately 45 nm @1 dB | TE | Leading research with fair loss and low polarization dependence with featured multi-layer SiN-on-SOI platform fabrication process. |
| 5.5 | >100 nm @1 dB | TM | ||
| SiN grating coupler without SOI reflector [136] | 1.3 | 80 nm @ 1 dB | TE | Novel design, low loss, wide bandwidth, and simplified fabrication. |
| Edge coupler based on SOI inverse taper [54] | 1.37 | Approximately 100 nm @1 dB | TE | Low loss, broadband width, and easy fabrication practical for mass production. |
| 2.13 | TM | |||
| Edge coupler assisted with SiN multiple upper waveguides [74] | 0.9 | >50 nm @1 dB | TE and TM | Ultra-low loss, limited bandwidth, and too large footprint for integration. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, X.; Wu, S.; Cheng, L.; Fu, H.Y. Edge Couplers in Silicon Photonic Integrated Circuits: A Review. Appl. Sci. 2020, 10, 1538. https://doi.org/10.3390/app10041538
Mu X, Wu S, Cheng L, Fu HY. Edge Couplers in Silicon Photonic Integrated Circuits: A Review. Applied Sciences. 2020; 10(4):1538. https://doi.org/10.3390/app10041538
Chicago/Turabian StyleMu, Xin, Sailong Wu, Lirong Cheng, and H.Y. Fu. 2020. "Edge Couplers in Silicon Photonic Integrated Circuits: A Review" Applied Sciences 10, no. 4: 1538. https://doi.org/10.3390/app10041538
APA StyleMu, X., Wu, S., Cheng, L., & Fu, H. Y. (2020). Edge Couplers in Silicon Photonic Integrated Circuits: A Review. Applied Sciences, 10(4), 1538. https://doi.org/10.3390/app10041538






