Numerical Simulation of Breaking Wave Loading on Standing Circular Cylinders with Different Transverse Inclined Angles
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations
2.2. Free Surface Capture
2.3. Numerical Wave Tank
2.4. Boundary Conditions
- (i)
- At the inlet boundary, the velocity for the water is given according to the wave theory, while the air velocity is zero. The pressure is set as a zero normal gradient boundary condition.
- (ii)
- At the outlet of the domain, the velocities for both water and air are set to zero. The zero normal gradient condition is applied for the pressure.
- (iii)
- At the top boundary, the velocity for the inflow is calculated from the flux in the patch-normal direction. The velocity for the outflow is set as the zero normal gradient boundary condition. The patch pressure on the top boundary is obtained by subtracting the dynamic pressure from the total pressure, expressed as follows,where is total pressure and is the mean velocity vector.
- (iv)
- The no-slip condition is employed in four boundaries, i.e., front, back, bottom, and the cylinder’s surface, where the velocity is zero. Meanwhile, the wall functions are employed on these boundaries. The distance of the first layer center to the wall is 0.002 D, where D is the diameter of the cylinder. It ensures that the dimensionless wall distance for the present simulation is at the range of 40–200.
2.5. Calculation of Wave Forces
2.6. Numerical Scheme
3. Numerical Implementation
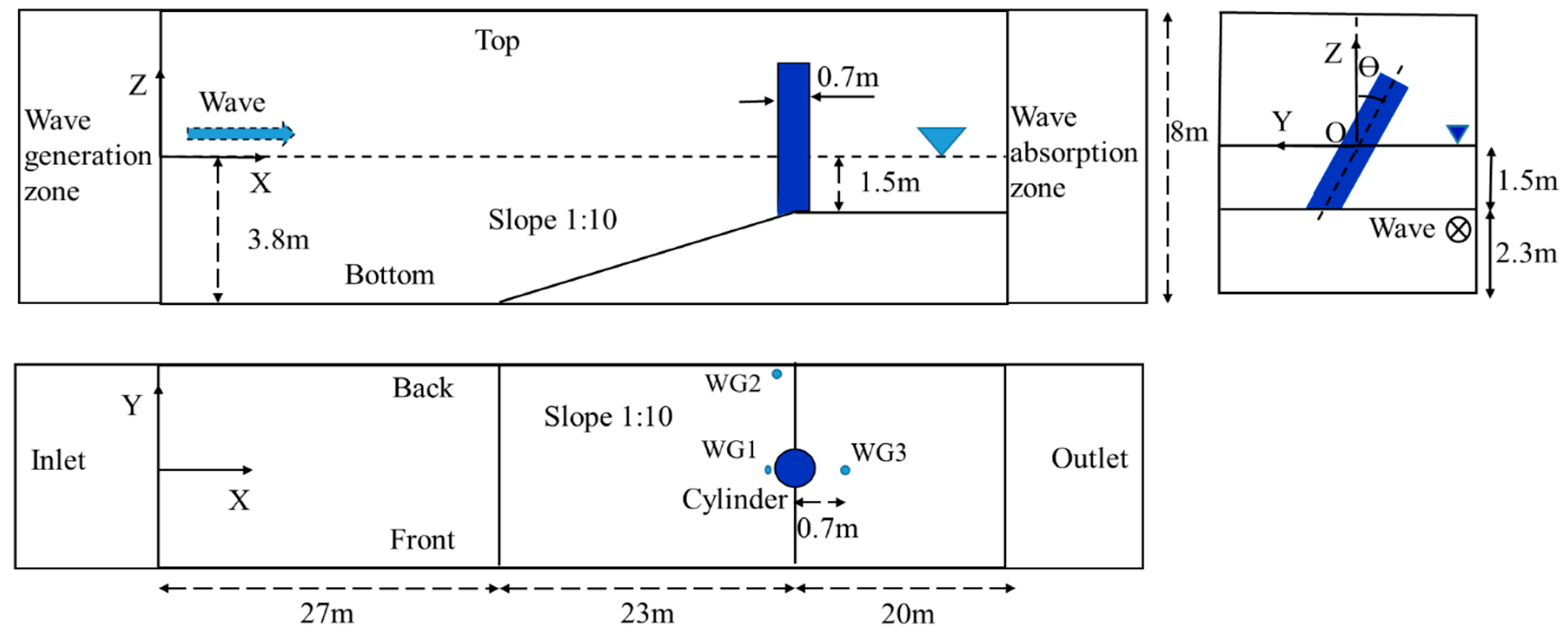
3.1. Setup of the Numerical Wave Tank
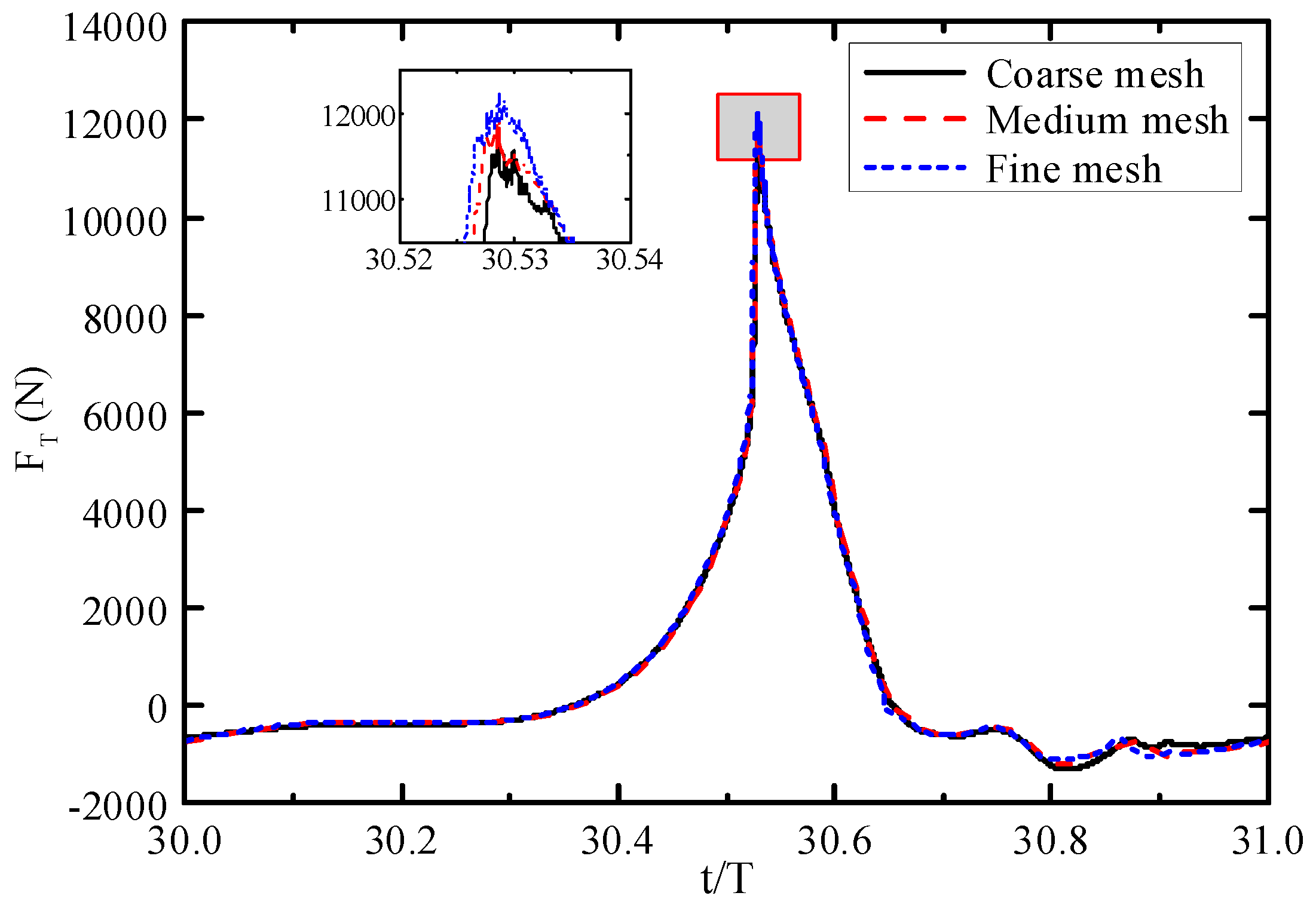
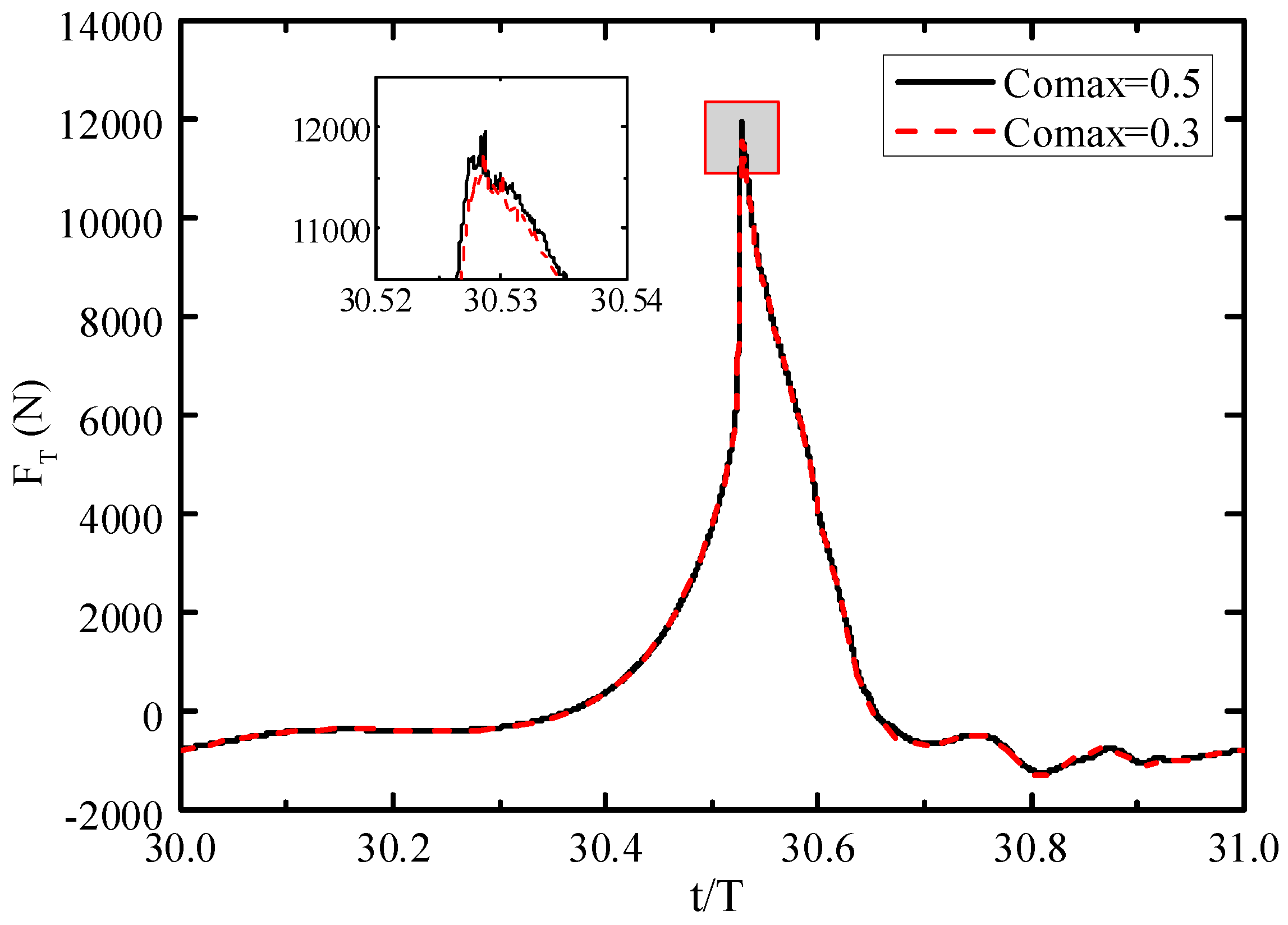
3.2. Grid and Time-Step Refinement Studies
4. Results
4.1. Validation of the Numerical Model
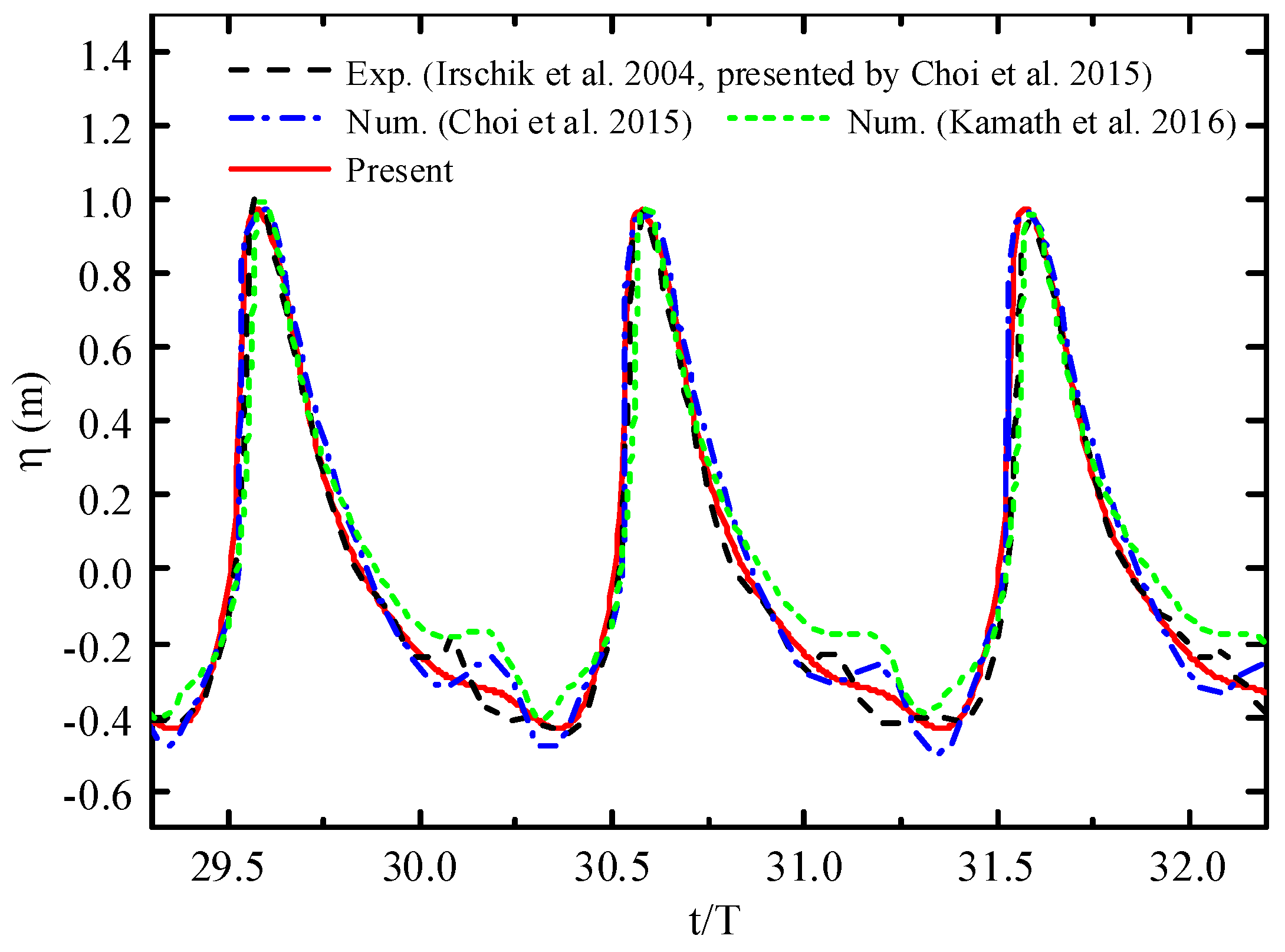
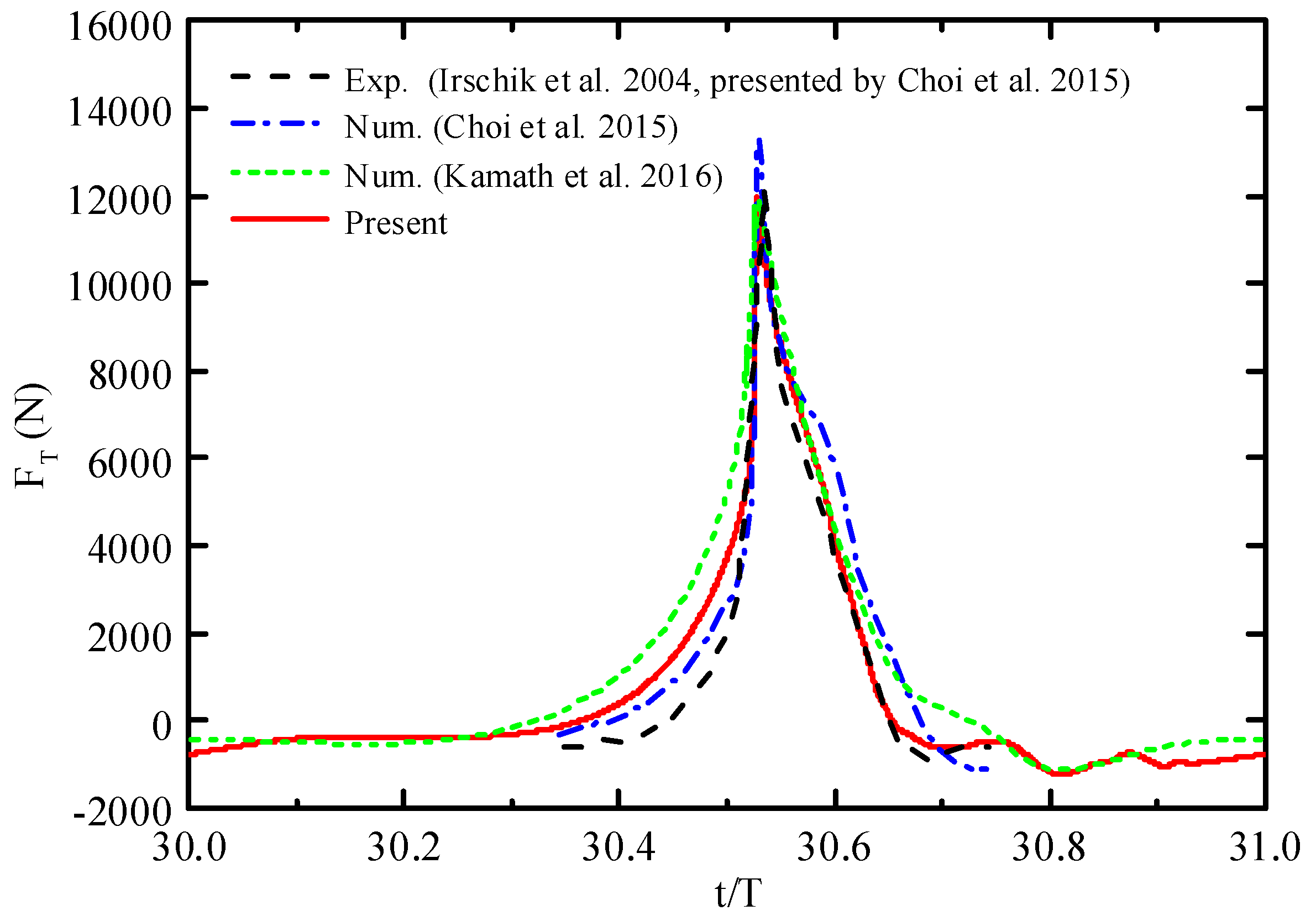
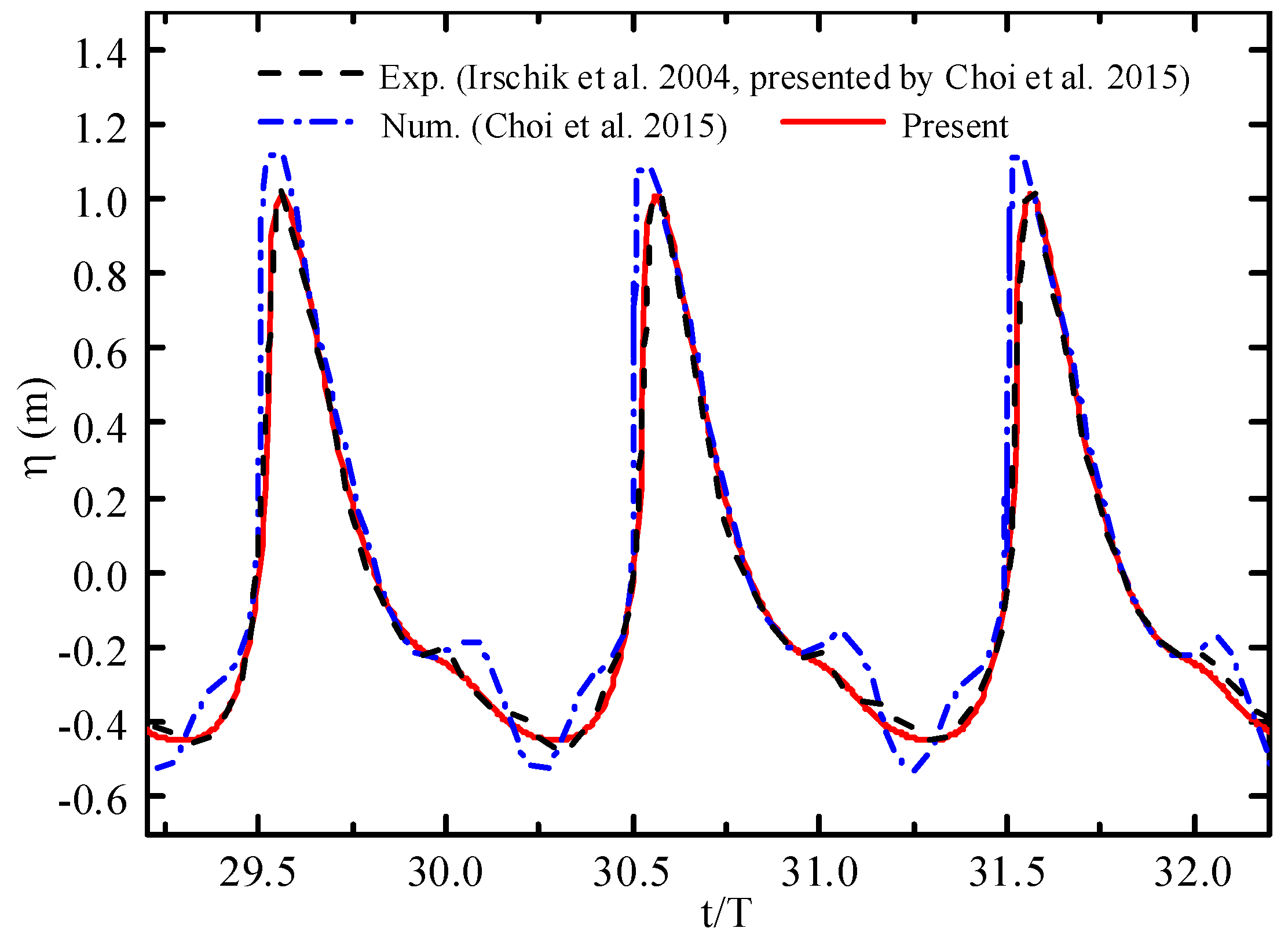
4.1.1. Comparisons of the Present Numerically Simulated Results with the Published Data for a Vertical Cylinder
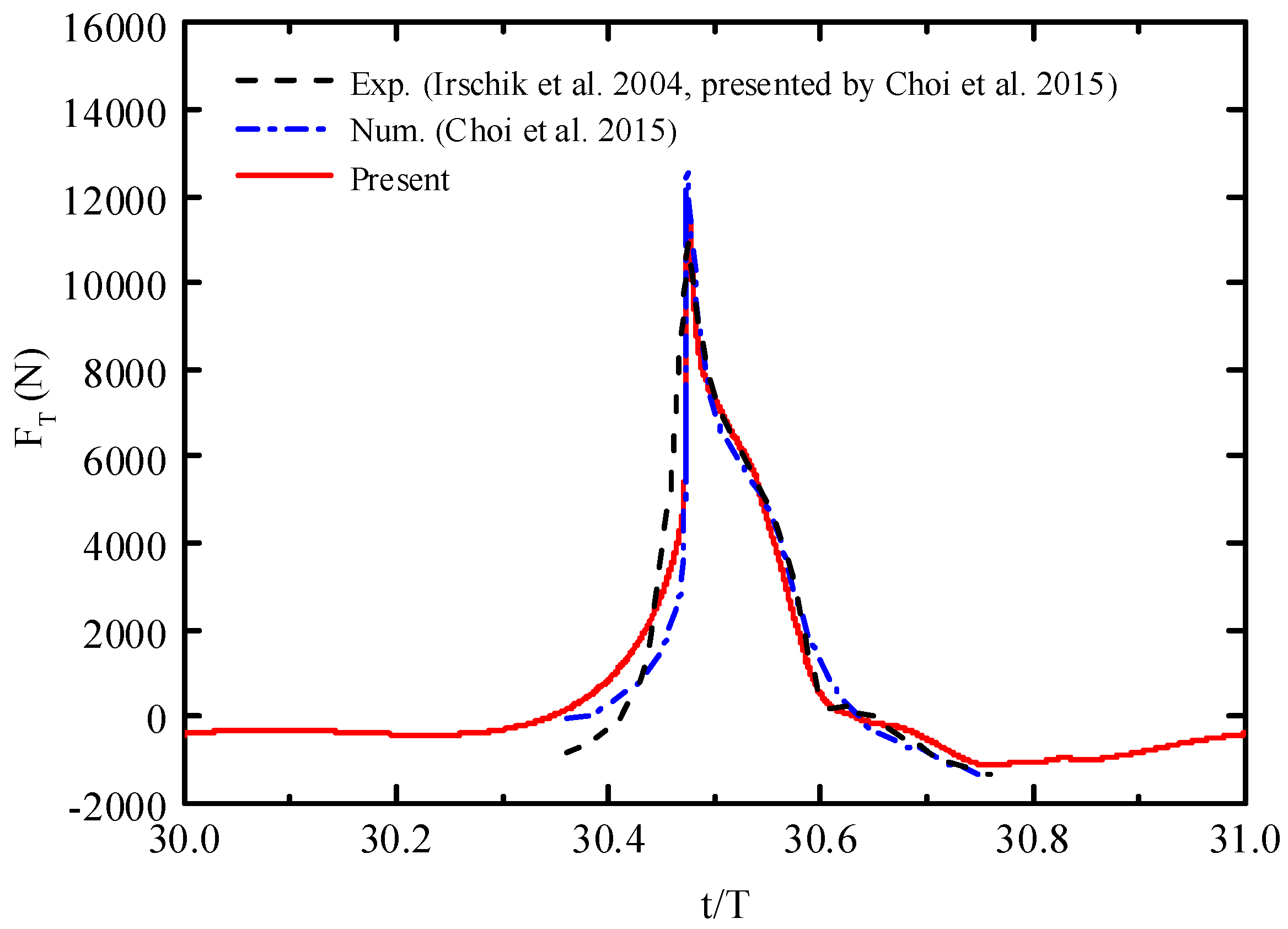
4.1.2. Comparisons of the Present Numerically Simulated Results with the Published Data for an Inclined Cylinder
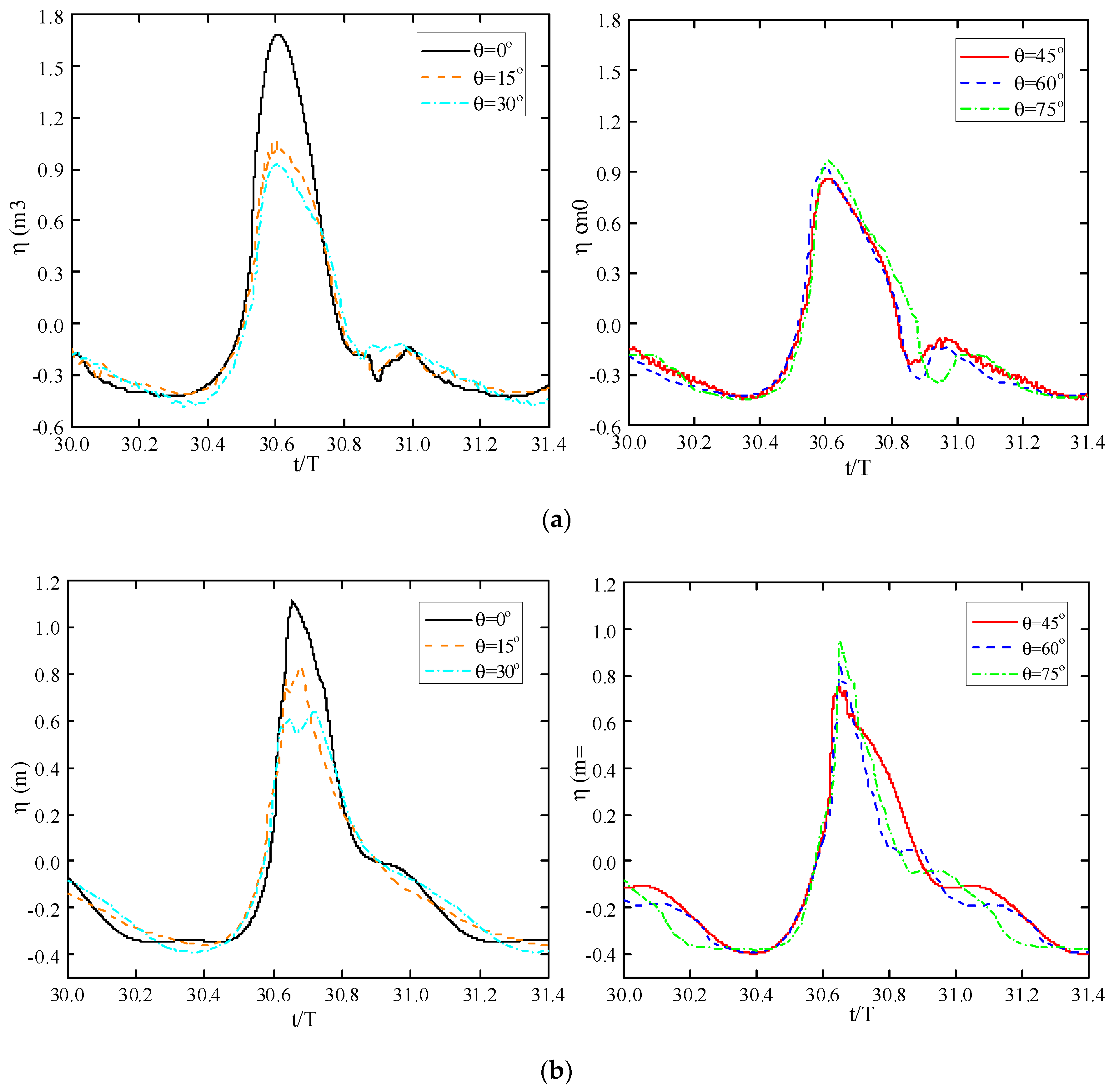
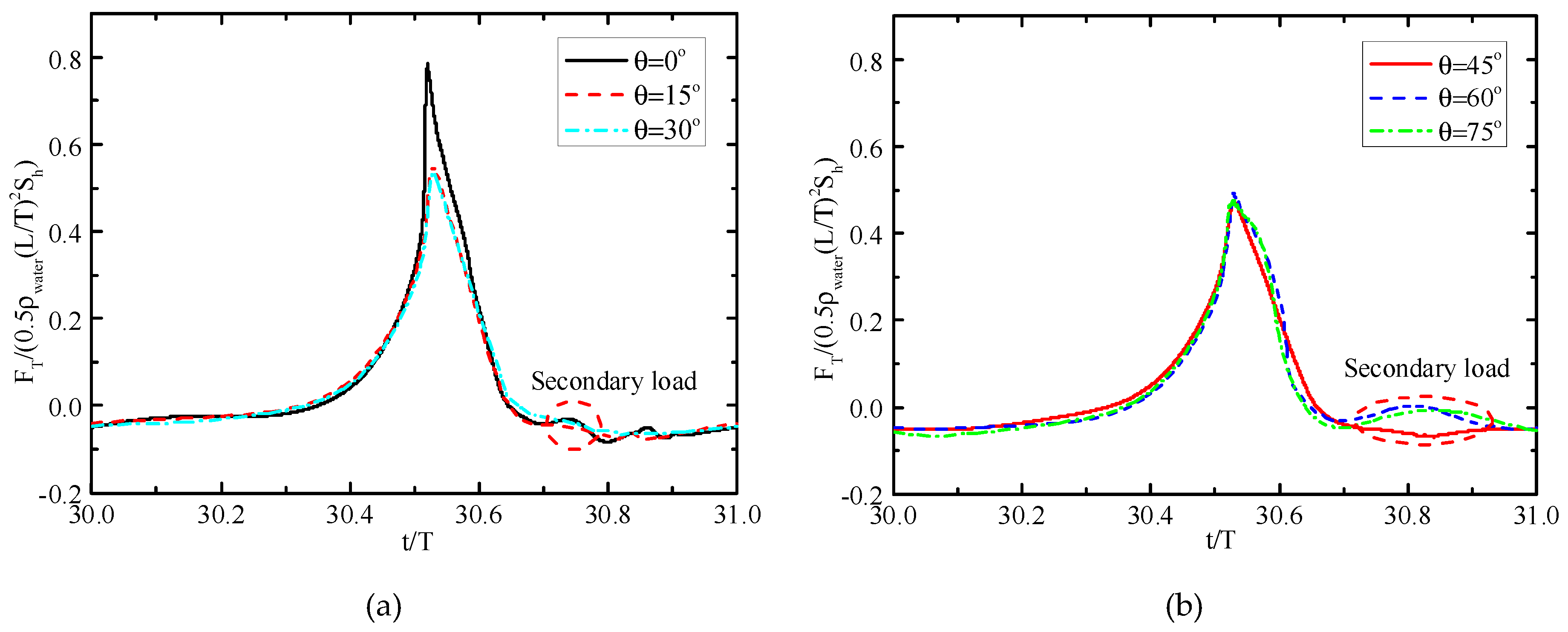
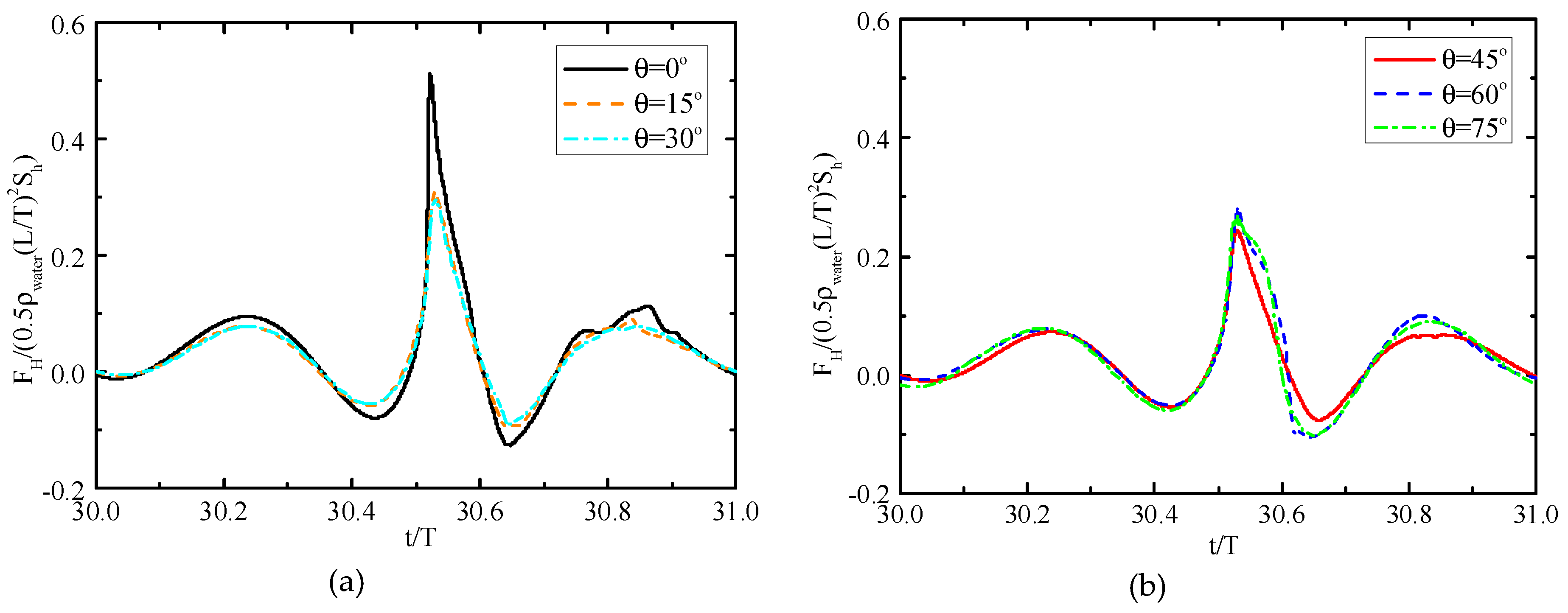
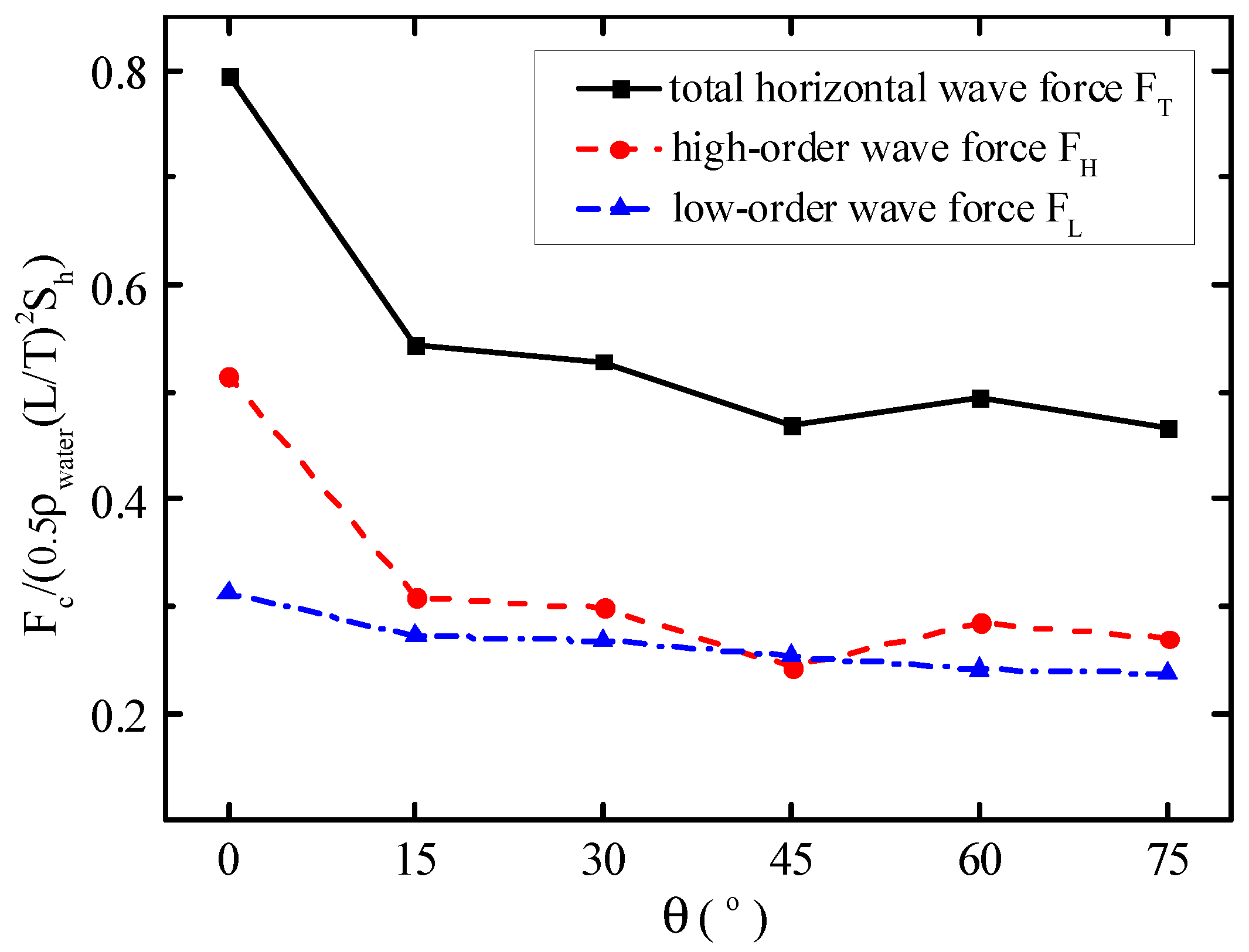
4.2. Characteristics of the Free Surface Elevations and the Breaking Wave Forces on the Standing Cylinder with Different Transverse Inclined Angles
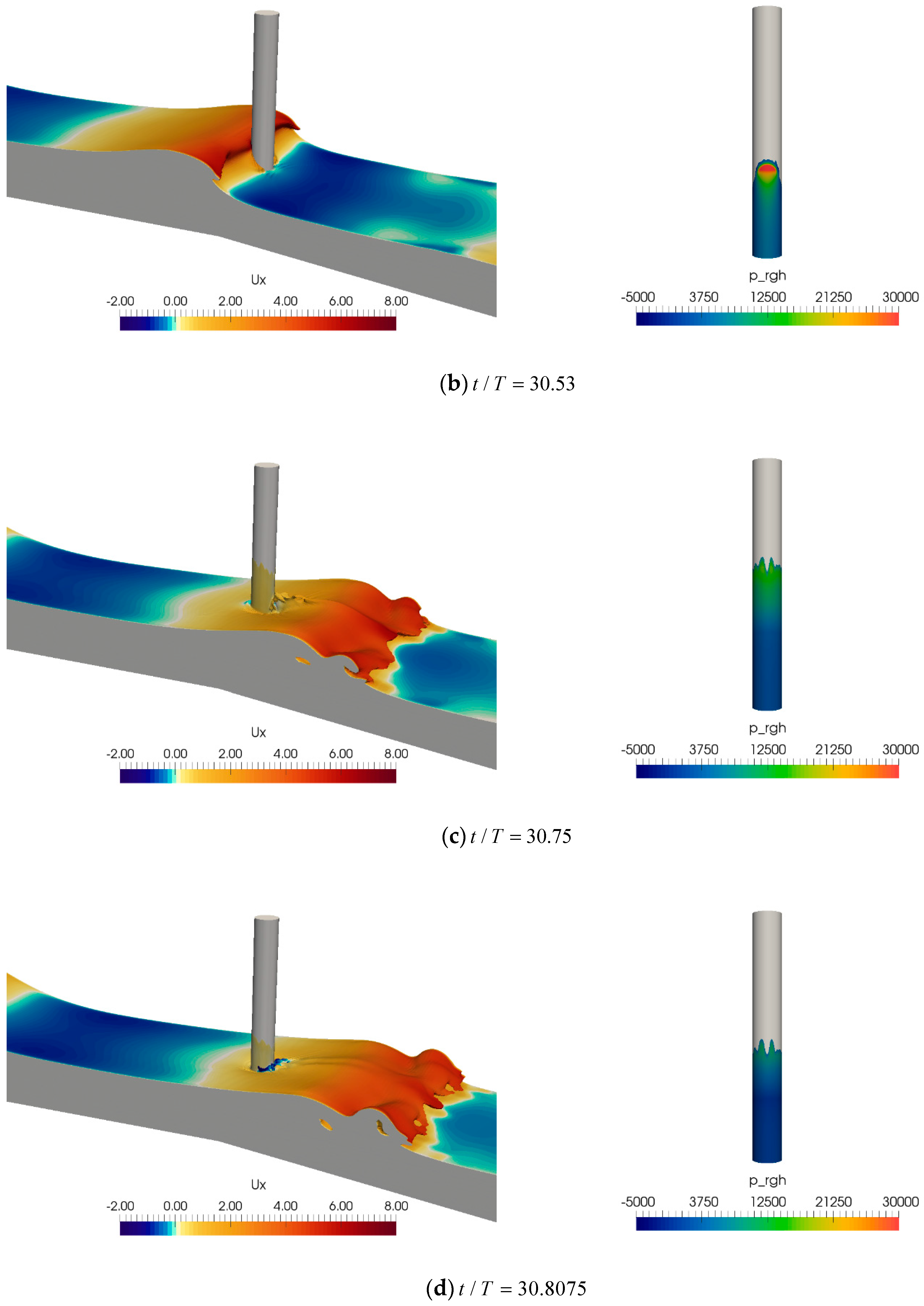
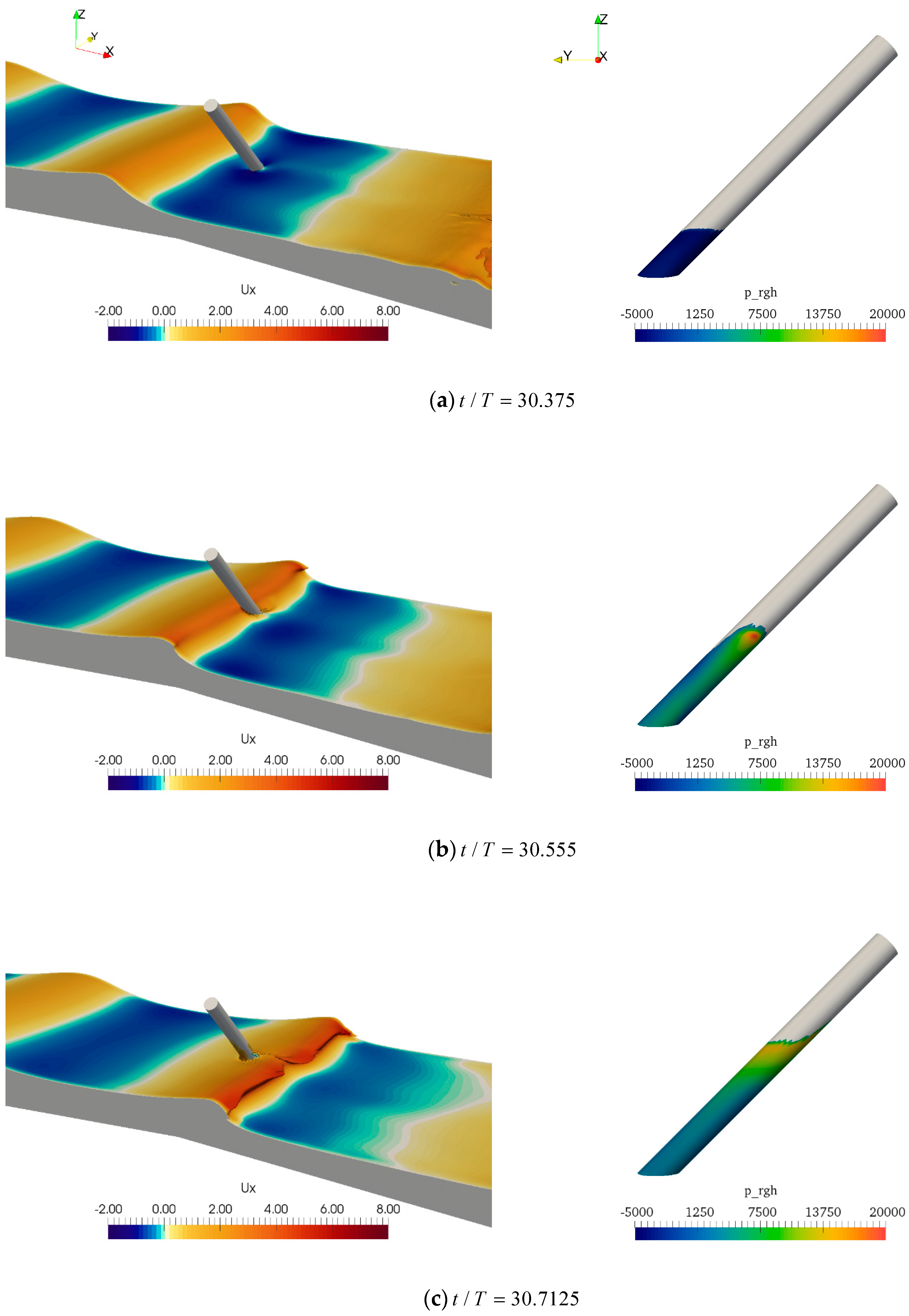
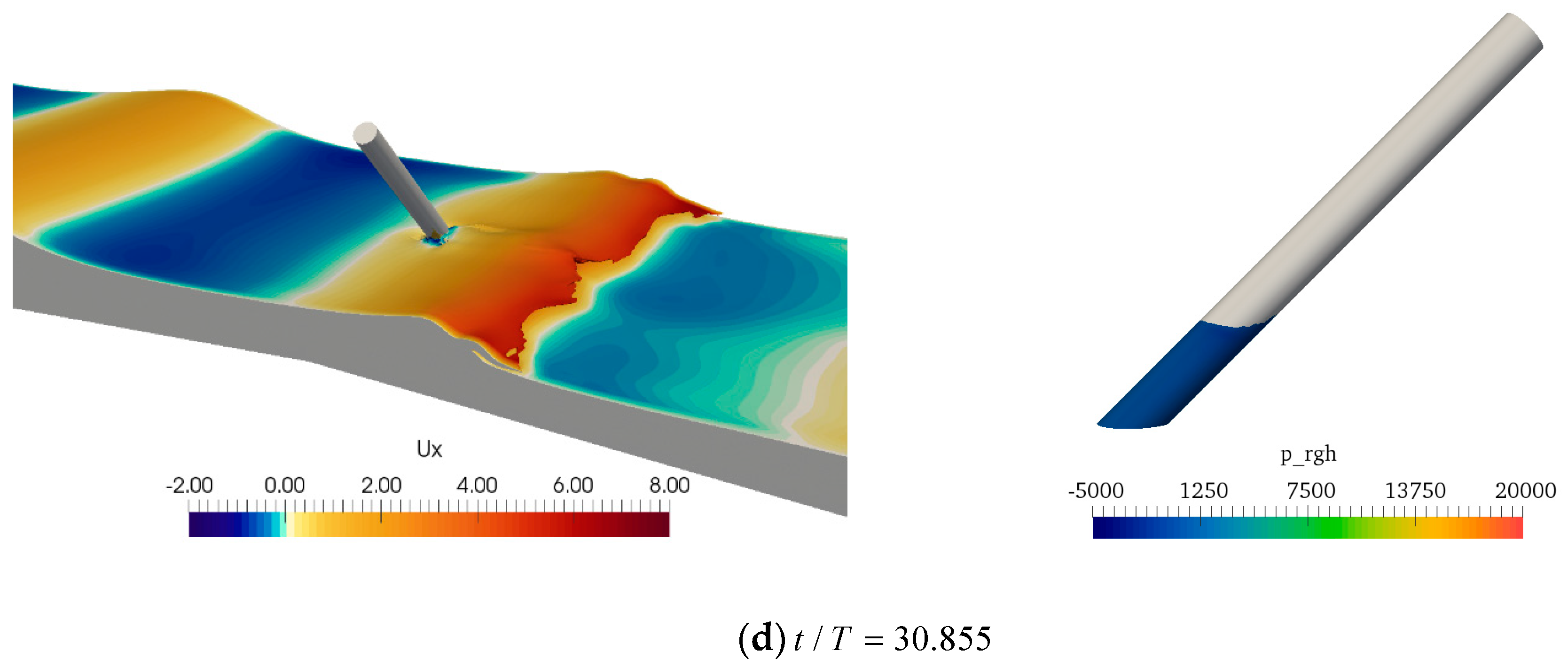
4.3. The Processes of Breaking Waves past the Cylinder
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Apelt, C.; Piorewicz, J. Interference effects on breaking wave forces on rows of vertical cylinders. In Proceedings of the First Australasian Port, Harbour & Offshore Engineering Conference 1986, Sydney, Australia, 29 September–2 October 1986; p. 191. [Google Scholar]
- Wienke, J.; Sparboom, U.; Oumeraci, H. Breaking wave impact on a slender cylinder. Coast. Eng. 2000, 2001, 1787–1798. [Google Scholar]
- Irschik, K.; Sparboom, U.; Oumeraci, H. Breaking wave loads on a slender pile in shallow water. Coast. Eng. 2005, 4, 568–580. [Google Scholar]
- Arntsen, Ø.; Ros Collados, X.; Tørum, A. Impact forces on a vertical pile from plunging breaking waves. Coast. Struct. 2013, 2, 533–544. [Google Scholar]
- Christensen, E.D.; Bredmose, H.; Hansen, E.A. Extreme wave forces and wave run-up on offshore wind turbine foundations. In Proceedings of the Copenhagen Offshore Wind, Copenhagen, Denmark, 26–28 October 2005; pp. 1–10. [Google Scholar]
- Shao, S. Simulation of breaking wave by SPH method coupled with k-ε model. J. Hydraul. Res. 2006, 44, 338–349. [Google Scholar] [CrossRef]
- Chow, A.D.; Rogers, B.D.; Lind, S.J.; Stansby, P.K. Numerical wave basin using incompressible smoothed particle hydrodynamics (ISPH) on a single GPU with vertical cylinder test cases. Comput. Fluids 2019, 179, 543–562. [Google Scholar] [CrossRef]
- Bredmose, H.; Jacobsen, N.G. Breaking wave impacts on offshore wind turbine foundations: Focused wave groups and CFD. In Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; pp. 397–404. [Google Scholar]
- Xiao, H.; Huang, W. Three-dimensional numerical modeling of solitary wave breaking and force on a cylinder pile in a coastal surf zone. J. Eng. Mech. 2014, 141, A4014001. [Google Scholar] [CrossRef]
- Choi, S.-J.; Lee, K.-H.; Gudmestad, O.T. The effect of dynamic amplification due to a structure׳ s vibration on breaking wave impact. Ocean Eng. 2015, 96, 8–20. [Google Scholar] [CrossRef]
- Kamath, A.; Chella, M.A.; Bihs, H.; Arntsen, Ø.A. Breaking wave interaction with a vertical cylinder and the effect of breaker location. Ocean Eng. 2016, 128, 105–115. [Google Scholar] [CrossRef]
- Chella, M.A.; Bihs, H.; Myrhaug, D.; Muskulus, M. Breaking solitary waves and breaking wave forces on a vertically mounted slender cylinder over an impermeable sloping seabed. J. Ocean Eng. Mar. Energy 2017, 3, 1–19. [Google Scholar]
- Jose, J.; Choi, S.-J. Estimation of slamming coefficients on local members of offshore wind turbine foundation (jacket type) under plunging breaker. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 624–640. [Google Scholar] [CrossRef]
- Liu, S.; Jose, J.; Ong, M.C.; Gudmestad, O.T. Characteristics of higher-harmonic breaking wave forces and secondary load cycles on a single vertical circular cylinder at different Froude numbers. Mar. Struct. 2019, 64, 54–77. [Google Scholar] [CrossRef]
- Liu, S.; Ong, M.C.; Obhrai, C. Numerical Simulations of Breaking Waves and Steep Waves Past a Vertical Cylinder at Different Keulegan–Carpenter Numbers. J. Offshore Mech. Arctic Eng. 2019, 141. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Brown, S.; Greaves, D.; Magar, V.; Conley, D. Evaluation of turbulence closure models under spilling and plunging breakers in the surf zone. Coast. Eng. 2016, 114, 177–193. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Mayer, S.; Garapon, A.; Sørensen, L.S. A fractional step method for unsteady free-surface flow with applications to non-linear wave dynamics. Int. J. Numer. Methods Fluids 1998, 28, 293–315. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoam®. Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Openfoam User Guide. Available online: https://cfd.direct/openfoam/user-guide/ (accessed on 2 March 2017).
- Stansberg, C. Comparing ringing loads from experiments with cylinders of different diameters—an empirical study. In Proceedings of the BOSS ‘97 Conference, Delft, The Netherlands, 1 July 1997. [Google Scholar]




| Case | Transverse Inclined Angle θ (°) |
|---|---|
| A | 0 |
| B | 15 |
| C | 30 |
| D | 45 |
| E | 60 |
| F | 75 |
| Mesh | Near the Cylinder (m) Max(Δx, Δy, Δz) | At Wave Generator (m) Max(Δx, Δy, Δz) | Number of Total Grids |
|---|---|---|---|
| Coarse mesh | (0.12, 0.1, 0.08) | (0.15, 0.10, 0.08) | 5,791,152 |
| Medium mesh | (0.10, 0.06, 0.05) | (0.12, 0.08, 0.05) | 7,787,600 |
| Fine mesh | (0.08, 0.06, 0.045) | (0.10, 0.08, 0.045) | 8,564,864 |
| Case | Total Horizontal Wave Forces FT (N) | Low-Order Wave Forces FL (N) | High-Order Wave Forces FH (N) |
|---|---|---|---|
| A | 11,952 | 4554 | 7458 |
| B | 8103 | 4058 | 4605 |
| C | 8793 | 4459 | 4962 |
| D | 9553 | 5161 | 4963 |
| E | 14228 | 6957 | 8200 |
| F | 25,965 | 13,213 | 15,016 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, S.; Liu, S.; Ong, M.C.; Sun, S.; Ren, H. Numerical Simulation of Breaking Wave Loading on Standing Circular Cylinders with Different Transverse Inclined Angles. Appl. Sci. 2020, 10, 1347. https://doi.org/10.3390/app10041347
Qu S, Liu S, Ong MC, Sun S, Ren H. Numerical Simulation of Breaking Wave Loading on Standing Circular Cylinders with Different Transverse Inclined Angles. Applied Sciences. 2020; 10(4):1347. https://doi.org/10.3390/app10041347
Chicago/Turabian StyleQu, Sen, Shengnan Liu, Muk Chen Ong, Shuzheng Sun, and Huilong Ren. 2020. "Numerical Simulation of Breaking Wave Loading on Standing Circular Cylinders with Different Transverse Inclined Angles" Applied Sciences 10, no. 4: 1347. https://doi.org/10.3390/app10041347
APA StyleQu, S., Liu, S., Ong, M. C., Sun, S., & Ren, H. (2020). Numerical Simulation of Breaking Wave Loading on Standing Circular Cylinders with Different Transverse Inclined Angles. Applied Sciences, 10(4), 1347. https://doi.org/10.3390/app10041347






