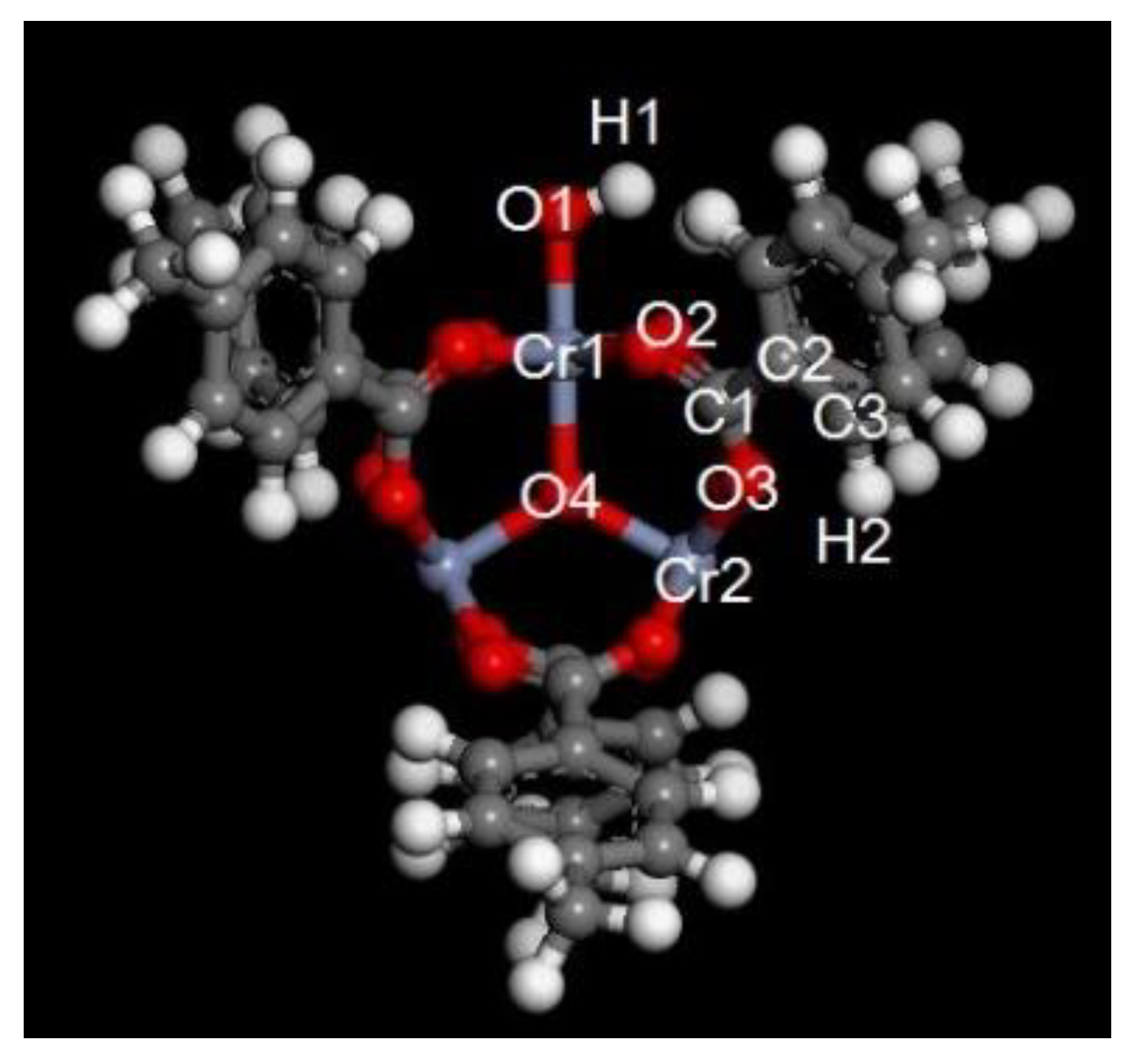
4.1. Adsorption Capacity and Adsorption Energy
To verify the reliability of simulation results, the simulated adsorption isotherms of CO
2 on MIL-101 (Cr) at 298 K were compared to experimental data [
33,
34]. As shown in
Figure 3, the simulated adsorption isotherms were slightly higher than the experimental values, and the deviation from the experimental value increased with the increase of pressure. These phenomena provide reasonable explanations: (1) the model of MIL-101 (Cr) that was used in the calculations contained no crystal defects and no impurities. However, actual MIL-101 (Cr) may have defects, and its pores may contain residual terephthalic acid, which can result in a relatively low CO
2 adsorption capacity; (2) when the pressure was low, the CO
2 adsorption capacity on MIL-101 (Cr) was also low, CO
2 molecules only occupied a small amount of space, and the residual impurities in the pores had little effect on the adsorption capacity. With the increase of pressure, the adsorption capacity also increased, and CO
2 molecules occupied more and more space in the pores. The existence of impurities hindered the adsorption of CO
2, resulting in the increase of deviation between the experimental and simulated values. In addition,
Table 5 shows the standard deviations of adsorption capacity. The value of the standard deviations of adsorption capacity are all less than 0.2, which indicated that the results could be repeated and the MC method could be applied to this system. Therefore, this simulation method, which is based on an MC simulation in a grand canonical ensemble, was utilized for further study, and the simulation results were considered to be accurate and reliable.
When calculating the adsorption isotherm, the adsorption energy reflecting the strength of the interaction between an adsorbent and an adsorbate can also be obtained. In this process, the adsorption energy was not constant. As summarized in
Table 5, the absolute value of the adsorption energy decreased, as the pressure increased, indicating that the interaction between the adsorbent and the adsorbate decreased as the pressure and adsorption capacity increased.
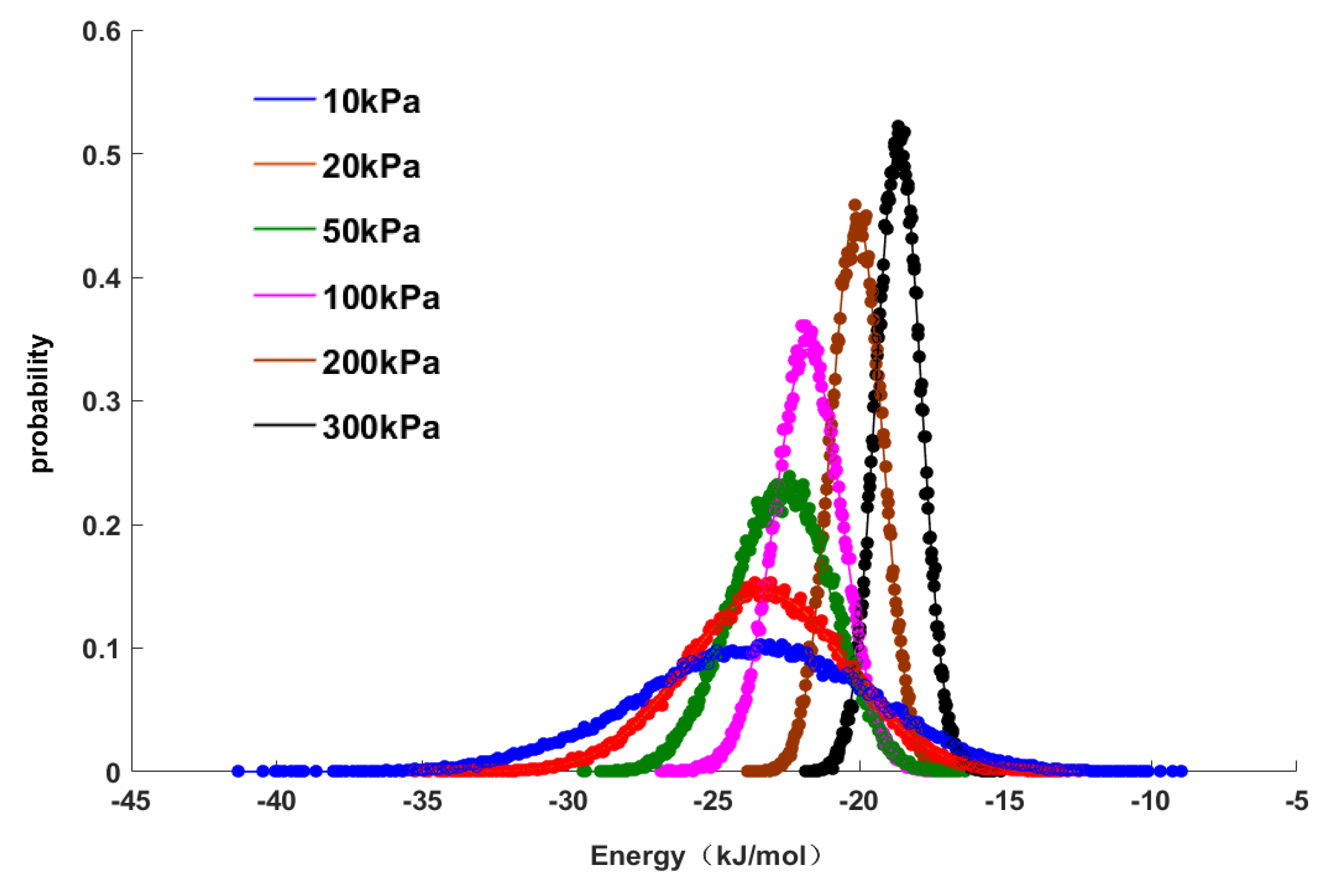
Figure 4 shows the characteristics and distributions of the adsorption energy. The data points in
Figure 4 represent the distribution points of the adsorption energy characteristics determined by GCMC molecular simulations, and the curve represents the curve fitted by a normal distribution model in the mathematical software MATLAB to correlate all data points. It can be seen in
Figure 4 that the normal distribution model had a good regression effect for the data points. Under different pressures, the values of the distributions of adsorption energy were different, but they all obeyed a normal distribution. The purpose of this study is to explore the relationship between adsorption energy and pressure, so the average value of the adsorption energy was used in subsequent work and is shown as the peak value of the normal distribution (
Figure 4). As the pressure increased, the peak value of the normal distribution shifted to the right, and the distribution area of adsorption energy narrowed, that is, the absolute average value of adsorption energy decreased. This result indicated that the adsorption was gradually weakened, which was also consistent with the change in adsorption energy shown in
Table 5. From the above results, it can be seen that the average adsorption energy was correlated with the adsorption pressure, that is, there was a linear relationship between them that can be expressed as follows:
where
E is the average adsorption energy,
P is the adsorption pressure, and
a and
c are the coefficients of the linear relationship between the adsorption energy and the adsorption pressure.
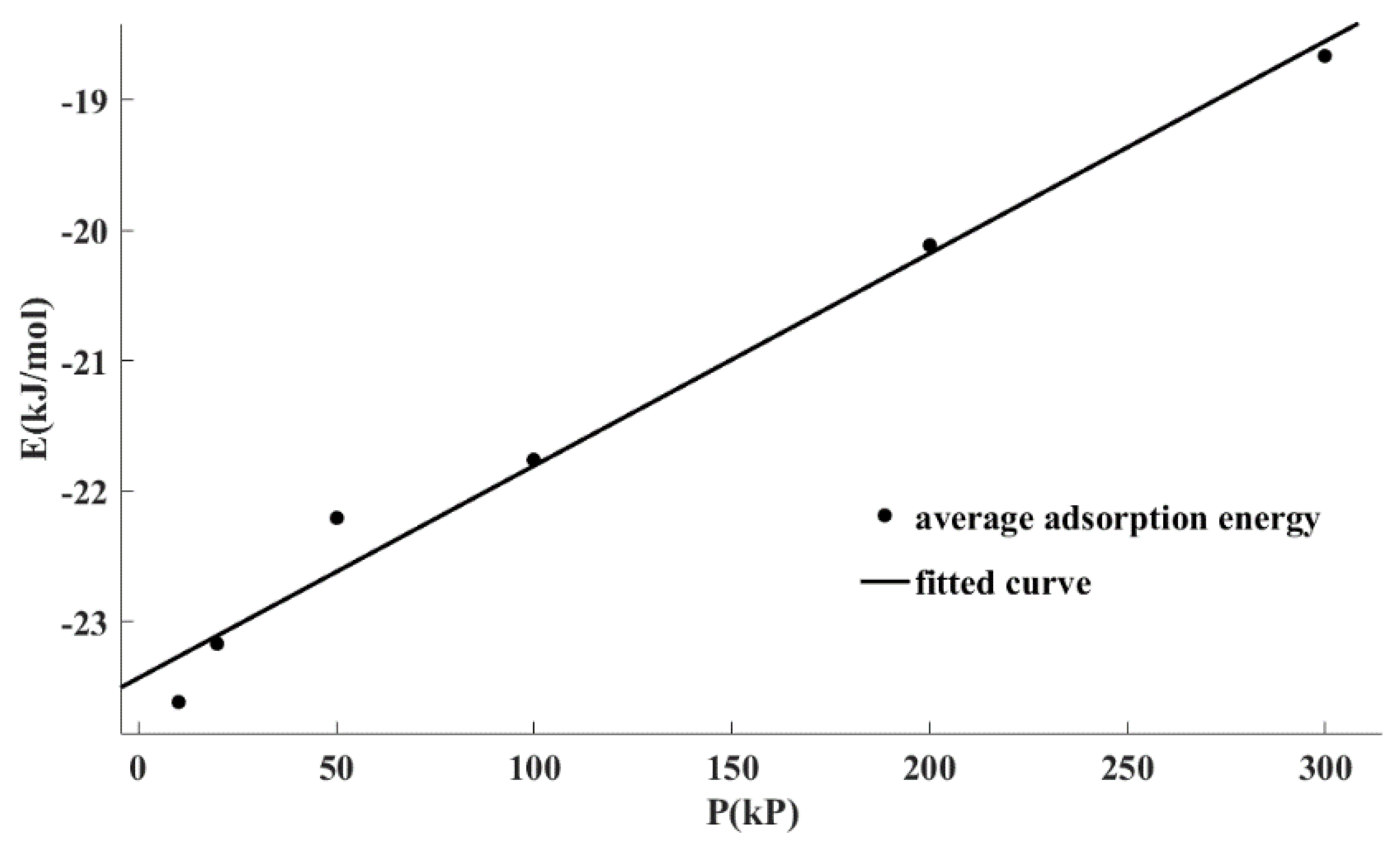
Figure 5 shows the fitting correlation curve of the average adsorption energy data points under different pressures using Equation (3). It can be seen that Equation (3) can well describe the relationship between the adsorption energy and pressure. It also can be seen from
Table 6 that the determination coefficient (R
2) for linear regression was greater than 0.98 and the residual sum of squared estimate of errors (SSE) was only 0.12. In conclusion, there was a linear relationship between the adsorption energy and the adsorption pressure, which can be written as Equation (3).
4.3. Regression of Adsorption Equilibrium Data with the DSL Model and the M-DSL Model
The DSL model and the M-DSL model were used to regress the adsorption equilibrium data by the nonlinear regression method, and the corresponding model parameters were obtained. The nonlinear regression was realized by the lsqnonlin function in MATLAB, and we used the Levenberg–Marquardt algorithm. The results were calculated with Equation (9), which was written as:
where
i is the number of experimental data points,
N is the total number of experimental data points,
qi,exp is the experimental value, and
qi,pre is the regression value. The lsqnonlin function in MATLAB is based on the nonlinear least squares method. In the process of regression using this method, the selection of an initial value is very important, different initial values may obtain different results. The specific operation process is as follows: (1) an appropriate initial value is selected according to experience of regression calculation; (2) the results of the first regression are taken as the initial values of regression; and (3) regression is carried out, until the obtained model parameter value no longer changes. After the operation process is completed, the R
2 of the model reaches the maximum, and the SSE has the minimum value, and the results are the final model parameter values. Therefore, using this method to regress the same system could get the same results, which showed that the results had good repeatability, and the model parameters obtained by this method were considered to be accurate and reasonable.
The accuracy of the regression was evaluated by the square sum of the error between the original experimental data and the fitting data, that is, the SSE, which was shown in Equation (10):
where
i is the number of experimental data points,
N is the total number of experimental data points,
yi,exp is the experimental value, and
yi, pre is the regression value. The closer the SSE is to 0, the closer the predicted values of the model are to the experimental values, and the better the model describes the experimental data.
The square of the correlation coefficient (R
2) can also be used as an evaluation index of data fitting. It is defined as the ratio of the sum of squares of the fitting deviation to the sum of squares of the actual deviation and can be calculated with Equation (11):
where
i is the number of experimental data points,
N is the total number of experimental data points,
yi,exp is the experimental value,
yi,pre is the regression value, and ȳ is the average number of experimental values used to determine the adsorption capacity. R
2 ranges from 0 to 1. The smaller the value is, the worse the fit between the model and the data is; the closer the value is to 1, the better the fit of the model is. In this study, SSE and R
2 were combined in order to analyze the regression results.
We used the adsorption equilibrium data on C
2H
4-HHPAC, CO
2-MIL-101 (Cr), CH
4-BPL active carbon, and a CO
2-H-Mordenite molecular sieve [
31,
32], as determined by experiments, in the DSL model and the M-DSL model for the nonlinear regression. The reason why we selected these data is that they have a wide range of adsorption temperatures and pressures and are commonly used to test adsorption equilibrium models. In addition, the adsorbents used in these systems are commonly used in industry, among which BPL is cylindrical, H-Mordenite is spherical and HHPAC is powder. Therefore, the shapes of adsorbents selected in this study almost contained the shapes of adsorbents commonly used in industry. Similarly, the adsorbates in these systems contained common organic gases such as CH
4 and C
2H
4 and common inorganic gas CO
2. Therefore, it could be said that the adsorption systems studied in this paper were sufficiently comprehensive, and the conclusions could be applied to most systems in industry.
Supplementary Figure S1 compares the correlation curves of the DSL model and the M-DSL model for different systems.
Table 7 and
Table 8 show the corresponding parameter values that were obtained by the regression of the adsorption equilibrium data on each system by using the DSL and M-DSL models, respectively. As shown in
Figure S1, for the C
2H
4-HHPAC system, the DSL model was able to relate the entire adsorption isotherm, and the regression effects were quite different under different temperatures and pressures. From
Table 7 and
Table 8, when the temperature was 253.15, 273.15, and 293.15 K, the DSL model was able to correlate the adsorption equilibrium data, which verified the applicability of the DSL model in the normal temperature range. However, the M-DSL model can better describe the adsorption isotherms of the system at these temperatures. The value of R
2 was greater than 0.998, and the SSE value was less than 0.1. By calculating the change in the SSE, we can see that the regression accuracy of the data with the M-DSL model was approximately 30% higher than that with the DSL model. These results indicated that the M-DSL model inherited the advantages of the DSL model in the normal temperature range and had better applicability.
When the temperatures were 223.15 and 233.15 K, the adsorption pressure gradually increased close to the saturated vapor pressure of C2H4, and, during this time, the adsorption capacity increased rapidly. At the temperature of 313.15 K, the adsorption capacity decreased significantly. These results showed that the DSL model was unable to well correlate the adsorption equilibrium data on C2H4-HHPAC in the low-temperature range and the high-temperature range. Under these conditions, the R2 of the DSL model was only 0.98, and the SSE was greater than 0.8. However, the M-DSL model can accurately describe adsorption isotherms in the low-temperature range. The regression accuracy of the M-DSL model to the adsorption equilibrium data was improved by more than 50%, the R2 was greater than 0.995, and the SSE was less than 0.3. In addition, the M-DSL model had obvious advantages in the high-temperature range. When the temperature was 313.15 K, the correlation curve of the M-DSL model was smoother than that of the DSL model. The R2 of the M-DSL model increased to 0.999, the SSE decreased to 0.03, and the regression accuracy increased by 94%. We drew similar conclusions for the CH4-BPL activated carbon and CO2-H-Mordenite systems. The regression accuracies of the M-DSL model and the DSL model were 22% and 8%, respectively. In conclusion, in ranges, in which large changes in adsorption capacity occur, such as high-temperature or low-temperature ranges, the adsorption energy cannot be simply assumed to be constant. The M-DSL model, which takes into account the linear relationship between adsorption energy and adsorption pressure, has a wider application range than the DSL model. It is also able to correlate adsorption equilibrium data well in the low-temperature range, the high-temperature range, and a relatively high-pressure range, where the DSL model is inapplicable.
Regarding the MIL-101 (Cr)-CO2 system, because the pore structure of the adsorbent was more complex than that of carbon materials and molecular sieves, the regression effect of the DSL model was poor. The value of R2 was only 0.98, which cannot produce the expected effect. The regression effect of CO2-MIL-101 (Cr) was greatly improved when using the M-DSL model. The R2 value was 0.9999, which is close to its upper limit (1), and the SSE was also very small (almost 0). The accuracy of the regression was 98% higher than that of the original DSL model. This result showed that the M-DSL model better correlated the adsorption equilibrium data on systems with a complex structure. Considering the linear relationship between the adsorption energy and pressure in an adsorption system with a complex pore structure can greatly improve the accuracy of the DSL model and improve the universality of the DSL model.
4.4. Modification of the TDSL Model That Reflects Temperature Changes
In the model parameter regression, we found that the parameters that were obtained by the DSL model and the M-DSL model were quite different at different temperatures and that the adsorption energy, which was found to have a linear relationship with the pressure obtained by a GCMC simulation, can modify the DSL model at different temperatures and had a good effect. In order to further verify this conclusion, we chose the DSL model that reflects temperature changes (TDSL), which is used in the adsorption module of Aspenplus and has been used in previous research [
16,
17,
18], and attempted to improve its accuracy and universality. The TDSL model is a two-parameter adsorption equilibrium model that is based on the DSL model and takes temperature and pressure as variables together. It is also based on the three assumptions of the Langmuir model. With this model, the adsorption equilibrium data obtained at different temperatures in the same system can be correlated at the same time. The form of the TDSL model is shown in Equation (12):
where
P is the adsorption equilibrium pressure,
q is the adsorption capacity at the equilibrium pressure, R is the gas constant, T is the adsorption temperature,
k1,
k2,
k5, and
k6 are the coefficients of the linear relationship between the saturated adsorption capacity and temperature in the original DSL model,
k 3 and
k7 are the adsorption energies corresponding to different adsorption sites, and
k4 and
k8 are pre-exponential factors.
Based on the conclusion that adsorption energy has a linear relationship with pressure, the TDSL model can be modified to obtain the M-TDSL model by substituting Equation (5) into Equation (12). The form of the modified TDSL (M-TDSL) model is shown in Equation (13):
where
a1,
c1,
a2, and c
2 are coefficients of the linear relationship between the adsorption energy and the adsorption pressure. The TDSL model and the obtained M-TDSL model were used to correlate the adsorption equilibrium data of the above systems at different temperatures at the same time. The results are shown in
Table 9 and
Table 10.
Supplementary Figure S2 shows the correlation curves of the TDSL model and the M-TDSL model for different systems.
Table 9 and
Table 10 show the corresponding parameter values that were obtained by the regression of the adsorption equilibrium data on each system by using the TDSL and M-TDSL models, respectively. Overall, the TDSL model was able to correlate the adsorption equilibrium data on CO
2-HHPAC well. Its R
2 was greater than 0.99, and its SSE was in a reasonable range. From the physical meaning of the parameters, it can be seen that the values of
k3 and
k7 were the adsorption energies at the two adsorption sites, respectively, and the results also showed that the adsorption energies were −19.98 and −28.99 kJ·mol
−1, respectively, which are in the general range of physical adsorption energies. This indicated that the regression results were reliable and accurate and that the physical meanings of the corresponding parameters were clear and definite. The regression effect of the M-TDSL model on the adsorption equilibrium data was slightly improved as compared to that of the original model, and the accuracy of the regression was increased by 14%. For the CH
4-BPL and CO
2-H-Mordenite systems, the TDSL model had a poor correlation, which cannot produce the expected effect. In fact, the M-TDSL model was better than the TDSL model with respect to the fitting correlation effects of these systems. Its R
2 was greater than 0.99, its SSE was significantly smaller than that of the TDSL model, and the regression accuracies of the M-TDSL and TDSL were also improved by 23% and 31%, respectively, compared with that of the original TDSL model. In the M-TDSL model, the two adsorption energies were numerically equal to the values of (
c1 +
a1P) and (
c2 +
a2P), both of which were in the general range of physical adsorption energies. In conclusion, the average regression accuracy when using the M-TDSL model was 23% higher than that when using the original TDSL model. Therefore, the obtained M-TDSL model had higher precision and a wider application range than the TDSL model, and the model parameters also had clear physical significance.
In addition, the results also showed that our conclusion—adsorption energy has a linear relationship with pressure—has certain universality across different adsorption equilibrium models. This relationship provides a basis for modifying other forms of adsorption equilibrium models and can be further tested when modifying other adsorption equilibrium models.