Net-Net AutoML Selection of Artificial Neural Network Topology for Brain Connectome Prediction

Abstract

Brain Connectome Networks (BCNs) are defined by brain cortex regions (nodes) interacting with others by electrophysiological co-activation (edges). The experimental prediction of new interactions in BCNs represents a difficult task due to the large number of edges and the complex connectivity patterns. Fortunately, we can use another special type of networks to achieve this goal—Artificial Neural Networks (ANNs). Thus, ANNs could use node descriptors such as Shannon Entropies (Sh) to predict node connectivity for large datasets including complex systems such as BCN. However, the training of a high number of ANNs for BCNs is a time-consuming task. In this work, we propose the use of a method to automatically determine which ANN topology is more efficient for the BCN prediction. Since a network (ANN) is used to predict the connectivity in another network (BCN), this method was entitled Net-Net AutoML. The algorithm uses Sh descriptors for pairs of nodes in BCNs and for ANN predictors of BCNs. Therefore, it is able to predict the efficiency of new ANN topologies to predict BCNs. The current study used a set of 500,470 examples from 10 different ANNs to predict node connectivity in BCNs and 20 features. After testing five Machine Learning classifiers, the best classification model to predict the ability of an ANN to evaluate node interactions in BCNs was provided by Random Forest (mean test AUROC of 0.9991 ± 0.0001, 10-fold cross-validation). Net-Net AutoML algorithms based on entropy descriptors may become a useful tool in the design of automatic expert systems to select ANN topologies for complex biological systems. The scripts and dataset for this project are available in an open GitHub repository.

1. Introduction

Any system may be represented as a complex network of nodes connected by edges, which can be any property or node interaction (L_ij = connection between nodes i and j) [1,2,3,4,5,6,7]. The diversity of systems susceptible to be studied with complex networks is very high. An important example is the representation of the human brain. Brain Connectome Networks (BCNs) are defined by anatomical connections and/or functional co-activations (L_ij) between brain regions (large collections of neurons). BCNs are so large and it is impossible for a person to remember and rationalize all possible connections and assign/predict correct connections in different situations [8]. Machine Learning (ML) algorithms may be useful to create classifiers for the prediction of properties of complex biological systems [9,10,11,12].

The first step in this process requires the quantification of relevant structural information of the biological system. Shannon’s entropy, introduced by Claude E. Shannon in his 1948 seminar paper “A Mathematical Theory of Communication” [13] could be used to quantify the information related to network nodes or the entire network. In fact, Shannon entropy information indices have become one of the universal indices used to quantify information [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Related indices, called Shannon–Markov information-theoretic entropy measures (Sh_k) of order (k) have been used to codify structural information of complex biological systems in ML studies [31]. We can calculate 1D, 2D, or 3D Sh_k descriptors for chemical structure of drugs [32], DNA/protein sequences [33,34,35], RNA secondary structures [36], protein spatial structures [37], protein–protein complexes [38], and complex networks [31]. Riera-Fernandez et al. [31] published ML prediction models of a BCN using information measures.

Artificial Neural Networks (ANNs) are powerful bio-inspired predictors able to learn/infer large datasets. There are many examples of ANN applications used to build predictive models [39,40,41,42]. ANNs are also able to learn large datasets related to the connectivity (structure) of bio-systems and other complex networks [43]. In the second step, an ML classifier should be constructed to evaluate the ability of any ANN to predict BCN node connectivity. Thus, the best ANN topology could be selected for the optimal BCN prediction. For nonexperts in ML, this is a complex task. In this context, the Automated Machine Learning (AutoML) method can help automatically select ANN topologies for complex network connectivity prediction, in the development of practical ML applications by non-experts [44,45]. In order to obtain the current Net-Net AutoML classifier, we need to quantify the information about the BCN nodes and ANN topologies.

In our previous work, we have introduced the idea of the Net-Net AutoML methodology for Biological Ecosystem Networks (BENs) [46]. BENs are webs of biological species (nodes) that can establish trophic relationships (interactions/edges). Considering that the experimental confirmation of all possible interactions is difficult and generates a huge volume of information, computational prediction becomes an important goal. We used ANNs to predict BENs with inputs as node Sh_k descriptors from known ecosystems. The complex task of a priori selecting the best ANN topology for the BEN node connectivity prediction, Net-Net AutoML method was able to help us. Twelve types of classifiers have been tested as Net-Net models for BENs. The best model used 338,050 examples from 10 ANN topologies for node pairs in 69 BENs and it was obtained with a deep fully connected neural network (test AUROC (Area Under Receiver Operating Characteristic) of 0.935).

In the current work, we apply the same Net-Net AutoML methodology to predict the ability of ANNs to predict BCNs. The dataset is based on predictions of 10 different ANN topologies for 52,690 pairs of brain region co-activations in the BCN (reported in the CoCoMac experiment) [47]. Therefore, we propose Net-Net AutoML models for the selection of ANNs for the study of BCNs, with the subsequent reduction of time and computational resources for the design of new expert systems.

2. Materials and Methods

2.1. Brain Connectome Dataset

This dataset is represented by a version of the CoCoMac network with 383 hierarchically organized regions covering cortex, thalamus, and basal ganglia. It contains 6602 directed long-distance connections and encloses different subnetworks such as cortico-cortical, cortico-subcortical, and subcortico-subcortical fiber systems [47].

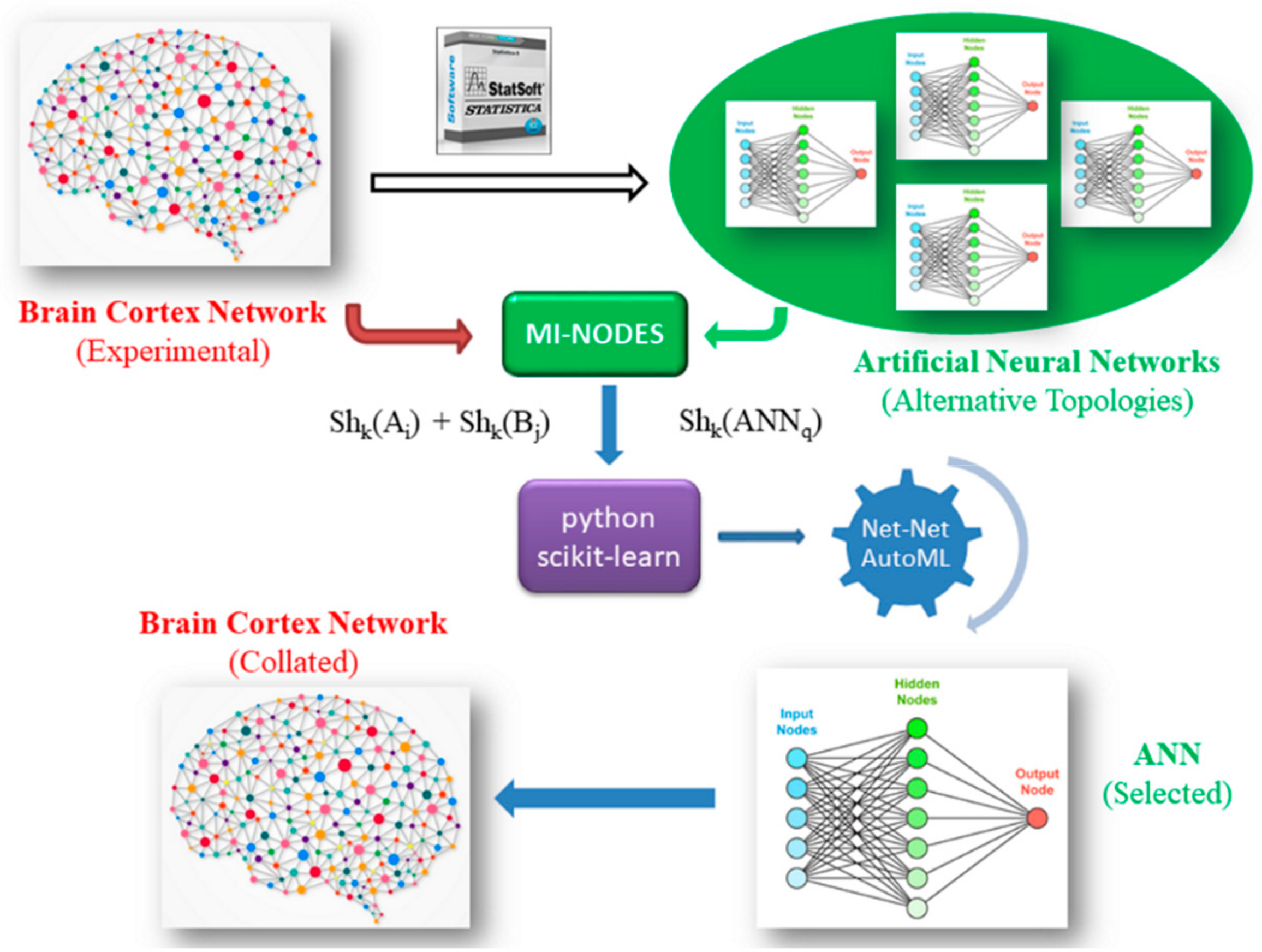
2.2. ANN Datasets and General Workflow

Figure 1 shows the workflow for the Net-Net AutoML method applied to BCNs. Our goal was to find a tool that would be able to predict BCN node connectivity (communications between brain regions). This task can be solved by training an ANN classifier using as dataset the previous known node connections (output) with any type of node descriptors (inputs). This solution involves intensive training of ANNs. Net-Net AutoML proposed a shortcut: The creation of another classifier with any ML method that can evaluate whether an ANN is able to predict with accuracy the node connectivity in BCNs, without any ANN training. In order to obtain this classifier, one should previously train different ANNs to predict BCN connectivity. Thus, this Net-Net AutoML classifier is a relationship between the ANN topologies trained for BCN prediction and the ability of these ANNs to provide good predictions.

In order to build ANNs for BCN prediction and Net-Net AutoML classifiers for the best ANN, both types of networks (BCNs and ANNs) should provide numerical descriptors. Therefore, for each BCN pair of nodes (brain regions), we knew the experimental connectivity (connected or not) and we could calculate the node descriptors such as Sh_k. This dataset was used to train different ANN topologies for the BCN prediction. In order to include information about ANNs to build a Net-Net AutoML classifier, we needed to include ANN information such as Sh_k of the entire ANN. Thus, we combined two types of descriptors in order to mix information about the BCN connectivity and ANN topology: We mixed Sh_k of BCN nodes (A_i–B_j pairs) with Sh_k for an ANN (S_hk(ANN)). We took into account the Shannon entropy from both types of networks but for different quantification: For nodes in BCN and for the entire network in ANN. The output of the Net-Net AutoML best classifier is the ability of S_hk(ANN) to predict connectivity between BCN nodes A_i and B_j.

We calculated the values of entropy Sh_k(A_i) and Sh_k(B_i) for a large number of pair of nodes in the BCN of the CoCoMac experiment [47]. The values Sh_k(A_i) are for the activated brain regions and the values Sh_k(B_i) for the co-activated brain regions. With these values we created a large dataset with output values L_ij = 1 (BCN links) or L_ij = 0 (absence of region co-activation), and input values Sh_k(A_i) and Sh_k(B_i). The dataset was used to train 10 different ANNs with the STATISTICA software [48]. This work is a proof-of-concept method, so at this point we applied the default behavior of STATISTICA that used an automatic algorithm to calculate the best ANN by means of feature selection and topology modification. Future studies should include more ANNs. In the second step, we created the final dataset to find a Net-Net AutoML classifier: We used the outputs of 10 previously trained ANNs to predict BCN connections for 52,690 pairs of BCN nodes (500,740 examples after pre-processing). Thus, the final dataset had the output as the ability of a specific ANN to predict the type of connection between BCN nodes, and the inputs as different entropies for BCN nodes and entire ANNs. In the next step, linear and nonlinear ML methods were tested to find the best Net-Net AutoML classifier to evaluate the ANN topology for BCN predictions.

Net-Net AutoML algorithm (Figure 1) has the following steps:

• (1) For each BCN:
• (1.1) Extract the connectivity matrix.
• (1.2) Add weights for the BCN connections (if present).
• (1.3) For each node A_i:
• (1.3.1) Calculate Shannon entropies for nodes using MI-NODES: Sh_k(A_i).
• (1.3.2) Create pairs of entropies for all the other nodes B: Sh_k(A_i)–Sh_k(B_j).
• (2) Build ANNs to predict BCN connectivity for nodes A_j–B_j:
• (2.1) For each ANN_q classifier:
• (2.1.1) Calculate network Shannon entropy: Sh_k(ANN).
• (3) Mix the BCN node descriptors with the ANN descriptors in the Net-Net AutoML dataset: Sh_k(A_i), Sh_k(B_j), Sh_k(ANN).
• (4) Split the dataset into training and testing subsets (n-folds).
• (5) Search for the best Net-Net AutoML classifier to evaluate whether a specific ANN can predict the BCN connectivity:
• (5.1) For each ML method:
• (5.1.1) Use a subset to train a classifier.
• (5.1.2) Evaluate the model with a testing subset, calculating AUROC accuracy.
• (6) Choose the best Net-Net AutoML classifier using AUROC metric.

2.3. Computational Methods

2.3.1. Markov–Shannon Entropy Centralities for Nodes

In the present work, we used the MI-NODES application [49]. In the first step, the connectivity matrix L for the BCN was obtained using the CoCoMac experiment [47]: n × n matrix with n vertices/nodes with values of 1 for the connected nodes and 0 for not connected ones. In the next step, a Markov matrix Π was derived from L by calculating the probabilities of vertices p_ij as matrix P. The power k (k = 1–5) of the probability matrix Π noted with (¹Π)^k was multiplied with a vector containing the initial probabilities (⁰p_j). The results are vectors with the absolute probabilities to reach nodes by walking throughout k nodes n_i (^kp_j). These vectors for each k value were used to calculate the entropy centrality (Sh_k) (see Equations (1) and (2)). For more mathematical details about combining the Markov chain theory and Shannon entropy see Reference [49] for MI-NODES desktop application and Reference [46] for the previous Net-Net AutoML application on Biological Ecosystem Networks. G represents any graph/network with j nodes. Thus, the input descriptors for BCN nodes or entire networks as ANNs are modified Shannon entropies that include the data about the path throughout k nodes based on probabilities.

$${}^{k}P={}^{0}P\times {\left({}^1\Pi \right)}^k=\left[{{}^{k}p}_1, {{}^{k}p}_2,\dots , {{}^{k}p}_j\right]$$

(1)

$${}_{\mathsf{k}}\left(\mathsf{G}\right)={{\displaystyle \sum }}_{\mathsf{j}\in \mathsf{G}}{\mathsf{S}\mathsf{h}}_{\mathsf{k}}\left(\mathsf{j}\right)=-{{\displaystyle \sum }}_{\mathsf{j}\in \mathsf{G}}{}^{\mathsf{k}}{\mathsf{p}}_{\mathsf{j}}{\mathbf{log}}^{\mathsf{k}}{\mathsf{p}}_{\mathsf{j}}$$

(2)

2.3.2. Net-Net AutoML Models

Once the values of the Markov–Shannon entropies were obtained for the BCN nodes and ANNs, twelve Machine Learning classifiers from scikit-learn (python) were tested to find the best Net-Net AutoML classifier able to determine the optimal ANN topology to predict BNCs (co-activations between brain regions):

• KNeighborsClassifier = KNN—k-nearest neighbors: A nonparametric classifier that assigns an unclassified sample to the same class as the nearest of k samples in the training set [50].
• LinearDiscriminantAnalysis = LDA—linear discriminant analysis [51]: A statistical supervised method that projects the input data to a lower dimension in order to maximize the scatter between classes versus the scatter within each class.
• GaussianNB = GBN—Gaussian Naive Bayes, a simple “probabilistic classifier” [52].
• SVC(kernel = ‘rbf’) = SVM_RBF—support-vector machines with nonlinear radial basis functions [53].
• LogisticRegression = LogR—Logistic regression [54] is a linear model that estimates the probability of a binary response using different factors.
• MLPClassifier = MLP—multilayer perceptron (artificial neural network) using 20 neurons in a hidden layer [55].
• DecisionTreeClassifier = DT—Decision Tree (DT) represents a set of decision rules inferred from the features as a tree of rules (the paths from root to leaf represent classification rules) [56].
• RandomForestClassifier = RF—Random Forest [57] aggregates several decision trees (parallel trees). Each tree is generated using a bootstrap sample randomly drawn from the original dataset.
• XGBClassifier = XGB—an optimized distributed gradient boosting library based on serial trees [58].
• GradientBoostingClassifier = GB—gradient boosting library [59].
• AdaBoostClassifier = Ada—is a meta-estimator that starts the fitting with a classifier based on the original dataset and then adds additional copies of the original classifier to the adjusted weights for the incorrectly classified instances [60].
• BaggingClassifier = Bagging—similar with Ada but the additional classifiers are based on subsets of the original dataset [61].

LDA could represent the simplest model equation. Let ^qS(L_ij) be the output variable of a Net-Net AutoML classifier used to score the ability of a given q ANN to correctly predict the link or brain region co-activation L_ij between two nodes/brain regions, A_i–B_j (L_ij = 1). Equation (3) describes the general formula for the LDA model. k means Sh_k codifies information for nodes placed at least at a topological distance k (from the reference node).

$${}^{q}S\left(L_{ij}\right)={\displaystyle \sum }_{k=1}^5{a}_{ki}·{Sh}_k\left(A_i\right)+{\displaystyle \sum }_{k=1}^5{b}_{ki}·{Sh}_k\left(B_j\right)+{\displaystyle \sum }_{k=1}^5{c}_{ki}·{Sh}_k\left(A_i-B_j\right)+{\displaystyle \sum }_{k=1}^5{d}_{ki}·{Sh}_k\left(\mathrm{ANN}\right)$$

(3)

Therefore, 20 features were obtained for the final dataset: Sh₁(A), Sh₁(B), Sh₁(A-B), Sh₁(ANN), Sh₂(A), Sh₂(B), Sh₂(A-B), Sh₂(ANN), Sh₃(A), Sh₃(B), Sh₃(A-B), Sh₃(ANN), Sh₄(A), Sh₄(B), Sh₄(A-B), Sh₄(ANN), Sh₅(A), Sh₅(B), Sh₅(A-B), and Sh₅(ANN). In order to avoid overfitting, a 10-fold cross-validation was performed. The performance of the models was measured using the Area Under the Receiver Operating Characteristics (AUROC) [62]. The scripts and dataset are available at an open repository in GitHub from one of the authors, Cristian R. Munteanu [63].

3. Results and Discussion

This study used the CoCoMac BCN dataset in order to build a computational tool that is able to select the best ANN topologies for BCN connectivity prediction. A recent study conducted by Van Essen et al. [64] has reviewed The Human Connectome Project, an amazing five-year enterprise devoted to characterize brain connectivity and function in healthy adult human beings. Lang [65] discussed the need for computational methods to disentangle the relationships between anatomical and functional connections. However, we have to deal with the estimation of data reliability and the presence of contradictory reports to develop new BCN models. Consequently, there is a need for computational tools for data mining using integrated large sets of partially redundant or inconsistent data in brain maps [66]. More often, data on BCN have to be systematically re-evaluated (collated) [67].

ANNs can discriminate between the correct connectivity for nodes (n_j) in complex systems (L_ij) from the incorrect and/or randomly distributed links. In order to be able to select the best ANN topology for BCN node connectivity prediction, we propose the Net-Net AutoML method. This tool represents a classifier based on Shannon entropies (Sh_k) of BCN pairs of nodes and ANN topology. In the first step, the BCN was turned into numerical input parameters (Sh_k(ANN) values) for all pairs of nodes to feed alternative ANN classifiers. Next, we trained different ANNs to predict the BCN connectivity. In the final step, we joined all the data (Sh_k values of BCNs and ANNs) of selected pre-trained cases to search the best AutoML classifier using twelve Machine Learning methods.

Table 1. Information indices Sh_k(ANN) of the ANNs used as inputs to find the best Net-Net Automated Machine Learning (AutoML) model.

ANN No.	ANN Profile (inputs:hidden layers EPs:outputs)	Shk(ANN)
		k = 0	k = 1	k = 2	k = 3	k = 4	k = 5
1	MLP15:15-14-1:1	0.05	0.054	0.054	0.054	0.054	0.054
2	MLP4:4-6-11-1:1	0.06	0.067	0.069	0.072	0.072	0.072
3	MLP5:5-8-1:1	0.078	0.088	0.097	0.097	0.097	0.097
4	MLP7:7-11-1:1	0.067	0.074	0.081	0.081	0.081	0.081
5	MLP9:9-12-1:1	0.061	0.067	0.071	0.071	0.071	0.071
6	MLP10:10-12-1:1	0.061	0.067	0.071	0.071	0.071	0.071
7	MLP4:4-8-11-1:1	0.057	0.059	0.06	0.061	0.061	0.061
8	MLP10:10-11-12-1:1	0.046	0.048	0.044	0.046	0.046	0.046
9	LNN14:14-1:1	0.056	0.146	0.146	0.146	0.146	0.146
10	LNN15:15-1:1	0.053	0.146	0.146	0.146	0.146	0.146

shows the values of Sh_k(ANN) for 10 different topologies. As previously explained, Sh_k(A_i) and Sh_k(B_i) were used as inputs and L_ij = 1 (BCN links) or L_ij = 0 as outputs. At that point, we used Multilayer Perceptron (MLP) and Liner Neural Network (LNN) as topologies with the default values provided by STATISTICA after its automatic algorithm based on feature selection and topology modification to improve them. In order to obtain a better generalization, the future studies should use more ANN topologies and/or different configurations thereof. We may need to use a High Performance Computing (HPC) service if we want to test a high number of ANNs for many complex systems [68,69,70,71,72,73].

Thus, our final classifier is based on entropies for different nodes of the BCN—Sh_k(A_i) and Sh_k(B_j)—and entropies of different ANNs topologies—Sh_k(ANN). The best Net-Net AutoML model determined the scores ^qS(L_ij) for a given ANN topology to predict the connectivity of BCN pair of nodes. This study presents a proof-of-concept model that fits very well, 500,740 outcomes obtained with 10 different ANNs.

Twelve ML classifiers were tested and the AUROC values were calculated using a 10-fold cross-validation (see

Table 2. AUROC for Net-Net AutoML classification models.

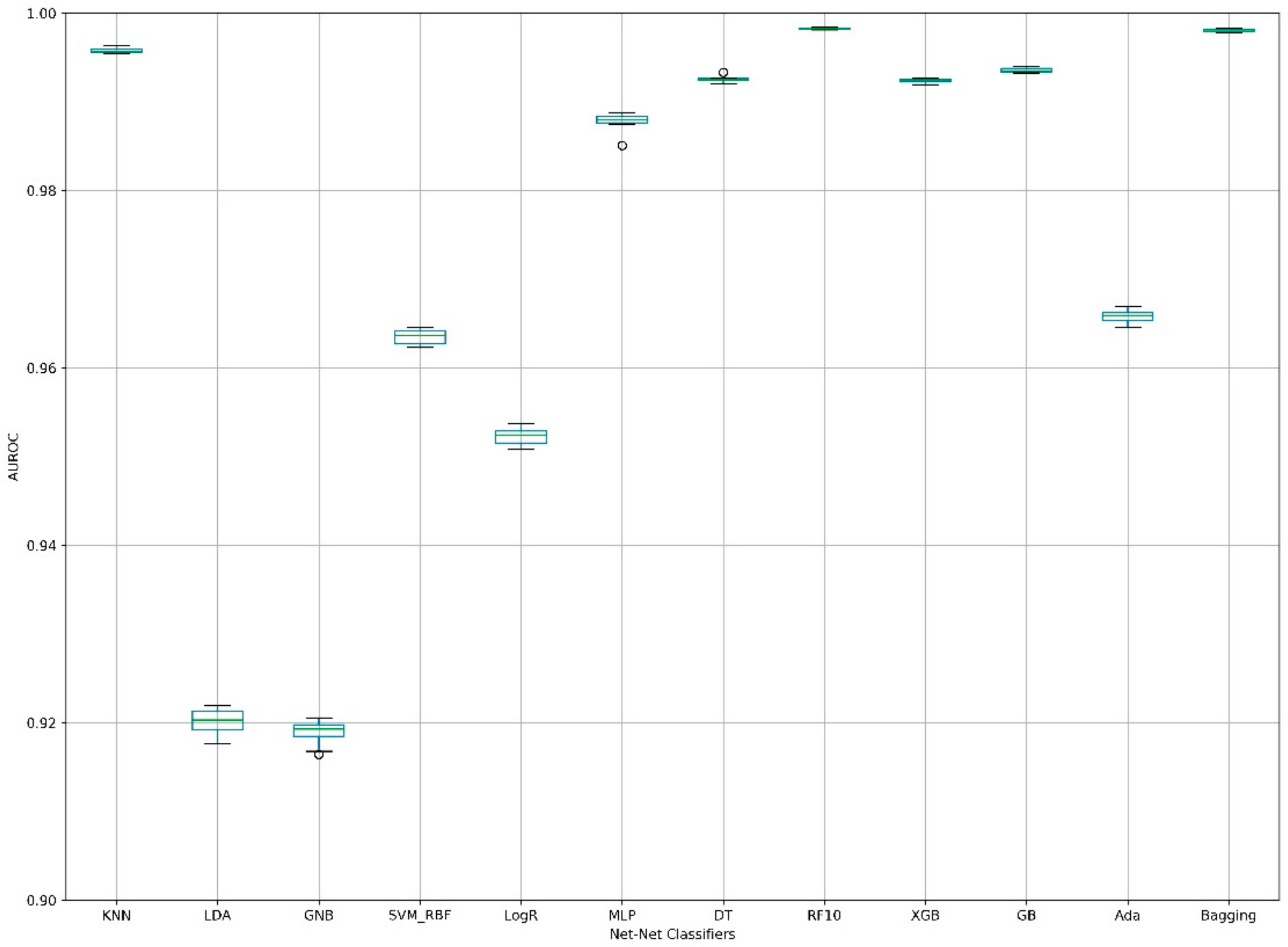
Fold	KNN	LDA	GNB	SVM_RBF	LogR	MLP	DT	RF10 1	XGB	GB	Ada	Bagging
1	0.9956	0.9195	0.9164	0.9625	0.9510	0.9876	0.9926	0.9983	0.9923	0.9937	0.9652	0.9983
2	0.9955	0.9217	0.9198	0.9642	0.9529	0.9879	0.9924	0.9982	0.9923	0.9933	0.9662	0.9980
3	0.9957	0.9203	0.9193	0.9637	0.9524	0.9880	0.9920	0.9983	0.9919	0.9934	0.9659	0.9980
4	0.9962	0.9207	0.9192	0.9637	0.9525	0.9851	0.9927	0.9981	0.9926	0.9938	0.9660	0.9982
5	0.9957	0.9204	0.9204	0.9645	0.9538	0.9882	0.9924	0.9983	0.9926	0.9934	0.9662	0.9980
6	0.9960	0.9192	0.9190	0.9633	0.9518	0.9885	0.9925	0.9982	0.9925	0.9936	0.9656	0.9979
7	0.9958	0.9219	0.9205	0.9645	0.9535	0.9888	0.9925	0.9983	0.9926	0.9940	0.9669	0.9982
8	0.9955	0.9215	0.9196	0.9642	0.9529	0.9884	0.9927	0.9981	0.9925	0.9940	0.9664	0.9978
9	0.9959	0.9176	0.9183	0.9625	0.9514	0.9875	0.9922	0.9982	0.9923	0.9933	0.9646	0.9979
10	0.9964	0.9182	0.9168	0.9623	0.9508	0.9879	0.9933	0.9984	0.9922	0.9933	0.9651	0.9982
Mean	0.9958	0.9201	0.9189	0.9635	0.9523	0.9878	0.9925	0.9983	0.9924	0.9936	0.9658	0.9980
SD	0.0003	0.0015	0.0014	0.0009	0.0010	0.0010	0.0003	0.0001	0.0002	0.0003	0.0007	0.0002

¹ RF10 = Random Forest with 10 trees.

). The best model was obtained with RF10 (RF based on 10 trees) and AUROC was 0.9983 ± 0.0001. Figure 2 shows the box-plot for the AUROC values of 12 ML methods (10-fold CV). The boxplot suggests that the AUROC values for all ML methods were stable within each fold. In addition, the difference between the RF and the other methods (box-plots are far from overlapping) proved to be statistically significant. All the Net-Net classifiers obtained good performance with an AUROC value greater than 0.90. An interesting result was provided by the simple KNN method with a mean AUROC value of 0.9958, still less than RF10 with a mean AUROC value of 0.9983. The linear methods (LDA and LogR) can provide models with a mean AUROC value > 0.92 and 0.95. The change to a tree-based method provided a better AUROC with values greater than 0.99, except for Ada. Bagging had a performance very similar to the RF classifier with a mean AUROC value of 0.9980.

In the next step, we performed a grid search for the RF number of trees: 1 tree (DT), and 2, 5, 10, 50, 100 trees (RF2, RF5, RF10, RF50, RF100). The results show that by using two trees with Random Forest, it is possible to increase the mean AUROC value from 0.9925 to 0.9944 (DT) (see

Table 3. AUROC for Net-Net AutoML classification models.

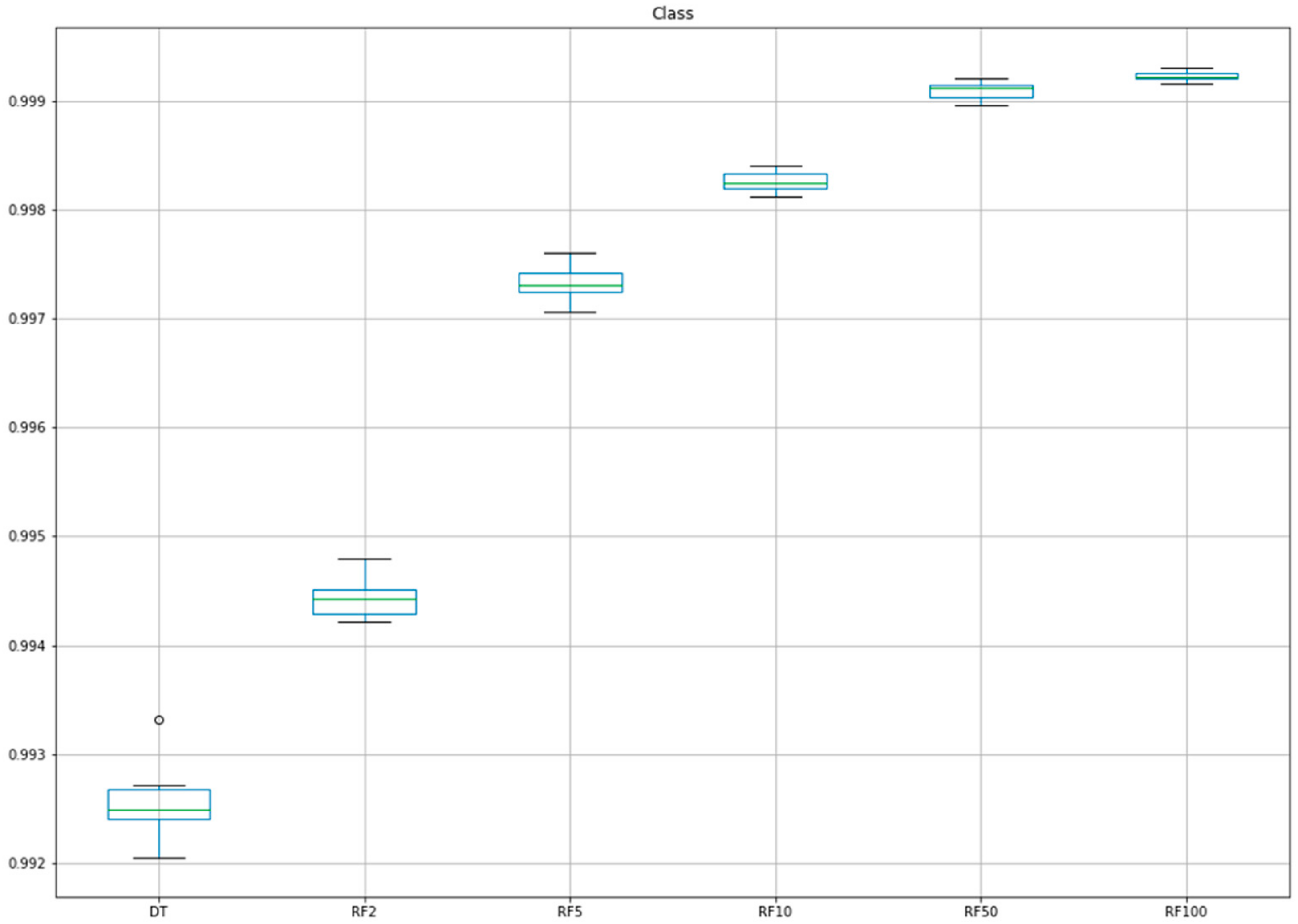
Fold	DT	RF2 1	RF5 2	RF10 3	RF50 4	RF100 5
1	0.9926	0.9948	0.9976	0.9983	0.9990	0.9992
2	0.9924	0.9944	0.9971	0.9982	0.9990	0.9992
3	0.9920	0.9943	0.9971	0.9983	0.9992	0.9993
4	0.9927	0.9945	0.9974	0.9981	0.9992	0.9993
5	0.9924	0.9942	0.9972	0.9983	0.9991	0.9993
6	0.9925	0.9945	0.9974	0.9982	0.9991	0.9992
7	0.9925	0.9944	0.9974	0.9983	0.9992	0.9992
8	0.9927	0.9943	0.9973	0.9981	0.9990	0.9992
9	0.9922	0.9942	0.9972	0.9982	0.9991	0.9992
10	0.9933	0.9948	0.9975	0.9984	0.9991	0.9992
Mean	0.9925	0.9944	0.9973	0.9983	0.9991	0.9992
SD	0.0003	0.0002	0.0002	0.0001	0.0001	0.0000

¹ RF with two trees; ² RF with five trees; ³ RF with 10 trees; ⁴ RF with 50 trees; ⁵ RF with 100 trees.

and Figure 3). By doubling the number of trees from 50 to 100, the difference between RF50 and RF100 for the mean AUROC value was just 0.0001. Therefore, we chose the best Net-Net AutoML model as RF50 with a mean AUROC value of 0.9991 (SD = 0.0001). The dataset, scripts, and results are available as an open GitHub repository [63].

Figure 4 shows the feature importance for the best Random Forest model based on 50 trees. We can observe that the entropies of the BCN nodes are the most important features followed by the ANN entropies. The differences between the BCN node entropies are less important for this RF classifier. The most important feature was the BCN node entropy containing information about the nodes placed at a minimum distance of 2—Sh₂(B).

4. Conclusions

This work confirms that Markov chains are useful to calculate Shannon entropy information indices Sh_k that quantify the connectivity patterns on both BCNs and ANNs. We demonstrated how to develop Net-Net AutoML models based on Sh_k values of both networks. The dataset contains 500,470 examples and 20 features. Twelve linear and non-linear Machine Learning classifiers were tested and the best classification model was provided by Random Forest (50 trees) with the mean test AUROC of 0.9991 ± 0.0001 (10-fold cross-validation). The Net-Net AutoML models are useful to determine the ANN topology, which is better to predict the connectivity in the BCN system. Consequently, we can use this methodology to predict the ANN topologies, with better performance before training them. This may lead to an optimization of computing resources. The scripts and dataset for this project are available in an open GitHub repository from one of the authors, Cristian R. Munteanu [63].