Sensor Fault Reconstruction based on Adaptive Sliding Mode Observer for Forklift Fault-Tolerant Control System
Abstract
1. Introduction
2. Forklift Model
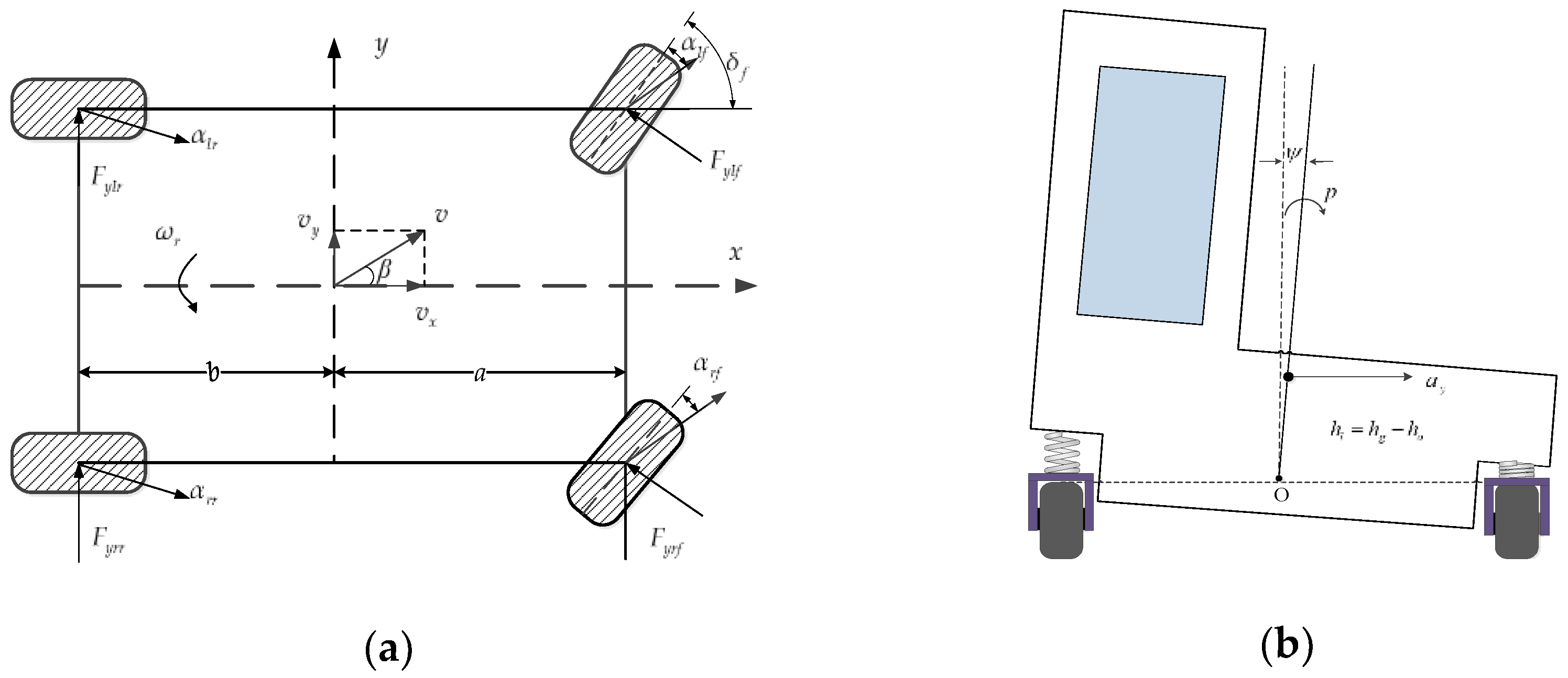
2.1. 3-DOF Forklift Model
2.2. Sensor Fault Model of a Forklift
3. Design of the Adaptive Sliding Mode Observer
- (1)
- (2) LMI:,
4. Design of the Sensor Fault Reconstruction
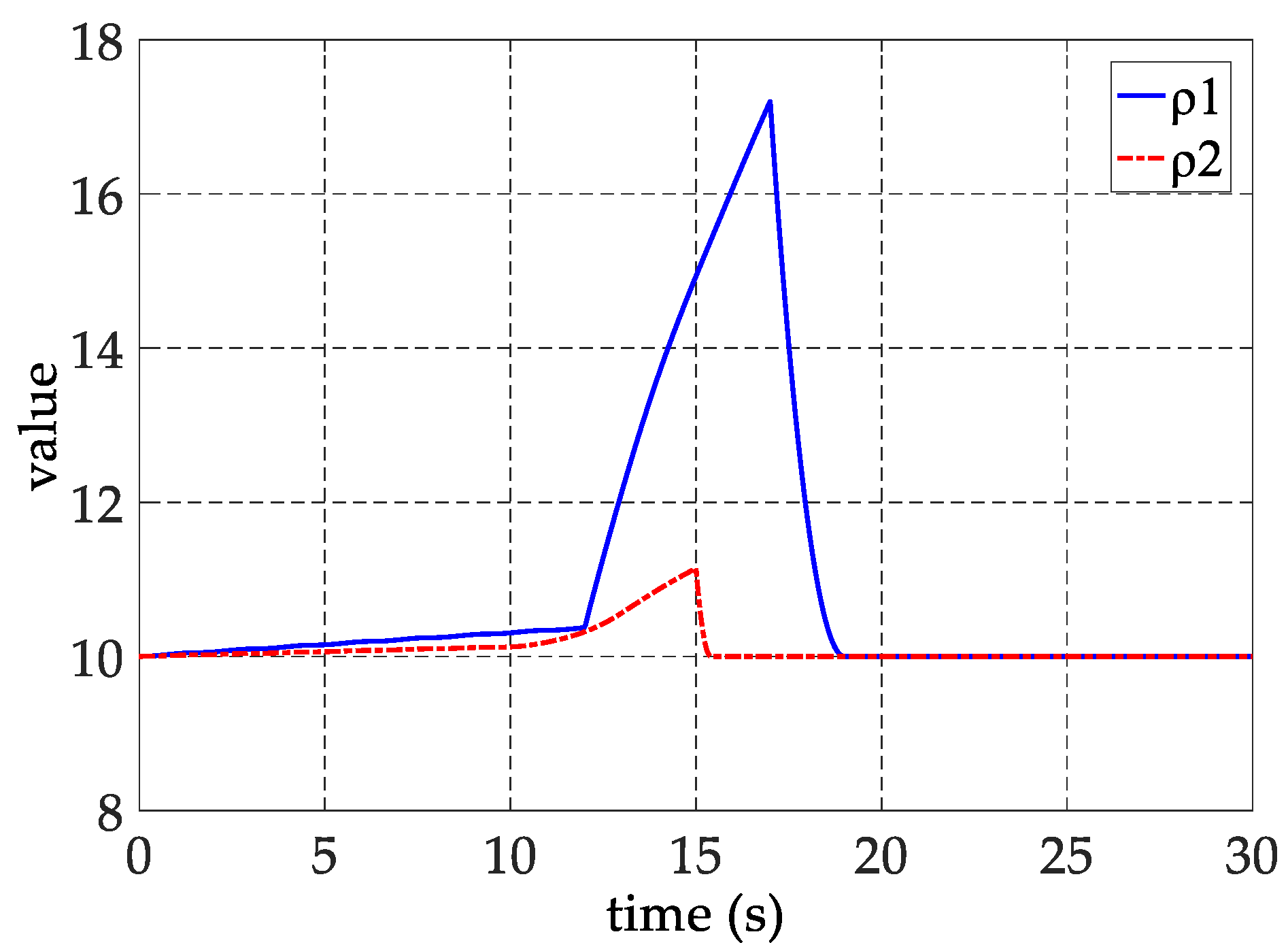
5. Improvement for Fault Reconstruction
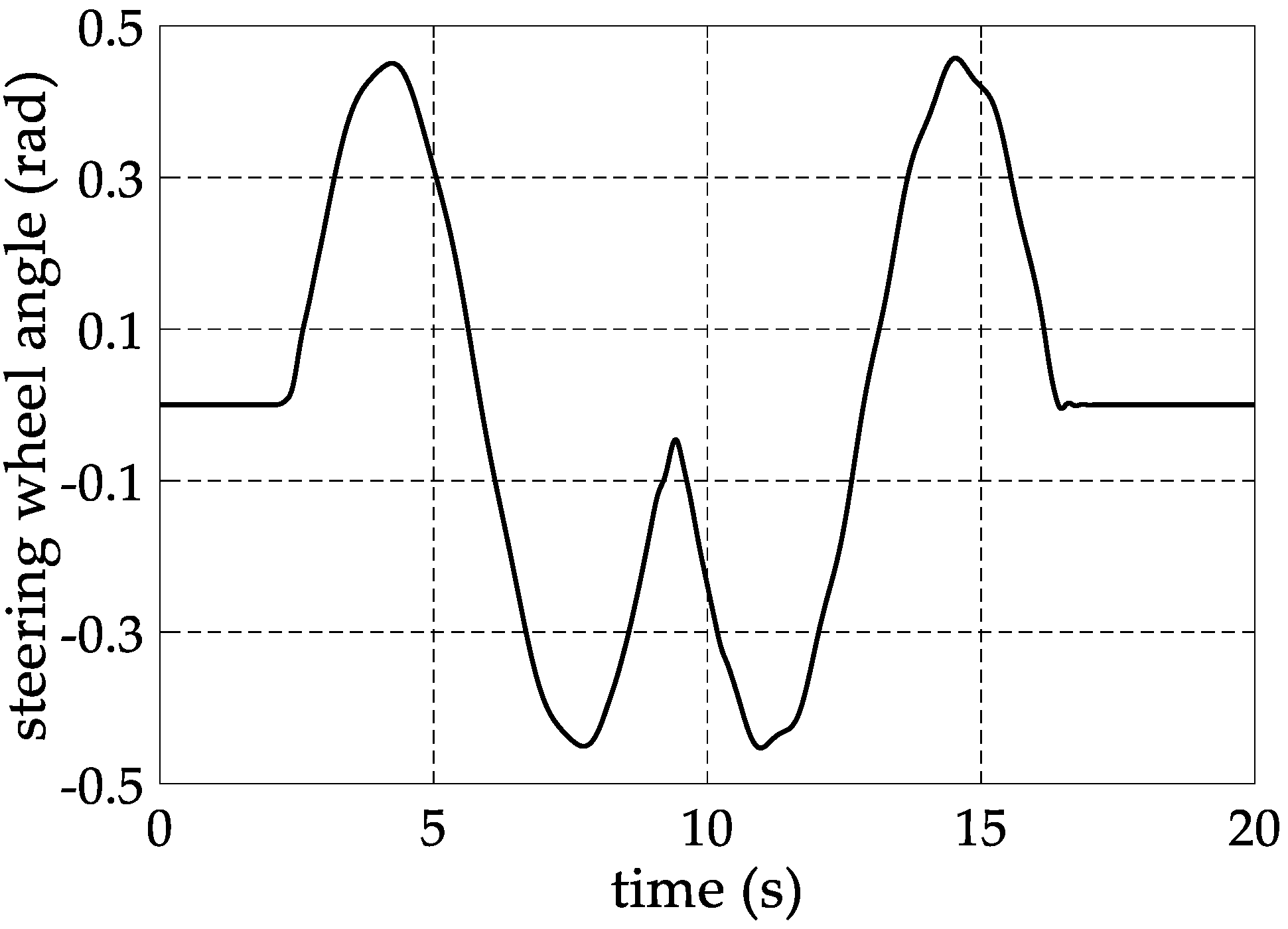
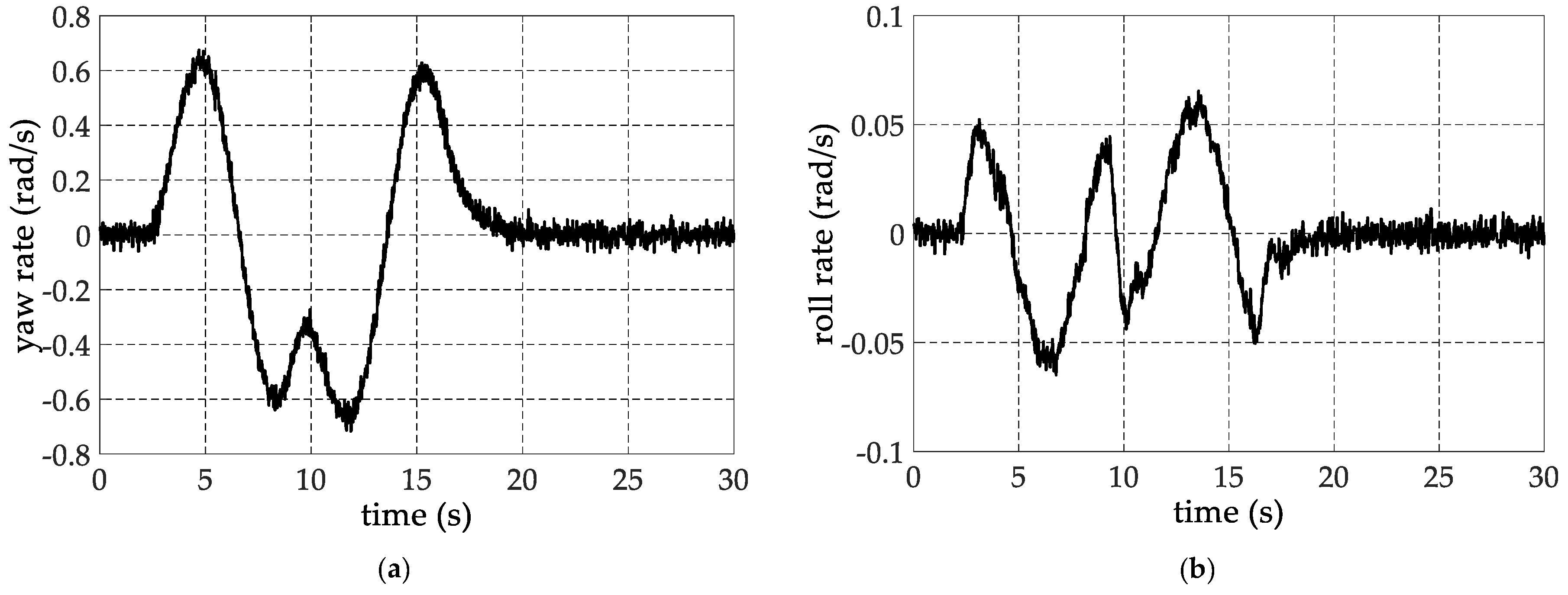
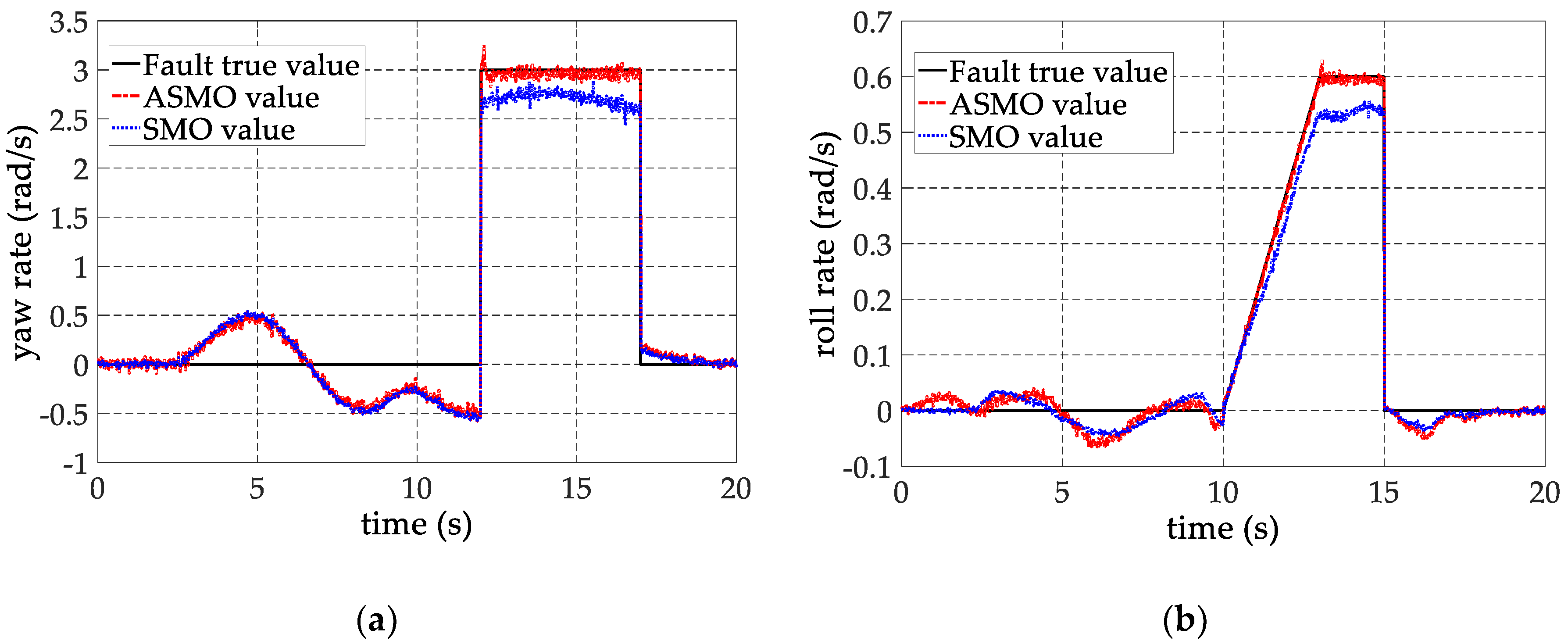
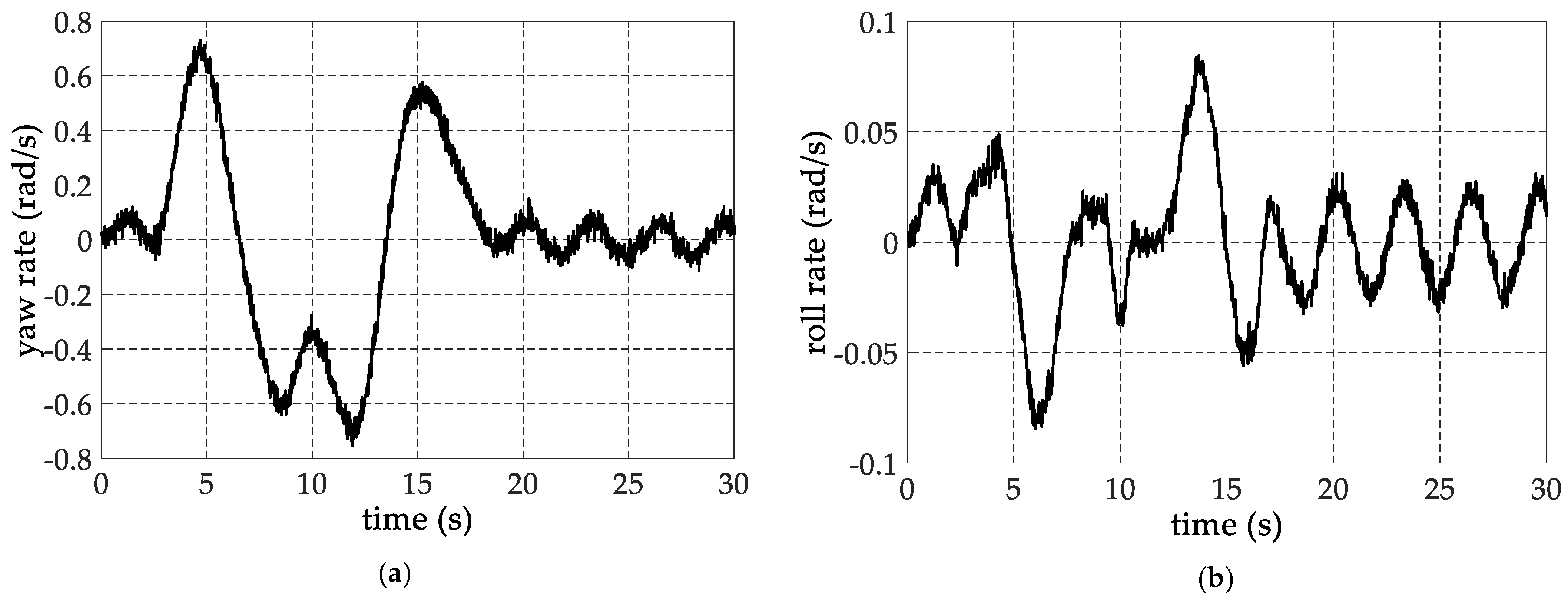
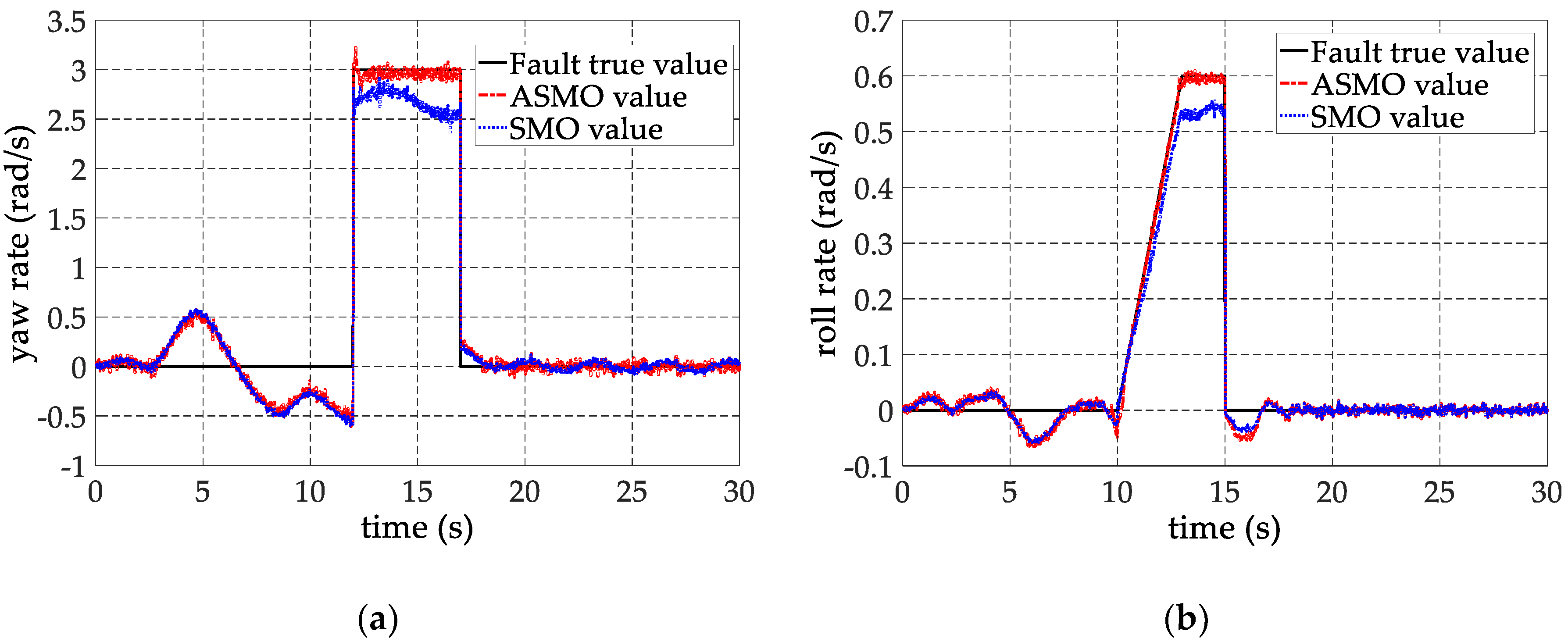
6. Experimental Verification
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, L.; Tseng, H.E. Robust Model-Based Fault Detection for a Roll Stability Control System. IEEE Trans. Control. Syst. Technol. 2007, 15, 519–528. [Google Scholar] [CrossRef]
- Boukhari, M.R.; Chaibet, A.; Boukhnifer, M.; Glaser, S. Proprioceptive Sensors’ Fault Tolerant Control Strategy for an Autonomous Vehicle. Sensors 2018, 18, 1893. [Google Scholar] [CrossRef]
- Zhao, W.; Qin, X.; Wang, C. Yaw and lateral stability control for four-wheel steer-by-wire system. IEEE/ASME Trans. Mechatron. 2018, 23, 2628–2637. [Google Scholar]
- Zhou, Y.; Liu, J.; Dexter, A.L. Estimation of an incipient fault using an adaptive neurofuzzy sliding-mode observer. Energy Build. 2014, 77, 256–269. [Google Scholar] [CrossRef]
- Boulaabi, I.; Sellami, A.; Ben Hmida, F. A robust sensor fault reconstruction based on a new sliding mode observer design method for uncertain delayed systems: A satellite system application. Control Eng. Appl. Inf. 2015, 17, 88–97. [Google Scholar]
- Cherni, H.; Boulaabi, I.; Sellami, A.; Ben Hmida, F. Robust actuator and sensor faults reconstruction based on new sliding mode observer for a class of output time-delay systems. IETE J. Res. 2016, 62, 812–821. [Google Scholar] [CrossRef]
- Ben Brahim, A.; Dhahri, S.; Ben Hmida, F.; Sellami, A. Simultaneous actuator and sensor faults reconstruction based on robust sliding mode observer for a class of nonlinear systems. Asian J. Control 2017, 19, 362–371. [Google Scholar] [CrossRef]
- Zhao, K.; Li, P.; Zhang, C.; Li, X.; He, J.; Lin, Y. Sliding mode observer-based current sensor fault reconstruction and unknown load disturbance estimation for PMSM driven system. Sensors 2017, 17, 2833. [Google Scholar] [CrossRef]
- Jia, Q.X.; Li, H.Y.; Zhang, Y.C.; Chen, X.Q. Robust observer-based sensor fault reconstruction for discrete-time systems via a descriptor system approach. Int. J. Control Autom. Syst. 2015, 13, 274–283. [Google Scholar] [CrossRef]
- Alaei, H.K.; Yazdizadeh, A. Robust output disturbance, actuator and sensor faults reconstruction using H∞ sliding mode descriptor observer for uncertain nonlinear boiler system. Int. J. Control Autom. Syst. 2018, 16, 1271–1281. [Google Scholar] [CrossRef]
- Abbaspour, A.; Aboutalebi, P.; Yen, K.K.; Sargolzaei, A. Neural adaptive observer-based sensor and actuator fault detection in nonlinear systems: Application in UAV. ISA Trans. 2017, 67, 317–329. [Google Scholar] [CrossRef]
- Djeziri, M.A.; Merzouki, R.; Bouamama, B.O.; Ouladsine, M. Fault diagnosis and fault-tolerant control of an electric vehicle overactuated. IEEE Trans. Veh. Technol. 2013, 62, 986–994. [Google Scholar] [CrossRef]
- Aboutalebi, P.; Abbaspour, A.; Forouzannezhad, P.; Sargolzaei, A. A novel sensor fault detection in an unmanned quadrotor based on adaptive neural observer. J. Intell. Robot. Syst. 2018, 90, 473–484. [Google Scholar] [CrossRef]
- Huang, C.; Naghdy, F.; Du, H. Observer-based fault-tolerant controller for uncertain steer-by-wire Systems using the delta operator. IEEE Trans. Mechatron. 2018, 23, 2587–2598. [Google Scholar] [CrossRef]
- Garramiola, F.; del Olmo, J.; Poza, J.; Madina, P.; Almandoz, G. Integral sensor fault detection and isolation for railway traction drive. Sensors 2018, 18, 1543. [Google Scholar] [CrossRef]
- Rkhissi-Kammoun, Y.; Ghommam, J.; Boukhnifer, M.; Mnif, F. Two current sensor fault detection and isolation schemes for induction motor drives using algebraic estimation approach. Math. Comput. Simulat. 2019, 157, 39–62. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, M.; Yao, F. Adaptive fault tolerant control and thruster fault reconstruction for autonomous underwater vehicle. Ocean Eng. 2018, 155, 10–23. [Google Scholar] [CrossRef]
- Simani, S.; Castaldi, P. Intelligent fault diagnosis techniques applied to an offshore wind turbine system. Appl. Sci. 2019, 9, 783. [Google Scholar] [CrossRef]
- Jiang, Z.Z.; Xiao, B.X. LQR optimal control research for four-wheel steering forklift based-on state feedback. J. Mech. Sci. Technol. 2018, 32, 2789–2801. [Google Scholar] [CrossRef]
- Sandy, R.; Meskin, N. Adaptive sliding mode observer for sensor fault diagnosis of an industrial gas turbine. Control Eng. Pract. 2015, 38, 57–74. [Google Scholar]
- Zhao, D.; Zhou, D.; Wang, Y. Sensor fault reconstruction for a class of 2-D nonlinear systems with application to fault compensation. Multidim. Syst. Sign. Process. 2015, 26, 1061–1080. [Google Scholar] [CrossRef]
- Wang, X.; Shen, Y.X. Fault-tolerant control strategy of a wind energy conversion system considering multiple fault reconstruction. Appl. Sci. 2018, 8, 794. [Google Scholar] [CrossRef]
- Plestan, F.; Shtessel, Y.; Bregeault, V.; Poznyak, A. New methodologies for adaptive sliding mode control. Int. J. Control 2010, 82, 1907–1919. [Google Scholar] [CrossRef]
- Jia, Q.; Chen, W.; Zhang, Y.; Li, Y. Integrated design of fault reconstruction and fault-tolerant control against actuator faults using learning observers. Int. J. Syst. Sci. 2016, 47, 3749–3761. [Google Scholar] [CrossRef]

| Symbol | Description | Values or Units |
|---|---|---|
| M | Mass of vehicle | 8720 kg |
| Sprung mass | 7500 kg | |
| Yaw rate of inertia around the z-axis | 3650 | |
| Yaw rate of inertia around the x-axis | 1800 | |
| Products of inertia around the x-axis and the z-axis | 500 | |
| Total roll rate | 65,690 Nm/rad | |
| Roll damping | 2100 Nm/(rad/s) | |
| Distance from the center of gravity to the roll center | 0.3 m | |
| a | Distance from the center of gravity to the rear axle | 1.2 m |
| b | Distance from the center of gravity to the front axle | 0.6 m |
| Corning stiffness of the front axle | 85,000 N/rad | |
| Corning stiffness of the rear axle | 55,000 N/rad | |
| Roll-steering parameter of the front axle | 0.07 | |
| Roll-steering parameter of the rear axle | 0.05 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Xiao, B. Sensor Fault Reconstruction based on Adaptive Sliding Mode Observer for Forklift Fault-Tolerant Control System. Appl. Sci. 2020, 10, 1278. https://doi.org/10.3390/app10041278
Zhang Z, Xiao B. Sensor Fault Reconstruction based on Adaptive Sliding Mode Observer for Forklift Fault-Tolerant Control System. Applied Sciences. 2020; 10(4):1278. https://doi.org/10.3390/app10041278
Chicago/Turabian StyleZhang, Zhilu, and Benxian Xiao. 2020. "Sensor Fault Reconstruction based on Adaptive Sliding Mode Observer for Forklift Fault-Tolerant Control System" Applied Sciences 10, no. 4: 1278. https://doi.org/10.3390/app10041278
APA StyleZhang, Z., & Xiao, B. (2020). Sensor Fault Reconstruction based on Adaptive Sliding Mode Observer for Forklift Fault-Tolerant Control System. Applied Sciences, 10(4), 1278. https://doi.org/10.3390/app10041278





