Semantic 3D Reconstruction with Learning MVS and 2D Segmentation of Aerial Images
Abstract
1. Introduction
- We present an end-to-end, learning-based, semantic 3D reconstruction framework, which reaches high Pixel Accuracy on the Urban Drone Dataset (UDD) [7].
- We propose a probability-based semantic MVS method, which combines the 3D geometry consistency and 2D segmentation information to generate better point-wise semantic labels.
- We design a joint local and global refinement method, which is proven effective by computing re-projection errors.
2. Related Work
3. Method
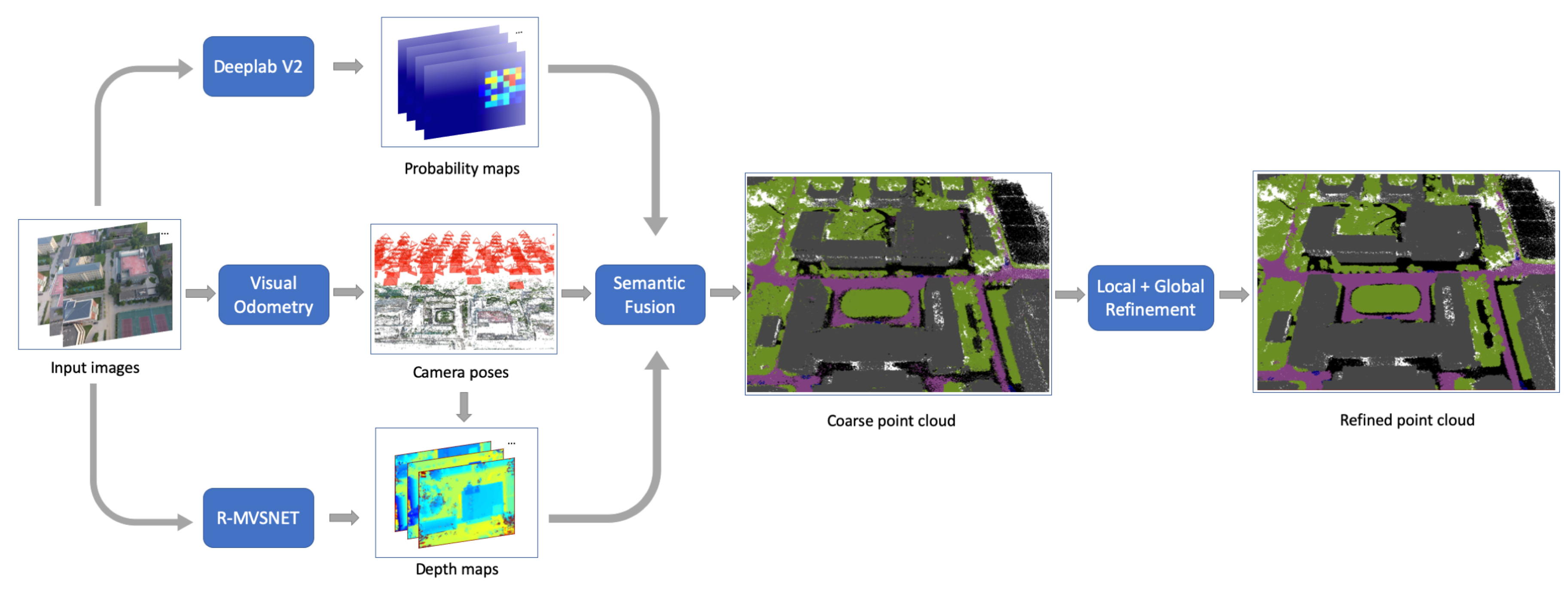
3.1. Overall Framework
3.2. 2D Segmentation
3.3. Learning-Based MVS
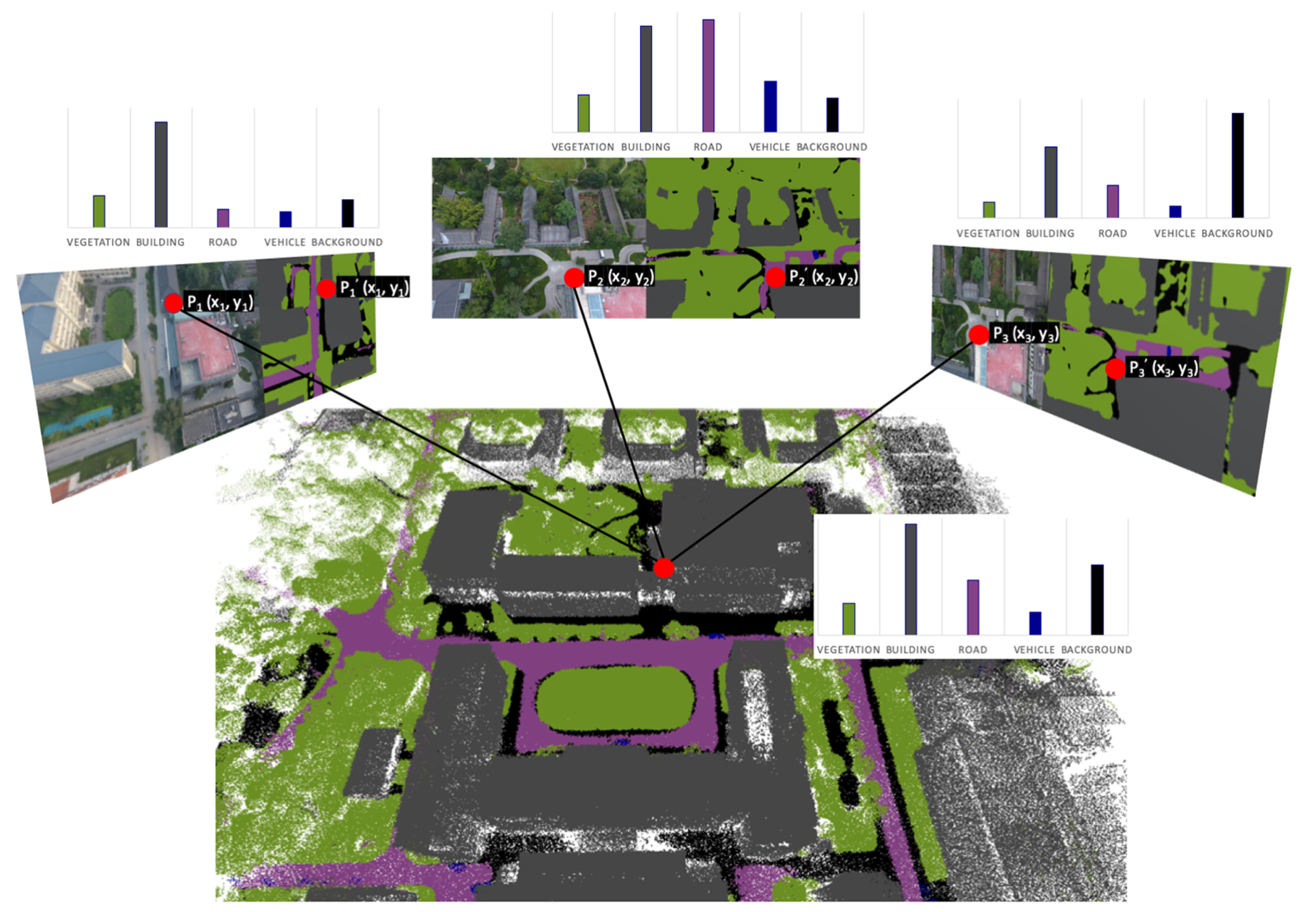
3.4. Semantic Fusion
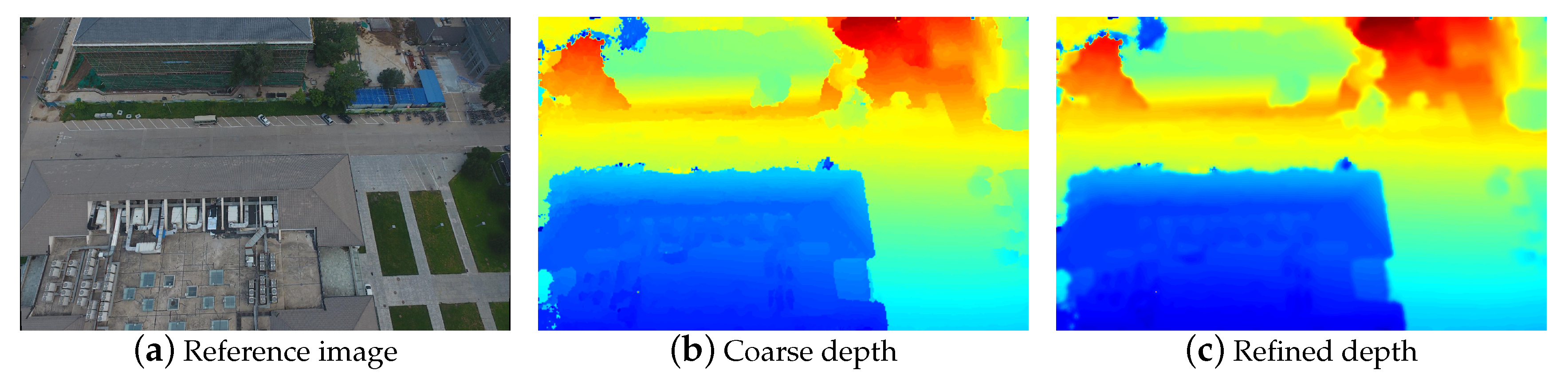
3.5. Point Cloud Refinement
4. Experimental Evaluation
4.1. Experimental Protocol
4.2. Evaluation Process
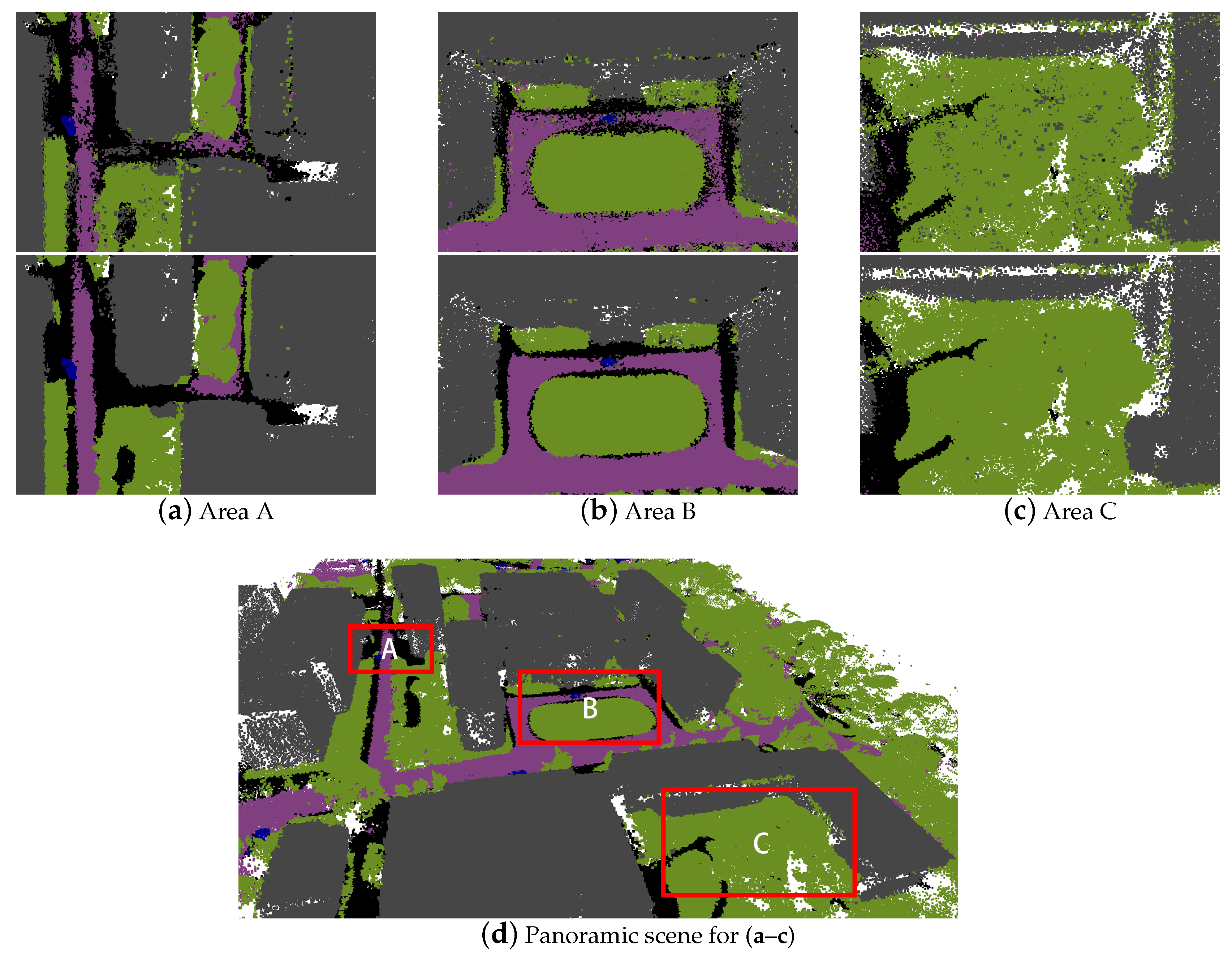
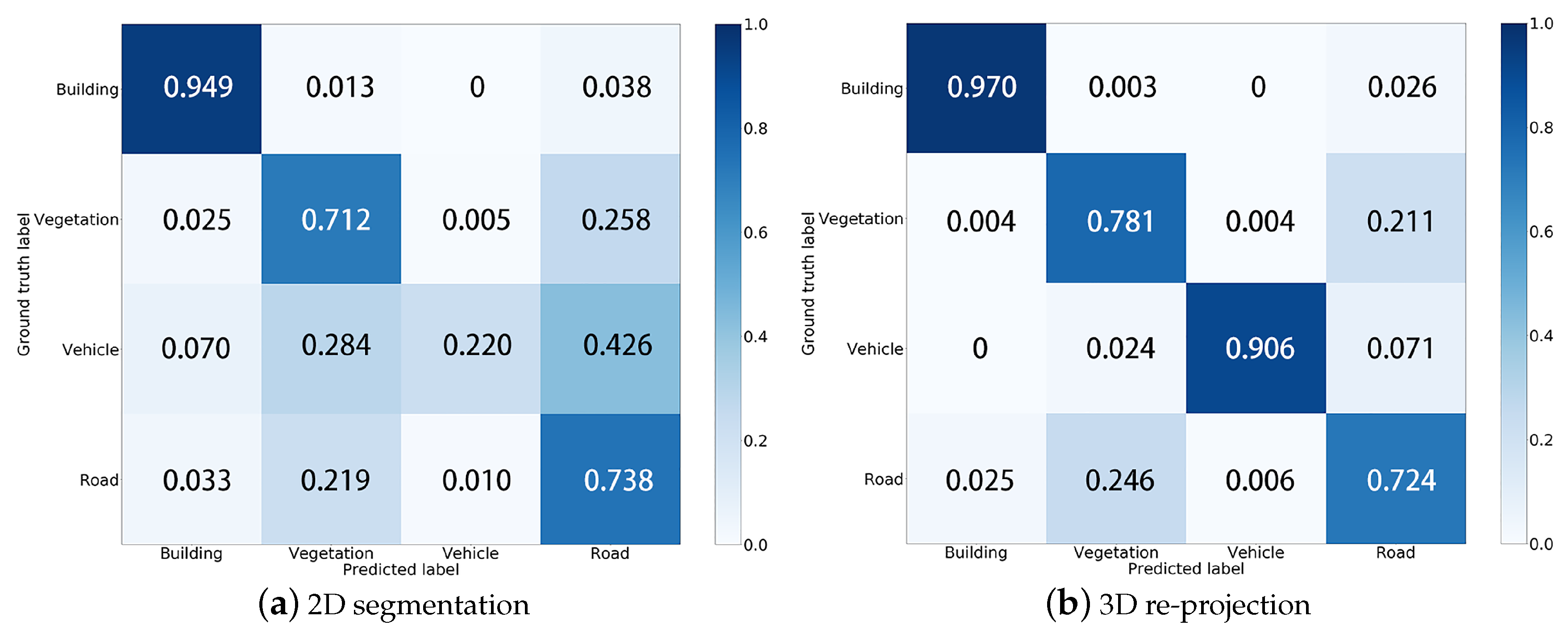
5. Results and Discussion
5.1. Quantitative Results
5.2. Discussion
5.2.1. Parameter Selection for K-Nearest Neighbors
5.2.2. Soft vs. Hard Decision Strategy
5.2.3. Down-Sample Rate
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. Mvsnet: Depth inference for unstructured multi-view stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Yao, Y.; Luo, Z.; Li, S.; Shen, T.; Fang, T.; Quan, L. Recurrent mvsnet for high-resolution multi-view stereo depth inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5525–5534. [Google Scholar]
- Chen, Y.; Wang, Y.; Lu, P.; Chen, Y.; Wang, G. Large-scale structure from motion with semantic constraints of aerial images. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Guangzhou, China, 23–26 November 2018; pp. 347–359. [Google Scholar]
- Bao, S.Y.; Savarese, S. Semantic structure from motion. In Proceedings of the CVPR 2011, Providence, RI, USA, 20–25 June 2011; pp. 2025–2032. [Google Scholar]
- Martinovic, A.; Knopp, J.; Riemenschneider, H.; Van Gool, L. 3D all the way: Semantic segmentation of urban scenes from start to end in 3d. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Santiago, Chile, 7–13 December 2015; pp. 4456–4465. [Google Scholar]
- Wolf, D.; Prankl, J.; Vincze, M. Fast semantic segmentation of 3D point clouds using a dense CRF with learned parameters. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4867–4873. [Google Scholar]
- Häne, C.; Zach, C.; Cohen, A.; Pollefeys, M. Dense semantic 3d reconstruction. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1730–1743. [Google Scholar] [CrossRef] [PubMed]
- Hane, C.; Zach, C.; Cohen, A.; Angst, R.; Pollefeys, M. Joint 3D scene reconstruction and class segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 97–104. [Google Scholar]
- Savinov, N.; Ladicky, L.; Hane, C.; Pollefeys, M. Discrete optimization of ray potentials for semantic 3d reconstruction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Santiago, Chile, 7–13 December 2015; pp. 5511–5518. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Santiago, Chile, 7–13 December 2015; pp. 1912–1920. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 922–928. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5099–5108. [Google Scholar]
- Vineet, V.; Miksik, O.; Lidegaard, M.; Nießner, M.; Golodetz, S.; Prisacariu, V.A.; Kähler, O.; Murray, D.W.; Izadi, S.; Pérez, P.; et al. Incremental dense semantic stereo fusion for large-scale semantic scene reconstruction. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 75–82. [Google Scholar]
- Zhao, C.; Sun, L.; Stolkin, R. A fully end-to-end deep learning approach for real-time simultaneous 3D reconstruction and material recognition. In Proceedings of the 2017 18th International Conference on Advanced Robotics (ICAR), Hong Kong, China, 10–12 July 2017; pp. 75–82. [Google Scholar]
- McCormac, J.; Handa, A.; Davison, A.; Leutenegger, S. Semanticfusion: Dense 3d semantic mapping with convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, Singapore, 29 May–3 June 2017; pp. 4628–4635. [Google Scholar]
- Li, X.; Wang, D.; Ao, H.; Belaroussi, R.; Gruyer, D. Fast 3D Semantic Mapping in Road Scenes. Appl. Sci. 2019, 9, 631. [Google Scholar] [CrossRef]
- Zhou, Y.; Shen, S.; Hu, Z. Fine-level semantic labeling of large-scale 3d model by active learning. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 523–532. [Google Scholar]
- Stathopoulou, E.; Remondino, F. Semantic photogrammetry: boosting image-based 3D reconstruction with semantic labeling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 2/W9. [Google Scholar] [CrossRef]
- Zhang, R.; Li, G.; Li, M.; Wang, L. Fusion of images and point clouds for the semantic segmentation of large-scale 3D scenes based on deep learning. ISPRS J. Photogramm. Remote Sens. 2018, 143, 85–96. [Google Scholar] [CrossRef]
- Schonberger, J.L.; Frahm, J.M. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Jensen, R.; Dahl, A.; Vogiatzis, G.; Tola, E.; Aanæs, H. Large scale multi-view stereopsis evaluation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 406–413. [Google Scholar]
- Galliani, S.; Lasinger, K.; Schindler, K. Massively parallel multiview stereopsis by surface normal diffusion. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 873–881. [Google Scholar]
- Sedlacek, D.; Zara, J. Graph cut based point-cloud segmentation for polygonal reconstruction. In Proceedings of the International Symposium on Visual Computing, Las Vegas, NV, USA, 30 November–2 December 2009; pp. 218–227. [Google Scholar]
- Boykov, Y.; Kolmogorov, V. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1124–1137. [Google Scholar] [CrossRef] [PubMed]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The cityscapes dataset for semantic urban scene understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3213–3223. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-scale machine learning on heterogeneous systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of COMPSTAT’2010; Springer: Paris, France, 2010; pp. 177–186. [Google Scholar]


| Category | Accuracy(%) | Precision(%) | Recall(%) | F1 score(%) |
|---|---|---|---|---|
| Building | 95.60 | 98.25 | 94.87 | 96.53 |
| Vegetation | 89.85 | 76.96 | 71.24 | 73.99 |
| Vehicle | 97.95 | 67.09 | 22.02 | 33.15 |
| Road | 87.91 | 52.58 | 73.84 | 61.42 |
| Pixel Accuracy(%) | |||||
| Method | Building | Vegetation | Vehicle | Road | All |
| 2D prediction | 95.60 | 89.85 | 97.95 | 87.91 | 85.66 |
| 3D baseline | 97.51 | 90.06 | 99.76 | 75.59 | 87.76 |
| Local | 96.20 | 91.38 | 99.74 | 68.61 | 88.24 |
| Global | 96.16 | 91.40 | 99.45 | 71.44 | 88.21 |
| 96.19 | 91.40 | 99.76 | 68.16 | 88.40 | |
| F1-Score(%) | |||||
| Method | Building | Vegetation | Vehicle | Road | |
| 2D prediction | 96.53 | 73.99 | 33.15 | 61.42 | |
| 3D baseline | 97.00 | 74.69 | 63.66 | 75.79 | |
| Local | 97.13 | 74.87 | 62.72 | 75.63 | |
| Global | 97.15 | 74.69 | 73.17 | 75.03 | |
| 97.85 | 76.07 | 81.40 | 76.57 | ||
| Method | k-Nearest Neighbor | Down-Sample Rate | Pixel Accuracy(%) |
|---|---|---|---|
| 2D prediction | 0 | 1 | 85.66 |
| 3D baseline | 0 | 0.1 | 87.76 |
| Local | 15 | 0.1 | 88.14 |
| Local | 15 | 0.2 | 88.02 |
| Local | 15 | 0.5 | 88.21 |
| Local | 15 | 1 | 88.24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Wang, Y.; Yi, H.; Chen, Y.; Wang, G. Semantic 3D Reconstruction with Learning MVS and 2D Segmentation of Aerial Images. Appl. Sci. 2020, 10, 1275. https://doi.org/10.3390/app10041275
Wei Z, Wang Y, Yi H, Chen Y, Wang G. Semantic 3D Reconstruction with Learning MVS and 2D Segmentation of Aerial Images. Applied Sciences. 2020; 10(4):1275. https://doi.org/10.3390/app10041275
Chicago/Turabian StyleWei, Zizhuang, Yao Wang, Hongwei Yi, Yisong Chen, and Guoping Wang. 2020. "Semantic 3D Reconstruction with Learning MVS and 2D Segmentation of Aerial Images" Applied Sciences 10, no. 4: 1275. https://doi.org/10.3390/app10041275
APA StyleWei, Z., Wang, Y., Yi, H., Chen, Y., & Wang, G. (2020). Semantic 3D Reconstruction with Learning MVS and 2D Segmentation of Aerial Images. Applied Sciences, 10(4), 1275. https://doi.org/10.3390/app10041275





