Effect of the Lubrication Parameters on the Ceramic Ball Bearing Vibration in Starved Conditions
Abstract
1. Introduction
2. Dynamic Model
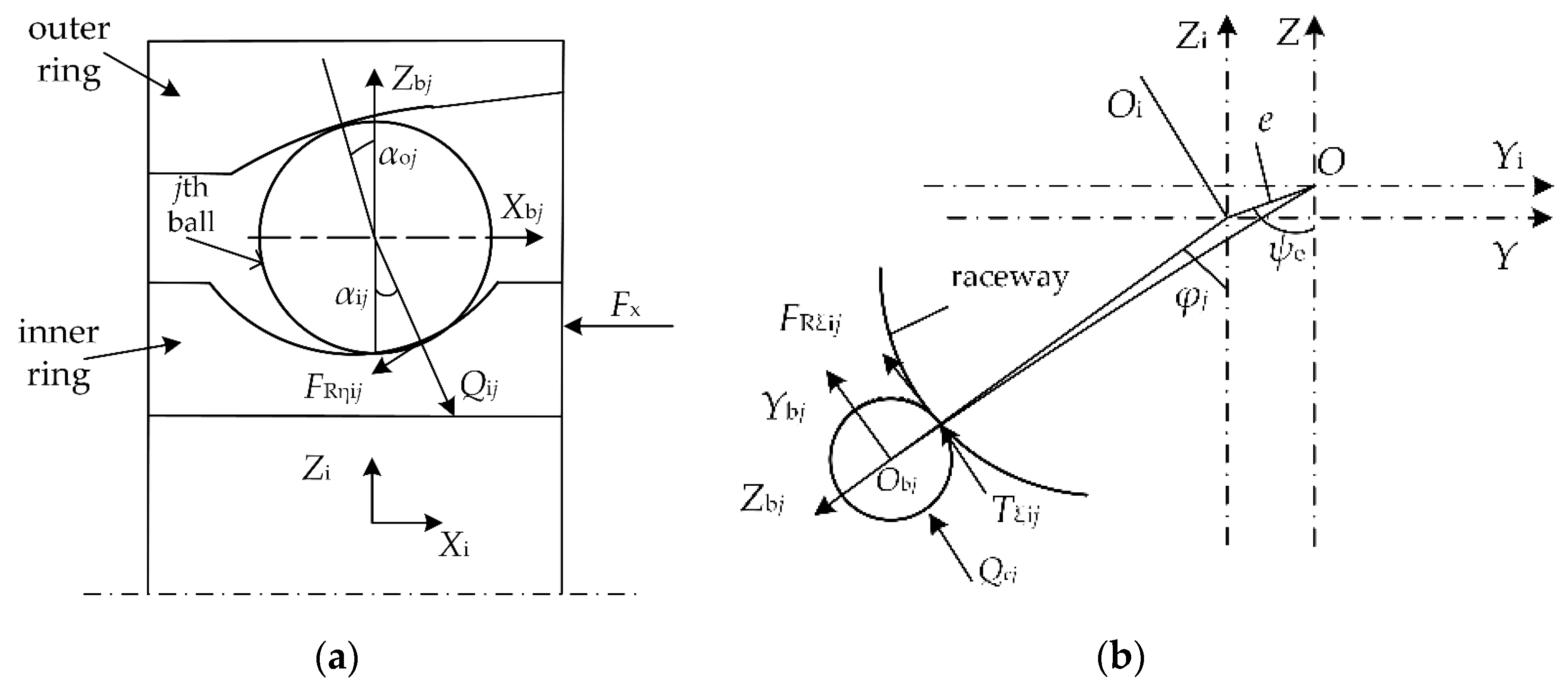
2.1. Contact Model between the Balls and Inner Ring
Model of the Inner Ring
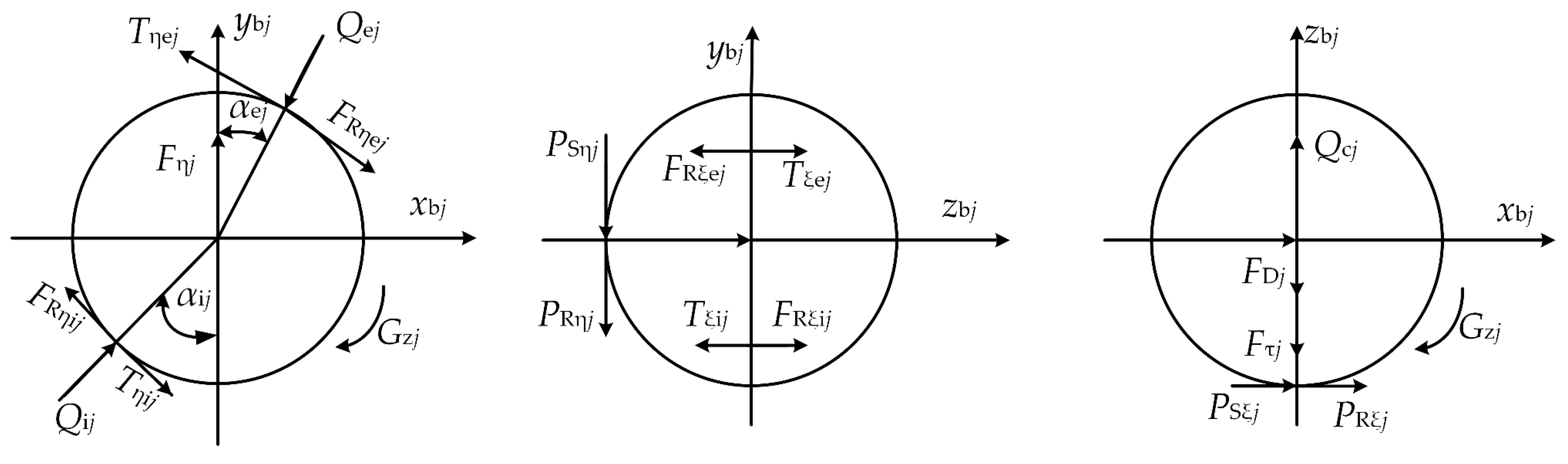
2.2. Model of the Ball at Normal Lubricated Conditions
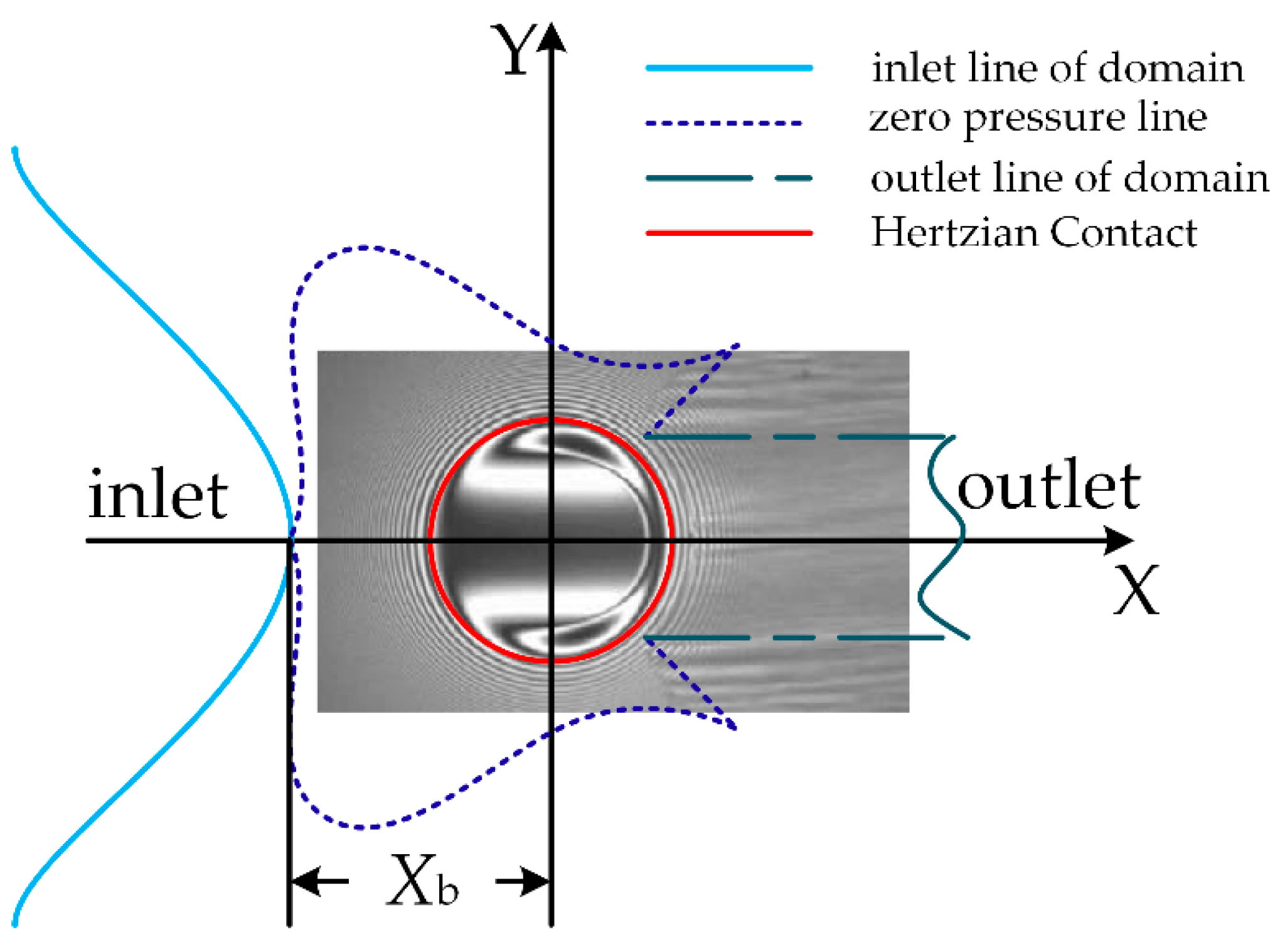
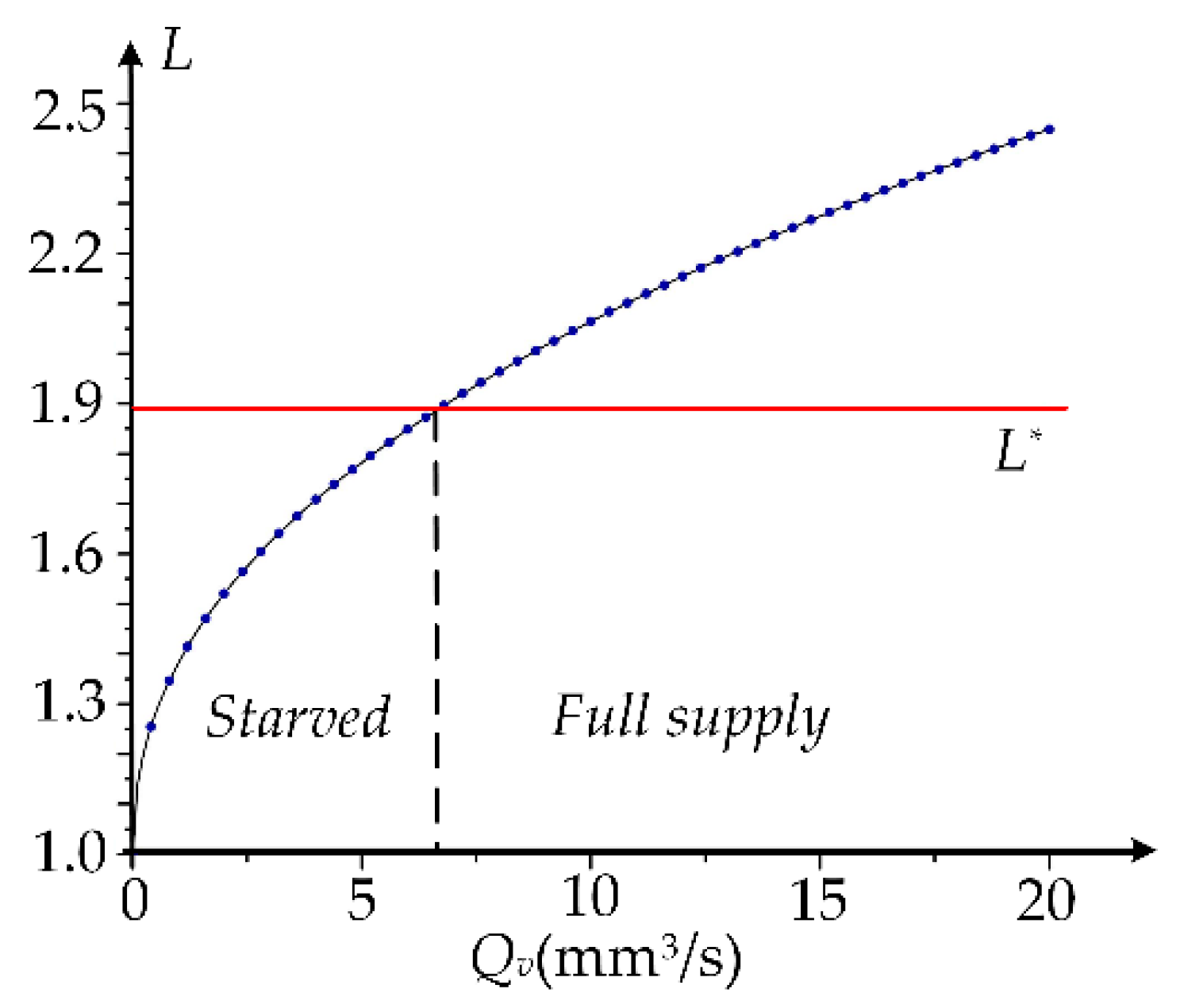
2.3. Model of the Ball at Starved Lubricated Conditions
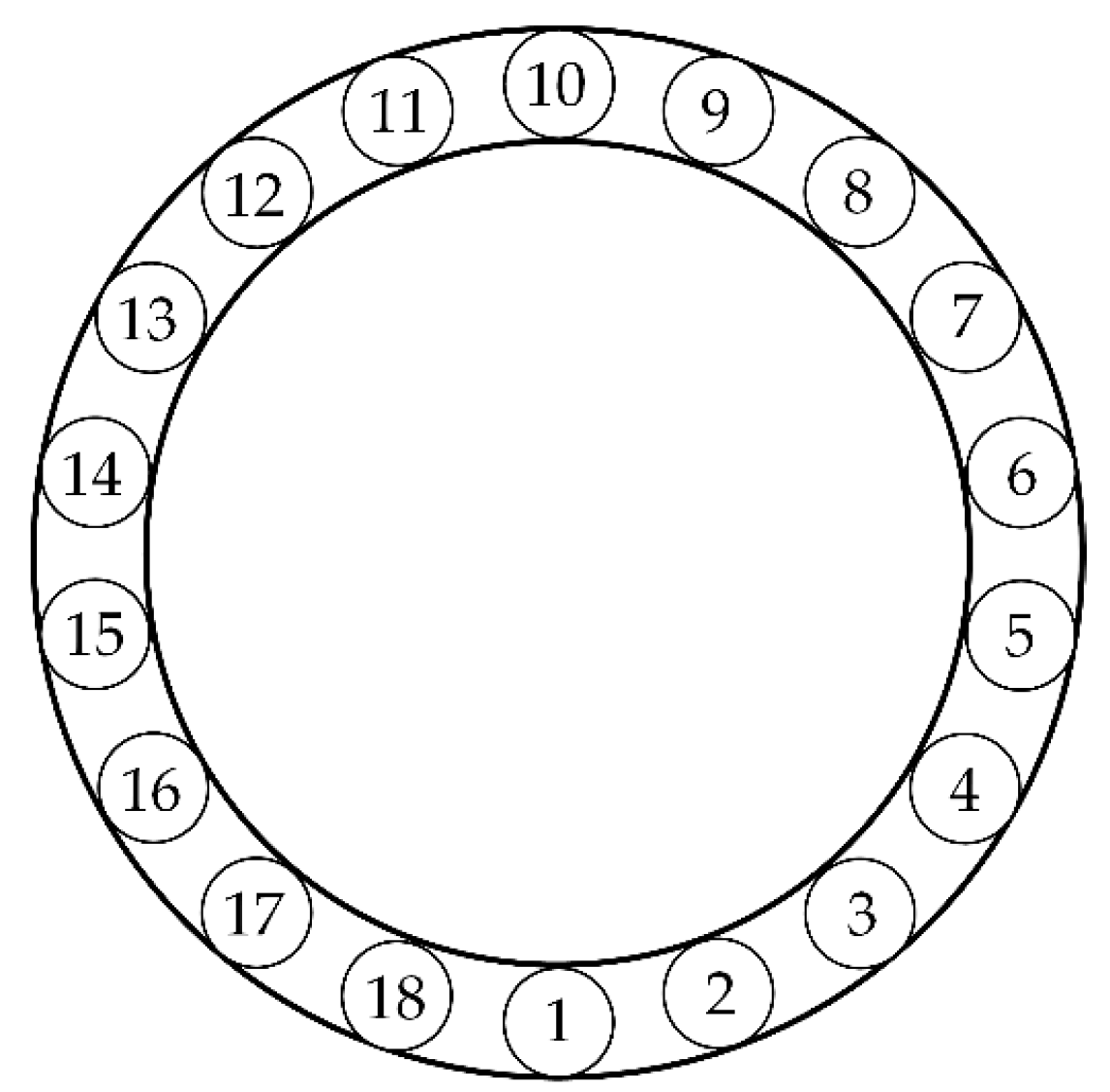
3. Numerical Simulation
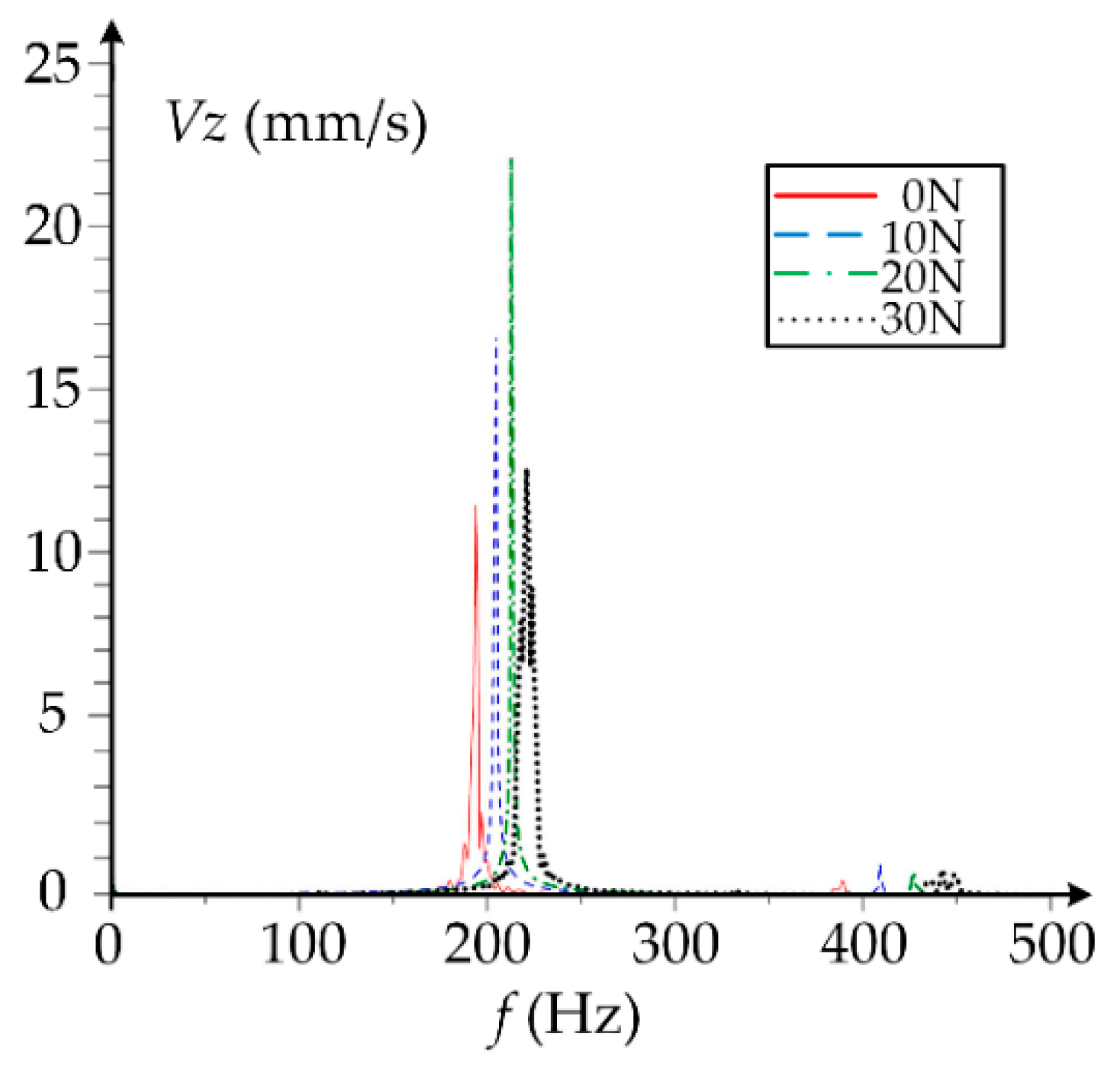
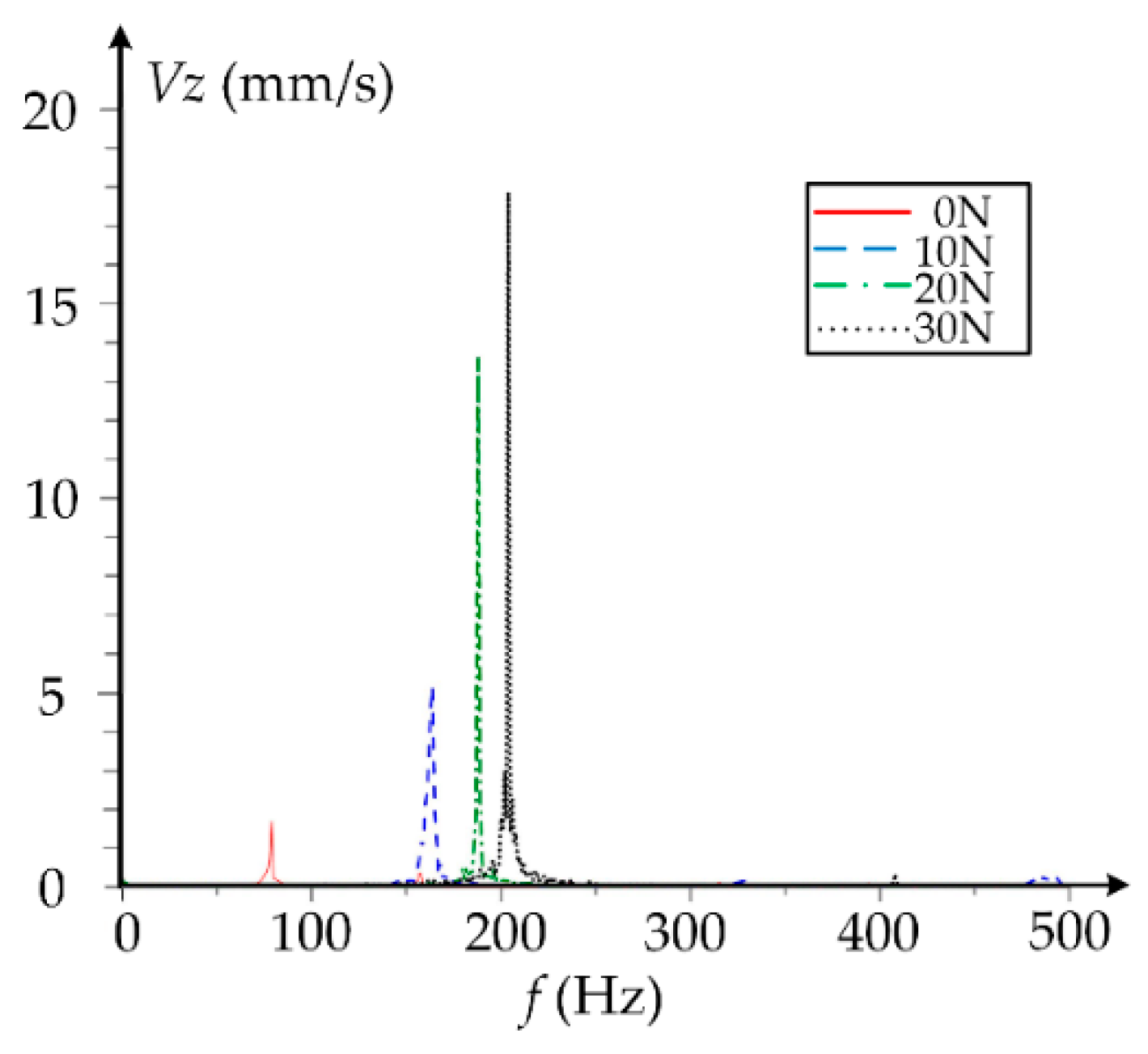
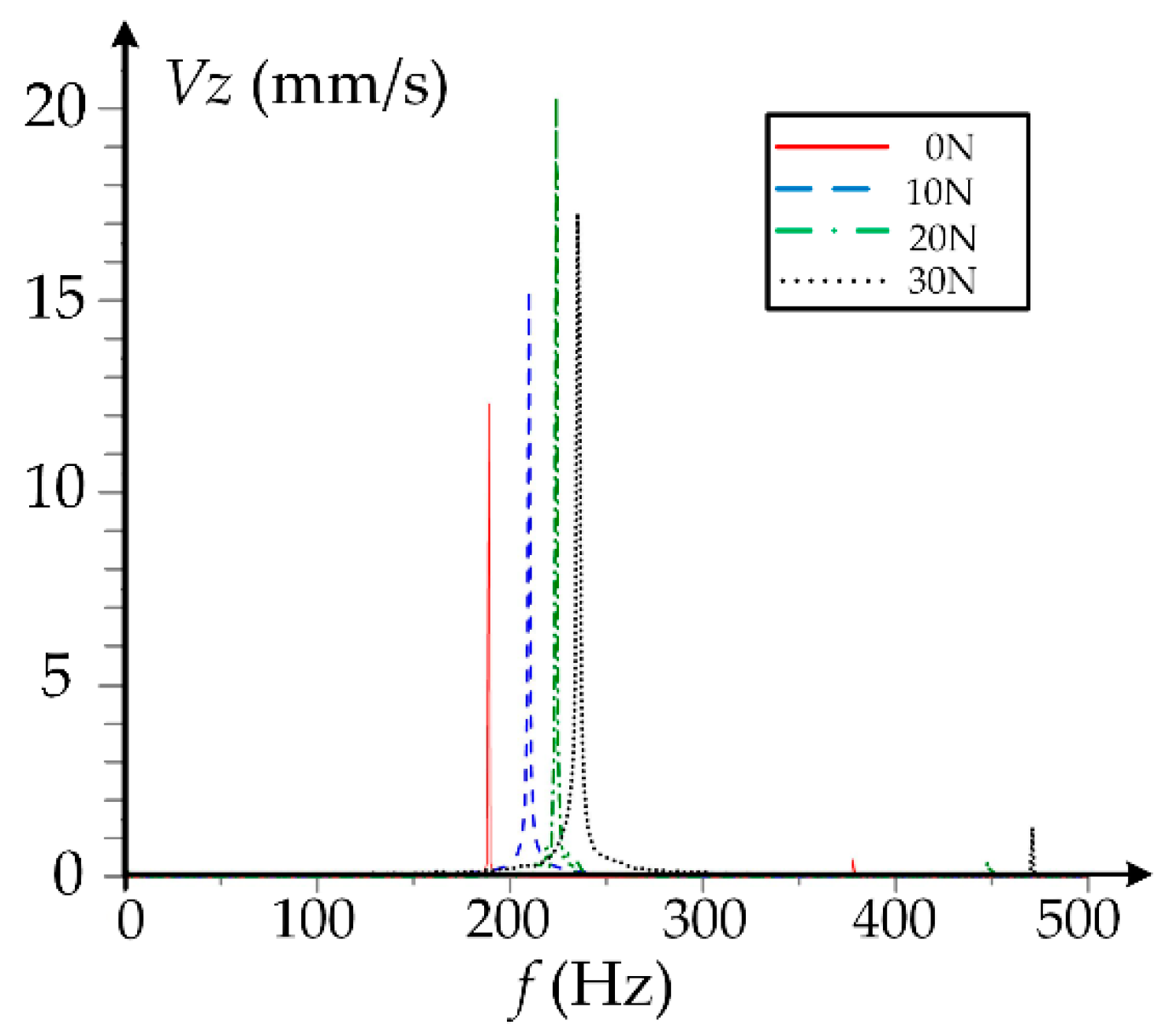
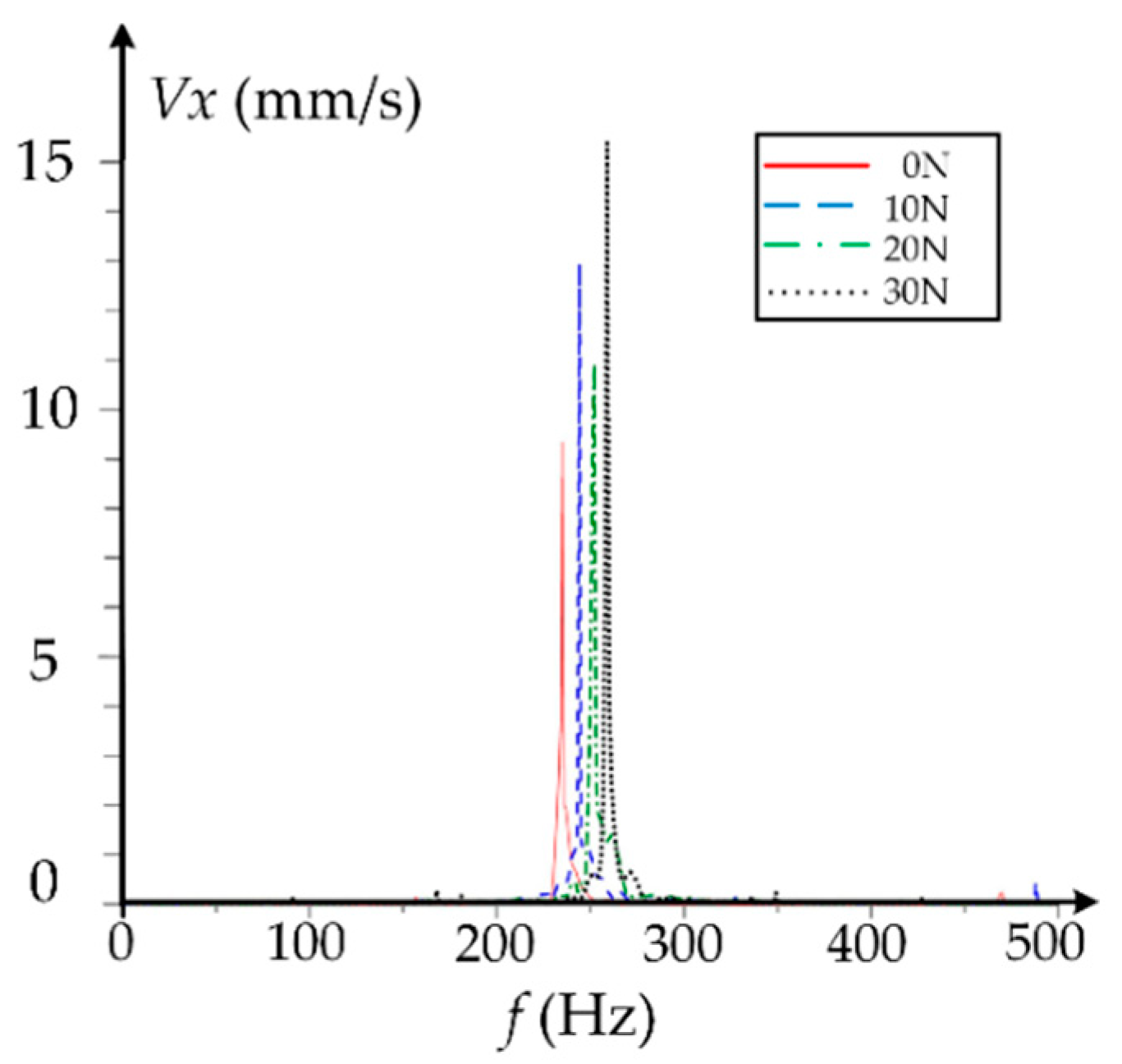
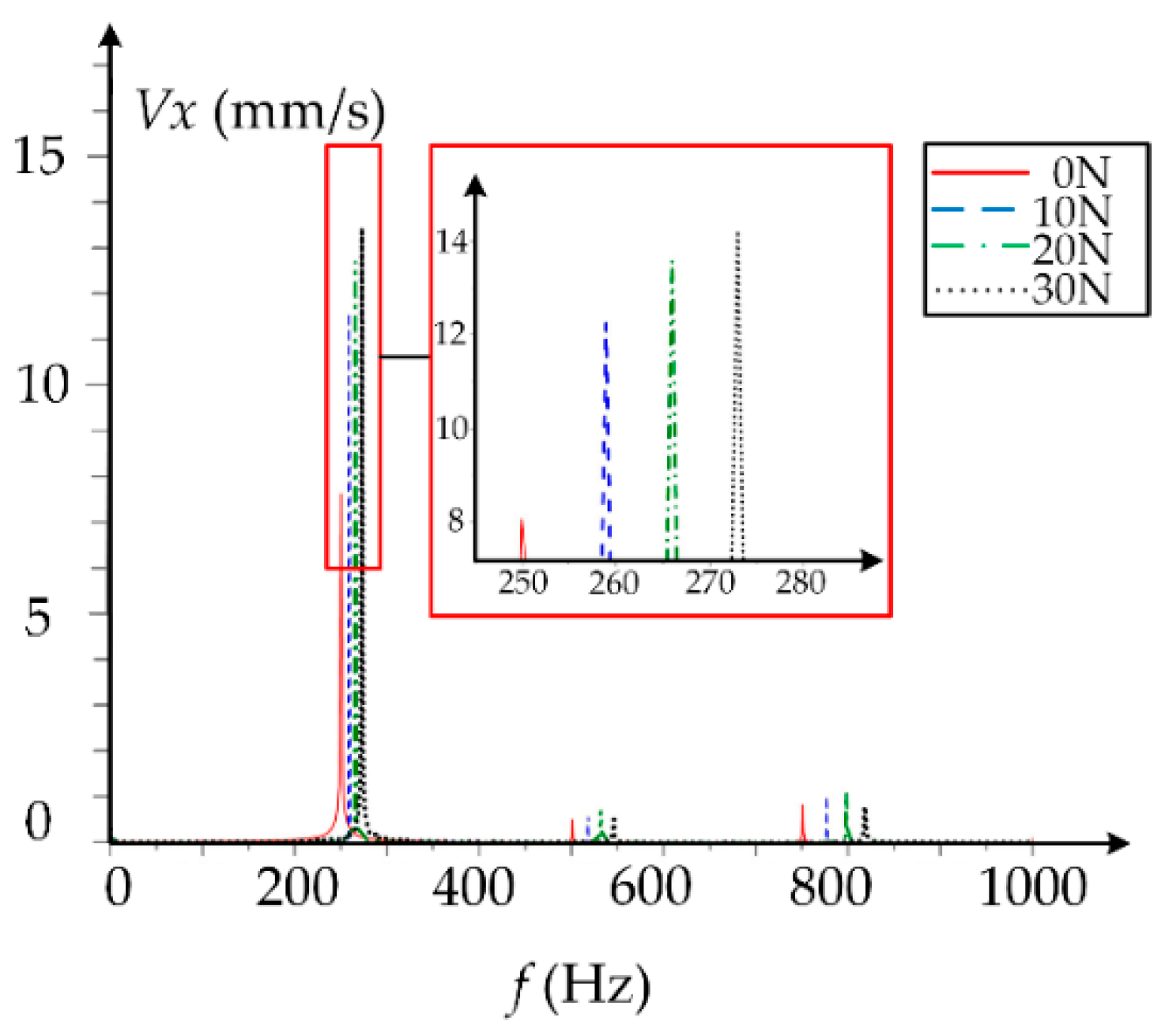
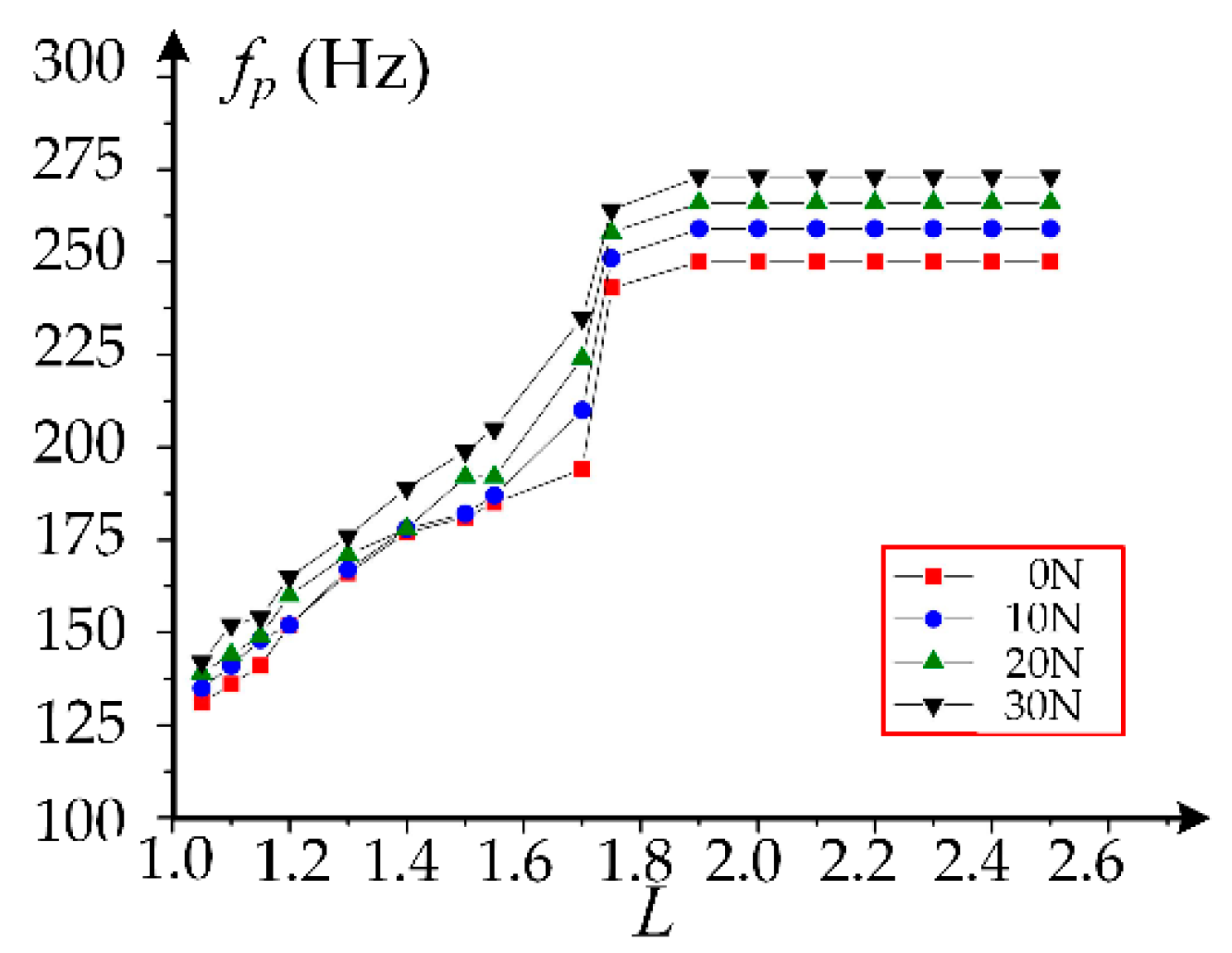
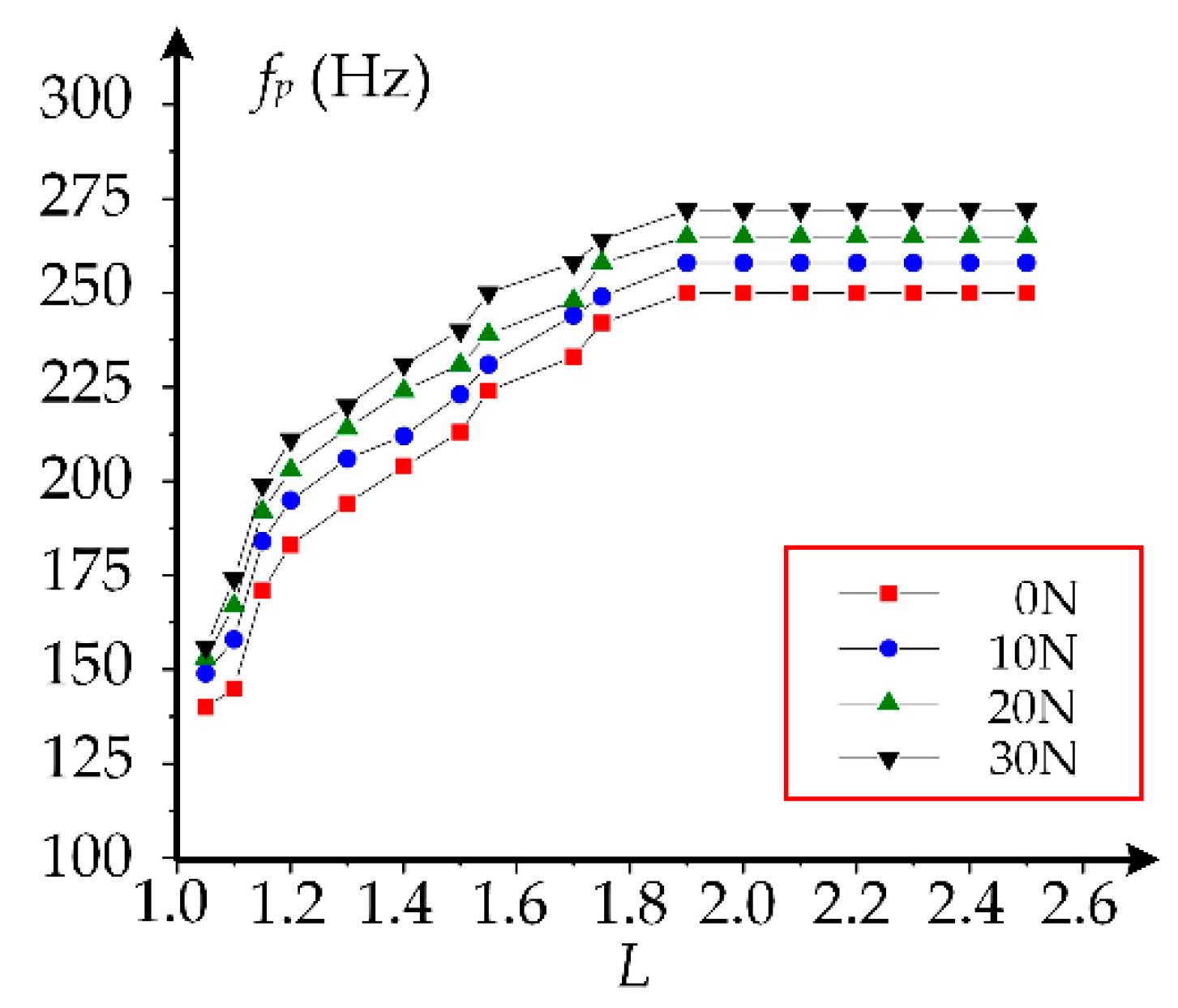
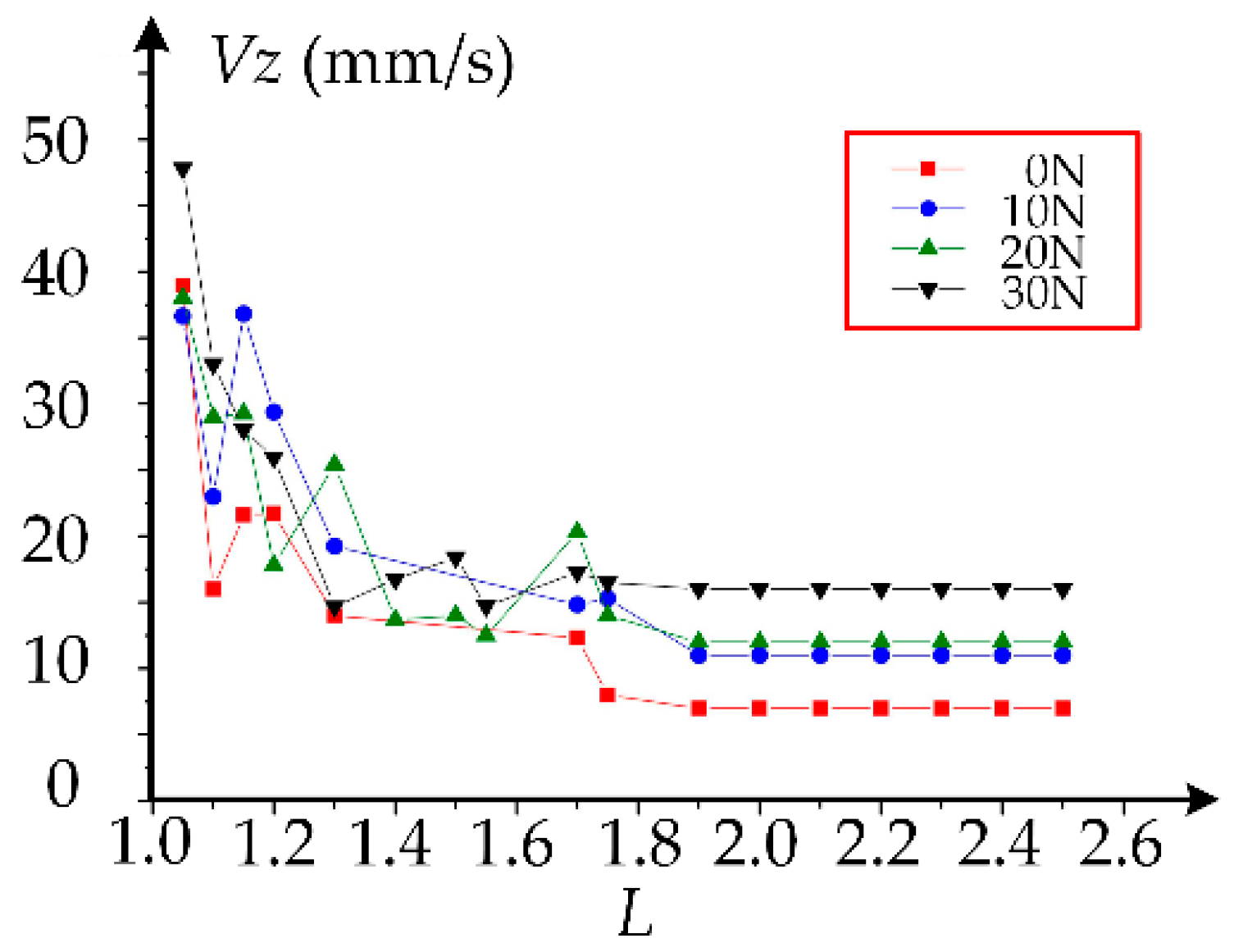
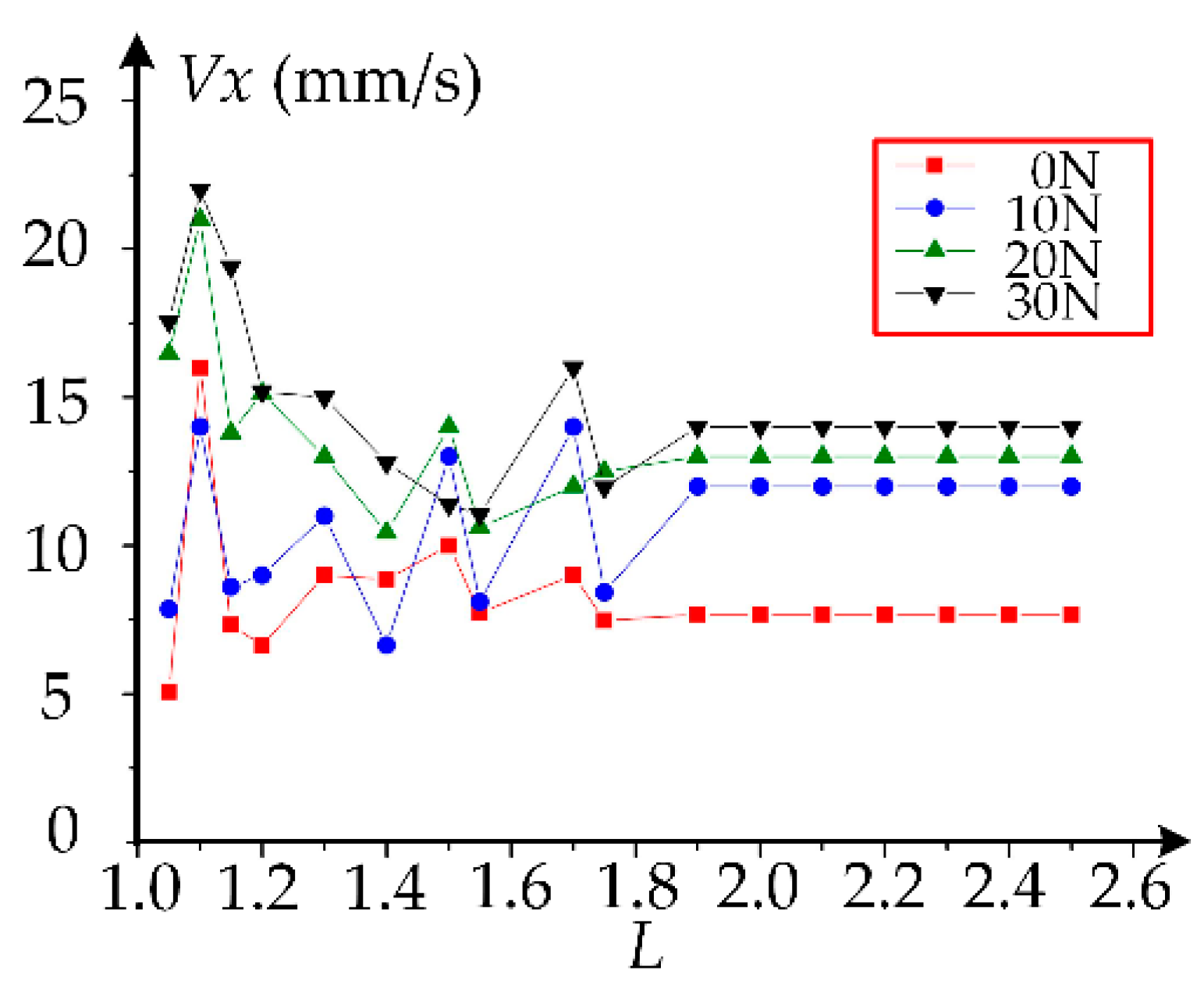
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a | The long half axis of the ellipse |
| b | The short half axis of the ellipse |
| D | The normal ball diameter |
| d | The pitch diameter of the bearing |
| e | The constant of nature |
| E | Equivalent elastic modulus |
| E1, E2 | Elastic moduli of the two contact materials |
| Fx, Fy, Fz | Components externally applied forces of X, Y, and Z directions |
| FRηij, FRηej, FRξij, FRξej | Hydrodynamic frictional forces at the inlet zone |
| Fηj, Fτj | Inertial force component of the ball |
| FDj | Aerodynamic resistance acting on the ball by the gas–oil mixture; |
| fx, fy | The natural frequency of bearing vibration in axial and radial directions |
| G | Material parameter |
| Gyj, Gzj | Components of the ball’s inertia moment of ybj and zbj directions |
| hb | The oil film thickness at the lubrication inlet |
| Hc | A dimensionless central oil film thickness |
| hc | The central oil film thickness |
| hmin | The minimum oil film thickness |
| hc1 | The actual central oil film thickness |
| Ibj | Moments of inertia of the jth ball |
| Iix, Iiy, Iiz | The principal moments of inertia of the inner ring in the inertial coordinate system |
| Jx, Jy, Jz | Components of the ball’s moment of inertia of xbj, ybj, and zbj directions |
| j | The jth ball |
| Koil | The oil film stiffness between the ball and the raceway |
| Kc | The contact stiffness |
| K | The contact coefficient between the ball and the raceway |
| Krij | The radial component of the comprehensive stiffness between the jth ball and the inner ring |
| Kaij | The axial component of the comprehensive stiffness between the jth ball and the inner ring |
| Kaej | The axial component of the comprehensive stiffness between the jth ball and the outer ring |
| Krej | The radial component of the comprehensive stiffness between the jth ball and the outer ring |
| (Koil)ij | The oil film stiffness of the jth ball and the inner ring |
| (Koil)ej | The oil film stiffness of the jth ball and the outer ring |
| (Kc)ij | The contact stiffness between the jth ball and the inner ring |
| (Kc)ej | The contact stiffness between the jth ball and the outer ring |
| Ka | Axial stiffness |
| Kr | Radial stiffness |
| k | Ellipticity |
| L | The dimensionless distance between the inlet and the Hertz contact center |
| L* | The boundary between fully flooded and starved |
| My, Mz | Externally applied torques |
| mi | Mass of the inner ring |
| mb | Mass of the ball |
| M | Mass of the bearing system |
| {O; X, Y, Z} | The inertial coordinate system of the bearing |
| {O; Xi, Yi, Zi} | The inner ring coordinate system of the bearing |
| {Obj; Xbj, Ybj, Zbj} | The coordinate system of the jth ball |
| PRηj, PRξj | Rolling frictional forces acting on the ball’s surface |
| PSηj, PSξj | Sliding frictional forces acting on the ball’s surface |
| Qij, Qej | Normal contact forces between the ball and raceway |
| Qcj | Collision force between the jth ball and the cage |
| Qv | The supplied oil flow rate |
| Q | Normal contact force between the ball and raceway |
| rij | The rolling radius |
| Ri | Groove curvature radius of inner race raceway |
| R | The equivalent radius of curvature |
| Rx | The equivalent radius of curvature in the long axis direction |
| Ry | The equivalent radius of curvature in the short axis direction |
| r | The inner ring radius |
| Tηij, Tηej, Tξij, Tξej | Traction forces of the contact surfaces |
| u | The average surface velocity |
| U | Velocity parameter |
| v1 and v2 | Poisson’s ratios of the two contact materials |
| W | Load parameter |
| The acceleration of the inner ring in the inertial coordinate system | |
| Displacement accelerations of the jth ball in the inertial coordinate system | |
| Xb | The actual distance between the inlet and the Hertz contact center |
| αij, αej | Contact angles between the ball and raceway |
| α0 | The pressure index of viscosity |
| δ | The contact deformation between the ball and the inner ring |
| η | The short axis of the ellipse |
| η0 | The dynamic viscosity at normal pressure |
| τ | The kinematic viscosity of the lubricating oil |
| The azimuth of the jth ball | |
| ξ | The long axis of the ellipse |
| Orbit speed of the jth ball in the inertial coordinate system | |
| ω | The angular velocity of the inner ring |
| Represent the angular velocity of the inner ring in the inertial coordinate system | |
| The angular accelerations of the inner ring in the inertial coordinate system | |
| ωxj, ωyj, ωzj | The angular velocity of the jth ball in {Obj; Xbj, Ybj, Zbj} |
| The angular accelerations of the jth ball in {Obj; Xbj, Ybj, Zbj} | |
| ωbjx, ωbjy, ωbjz | The angular velocities of the jth ball in the inertial coordinate system |
| The angular accelerations of the jth ball in the inertial coordinate system | |
| Subscript i | Represents the inner ring |
| Subscript e | Represents the outer ring |
References
- Wu, Y.H.; Zhang, L.X.; Zhang, K.; Li, S.H. Design on High-Speed Precision Grinder. Key Eng. Mater. 2006, 304, 492–496. [Google Scholar] [CrossRef]
- Li, S.H.; Wu, Y.H.; Zhang, K. Parameter Optimization for Oil/Air Lubrication of High Speed Ceramic Motorized Spindle without Bearing Inner Rings. Appl. Mech. Mater. 2010, 37, 839–843. [Google Scholar] [CrossRef]
- Tiwari, M.; Gupta, K.; Prakash, O. Dynamic response of an unbalanced rotor supported on ball bearings. J. Sound Vib. 2000, 238, 757–779. [Google Scholar] [CrossRef]
- Harsha, S.P. Nonlinear dynamic response of a balanced rotor supported by rolling element bearings due to radial internal clearance effect. Mech. Mach. Theory 2006, 41, 688–706. [Google Scholar] [CrossRef]
- Tripathi, J.S.; Agrawal, J.F. Development of Analytical Model of Ball Bearings for EHL Contact. IJRMEE 2018, 5, 5–12. [Google Scholar]
- Shi, H.T.; Bai, X.T. Model-based uneven loading condition monitoring of full ceramic ball bearings in starved lubrication. Mech. Syst. Signal Pr. 2020, 139, 106583. [Google Scholar] [CrossRef]
- Nonato, F.; Cavalca, K.L. An approach for including the stiffness and damping of elastohydrodynamic point contacts in deep groove ball bearing equilibrium models. J. Sound Vib. 2014, 333, 6960–6978. [Google Scholar] [CrossRef]
- Shi, H.T.; Bai, X.T.; Zhang, K.; Wang, Z.N.; Liu, Z.M. Spalling localization on the outer ring of hybrid ceramic ball bearings based on the sound signals. IEEE Access 2019, 7, 134621–134634. [Google Scholar] [CrossRef]
- Bai, X.T.; Wu, Y.H.; Zhang, K.; Chen, C.Z.; Yan, H.P. Radiation noise of the bearing applied to the ceramic motorized spindle based on the sub-source decomposition method. J. Sound Vib. 2017, 410, 35–48. [Google Scholar] [CrossRef]
- Zhang, W.H.; Deng, S.E.; Chen, G.D.; Cui, Y.C. Study on the impact of roller convexity excursion of high-speed cylindrical roller bearing on roller’s dynamic characteristics. Mech. Mach. Theory 2016, 103, 21–39. [Google Scholar] [CrossRef]
- Cui, Y.C.; Zhang, W.H.; Deng, S.E.; Chen, G.D. The impact of roller dynamic unbalance of high-speed cylindrical roller bearing on the cage nonlinear dynamic characteristics. Mech. Mach. Theory 2017, 118, 65–83. [Google Scholar]
- Bai, X.T.; Wu, Y.H.; Rosca, I.C.; Zhang, K.; Shi, H.T. Investigation on the effects of the ball diameter difference in the sound radiation of full ceramic bearings. J. Sound Vib. 2019, 450, 231–250. [Google Scholar] [CrossRef]
- Shah, D.S.; Patel, V.N. A Dynamic Model for Vibration Studies of Dry and Lubricated Deep Groove Ball Bearings Considering Local Defects on Races. Measurement 2019, 137, 535–555. [Google Scholar] [CrossRef]
- Adiyanto, O.; Pratama, P.S.; Choi, W. Tribological characteristics of SCM 440 bearing steel under gas and oil lubricant in the cylinder block tractor engine. Ind. Lubr. Tribol. 2018, 70, 1361–1366. [Google Scholar] [CrossRef]
- Fischer, D.; Jacobs, G.; Stratmann, A.; Burghardt, G. Effect of base oil type in grease composition on the lubricating film formation in EHD contacts. Lubricants 2018, 6, 32. [Google Scholar] [CrossRef]
- Jablonka, K.; Glovnea, R.; Bongaerts, J. Quantitative measurements of film thickness in a radially loaded deep-groove ball bearing. Tribol. Int. 2018, 119, 239–249. [Google Scholar] [CrossRef]
- Kostal, D.; Sperka, P.; Krupka, I.; Hartl, M. Experimental Comparison of the Behavior between Base Oil and Grease Starvation Based on Inlet Film Thickness. Tribol. Ind. 2017, 39, 110–119. [Google Scholar] [CrossRef][Green Version]
- Liu, Z.; Meng, X.; Wen, C.; Yu, S.; Zhou, Z. On the oil-gas-solid mixed bearing between compression ring and cylinder liner under starved lubrication and high boundary pressures. Tribol. Int. 2019, 105869. [Google Scholar] [CrossRef]
- Nogi, T. An analysis of starved EHL point contacts with reflow. Tribol. Online 2015, 10, 64–75. [Google Scholar] [CrossRef]
- Vengudusamy, B.; Kuhn, M.; Rankl, M.; Spallek, R. Film forming behavior of greases under starved and fully flooded EHL conditions. Tribol. Trans. 2016, 59, 62–71. [Google Scholar] [CrossRef]
- Fischer, D.; Mues, H.; Jacobs, G.; Stratmann, A. Effect of Over Rolling Frequency on the Film Formation in Grease Lubricated EHD Contacts under Starved Conditions. Lubricants 2019, 7, 19. [Google Scholar] [CrossRef]
- Bijani, D.; Deladi, E.; de Rooij, M.; Schipper, D. The influence of surface texturing on the film thickness in starved lubricated parallel sliding contacts. Lubricants 2018, 6, 61. [Google Scholar] [CrossRef]
- Tanaka, M. Journal bearing performance under starved lubrication. Tribol. Int. 2000, 33, 259–264. [Google Scholar] [CrossRef]
- Maruyama, T.; Saitoh, T. Relationship between supplied oil flow rates and oil film thicknesses under starved elastohydrodynamic lubrication. Lubricants 2015, 3, 365–380. [Google Scholar] [CrossRef]
- Ebner, M.; Yilmaz, M.; Lohner, T.; Michaelis, K.; Höhn, B.-R.; Stahl, K. On the effect of starved lubrication on elastohydrodynamic (EHL) line contacts. Tribol. Int. 2018, 118, 515–523. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal elastohydrodynamic lubrication of point contacts. 3. Fully flooded results. J. Lubr. Technol. 1977, 99, 64–76. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal elastohydrodynamic lubrication of point contacts, Part IV–Starvation results. J. Lubr. Technol. 1977, 99, 15–23. [Google Scholar] [CrossRef]
- Wedeven, L.D.; Evans, D.; Cameron, A. Optical analysis of ball bearing starvation. Mech. Eng. 1971, 93, 44–50. [Google Scholar] [CrossRef]
- Liu, C.L.; Guo, F.; Wong, P.L. Characterisation of starved hydrodynamic lubricating films. Tribol. Int. 2019, 31, 694–701. [Google Scholar] [CrossRef]
- Venner, C.H.; Zoelen, M.T.; Lugt, P.M. Thin layer flow and film decay modeling for grease lubricated rolling bearings. Tribol. Int. 2012, 47, 175–187. [Google Scholar] [CrossRef]
- Shi, H.T.; Bai, X.T.; Zhang, K.; Wu, Y.H.; Yue, G.D. Influence of uneven loading condition on the sound radiation of starved lubricated full ceramic ball bearings. J. Sound Vib. 2019, 461, 114910. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Johns-Rahnejat, P.M.; Rahnejat, H.; Gohar, R. Boundary conditions for elastohydrodynamics of circular point contacts. Tribol. Lett. 2014, 53, 107–118. [Google Scholar] [CrossRef]

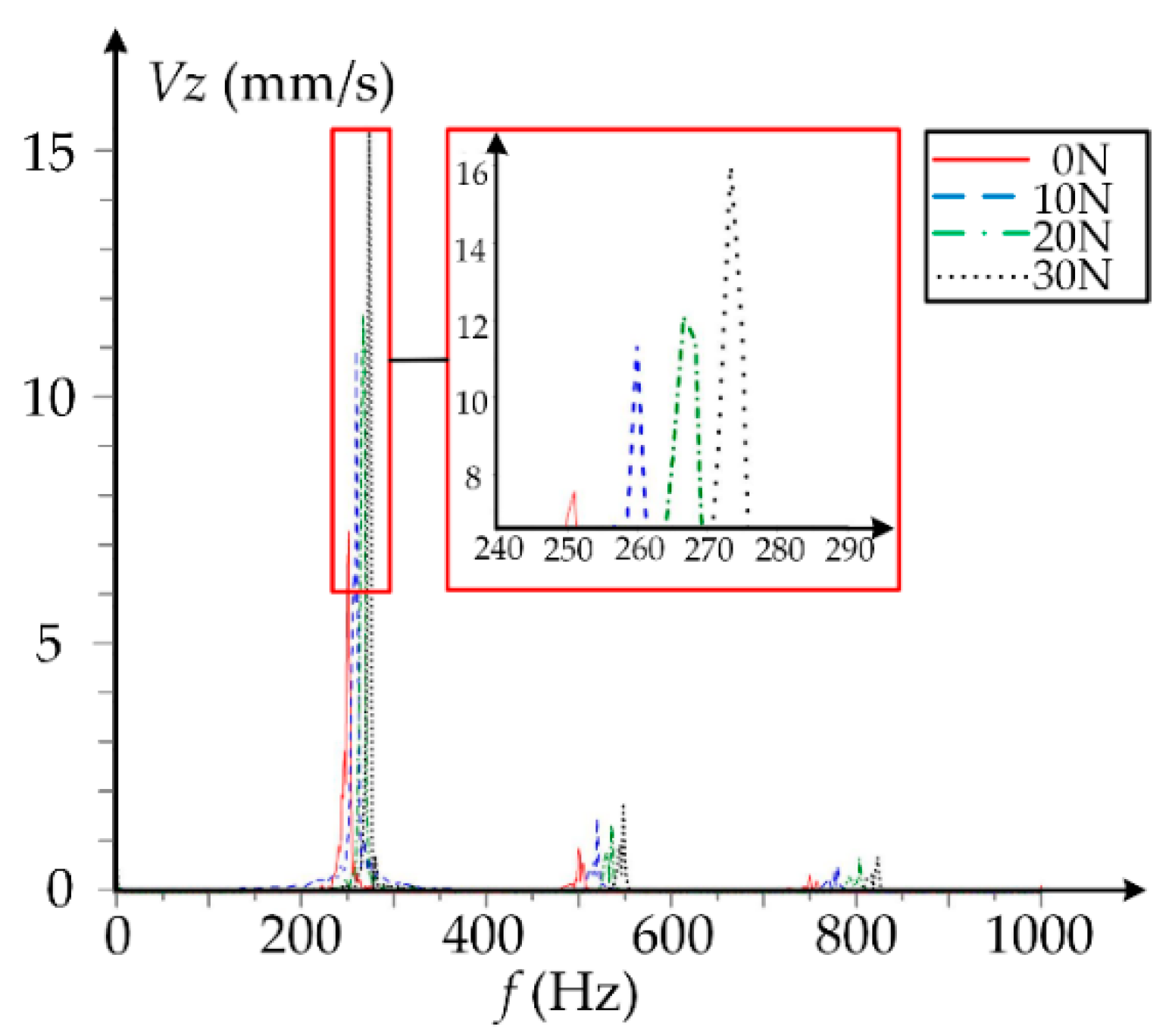
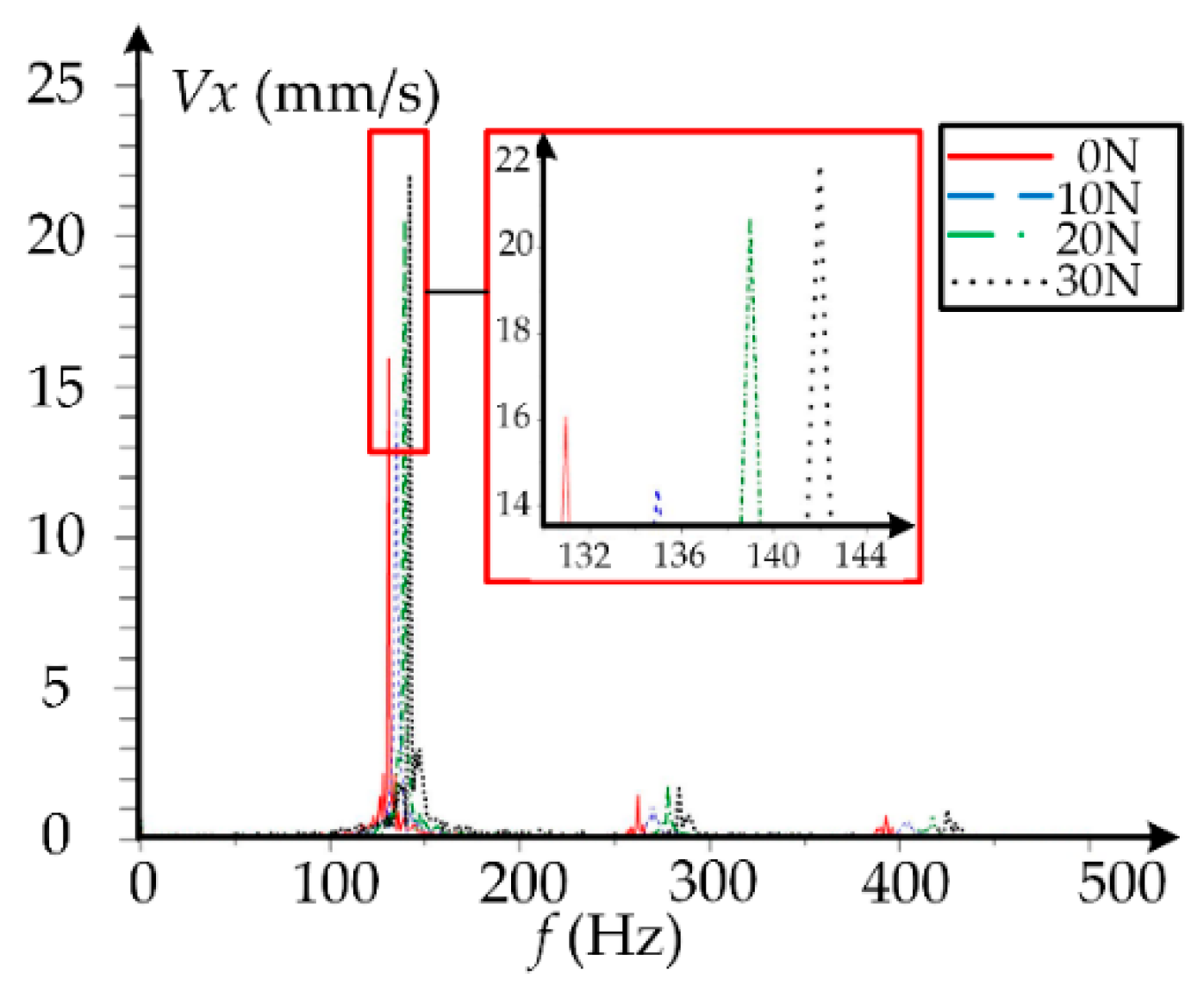
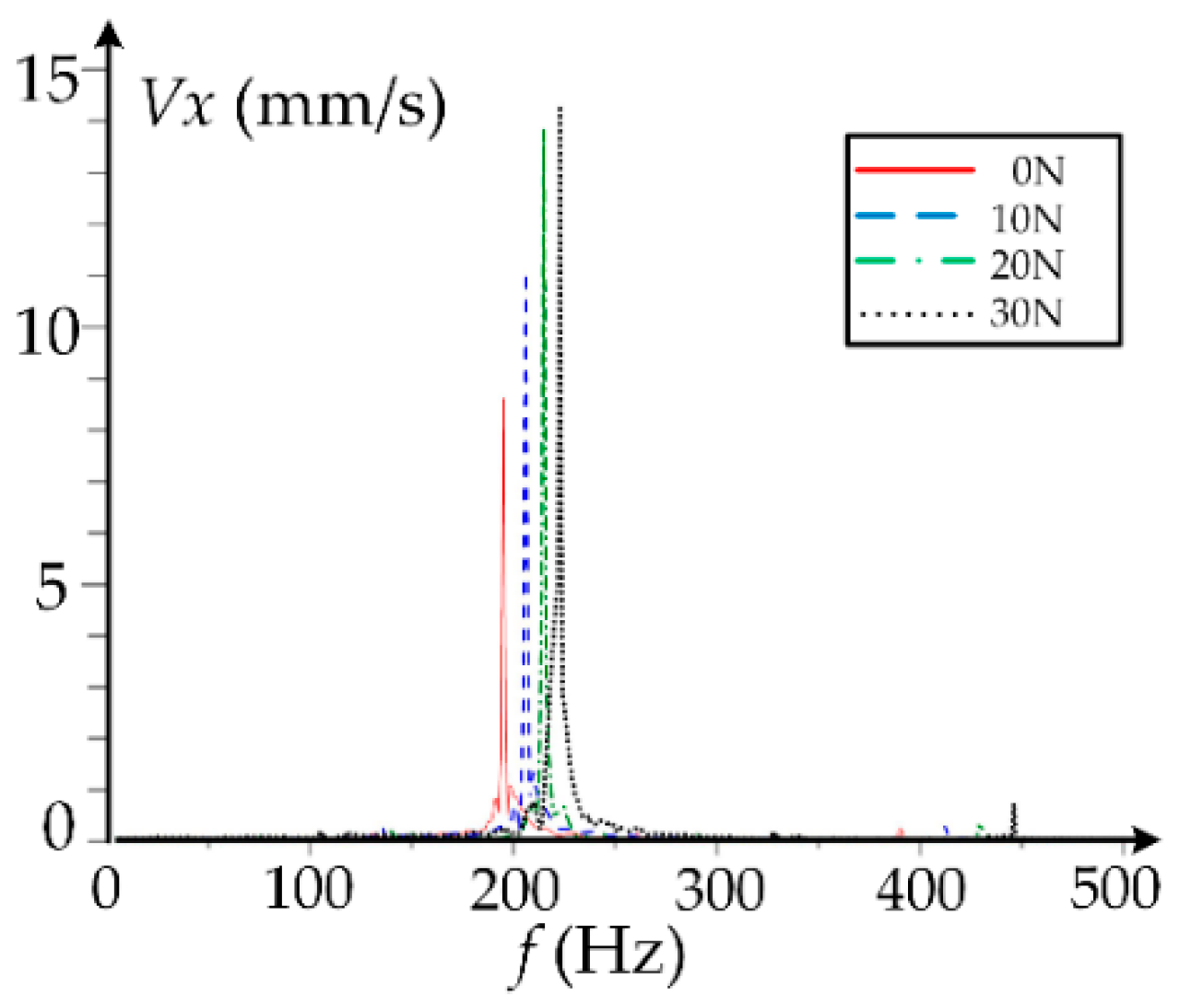
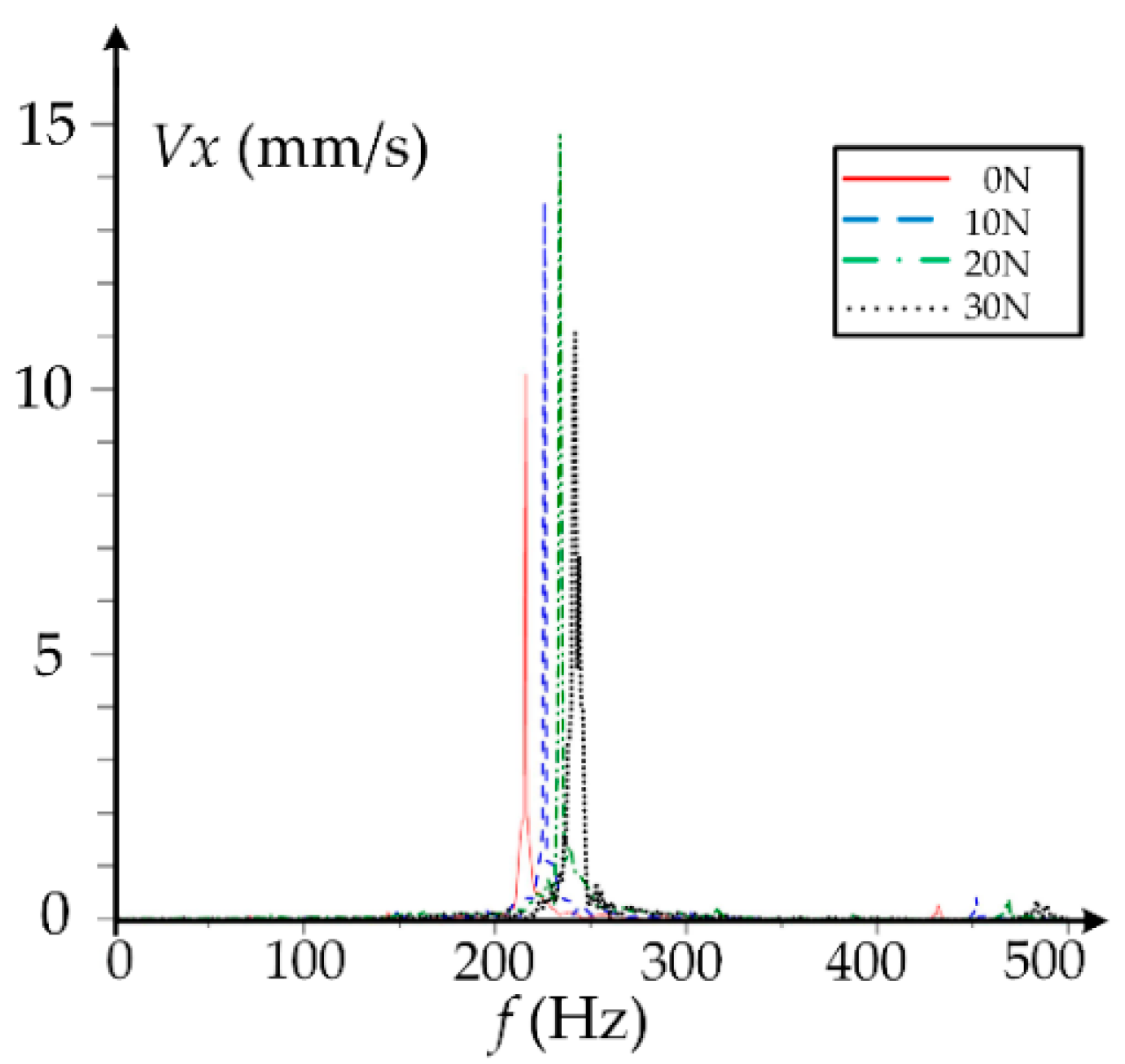
| Item | Value |
|---|---|
| Outer ring diameter (mm) | 75 |
| Inner ring diameter (mm) | 45 |
| Ball number | 18 |
| Nominal Ball diameter (mm) | 8 |
| Initial contact angle (degree) | 15 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Wu, X.; Bai, X.; Wang, Z.; Zou, D.; Sun, J. Effect of the Lubrication Parameters on the Ceramic Ball Bearing Vibration in Starved Conditions. Appl. Sci. 2020, 10, 1237. https://doi.org/10.3390/app10041237
Zhang K, Wu X, Bai X, Wang Z, Zou D, Sun J. Effect of the Lubrication Parameters on the Ceramic Ball Bearing Vibration in Starved Conditions. Applied Sciences. 2020; 10(4):1237. https://doi.org/10.3390/app10041237
Chicago/Turabian StyleZhang, Ke, Xianchao Wu, Xiaotian Bai, Zinan Wang, Defang Zou, and Jie Sun. 2020. "Effect of the Lubrication Parameters on the Ceramic Ball Bearing Vibration in Starved Conditions" Applied Sciences 10, no. 4: 1237. https://doi.org/10.3390/app10041237
APA StyleZhang, K., Wu, X., Bai, X., Wang, Z., Zou, D., & Sun, J. (2020). Effect of the Lubrication Parameters on the Ceramic Ball Bearing Vibration in Starved Conditions. Applied Sciences, 10(4), 1237. https://doi.org/10.3390/app10041237





