Seismic Response Mitigation of Base-Isolated Buildings
Abstract
1. Introduction
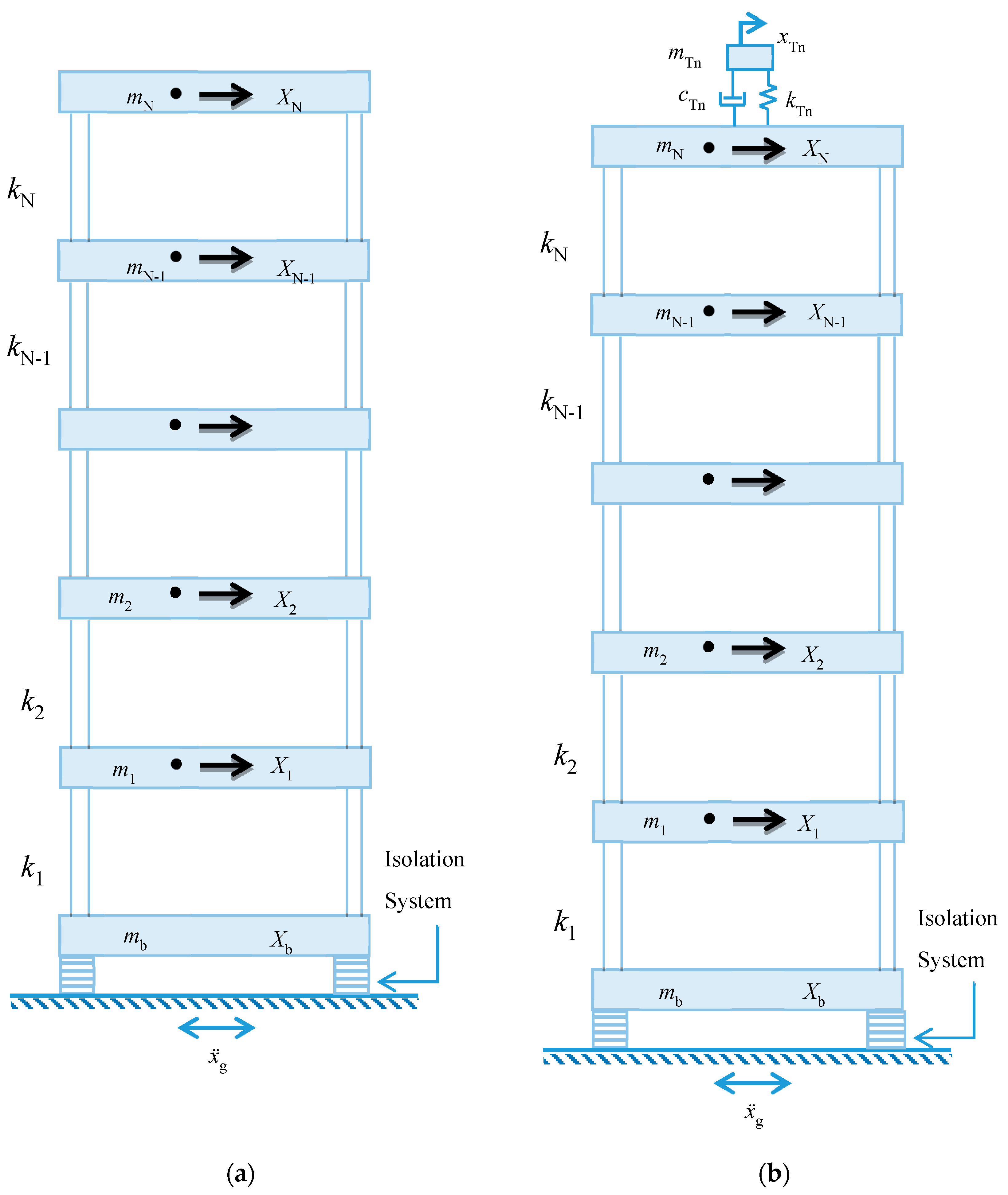
2. Structural Model
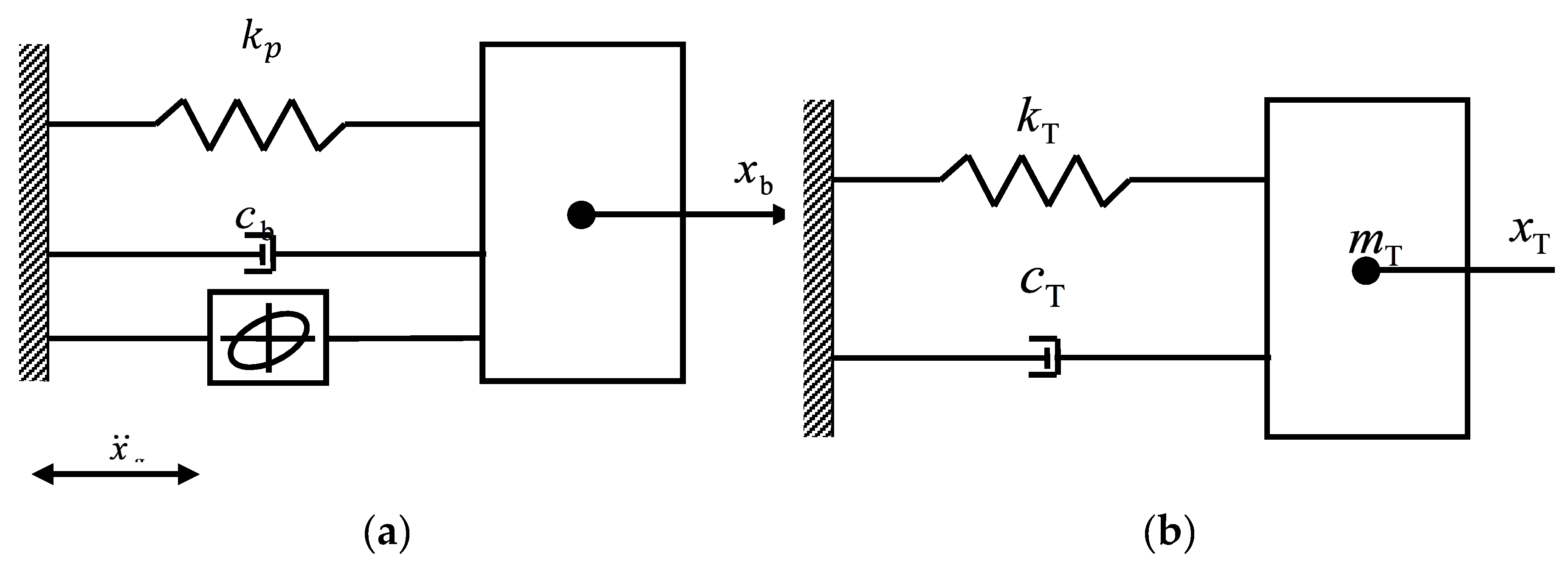
3. Mathematical Model of Isolator
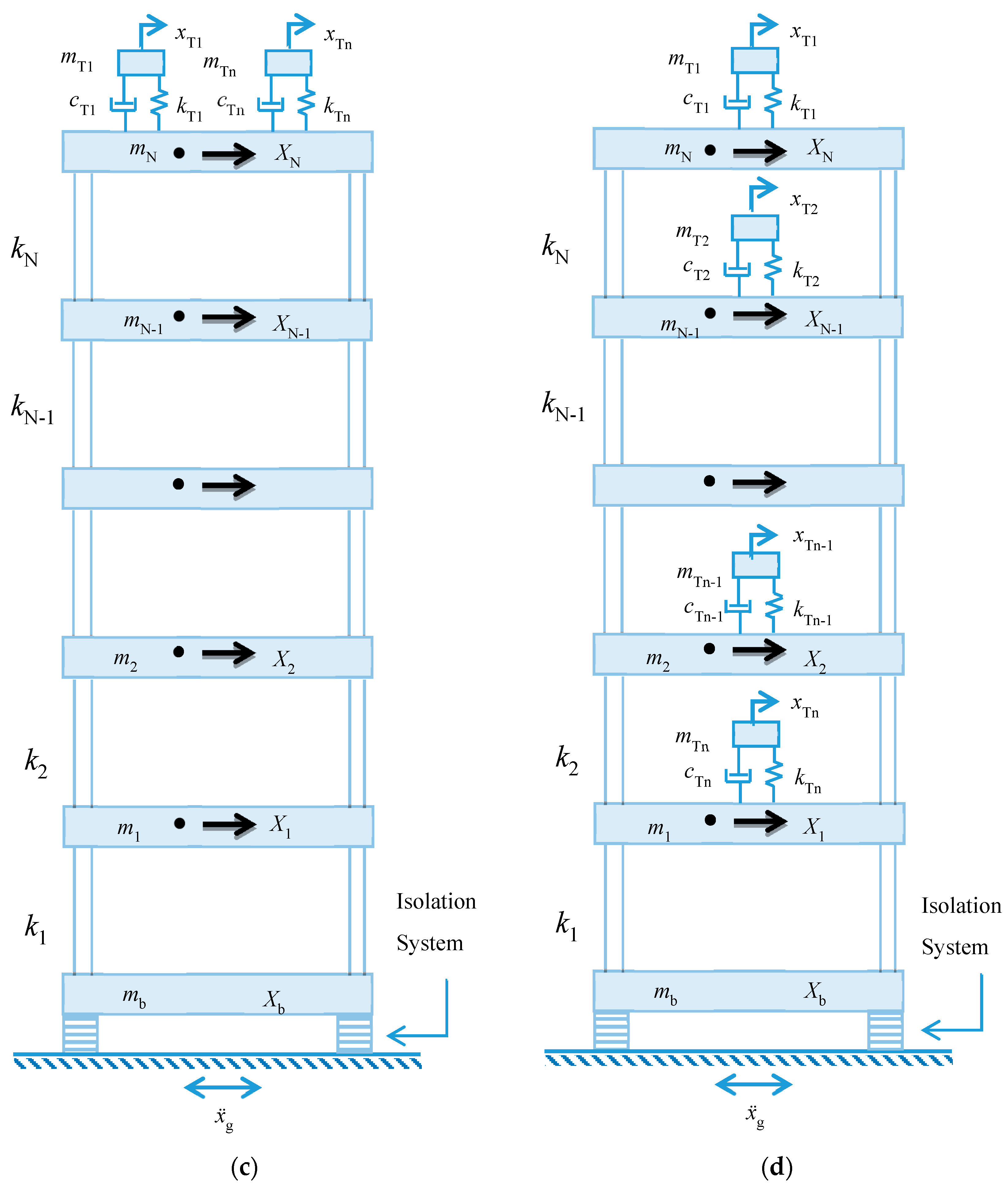
4. Mathematical Model of the TMD
5. Numerical Study
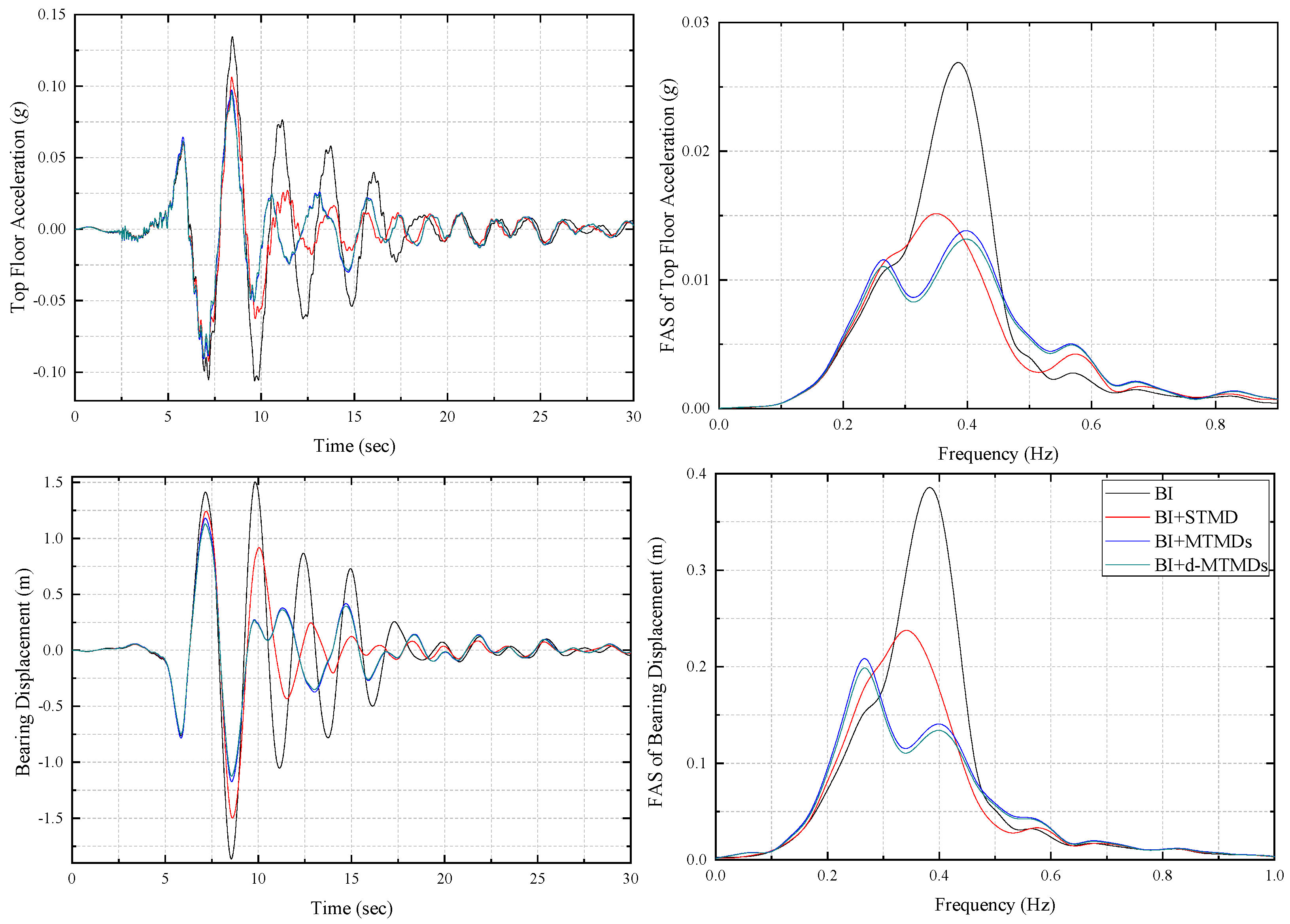
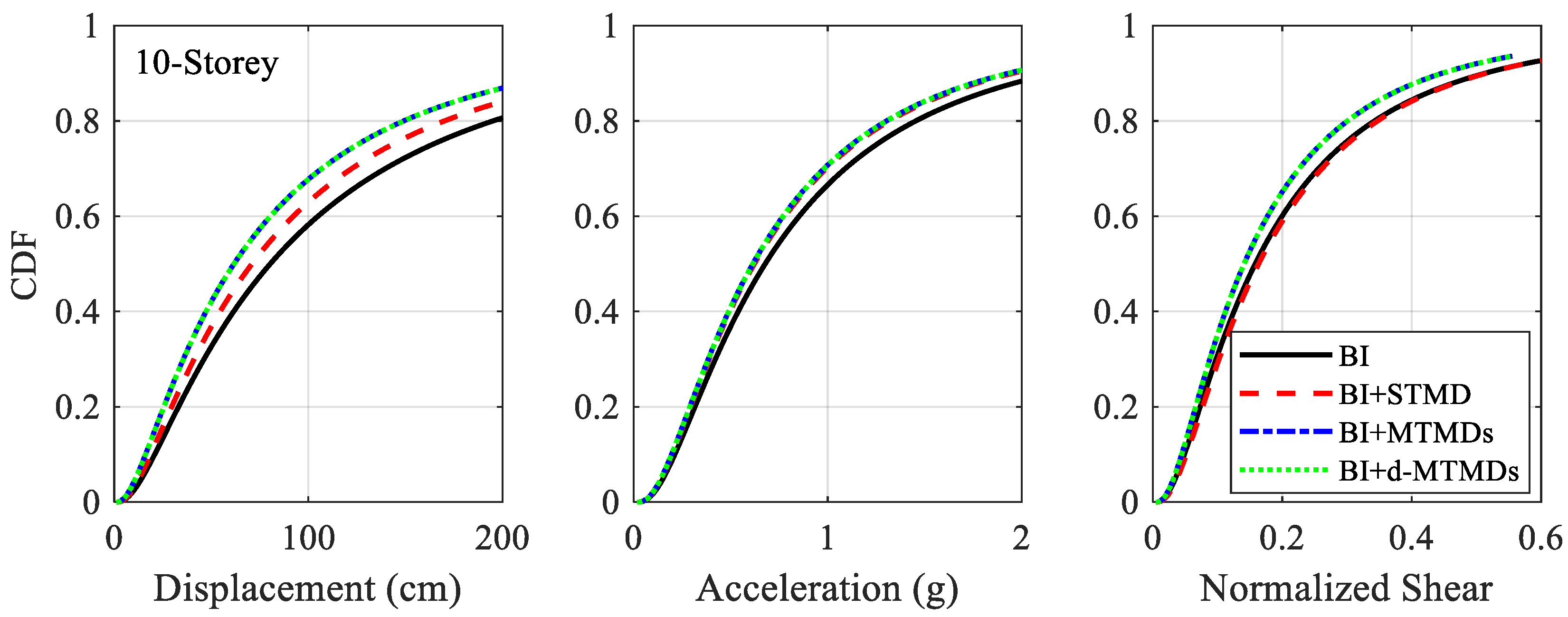
5.1. Performance of TMDs in Response Mitigation
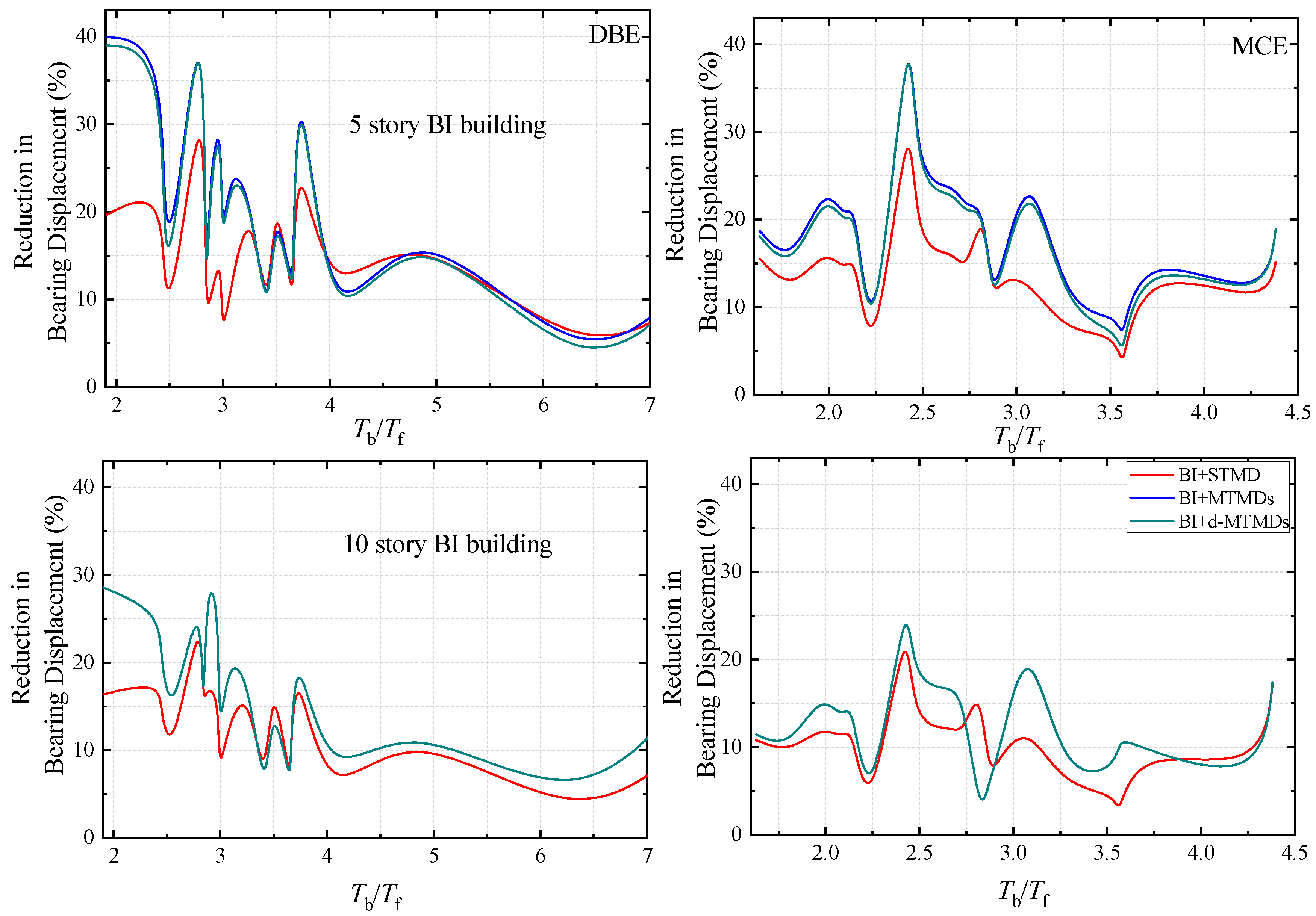
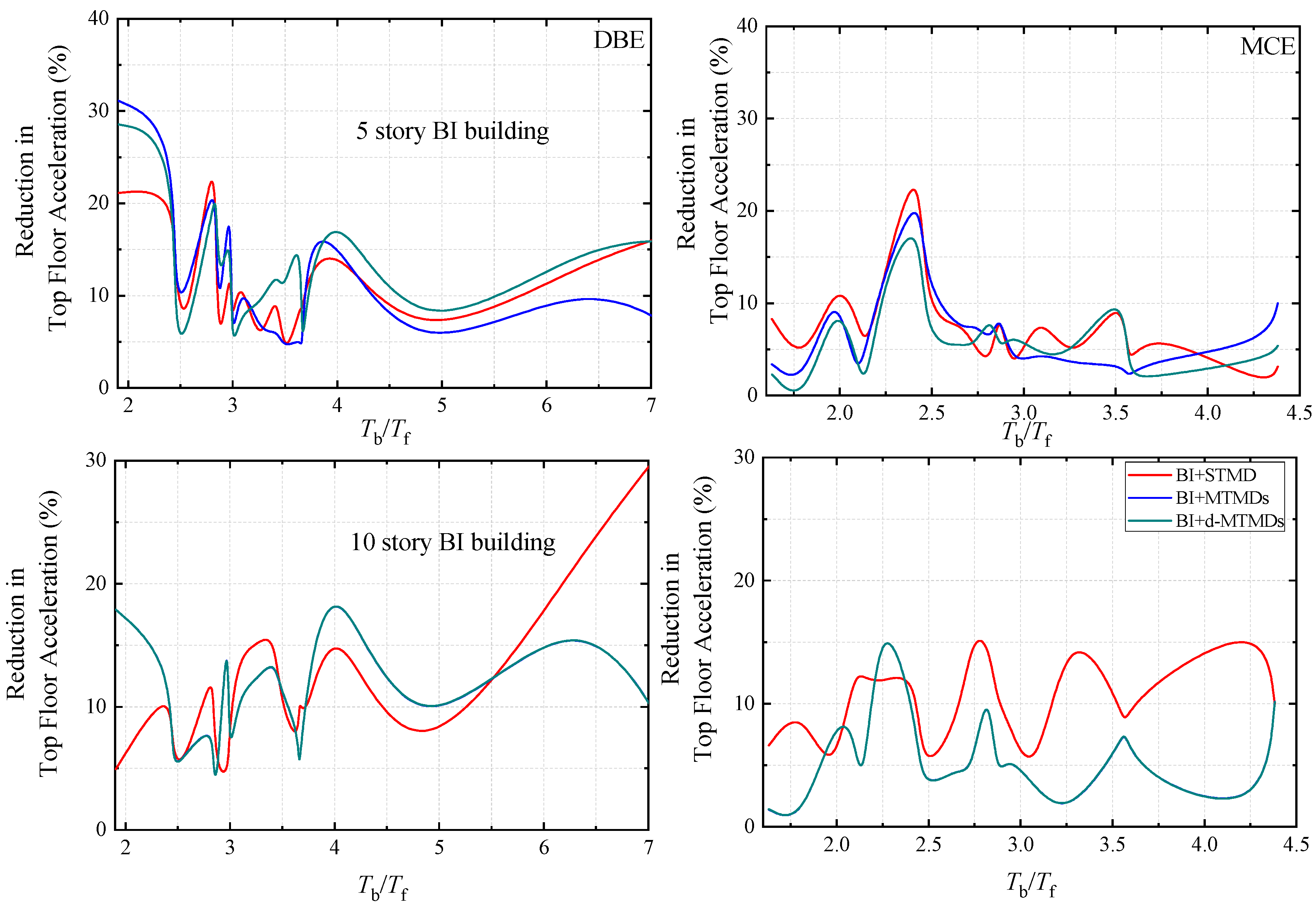
5.2. Seismic Effectiveness of Hybrid System
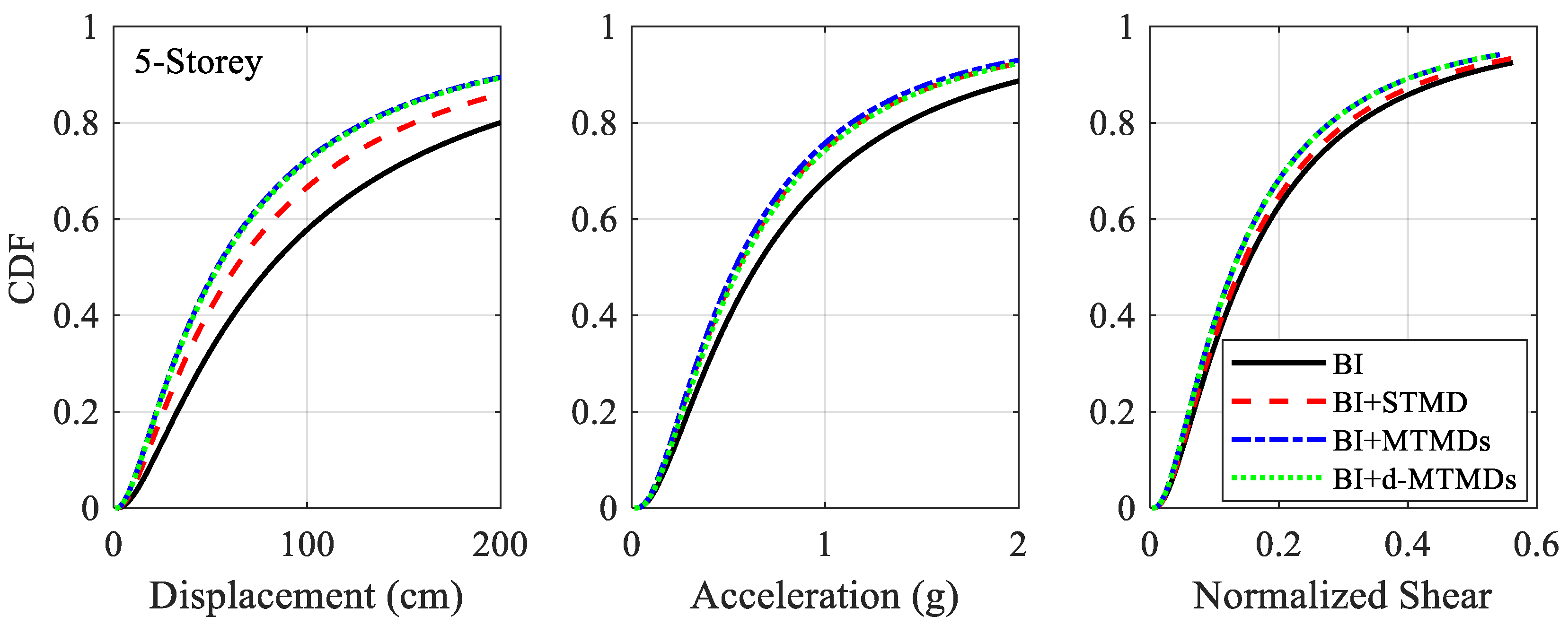
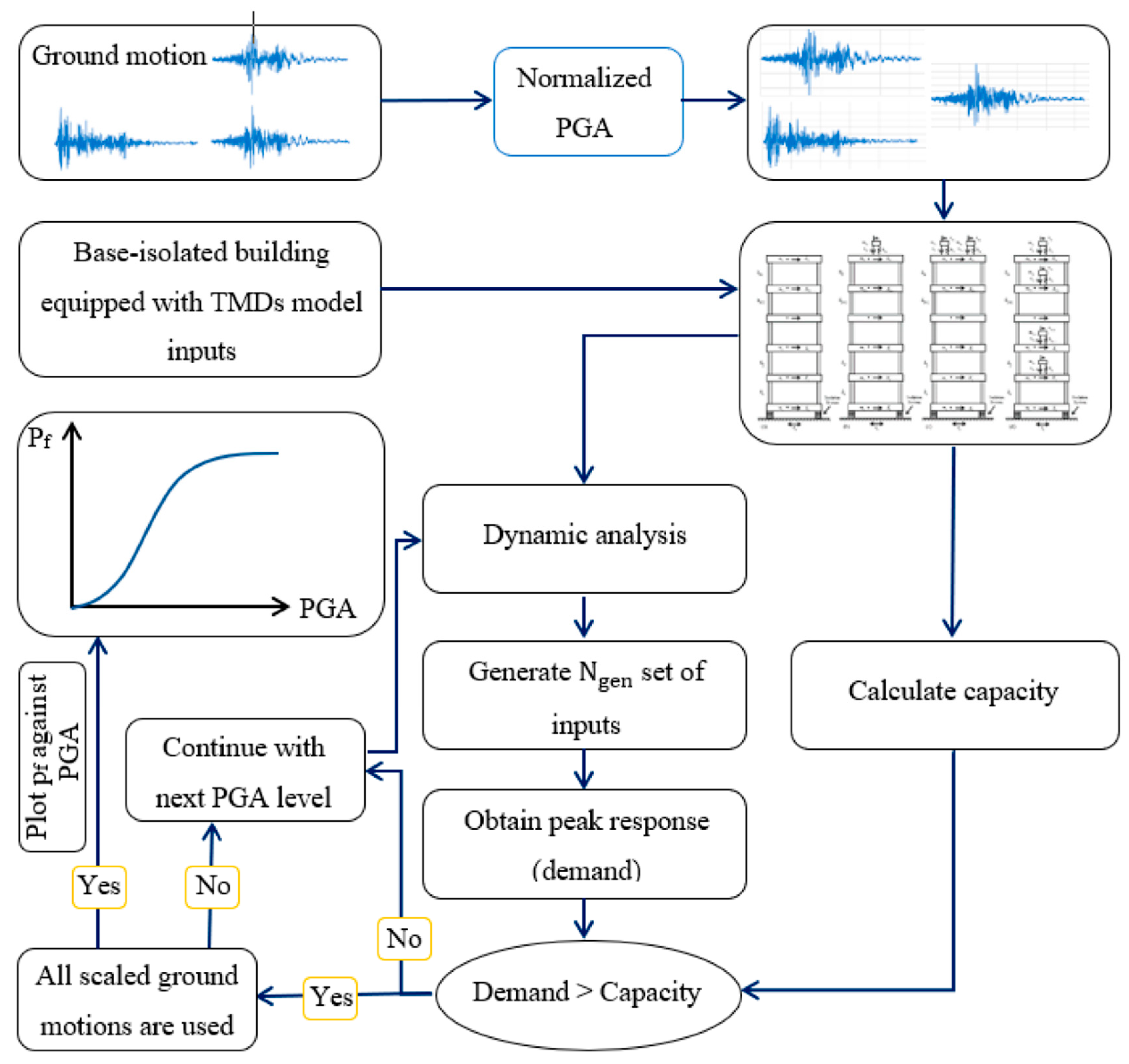
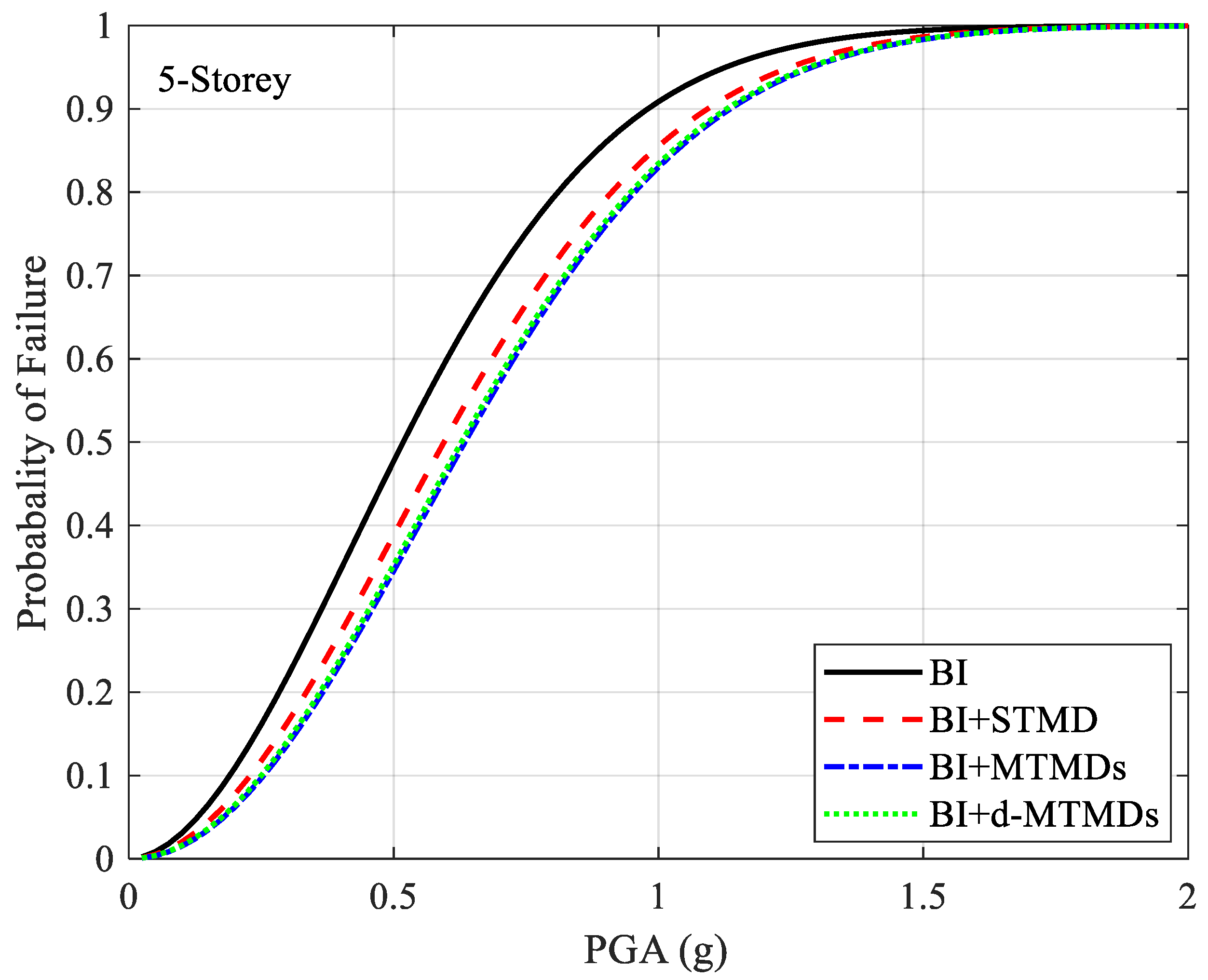
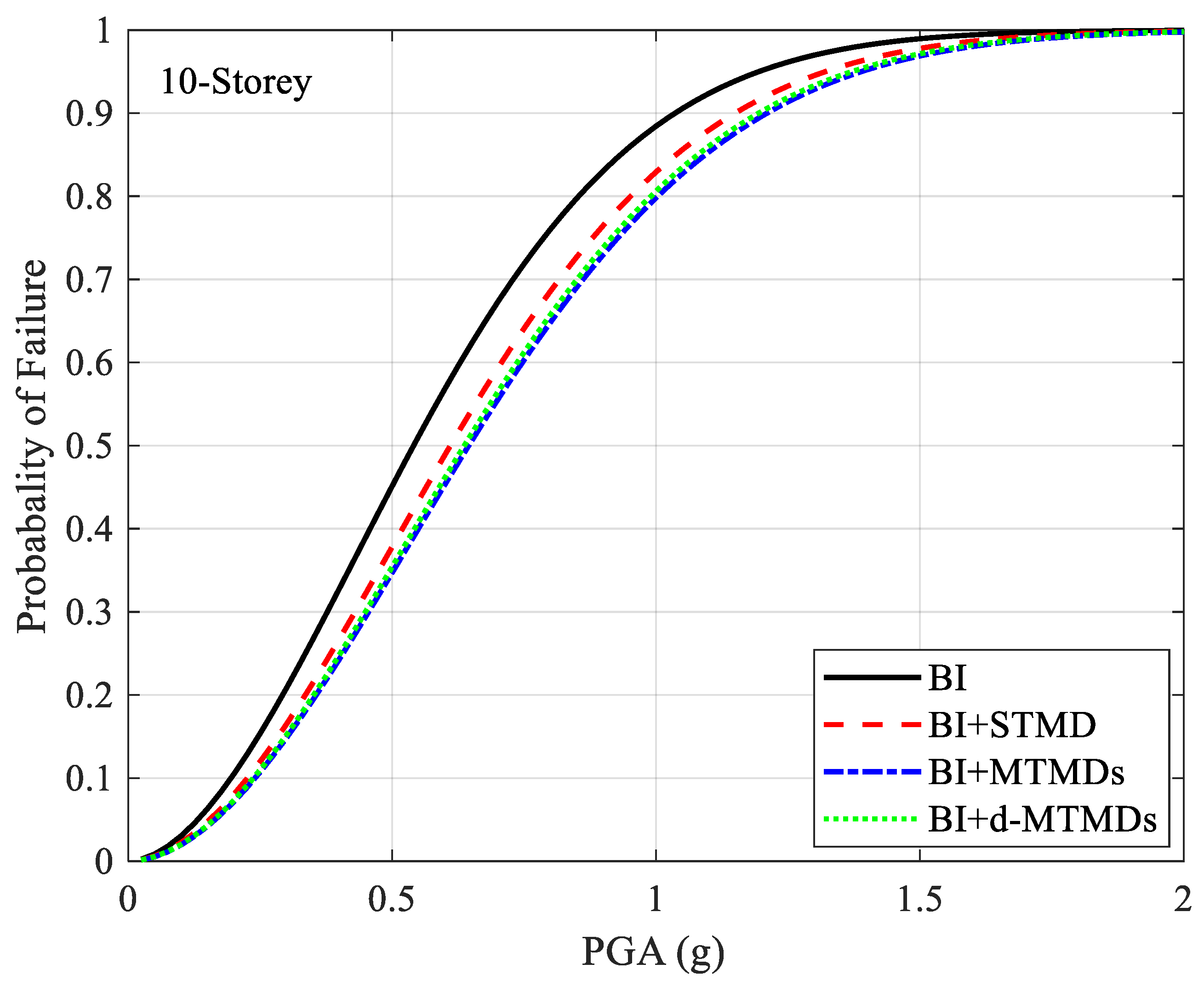
5.3. Seismic Fragility Analysis
6. Conclusions
- TMD schemes are can be used to control bearing displacement of BI buildings subjected to earthquake ground excitations without compromising the control in acceleration response achieved by BI.
- MTMDs and d-MTMDs are marginally better than STMD in controlling the bearing displacement of the BI building. The effectiveness of MTMDs and d-MTMDs are same as STMD for mitigating top floor acceleration.
- The TMD schemes reduce the fragility of the structure by about 5% in a wide range of PGA of 0.5g to 1g. For weaker and stronger shaking, the reduction in fragility is not significant. It is to be noted that the TMDs used in this study are not optimized for specific type of ground motions and might experience detuning effects for some ground motions. Designing such TMDs based on effective period of vibration of a structure for a well-established target displacement obtained from appropriate hazard analysis might provide additional benefits.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Greco, R.; Marano, G.C. Optimum design of Tuned Mass Dampers by displacement and energy perspectives. Soil Dyn. Earthq. Eng. 2013, 49, 243–253. [Google Scholar] [CrossRef]
- Longarini, N.; Zucca, M. A chimney’s seismic assessment by a tuned mass damper. Eng. Struct. 2014, 79, 290–296. [Google Scholar] [CrossRef]
- Reggio, A.; Angelis, M.D. Optimal energy-based seismic design of non-conventional Tuned Mass Damper (TMD) implemented via inter-story isolation. Earthq. Eng. Struct. Dyn. 2015, 44, 1623–1642. [Google Scholar] [CrossRef]
- Lu, Z.; Li, K.; Zhou, Y. Comparative Studies on Structures with a Tuned Mass Damper and a Particle Damper. J. Aerosp. Eng. 2018, 31, 04018090. [Google Scholar] [CrossRef]
- Rezaee, M.; Aly, A.M. Vibration Control in Wind Turbines to Achieve De-sired System-Level Performance under Single and Multiple Hazard Loadings. Struct. Control Health Monit. 2018. [Google Scholar] [CrossRef]
- Wang, C.; Shi, W. Optimal Design and Application of a Multiple Tuned Mass Damper System for an In-Service Footbridge. Sustainability 2019, 11, 2801. [Google Scholar] [CrossRef]
- Cao, L.; Li, C. Tuned tandem mass dampers-Inerters with broadband high effectiveness for structures under white noise base excitations. Struct. Control Health Monit. 2019, 26, e2319. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V.; Datta, T.K. Effectiveness of distributed tuned mass dampers for multi-mode control of chimney under earthquakes. Eng. Struct. 2016, 124, 1–16. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V.; Datta, T.K. Distributed tuned mass dampers for multi-mode control of benchmark building under seismic excitations. J. Earthq. Eng. 2019, 23, 1137–1172. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V.; Datta, T.K. Along-Wind response control of chimneys with distributed multiple tuned mass dampers. Struct. Control Health Monit. 2019, 26, e2275. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V.; Datta, T.K. Dynamic response control of a wind-excited tall building with distributed multiple tuned mass dampers. Int. J. Struct. Stab. Dyn. 2019, 19, 1950059. [Google Scholar] [CrossRef]
- Gill, D.; Elias, S.; Steinbrecher, A.; Schröder, C.; Matsagar, V. Robustness of multi-mode control using tuned mass dampers for seismically excited structures. Bull. Earthq. Eng. 2017, 15, 5579–5603. [Google Scholar] [CrossRef]
- Elias, S. Seismic energy assessment of buildings with tuned vibration absorbers. Shock Vib. 2018, 2018. [Google Scholar] [CrossRef]
- Elias, S. Effect of SSI on vibration control of structures with tuned vibration absorbers. Shock Vib. 2019, 2019. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Seismic vulnerability of non-linear building with distributed multiple tuned vibration absorbers. Struct. Infrastruct. Eng. 2019, 15. [Google Scholar] [CrossRef]
- Matin, A.; Elias, S.; Matsagar, V. Distributed multiple tuned mass dampers for seismic response control in bridges. Proc. Inst. Civ. Eng. Struct. Build. 2019, 1–18. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 2017, 44, 129–156. [Google Scholar] [CrossRef]
- Zelleke, D.H.; Elias, S.; Matsagar, V.A.; Jain, A.K. Supplemental Dampers in Base-Isolated Buildings to Mitigate Large Isolator Displacement Under Earthquake Excitations. Bull. N. Z. Soc. Earthq. Eng. 2015, 48, 100–117. [Google Scholar] [CrossRef]
- Tsai, H. The Effect of Tuned-Mass Dampers on the Seismic Response of Base-Isolated Structures. Int. J. Solid Struct. 1995, 32, 1199–1210. [Google Scholar] [CrossRef]
- Yang, J.; Danielianns, A.; Liu, S. Aseismic Hybrid Control Systems for Building Structures. J. Eng. Mech. 1991, 117, 836–853. [Google Scholar] [CrossRef]
- Xiang, P.; Nishitani, A. Optimally Design for More Effective Tuned Mass Damper and Its Application to Base-Isolated Buildings. Struct. Control Health Monit. 2014, 21, 98–114. [Google Scholar] [CrossRef]
- De Domenico, D.; Deastra, P.; Ricciardi, G.; Sims, N.D.; Wagg, D.J. Novel fluid inerter based tuned mass dampers for optimised structural control of base-isolated buildings. J. Frankl. Inst. 2018, 356, 7626–7649. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Optimal design and seismic performance of tuned mass damper inerter (TMDI) for structures with nonlinear base isolation systems. Earthq. Eng. Struct. Dyn. 2018, 47, 2539–2560. [Google Scholar]
- De Domenico, D.; Ricciardi, G. An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthq. Eng. Struct. Dyn. 2018, 47, 1169–1192. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Earthquake-resilient design of base isolated buildings with TMD at basement: Application to a case study. Soil Dyn. Earthq. Eng. 2018, 113, 503–521. [Google Scholar] [CrossRef]
- Rabiee, R.; Chae, Y. Adaptive Base-isolation System to Achieve Structural Resiliency under Both Short-and Long-period Earthquake Ground Motions. J. Intell. Mater. Syst. Struct. 2019, 30, 16–31. [Google Scholar] [CrossRef]
- Stanikzai, M.H.; Elias, S.; Matsagar, V.A.; Jain, A.K. Seismic response control of base-isolated buildings using tuned mass damper. Aust. J. Struct. Eng. 2019, 1–12. [Google Scholar] [CrossRef]
- Stanikzai, M.H.; Elias, S.; Matsagar, V.A.; Jain, A.K. Seismic Response Control of Base-Isolated Buildings Using Multiple Tuned Mass Dampers. Struct. Des. Tall Spec. Build. 2019, 28, e1576. [Google Scholar] [CrossRef]
- Bertero, V.V. Strength and Deformation Capacities of Buildings under Extreme Environments. Struct. Eng. Struct. Mech. 1977, 53, 29–79. [Google Scholar]
- Kennedy, R.P.; Cornell, C.; Campbell, R.; Kaplan, S.; Perla, H. Probabilistic Seismic Safety Study of An Existing Nuclear Power Plant. Nuclear Eng. Des. 1980, 59, 315–338. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, C.A. Seismic Hazard Analysis for Non-linear Structures. II: Applications. ASCE J. Struct. Eng. 1994, 120, 3345–3365. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, C.A. Seismic Hazard Analysis for Non-linear Structures. I: Methodology. ASCE J. Struct. Eng. 1994, 120, 3320–3344. [Google Scholar] [CrossRef]
- Luco, N.; Cornell, C.A. Effects of random connection fractures on demands and reliability for a 3-story pre-Northridge SMRF structure. In Proceedings of the 6th U.S. National Conference on Earthquake Engineering; paper 244; EERI: El Cerrito, CA, USA; Seattle, DC, USA, 1998; pp. 1–12. [Google Scholar]
- Luco, N.; Cornell, C.A. Effects of Connection Fractures on SMRF Seismic Drift Demands. ASCE J. Struct. Eng. 2000, 126, 127–136. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- FEMA. Recommended Seismic Design Criteria for New Steel Moment-Frame Buildings; Report No. FEMA-350, SAC Joint Venture; Federal Emergency Management Agency: Washington, DC, USA, 2000.
- FEMA. Recommended Seismic Evaluation and Upgrade Criteria for Existing Welded Steel Moment-Frame Buildings; Report No. FEMA-351, SAC Joint Venture; Federal Emergency Management Agency: Washington, DC, USA, 2000.
- Wen, Y.K. Method for random vibration of hysteretic systems. J. Eng. Mech. Am. Soc. Civ. Eng. 1976, 102, 249–263. [Google Scholar]
- Sadek, F.; Mohraz, B.; Taylor, A.W.; Chung, R.M. A Method of Estimating the Parameters of Tuned Vibration Absorbers for Seismic applications. Earthq. Eng. Struct. Dyn. 1997, 26, 617–635. [Google Scholar] [CrossRef]
- Matsagar, V.A.; Jangid, R.S. Influence of isolator characteristics on the response of base-isolated structures. Eng. Struct. 2004, 26, 1735–1749. [Google Scholar] [CrossRef]
- Somerville, P.G.; Smith, M.; Punyamurthula, S.; Sun, J. Development of Ground Motion Time Histories for Phase 2 of the FEMA/SAC Steel Project; Report. No. SAC/BD-97/ 04; SAC Joint Venture: Sacramento, CA, USA, 1997. [Google Scholar]
- Bhandari, M.; Bharati, S.D.; Sharimali, M.K.; Datta, T.K. Assessment of Proposed Lateral Load Patterns in Pushover Analysis for Base-isolated Frames. Eng. Struct. 2018, 175, 531–548. [Google Scholar] [CrossRef]
- Rathje, E.M.; Faraj, F.; Russell, S.; Bray, J.D. Empirical relationships for frequency content parameters of earthquake ground motions. Earthq. Spectra 2004, 20, 119–144. [Google Scholar] [CrossRef]
- Rupakhety, R.; Sigurdsson, S.U.; Papageorgiou, A.S.; Sigbjörnsson, R. Quantification of ground-motion parameters and response spectra in the near-fault region. Bull. Earthq. Eng. 2011, 9, 893–930. [Google Scholar] [CrossRef]
- Quaglini, V.; Dubini, P.; Furinghetti, M.; Pavese, A. Assessment of Scale Effects in the Experimental Evaluation of the Coefficient of Friction of Sliding Isolators. J. Earthq. Eng. 2019, 1–21. [Google Scholar] [CrossRef]
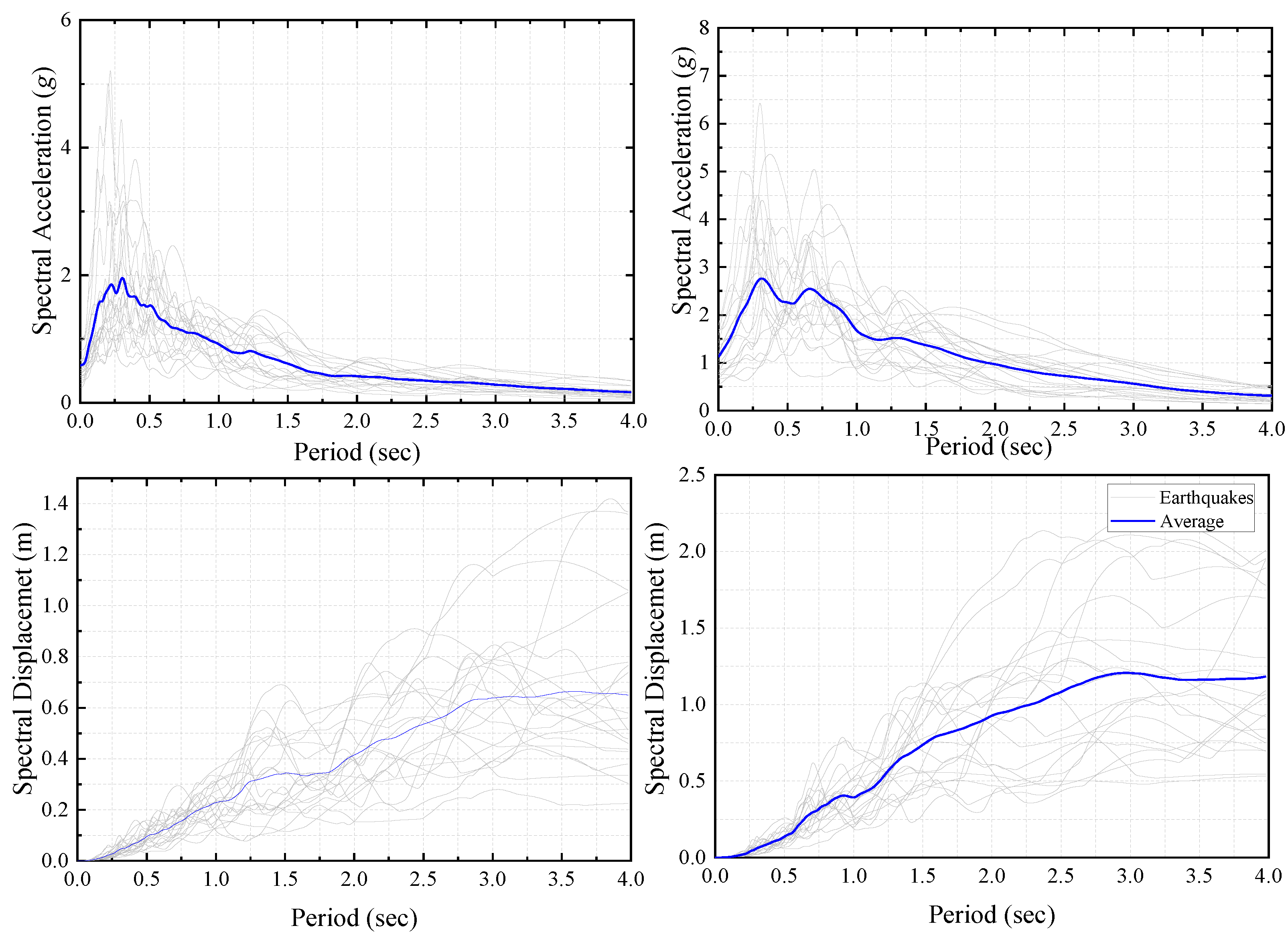
| SAC Name | Record | Year | Earthquake Magnitude | Distance (km) | Scale Factor | Number of points | ∆t (s) | Duration (s) | PGA (g) |
|---|---|---|---|---|---|---|---|---|---|
| LA01 | Imperial Valley | 1940 | 6.9 | 10 | 2.01 | 2674 | 0.02 | 53.46 | 0.46 |
| LA02 | Imperial Valley | 1940 | 6.9 | 10 | 2.01 | 2674 | 0.02 | 53.46 | 0.68 |
| LA03 | Imperial Valley | 1979 | 6.5 | 4.1 | 1.01 | 3939 | 0.01 | 39.38 | 0.39 |
| LA04 | Imperial Valley | 1979 | 6.5 | 4.1 | 1.01 | 3939 | 0.01 | 39.38 | 0.49 |
| LA05 | Imperial Valley | 1979 | 6.5 | 1.2 | 0.84 | 3909 | 0.01 | 39.08 | 0.3 |
| LA06 | Imperial Valley | 1979 | 6.5 | 1.2 | 0.84 | 3909 | 0.01 | 39.08 | 0.23 |
| LA07 | Landers | 1992 | 7.3 | 36 | 3.2 | 4000 | 0.02 | 79.98 | 0.42 |
| LA08 | Landers | 1992 | 7.3 | 36 | 3.2 | 4000 | 0.02 | 79.98 | 0.43 |
| LA09 | Landers | 1992 | 7.3 | 25 | 2.17 | 4000 | 0.02 | 79.98 | 0.52 |
| LA10 | Landers | 1992 | 7.3 | 25 | 2.17 | 4000 | 0.02 | 79.98 | 0.36 |
| LA11 | Loma Prieta | 1989 | 7 | 12 | 1.79 | 2000 | 0.02 | 39.98 | 0.67 |
| LA12 | Loma Prieta | 1989 | 7 | 12 | 1.79 | 2000 | 0.02 | 39.98 | 0.97 |
| LA13 | Northridge | 1994 | 6.7 | 6.7 | 1.03 | 3000 | 0.02 | 59.98 | 0.68 |
| LA14 | Northridge | 1994 | 6.7 | 6.7 | 1.03 | 3000 | 0.02 | 59.98 | 0.66 |
| LA15 | Northridge | 1994 | 6.7 | 7.5 | 0.79 | 2990 | 0.005 | 14.945 | 0.53 |
| LA16 | Northridge | 1994 | 6.7 | 7.5 | 0.79 | 2990 | 0.005 | 14.945 | 0.58 |
| LA17 | Northridge | 1994 | 6.7 | 6.4 | 0.99 | 3000 | 0.02 | 59.98 | 0.57 |
| LA18 | Northridge | 1994 | 6.7 | 6.4 | 0.99 | 3000 | 0.02 | 59.98 | 0.82 |
| LA19 | North Palm Springs | 1986 | 6 | 6.7 | 2.97 | 3000 | 0.02 | 59.98 | 1.02 |
| LA20 | North Palm Springs | 1986 | 6 | 6.7 | 2.97 | 3000 | 0.02 | 59.98 | 0.99 |
| ZSAC Name | Record | Year | Earthquake Magnitude | Distance (km) | Scale Factor | Number of Points | ∆t (s) | Duration (s) | PGA (g) |
|---|---|---|---|---|---|---|---|---|---|
| LA21 | Kobe | 1995 | 6.9 | 3.4 | 1.15 | 3000 | 0.02 | 59.98 | 1.28 |
| LA22 | Kobe | 1995 | 6.9 | 3.4 | 1.15 | 3000 | 0.02 | 59.98 | 0.92 |
| LA23 | Loma Prieta | 1989 | 7 | 3.5 | 0.82 | 2500 | 0.01 | 24.99 | 0.42 |
| LA24 | Loma Prieta | 1989 | 7 | 3.5 | 0.82 | 2500 | 0.01 | 24.99 | 0.47 |
| LA25 | Northridge | 1994 | 6.7 | 7.5 | 1.29 | 2990 | 0.005 | 14.945 | 0.87 |
| LA26 | Northridge | 1994 | 6.7 | 7.5 | 1.29 | 2990 | 0.005 | 14.945 | 0.94 |
| LA27 | Northridge | 1994 | 6.7 | 6.4 | 1.61 | 3000 | 0.02 | 59.98 | 0.93 |
| LA28 | Northridge | 1994 | 6.7 | 6.4 | 1.61 | 3000 | 0.02 | 59.98 | 1.33 |
| LA29 | Tabas, | 1974 | 7.4 | 1.2 | 1.08 | 2500 | 0.02 | 49.98 | 0.81 |
| LA30 | Tabas, | 1974 | 7.4 | 1.2 | 1.08 | 2500 | 0.02 | 49.98 | 0.99 |
| LA31 | Elysian Park (simulated) | 7.1 | 17.5 | 1.43 | 3000 | 0.01 | 29.99 | 1.3 | |
| LA32 | Elysian Park (simulated) | 7.1 | 17.5 | 1.43 | 3000 | 0.01 | 29.99 | 1.19 | |
| LA33 | Elysian Park (simulated) | 7.1 | 10.7 | 0.97 | 3000 | 0.01 | 29.99 | 0.78 | |
| LA34 | Elysian Park (simulated) | 7.1 | 10.7 | 0.97 | 3000 | 0.01 | 29.99 | 0.68 | |
| LA35 | Elysian Park (simulated) | 7.1 | 11.2 | 1.1 | 3000 | 0.01 | 29.99 | 0.99 | |
| LA36 | Elysian Park (simulated) | 7.1 | 11.2 | 1.1 | 3000 | 0.01 | 29.99 | 1.1 | |
| LA37 | Palos verdes (simulated) | 7.1 | 1.5 | 0.9 | 3000 | 0.02 | 59.98 | 0.71 | |
| LA38 | Palos verdes (simulated) | 7.1 | 1.5 | 0.9 | 3000 | 0.02 | 59.98 | 0.78 | |
| LA39 | Palos verdes (simulated) | 7.1 | 1.5 | 0.88 | 3000 | 0.02 | 59.98 | 0.5 | |
| LA40 | Palos verdes (simulated) | 7.1 | 1.5 | 0.88 | 3000 | 0.02 | 59.98 | 0.63 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanikzai, M.H.; Elias, S.; Rupakhety, R. Seismic Response Mitigation of Base-Isolated Buildings. Appl. Sci. 2020, 10, 1230. https://doi.org/10.3390/app10041230
Stanikzai MH, Elias S, Rupakhety R. Seismic Response Mitigation of Base-Isolated Buildings. Applied Sciences. 2020; 10(4):1230. https://doi.org/10.3390/app10041230
Chicago/Turabian StyleStanikzai, Mohammad Hamayoun, Said Elias, and Rajesh Rupakhety. 2020. "Seismic Response Mitigation of Base-Isolated Buildings" Applied Sciences 10, no. 4: 1230. https://doi.org/10.3390/app10041230
APA StyleStanikzai, M. H., Elias, S., & Rupakhety, R. (2020). Seismic Response Mitigation of Base-Isolated Buildings. Applied Sciences, 10(4), 1230. https://doi.org/10.3390/app10041230







