A Radial-In-Plane Sensitivity Interferometer with Divergent Illumination for Displacement Measurement

Abstract

An in-plane radial sensitivity interferometer that uses the divergent illumination for displacement measurement in the radial direction is presented. A description and mathematical model for calculating the sensitivity vector are also presented. The interferometer has two polarizing filters: a circular one and a linear one to implement the phase stepping technique. A measurement of the radial deformation by thermal expansion is performed over an aluminium plate in order to test the interferometer. The results indicate that the maximum contribution of the out-of-plane with respect to the radial-in-plane sensitivity vector is less than 3% and decreases by less than 1% when measurements are performed near the optical axis. The measurement is compared with the results obtained by a finite element analysis on a virtual specimen model.

1. Introduction

Many studies employ Electronic Speckle Pattern Interferometry (ESPI) for the measurement of displacements, deformations, and surface shape. The optical system used in ESPI can be configured to favour displacement measurements in a certain direction. Usually, measurements are made by observing perpendicular or parallel displacements to an observer plane. Therefore, the technique is typically divided into two types of interferometers according to the main sensitivity vector direction of the optical system: in-plane and out-of-plane sensitivity interferometers. Robert Jones et al. show several techniques based on ESPI and holographic interferometry ESPI, as well as an optical configuration for several interferometric systems [1].

ESPI is an instrumental technique for full-field displacement and surface topography measuring when it is not possible to make contact with the object. This technique is highly accurate in recording measurements, and its resolution can be adjusted in a wide range, from nanometres to micrometres [2]. ESPI is widely used as a non-destructive test in mechanical elements [3], vibration analysis [4], dynamic deformation analysis [5,6], and surface topometric measurement [7]. Unfortunately, optical configurations in ESPI can only record displacement in one direction, making it necessary to employ an optical system for each direction of the displacement—preferably orthogonal and simultaneous ones. To measure the mechanical stresses around a crack, it is necessary to determine the deformation in the radial direction on the edge of the crack tip [8]. Since determining the direction in which displacement occurs is essential to the study of deformations, several methods have been proposed to overcome this limitation. Hua Fan et al. [9], A.J. Moore et al. [10], Guillaume Richoz et al. [11], and David-Ignacio Serrano-Garcia et al. [12] show distinct approaches to simultaneous orthogonal deformation measurements based on ESPI, and using different elements, such as polarizers, alternating measurements between optical systems, and simultaneous illumination with different wavelengths and interferometers.

On the other hand, Matías R. Viotti et al. and A. Albertazzi et al. introduced a device based on two conic mirrors and collimated illumination to measure residual stresses by interferometry with radial-in-plane sensitivity [13,14,15]. The conic mirrors are interconnected with piezoelectric actuators, which are needed to implement the phase shift technique to find the deformation-associated optical phase. To diminish the measurement mistakes due to the wavefront of illumination, it is necessary to keep the radial direction of the sensitivity vector consistent by using collimated illumination over the full conic mirror surface. This becomes increasingly expensive if the outer diameter of the conic mirror is large because it requires a collimating lens with the same diameter. In this work, we reduce costs by introducing a radial interferometer with divergent illumination that uses a linear polarizer and a one-quarter wave retarder to perform the phase shift technique by polarization [16]. With this method, we present a proposal for a solution to the problem of collimated illumination of an extended beam diameter through a simplification of the typical optical system used in radial interferometry. To verify the functionality of the radial interferometer with divergent illumination, without the need of a collimated illumination, we performed deformation measurements in a thin aluminium plate when it was heated from the rear by a point heat source. Results are compared to a finite element analysis simulation.

2. Theoretical Background

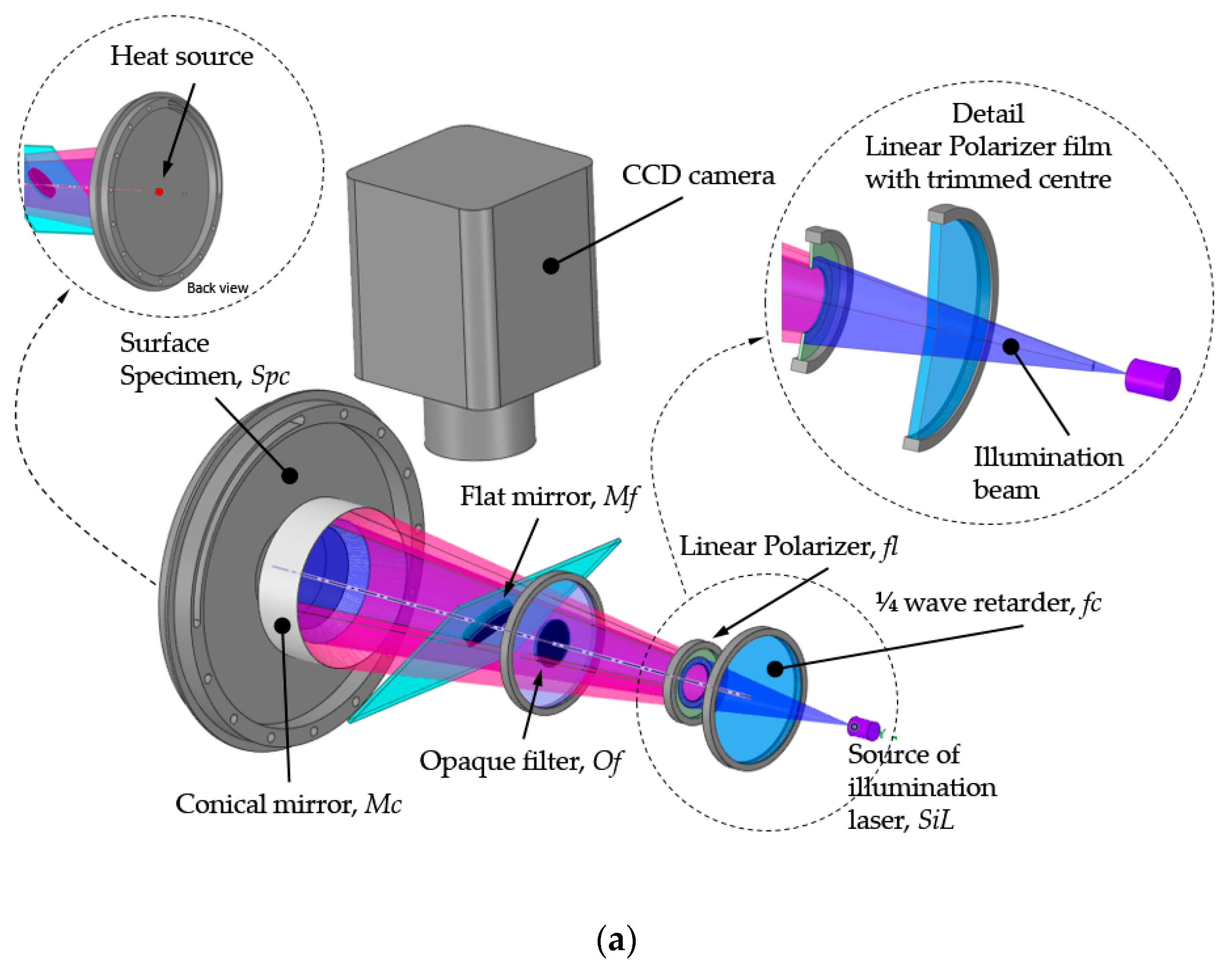
Figure 1 shows a diagram of the optical arrangement used for ESPI interferometry with radial-in-plane sensitivity. A laser illumination beam strikes an optical fibre at one end, emerging from the other end in such a way that it can be considered as a point source (spherical wavefront), which generates divergent illumination, $SiL$.

There is an extensive literature explaining the polarization phase shifting method; e.g., E. M. Frins et al. [17] show in detail the mathematical formulation, theory, and implementation of this technique. To implement our polarization phase shifting system, the illumination beam passes through a quarter-wave retarding plate ($fc$). With its fast axis tilted in a 0 rad angle, the linearly polarized filter ($fl$) is set in a $\pi /4$ rad angle in front the first polarizer filter. A ring-shaped film with linear polarization is used to polarize only the illumination beam bc reflected in the upper half of the conic mirror, while the illumination beam ac remains with the illumination passed through the one-quarter wave retarder film. An opaque body, $Of$, blocks the illumination that would otherwise strike on the observation surface. 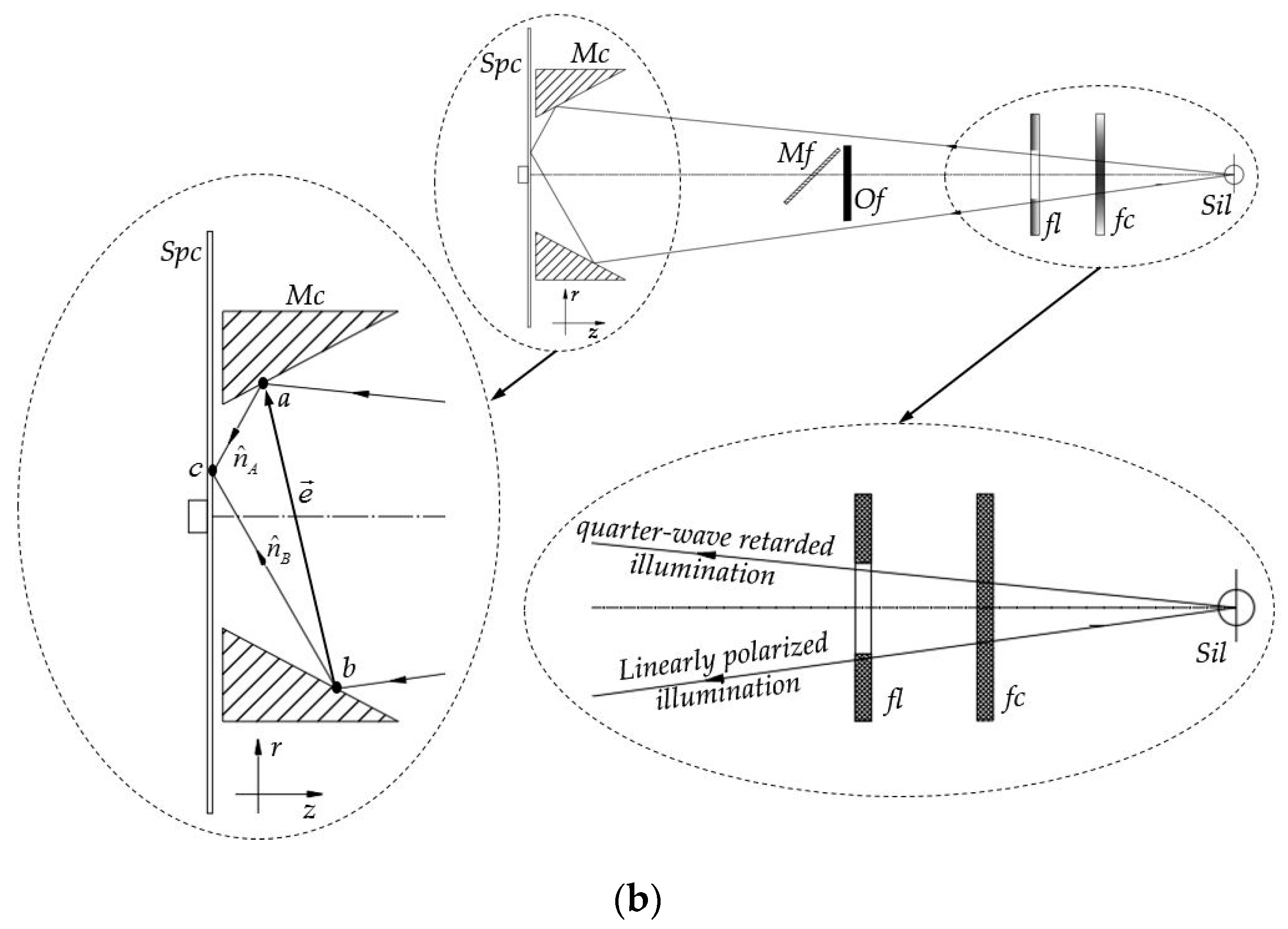A flat mirror, $Mf$, placed in front the opaque body allows for observation of the specimen surface through a charge-coupled device (CCD) camera. The two illumination beams, ac and bc, converge at point c (Figure 1b), where a Speckle pattern can be observed. The conic mirror is made from polished stainless steel and provides a way of magnifying the image of an object on an opaque screen so that it can be viewed from directly in front of the screen, with a short projecting distance necessary to produce the magnification. The central part of the specimen surface has been excluded due to the convergence of the illumination reflected by the conic mirror. The unitary vector of illumination, ${\widehat{n}}_A$, keeps a circular polarization, while the unitary vector, ${\widehat{n}}_B$, is linearly polarized. The difference between the illumination unitary vectors is related to the sensitivity vector, $\overrightarrow{e}$, by the following equation [18]:

$$\overrightarrow{e}=\frac{2\pi }{\lambda }\left({\widehat{n}}_A-{\widehat{n}}_B\right)$$

(1)

where $\lambda$ is the illumination beam’s wavelength.

The illumination unitary vectors ${\widehat{n}}_A$ and ${\widehat{n}}_B$ are obtained by considering: the polar coordinates from the illumination source, $SiL\left(r_s,0,z_s\right)$; the cutting surface of the conical mirror at points a and b, where the coordinates are $Mc\left(r_{ma},\theta ,z_{ma}\right)$ and $Mc\left(r_{mb},\theta +\pi ,z_{mb}\right),$ respectively; and, finally, a point in the plane of the specimen surface c with the coordinate $Spc\left(r_p,\theta ,z_p\right)$.

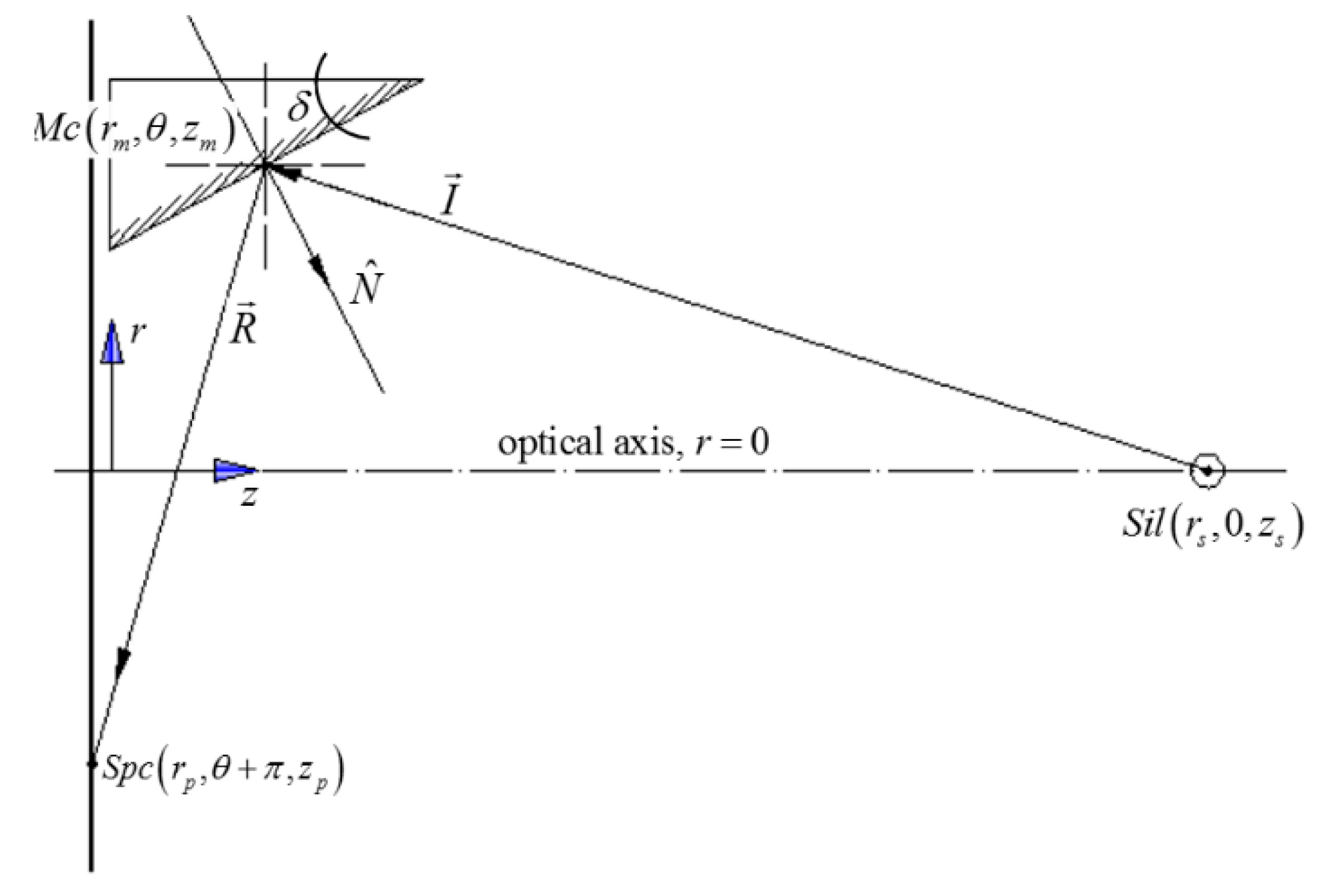
The quantities $r_s$, $z_s$, $r_p$, $z_p$, $r_{ma}$, $z_{ma}$, $r_{mb}$, and $z_{mb}$ represent radial coordinates and the z-direction of the source, the specimen, and the conic mirror at points a and b, respectively, while $\theta$ is the angular coordinate. In applying the reflection geometry in the mirror, as observed in Figure 2, we can describe the relationship for the reflection of the illumination on the conic mirror on the plane $\left(r,z\right)$ as [19]:

$${\overrightarrow{R}}_i={\overrightarrow{I}}_i-2\left({\overrightarrow{I}}_i·{\widehat{N}}_i\right){\widehat{N}}_i,i=A,B$$

(2)

where ${\overrightarrow{R}}_i$ is the illumination vector reflected by the conic mirror to the specimen surface; ${\overrightarrow{I}}_i$ is the illumination vector from the illumination source to the conic mirror; and ${\widehat{N}}_i$ is the normal unitary vector to the surface of the conic mirror, with the feature that it is a vector with a constant direction on the full surface, of which the component in cylindrical coordinates is $\widehat{N}\left(r,\theta ,z\right)=\left[\cos \left(\delta \right),\theta ,\sin \left(\delta \right)\right]$.

Considering the coordinates of each element, the illumination vectors reflected, ${\overrightarrow{R}}_i$, can be expressed as shown in the following equation:

$$\begin{array}{c}{\overrightarrow{R}}_A=\left(\begin{array}{c}{r}_p-r_{ma}\\ \theta +\pi \\ z_p-z_{ma}\end{array}\right)=\left(\begin{array}{c}{r}_{ma}-r_s\\ \theta +\pi \\ z_{ma}-z_s\end{array}\right)-2\left[\left(\begin{array}{c}{r}_{ma}-r_s\\ \theta +\pi \\ z_{ma}-z_s\end{array}\right)·\left(\begin{array}{c}\cos \left({\delta }_a\right)\\ \theta +\pi \\ \sin \left({\delta }_a\right)\end{array}\right)\right]\left(\begin{array}{c}\cos \left({\delta }_a\right)\\ \theta +\pi \\ \sin \left({\delta }_a\right)\end{array}\right)\\ {\overrightarrow{R}}_B=\left(\begin{array}{c}{r}_p-r_{mb}\\ \theta \\ z_p-z_{mb}\end{array}\right)=\left(\begin{array}{c}{r}_{mb}-r_s\\ \theta \\ z_{mb}-z_s\end{array}\right)-2\left[\left(\begin{array}{c}{r}_{mb}-r_s\\ \theta \\ z_{mb}-z_s\end{array}\right)·\left(\begin{array}{c}\cos \left({\delta }_b\right)\\ \theta \\ \sin \left({\delta }_b\right)\end{array}\right)\right]\left(\begin{array}{c}\cos \left({\delta }_b\right)\\ \theta \\ \sin \left({\delta }_b\right)\end{array}\right)\end{array}$$

(3)

in such a way that the unitary vectors ${\widehat{n}}_A$ and ${\widehat{n}}_B$ can be calculated by means of the definition of the unitary vector.

$${\widehat{n}}_A=\frac{{\overrightarrow{R}}_A}{\left|{\overrightarrow{R}}_A\right|},{\widehat{n}}_B=\frac{{\overrightarrow{R}}_B}{\left|{\overrightarrow{R}}_B\right|}$$

(4)

The optical phase $\Delta \varphi$ associated with the displacements $\overrightarrow{d}=\left[u_r,u_{\theta },u_z\right]$ from all of the points that confirm the specimen surface is related to the vector sensitivity $\overrightarrow{e}$ (Equation (1)) by the expression [20]:

$$\Delta \varphi =\overrightarrow{e}·\overrightarrow{d}.$$

(5)

By analyzing the previous equations, we can simplify the optical phase into two components, since the sensitivity vector always coincides with the rz plane. The optical phase will be composed by in-plane and out-of-plane radial sensitivity depending on the displacement vector, $\overrightarrow{e}\left(r,z\right)=e_r\widehat{\rho }+e_z\widehat{k}$, where $\widehat{\rho }$ and $\widehat{k}$ are the unitary vectors in the radial and z axis directions for the components $e_x$ and $e_z$, respectively. Simplifying Equation (5) by disregarding the associated quantity to $e_z$ and assuming that the contribution to sensitivity is small, we can rewrite it as:

$$u_r\left(r,\theta \right)\approx \frac{\lambda \Delta \varphi \left(r,\theta \right)}{2\pi \left({\widehat{n}}_A-{\widehat{n}}_B\right)}.$$

(6)

A numerical analysis can be done by taking into account the dimensions shown in

Table 1. Data for the numerical analysis.

Laser Illumination Data	Wavelength, $\lambda =552$ nm Laser Power: 1 W
Digital camera CCD data	Resolution: 804 × 556 pixels
Divergent illumination source coordinates, $SiL\left(r_s,0,z_s\right)$	$r_s=0$
	$z_s=265$ mm
Conic mirror dimensions	Outer radius: 37.5 mm
	Inner radius: 25.0 mm
	High: 20 mm
	Conic mirror angle: $\delta =32°$
Illuminated surface radius	Radius: 25.0 mm

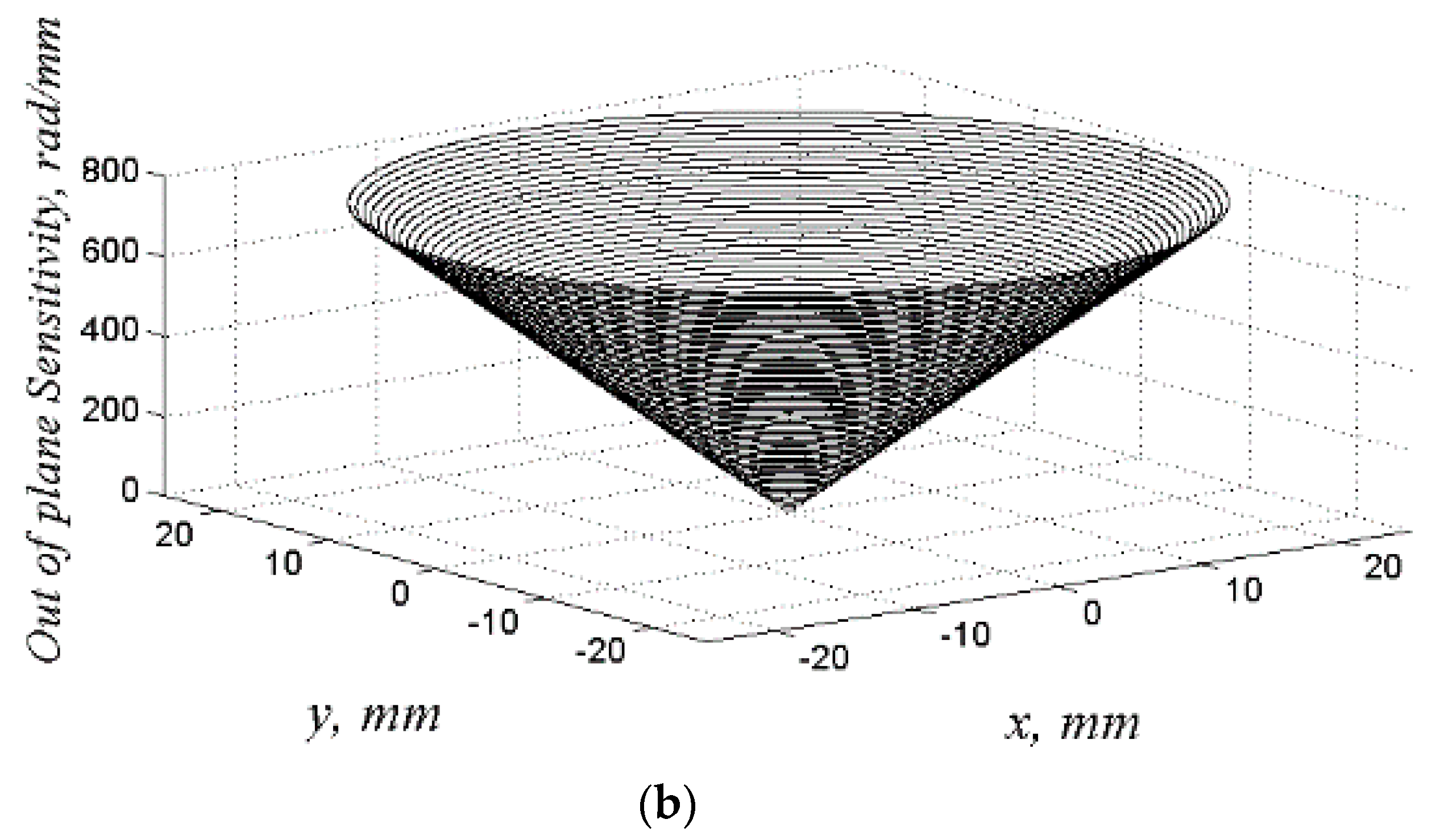
for the optical arrangement of ESPI interferometry with in-plane radial sensitivity and divergent illumination. Considering the Equations (1), (3), and (4), we can calculate the in-plane and out-of-plane radial component of the sensitivity vector. As observed in Figure 3a, maximum sensitivity in the radial plane is obtained in the centre of the cone and decreases towards the ends; it is unlikely that the sensitivity component out-of-plane is minimal at the centre and increases towards the ends (see Figure 3b).

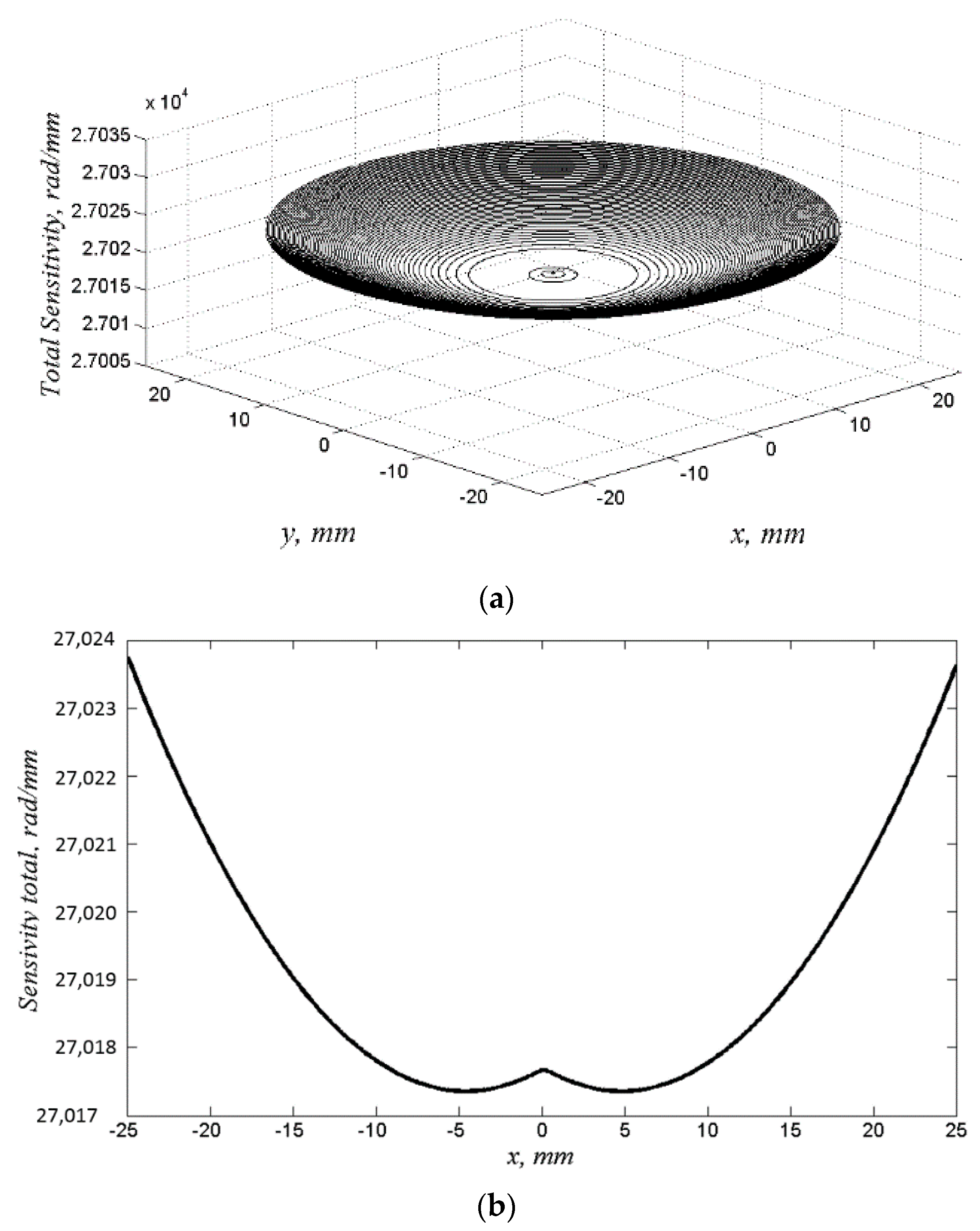
As observed, the maximum in-plane radial sensitivity is obtained from the cone’s centre and decreases towards the ends. In contrast, the sensitivity component out of the plane is minimal at the centre and increases towards the ends. However, the contribution of the out-of-plane sensitivity is much smaller (less than 3%) than the in-plane radial sensitivity. Figure 4 shows the calculation of the total sensitivity of the system using the data in Table 1.

As shown here, the out-of-plane component of the sensitivity vector on the outer side of the observed area only represents less than 3% of the total sensitivity of the system, and this decreases to zero as the observer moves towards the centre.

3. Experimental Results and Discussion

A convex cone mirror was manufactured by the machining and high-quality polishing of a stainless-steel block, as shown in Figure 5. Micro-roughness measurement of the optical surface was 0.05 µm RMS (Root Mean Square). An aluminium plate mounted in a rigid frame was used as a specimen. Deformations by dilatation in the plate were induced by heating it to 80 °C with an electric resistance set in a small cylinder of 6 mm in diameter and 4 mm in thickness in contact with the rear. This heating temperature was low enough to minimize out-of-plane displacements due to buckling deformations. In consequence, deformations by heat convection effects were neglected.

A 552 nm laser was used as a divergent illumination source set to $z_s=265$ mm in front of the specimen, as shown in Figure 1. This position was required with respect to the vertex of the conical mirror to avoid convergence and ensure full field analysis due to the geometrical design of the mirror. The retarder-polarized system $\left(fc-fl\right)$ generated circular and linear polarizing states for both the beam that crossed the polarizing ring and the beam that propagated freely. When the linear polarizer rotated, linear polarizing states were generated, which allowed for the interference of the two beams with different curvature radiuses, and this generated the observed patterns with radial symmetry.

The generated interferograms were captured by a CCD camera. The images were a monochromatic 640 × 480 pixels resolution of 8 bits. To obtain the optical phase, $\Delta \varphi$, we used the polarizing [21] shifting phase technique [22]. For this, a deformation in the sample was generated by heating in such a way that temporal variations were longer than the capture time of the five interferograms. Each phase shift was produced by changing the angle of the linear polarized filter (fl) so that five interferograms with a relative shift of $\frac{2\pi }{5}$ rad were obtained. The acquired images were filtered to normalize the contrast of the interference fringes with digital image processing.

The result is shown in Figure 6. The optical unwrapping phase $\Delta \varphi$ was obtained by the algorithm of the unwrapping phase proposed by Quiroga [23]. This algorithm had the advantage of no error propagation during the unwrapping phase by means of adaptation of the evaluation trajectory during the progression of the algorithm.

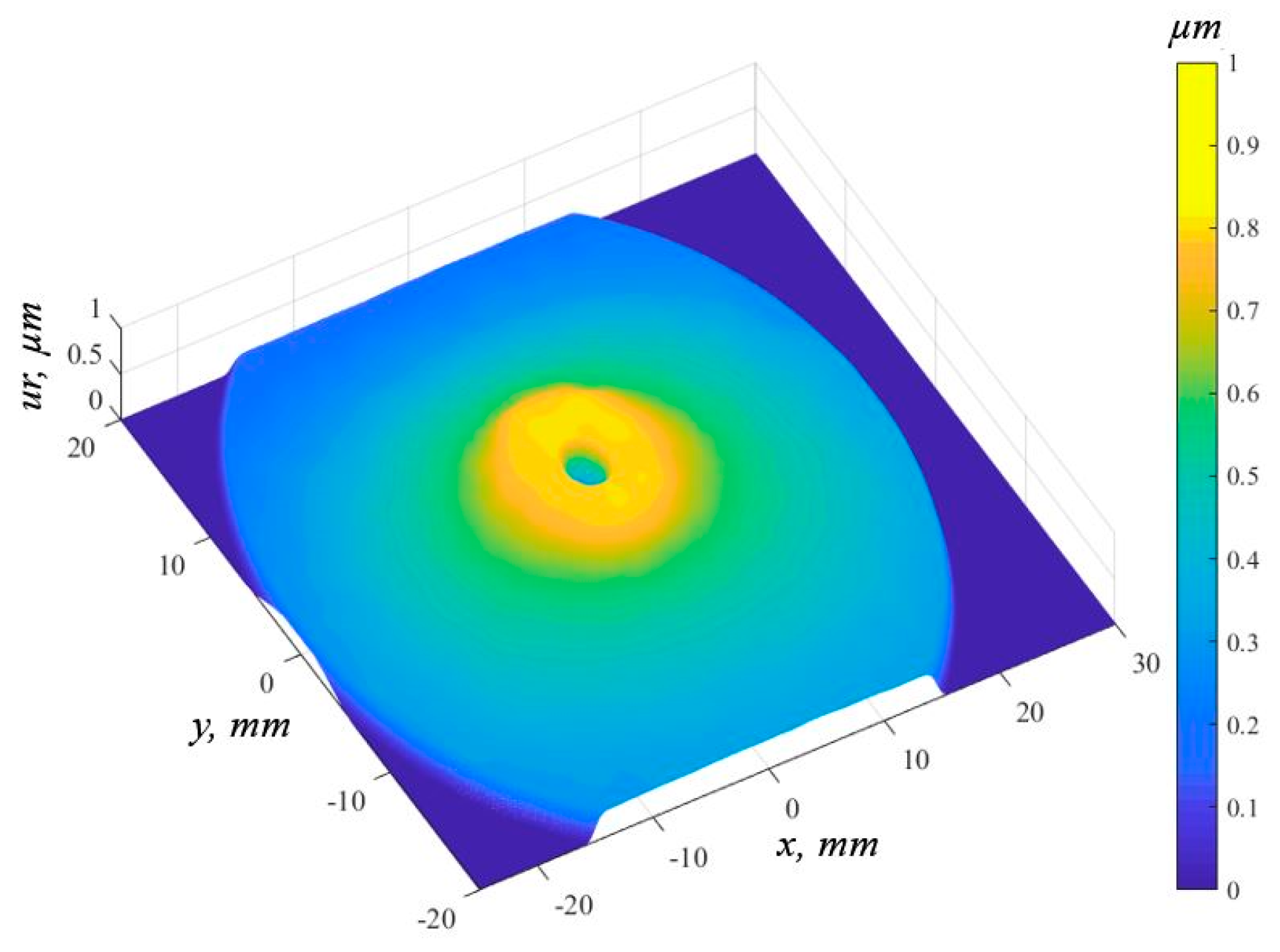
Considering the system sensitivity shown in Figure 4 and using Equation (6), Figure 7 shows the radial deformation of the surface. As mentioned above, it was not possible to take measurements in the centre due to the convergence of the illumination at this point from the other directions.

The measurement achieved for the maximum radial deformation was 0.8 µm when the plate was heated to 80 °C by the rear in the centre point. The deformation decreased according to the increasing radial distance. The contribution of the out-of-plane component of the sensitivity vector represented less than 3% towards the outer edges. In maximum deformations, its contribution was estimated at less than 1%, and that is why it was neglected.

Numerical simulations were performed using ANSYS software for finite element analysis applied only to a three-dimensional (3D) geometrical model of the specimen plate. The finite elements were created using a rotational sweeping method around the centre of the specimen plate according to the spectated radial deformation. There were 144 angular and 72 radial divisions, which obtained 21,850 nodes and 21,582 elements. The thickness of each element was 2 mm. A heating point was applied near the specimen plate located at the centre with the purpose of inducing a deformation by dilatation. The maximum temperature applied to the simulation was 80 °C. The perimetral contour of the 3D geometrical model was fixed without an assigned displacement. The setting of the plate and the result of the simulation are shown in Figure 8.

Figure 9 illustrates the comparison between the result of the simulation by finite element analysis and ESPI with in-plane radial sensitivity.

In the simulations, we can observe that the maximum radial deformation is 0.95 µm for a radius of 4 mm and that it approaches the position of the circular plate used to induce deformation by dilatation. However, in the measurements of radius higher than 8 mm, we can see a strong correlation between the ESPI measurements and the finite element analysis. In the geometrical model, near to the centre (radius [−5, 5]), we can see an inconsistent measurement related to the meshing size of the finite elements. These data were not considered for analysis.

4. Discussion, Advantages, and Disadvantages

The setup of this new radial-in-plane sensitivity interferometer that uses the divergent illumination is very simple and provides accurate measurements in radial directions. However, it does not allow for adjustments to the sensitivity vectors without losses in convergence in the illumination on the test surface. The measurements obtained by the proposed interferometer successfully support the presented mathematical model. It is shown that the radial-in-plane component contribution of the sensitivity vector is higher in comparison with the out-of-plane component; however, we can expect an error (less than 3%) near the centre of the observed area. Given the illumination convergence at the centre of the observed surface, it is difficult to obtain accurate measurements around the optical axis, so an alternative analysis is required.

5. Conclusions

We showed a new configuration for the polarized interferometer with in-plane radial sensitivity using divergent illumination. We performed measurements of deformations due to the dilatation of an aluminium plate that was heated by the rear by contact with a small cylindrical element connected to electric resistance. The implemented system allowed us to measure deformations mainly in the radial direction. The results were compared to a simulation by the finite element analysis technique, which had comparable results. According to the mathematical model, the contribution of the out-of-plane sensitivity vector is less than 1% near the centre of the measurement, and this increases in function of the radius of less than 3%. We can conclude that the contribution of the out-of-plane sensitivity vector increases proportionally to the radius; this represents a disadvantage in determining the in-plane deformation at these points. On the other hand, it is not possible to obtain reliable measurements at the centre of the conic mirror due to the convergence of the illumination beam. As a perspective, we propose to carry out further research to determine the error of the measurement in this condition.