On the Cattaneo–Christov Heat Flux Model and OHAM Analysis for Three Different Types of Nanofluids

Abstract

In this article, the boundary layer flow of a viscous nanofluid induced by an exponentially stretching surface embedded in a permeable medium with the Cattaneo–Christov heat flux model (CCHFM) is scrutinized. We took three distinct kinds of nanoparticles, such as alumina (Al₂O₃), titania (TiO₂) and copper (Cu) with pure water as the base fluid. The features of the heat transfer mechanism, as well as the influence of the relaxation parameter on the present viscous nanofluid flow are discussed here thoroughly. The thermal stratification is taken in this phenomenon. First of all, the problem is simplified mathematically by utilizing feasible similarity transformations and then solved analytically through the OHAM (optimal homotopy analysis method) to get accurate analytical solutions. The change in temperature distribution and axial velocity for the selected values of the specific parameters has been graphically portrayed in figures. An important fact is observed when the thermal relaxation parameter (TRP) is increased progressively. Graphically, it is found that an intensification in this parameter results in the exhaustion of the fluid temperature together with an enhancement in the heat transfer rate. A comparative discussion is also done over the Fourier’s law and Cattaneo–Christov model of heat.

1. Introduction

Heat transfer analysis is involved in different aspects of engineering and biomedical applications such as continuous stretching of plastic films, energy production process, drawing of copper wires, conduction of heat in tissues, hot rolling, magnetic drug targeting, nuclear reactor cooling, space cooling, metal spinning’s and many other important fields. The heat transfer phenomenon arises due to the differences in the temperature between two objects or in the same object. When one considers distinct materials with distinct temperature then the flow of heat occurs from the peak temperature to the body at minimum temperature. Until now, Fourier’s popular law [1] was used for the heat transfer mechanism. This law states that any initial change in temperature is immediately spread all through the entire medium under examination. However, in fact, no such material or object existed there, which gives the proof of Fourier’s heat conduction law. To solve this problem, Cattaneo [2] proposed an adjusted Fourier’s law by involving a term called the relaxation term. Thus, Christov [3] utilized the upper-convected derivative model of Oldroyd [4] to describe Cattaneo heat flux law. The physical interpretation of the heat flux Cattaneo–Christov model is that the heat transfer throughout the whole medium at a slow rate. The influences of the Cattaneo–Christov model of heat flux with initial and boundary problems and their structural stability solutions have been discussed by Tibullo and Zampoli [5]. The Cattaneo–Christov model to explore the transfer of heat for fluid with viscoelasticity enclosed by a sheet (stretching) and flow with slip is studied by Khan et al. [6]. Straughan [7] and Haddad [8] examined the law of the Cattaneo–Christov model of heat flux with thermal convection and obtained the computational solutions. Crane and Carragher [9] observed the heat transfer mechanism on a continuous shrinking surface. Later on, lots of investigations were made to consider the flow past an exponentially expanding surface. Keller and Magyari [10] inspected the flow where the viscous effects are dominant past an exponentially stretching sheet through exponential temperature profile distribution. Mustafa [11] investigated the spinning flow of viscoelastic fluids due to a stretching sheet by employing the Cattaneo–Christov heat flux model (CCHFM). Khan [12] studies the heat transfer mechanism and three dimensions Burgers liquid flow by assuming the model of heat flux called Cattaneo–Christov.

The phenomenon of heat transport over a stretchable surface is a broad field of new thinking and idea in the current time. Some key fluid velocity problems for the diverse liquid flow for exponential stretchable sheet are obtainable [13,14,15]. Partha et al. [16] initiated the fluid flow in more than one dimension, which is induced by an exponentially stretching sheet with the combined impacts of mixed convection and viscous dissipation. Nadeem et al. [17] scrutinized the transfer rate of heat and the boundary layer fluid flow of a Maxwell fluid past exponentially stretching. In recent time, the main focus on the subject of various examinations, which is the flow through a permeable source. The survey has been animated in this field, to a degree, which is the expansive one and by the fact that in various discipline engineering, physics, applied mathematics and industries they have various applications of the heat transfer motivated fluid flows in permeable source types media like fibrous insulations and the ground dumping of non-atomic or atomic waste, earth science systems, etc. A comprehensive review of the literature can be seen in the books by Pop and Ingham [18] and Vafai [19]. The magnetohydrodynamic (MHD) two-dimensional boundary layer flows of a Maxwell fluid, which is upper-convected were investigated in [20,21] for porous objects. Further, Lesnic et al. [22,23] combined the natural convection via the theory of boundary layer and the Newtonian heating (NH) past a slope zero and a sheet vertically saturated in permeable media. Aliakbar et al. [24] showed the results of different embedded arbitrary constants on the temperature profile above the sheet. Nadeem et al. [25] considered the transfer of heat phenomenon past an exponentially stretching sheet with Newtonian heating.

Nanofluid are fluids that are taken to be in a nanosize arrangement. These liquids are a mixture of nanoparticles i.e., (carbon nanotubes or carbides, oxides and metal) and base liquids (including glycol, ethylene, oil, water, etc.). We called these types of liquid a nanofluid and were familiarized by Choi [26]. These liquids having a much-augmented conductivity for the escalating thermal performance. Eastman et al. [27] examined that boost up the thermal conductivity depends upon the body, shape and thermal properties of the nanoparticles. Nanoparticles are the important features of the rapidly developing field of nanotechnology. Their uniqueness and existence properties make these particles vital and major in many fields of human action. This review tries to abridge the short and the latest advancements in the field of applied nanoparticles, specifically, their application in medicine, chemistry and biology and many other fields of education like science and technology. Nadeem et al. [28] considered the nonlinear stretching sheet to explored the feature of heat transfer in the presence of three different nanoparticles, such as Cu, Al₂O₃, and TiO₂. Khan et al. [29] examined the three-dimensional unsteady CNTs nanofluid flow in the existence of velocity and thermal slip. Recently many researchers investigated the influence of different nanoparticle in various flow fields [30,31,32,33,34,35].

Analytical solutions have great importance in physical problems. The analysis of OHAM is functional to solve the formulated boundary value problem and obtained analytical results. Liao [36,37] suggested the homotopy analysis method and optimal HAM approach to get analytical solutions for non-linear differential equations. Other interesting related numerical investigations can be found in [38,39,40,41,42,43,44,45,46,47,48,49].

In this work, we applied the Cattaneo–Christov model of heat flux to study the boundary layer flow of a viscous nanofluid induced by an exponentially stretching surface embedded in a porous medium. The guess of thermal stratification is to be invoked. The given problem is mathematically constructed and their dimensionless ordinary differential equations (ODEs) are computed by exercising the appropriate transformations and then obtain the exact solutions through OHAM (optimal homotopy analysis method). The differences in the fluid flow movement for the two fields of velocity and the temperature for diverse approximations of relevant interesting parameters of aforementioned nanofluids have been explained graphically. Stress is given to the fact that augmentation in the thermal relaxation parameter shows interesting exhaustion in the field of temperature distribution and the rate of heat transfer advancements.

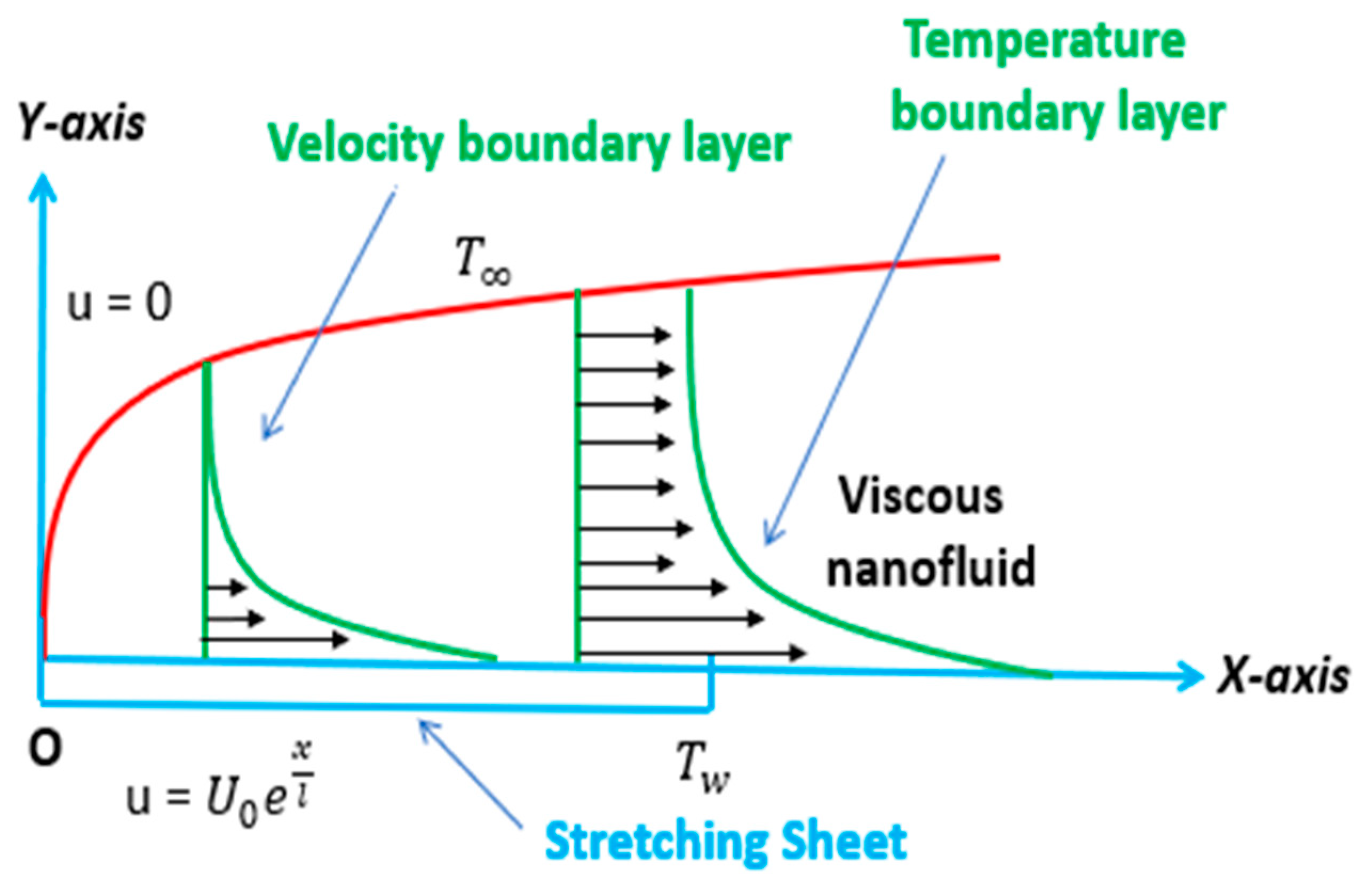
2. Problem Formulation

Let us take the steady two-dimensional boundary layer flow of an incompressible viscous nanofluid past an exponentially stretching sheet flooded in a permeable medium. Utilizing the boundary layer estimates the governing equations for the flow problem are obtained as

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

$${\rho }_{nf}\left(u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}\right)+\frac{\partial p}{\partial x}-{\mu }_{nf}\frac{{\partial }^{2}u}{\partial y^2}=-\frac{{\mu }_{nf}\epsilon }{K}u.$$

(2)

In the aforementioned equations, $u$ and $v$ represent the velocity components along with the x and y directions respectively, $\epsilon$ indicates the porosity of the medium and $K$ is regarded as the permeability of the fluidic medium. The parameters ${\mu }_{nf}$ (nanofluid viscosity) and ${\rho }_{nf}$ (nanofluid density) are defined below by

$${\mu }_{nf}=\frac{{\mu }_f}{{\left(1-\varphi \right)}^{2.5}}, {\rho }_{nf}=\left(1-\varphi \right){\rho }_f+\varphi {\rho }_s.$$

(3)

Here $\varphi$ indicates the nanoparticles volume fraction of nanofluid, ${\rho }_f$ denotes the fluid density of the base fluid, ${\rho }_s$ specifies nanoparticles density and ${\mu }_f$ represents base fluid viscosity. For the steady boundary layer flow, the equation of energy is

$$-\mathbf{V}.\nabla T=\frac{\nabla .\mathbf{q}}{{\left(\rho c_p\right)}_{nf}},$$

(4)

where ${\left(\rho c_p\right)}_{nf}$ signifies specific heat capacity of nanofluid,$\hspace{0.17em}T$ demonstrates local fluid temperature and $q$ represents heat flux satisfying Cattaneo–Christov heat flux law given below

$$\mathbf{q}+{\lambda }_2\left[\frac{\partial \mathbf{q}}{\partial t}+ \left(\nabla .\mathbf{V}\right)\hspace{0.17em}\mathbf{q}-\mathbf{q}.\nabla \mathbf{V}+\mathbf{V}.\nabla \mathbf{q}\right]=-k_{nf}\nabla T,$$

(5)

in which ${\lambda }_2$ indicates thermal relaxation time, $\mathbf{V}$ denotes the velocity vector and $k_{nf}$ represents the thermal conductivity of the nanofluid. Using the fact that fluid is incompressible and utilizing Equation (5) in Equation (4), the temperature equation takes the form

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+{\lambda }_2\left(\begin{array}{l}\left\{u\frac{\partial u}{\partial x}\frac{\partial T}{\partial x}\right\}+\left\{v\frac{\partial v}{\partial y}\frac{\partial T}{\partial y}\right\}+\left\{u\frac{\partial v}{\partial x}\frac{\partial T}{\partial y}\right\}+\left\{v\frac{\partial u}{\partial y}\frac{\partial T}{\partial x}\right\}+\\ \left\{2uv\frac{{\partial }^{2}T}{\partial x\partial y}\right\}+\left\{u^2\frac{{\partial }^{2}T}{\partial x^2}\right\}+\left\{v^2\frac{{\partial }^{2}T}{\partial y^2}\right\}\end{array}\right)={\alpha }_{nf}\frac{{\partial }^{2}T}{\partial y^2}.$$

(6)

Here, the parameter ${\alpha }_{nf}$ denotes the thermal diffusivity of nanofluid defined as follow

$$\begin{array}{c}{\alpha }_{nf}{\left(\rho c_p\right)}_{nf}=k_{nf},\hspace{0.17em} {\left(\rho c_p\right)}_{nf}-\left(1-\varphi \right)\hspace{0.17em}{\left(\rho c_p\right)}_f=\varphi {\left(\rho c_p\right)}_s,\hspace{0.17em}\\ \frac{k_{nf}}{k_f}=\frac{\left(2k_f+k_s\right)-2\varphi \left(k_f-k_s\right)}{\left(2k_f+k_s\right)+\varphi \left(k_f-k_s\right)},\hspace{0.17em} {\nu }_{nf}{\rho }_{nf}={\mu }_{nf}.\end{array}$$

(7)

Here $k_f$ indicates the thermal conductivity of base fluid whereas $k_s$ indicates solid thermal conductivity. The associated boundary conditions are imposed as below

$$\begin{array}{c}{v|}_{y=0}=0,{u|}_{y=0}=U_w(x)=U_0{e}^{(x/l)},\hspace{0.17em}{T|}_{y=0}=T_w(x)=T_0+a{e}^{(x/l)},\\ {u|}_{y\to \infty }\to 0,\hspace{0.17em} {T|}_{y\to \infty }\to T_{\infty }=T_0+b{e}^{(x/l)}.\end{array}$$

(8)

Here $U_w(x)$ denotes the velocity of the stretching surface, $U_0$ identifies the reference velocity, $l$ signifies a characteristic length, $\left(a,b\right)$ are dimensional constants, $T_w(x)$ and $T_{\infty }$ represent the wall and ambient temperature or far away temperature, respectively.

The geometrical structure of the problem is given in Figure 1.

The problem considered here is based on the following suitable similarity transformations [13,17,25].

$$\begin{array}{l}\eta =\sqrt{\frac{U_0}{2\nu l}}{e}^{(x/2l)}y,\hspace{0.17em}u=U_0{e}^{(x/l)}{f}^{\prime }\left(\eta \right),\\ v=-\sqrt{\frac{\upsilon U_0}{2l}}{e}^{(x/2l)}\left\{\eta f^{\prime }+f\right\},\hspace{0.17em}\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_0}.\end{array}$$

(9)

Equation (1) is equivalently satisfied and Equations (2)–(8) are transformed into the following form

$$\frac{1}{{\left(1-\varphi \right)}^{2.5}\left(1-\varphi +\varphi \left({\rho }_s/{\rho }_f\right)\right)}{f}^{‴}+f{f}^{″}-2{\left(f’\right)}^2-\frac{2P_m}{\left(1-\varphi +\varphi \left({\rho }_s/{\rho }_f\right)\right)}{f}^{\prime }=0,$$

(10)

$$\frac{1}{\mathrm{Pr}}\frac{k_{nf}/k_f}{\left(1-\varphi +\varphi {\left(\rho c_p\right)}_{{}_s}/{\left(\rho c_p\right)}_f\right)}{\theta }^{″}+{\theta }^{\prime }f-\frac{1}{2}{\lambda }_t\left(f^2{\theta }^{″}-f{f}^{\prime }{\theta }^{\prime }\right)=0,$$

(11)

$$\begin{array}{l}{f}^{\prime }\left(\eta \right)=1,f\left(\eta \right)=0,\theta \left(\eta \right)=1-S \mathrm{at} \eta =0,\\ f^{\prime }\left(\eta \right)\to 0, \theta \left(\eta \right)\to 0 \mathrm{as} \eta \to \infty .\end{array}$$

(12)

In the above equations, the embedded parameters thermal stratification (TS) is denoted by $S$, the porous medium parameter (PMP) is designated by $P_m$, the Prandtl number (PN) is symbolized by $\mathrm{Pr}$ and the non-dimensional thermal relaxation time (TRT) is represented by ${\lambda }_t$. These physical parameters are defined as

$$P_m=\frac{\nu \epsilon }{U_{0}K},\hspace{0.17em} \mathrm{Pr}=\nu /\alpha ,\hspace{0.17em} {\lambda }_t={\lambda }_2{U}_0,\hspace{0.17em} S=b/a.$$

(13)

Note that for ${\lambda }_t=0$ leads to the classical Fourier’s heat conduction law.

3. Variables of Engineering Interest

The physical quantity such as the shear stress rate (local coefficient of skin friction) is given by

$$C_f=\frac{{\tau }_w}{{\rho }_f{U}_{\infty }^2},\hspace{0.17em}{\tau }_w={\mu }_{nf}{\left(\frac{\partial u}{\partial y}\right)}_{y=0}.$$

(14)

Consuming the similarity transformation (9) the above equation becomes

$$\sqrt{{\mathrm{Re}}_x}{C}_f=\frac{1}{{(1-\varphi )}^{2.5}}{f}^{″}(0).$$

(15)

By making use of Equation (15), extensive data results are outputted in

Table 1. Numerical data set for skin friction of three different types of water-base nanofluids.

$\mathit{\varphi }$	${\mathit{P}}_{\mathit{m}}$	${\mathit{\lambda }}_{\mathit{t}}$	$\sqrt{\mathbf{R}{\mathbf{e}}_{\mathit{x}}}{\mathit{C}}_{\mathit{f}}$
			Cu	Al2O3	TiO2
0.01	0.1	0.3	1.3228	1.4760	1.5230
0.03			1.6384	1.7334	1.8384
0.05			1.8550	2.0755	2.2550
0.05	0.2	0.3	1.3230	1.3759	1.4229
	0.4		1.5307	1.5898	1.6306
	0.6		1.7151	1.7785	1.8150
0.05	0.6	0.1	1.3312	1.4211	1.5311
		0.2	1.3312	1.4212	1.5312
		0.4	1.3312	1.4212	1.5312

for reduced skin friction coefficient $\sqrt{{\mathrm{Re}}_x}{C}_f$. However the values specified to the parameters $\varphi ,P_m \mathrm{and} {\lambda }_t$, it is found that the nanoparticles TiO₂ exhibit higher frictional effect that the other nanoparticles.

4. Optimal Homotopy Analysis Method (OHAM)

The initial estimates and linear operators for optimal HAM results are

$$\begin{array}{c}{f}_0\left(\eta \right)=\left(1-e^{\left(-\eta \right)}\right),\hspace{0.17em} {\theta }_0\left(\eta \right)=\left(1-S\right)\hspace{0.17em}{e}^{\left(-\eta \right)},\\ L_f\left(f\right)+\frac{df}{d\eta }-\frac{d^{3}f}{d{\eta }^3}=0,\hspace{0.17em} L_{\theta }\left(\theta \right)+\theta -\frac{d^2\theta }{d{\eta }^2}=0.\end{array}$$

(16)

Here linear operators are denoted by $L_f\left(f\right)$ and $L_{\theta }\left(\theta \right)$, whereas the initial guesses of the functions $\left\{f(\eta ),\theta (\eta )\right\}$ are represented by $\left\{f_0(\eta ),{\theta }_0(\eta )\right\}$.

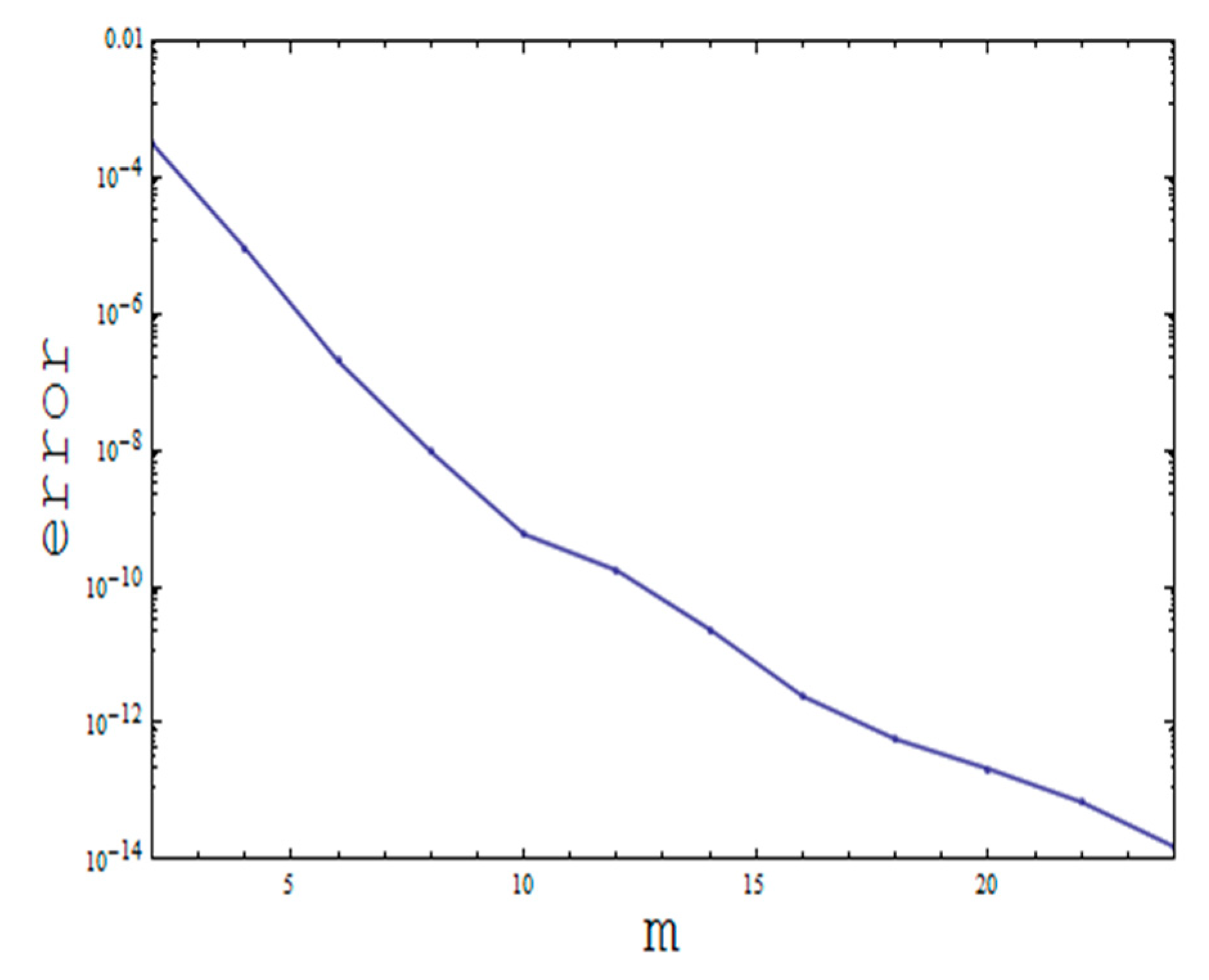
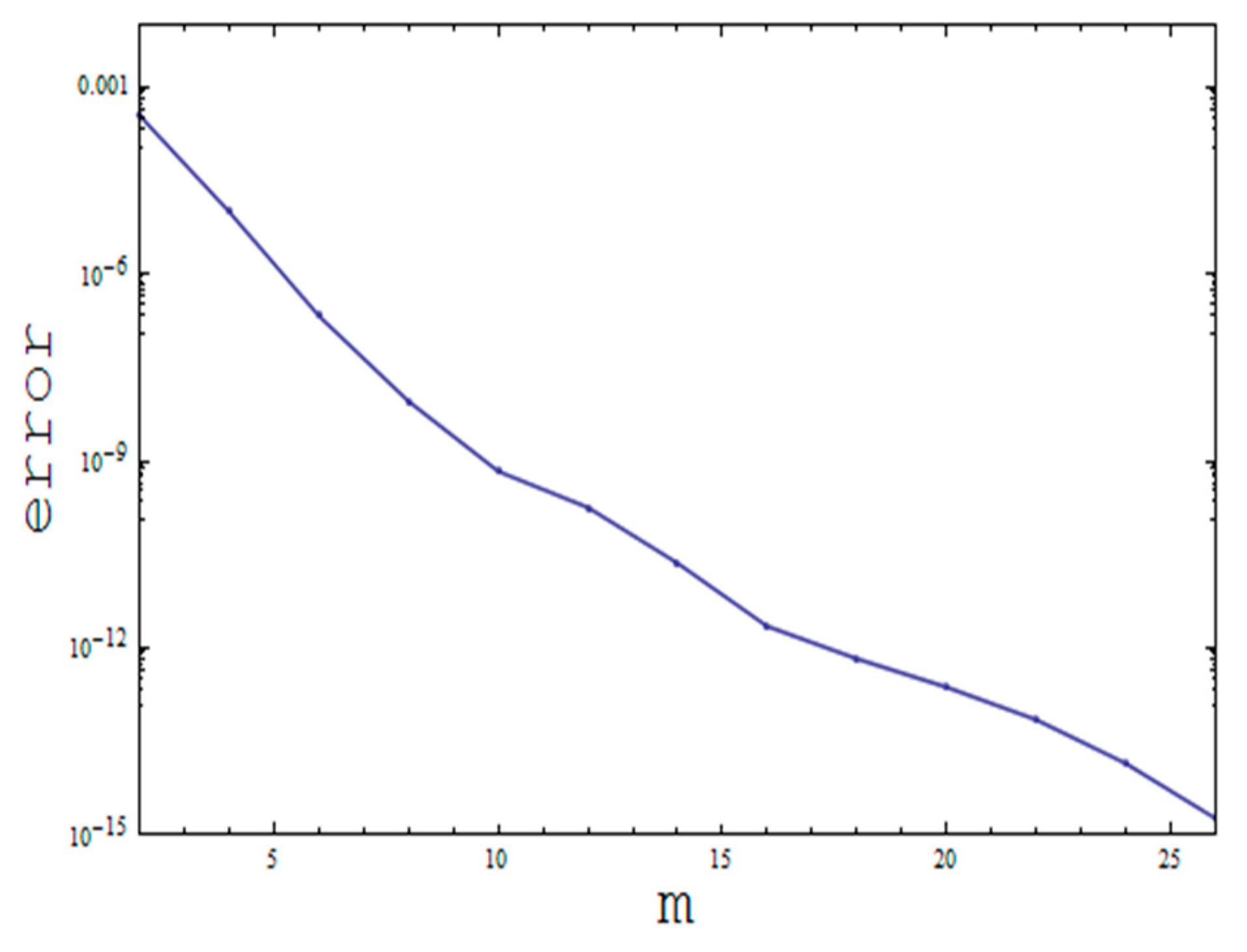
Convergence Analysis

We utilized the optimal homotopy analysis techniques to alter and control the resulting convergence series results. Suitable values are assigned to auxiliary parameters $\left\{h_f,h_{\theta }\right\}$ to get the convergent solutions. The errors residual are obtained for velocity and temperature equations by expressions defined below.

$$\begin{array}{l}{\Delta }_m{}^f={\displaystyle \underset{0}{\overset{1}{\int }}{\left[R_m{}^f(\eta ,h_f)\right]}^{2}d\eta ,}\\ {\Delta }_m{}^{\theta }={\displaystyle \underset{0}{\overset{1}{\int }}{\left[R_m{}^{\theta }(\eta ,h_{\theta })\right]}^{2}d\eta .}\end{array}$$

(17)

The parametric values convergence exercising by utilizing the procedure OHAM, which is enumerated below in

Table 2. Average residual square errors (${\epsilon }_m^t$).

$\frac{values\to }{order\downarrow }$	$h_f$	$h_{\theta }$	${\epsilon }_m^t$
$8$	$-0.573983$	$-0.918049$	$6.98675\times {10}^{-6}$
$10$	$-0.565917$	$-0.931985$	$9.05515\times {10}^{-7}$
$12$	$-0.539285$	$-1.38686$	$1.45651\times {10}^{-8}$
$14$	$-0.535106$	$-1.37685$	$2.06408\times {10}^{-9}$
$16$	$-0.531844$	$-1.36636$	$3.99551\times {10}^{-10}$

and

Table 3. Discrete residual square errors for ${\epsilon }_m^f$ and ${\epsilon }_m^{\theta }$

$\frac{values\to }{order\downarrow }$	$h_f=-0.570464$	$h_{\theta }=-1.23274$
	${\epsilon }_m^f$	${\epsilon }_m^{\theta }$
$4$	$1.72569\times {10}^{-6}$	$0.000020310$
$8$	$2.87068\times {10}^{-9}$	$5.78132\times {10}^{-7}$
$12$	$9.29003\times {10}^{-12}$	$1.7193\times {10}^{-11}$
$20$	$2.74651\times {10}^{-15}$	$6.16398\times {10}^{-15}$

. The values assigned to residual parameters are $\mathrm{Pr}=6.2,$ $S=0.8,$ $Pm=0.5,$$\lambda =1.$

The graphical picture for 8th and 10th order approximations show the error decline in the subsequent figures (Figure 2 and Figure 3).

Here, the quantity ${\epsilon }_m^t\left(={\epsilon }_m^f+{\epsilon }_m^{\theta }\right)$ represents the total squared of the residual error, which is utilized to achieve the control parameters for the convergence of the optimal solution.

5. Results and Discussion

The physical impacts of the miscellaneous emerging parameters containing nanoparticles volume fraction ($0\le \varphi \le 0.3$), porosity parameter ($0.2\le P_m\le 0.8$), thermal stratification ($0\le S\le 0.4$), of the dimensionless thermal relaxation time ($0\le {\lambda }_t\le 4$) on the axial velocity and the distribution of temperature were well explained in this part. Note that in all these graphs and tables, the value of Prandtl number ($\mathrm{Pr}$) was kept fixed, i.e., $\mathrm{Pr}=6.2$ for the base fluid water. Graphical results are portrayed in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12.

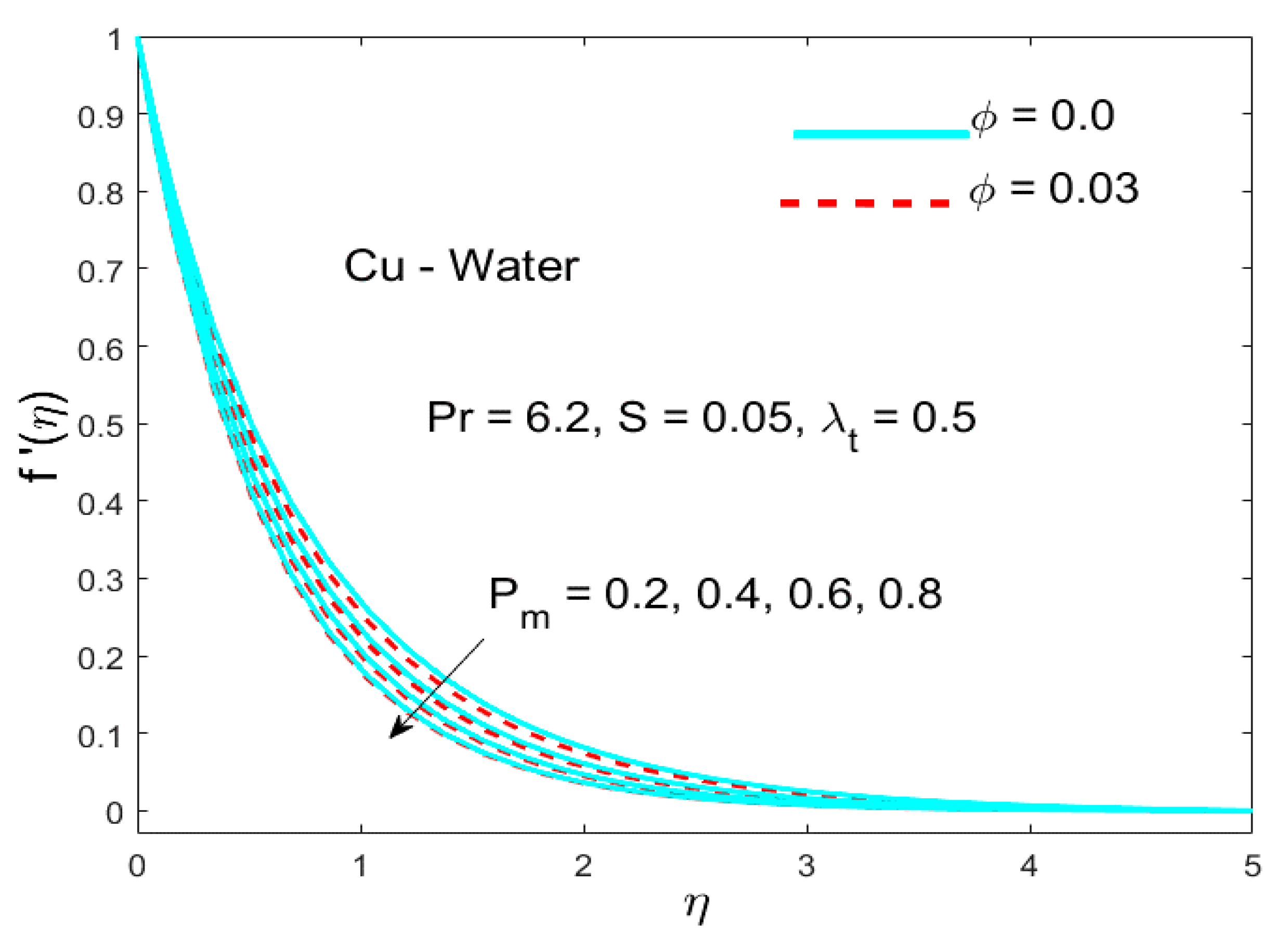
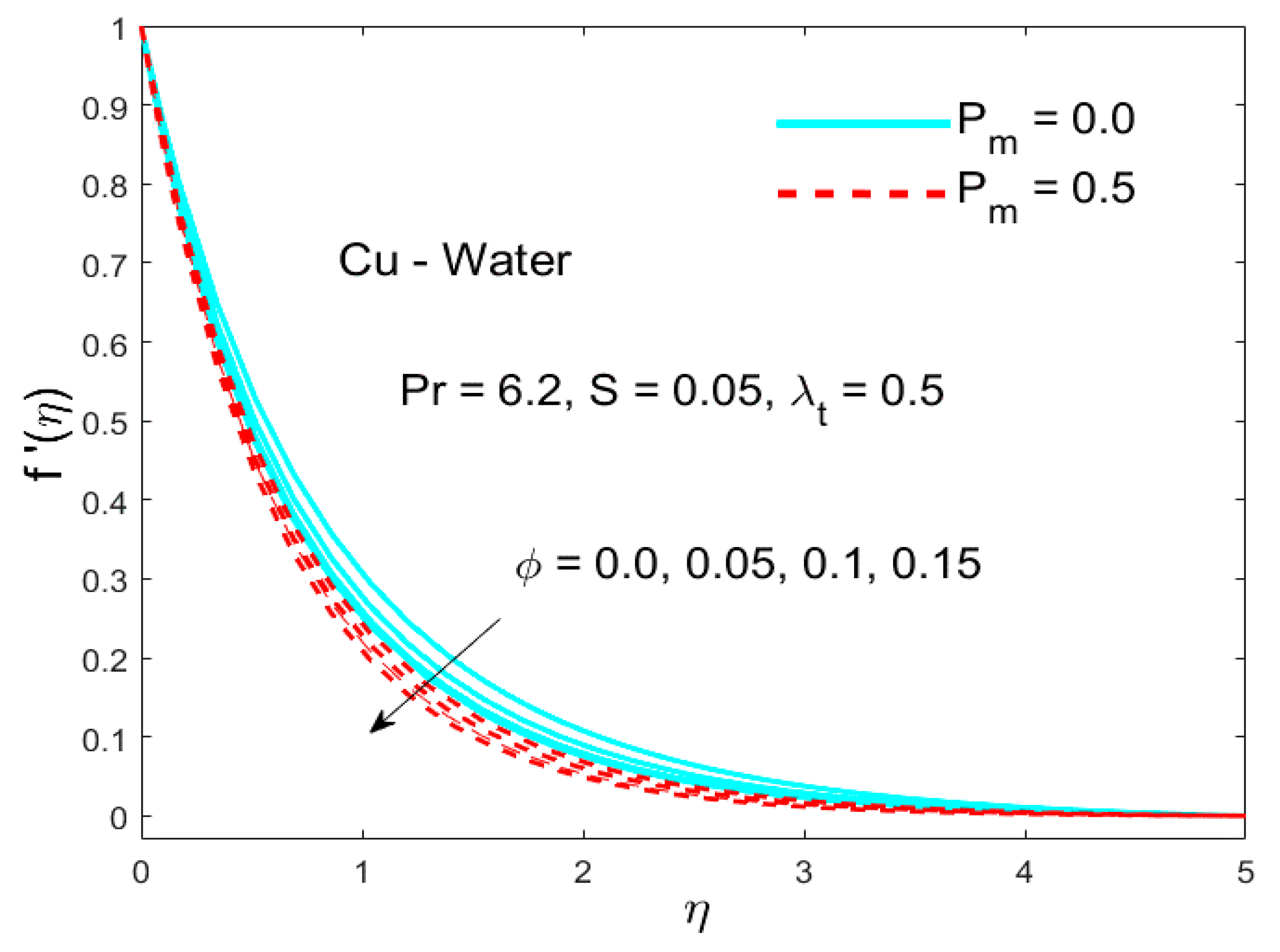
5.1. The Impact of the Parameter $P_m$ (Called Porosity Parameter)

In this subclass, we discussed the behavior of $P_m$ (non-dimension porosity parameter) on velocity and temperature profiles. Figure 4 shows the effect of $P_m$ on the behavior of axial velocity. As expected, the reduction in the velocity distribution was seen with an augmentation in the estimation of $P_m$. Further, the flow profile of velocity was higher in the absence of solid volume fraction parameter $\varphi$. 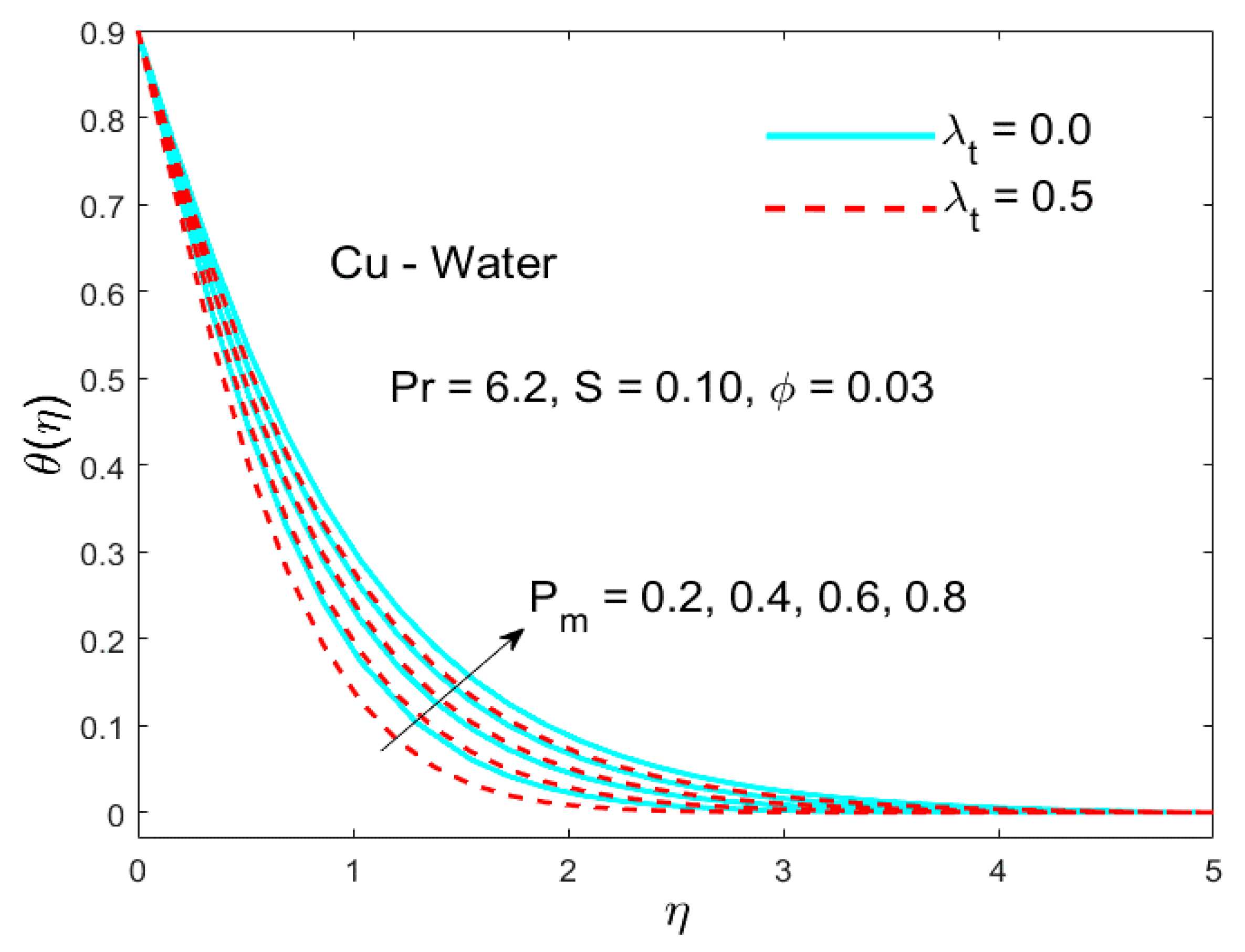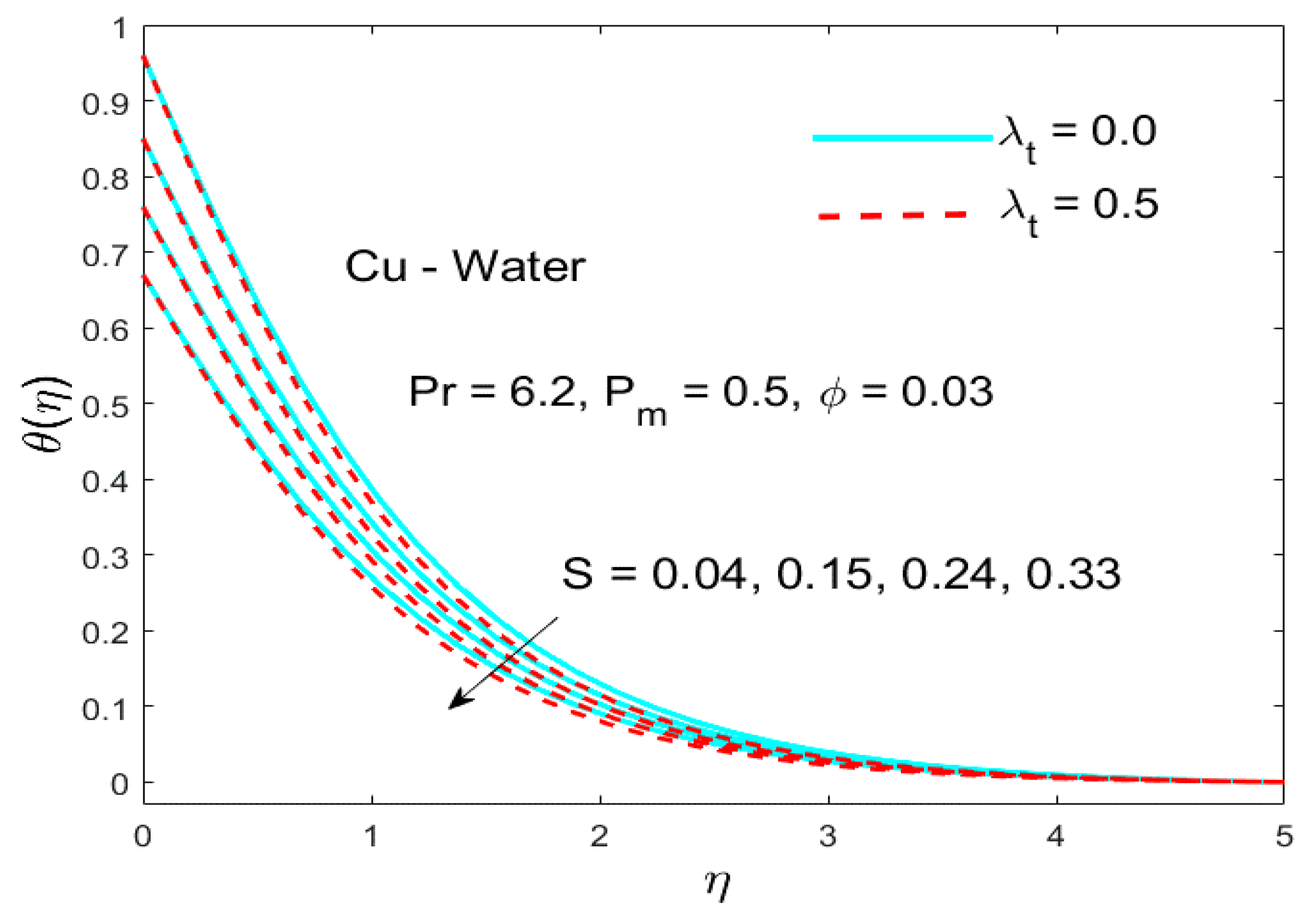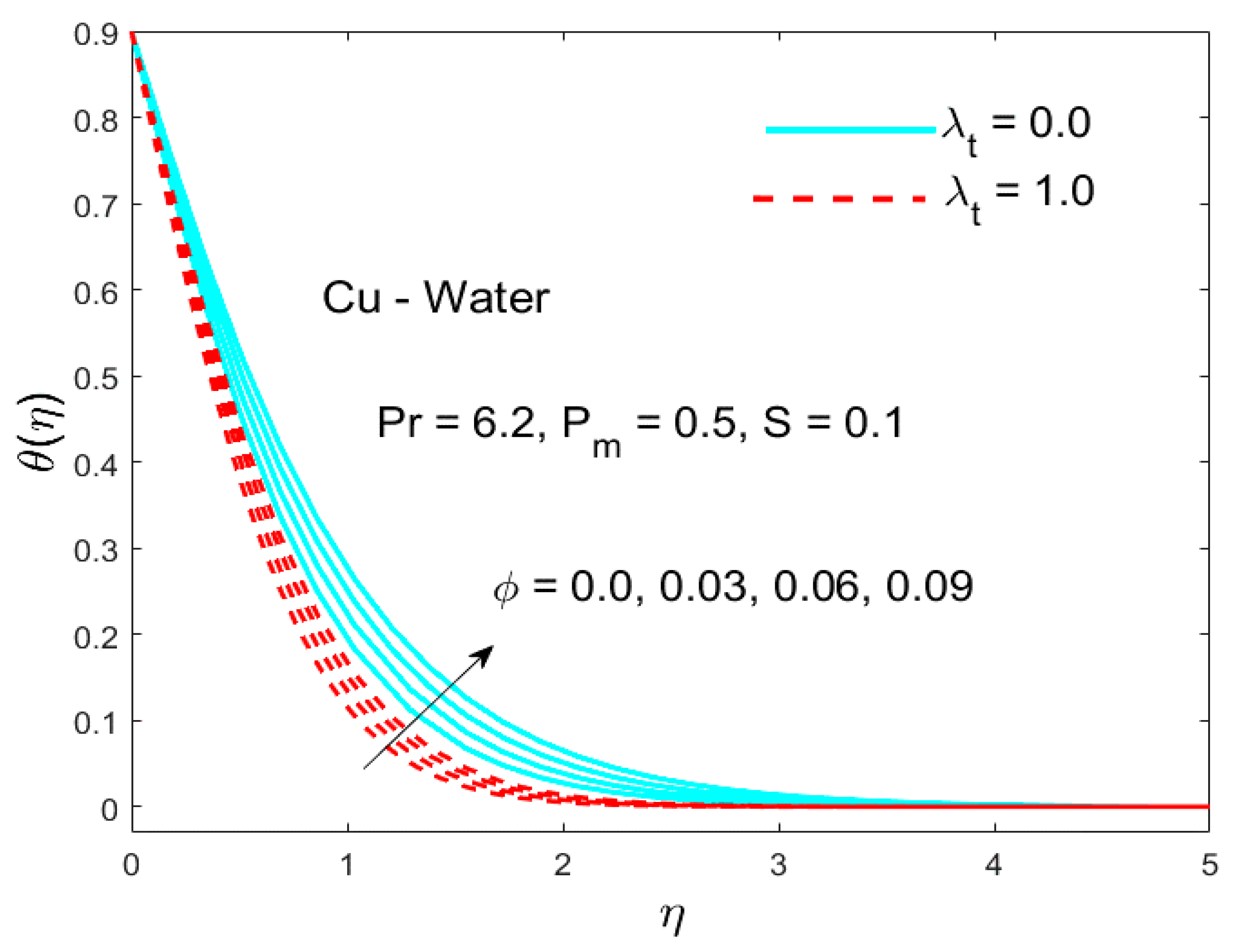Figure 5 displays that due to the enhancement in the value of $P_m$ (porosity parameter), the dimensionless temperature profile increased. Physically, it happened due to the decrease in the permeability $K$ of the permeable source and the fluid effective viscosity. Notably, the variation in the temperature $\theta$ for ${\lambda }_t=0.5$ was lower as compared to ${\lambda }_t=0.$

5.2. The Impact of the Parameter $S$ (Thermal Stratification)

Figure 6 portrays the stimulus of parameter $S$, i.e., TSP on the field of temperature. Here it is fascinating to note that the enrichment in the values of the thermal stratified parameter $S$ caused the temperature distribution to become thinner. Physically, this is on the grounds that reasonably temperature differences decrease between the surrounding and surface of the sheet, and this fact reduces the fluid temperature.

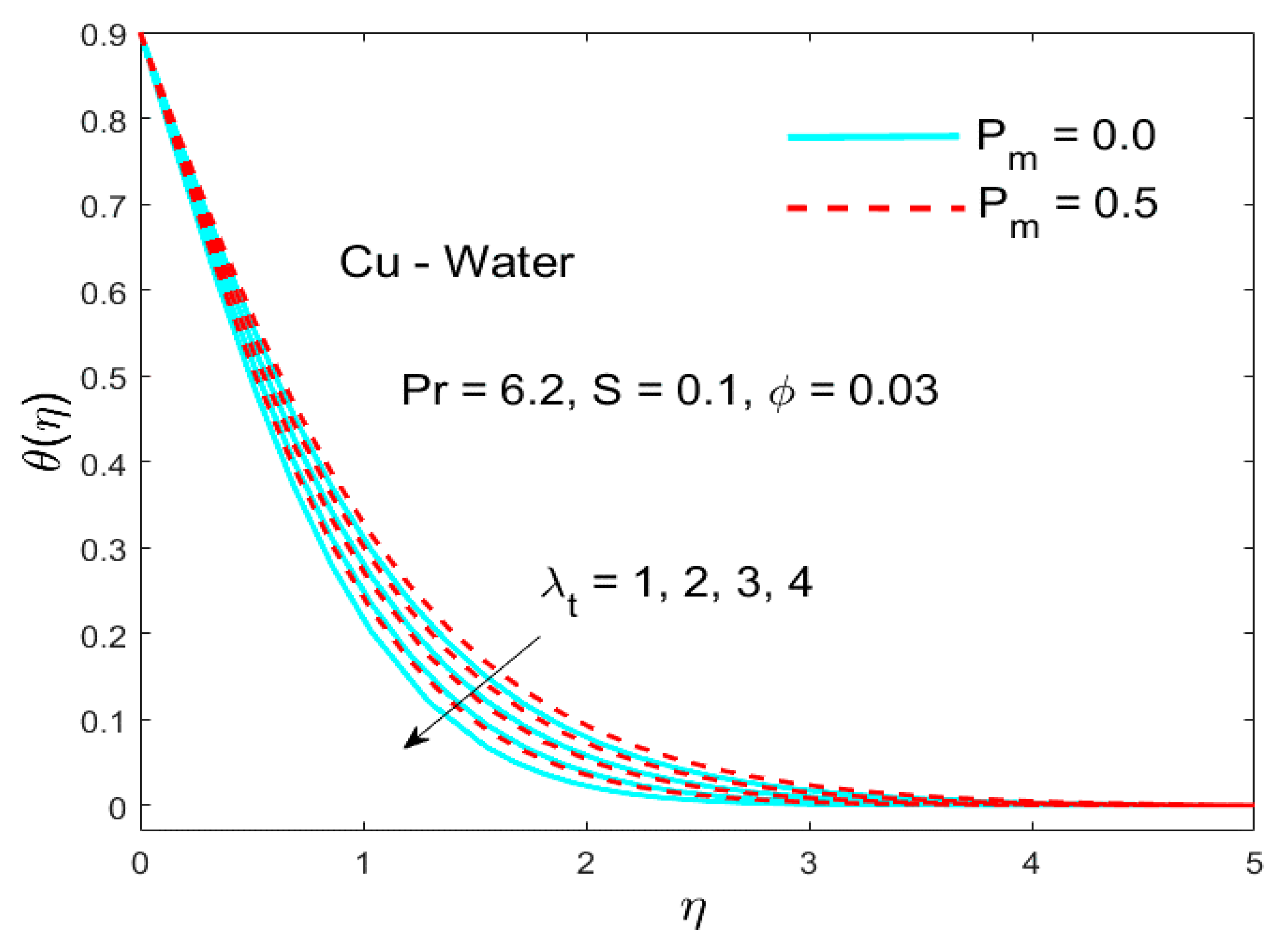
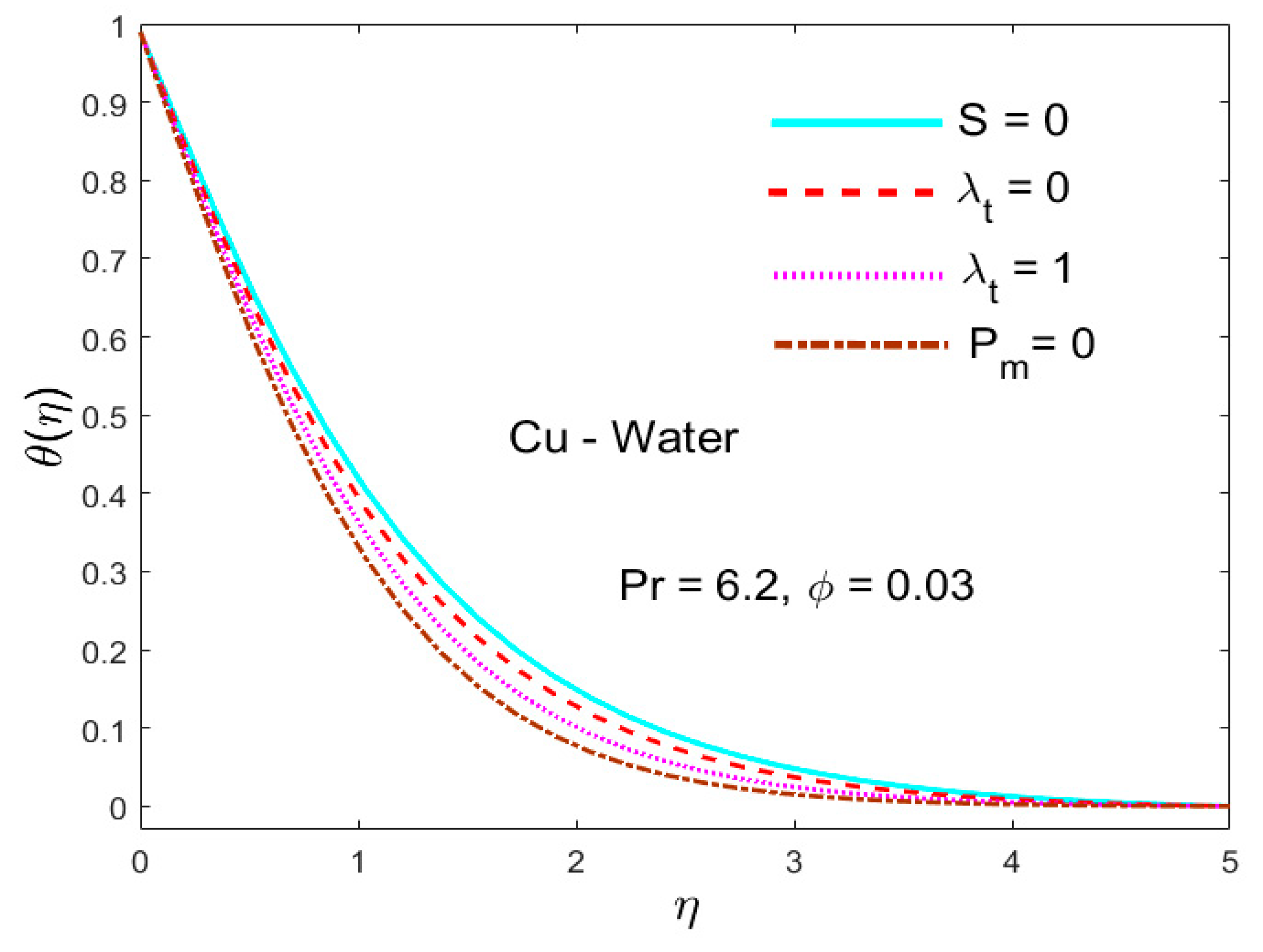
5.3. The Influence of the Parameter ${\lambda }_t$ Called (Thermal Relaxation)

The characteristics of the dimensionless thermal relaxation parameter ${\lambda }_t$ on $\theta (\eta )$ are revealed in Figure 7. The temperature distribution and the thickness of the thermal boundary layer were reduced for the greater values of ${\lambda }_t$. The physical interpretation is that the physical object like particles need more additional time to transfer heat to its nearest particles as we enhanced the value of ${\lambda }_t$. Further, we could state that for larger ${\lambda }_t$, the material demonstrated a non-conducting behavior, due to this reason the temperature distribution reduced. Fourier’s heat conduction law and the Cattaneo–Christov model of heat flux comparison are elaborated in Figure 8. It is observed that for ${\lambda }_t=0$, heat transferred sharply all the way through the material. The worth mentioning point is that the temperature got larger for ${\lambda }_t=0$, i.e., for Fourier’s law than the Cattaneo–Christov model law but qualitatively similar in both cases.

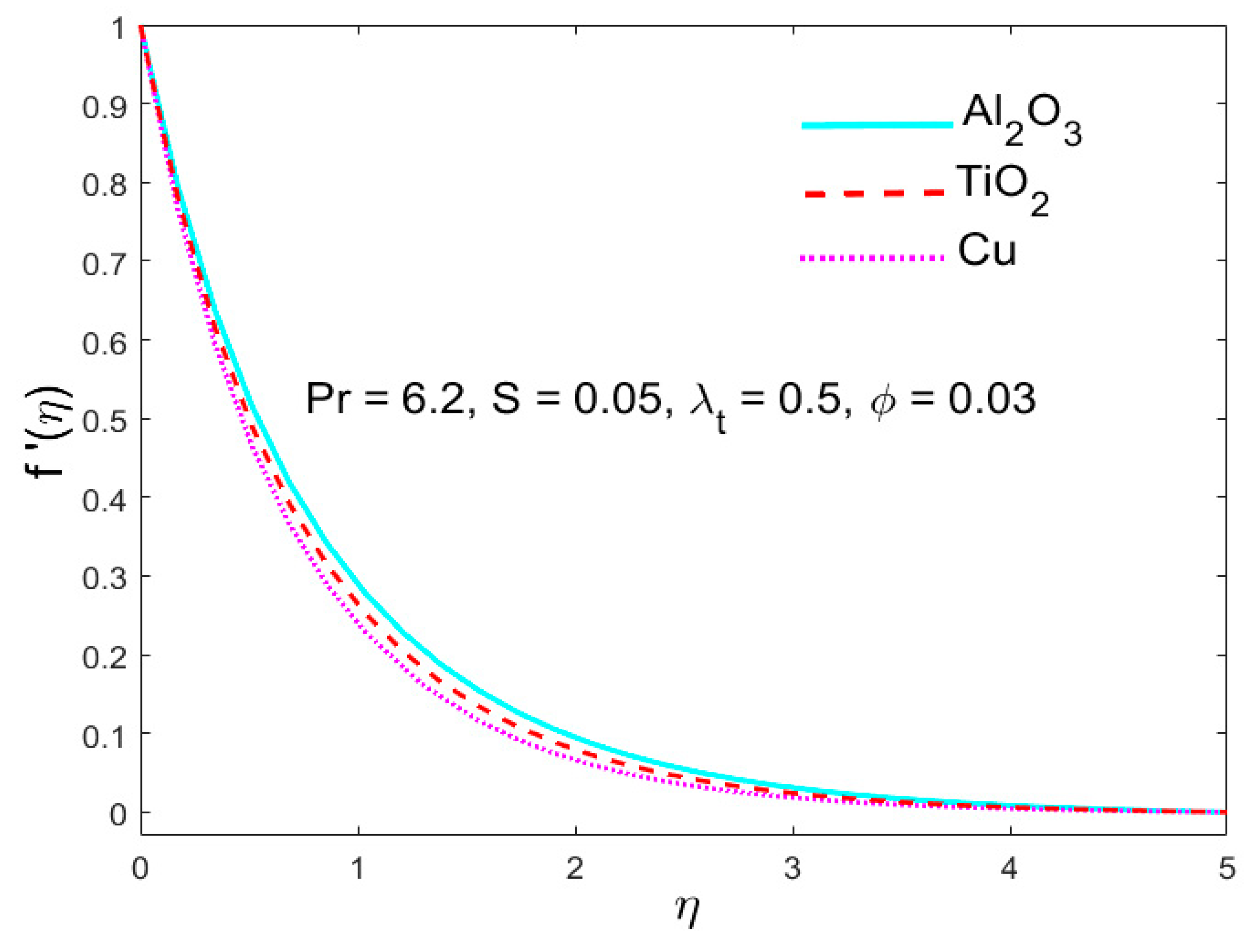
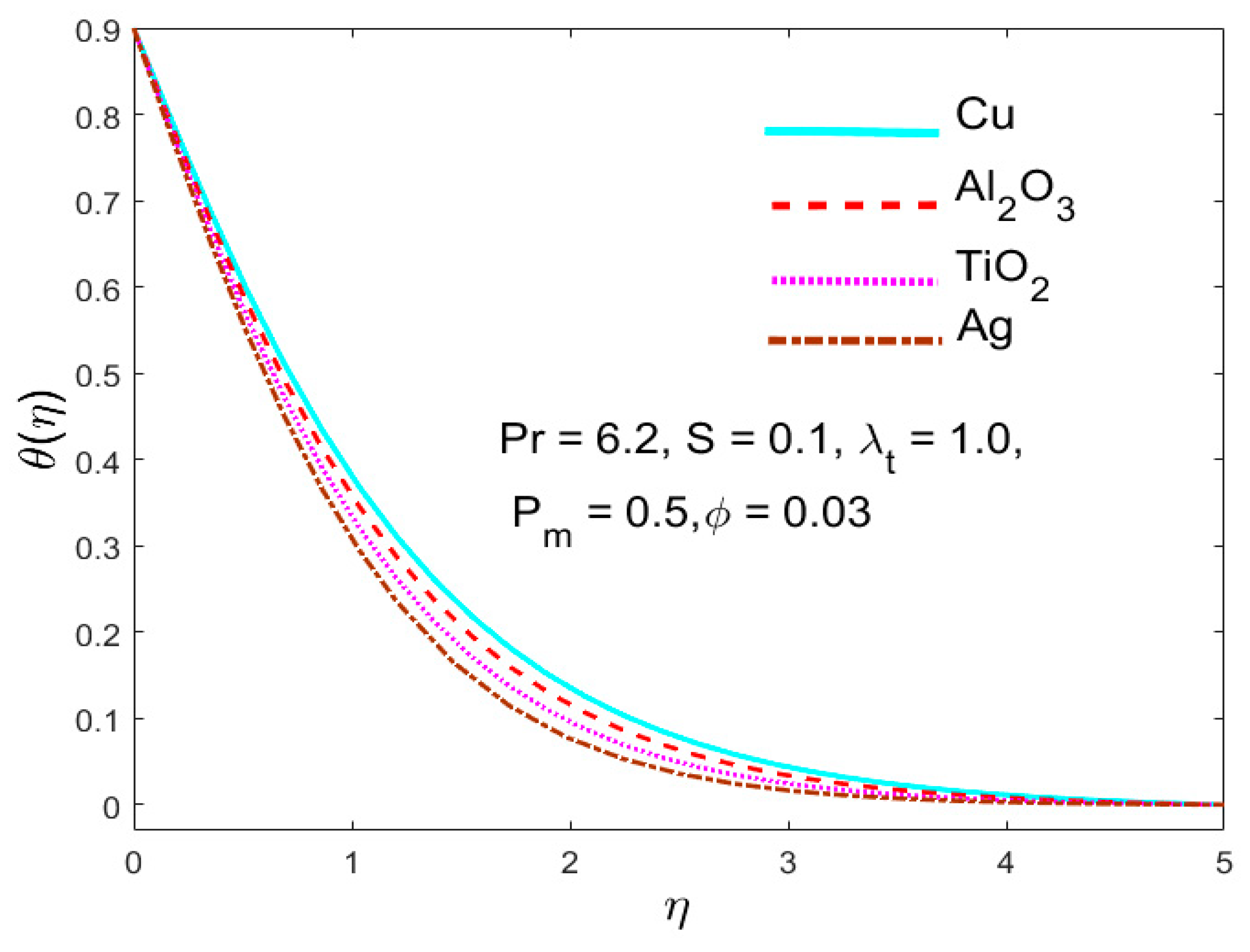
5.4. The Stimulus of the Parameter $\varphi$ (Nanoparticle Volume Fraction)

Using the thermophysical characteristics of nanoparticles and base liquid is mentioned in

Table 4. Thermophysical key properties of the nanoparticles and the water (base fluid).

Physical Properties	H2O	Cu	Al2O3	TiO2
$c_p(\mathrm{J}/\mathrm{kg} \mathrm{K})$	4179	385	765	686.2
$\rho ({\mathrm{kg}/\mathrm{m}}^3)$	997	8933	3970	4250
$\mathrm{k}(\mathrm{W}/\mathrm{m} \mathrm{K})$	0.613	400	40	8.9538

. The influence of developing parameters on the flow of fluid motion and temperature was carried out through graphs and tables. The impact of the volume fraction of Cu-water nanofluid on the velocity field is sketched in Figure 9. The enhancement in the volume fraction of Cu-water nanofluid tended to reduce the dimensionless velocity profile. Figure 10 shows that the expansion of Cu-nanoparticles in liquid, the opposite force to the flow of motion was advanced as compared to titanium dioxide and alumina. From Figure 11, we observed that the larger value of Cu-nanoparticles volume fraction shows an increasing trend in the temperature profile. Figure 12. illustrates the influence of the three changed water-base nanofluids such as alumina (Al₂O₃), titanium dioxide (TiO₂) and copper (Cu) on the non-dimensional temperature profiles. On the other hand, clearly observed that the Cu-water nanofluids had the highest temperature profile in comparison with Al₂O₃ (alumina) and TiO₂ (titanium dioxide) nanofluids.

6. Concluding Remarks

In this final section, we scrutinized the key features of the Cattaneo–Christov model of heat flux to highlight the transfer heat of viscous fluid in the existence of nanoparticles with porous media. The motion of the liquid is produced by an exponentially exercising the stretching surface. The worth mentioning remarks of the above work are summarized below.

➢

The enhancement in the porosity parameter $P_m$ shows a decreasing trend in the velocity profile.

➢

Both the temperature field and its associated layer thickness were condensed for bigger values of the thermal stratification parameter $S$.

➢

A larger thermal relaxation parameter ${\lambda }_t$ reduced the temperature field and corresponding boundary layer thickness.

➢

The effect of the thermal relaxation parameter was qualitatively identical in both the Cattaneo–Christov model of heat flux and Fourier models.

➢

For nanofluids with copper nanoparticles, the velocity components show a decreasing behavior as the volume fraction of nanoparticle rose along with the saddle and nodal points.

➢

For Cu-nanoparticles expansion in liquid, the resistance to the motion of the liquid (along x- and y-axes) was found to be higher as compared to titanium dioxide (TiO₂) and alumina (Al₂O₃).

➢

The temperature also improved for the Cu-water nanofluid with the increment in the volume fraction of the nanoparticles.