Synthetic Microstructure Generation and Multiscale Analysis of Asphalt Concrete
Abstract
1. Introduction
2. Materials and Methods
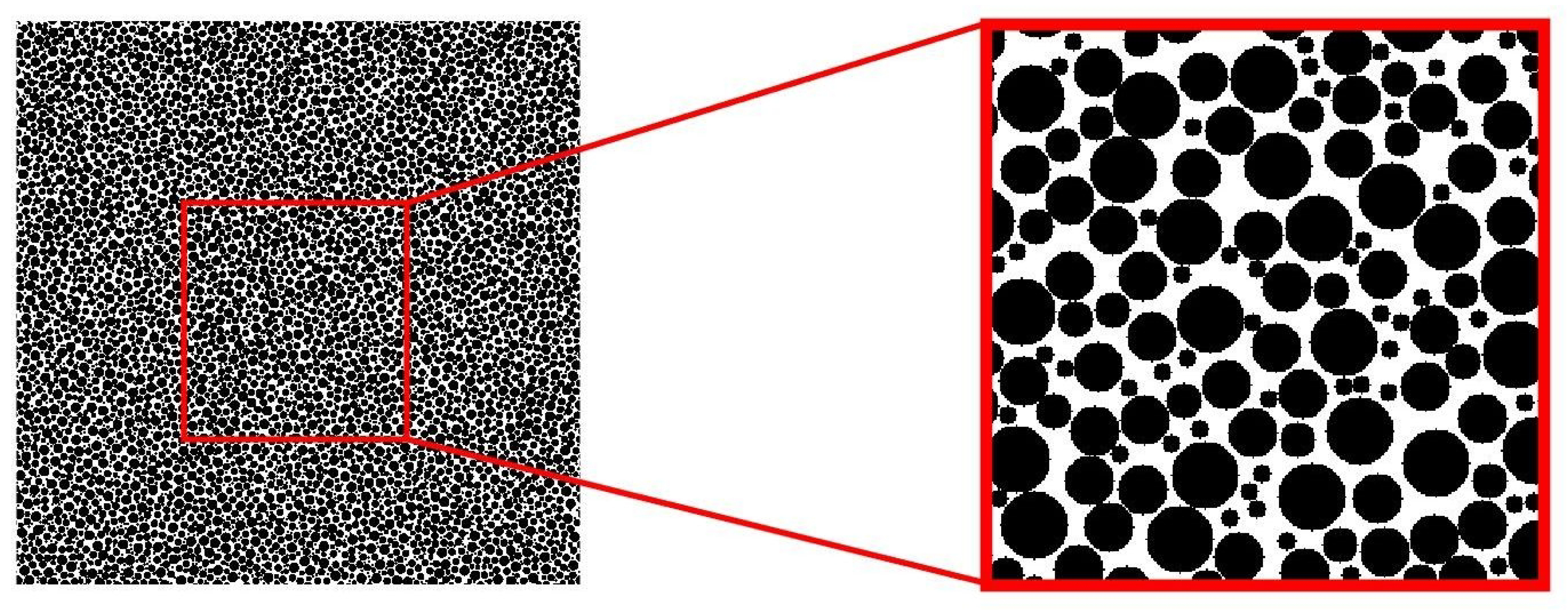
2.1. Microstructure Generation
2.1.1. Generation of Spheres (Circles)
2.1.2. Voronoi Tessellation
2.1.3. Shrinkage Procedure
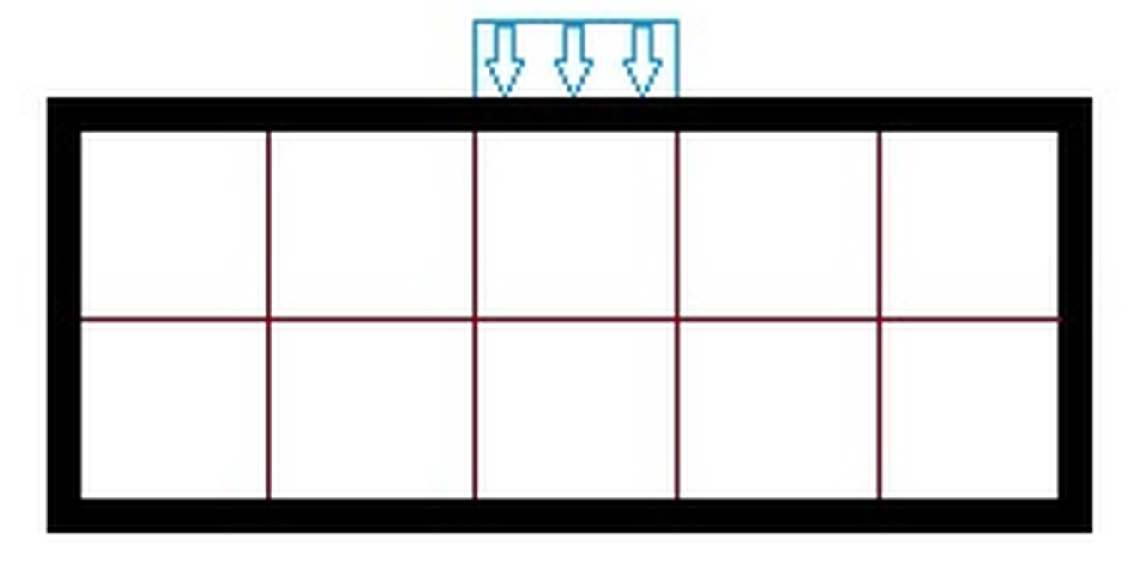
2.2. Multiscale Modeling
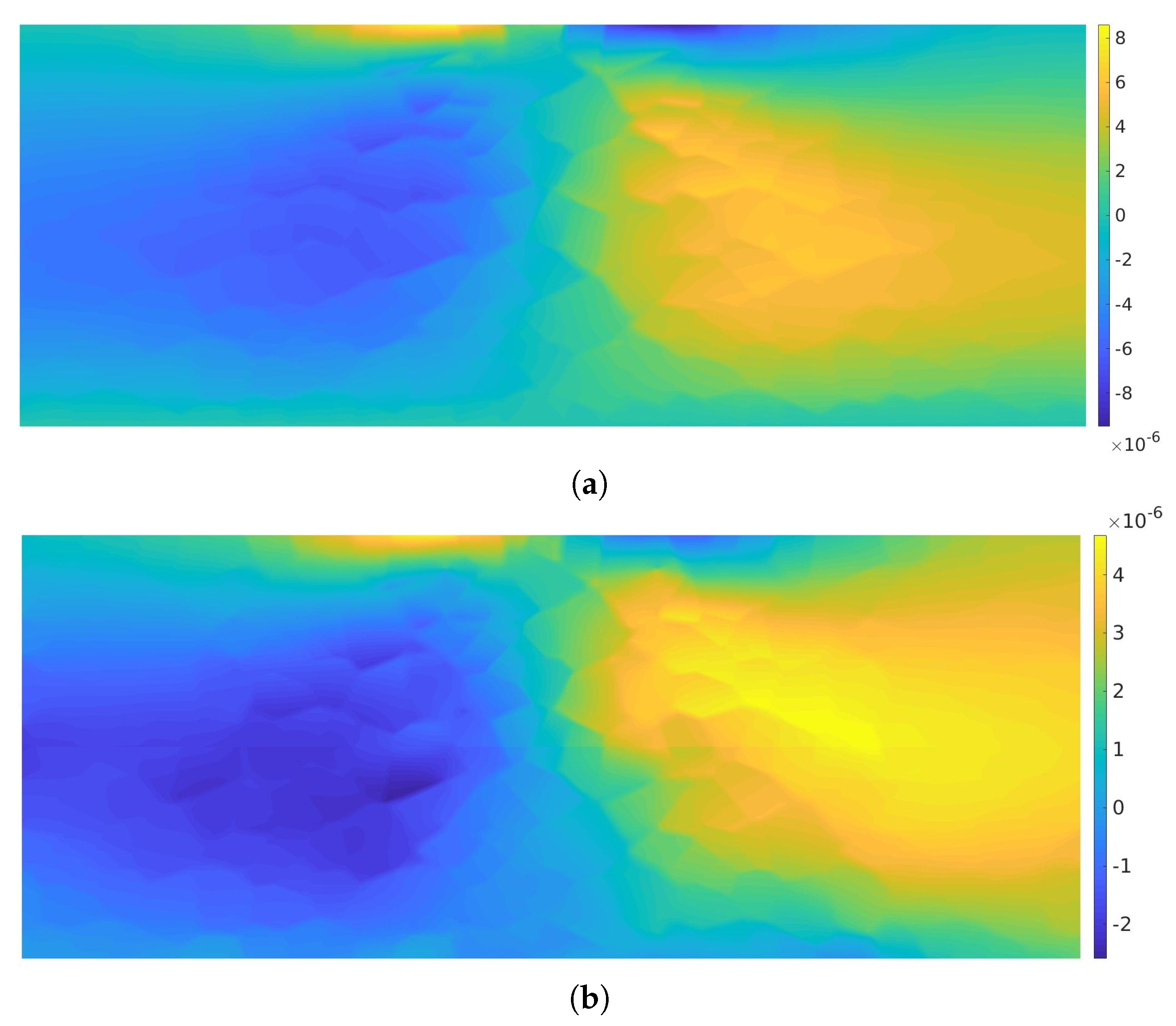
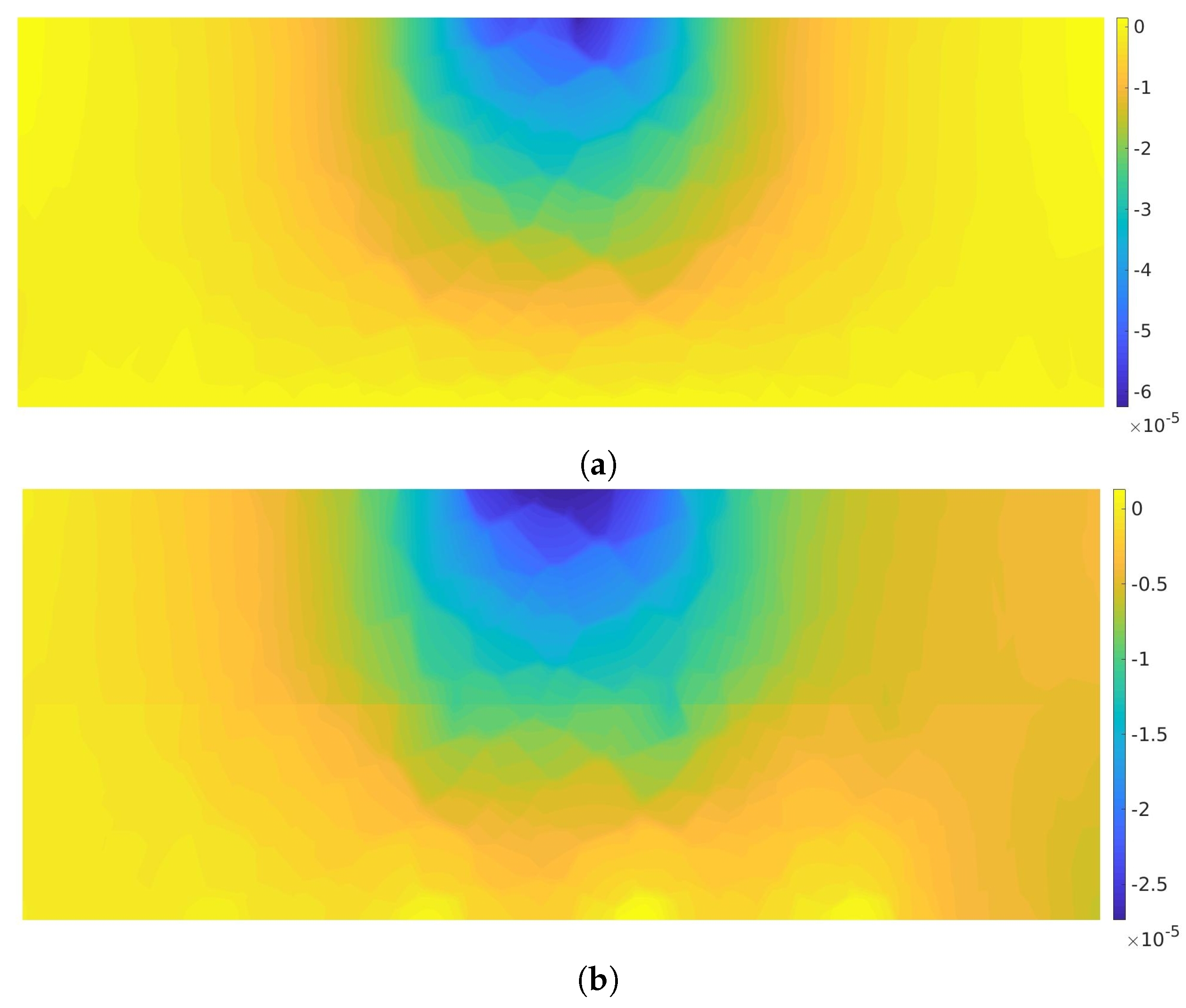
3. Results
- for the aggregate particles (inclusions) − GPa, , and
- for the mastic (matrix) − GPa, .
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Porto, M.; Caputo, P.; Loise, V.; Eskandarsefat, S.; Teltayev, B.; Rossi, C.O. Bitumen and Bitumen Modification: A Review on Latest Advances. Appl. Sci. 2019, 9, 742. [Google Scholar] [CrossRef]
- Collop, A.; Scarpas, A.; Kasbergen, C.; de Bondt, A. Development and finite element implementation of a stress dependent elasto-visco-plastic constitutive model with damage for asphalt. Transp. Res. Rec. 2003, 1832, 96–104. [Google Scholar] [CrossRef]
- Kim, Y.; Souza, F.; Teixeira, J. A two-way coupled multiscale model for predicting damage-associated performance of asphaltic roadways. Comput. Mech. 2013, 51, 187–201. [Google Scholar] [CrossRef]
- Liu, P.; Hu, J.; Wang, D.; Oeser, M.; Alber, S.; Ressel, W.; Fala, G. Modelling and evaluation of aggregate morphology on asphalt compression behavior. Constr. Build. Mater. 2017, 133, 196–208. [Google Scholar] [CrossRef]
- Mitra, K.; Das, A.; Basu, S. Mechanical behavior of asphalt mix: An experimental and numerical study. Constr. Build. Mater. 2012, 27, 545–552. [Google Scholar] [CrossRef]
- Schüller, T.; Manke, R.; Jänicke, R.; Radenberg, M.; Steeb, H. Multi-scale modelling of elastic/viscoelastic compounds. ZAMM J. Appl. Math. Mech. 2013, 93, 126–137. [Google Scholar] [CrossRef]
- Schüller, T.; Jänicke, R.; Steeb, H. Nonlinear modeling and computational homogenization of asphalt concrete on the basis of XRCT scans. Constr. Build. Mater. 2016, 109, 96–108. [Google Scholar] [CrossRef]
- Woldekidan, M.; Huurman, M.; Pronk, A. Linear and Nonlinear Viscoelastic Analysis of Bituminous Mortar. Transp. Res. Rec. J. Transp. Res. Board 2013, 2370, 53–62. [Google Scholar] [CrossRef]
- Dai, Q.; You, Z. Prediction of creep stiffness of asphalt mixture with micromechanical finite-element and discrete-element models. J. Eng. Mech. 2007, 133, 163–173. [Google Scholar] [CrossRef]
- Arshadi, A.; Bahia, H. Development of an image-based multi-scale finite-element approach to predict mechanical response of asphalt mixtures. Road Mater. Pavement Des. 2015, 16, 214–229. [Google Scholar] [CrossRef]
- Aigner, E.; Lackner, R.; Pichler, C. Multiscale Prediction of Viscoelastic Properties of Asphalt Concrete. J. Mater. Civ. Eng. 2009, 21, 771–780. [Google Scholar] [CrossRef]
- Al-Rub, R.; You, T.; Masad, E.; Little, D. Mesomechanical modeling of the thermo-viscoelastic, thermo-viscoplastic, and thermo-viscodamage response of asphalt concrete. Int. J. Adv. Eng. Sci. Appl. Math. 2011, 3, 14–33. [Google Scholar] [CrossRef]
- You, T.; Al-Rub, R.; Darabi, M.; Masad, E.; Little, D. Three-dimensional microstructural modeling of asphalt concrete using a unified viscoelastic-viscoplastic-viscodamage model. Constr. Build. Mater. 2012, 28, 531–548. [Google Scholar] [CrossRef]
- Ziaei-Rad, V.; Nouri, N.; Ziaei-Rad, S.; Abtahi, M. A numerical study on mechanical performance of asphalt mixture using a meso-scale finite element model. Finite Elem. Anal. Des. 2012, 57, 81–91. [Google Scholar] [CrossRef]
- Klimczak, M.; Cecot, W. An adaptive MsFEM for non periodic viscoelastic composites. Int. J. Numer. Methods Eng. 2018, 114, 861–881. [Google Scholar] [CrossRef]
- Wimmer, J.; Stier, B.; Simon, J.W.; Reese, S. Computational homogenisation from a 3D finite element model of asphalt concrete–linear elastic computations. Finite Elem. Anal. Des. 2016, 110, 43–57. [Google Scholar] [CrossRef]
- Mo, L.; Huurman, M.; Wu, S.; Molenaar, A. 2D and 3D meso-scale finite element models for ravelling analysis of porous asphalt concrete. Finite Elem. Anal. Des. 2008, 44, 186–196. [Google Scholar] [CrossRef]
- Tschopp, M.; Wilks, G.; Spowart, J. Multi-scale characterization of orthotropic microstructures. Model. Simul. Mater. Sci. Eng. 2008, 16, 065009. [Google Scholar] [CrossRef]
- Cecot, W.; Oleksy, M. High order FEM for multigrid homogenization. Comput. Math. Appl. 2015, 70, 1391–1400. [Google Scholar] [CrossRef]
- Efendiev, Y.; Hou, T. Multiscale finite element methods for porous media flows and their applications. Appl. Numer. Math. 2007, 57, 577–596. [Google Scholar] [CrossRef]
- Hou, T.; Wu, X. A multiscale finite element method for elliptic problems in composite materials and porous media. J. Comput. Phys. 1997, 134, 169–189. [Google Scholar] [CrossRef]
- Cecot, W. Adaptive FEM analysis of selected elastic-visco-plastic problems. Comput. Methods Appl. Mech. Eng. 2007, 196, 3859–3870. [Google Scholar] [CrossRef]
- Cecot, W. Application of h-adaptive FEM and Zarka’s approach to analysis of shakedown problems. Int. J. Numer. Methods Eng. 2004, 61, 2139–2158. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimczak, M.; Cecot, W. Synthetic Microstructure Generation and Multiscale Analysis of Asphalt Concrete. Appl. Sci. 2020, 10, 765. https://doi.org/10.3390/app10030765
Klimczak M, Cecot W. Synthetic Microstructure Generation and Multiscale Analysis of Asphalt Concrete. Applied Sciences. 2020; 10(3):765. https://doi.org/10.3390/app10030765
Chicago/Turabian StyleKlimczak, Marek, and Witold Cecot. 2020. "Synthetic Microstructure Generation and Multiscale Analysis of Asphalt Concrete" Applied Sciences 10, no. 3: 765. https://doi.org/10.3390/app10030765
APA StyleKlimczak, M., & Cecot, W. (2020). Synthetic Microstructure Generation and Multiscale Analysis of Asphalt Concrete. Applied Sciences, 10(3), 765. https://doi.org/10.3390/app10030765




