1. Introduction
The study of heat transport can provide engineering solutions for a plethora of important problems in many scientific and technological disciplines [
1,
2]. The complexity of the description of heat transport is increased when the system under study is a heterogeneous material, consisting of more than one phases or materials in discrete forms. Many natural substances, such as stones, soil, and sand (aquifers, oil reservoirs), zeolites, biological tissues (bones, wood), as well as man-made materials, such as cement, ceramics, foams, and colloidal solutions, are considered heterogeneous materials [
3]. The characteristic length of heat transport ranges from a few tens of nanometers, for colloidal solutions and nanofibers, to the field scale, for geological applications.
A very useful parameter for characterizing heat conduction in a material is the effective thermal conductivity (
) [
3,
4,
5]. For isotropic materials, the effective thermal conductivity is the ratio of the magnitude of the heat flux to that of the temperature gradient in the material. In most occasions, the conductivity and the volume fraction of each component are not sufficient to determine the effective thermal conductivity of the medium. Parameters such as the composition, the shape, and the layout of the various components also play an important role. Thus, the thermal conductivity of a heterogeneous material is related to the thermal conductivity of individual phases (air, water, solid particles), the volume fraction, and the microstructure geometry [
3,
4,
5].
Maxwell introduced the idea of increasing the thermal conductivity of a fluid by mixing suspended metallic or non-metallic solid particles [
1,
3,
6]. He was also the first to calculate the effective conductivity of a set of spheres in a dilute solution. Since then, many models were proposed to describe the thermal conductivity of composite materials, the most popular being Bruggeman’s expressions [
3]. However, these models are unable to include the particularities of each structure. Ultrafine particles tend to form aggregates, as a result of their random movement and the action of Van der Waals interparticle forces. Given the increased connectivity of the particles between themselves, as well as between them and the walls, aggregated systems have different thermal properties from fully dispersed particles. Nanofluids and aerogels are typical systems that are comprised of fractal-like aggregates [
7]. For the calculation of the equivalent properties in such systems, numerical simulations of the underlying internal transport phenomena should be performed.
Conventional numerical techniques, such as finite differences (FD) and finite elements (FE), have been used extensively with success in a wide range of problems [
8,
9]. The FE method, in particular, has enjoyed extensive use and found vast commercialization, due to its stability and applicability. However, the above methods present certain inherent problems associated with the requirement for a well-organized and connected mesh in the boundaries and the main domain of the problem. Creating this well-coherent mesh can be particularly difficult and usually requires timely user involvement, especially in complex geometries with steep gradients of the field variables, where substantial mesh refinement is usually needed. Because of this difficulty, new numerical methods have appeared recently, commonly called meshfree methods [
10,
11,
12,
13]. These methods overcome many of the problems associated with well-connected mesh creation through its complete elimination in the solution process. This makes them more flexible in difficult geometries, as the grid can be easily refined in strenuous areas, such as the interface between the materials.
The main advantage over traditional mesh-based numerical methods is related to the approximation of the field variables. Local-type interpolation is used without the necessity of a connected mesh in the domain. Meshless methods use regularly or irregularly distributed spatial points, usually called nodes, with a weight function and local support defined in each of these nodes. This reduces considerably the difficulties associated with mesh generation. In recent years, many authors used meshless methods to solve heat conduction problems. The smooth particle hydrodynamics method was reported for solving unsteady-state heat conduction problems [
14]. The element-free Galerkin method was used for solving heat transport problems [
15,
16]. The meshless local Petrov-Galerkin (MLPG) method created by Atluri and Zhu [
17] was also applied in heat conduction systems [
18,
19,
20].
In the present work, three dimensional (3D) thermal conduction problems within particulate systems were solved. The MLPG method, which is based on the expression of differential equations in the local weak form, was implemented. Two distinctive methods for the approximation of differential operators and unknown functions, moving least squares (MLS) [
21] and discretization-corrected particle strength sxchange (DC PSE) [
22], were examined, and a new sophisticated interpolation procedure was proposed, allowing easier grid refinement. The predictions of the method were compared with analytical ones, with the predictions of other numerical techniques and commercial software packages, as well as with experimental data from the literature. Initially, the method was validated for a well-known literature problem. The convergence of the method was compared on the basis of two field descriptors, locally with the temperature distribution resulting from the finite difference (FD) method, and globally with the derived effective conductivity.
Particle aggregates were constructed with the diffusion limited aggregation (DLA) method and with a ballistic aggregation (BA) technique. The effective thermal conductivity of the aggregates was studied, addressing successfully the problem that is associated with the contact between neighboring particles. It was shown that the present work offers a further utilization of the MLPG approach, providing robust, fast, and very accurate solutions.
2. Materials and Methods
A truly meshless method based on the MLPG approach is presented below for the solution of heat conduction problems. The success of the MLPG method depends on three important parameters, namely, the approximation of the unknown function and its derivatives (trial function), the weight function of the integration (test function), and the shape of the integration domain. As trial function, the widely used approach of the MLS method was implemented. Also, the DS PSE operator was tested for the first time, to the authors’ knowledge, as a trial function of the MLPG method.
The solution approximation,
, is described following the MLS technique [
21], as the product of a vector of polynomial base,
, and a vector of coefficients,
,
is a number related with the order of the polynomial base. In order to determine the form of
, a weighted discrete error norm is constructed and minimized. This process results to the construction of the shape function,
is a vector containing the nodal data, and
are matrix functions of the polynomial base and an exponential weight function, and
is the number of nodes in the support of domain of node
. Derivatives of the shape function,
, can be calculated with the product rule.
DC PSE [
22,
23] was originally formulated as a correction of the particle strength exchange method (PSE) [
24]. Considering a continuous field
, any derivative can be expressed as
where
and
are integers that determine the order of the operator. The DC PSE operator for this derivative is
where
is a resolution function,
are the nodes of the support domain, and
is a kernel function.
The weighted integral of the heat conduction equation at the domain
around a point
is given by
where
is the weight function (here, the step function), and
is the thermal conductivity. Reduced quantities are determined based on the physical values of the media, the domain geometry, and the boundary conditions
is the length of the domain, and
,
are the values of the temperature imposed at the hot and cold boundary boundaries, respectively.
and
are the domains of medium
(exterior) and
(interior) of the enclosure. Using the Gauss divergence theorem, the local symmetric weak form of the heat equation is
where
is the step function defined at the domain of the interior medium (unit there, zero elsewhere). Solution of the equation provides the temperature distribution throughout the cavity. One can calculate the dimensionless effective thermal conductivity of the medium by the following integral
Surfaces are perpendicular to the heat flux. To determine the conductivity with sufficient statistical accuracy, at least 10 such equidistant surfaces within the domain were obtained, and their averaged conductivity gave the effective thermal conductivity.
One of the main advantages of the meshless methods is the straightforward implementation of node refinement. In fact, it is necessary that the entire node generation process be fully automated without the user’s intervention. A determining factor in this direction is the relative positions of all nodes of the influence domain around any given point. In the case of a sharp increase in discretization, the nodes near the boundaries of the refinement have most of their neighbors in the direction of the refined mesh. In this case, the MLS method usually fails to calculate the shape functions accurately. Also, the DC PSE method has no stable resulting solutions while calculating the operators [
23].
A solution to this problem could be the gradual refinement of the grid, so that the transition to the higher discretization region becomes sufficiently smooth [
12]. However, defining the nodes and the vectors normal to the interfaces at the limits of the refinement in complex three-dimensional geometries with multiple interconnections has proven computationally difficult and time-consuming.
To overcome this impediment, an alternative way of interpolation in these complex regions was introduced. Problematic nodes near the edge of the refinement do not require all neighboring nodes to calculate the shape functions, but only those of the initial (low) spatial resolution. In addition, a thin layer of nodes belonging to the high resolution can have their shape function definition influenced not by the entire refined node distribution, but by the nodes belonging to the low (base) resolution only. The remaining nodes are both affected and affecting the entire grid.
Figure 1 shows the nodes that are contained in the support domain of three representative nodes located at the edge of the refinement.
The process of node generation begins with spatial discretization using a homogeneous grid of accuracy sufficient for a single-component medium with no expected steep gradients, from here on called low-density (low-resolution, d0). For heat transport in a medium that includes two or more components, the thermal conductivity is a characteristic property of each part. Considering the conductivity of two materials with distinct conductivities, and , each node in this grid is characterized by the thermal conductivity of its location ( or ) and this value is stored in a vector ().
By calculating the shape function derivatives in the MLS method, or the first order operators for the DC PSE method, in the original, low-density grid, the gradient of the thermal conductivity can be calculated at each node of the medium. The gradient will be zero everywhere (), except for the areas near the interfaces of the components (). The thickness of each such area depends on the size of the support domain. The support domain is set equal to 1.5 times the initial grid spacing (). The nodes near the interface are deleted and the space is discretized there in double resolution (), with no change on the size of the support domain (). Upon calculating the conductivity gradient, the nodes that will remain near the interface () will be the ones from the aforementioned resolution. Thus, the grid is constructed automatically and speedily, without user intervention at any creation stage. This process can be continued for successively higher discretizations, doubling the discretization locally every time.
The integration part is of key importance for the success of the MLPG method. The size and shape of the sectors on which the weight function is non-zero may vary. Using the MLS approach and the DC PSE method for the trial function, and based on the concept of the MLPG method, the weight function in each local integral can be selected in several ways [
11]. Each weight function offers a specific expression of the MLPG method. It has been reported [
10,
11] that the most promising expression is the MLPG which uses the step function as a weight function for the integration, which is defined in the space
of the integration. In this case, the spatial integrals in the
are avoided on account of the Gauss theorem. The overall matrix includes surface integrals only, which makes this method more efficient and attractive, with the solution being faster and more accurate than most other MLPG implementations, due to the simplicity of the calculations and the stability of the resulting solutions.
Apart from the form of the weight function, the shape of the integration domain is also critical to the success of the method. Notable increase of the stability and robustness of the method has been reported using rectangular type domains in 2D problems [
18]. Usually, equidistant domains around each node are used in MLPG implementations, with a radius around 60% of the local grid distance. Cubic integration domains around each node are used in the present 3D cases and, thus, the whole domain is covered without overlapping. During refinement in regions close to the interfaces, overlapping cannot be avoided without significant increase in the computational time. However, the overlapping is effectively restricted in small areas and does not affect the stability of the method.
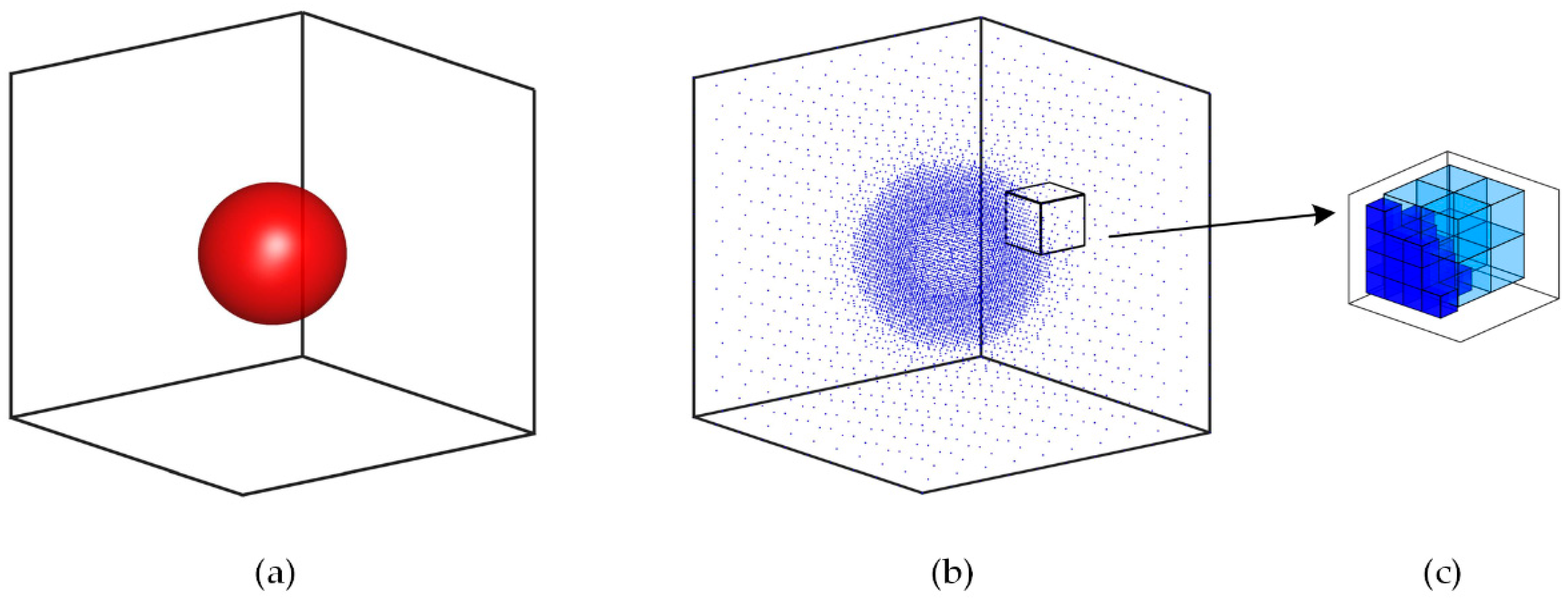
Figure 2 shows a domain comprising of a test sphere,
Figure 2a, and the resulting computational grid, with integration sites around each node in the inlet,
Figure 2b, consisting of cubes equal to the local grid spacing of each node. During numerical integration, one can have increased accuracy of the results either by increasing the order of the Gaussian quadrature integration, or by dividing the field of integration into smaller parts while keeping the integration order low. It was reported that the algorithm which computes integrals using subdivisions was more efficient than the one that integrates across the support domain with higher quadrature order [
10,
11]. Thus, the surface integrals for the cubic domains are calculated here as the sum of the integrals on the cube sides, and 3-point Gaussian quadrature is used in each side integral.
For heat conduction problems, it has been proven [
18] that first-order interpolation is computationally efficient, fast and accurate. The optimal size of the support domain for the interpolation is ca 1.7 times the local grid spacing. The process of the grid generation, the construction of the shape functions, and the calculation of the integrals are performed here using Matlab kernels. The biconjugate gradient stabilized method (BiCGSTAB) [
25] was used for the numerical solution of the resulting linear system.
For validation purposes, the thermal conductivity was calculated for various particulate systems using Comsol Multiphysics
® and in-house developed automation Matlab
® scripts for the generation of the CAD geometry. Once the geometry was created, the heat transport equation was solved using FE discretization (Galerkin approach), with free tetrahedral elements in the whole domain, and boundary layers (local refinement) developed along each side of the boundary interfaces. Details of the FE resolution are provided in the
Section 5.
3. Simulation of Aggregate Formation
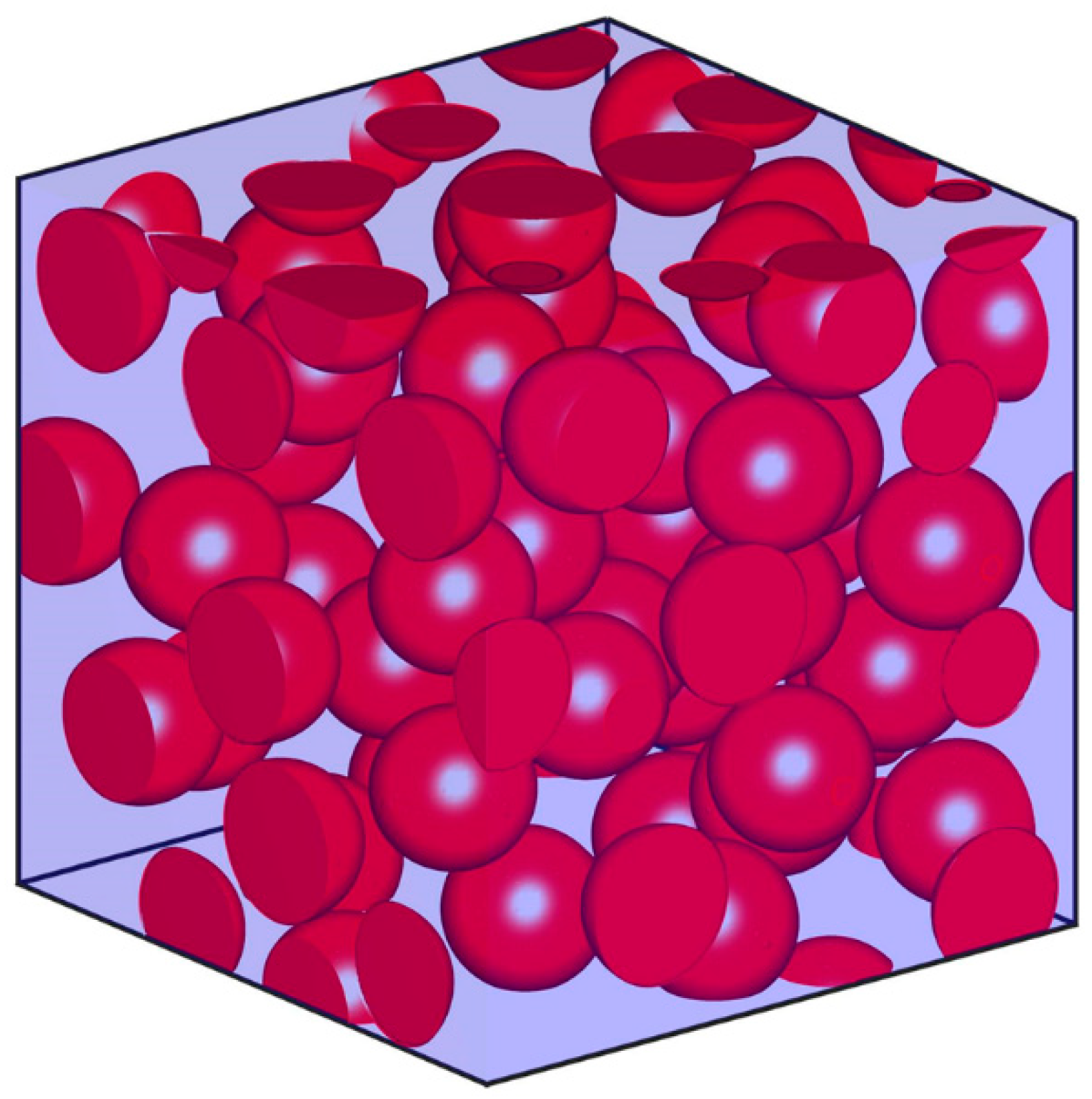
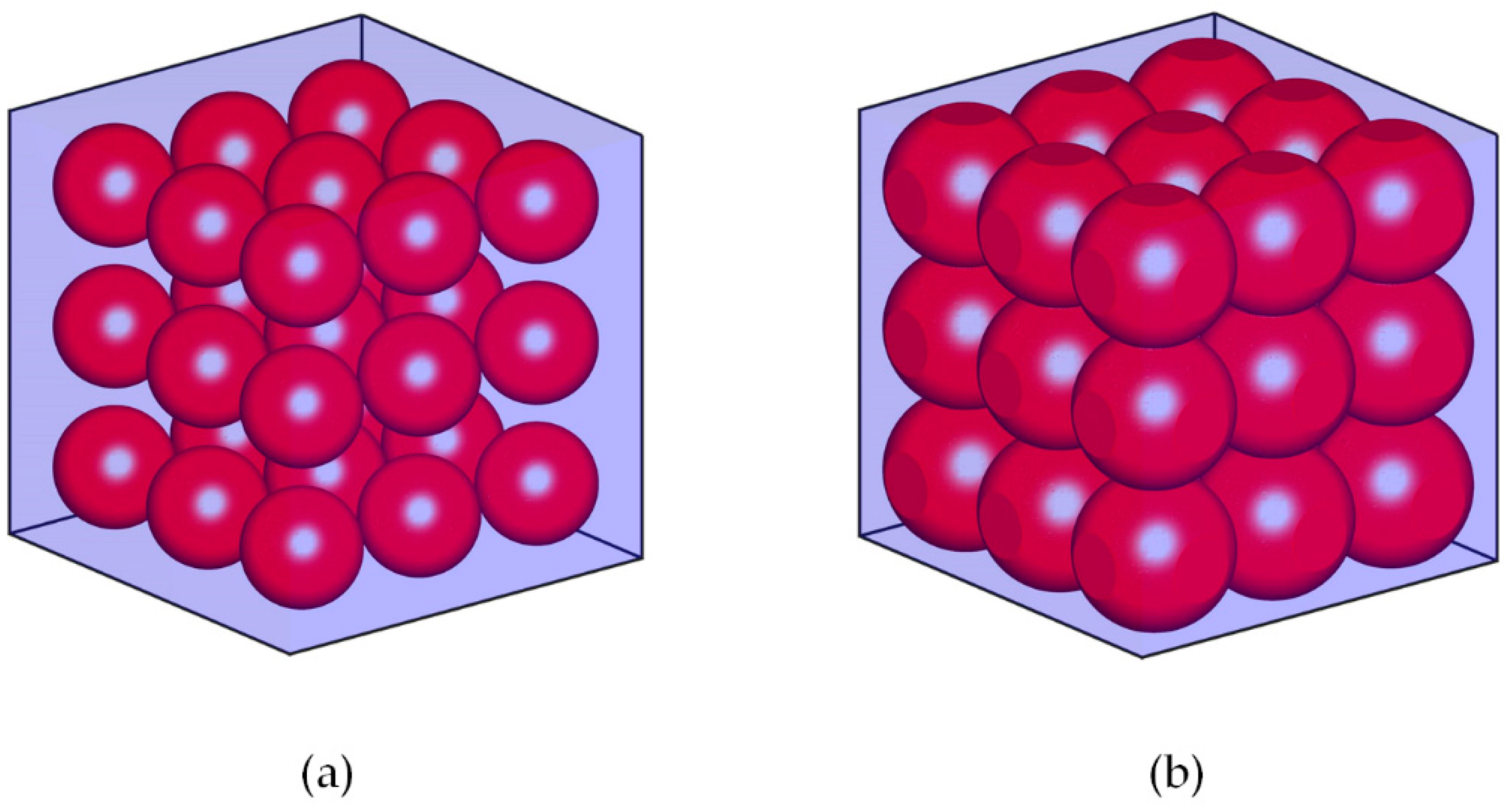
In the present work, the effective thermal conductivity of biphasic systems was calculated. Particularly, heat transport in particle systems and granular porous media was simulated. All the structures encompass a number of spheres within a cubic cavity. Algorithms based on Monte Carlo techniques were used to represent the particulate systems and granular porous media. Equally sized spheres were assumed, and the structures were periodic in every direction. The algorithm allowed random placement of the spheres over the working domain. The first, simple, case that was considered was that of granular media that were made up of spheres with no contact between them [
26]. An example of a granular medium with porosity 0.7 is presented in
Figure 3.
In addition, structures with aggregates of particles were simulated. In this case, every particle was in contact with at least another one. One of the determining parameters for the morphology of particle aggregates is their fractal dimension (
) [
27,
28]. For an aggregate consisting of
particles, the fractal dimension (
) relates the number of particles in the aggregate with its gyroscopic radius (
), through:
, where
is the radius of the particles. As a basic rule, one expects that the higher the fractal dimension, the more cohesive the aggregate.
For the representation of the aggregates, the well-known DLA [
29] and the BA method [
30] were used here, as well as modifications of these models, to represent denser aggregates. The DLA model describes the appropriate phenomena for the formation of fractal structures [
29]. An important parameter of this method is the mean free path of the Brownian diffusion of particles [
30]. If the mean free path is smaller than the size of the aggregate, the morphological characteristics of the clusters are the same and the fractal dimension is approximately
. In the extreme case that the mean free path remains always larger than the aggregate size, the BA model is defined. The resulting aggregates are denser than those of the DLA model [
30,
31]. In these cases, every particle was assumed to cease its motion as soon as it gets in contact with another one. Extension of these models allows the particle to move along the surface of the cluster in order to find a suitable second contact point (DLA 2p, BA 2p) [
30]. This method results in more compact aggregates. In
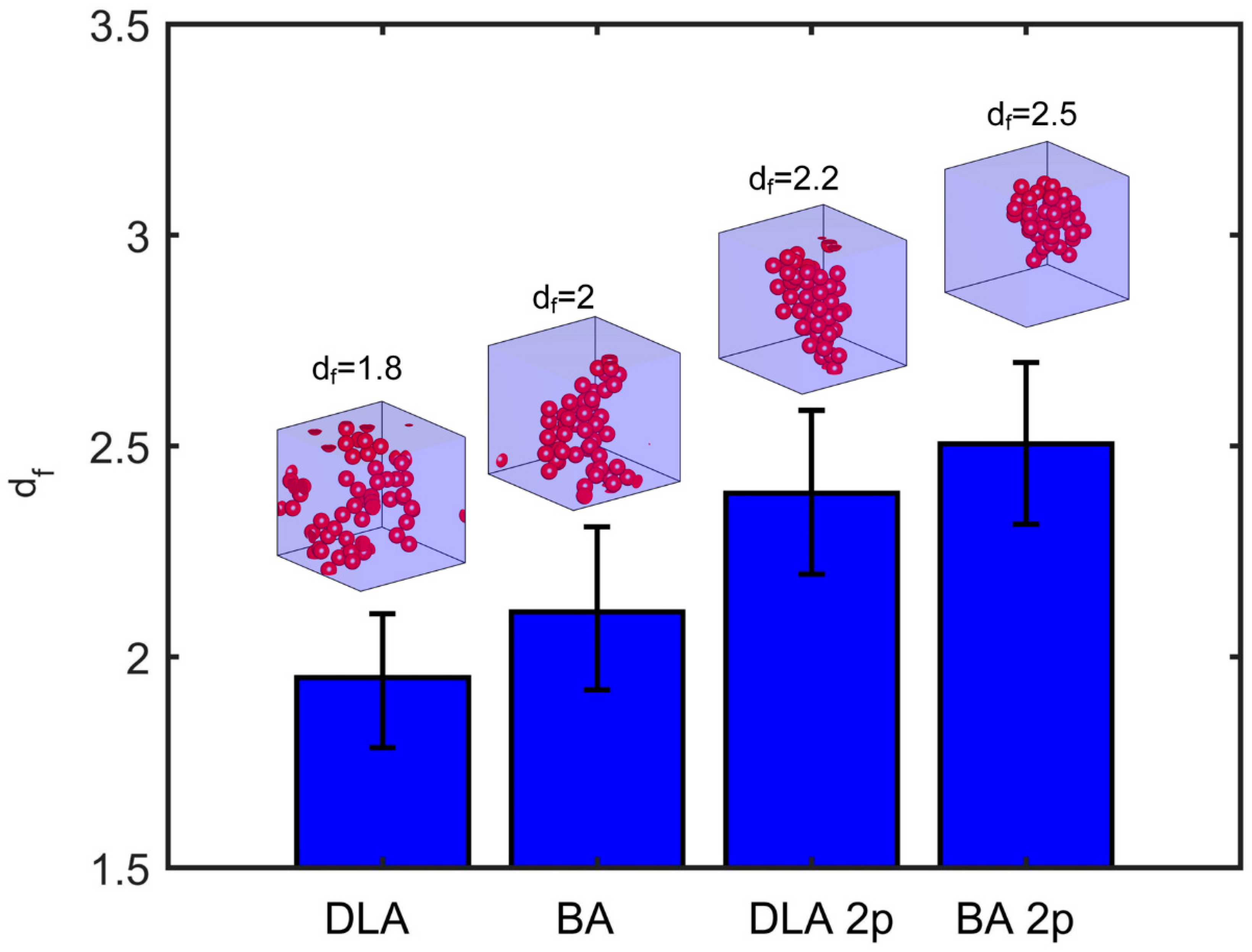
Figure 4, the mean fractal dimension of 50 particles forming a single aggregate is presented along with its standard derivation for the DLA, BA, and their 2p counterpart aggregation methods. A visualization of aggregates resulting from each method is also shown accordingly.
The heat transport equation is solved in each of the aforementioned structures. The heat transfer is caused by the temperature difference imposed on the walls along the vertical axis. The rest of the boundaries are subject to periodic conditions.
6. Conclusions
A novel numerical method that combines the discretization-corrected particle strength exchange (DC PSE) operators with the meshless local Petrov–Galerkin (MLPG) technique was developed in order to simulate heat transport phenomena in particulate systems. Local refinement of the grid was shown to improve the accuracy of the calculations at reference geometries. An alternative, more efficient approach of interpolation was introduced, increasing the stability of the method and reducing the computational cost for grid construction. An automated method for grid refinement was introduced in multiple discretization levels inside the folds of the structures bypassing the necessity for user intervention. Moreover, the use of cubic domains to calculate local integrals, aiming at full geometry coverage with minimal overlapping, produced adequately stable and accurate results.
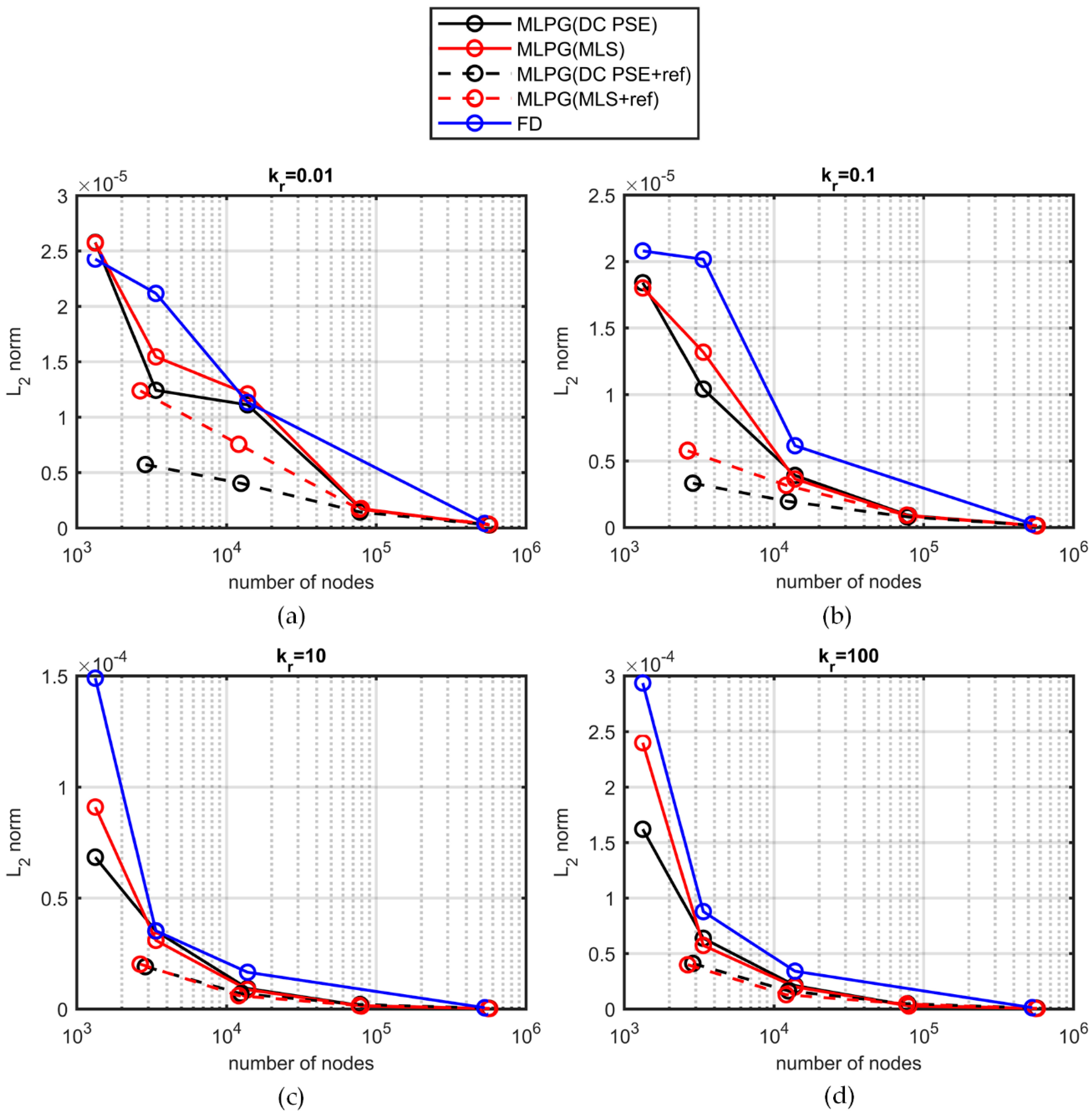
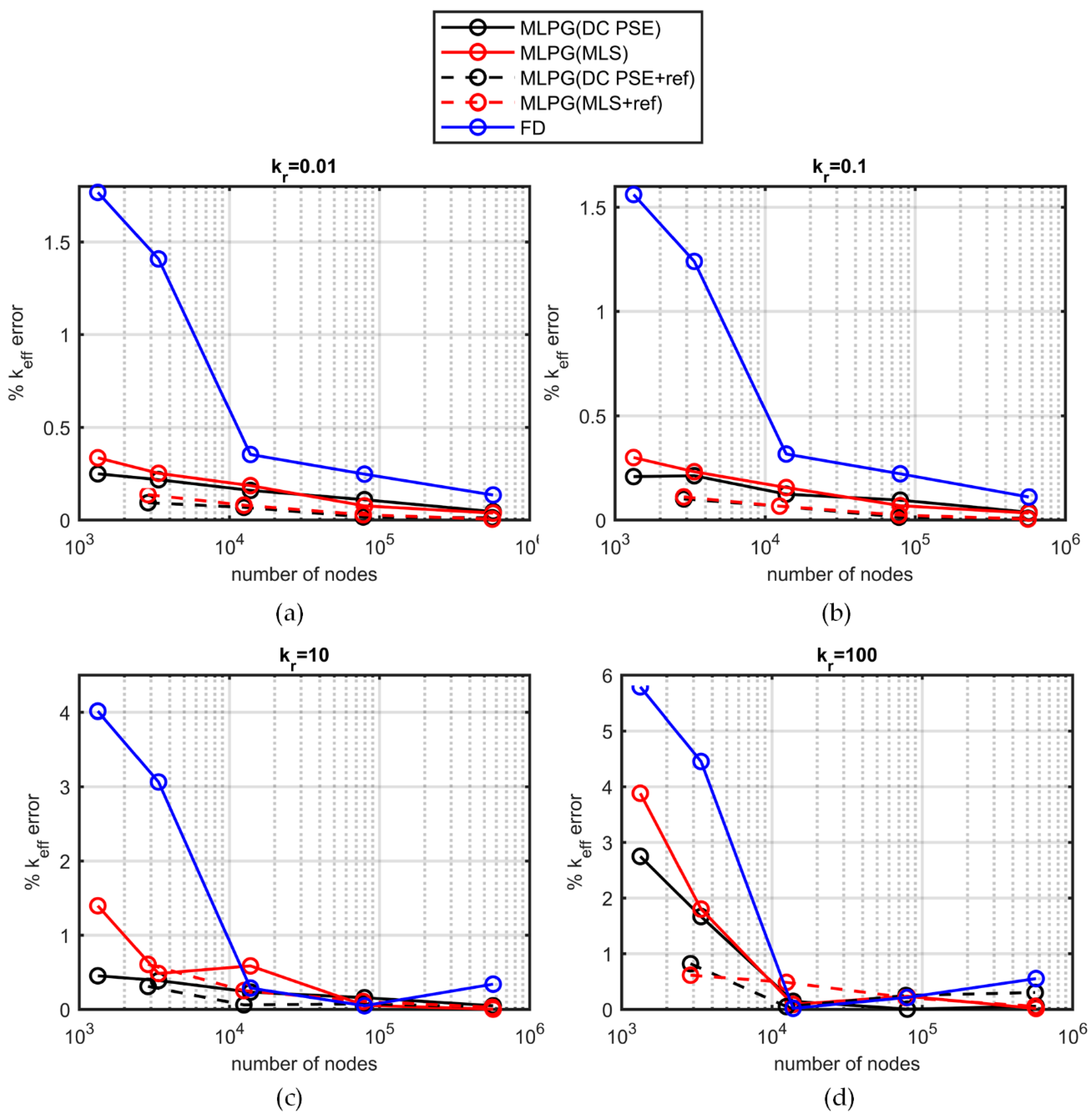
In addition, two different versions of the MLPG and the finite differences (FD) methods were compared in terms of the accuracy of the solutions. One version of the method used the moving least squares (MLS) approach for the trial function, while the other one used the DC PSE method. The DC PSE operators, which were used for the first time in this work as trial functions for the MLPG method, enhanced the solution stability and accuracy. It appears that the MLPG methods outweighed the FD one in the accuracy of the calculation for both the temperature distribution and the effective thermal conductivity. Additionally, the use of DC PSE operators reduced the computational cost required, as solutions converged using a smaller number of nodes.
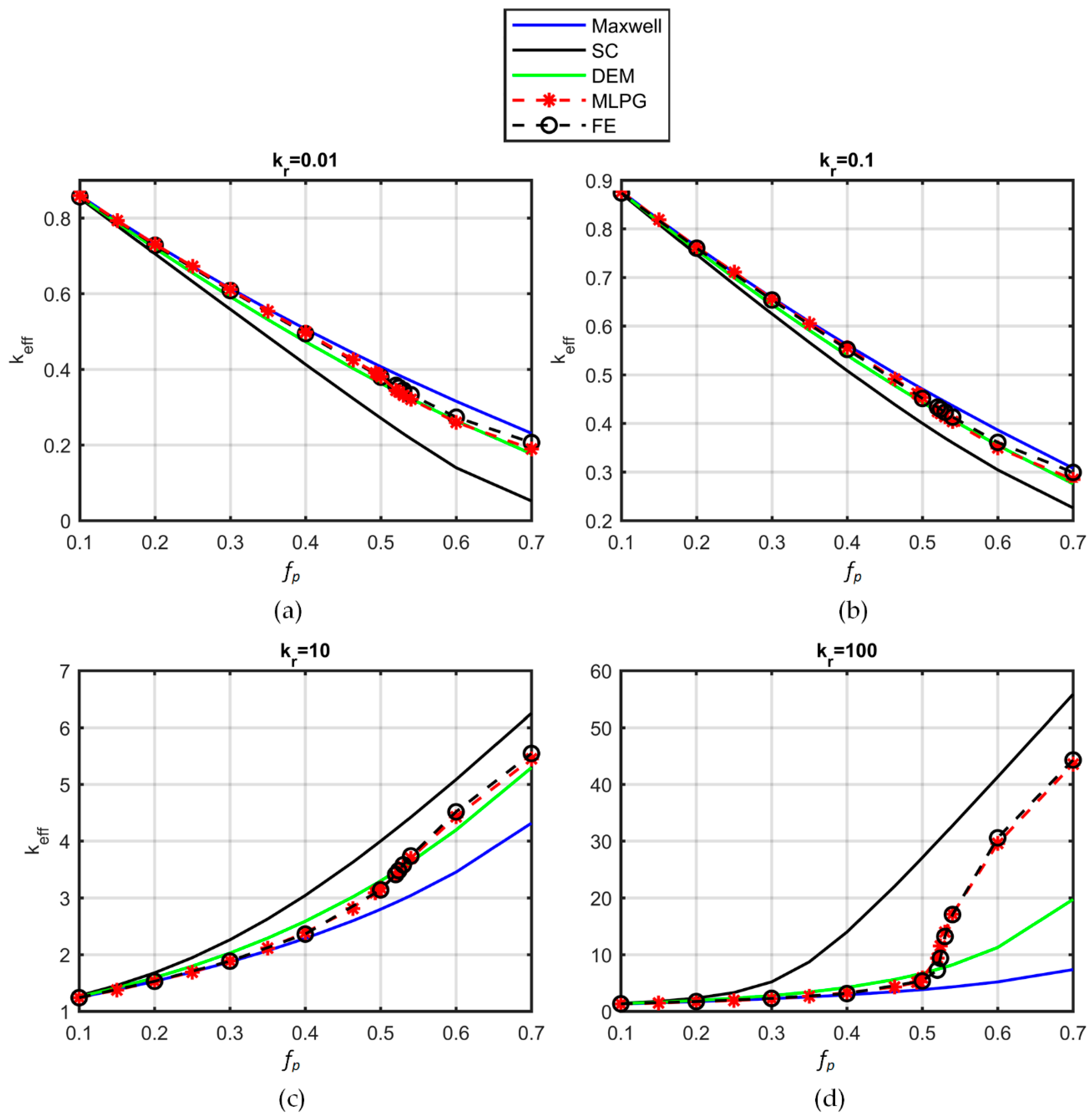
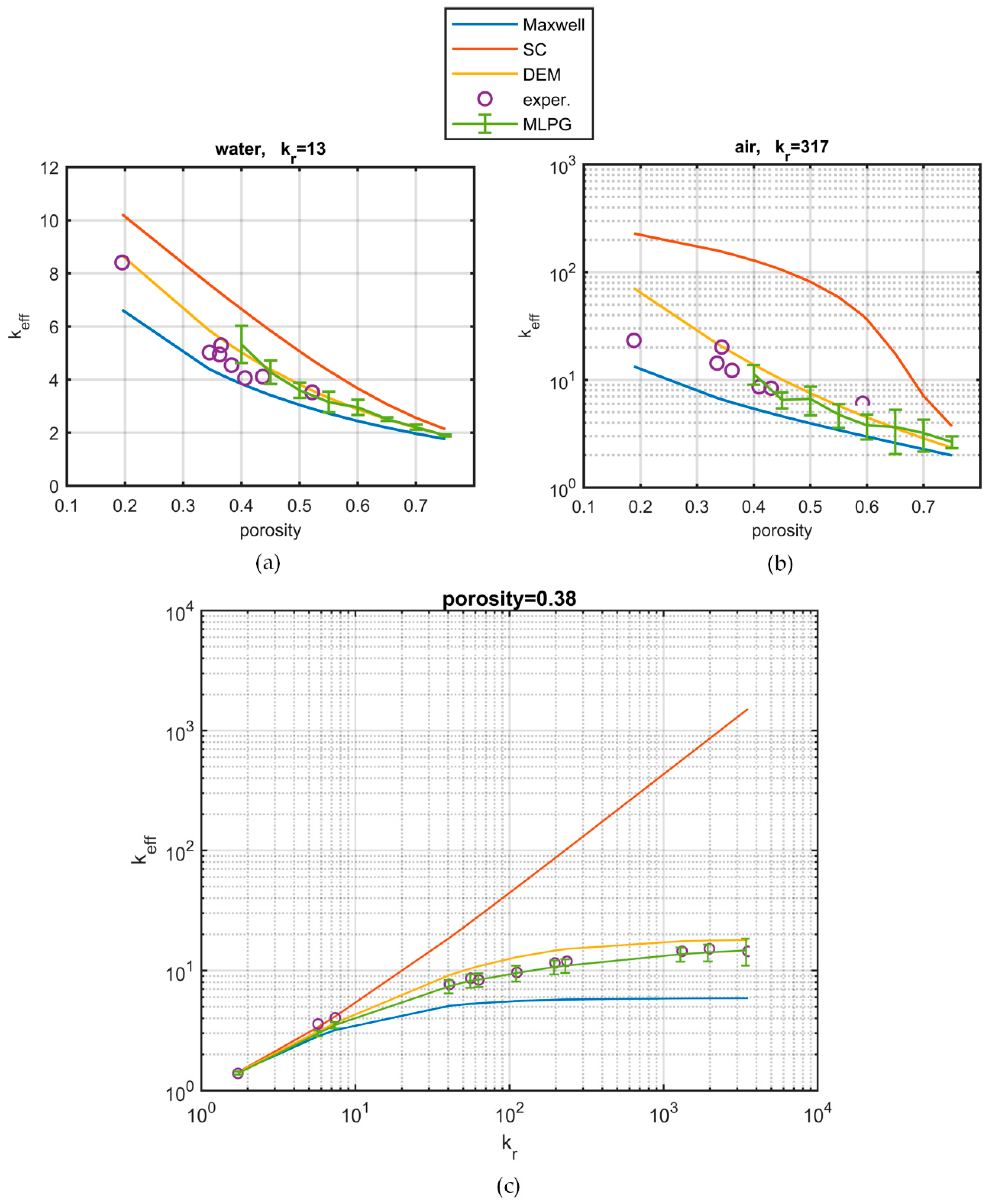
The MLPG performance was tested against the performance of the finite element (FE) method-based software for the calculation of the effective conductivity in systems of fully dispersed spheres. The MLPG method with DC PSE operators and fourfold discretization near the interfaces had a convergence similar to that of the FE method. Experimental data from the literature were used for the sake of comparison with simulations. Sample structures were reconstructed with the Monte Carlo technique, and the heat transport problem was solved therein. The results of the MLPG method were in excellent agreement with experimental data. An important side outcome of this work is the observation that the differential effective medium (DEM) approximation predicted well the conductivity of unconsolidated granular media.
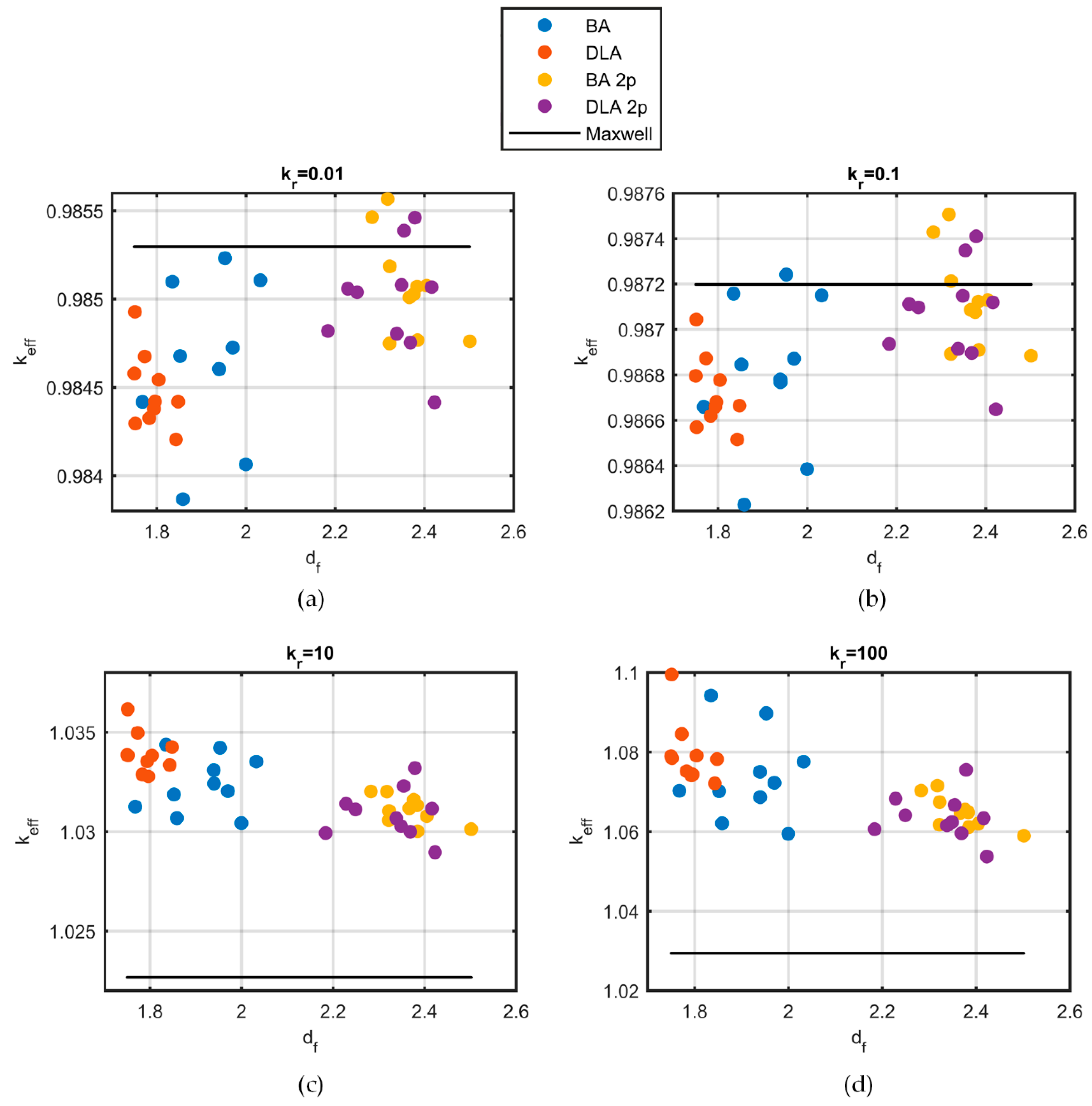
Finally, the convergence of the method for dense granular structures was studied, where the extension of particle overlapping significantly influenced the conduction, and therefore, the thermal conductivity. Aggregate structures with different morphological properties were reconstructed, and the effective conductivity was calculated with elevated accuracy, a result of great value in practical applications. For particles with conductivity lower than that of the bulk medium, the effective conductivity was not affected by aggregation, and the results were in full agreement with the Maxwell approximation. Conversely, for highly conducting particles, aggregation enhanced conduction. The thermal conductivity was a function of the fractal dimension of the aggregates. It was found that, as the fractal dimension decreased, the thermal conductivity increased monotonically.