Cross-Domain Data Augmentation for Deep-Learning-Based Male Pelvic Organ Segmentation in Cone Beam CT
Abstract
1. Introduction
2. Materials and Methods
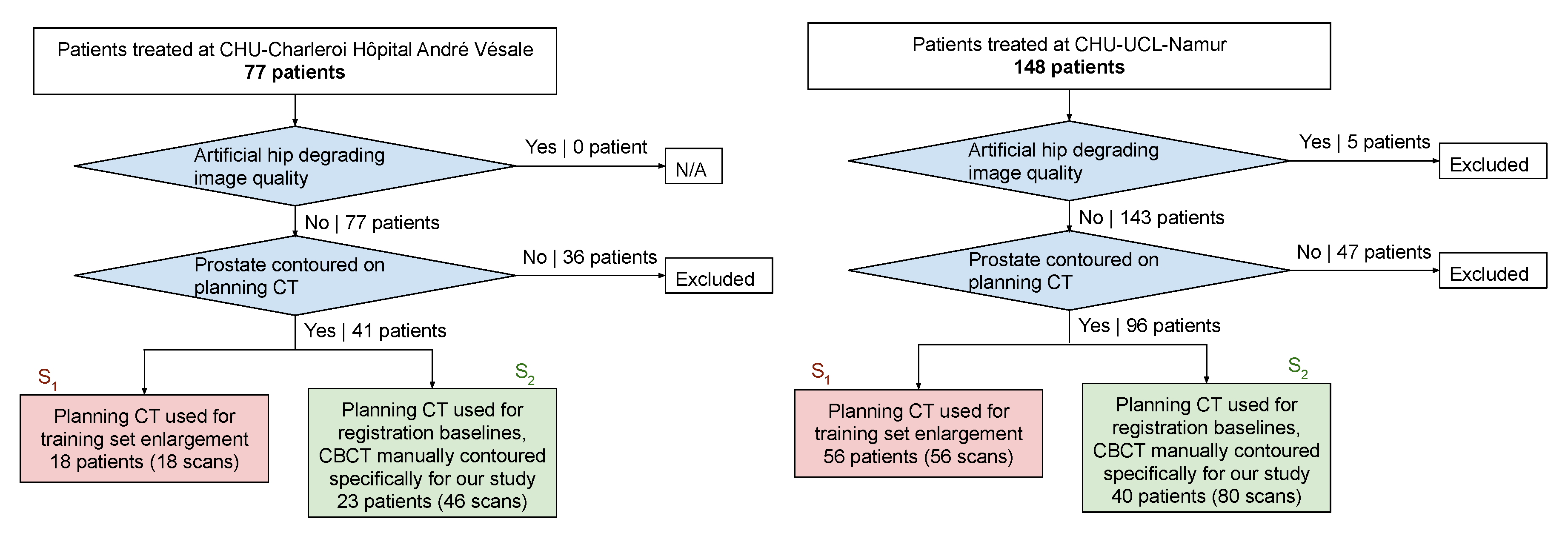
2.1. Data and Preprocessing
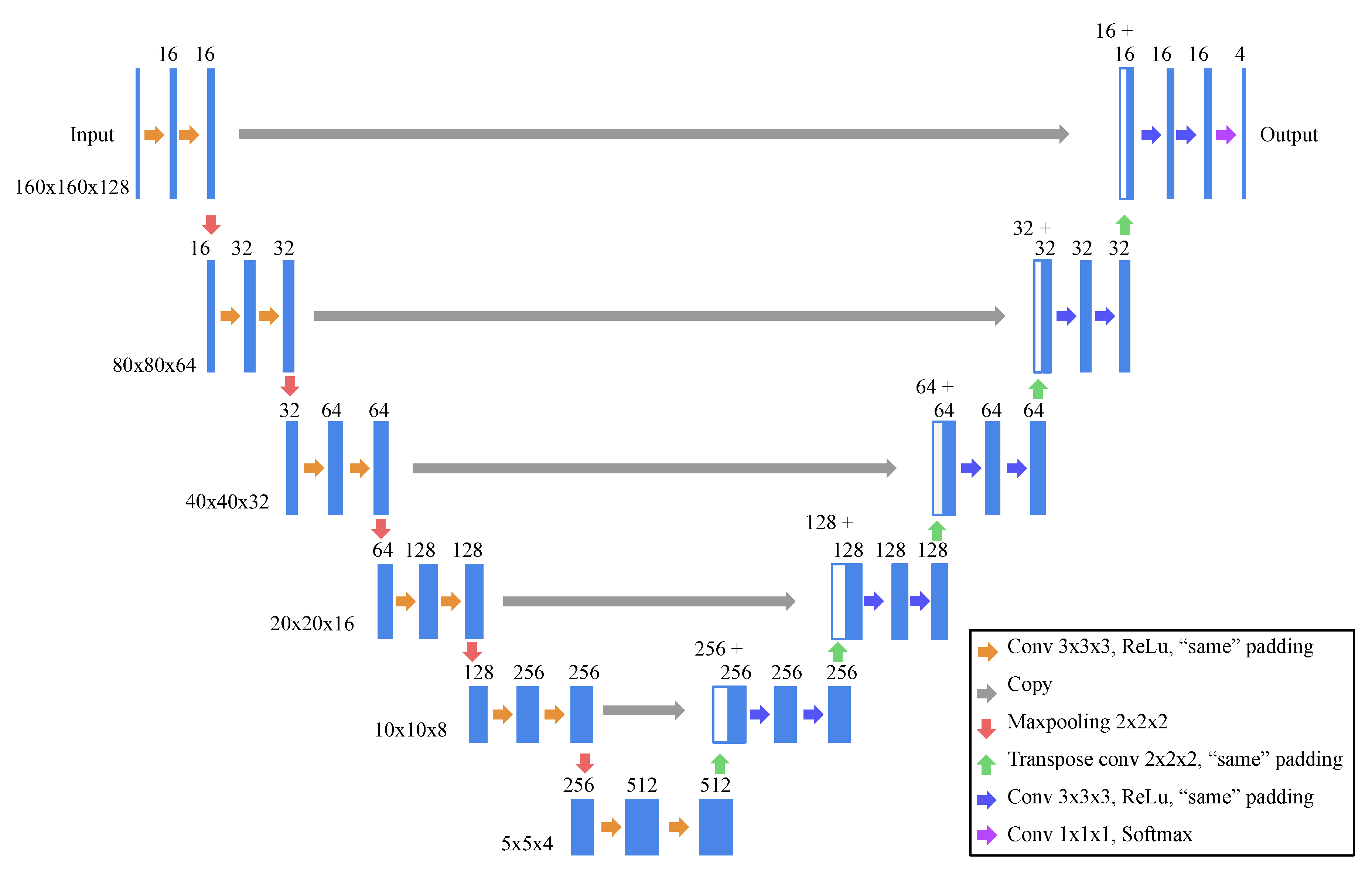
2.2. Model Architecture and Learning Strategy
2.3. Validation and Comparison Baselines
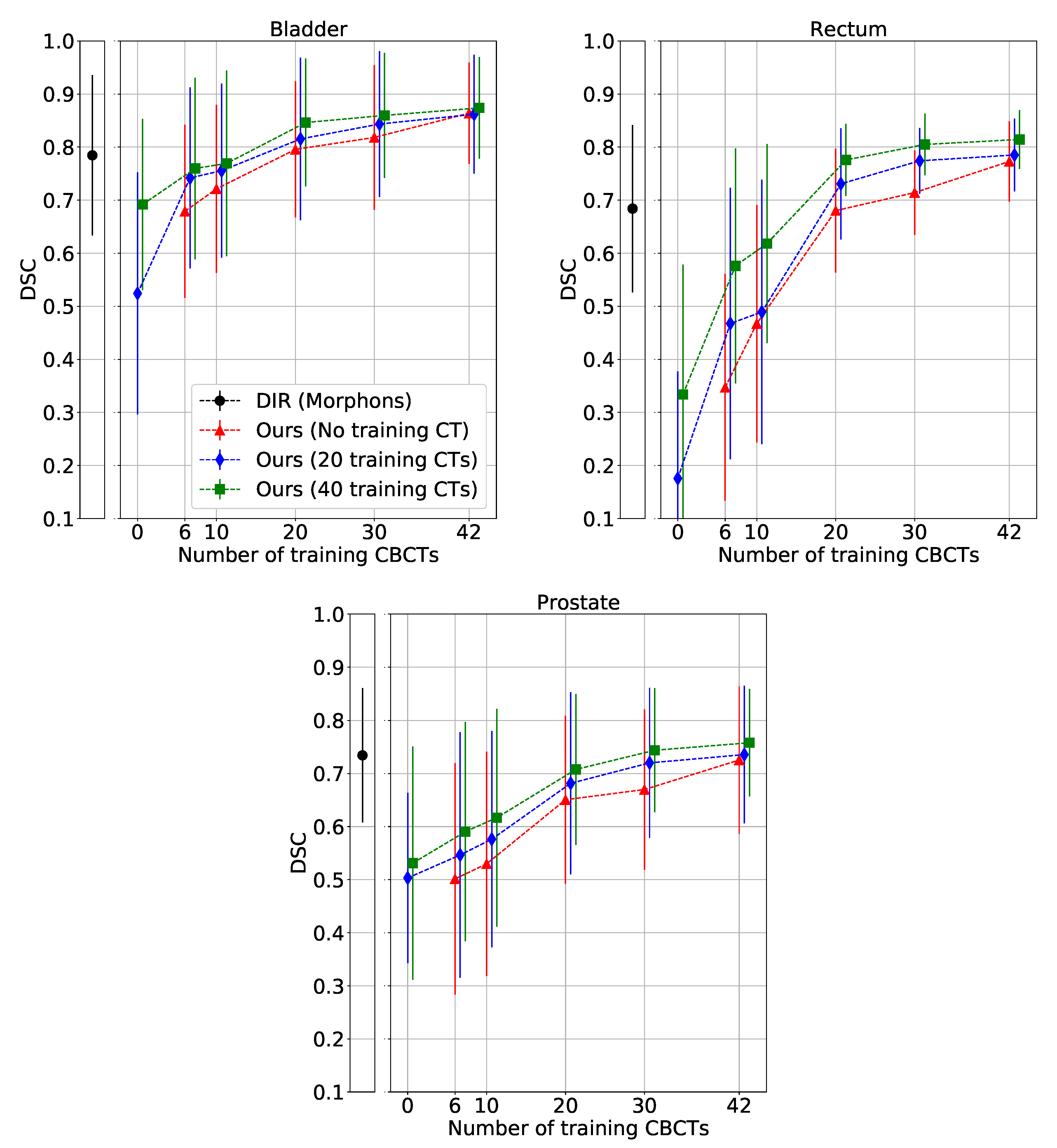
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CBCT | Cone beam computed tomography |
| CT | Computed tomography |
| CTV | Clinical target volume |
| DIR | Deformable image registration |
| DL | Deep learning |
| DSC | Dice similarity coefficient |
| DVF | Deformation vector field |
| EBRT | External beam radiation therapy |
| FCN | Fully convolutional neural network |
| GPU | Graphical processing unit |
| JI | Jaccard index |
| LoA | Limit of agreement |
| OAR | Organ at risk |
| ROI | Region of interest |
| SMBD | Symmetric mean boundary distance |
References
- Brousmiche, S.; Orban de Xivry, J.; Macq, B.; Seco, J. SU-E-J-125: Classification of CBCT Noises in Terms of Their Contribution to Proton Range Uncertainty. Med. Phys. 2014, 41, 184. [Google Scholar] [CrossRef]
- Peng, C.; Ahunbay, E.; Chen, G.; Anderson, S.; Lawton, C.; Li, X.A. Characterizing interfraction variations and their dosimetric effects in prostate cancer radiotherapy. Int. J. Radiat. Oncol. Biol. Phys. 2011, 79, 909–914. [Google Scholar] [CrossRef] [PubMed]
- Ghilezan, M.; Yan, D.; Martinez, A. Adaptive Radiation Therapy for Prostate Cancer. Semin. Radiat. Oncol. 2010, 20, 130–137. [Google Scholar] [CrossRef] [PubMed]
- Pos, F.; Remeijer, P. Adaptive Management of Bladder Cancer Radiotherapy. Semin. Radiat. Oncol. 2010, 20, 116–120. [Google Scholar] [CrossRef]
- Wang, Y.; Efstathiou, J.A.; Sharp, G.C.; Lu, H.M.; Ciernik, I.F.; Trofimov, A.V. Evaluation of the dosimetric impact of interfractional anatomical variations on prostate proton therapy using daily in-room CT images. Med. Phys. 2011, 38, 4623–4633. [Google Scholar] [CrossRef]
- Moteabbed, M.; Trofimov, A.; Sharp, G.C.; Wang, Y.; Zietman, A.L.; Efstathiou, J.A.; Lu, H.M. Proton therapy of prostate cancer by anterior-oblique beams: Implications of setup and anatomy variations. Phys. Med. Biol. 2017, 62, 1644–1660. [Google Scholar] [CrossRef]
- Rigaud, B.; Simon, A.; Castelli, J.; Lafond, C.; Acosta, O.; Haigron, P.; Cazoulat, G.; de Crevoisier, R. Deformable image registration for radiation therapy: Principle, methods, applications and evaluation. Acta Oncol. 2019, 58, 1225–1237. [Google Scholar] [CrossRef]
- Oh, S.; Kim, S. Deformable image registration in radiation therapy. Radiat. Oncol. J. 2017, 35, 101. [Google Scholar] [CrossRef]
- Motegi, K.; Tachibana, H.; Motegi, A.; Hotta, K.; Baba, H.; Akimoto, T. Usefulness of hybrid deformable image registration algorithms in prostate radiation therapy. J. Appl. Clin. Med. Phys. 2019, 20, 229–236. [Google Scholar] [CrossRef]
- Takayama, Y.; Kadoya, N.; Yamamoto, T.; Ito, K.; Chiba, M.; Fujiwara, K.; Miyasaka, Y.; Dobashi, S.; Sato, K.; Takeda, K.; et al. Evaluation of the performance of deformable image registration between planning CT and CBCT images for the pelvic region: Comparison between hybrid and intensity-based DIR. J. Radiat. Res. 2017, 58, 567–571. [Google Scholar] [CrossRef]
- Zambrano, V.; Furtado, H.; Fabri, D.; Lütgendorf-Caucig, C.; Góra, J.; Stock, M.; Mayer, R.; Birkfellner, W.; Georg, D. Performance validation of deformable image registration in the pelvic region. J. Radiat. Res. 2013, 54, i120–i128. [Google Scholar] [CrossRef] [PubMed]
- Thor, M.; Petersen, J.B.; Bentzen, L.; Høyer, M.; Muren, L.P. Deformable image registration for contour propagation from CT to cone-beam CT scans in radiotherapy of prostate cancer. Acta Oncol. 2011, 50, 918–925. [Google Scholar] [CrossRef] [PubMed]
- Söhn, M.; Birkner, M.; Chi, Y.; Wang, J.; Yan, D.; Berger, B.; Alber, M. Model-independent, multimodality deformable image registration by local matching of anatomical features and minimization of elastic energy. Med. Phys. 2008, 35, 866–878. [Google Scholar] [CrossRef] [PubMed]
- Thirion, J.P. Image matching as a diffusion process: An analogy with Maxwell’s demons. Med. Image Anal. 1998, 2, 243–260. [Google Scholar] [CrossRef]
- Woerner, A.J.; Choi, M.; Harkenrider, M.M.; Roeske, J.C.; Surucu, M. Evaluation of deformable image registration-based contour propagation from planning CT to cone-beam CT. Technol. Cancer Res. Treat. 2017, 16, 801–810. [Google Scholar] [CrossRef]
- König, L.; Derksen, A.; Papenberg, N.; Haas, B. Deformable image registration for adaptive radiotherapy with guaranteed local rigidity constraints. Radiat. Oncol. 2016, 11, 122. [Google Scholar] [CrossRef]
- Chai, X.; van Herk, M.; Betgen, A.; Hulshof, M.; Bel, A. Automatic bladder segmentation on CBCT for multiple plan ART of bladder cancer using a patient-specific bladder model. Phys. Med. Biol. 2012, 57, 3945. [Google Scholar] [CrossRef]
- Van de Schoot, A.; Schooneveldt, G.; Wognum, S.; Hoogeman, M.; Chai, X.; Stalpers, L.; Rasch, C.; Bel, A. Generic method for automatic bladder segmentation on cone beam CT using a patient-specific bladder shape model. Med. Phys. 2014, 41, 031707. [Google Scholar] [CrossRef]
- Kazemifar, S.; Balagopal, A.; Nguyen, D.; McGuire, S.; Hannan, R.; Jiang, S.; Owrangi, A. Segmentation of the prostate and organs at risk in male pelvic CT images using deep learning. arXiv 2018, arXiv:1802.09587. [Google Scholar] [CrossRef]
- Cha, K.H.; Hadjiiski, L.; Samala, R.K.; Chan, H.P.; Caoili, E.M.; Cohan, R.H. Urinary bladder segmentation in CT urography using deep-learning convolutional neural network and level sets. Med. Phys. 2016, 43, 1882–1896. [Google Scholar] [CrossRef]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 424–432. [Google Scholar]
- Haensch, A.; Dicken, V.; Gass, T.; Morgas, T.; Klein, J.; Meine, H.; Hahn, H. Deep learning based segmentation of organs of the female pelvis in CBCT scans for adaptive radiotherapy using CT and CBCT data. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 179–180. [Google Scholar]
- Hänsch, A.; Dicken, V.; Klein, J.; Morgas, T.; Haas, B.; Hahn, H.K. Artifact-driven sampling schemes for robust female pelvis CBCT segmentation using deep learning. In Medical Imaging 2019: Computer-Aided Diagnosis; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 10950, p. 109500T. [Google Scholar]
- Brion, E.; Léger, J.; Javaid, U.; Lee, J.; De Vleeschouwer, C.; Macq, B. Using planning CTs to enhance CNN-based bladder segmentation on cone beam CT. In Medical Imaging 2019: Image-Guided Procedures, Robotic Interventions, and Modeling; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 10951, p. 109511M. [Google Scholar]
- Schreier, J.; Genghi, A.; Laaksonen, H.; Morgas, T.; Haas, B. Clinical evaluation of a full-image deep segmentation algorithm for the male pelvis on cone-beam CT and CT. Radiother. Oncol. 2020, 145, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Hatton, J.A.; Greer, P.B.; Tang, C.; Wright, P.; Capp, A.; Gupta, S.; Parker, J.; Wratten, C.; Denham, J.W. Does the planning dose—Volume histogram represent treatment doses in image-guided prostate radiation therapy? Assessment with cone-beam computerised tomography scans. Radiother. Oncol. 2011, 98, 162–168. [Google Scholar] [CrossRef] [PubMed]
- Giavarina, D. Understanding bland altman analysis. Biochem. Med. Biochem. Med. 2015, 25, 141–151. [Google Scholar] [CrossRef]
- Weistrand, O.; Svensson, S. The ANACONDA algorithm for deformable image registration in radiotherapy. Med. Phys. 2015, 42, 40–53. [Google Scholar] [CrossRef]
- Janssens, G.; Jacques, L.; de Xivry, J.O.; Geets, X.; Macq, B. Diffeomorphic registration of images with variable contrast enhancement. J. Biomed. Imaging 2011, 2011, 3. [Google Scholar] [CrossRef][Green Version]
- Mattes, D.; Haynor, D.R.; Vesselle, H.; Lewellen, T.K.; Eubank, W. PET-CT image registration in the chest using free-form deformations. IEEE Trans. Med. Imaging 2003, 22, 120–128. [Google Scholar] [CrossRef]
- Oktay, O.; Ferrante, E.; Kamnitsas, K.; Heinrich, M.; Bai, W.; Caballero, J.; Cook, S.A.; De Marvao, A.; Dawes, T.; O‘Regan, D.P.; et al. Anatomically constrained neural networks (ACNNs): Application to cardiac image enhancement and segmentation. IEEE Trans. Med Imaging 2017, 37, 384–395. [Google Scholar] [CrossRef]
- Ravishankar, H.; Venkataramani, R.; Thiruvenkadam, S.; Sudhakar, P.; Vaidya, V. Learning and incorporating shape models for semantic segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Quebec, QC, Canada, 11–13 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 203–211. [Google Scholar]
- Kamnitsas, K.; Baumgartner, C.; Ledig, C.; Newcombe, V.; Simpson, J.; Kane, A.; Menon, D.; Nori, A.; Criminisi, A.; Rueckert, D.; et al. Unsupervised domain adaptation in brain lesion segmentation with adversarial networks. In Proceedings of the International Conference on Information Processing in Medical Imaging, Boone, NC, USA, 25–30 June 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 597–609. [Google Scholar]
Sample Availability: Access to the dataset is subjected to the authorization of the partner hospitals’ ethics committees. The dataset is not available by default. |
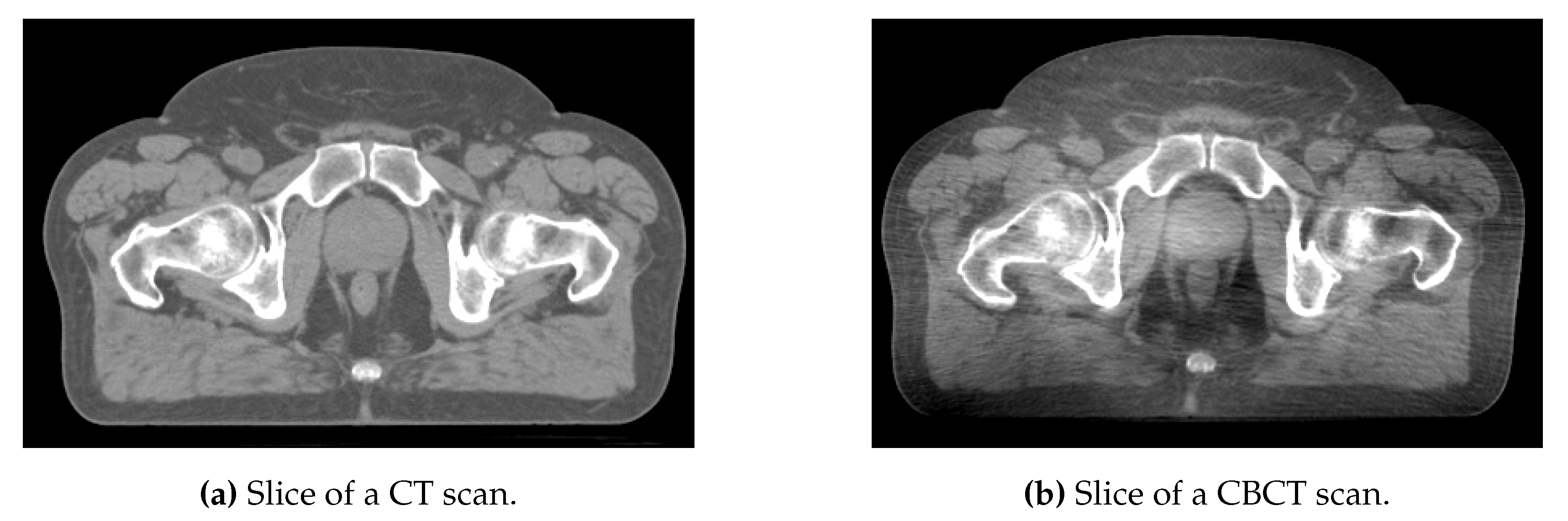
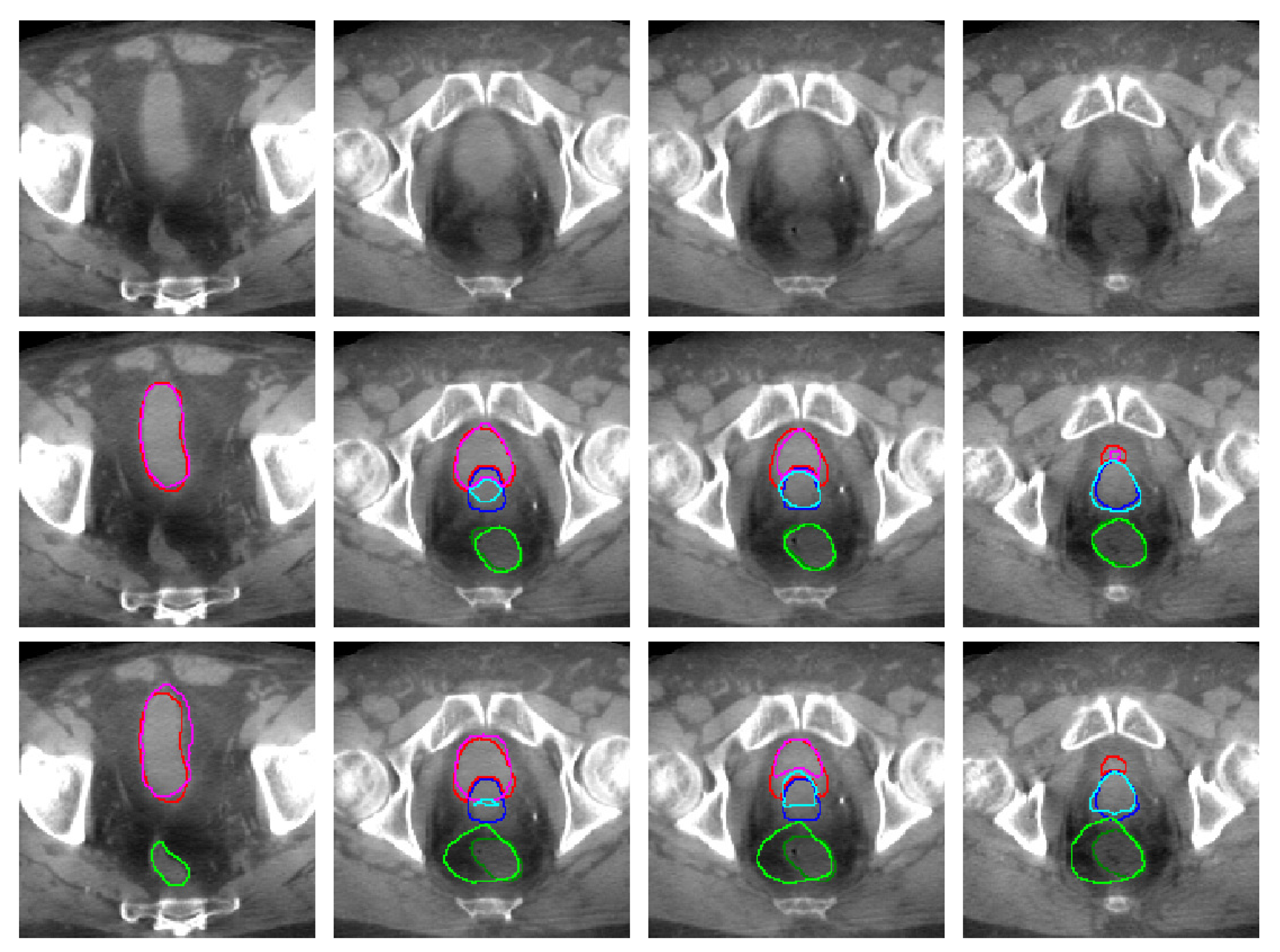
| (CT) | (CBCT) | ||
|---|---|---|---|
| fold 1 | fold 2 | fold 3 | |
| train | train | train | test |
| train | train | test | train |
| train | test | train | train |
| Study | Method | DSC | JI | SMBD (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bladder | Rectum | Prostate | Bladder | Rectum | Prostate | Bladder | Rectum | Prostate | ||
| Ours | DL () | 0.796 ± 0.128 | 0.680 ± 0.117 | 0.651 ± 0.158 | 0.677 ± 0.153 | 0.526 ± 0.123 | 0.501 ± 0.164 | 3.94 ± 2.18 | 3.85 ± 1.39 | 4.90 ± 2.85 |
| Ours | DL () | 0.846 ± 0.120 | 0.776 ± 0.068 | 0.708 ± 0.142 | 0.749 ± 0.155 | 0.638 ± 0.086 | 0.565 ± 0.157 | 3.02 ± 2.26 | 3.14 ± 1.43 | 3.87 ± 2.19 |
| Ours | DL () | 0.864 ± 0.096 | 0.773 ± 0.075 | 0.725 ± 0.139 | 0.771 ± 0.131 | 0.636 ± 0.098 | 0.585 ± 0.151 | 2.77 ± 1.95 | 3.06 ± 1.55 | 3.51 ± 2.03 |
| Ours | DL () | 0.874 ± 0.096 | 0.814 ± 0.055 | 0.758 ± 0.101 | 0.787 ± 0.131 | 0.690 ± 0.077 | 0.620 ± 0.120 | 2.47 ± 1.93 | 2.38 ± 0.98 | 3.08 ± 1.48 |
| DIR | Rigid image registration | 0.714 ± 0.149 | 0.646 ± 0.090 | 0.730 ± 0.108 | 0.576 ± 0.175 | 0.484 ± 0.102 | 0.585 ± 0.124 | 6.93 ± 4.09 | 5.30 ± 1.91 | 3.81 ± 1.44 |
| DIR | DIR, RS intensity-based | 0.737 ± 0.155 | 0.662 ± 0.100 | 0.739 ± 0.110 | 0.606 ± 0.187 | 0.504 ± 0.115 | 0.597 ± 0.127 | 6.27 ± 4.08 | 5.08 ± 2.04 | 3.61 ± 1.42 |
| DIR | DIR, morphons | 0.784 ± 0.151 | 0.684 ± 0.158 | 0.734 ± 0.127 | 0.668 ± 0.182 | 0.539 ± 0.165 | 0.594 ± 0.143 | 5.04 ± 3.90 | 5.00 ± 3.43 | 3.65 ± 1.64 |
| Schreier et al. (2019) [25] * | DL ( = 300, = 300) | 0.932 | 0.871 | 0.840 | - | - | - | 2.57 ± 0.54 | 2.47 ± 0.64 | 2.34 ± 0.68 |
| Brion et al. (2019) [24] * | DL ( = 32, = 64) | 0.848 ± 0.085 | - | - | 0.745 ± 0.114 | - | - | 2.8 ± 1.4 | - | - |
| Hänsch et al. (2018) [22] * | DL ( = 124, = 88) | 0.88 | 0.71 | - | - | - | - | - | - | - |
| Motegi et al. (2019) [9] * | DIR, MIM intensity-based | ∼ 0.80 | ∼ 0.40 | ∼ 0.55 | - | - | - | - | - | - |
| Motegi et al. (2019) [9] * | DIR, RS intensity-based | ∼ 0.78 | ∼ 0.70 | ∼ 0.75 | - | - | - | - | - | - |
| Takayama et al. (2017) [10] * | DIR, RS intensity-based | 0.69 ± 0.07 | 0.75 ± 0.05 | 0.84 ± 0.05 | - | - | - | - | - | - |
| Woerner et al. (2017) [15] * | DIR, cascade MI-based | ∼ 0.83 | ∼ 0.77 | ∼ 0.80 | - | - | - | ∼2.6 | ∼2.3 | ∼2.3 |
| Konig et al. (2016) [16] * | DIR, rigid on bone and prostate | 0.85 ± 0.05 | - | 0.82 ± 0.04 | - | - | - | - | - | - |
| Thor et al. (2011) [12] * | DIR, demons | 0.73 | 0.77 | 0.80 | - | - | - | - | - | - |
| van de Schoot et al. (2014) [18] * | Patient specific model | ∼ 0.87 | - | - | - | - | - | - | - | - |
| Chai et al. (2012) [17] * | Patient specific model | 0.78 | - | - | - | - | - | - | - | - |
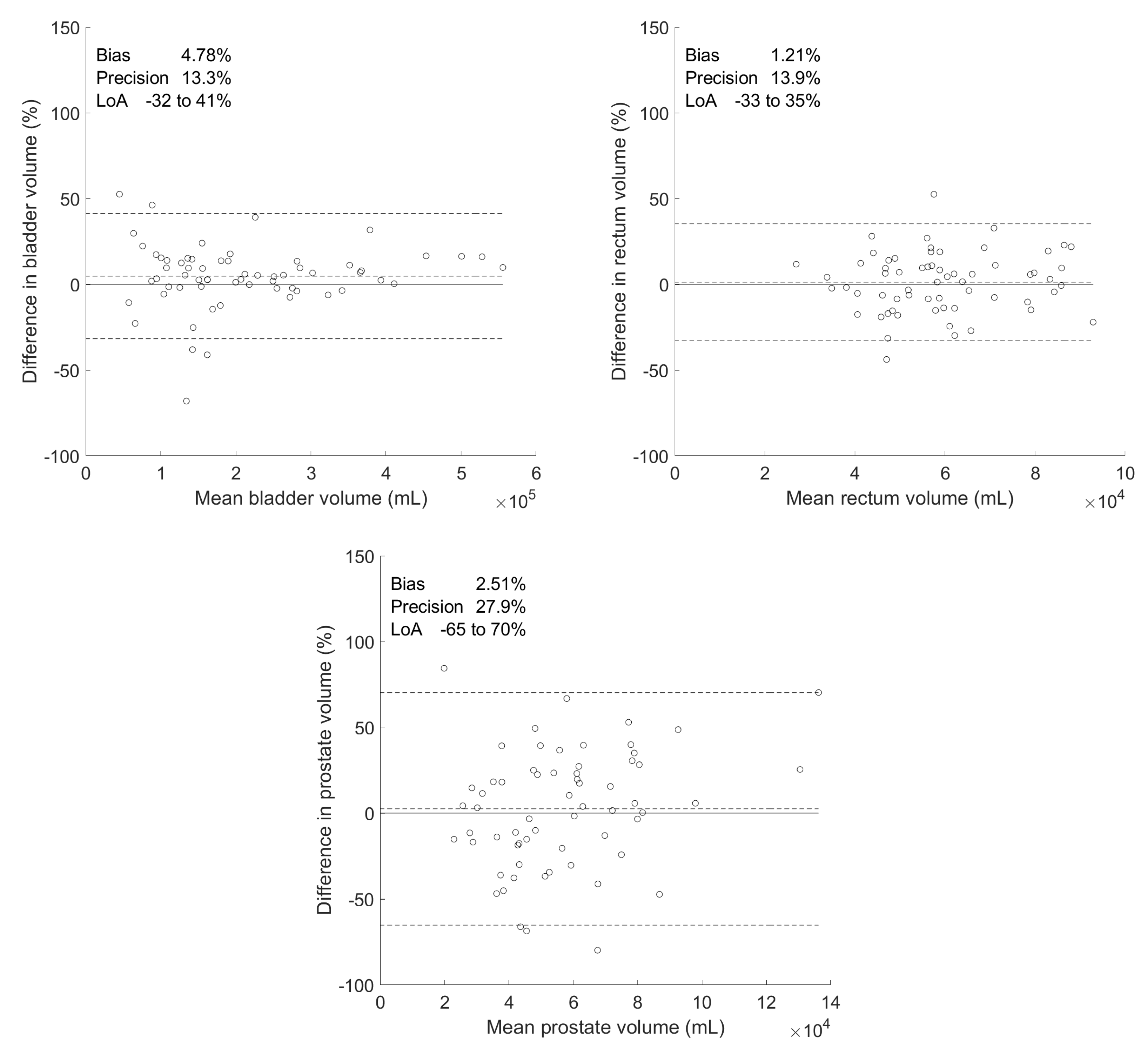
| Differences between Manual and Predicted Volumes | |||||||
|---|---|---|---|---|---|---|---|
| Organ | Volumes () | Absolute () | Percentage (%) | ||||
| Manual | Predicted | Bias | Precision | Bias | Precision | p-Value | |
| Bladder | 21.9 ± 12.9 | 20.7 ± 11.4 | 1.18 | 2.46 | 4.78 | 13.3 | 0.285 |
| Rectum | 5.96 ± 1.66 | 5.87 ± 1.55 | 0.094 | 0.826 | 1.21 | 13.9 | 0.897 |
| Prostate | 5.87 ± 2.98 | 5.53 ± 2.07 | 0.340 | 1.64 | 2.51 | 27.9 | 0.438 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Léger, J.; Brion, E.; Desbordes, P.; De Vleeschouwer, C.; Lee, J.A.; Macq, B. Cross-Domain Data Augmentation for Deep-Learning-Based Male Pelvic Organ Segmentation in Cone Beam CT. Appl. Sci. 2020, 10, 1154. https://doi.org/10.3390/app10031154
Léger J, Brion E, Desbordes P, De Vleeschouwer C, Lee JA, Macq B. Cross-Domain Data Augmentation for Deep-Learning-Based Male Pelvic Organ Segmentation in Cone Beam CT. Applied Sciences. 2020; 10(3):1154. https://doi.org/10.3390/app10031154
Chicago/Turabian StyleLéger, Jean, Eliott Brion, Paul Desbordes, Christophe De Vleeschouwer, John A. Lee, and Benoit Macq. 2020. "Cross-Domain Data Augmentation for Deep-Learning-Based Male Pelvic Organ Segmentation in Cone Beam CT" Applied Sciences 10, no. 3: 1154. https://doi.org/10.3390/app10031154
APA StyleLéger, J., Brion, E., Desbordes, P., De Vleeschouwer, C., Lee, J. A., & Macq, B. (2020). Cross-Domain Data Augmentation for Deep-Learning-Based Male Pelvic Organ Segmentation in Cone Beam CT. Applied Sciences, 10(3), 1154. https://doi.org/10.3390/app10031154





