Dynamic Balance Method for Grading the Chain Drive Double Threshing Drum of a Combine Harvester
Abstract
1. Introduction
2. Material and Methods
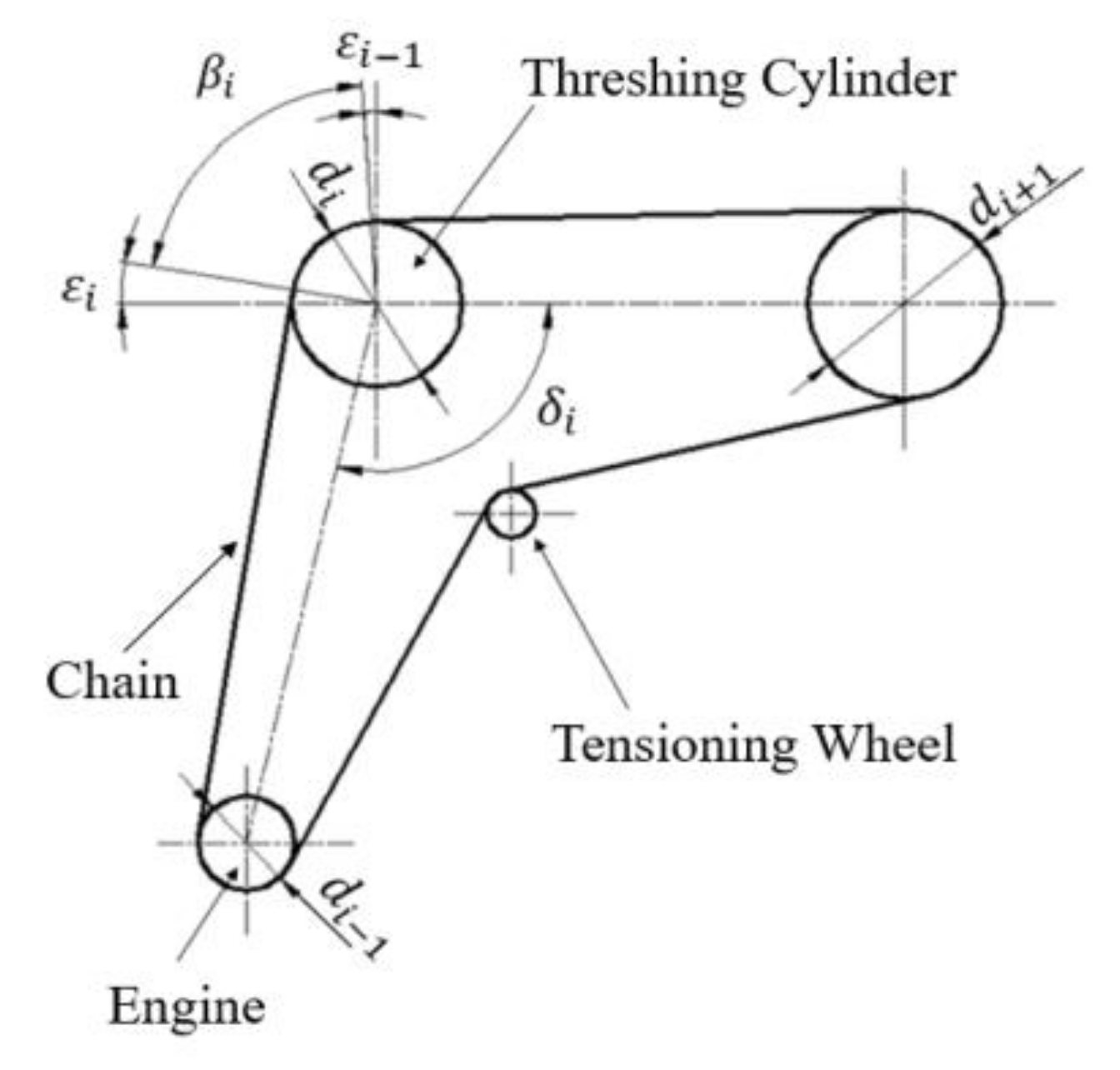
2.1. Double Drums Chain Grading Drive Structure Principle
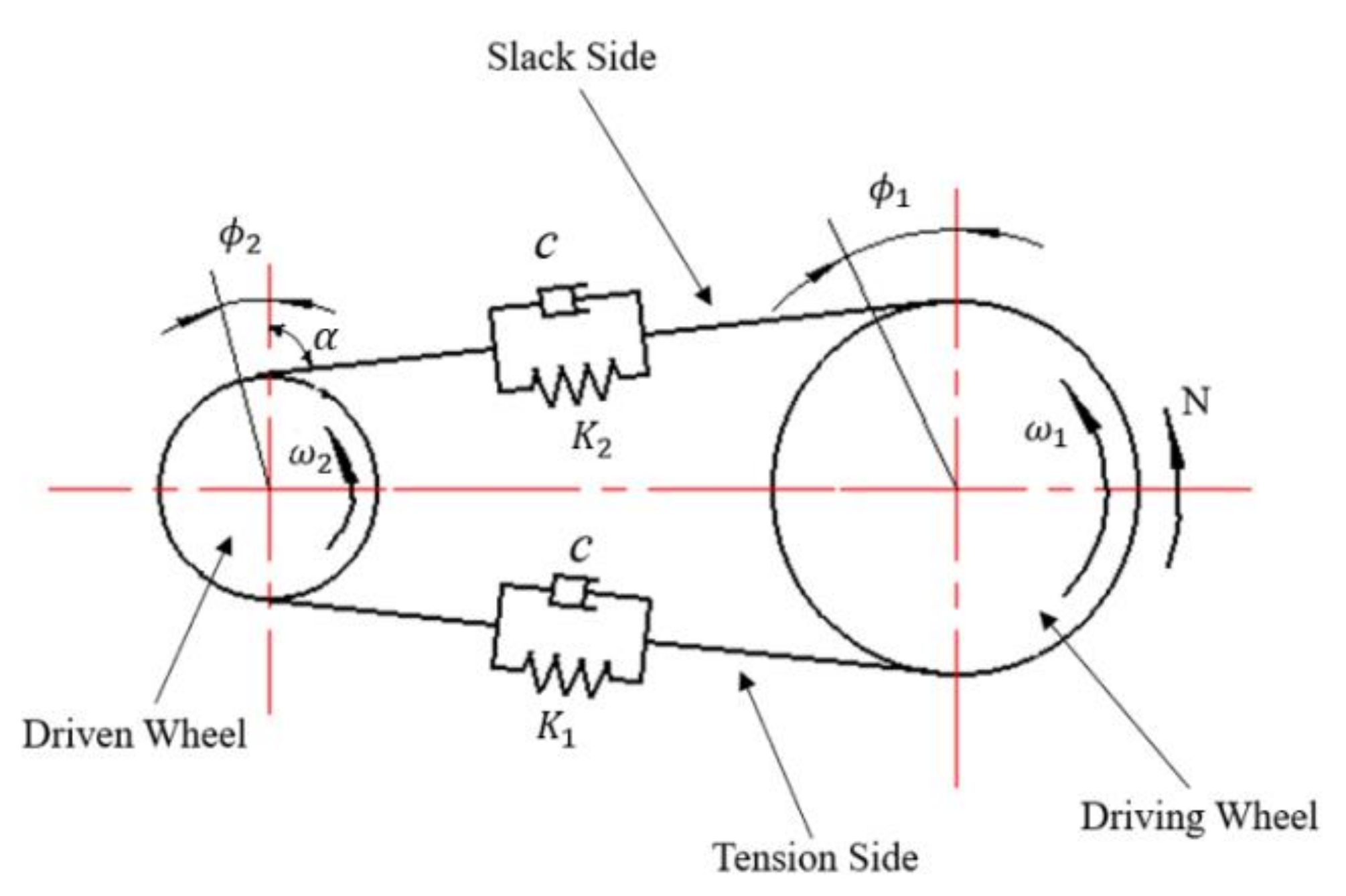
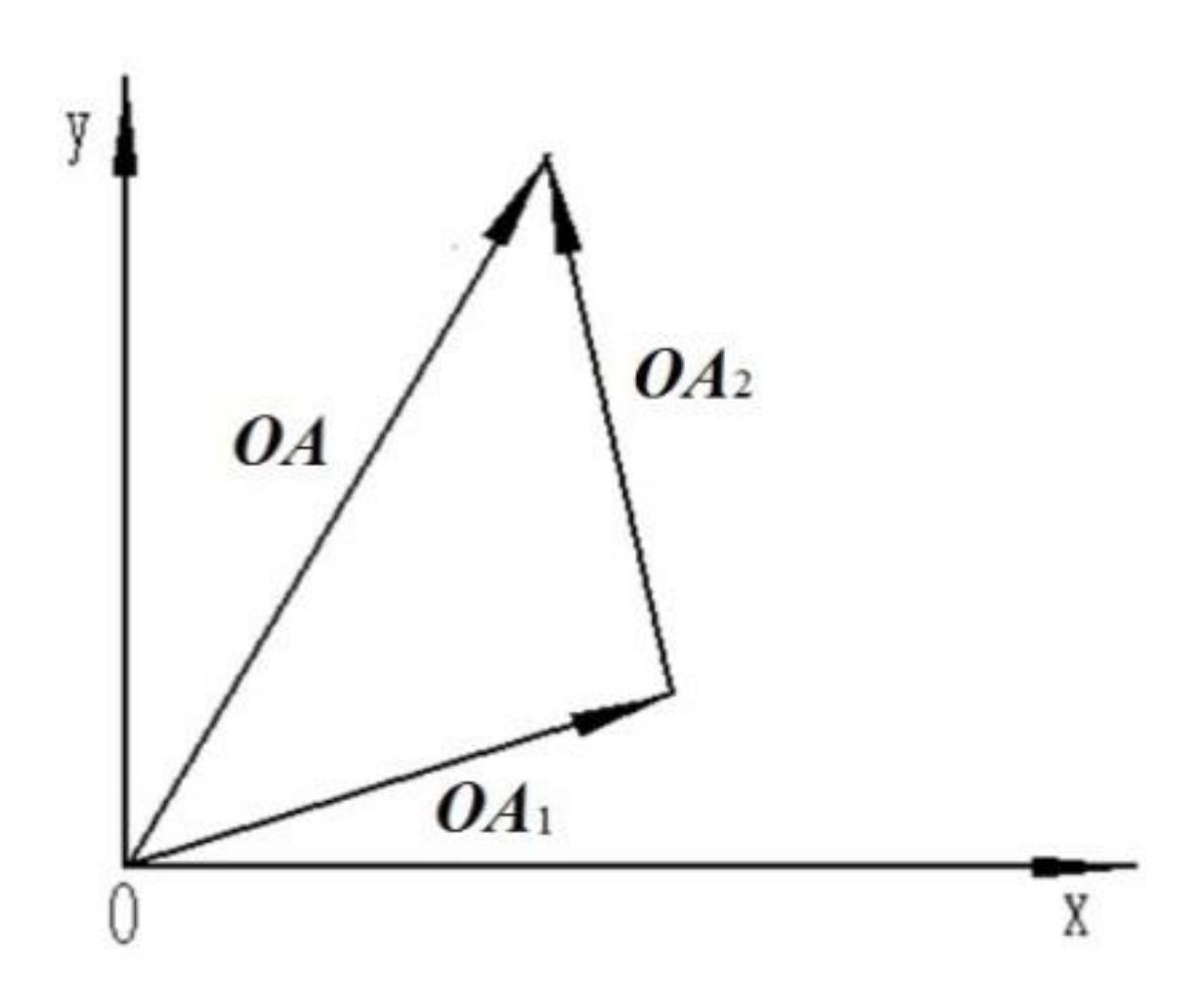
2.2. Unbalance Vibration Modeling of Grading Chain Drive Double Drums
2.3. Dynamic Balance Principle and Method
2.4. Balance Method Test Bench for Grading Chain Drive
Test Method for Dynamic Balance Characteristic
2.5. Engineering Application of Double Drum Balance of Combine Harvester
Combine Harvester Double Threshing Drum Dynamic Balance
2.6. Test Method for Vibration Characteristics and Axis Trajectory
2.6.1. Grading Chain Drive Double Drum Vibration Characteristic Test
2.6.2. Axis Trajectory of Double Threshing Drum Test
3. Results and Discussion
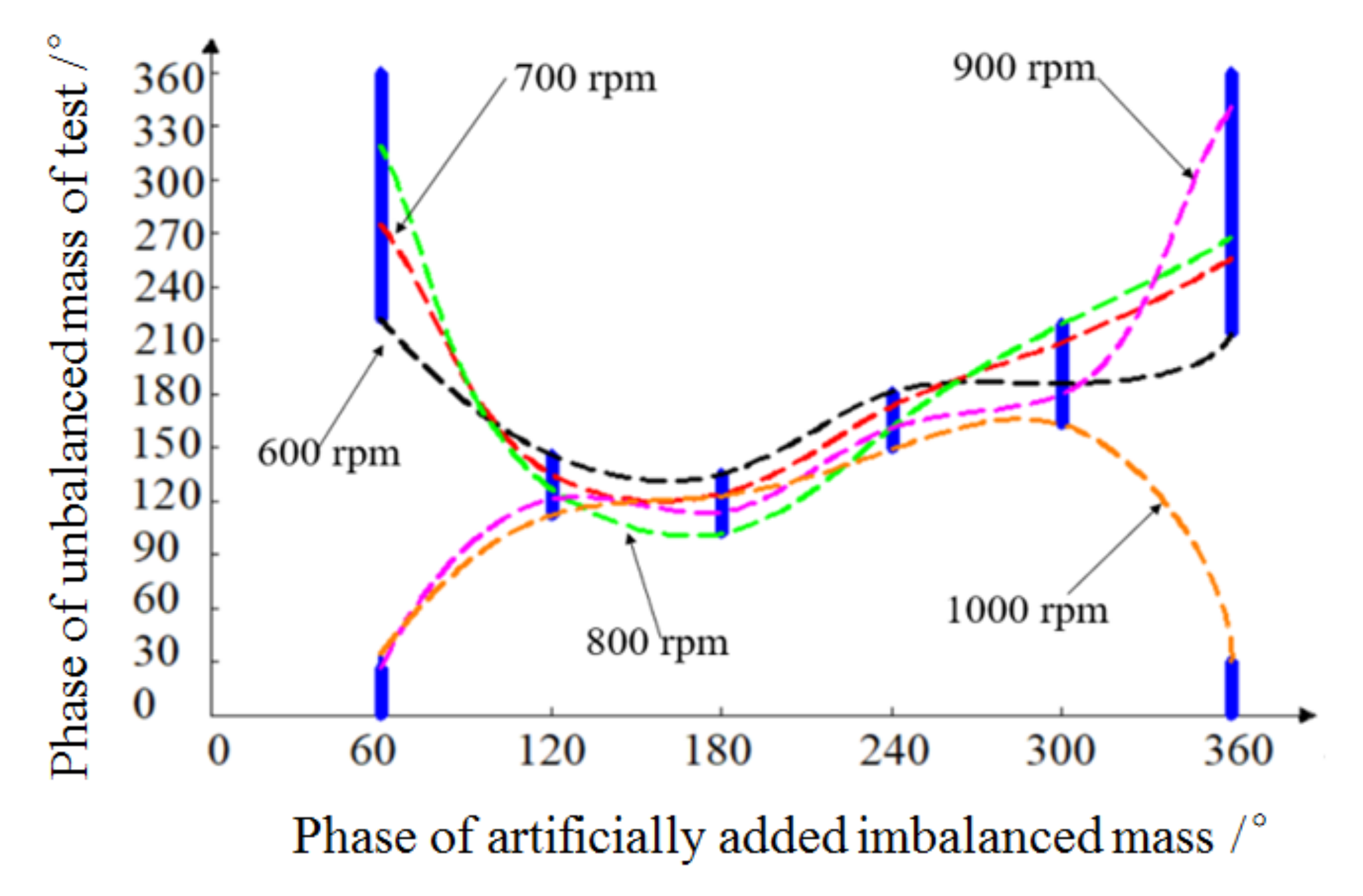
3.1. Dynamic Balancing Method of Driven Drum
3.2. Driven Drum End Surface Radial Weight Dynamic Balance Effects
3.3. Active and Driven Drum Dynamic Balance Effects
3.4. Double Threshing Drum Grading Chain Drive Dynamic Balance
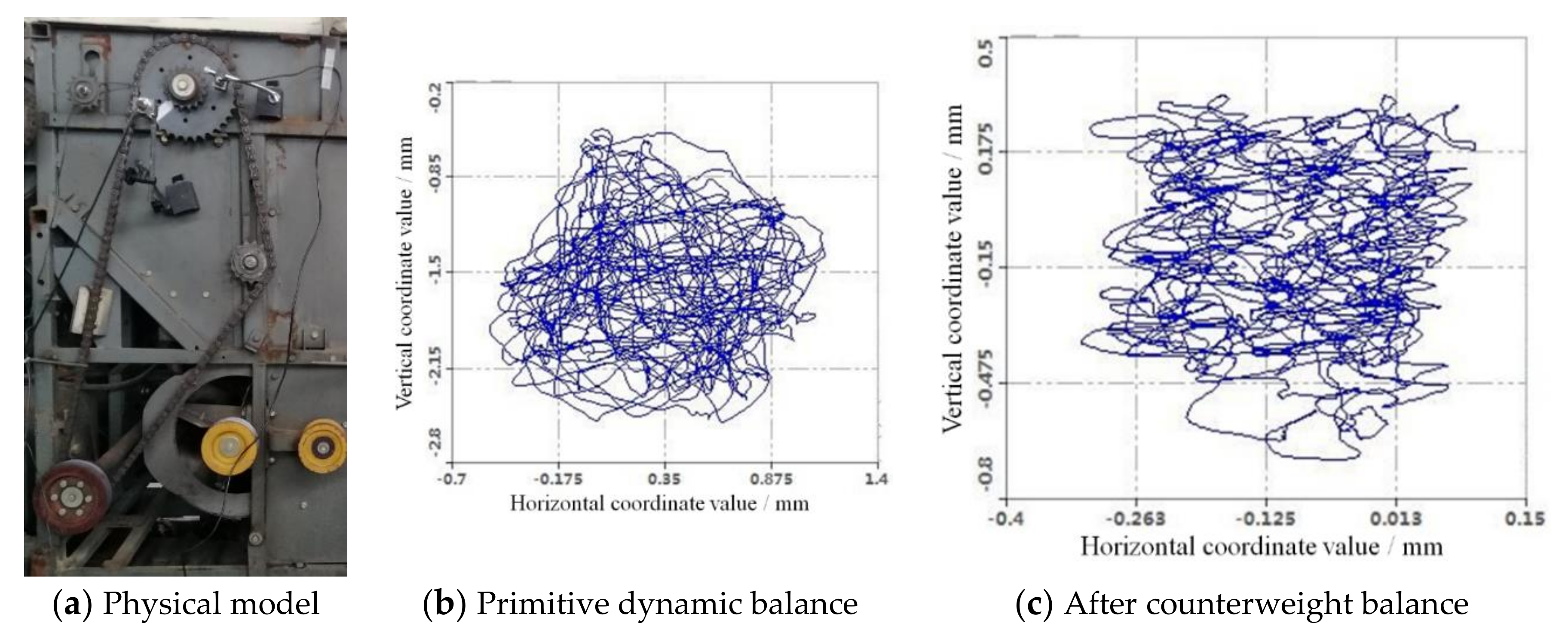
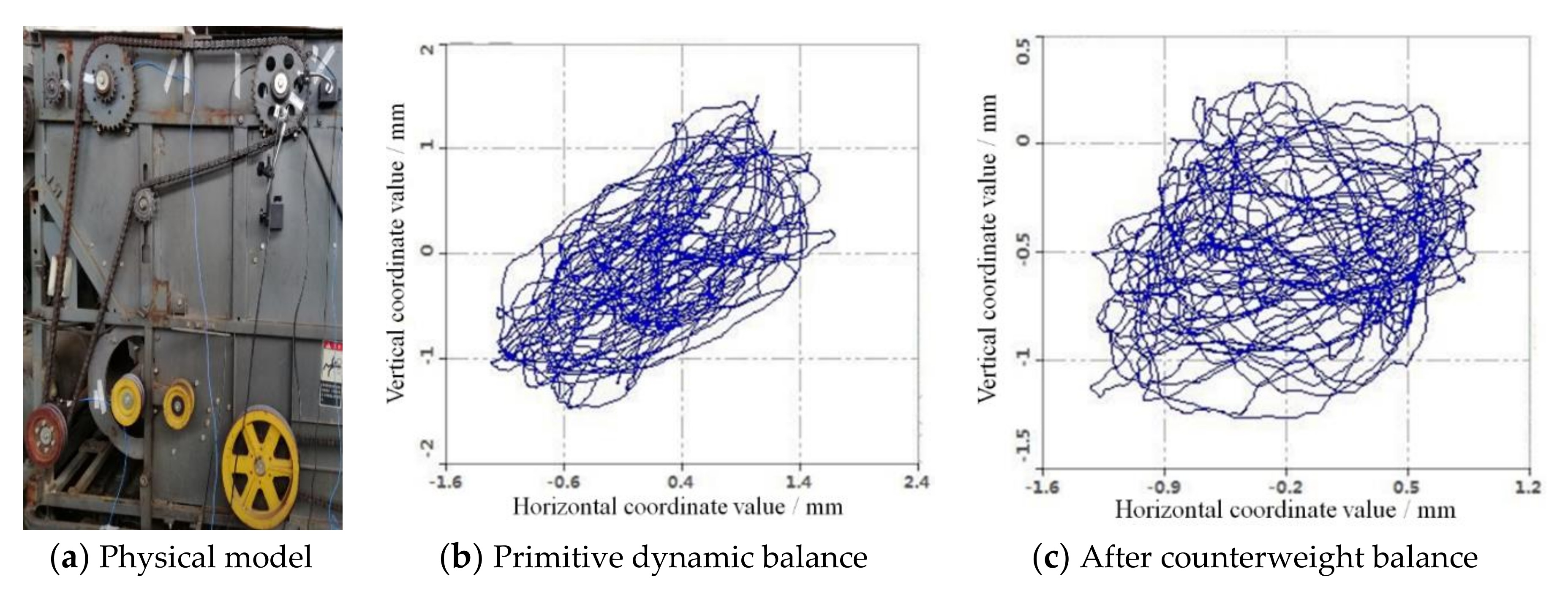
3.5. Double Threshing Drums Dynamic Balance Test Verification
4. Conclusions
- (1)
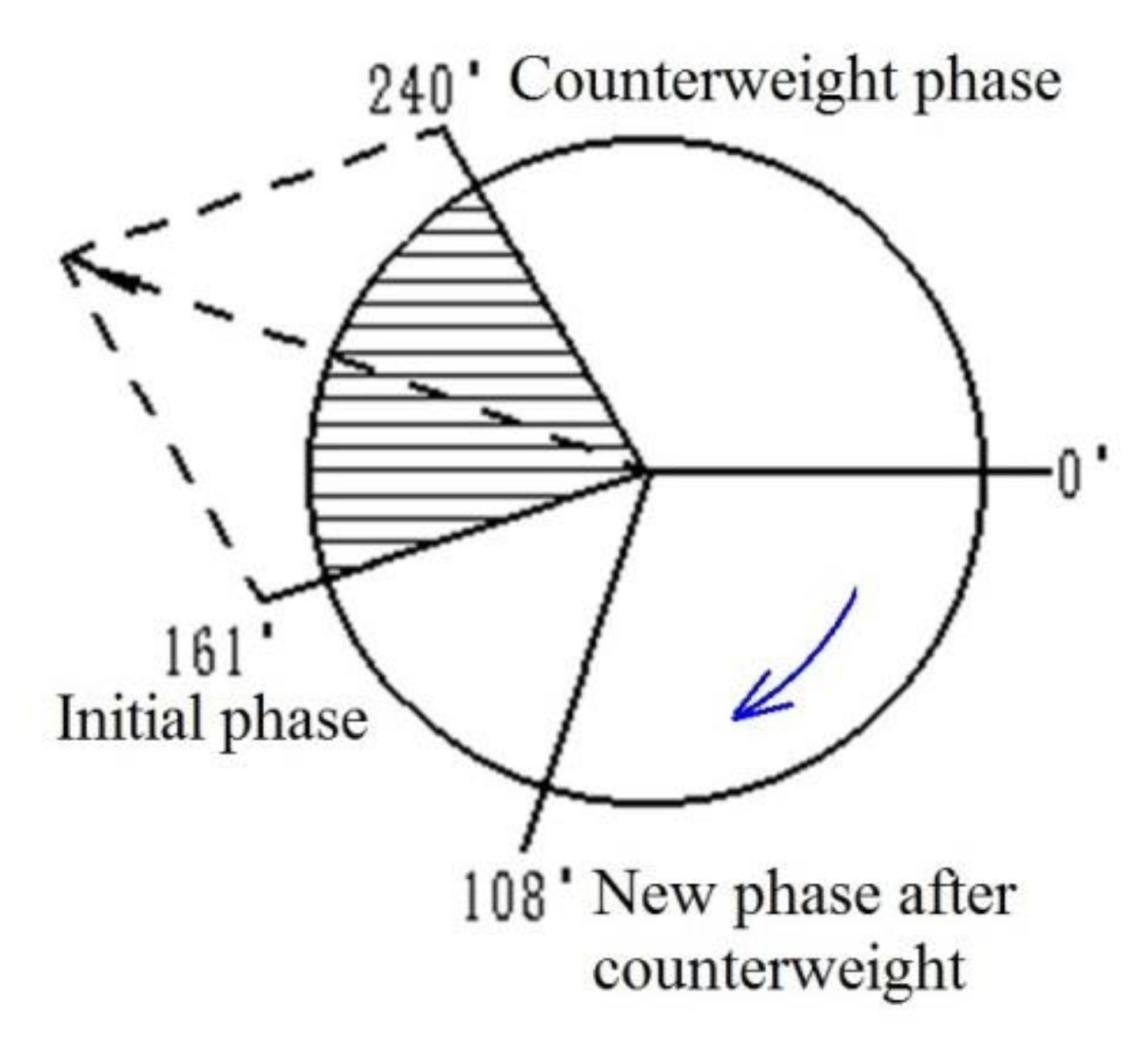
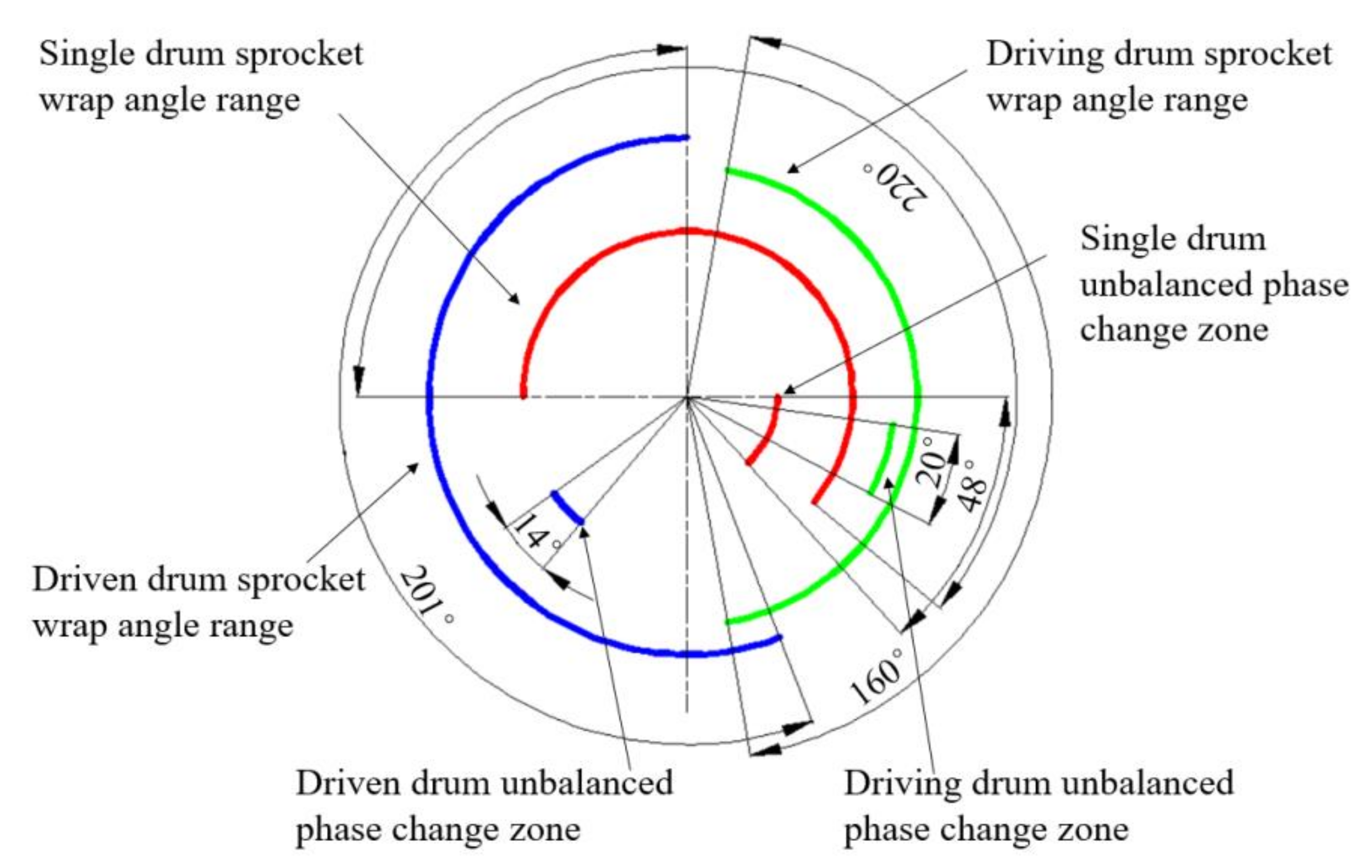
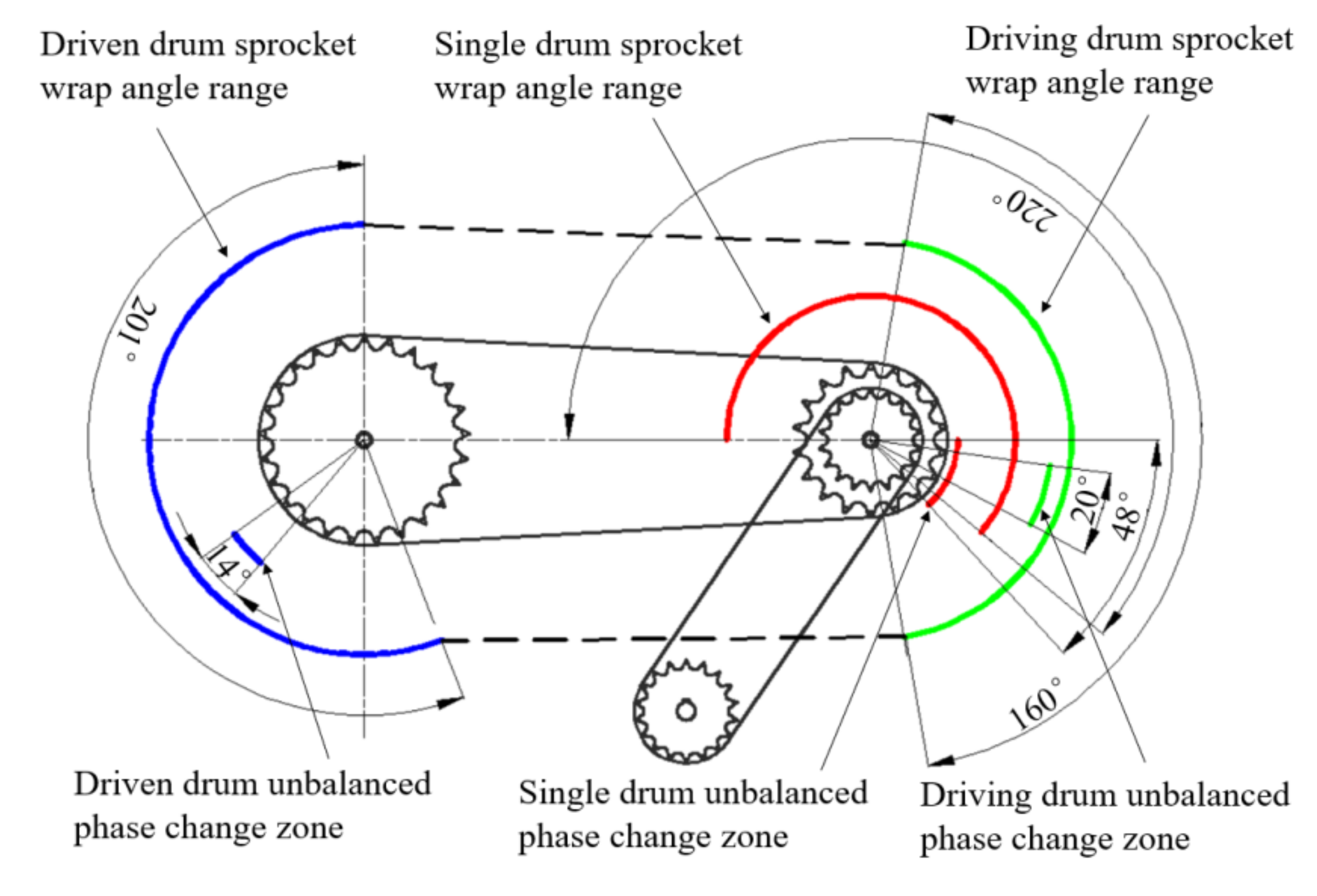
- In the dynamic balance test of the driven drum, a mass of 58.8 g was added in the direction of 240° of the drum, which artificially caused the drum to be unbalanced. The angle of the unbalance after the weighting was between the initial unbalanced phase 161° and the emphasis phase 240°. At the same rotational speed, the phase of the unbalanced amount after the actual measurement was 108°. It can be seen that the side chain drive affected the unbalanced state of the threshing drum from this phase change. The size and position of the wrap angle of the chain drive would directly affect the phase of the two equivalent unbalanced mass.
- (2)
- When double threshing drums were connected in parallel by the chain drive, the transmission characteristics based on the chain drive or the influence of the load on the unbalanced phase would affect the equilibrium state of the entire system. The unbalance of the load had little effect on the unbalanced amplitude of the active drum through the transmission characteristics of the chain drive. After the load was driven, the transmission chain between the load and the driving drum generated tensile force and lateral vibration, which had an obvious influence on the unbalanced phase of the main driven drum. Therefore, when determining the double threshing drums dynamic balance method, the influence of load and chain drive on the unbalanced phase of the active drum would be considered.
- (3)
- In the portable dynamic balancer system, the unbalanced amplitude after balancing threshing drum I chain transmission mode of combine harvester can be maximum reduced 91%. The axial trajectory of single threshing drum I was reduced after increasing the weight. When threshing drum II was dynamically balanced, the unbalanced amplitude of threshing drum II can be maximum reduced 69.2%. The horizontal and vertical amplitudes coordinate values of threshing drum II axis trajectory were significantly reduced. When constructing the double threshing drums dynamic balance model, the influence of the chain drive on the unbalanced phase should be considered.
Author Contributions
Funding
Conflicts of Interest
Data Availability
References
- Li, K.Z. Analysis, diagnosis and prevention of common faults in agricultural machinery. Sci. Technol. Innov. 2019, 23, 140–141. [Google Scholar]
- Yang, X.; Tian, M.Q.; Li, L.; Song, J.C.; Zhang, L.F.; Wu, J.K. Noise reduction method for vibration signal driven by mining belt conveyor. Ind. Autom. 2019, 45, 66–70. [Google Scholar]
- Li, Z.; Miao, F.; Yang, Z.; Wang, H. An anthropometric study for the anthropomorphic design of tomato-harvesting robots. Comput. Electron. Agric. 2019, 163, 104881. [Google Scholar] [CrossRef]
- Cui, Y.C.; Deng, S.E.; Zhang, W.H.; Chen, G.D. The impact of roller dynamic unbalance of high-speed cylindrical roller bearing on the cage nonlinear dynamic characteristics. Mech. Mach. Theory 2017, 118, 65–83. [Google Scholar]
- Xing, C.H.; Li, Y.L.; Zhang, L. Effective application of rotor unbalance fault in diagnosis. Equip. Manag. Maint. 2019, 11, 175–176. [Google Scholar]
- Wang, Z.; Tu, W.; Zhang, K.; Shi, Q.H.; Li, J.; Wei, C.Y. Research status of dynamic balance method for high speed spindles. Modern Manuf. Eng. 2019, 6, 154–160. [Google Scholar]
- Li, Z.Z.; He, L.D.; Zhang, L.H.; Zhang, Z.C.; Wan, F.T. Experimental study on low-speed dynamic balance of two-span four-supported shaft rotor. J. Beijing Univ. Chem. Technol. Nat. Sci. Ed. 2019, 46, 65–71. [Google Scholar]
- Kang, J.; Yuan, Y.; Liu, H.; He, J.; Jiang, M.; He, P. Load control of threshing cylinder of small-sized harvester based on current detection. Eng. Agric. Environ. Food 2017, 10, 150–156. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, H.T.; Zhou, Y.P. Unbalanced Vibration Identification of Tangential ThreshingCylinder Induced by Rice Threshing Process. Shock Vib. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Gen, D.Y.; He, K.; Wang, Q.; Jin, C.Q.; Zhang, G.H.; Lu, X.F. Design and experiment of horizontal axial flow corn flexible threshing device. Trans. Chin. Soc. Agric. Mach. 2019, 50, 101–108. [Google Scholar]
- Gu, D.; Zhang, X.; Zhang, J.; Liu, Y.; Wen, B. Synchronization and coupling dynamic characteristics of an exciter and two cylindrical rollers in a vibrating system. J. Sound Vib. 2019, 456, 353–373. [Google Scholar] [CrossRef]
- Cui, Y.; Deng, S.; Niu, R.; Chen, G. Vibration effect analysis of roller dynamic unbalance on the cage of high-speed cylindrical roller bearing. J. Sound Vib. 2018, 434, 314–335. [Google Scholar] [CrossRef]
- Hu, W.T.; Liu, Y.X. Optimization of mechanical high-speed fine-punching maneuver balance. Forg. Technol. 2018, 43, 83–88. [Google Scholar]
- Li, J.; Xue, K.P.; Yang, Z.; Hong, T.S. Nonlinear control of lateral vibration of freight chain in orchard. Trans. Chin. Soc. Agric. Mach. 2017, 33, 66–72. [Google Scholar]
- Robert, T.; Niels, B.; Ulrich, G.; Elmar, W. Experimental investigations of the internal friction in automotive bush chain drive systems. Tribol. Int. 2019, 140, 105871. [Google Scholar]
- Awwaluddin, M.; Hastuty, S.; Petrus, Z.; Putut, H.S.; Edi, S.; Nugroho, A. Chain and Sprocket Analysis of Control Rod Drive Mechanism of HTGR Experimental Power Reactor. J. Phys. Conf. Ser. 2019, 1198, 022053. [Google Scholar] [CrossRef]
- Zhang, W.X.; Ren, X.Q. Optimization design of sprocket entity in synchronous chain drive. Spec. Equip. Electron. Ind. 2019, 48, 63–65. [Google Scholar]
- Gong, H.C. Dynamic analysis of intermittent transmission chain system. Mech. Transm. 2019, 43, 131–133, 143. [Google Scholar]
- Velicu, R.; Săulescu, R.; Gavrilă, C.C. Kinematic Modelling of Contact Point between Chain Bush and Sprocket. IOP Conf. Ser. Mater. Sci. Eng. 2019, 514, 012029. [Google Scholar] [CrossRef]
- Chai, L.P.; Yu, J.F.; Li, Y. Pressure pulsation characteristics in series-parallel centrifugal pump with unequal blade pitch. J. Drain. Irrig. Mach. Eng. 2019, 37, 752–757. [Google Scholar]
- Song, M.W.; Chai, M.J. Equivalent mechanism and motion analysis of roller chain based on MATLAB coal mine. Coal Technol. 2018, 37, 304–307. [Google Scholar]
- Wang, Y.L.; Zeng, Y.; Xu, L.K. Shafting vibration model with torsion deformation in shaft of hydro-turbine generator units. J. Drain. Irrig. Mach. Eng. 2019, 37, 782–787. [Google Scholar]
- Zhao, Y.; Ru, R.T.; Wu, L.Y. Study on coupling vibration characteristics of double gearbox transmission system. Mech. Transm. 2018, 42, 1–6. [Google Scholar]
- Qiao, X.; Hu, G. Active Control for Multinode Unbalanced Vibration of Flexible Spindle Rotor System with Active Magnetic Bearing. Shock. Vib. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Liu, J.; Tang, C.; Shao, Y. An innovative dynamic model for vibration analysis of a flexible roller bearing. Mech. Mach. Theory 2019, 135, 27–39. [Google Scholar] [CrossRef]
- Bin, G.F.; Zhou, W.; Wang, W.M.; Li, X.J. Study on virtual dynamic balance of turbomachinery multi-rotor axis based on dynamic response analysis. J. Vib. Shock 2017, 36, 8–12, 28. [Google Scholar]
- Bin, G.F.; Li, X.J.; Chen, L.F.; Cui, Y.H. Effect of rotor unbalance on vibration characteristics of two-span three-supported shafting system. J. Power Eng. 2017, 37, 699–703, 725. [Google Scholar]
- Tang, Z.; Li, Y.; Cheng, C. Development of multi-functional combine harvester with grain harvesting and straw baling. Span. J. Agric. Res. 2017, 15, 202. [Google Scholar] [CrossRef]
- Tang, Z.; Li, Y.; Li, X.Y.; Xu, T.B. Structural damage modes for rice stalks undergoing threshing. Biosyst. Eng. 2019, 186, 323–336. [Google Scholar] [CrossRef]
- Liang, Z.; Xu, L.; De Baerdemaeker, J.; Li, Y.; Saeys, W. Optimisation of a multi-duct cleaning device for rice combine harvesters utilising CFD and experiments. Biosyst. Eng. 2020, 190, 25–40. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, H.; Zhou, Y.; Li, Y. Mutual Interference and Coupling Response of Multicylinder Vibration among Combine Harvester Co-Frame. Shock. Vib. 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Su, S.H.; Liu, Z.W. Hydraulic performance of guide vane mixed-flow pump based on loading distribution. J. Drain. Irrig. Mach. Eng. 2018, 36, 1233–1239. [Google Scholar]
- Wang, C.; Cui, Y.; Ge, S.; Sun, M.; Jia, Z. Experimental Study on Vortex-Induced Vibration of Risers Considering the Effects of Different Design Parameters. Appl. Sci. 2018, 8, 2411. [Google Scholar] [CrossRef]
- Lai, Z.N.; Yang, S.; Wu, P. Speed-throttling combined optimization for high reliability in parallel centrifugal pump system. J. Drain. Irrig. Mach. Eng. 2018, 36, 1205–1210. [Google Scholar]
- Wang, Z.; Yue, F.; Wang, H.; Gao, H.; Fan, B. Refined Study on Free Vibration of a Cable with an Inertial Mass Damper. Appl. Sci. 2019, 9, 2271. [Google Scholar] [CrossRef]
- Pan, D.; Fu, X.; Qi, W. The Direct Integration Method with Virtual Initial Conditions on the Free and Forced Vibration of a System with Hysteretic Damping. Appl. Sci. 2019, 9, 3707. [Google Scholar] [CrossRef]
- Ma, J.; Liu, T.; Zha, C.; Song, L. Simulation Research on the Time-Varying Meshing Stiffness and Vibration Response of Micro-Cracks in Gears under Variable Tooth Shape Parameters. Appl. Sci. 2019, 9, 1512. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, K. Integrated condition monitoring and fault diagnosis technology for wind turbine drive-train. J. Drain. Irrig. Mach. Eng. 2018, 36, 613–616. [Google Scholar]
- Xie, H.R.; Jin, C.Q.; Yin, X.; Qian, Z.J.; Teng, Y.J.; Yu, C.X. Vibration test and analysis of tracked soybean combine harvester. J. Agric. Mech. Res. 2019, 41, 158–163, 174. [Google Scholar]
- Li, Z.G.; Chen, N.X.; Shi, Y.C. Experimental study on lateral vibration law of PL-type multi-ribbed belt. J. Changchun Univ. 2016, 26, 1–4. [Google Scholar]





| Device Name | Performance Indicator | Parameter Value |
|---|---|---|
| S956Y-1 portable dynamic balance instrument | Frequency range (Hz) | 10~5000 |
| Frequency response error (%) | ±5 | |
| Maximum range (mm/s) | 100 | |
| Highest resolution (mm/s) | 0.1 | |
| L14A piezoelectric acceleration sensor | Sensitivity (pc/ms−2) | 3.5~5.2 |
| Frequency range (Hz) | 2~3000 | |
| Maximum acceleration (m/s2) | 2000 | |
| SGD-1-5V photoelectric speed sensor | Measuring range (rpm) | 1~60,000 |
| Operating Voltage (Vdc) | 5 | |
| Output signal type | TTLPulse signal |
| Instrument | Performance Index | Parameter | Performance Index | Parameter |
|---|---|---|---|---|
| 5E106 eddy current sensor | Sensitivity (V/mm) | 1 | Minimum measured surface (mm) | Φ58 |
| Nonlinear error (%) | ±1 | Frequency range (Hz) | 0–10,000 | |
| Range (mm) | 10 | Excitation voltage (Vdc) | ±15 | |
| Probe diameter (mm) | φ25 | Working temperature (°C) | −20–120 |
| Weight Holes Phase Angle | Item and Units | Threshing Drum with Different Rotation | ||||
|---|---|---|---|---|---|---|
| 600 rpm | 700 rpm | 800 rpm | 900 rpm | 1000 rpm | ||
| 60° | Amplitude (mm/s) | 0.532 | 0.426 | 0.486 | 1.16 | 1.716 |
| Phase (°) | 222 | 275 | 319 | 27 | 35 | |
| 120° | Amplitude (mm/s) | 0.431 | 0.502 | 0.735 | 1.869 | 2.662 |
| Phase (°) | 146 | 135 | 127 | 121 | 112 | |
| 180° | Amplitude (mm/s) | 0.22 | 0.382 | 0.538 | 2.028 | 2.868 |
| Phase (°) | 135 | 124 | 102 | 114 | 123 | |
| 240° | Amplitude (mm/s) | 0.383 | 0.513 | 0.972 | 1.487 | 2.725 |
| Phase (°) | 181 | 173 | 161 | 159 | 149 | |
| 300° | Amplitude (mm/s) | 0.631 | 0.483 | 0.661 | 1.271 | 1.863 |
| Phase (°) | 186 | 209 | 219 | 180 | 163 | |
| 360° | Amplitude (mm/s) | 0.618 | 0.465 | 0.622 | 0.861 | 1.094 |
| Phase (°) | 214 | 256 | 268 | 341 | 30 | |
| Rotating Speed (rpm) | Active Drum | Driven Drum | |||
|---|---|---|---|---|---|
| Amplitude (mm/s) | Phase (°) | Amplitude (mm/s) | Phase (°) | ||
| Single drum | 600 | 0.754 | 0 | - | - |
| 700 | 0.712 | 10 | - | - | |
| 800 | 1.285 | 33 | - | - | |
| 900 | 1.635 | 42 | - | - | |
| 1000 | 1.865 | 48 | - | - | |
| Double drum | 600 | 0.608 | 8 | 0.544 | 130 |
| 700 | 0.783 | 20 | 0.644 | 131 | |
| 800 | 1.213 | 17 | 0.754 | 136 | |
| 900 | 2.476 | 14 | 1.926 | 138 | |
| 1000 | 2.865 | 28 | 2.19 | 144 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Z.; Li, X.; Liu, X.; Ren, H.; Zhang, B. Dynamic Balance Method for Grading the Chain Drive Double Threshing Drum of a Combine Harvester. Appl. Sci. 2020, 10, 1026. https://doi.org/10.3390/app10031026
Tang Z, Li X, Liu X, Ren H, Zhang B. Dynamic Balance Method for Grading the Chain Drive Double Threshing Drum of a Combine Harvester. Applied Sciences. 2020; 10(3):1026. https://doi.org/10.3390/app10031026
Chicago/Turabian StyleTang, Zhong, Xiyao Li, Xin Liu, Hui Ren, and Biao Zhang. 2020. "Dynamic Balance Method for Grading the Chain Drive Double Threshing Drum of a Combine Harvester" Applied Sciences 10, no. 3: 1026. https://doi.org/10.3390/app10031026
APA StyleTang, Z., Li, X., Liu, X., Ren, H., & Zhang, B. (2020). Dynamic Balance Method for Grading the Chain Drive Double Threshing Drum of a Combine Harvester. Applied Sciences, 10(3), 1026. https://doi.org/10.3390/app10031026






