Compact Model of Latent Heat Thermal Storage for Its Integration in Multi-Energy Systems
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
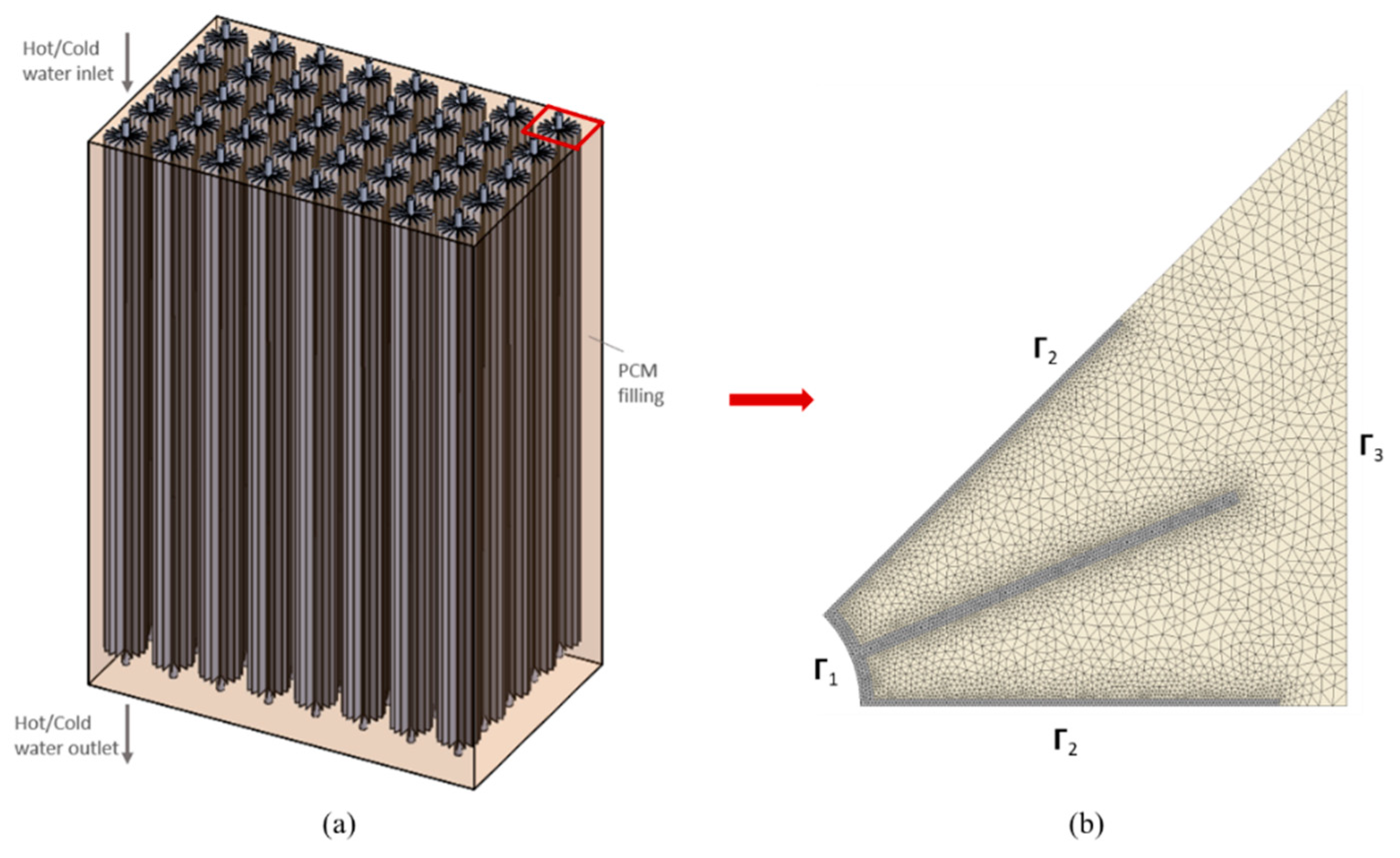
2.1. D Detailed Model
2.2. D Compact Model
3. Case Study
3.1. LHTS System Description
3.2. Model Application to Thermal Energy Networks
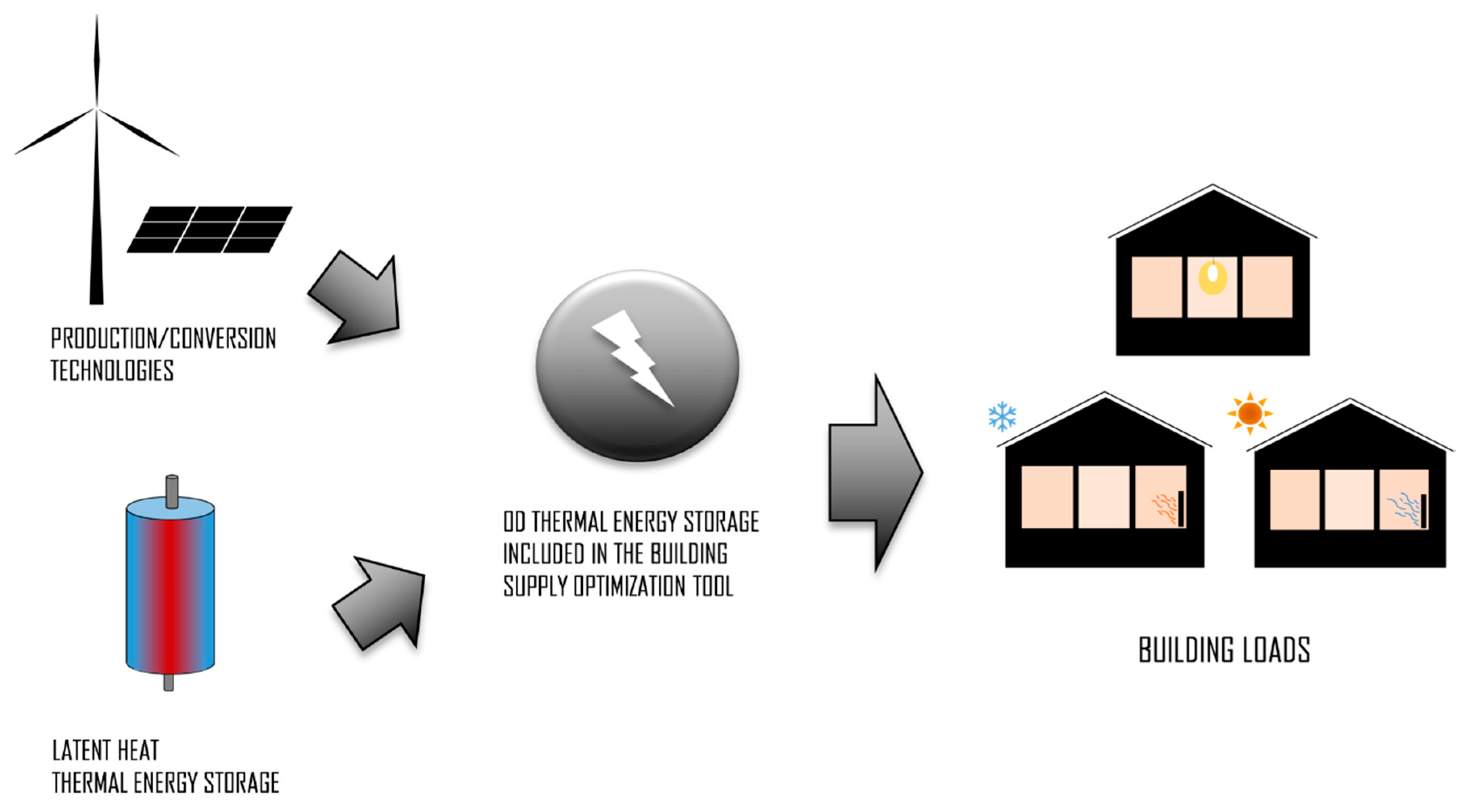
3.3. Model Application to Multi-Energy Systems
4. Results and Discussion
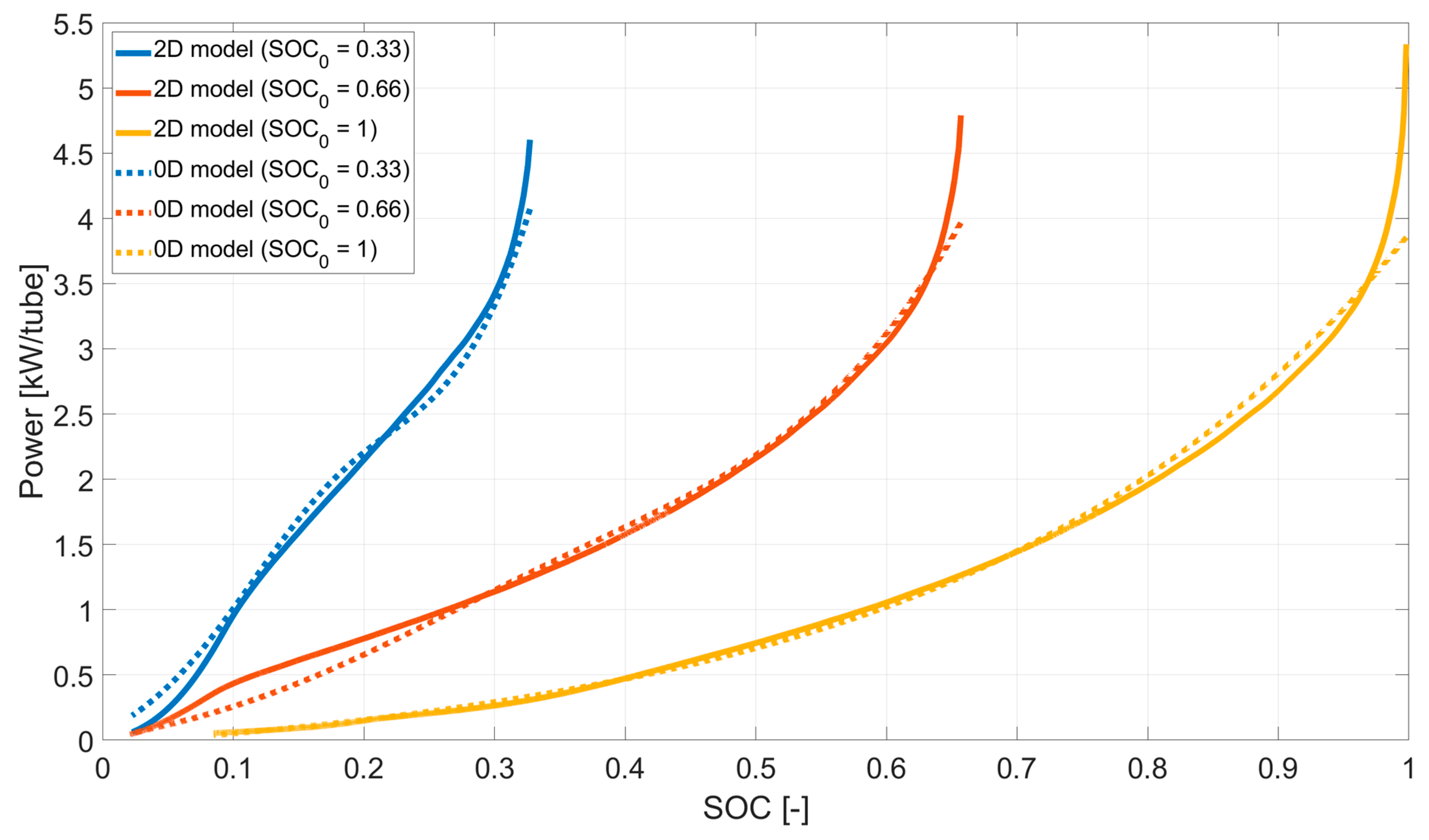
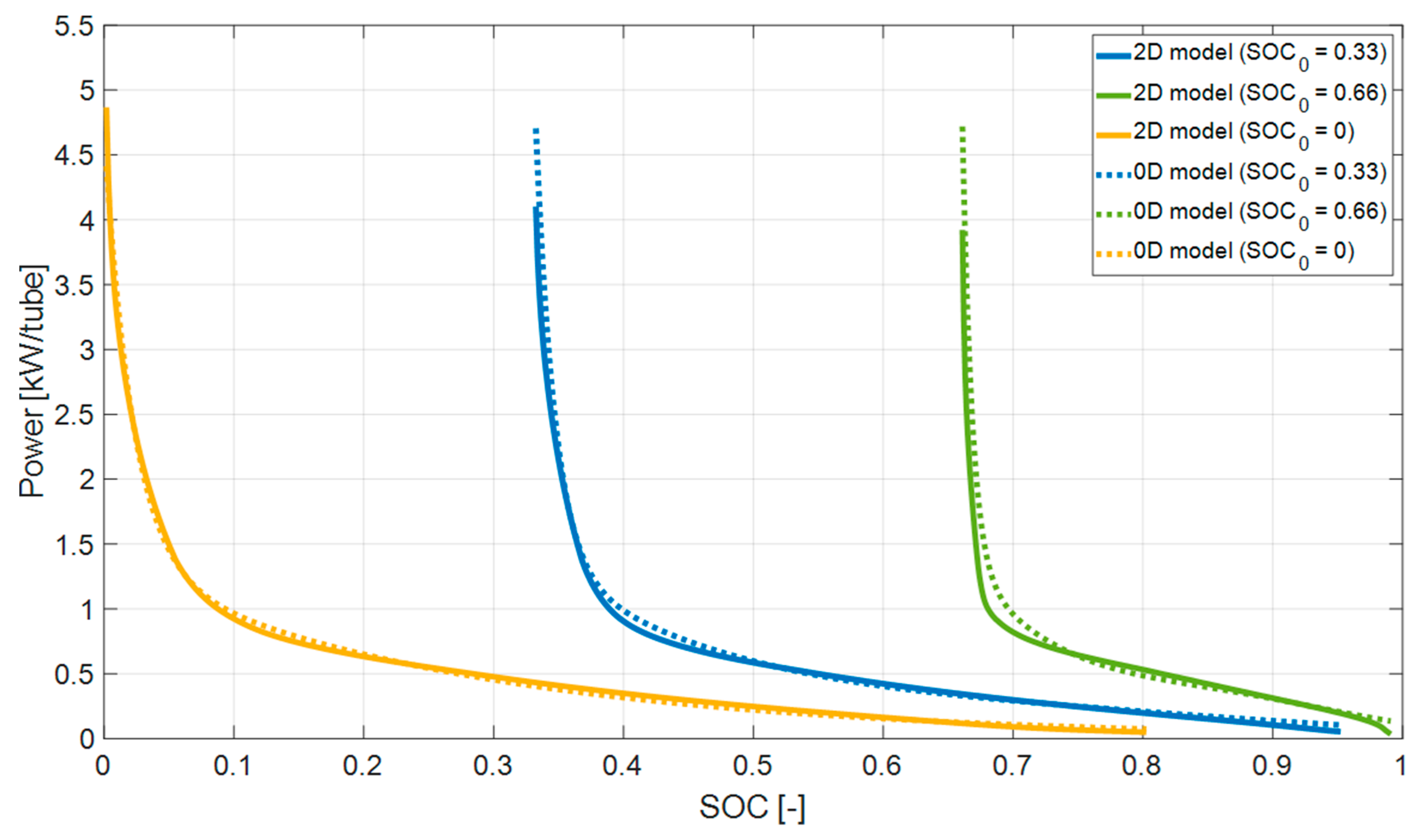
4.1. Comparison between 0D and 2D Models
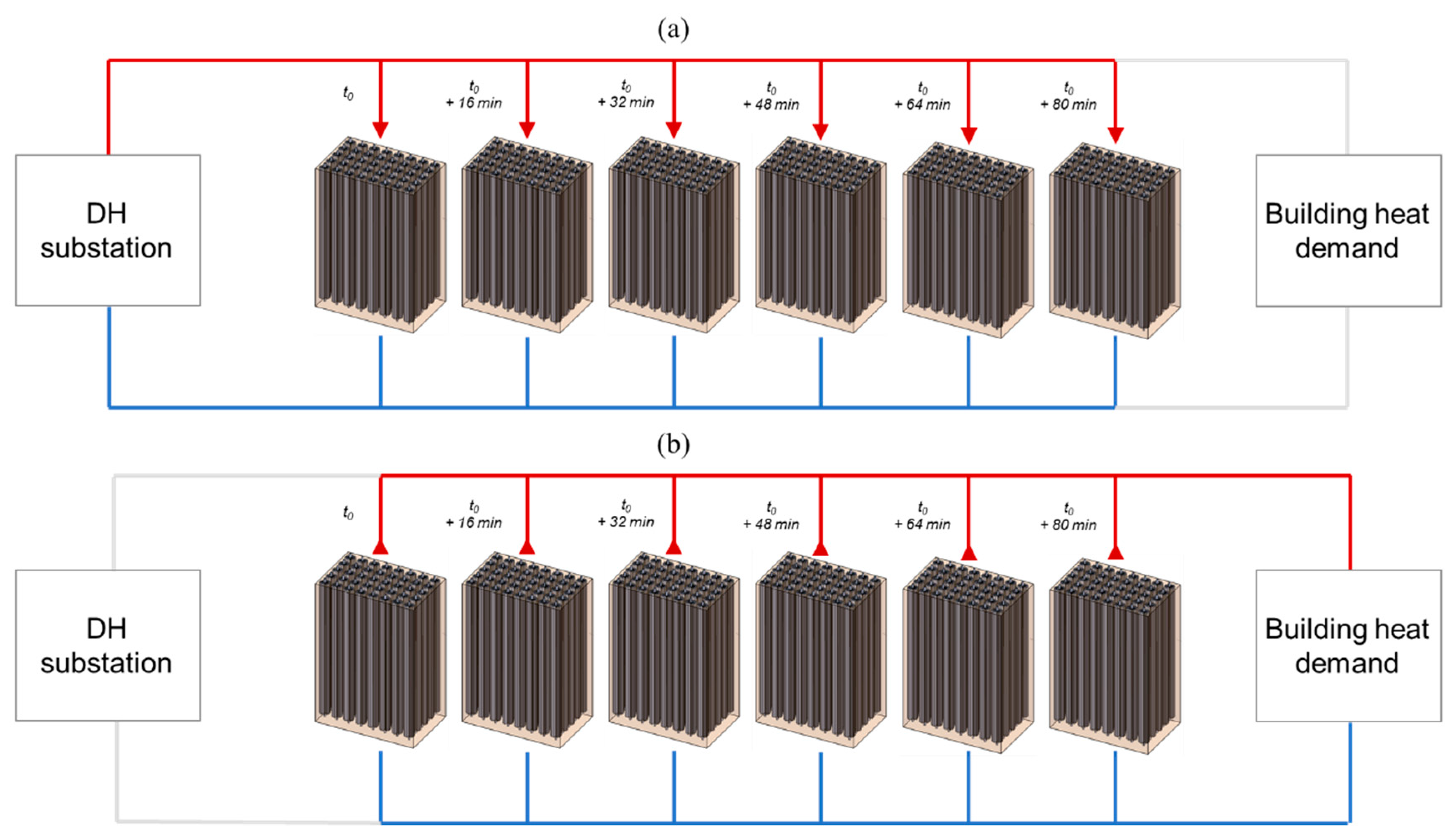
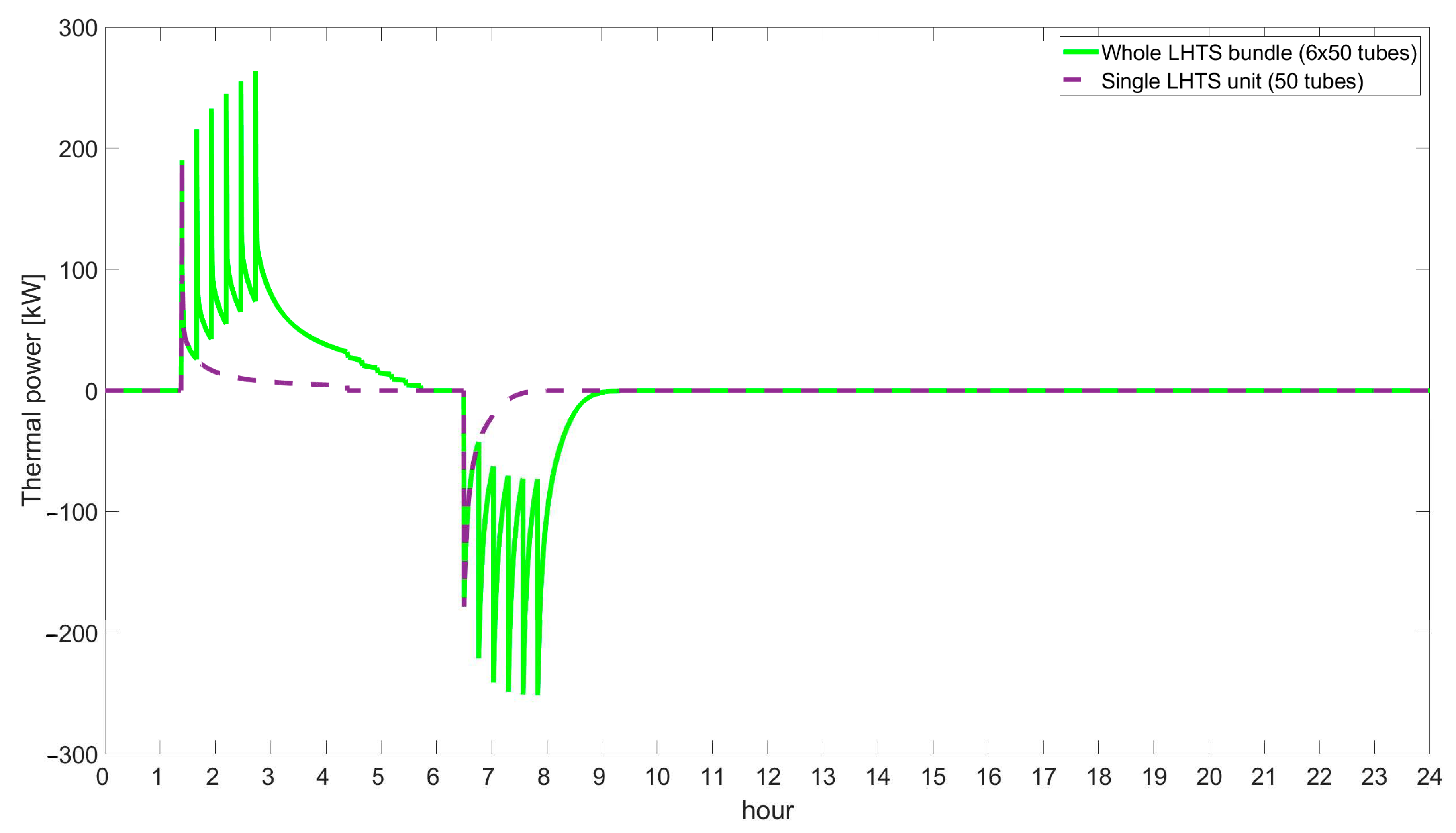
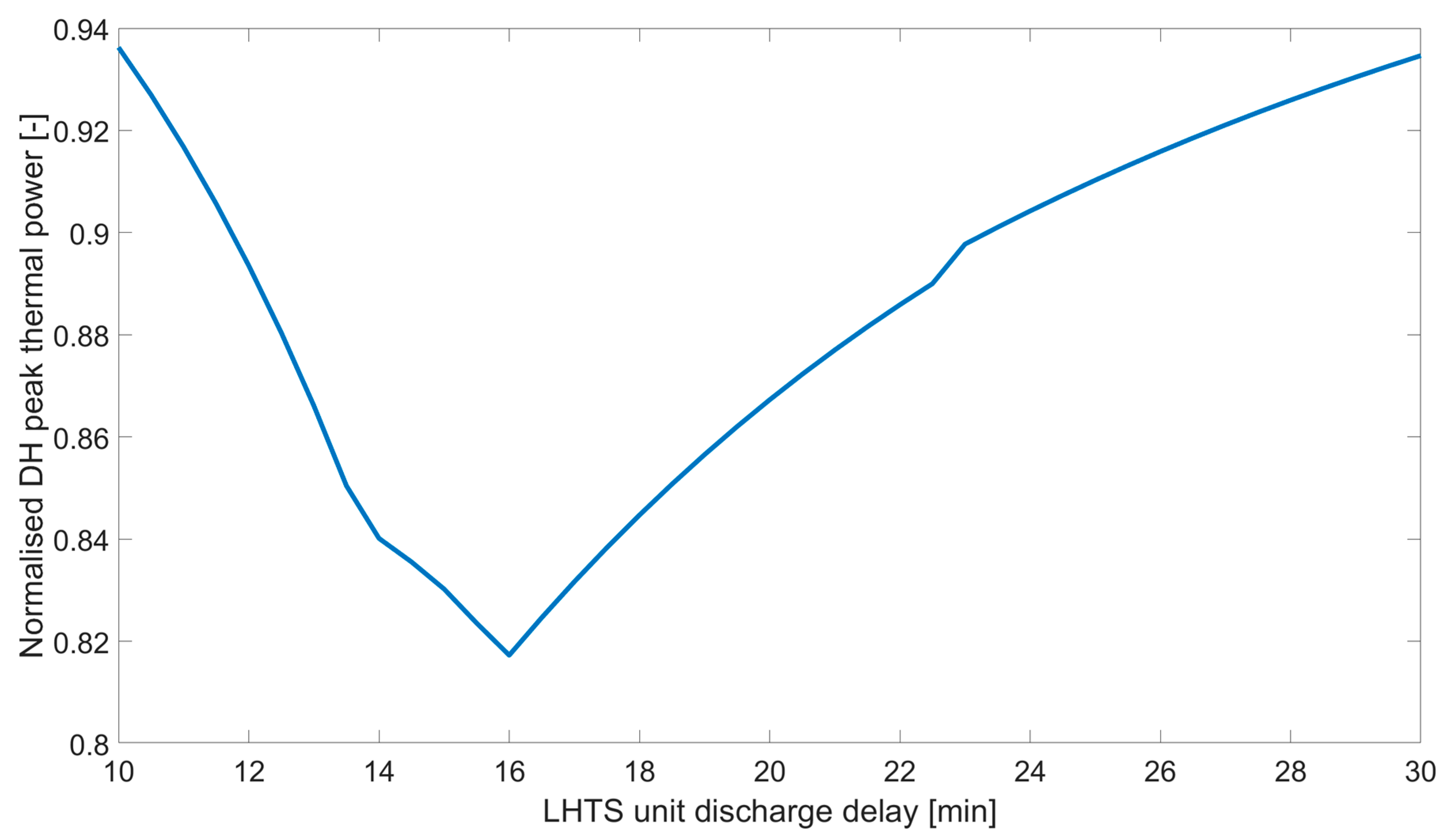
4.2. Distributed LHTS in DH Networks
- The charging phase of each LHTS unit lasts 3 h; thus, the whole LHTS bundle is charged between 1.20 and 5.40 am (due to the imposed delay between the activation of each unit);
- The discharging phase of each LHTS unit lasts 1.5 h; thus, the whole LHTS bundle is discharged between 6.30 am and 9.20 am (due to the imposed delay between the activation of each unit).
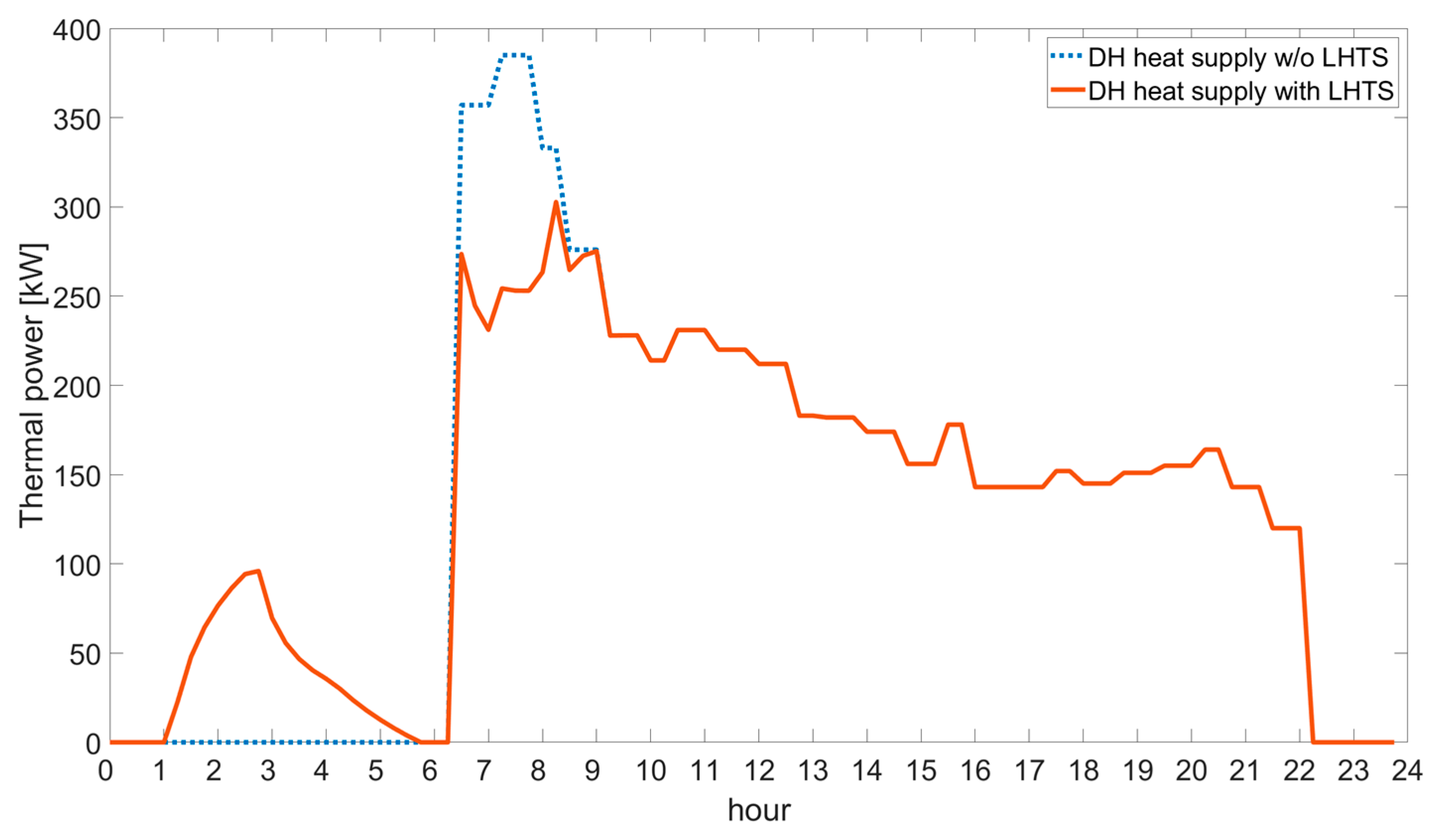
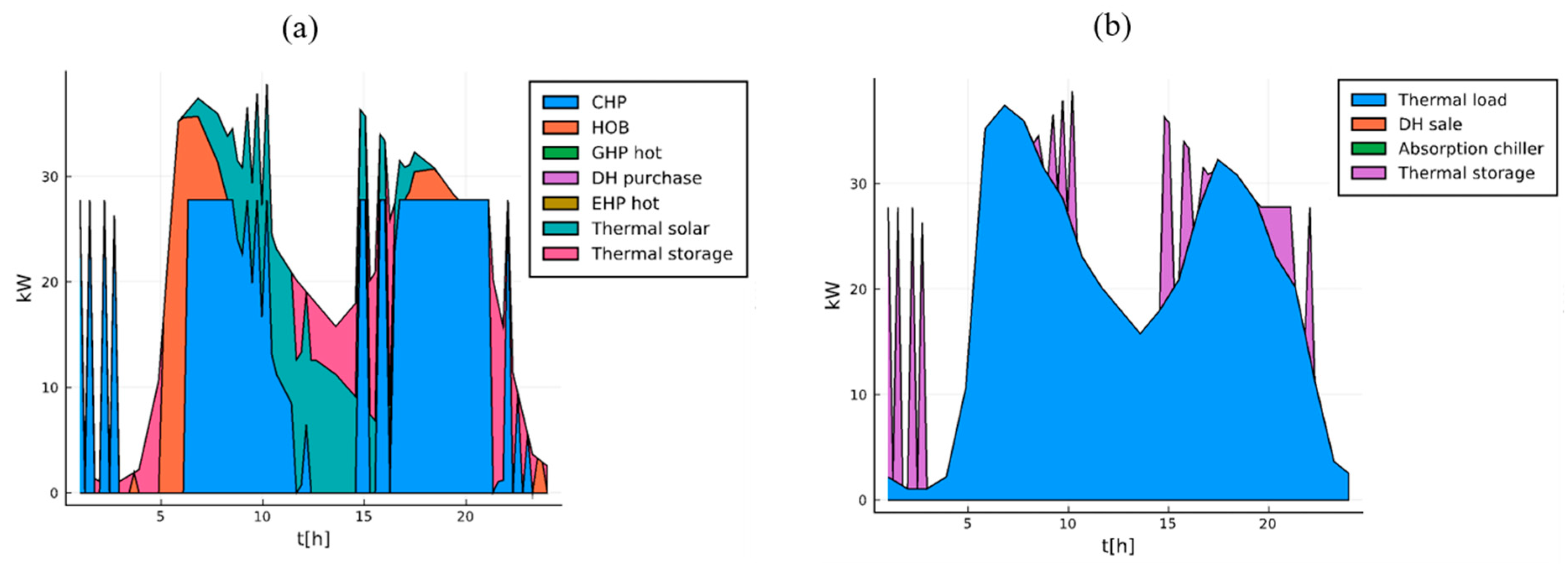
4.3. LHTS in Multi-Energy Systems
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nguyen, T.-T.; Martin, V.; Malmquist, A.; Silva, C.A.S. A review on technology maturity of small scale energy storage technologies. Renew. Energy Environ. Sustain. 2017, 2, 36. [Google Scholar] [CrossRef]
- Al-abidi, A.A.; Bin Mat, S.; Sopian, K.; Sulaiman, M.Y.; Mohammed, A.T. CFD applications for latent heat thermal energy storage: A review. Renew. Sustain. Energy Rev. 2013, 20, 353–363. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N.; Eames, P.; Smyth, M. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS). Renew. Sustain. Energy Rev. 2010, 14, 615–628. [Google Scholar] [CrossRef]
- Niyas, H.; Prasad, S.; Muthukumar, P. Performance investigation of a lab–scale latent heat storage prototype—Numerical results. Energy Convers. Manag. 2017, 135, 188–199. [Google Scholar] [CrossRef]
- Niyas, H.; Rao, C.R.C.; Muthukumar, P. Performance investigation of a lab-scale latent heat storage prototype—Experimental results. Sol. Energy 2017, 155, 971–984. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Gagliardi, F.; Verda, V. Maximization of performance of a PCM latent heat storage system with innovative fins. Appl. Energy 2015, 137, 707–715. [Google Scholar] [CrossRef]
- Pizzolato, A.; Sharma, A.; Maute, K.; Sciacovelli, A.; Verda, V. Topology optimization for heat transfer enhancement in Latent Heat Thermal Energy Storage. Int. J. Heat Mass Transf. 2017, 113, 875–888. [Google Scholar] [CrossRef]
- Pizzolato, A.; Sharma, A.; Maute, K.; Sciacovelli, A.; Verda, V. Design of effective fins for fast PCM melting and solidification in shell-and-tube latent heat thermal energy storage through topology optimization. Appl. Energy 2017, 208, 210–227. [Google Scholar] [CrossRef]
- Esapour, M.; Hosseini, M.J.; Ranjbar, A.A.; Pahamli, Y.; Bahrampoury, R. Phase change in multi-tube heat exchangers. Renew. Energy 2016, 85, 1017–1025. [Google Scholar] [CrossRef]
- Esapour, M.; Hosseini, M.J.; Ranjbar, A.A.; Bahrampoury, R. Numerical study on geometrical specifications and operational parameters of multi-tube heat storage systems. Appl. Therm. Eng. 2016, 109, 351–363. [Google Scholar] [CrossRef]
- Seddegh, S.; Wang, X.; Henderson, A.D. A comparative study of thermal behaviour of a horizontal and vertical shell-and-tube energy storage using phase change materials. Appl. Therm. Eng. 2016, 93, 348–358. [Google Scholar] [CrossRef]
- Neumann, H.; Palomba, V.; Frazzica, A.; Seiler, D.; Wittstadt, U.; Gschwander, S.; Restuccia, G. A simplified approach for modelling latent heat storages: Application and validation on two different fin-and-tubes heat exchangers. Appl. Therm. Eng. 2017, 125, 41–52. [Google Scholar] [CrossRef]
- Parry, A.J.; Eames, P.C.; Agyenim, F.B. Modeling of Thermal Energy Storage Shell-and-Tube Heat Exchanger. Heat Transf. Eng. 2014, 35, 1–14. [Google Scholar] [CrossRef]
- Tay, N.H.S.; Belusko, M.; Castell, A.; Cabeza, L.F.; Bruno, F. An effectiveness-NTU technique for characterising a finned tubes PCM system using a CFD model. Appl. Energy 2014, 131, 377–385. [Google Scholar] [CrossRef]
- Johnson, M.; Vogel, J.; Hempel, M.; Hachmann, B.; Dengel, A. Design of high temperature thermal energy storage for high power levels. Sustain. Cities Soc. 2017, 35, 758–763. [Google Scholar] [CrossRef]
- Colella, F.; Sciacovelli, A.; Verda, V. Numerical analysis of a medium scale latent energy storage unit for district heating systems. Energy 2012, 45, 397–406. [Google Scholar] [CrossRef]
- Xu, T.; Humire, E.N.; Chiu, J.N.-W.; Sawalha, S. Numerical thermal performance investigation of a latent heat storage prototype toward effective use in residential heating systems. Appl. Energy 2020, 278, 115631. [Google Scholar] [CrossRef]
- Vogel, J.; Johnson, M. Natural convection during melting in vertical finned tube latent thermal energy storage systems. Appl. Energy 2019, 246, 38–52. [Google Scholar] [CrossRef]
- Agyenim, F.; Eames, P.; Smyth, M. Heat transfer enhancement in medium temperature thermal energy storage system using a multitube heat transfer array. Renew. Energy 2010, 35, 198–207. [Google Scholar] [CrossRef]
- RT70HC Data Sheet. Available online: https://www.rubitherm.eu/media/products/datasheets/Techdata_-RT70HC_EN_06082018.PDF (accessed on 28 October 2020).
- Ansys Fluent Theory Guide. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v202/en/flu_th/flu_th_sec_melt_theory_energy.html%23flu_th_eq_melt_liq_frac (accessed on 28 October 2020).
- Stamatiou, A.; Maranda, S.; Eckl, F.; Schuetz, P.; Fischer, L.; Worlitschek, J. Quasi-stationary modelling of solidification in a latent heat storage comprising a plain tube heat exchanger. J. Energy Storage 2018, 20, 551–559. [Google Scholar] [CrossRef]
- Verda, V.; Colella, F. Primary energy savings through thermal storage in district heating networks. Energy 2011, 36, 4278–4286. [Google Scholar] [CrossRef]
- Hosseini, M.J.; Rahimi, M.; Bahrampoury, R. Experimental and computational evolution of a shell and tube heat exchanger as a PCM thermal storage system. Int. Commun. Heat Mass Transf. 2014, 50, 128–136. [Google Scholar] [CrossRef]
- District Heating Prices in Turin. Available online: https://www.irenlucegas.it/documents/66424/545179/Tariffe_TLR_nuovo_sito_1_10_2020.pdf/22923499-defa-4394-bc52-cf578e0602b6 (accessed on 28 October 2020).

| PCM Physical Property | Value |
|---|---|
| Density (ρ) [kg/m3] | 880 (constant) |
| Specific Heat [J/(kg*K)] | 2000 |
| Thermal Conductivity (k) [W/(m*K)] | 0.2 |
| Latent Heat [kJ/kg] | 214 |
| Solidus Temperature [°C] | 69 |
| Liquidus Temperature [°C] | 71 |
| Coefficient | Discharge Phase | Charge Phase |
|---|---|---|
| A | 0.1752 [kW] | 3.353 [kW] |
| B | 3.112 [-] | −45.93 [-] |
| C | −0.2078 [kW] | 1.337 [kW] |
| D | −0.9345 [-] | −3.606 [-] |
| K | 1.758 [kW] | 0.3296 [kW] |
| E | 0.5518 [-] | 0.5908 [-] |
| F | 0.3442 [-] | 0.4197 [-] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colangelo, A.; Guelpa, E.; Lanzini, A.; Mancò, G.; Verda, V. Compact Model of Latent Heat Thermal Storage for Its Integration in Multi-Energy Systems. Appl. Sci. 2020, 10, 8970. https://doi.org/10.3390/app10248970
Colangelo A, Guelpa E, Lanzini A, Mancò G, Verda V. Compact Model of Latent Heat Thermal Storage for Its Integration in Multi-Energy Systems. Applied Sciences. 2020; 10(24):8970. https://doi.org/10.3390/app10248970
Chicago/Turabian StyleColangelo, Alessandro, Elisa Guelpa, Andrea Lanzini, Giulia Mancò, and Vittorio Verda. 2020. "Compact Model of Latent Heat Thermal Storage for Its Integration in Multi-Energy Systems" Applied Sciences 10, no. 24: 8970. https://doi.org/10.3390/app10248970
APA StyleColangelo, A., Guelpa, E., Lanzini, A., Mancò, G., & Verda, V. (2020). Compact Model of Latent Heat Thermal Storage for Its Integration in Multi-Energy Systems. Applied Sciences, 10(24), 8970. https://doi.org/10.3390/app10248970






