On Mathematical Modelling of Automated Coverage Optimization in Wireless 5G and beyond Deployments
Abstract
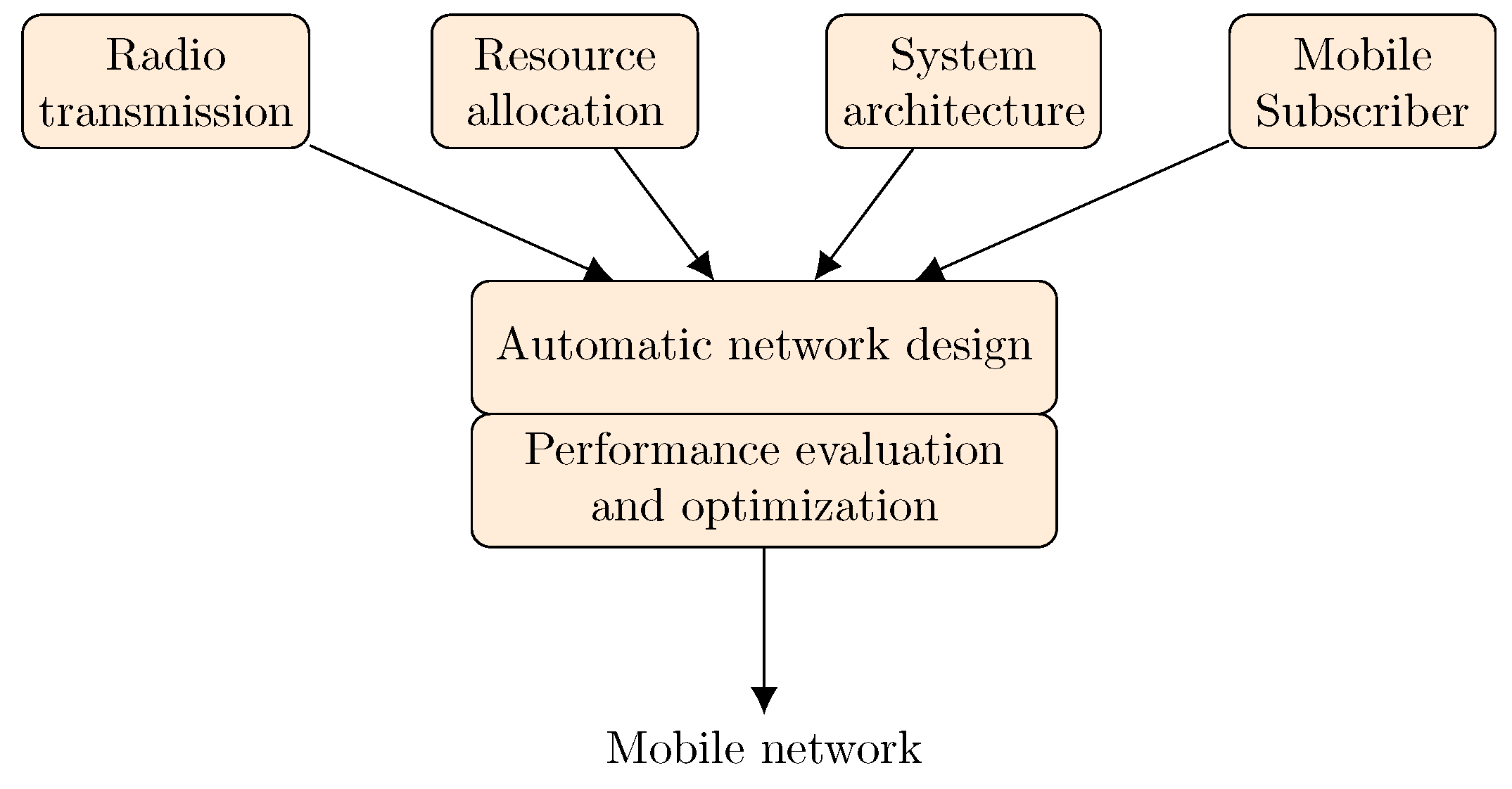
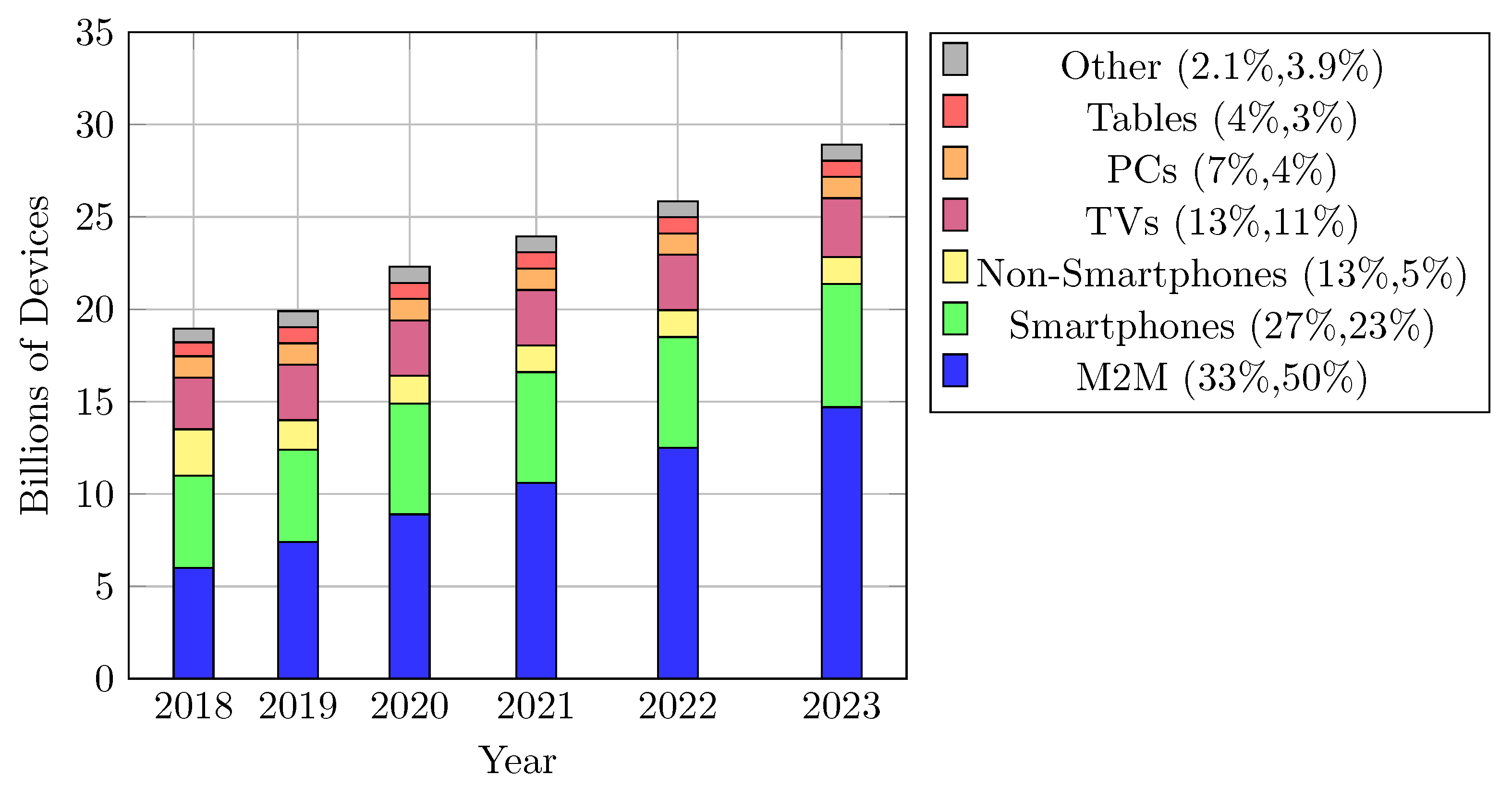
1. Introduction
1.1. Literature Review
1.1.1. Location Covering Problems
1.1.2. Base Station Optimization and Deployment
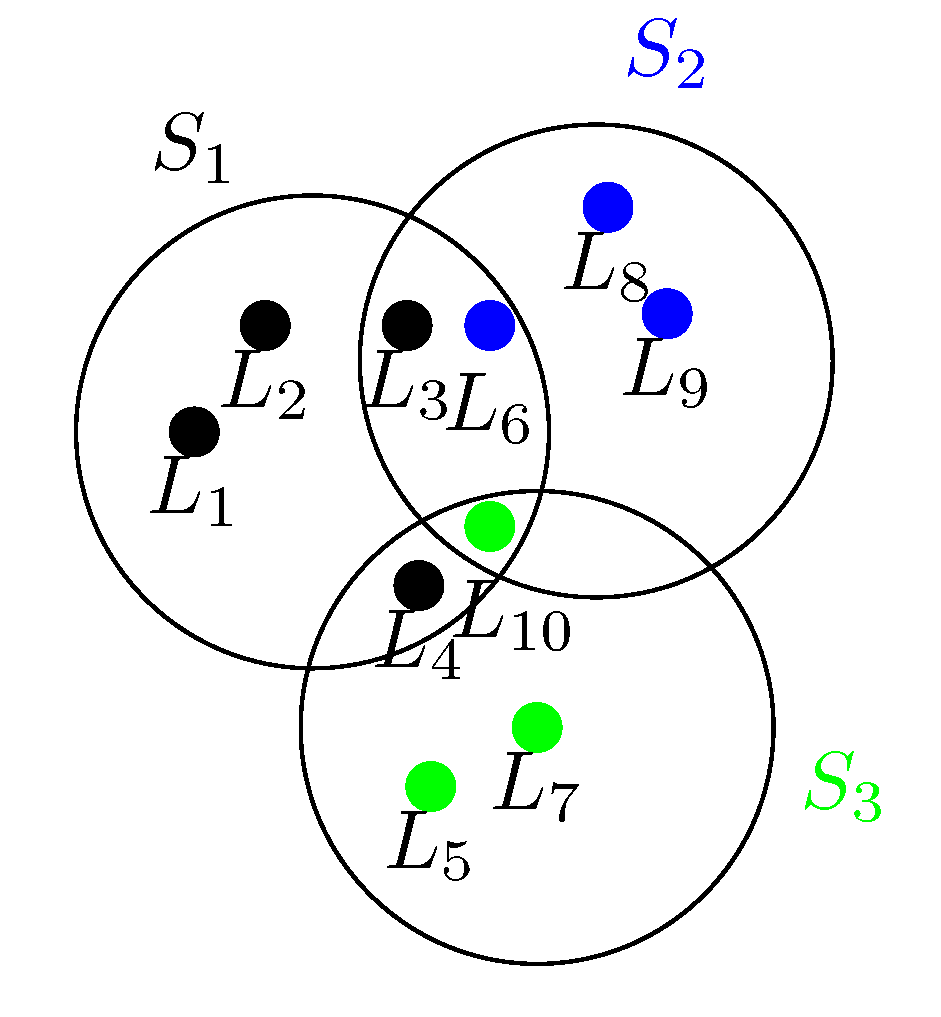
1.2. Problem Formulation and Related Work
- I is the set of service centres ,
- J is the set of customer locations .
- 1.
- A condition necessary to solve the task is that all of the customer locations are reachable from at least one location where an operating service centre is considered.
- 2.
- Customer location j is reachable from vertex i, which is designated as an operating service centre if . If this inequality is not satisfied, vertex j is unreachable from i.
1.3. Main Contribution
2. Models Developed for Network Coverage and Capacity Problems
- deploying service centres to the new area or reconfiguration of the whole network,
- deploying additional service centres to the area, where service centres already exist, but do not provide sufficient network capacity.
- —capacity of service centre i,
- —the list of devices from customer location j that need a service centre,
- —customer from location j is assigned or is not assigned to service centre i,
- —expresses the weights of service centre i (in practice, it represents the gNodeB installation costs).
2.1. Capacitated Network Area Coverage
2.2. Wireless Interference Considerations
2.3. Capacitated Network Area Coverage with Existing Services
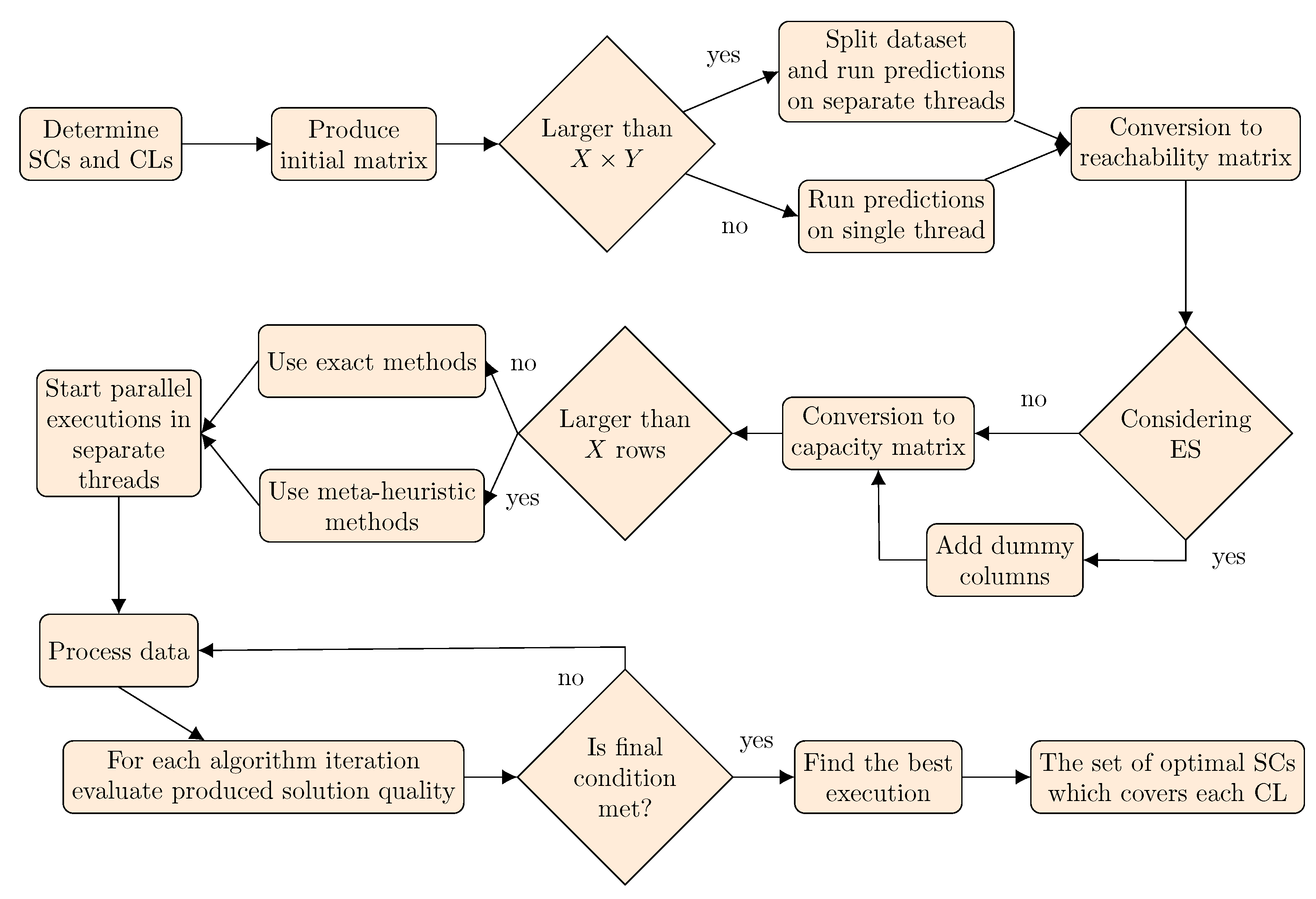
3. Computational Concept
3.1. Propagation Models
3.2. Employment of Developed Models
| Algorithm 1 The algorithm representing the whole computational concept to get the best locations to deploy service centres (gNodeB) nodes. |
|
3.3. Model Computational Complexity Considerations
4. Numerical Simulations and Results Discussion
4.1. gNodeB Parameters Settings
4.2. Simulation of Different Deployment Scenarios
4.3. Simulations Utilizing Dataset From District in Central Europe
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qamar, F.; Hindia, M.; Dimyati, K.; Noordin, K.A.; Majed, M.B.; Abd Rahman, T.; Amiri, I.S. Investigation of future 5G-IoT millimeter-wave network performance at 38 GHz for urban microcell outdoor environment. Electronics 2019, 8, 495. [Google Scholar] [CrossRef]
- Aranda, D.A.; Fernández, L.M.M.; Stantchev, V. Integration of Internet of Things (IoT) and Blockchain to increase humanitarian aid supply chains performance. In Proceedings of the 2019 5th International Conference on Transportation Information and Safety (ICTIS), Liverpool, UK, 14–17 July 2019; pp. 140–145. [Google Scholar]
- Al-Yasir, Y.I.; Ojaroudi Parchin, N.; Abd-Alhameed, R.A.; Abdulkhaleq, A.M.; Noras, J.M. Recent progress in the design of 4G/5G reconfigurable filters. Electronics 2019, 8, 114. [Google Scholar] [CrossRef]
- Shukla, S.; Hassan, M.F.; Khan, M.K.; Jung, L.T.; Awang, A. An analytical model to minimize the latency in healthcare internet-of-things in fog computing environment. PLoS ONE 2019, 14, e0224934. [Google Scholar] [CrossRef]
- Cisco Visual Networking Index. Cisco Visual Networking Index: Forecast and Trends, 2018–2023; White Papper; Cisco Visual Networking Index: San Jose, CA, USA, 2020. [Google Scholar]
- Bansal, G.; Jain, A.K.; Mishra, T. 5G Technology and Their Challenges. J. Adv. Database Manag. Syst. 2019, 6, 1–7. [Google Scholar]
- Shen, C.; Yun, M.; Arora, A.; Choi, H.A. Efficient mobile base station placement for first responders in public safety networks. In Proceedings of the Future of Information and Communication Conference, San Francisco, CA, USA, 14–15 March 2019; pp. 634–644. [Google Scholar]
- <i>Rios, R. 5G Network Planning and Optimisation Using Atoll. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2019. [Google Scholar]
- Tutschku, K. Demand-based radio network planning of cellular mobile communication systems. In Proceedings of the Conference on Computer Communications. Seventeenth Annual Joint Conference of the IEEE Computer and Communications Societies. Gateway to the 21st Century, San Francisco, CA, USA, 29 March–2 April 1998; Volume 3, pp. 1054–1061. [Google Scholar]
- Mohammed, M.E.; Bilal, K.H. LTE Radio Planning Using Atoll Radio Planning and Optimization Software. Int. J. Sci. Res. 2014, 3, 1460. [Google Scholar]
- Karp, R.M. Reducibility among combinatorial problems. In Complexity of Computer Computations; Springer: Berlin/Heidelberg, Germany, 1972; pp. 85–103. [Google Scholar]
- Dembski, W.A.; Marks, R.J. Bernoulli’s principle of insufficient reason and conservation of information in computer search. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 1–14 October 2009; pp. 2647–2652. [Google Scholar]
- Toregas, C. A Covering Formulation for the Location of Public Facilities. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1970. [Google Scholar]
- Sridharan, R. The capacitated plant location problem. Eur. J. Oper. Res. 1995, 87, 203–213. [Google Scholar] [CrossRef]
- Church, R.L.; Gerrard, R.A. The multi-level location set covering model. Geogr. Anal. 2003, 35, 277–289. [Google Scholar] [CrossRef]
- Cardei, M.; Du, D.Z. Improving wireless sensor network lifetime through power aware organization. Wirel. Netw. 2005, 11, 333–340. [Google Scholar] [CrossRef]
- Abrams, Z.; Goel, A.; Plotkin, S. Set k-cover algorithms for energy efficient monitoring in wireless sensor networks. In Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks, Berkeley, CA, USA, 26–27 April 2004; pp. 424–432. [Google Scholar]
- Jeong, I.J. An optimal approach for a set covering version of the refueling-station location problem and its application to a diffusion model. Int. J. Sustain. Transp. 2017, 11, 86–97. [Google Scholar] [CrossRef]
- Maher, S.J.; Murray, J.M. The unrooted set covering connected subgraph problem differentiating between HIV envelope sequences. Eur. J. Oper. Res. 2016, 248, 668–680. [Google Scholar] [CrossRef]
- Davoodi, S.M.R.; Goli, A. An integrated disaster relief model based on covering tour using hybrid Benders decomposition and variable neighborhood search: Application in the Iranian context. Comput. Ind. Eng. 2019, 130, 370–380. [Google Scholar] [CrossRef]
- Vianna, S.S. The set covering problem applied to optimisation of gas detectors in chemical process plants. Comput. Chem. Eng. 2019, 121, 388–395. [Google Scholar] [CrossRef]
- Basciftci, B.; Ahmed, S.; Shen, S. Distributionally robust facility location problem under decision-dependent stochastic demand. Eur. J. Oper. Res. 2020, in press. [Google Scholar] [CrossRef]
- Chauhan, D.; Unnikrishnan, A.; Figliozzi, M. Maximum coverage capacitated facility location problem with range constrained drones. Transp. Res. Part Emerg. Technol. 2019, 99, 1–18. [Google Scholar] [CrossRef]
- Murty, K.G.; Perin, C. A 1-matching blossom-type algorithm for edge covering problems. Networks 1982, 12, 379–391. [Google Scholar] [CrossRef]
- Dinur, I.; Safra, S. On the hardness of approximating minimum vertex cover. Ann. Math. 2005, 162, 439–485. [Google Scholar] [CrossRef]
- Guha, S.; Hassin, R.; Khuller, S.; Or, E. Capacitated vertex covering. J. Algorithms 2003, 48, 257–270. [Google Scholar] [CrossRef]
- Berge, C. Two theorems in graph theory. Proc. Natl. Acad. Sci. USA 1957, 43, 842. [Google Scholar] [CrossRef]
- Church, R.R.C. The maximal covering location model. Pap. Reg. Sci. Assoc. 1974, 32, 101–118. [Google Scholar] [CrossRef]
- Plane, D.R.; Hendrick, T.E. Mathematical programming and the location of fire companies for the Denver fire department. Oper. Res. 1977, 25, 563–578. [Google Scholar] [CrossRef]
- Schilling, D.; Elzinga, D.J.; Cohon, J.; Church, R.; ReVelle, C. The Team/Fleet models for simultaneous facility and equipment placement. Transp. Sci. 1979, 13, 163–175. [Google Scholar] [CrossRef]
- Margules, C.R. Conservation evaluation in practice. In Wildlife Conservation Evaluation; Springer: Berlin/Heidelberg, Germany, 1986; pp. 297–314. [Google Scholar]
- Current, J.R.; Storbeck, J.E. Capacitated covering models. Environ. Plan. Plan. Des. 1988, 15, 153–163. [Google Scholar] [CrossRef]
- Revelle, C.; Hogan, K. The maximum reliability location problem and α-reliablep-center problem: Derivatives of the probabilistic location set covering problem. Ann. Oper. Res. 1989, 18, 155–173. [Google Scholar] [CrossRef]
- Gerrard, R.A.; Church, R.L. Closest assignment constraints and location models: Properties and structure. Locat. Sci. 1996, 4, 251–270. [Google Scholar] [CrossRef]
- Berman, O.; Krass, D. The Generalized Maximal Covering Location Problem. Comput. Oper. Res. 2002, 29, 563–581. [Google Scholar] [CrossRef]
- Hong, S.; Kuby, M. A threshold covering flow-based location model to build a critical mass of alternative-fuel stations. J. Transp. Geogr. 2016, 56, 128–137. [Google Scholar] [CrossRef]
- Melo, M.T.; Nickel, S.; Saldanha-Da-Gama, F. Facility location and supply chain management—A review. Eur. J. Oper. Res. 2009, 196, 401–412. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Asgari, N.; Heidari, N.; Hosseininia, M.; Goh, M. Covering problems in facility location: A review. Comput. Ind. Eng. 2012, 62, 368–407. [Google Scholar] [CrossRef]
- Church, R.L.; Murray, A. Location Covering Models; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Brimberg, J.; Drezner, Z. A location–allocation problem with concentric circles. IIE Trans. 2015, 47, 1397–1406. [Google Scholar] [CrossRef]
- Boonmee, C.; Arimura, M.; Asada, T. Facility location optimization model for emergency humanitarian logistics. Int. J. Disaster Risk Reduct. 2017, 24, 485–498. [Google Scholar] [CrossRef]
- Eiselt, H.A.; Marianov, V. Location modeling for municipal solid waste facilities. Comput. Oper. Res. 2015, 62, 305–315. [Google Scholar] [CrossRef]
- Sitepu, R.; Puspita, F.M.; Romelda, S.; Fikri, A.; Susanto, B.; Kaban, H. Set covering models in optimizing the emergency unit location of health facility in Palembang. J. Physics: Conf. Ser. 2019, 1282, 012008. [Google Scholar] [CrossRef]
- García, S.; Marín, A. Covering location problems. In Location Science; Springer: Berlin/Heidelberg, Germany, 2015; pp. 93–114. [Google Scholar]
- Berman, O.; Huang, R. The minimum weighted covering location problem with distance constraints. Comput. Oper. Res. 2008, 35, 356–372. [Google Scholar] [CrossRef]
- Mattos, D.I.; Bosch, J.; Olsson, H.H.; Dakkak, A.; Bergh, K. Automated optimization of software parameters in a long term evolution radio base station. In Proceedings of the 2019 IEEE International Systems Conference (SysCon), Orlando, FL, USA, 8–11 April 2019; pp. 1–8. [Google Scholar]
- Dai, L.; Zhang, H. Propagation-Model-Free Base Station Deployment for Mobile Networks: Integrating Machine Learning and Heuristic Methods. IEEE Access 2020, 8, 83375–83386. [Google Scholar] [CrossRef]
- Yigitel, M.A.; Incel, O.D.; Ersoy, C. Dynamic BS topology management for green next generation HetNets: An urban case study. IEEE J. Sel. Areas Commun. 2016, 34, 3482–3498. [Google Scholar] [CrossRef]
- Sui, X.; Zhang, H.; Lv, Y. Coverage performance analysis of grid distribution in heterogeneous network. In Proceedings of the 2017 IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 27–30 October 2017; pp. 1424–1428. [Google Scholar]
- Foukas, X.; Patounas, G.; Elmokashfi, A.; Marina, M.K. Network slicing in 5G: Survey and challenges. IEEE Commun. Mag. 2017, 55, 94–100. [Google Scholar] [CrossRef]
- Mukherjee, A.; Keshary, V.; Pandya, K.; Dey, N.; Satapathy, S.C. Flying ad hoc networks: A comprehensive survey. In Information and Decision Sciences; Springer: Berlin/Heidelberg, Germany, 2018; pp. 569–580. [Google Scholar]
- Chen, H.; Mo, Y.; Qian, Q.; Xia, P. Research on 5G Wireless Network Deployment in Tourist Cities. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 398–402. [Google Scholar]
- Kenyeres, M.; Kenyeres, J. Synchronous Distributed Consensus Algorithms for Extrema Finding with Imperfect Communication. In Proceedings of the 2020 IEEE 18th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herlany, Slovakia, 23–25 January 2020; pp. 157–164. [Google Scholar]
- Ganame, H.; Yingzhuang, L.; Ghazzai, H.; Kamissoko, D. 5G Base Station Deployment Perspectives in Millimeter Wave Frequencies Using Meta-Heuristic Algorithms. Electronics 2019, 8, 1318. [Google Scholar] [CrossRef]
- Han, F.; Zhao, S.; Zhang, L.; Wu, J. Survey of strategies for switching off base stations in heterogeneous networks for greener 5G systems. IEEE Access 2016, 4, 4959–4973. [Google Scholar] [CrossRef]
- Xu, X.; Saad, W.; Zhang, X.; Xu, X.; Zhou, S. Joint deployment of small cells and wireless backhaul links in next-generation networks. IEEE Commun. Lett. 2015, 19, 2250–2253. [Google Scholar] [CrossRef]
- Kenyeres, M.; Kenyeres, J. Distributed Network Size Estimation Executed by Average Consensus Bounded by Stopping Criterion for Wireless Sensor Networks. In Proceedings of the 2019 International Conference on Applied Electronics (AE), Pilsen, Czech Republic, 10–11 September 2019; pp. 1–6. [Google Scholar]
- Cacciapuoti, A.S.; Caleffi, M.; Masone, A.; Sforza, A.; Sterle, C. Data Throughput Optimization for Vehicle to Infrastructure Communications. In New Trends in Emerging Complex Real Life Problems; Springer: Berlin/Heidelberg, Germany, 2018; pp. 93–101. [Google Scholar]
- González-Brevis, P.; Gondzio, J.; Fan, Y.; Poor, H.V.; Thompson, J.; Krikidis, I.; Chung, P.J. Base station location optimization for minimal energy consumption in wireless networks. In Proceedings of the 2011 IEEE 73rd Vehicular Technology Conference (VTC Spring), Yokohama, Japan, 15–18 May 2011; pp. 1–5. [Google Scholar]
- Valavanis, I.K.; Athanasiadou, G.; Zarbouti, D.; Tsoulos, G.V. Base-station location optimization for LTE systems with genetic algorithms. In Proceedings of the 20th European Wireless Conference, Barcelona, Spain, 14–16 May 2014; pp. 1–6. [Google Scholar]
- Kenyeres, M.; Kenyeres, J. Average Consensus over Mobile Wireless Sensor Networks: Weight Matrix Guaranteeing Convergence without Reconfiguration of Edge Weights. Sensors 2020, 20, 3677. [Google Scholar] [CrossRef]
- Teague, K.; Abdel-Rahman, M.J.; MacKenzie, A.B. Joint base station selection and adaptive slicing in virtualized wireless networks: A stochastic optimization framework. In Proceedings of the 2019 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 18–21 February 2019; pp. 859–863. [Google Scholar]
- Tayal, S.; Garg, P.; Vijay, S. Optimization Models for Selecting Base Station Sites for Cellular Network Planning. In Applications of Geomatics in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2020; pp. 637–647. [Google Scholar]
- Afuzagani, D.; Suyanto, S. optimizing BTS Placement Using Hybrid Evolutionary Firefly Algorithm. In Proceedings of the 8th International Conference on Information and Communication Technology (ICoICT), Yogyakarta, Indonesia, 24–26 June 2020; pp. 1–5. [Google Scholar]
- Seda, P.; Mark, M.; Su, K.; Seda, M.; Hosek, J.; Leu, J. The Minimization of Public Facilities With Enhanced Genetic Algorithms Using War Elimination. IEEE Access 2019, 7, 9395–9405. [Google Scholar] [CrossRef]
- Beasley, J.E.; Chu, P.C. A genetic algorithm for the set covering problem. Eur. J. Oper. Res. 1996, 94, 392–404. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Cuesta, R.; Paredes, F. Application of the artificial bee colony algorithm for solving the set covering problem. Sci. World J. 2014, 2014, 189164. [Google Scholar] [CrossRef] [PubMed]
- Lanza-Gutierrez, J.M.; Crawford, B.; Soto, R.; Berrios, N.; Gomez-Pulido, J.A.; Paredes, F. Analyzing the effects of binarization techniques when solving the set covering problem through swarm optimization. Expert Syst. Appl. 2017, 70, 67–82. [Google Scholar] [CrossRef]
- Coco, A.A.; Santos, A.C.; Noronha, T.F. Senario-based heuristics with path-relinking for the robust set covering problem. In Proceedings of the XI Metaheuristics International Conference (MIC), Agadir, Morocco, 7–10 June 2015. [Google Scholar]
- Vasko, F.J.; Lu, Y.; Zyma, K. What is the best greedy-like heuristic for the weighted set covering problem? Oper. Res. Lett. 2016, 44, 366–369. [Google Scholar] [CrossRef]
- Murray, A.T. Optimising the spatial location of urban fire stations. Fire Saf. J. 2013, 62, 64–71. [Google Scholar] [CrossRef]
- Maggenti, M.; Vassilovski, D. Method and Apparatus for Automatic Configuration of Wireless Communication Networks. U.S. Patent 9,888,393, 30 October 2018. [Google Scholar]
- Mangrulkar, S.; Kim, Y.S.; Duong, T.; Sung, S. Dynamic Configuration of eNodeB to Facilitate Circuit Switched Fallback Service. U.S. Patent 10,432,453, 2019. [Google Scholar]
- Ogbulezie, J. A Review of Path Loss Models for UHF Radio Waves Propagation: Trends and Assessment. Int. J. Res. Eng. Sci. 2016, 4, 67–75. [Google Scholar]
- Walfisch, J.; Bertoni, H.L. A theoretical model of UHF propagation in urban environments. IEEE Trans. Antennas Propag. 1988, 36, 1788–1796. [Google Scholar] [CrossRef]
- ETSI. Requirements for Support of Radio Resource Management (3GPP TS 38.133 Version 15.6.0 Release 15). Technical Report. Available online: https://www.etsi.org/deliver/etsi_ts/138100_138199/138133/15.06.00_60/ts_138133v150600p.pdf (accessed on 8 December 2020).
- Telkonika. Mobile Signal Strength Recommendations. 2019. Available online: https://wiki.teltonika.lt/view/Mobile_Signal_Strength_Recommendations (accessed on 8 December 2020).
- Balas, E.; Carrera, M.C. A dynamic subgradient-based branch-and-bound procedure for set covering. Oper. Res. 1996, 44, 875–890. [Google Scholar] [CrossRef]
- Beasley, J.E. An algorithm for set covering problem. Eur. J. Oper. Res. 1987, 31, 85–93. [Google Scholar] [CrossRef]
- Beasley, J.E.; Jörnsten, K. Enhancing an algorithm for set covering problems. Eur. J. Oper. Res. 1992, 58, 293–300. [Google Scholar] [CrossRef]
- Fisher, M.L.; Kedia, P. Optimal solution of set covering/partitioning problems using dual heuristics. Manag. Sci. 1990, 36, 674–688. [Google Scholar] [CrossRef]
- Galinier, P.; Hertz, A. Solution techniques for the large set covering problem. Discret. Appl. Math. 2007, 155, 312–326. [Google Scholar] [CrossRef][Green Version]
- Yelbay, B.; Birbil, Ş.İ.; Bülbül, K. The set covering problem revisited: An empirical study of the value of dual information. Eur. J. Oper. Res. 2012, 11, 575–594. [Google Scholar] [CrossRef]
- Williamson, D.P. Lecture Notes on Approximation Algorithms; Technical report, Technical Report RC–21409; IBM: Armonk, NY, USA, 1999. [Google Scholar]
- Beasley, J.E. A lagrangian heuristic for set-covering problems. Nav. Res. Logist. 1990, 37, 151–164. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 2, pp. 1470–1477. [Google Scholar]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Eberhart; Shi, Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No. 01TH8546), Seoul, Korea, 27–30 May 2001; pp. 81–86. [Google Scholar]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. BGSA: Binary gravitational search algorithm. Nat. Comput. 2010, 9, 727–745. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithm, Levy flights and global optimization. In Research and Development in Intelligent Systems XXVI; Springer: Berlin/Heidelberg, Germany, 2010; pp. 209–218. [Google Scholar]
- Rao, R.V.; Patel, V. An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems. Sci. Iran. 2013, 20, 710–720. [Google Scholar] [CrossRef]
- Lam, A.Y.; Li, V.O.; James, J. Real-coded chemical reaction optimization. IEEE Trans. Evol. Comput. 2011, 16, 339–353. [Google Scholar] [CrossRef]
- Sadollah, A.; Eskandar, H.; Kim, J.H. Water cycle algorithm for solving constrained multi-objective optimization problems. Appl. Soft Comput. 2015, 27, 279–298. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Back, T. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms; Oxford University Press: Oxford, MA, USA, 1996. [Google Scholar]
- Civicioglu, P. Transforming geocentric cartesian coordinates to geodetic coordinates by using differential search algorithm. Comput. Geosci. 2012, 46, 229–247. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Leung, Y.; Gao, Y.; Xu, Z.B. Degree of population diversity-a perspective on premature convergence in genetic algorithms and its markov chain analysis. IEEE Trans. Neural Netw. 1997, 8, 1165–1176. [Google Scholar] [CrossRef] [PubMed]
- Panichella, A.; Oliveto, R.; Di Penta, M.; De Lucia, A. Improving multi-objective test case selection by injecting diversity in genetic algorithms. IEEE Trans. Softw. Eng. 2015, 41, 358–383. [Google Scholar] [CrossRef]
- Frederick, W.G.; Sedlmeyer, R.L.; White, C.M. The Hamming metric in genetic algorithms and its application to two network problems. In Proceedings of the 1993 ACM/SIGAPP Symposium on Applied Computing: States of the Art and Practice; 1993; pp. 126–130. [Google Scholar]
- Calégari, P.; Guidec, F.; Kuonen, P.; Kobler, D. Parallel island-based genetic algorithm for radio network design. J. Parallel Distrib. Comput. 1997, 47, 86–90. [Google Scholar]
- Garey, M.; Johnson, D. Computers and Intractability: A Guide to the Theory of NP-Completeness, 19th ed.; W.H. Freeman and Company: New York, NY, USA, 1997. [Google Scholar]
- GSMA. The 5G Guide a Reference for Operators; Report itu-r;l GSMA: London, UK, 2019. [Google Scholar]
- 3GPP. Requirements for Further Advancements for Evolved Universal Terrestrial Radio Access (E-UTRA) (LTE-Advanced); Technical Report (TR) 36.913, 3rd Generation Partnership Project (3GPP), Version 15.0.0. 2018. Available online: https://www.etsi.org/deliver/etsi_tr/136900_136999/136913/15.00.00_60/tr_136913v150000p.pdf (accessed on 8 December 2020).
- Alliance, N. 5G white paper. In Next Generation Mobile Networks, White Paper; Next Generation Mobile Networks: Frankfurt am Main, Germany, 2015. [Google Scholar]
- ITU-R. Characteristics of Terrestrial IMT-Advanced Systems for Frequency Sharing/Interference Analyses; Report itu-r, Version M.2292-0; International Telecommunication Union: Geneva, Switzerland, 2017. [Google Scholar]
- Praha. Tomography Information about Prague 11. Available online: https://www.mistopisy.cz/pruvodce/obec/4861/praha-11/pocet-obyvatel/ (accessed on 8 December 2020).

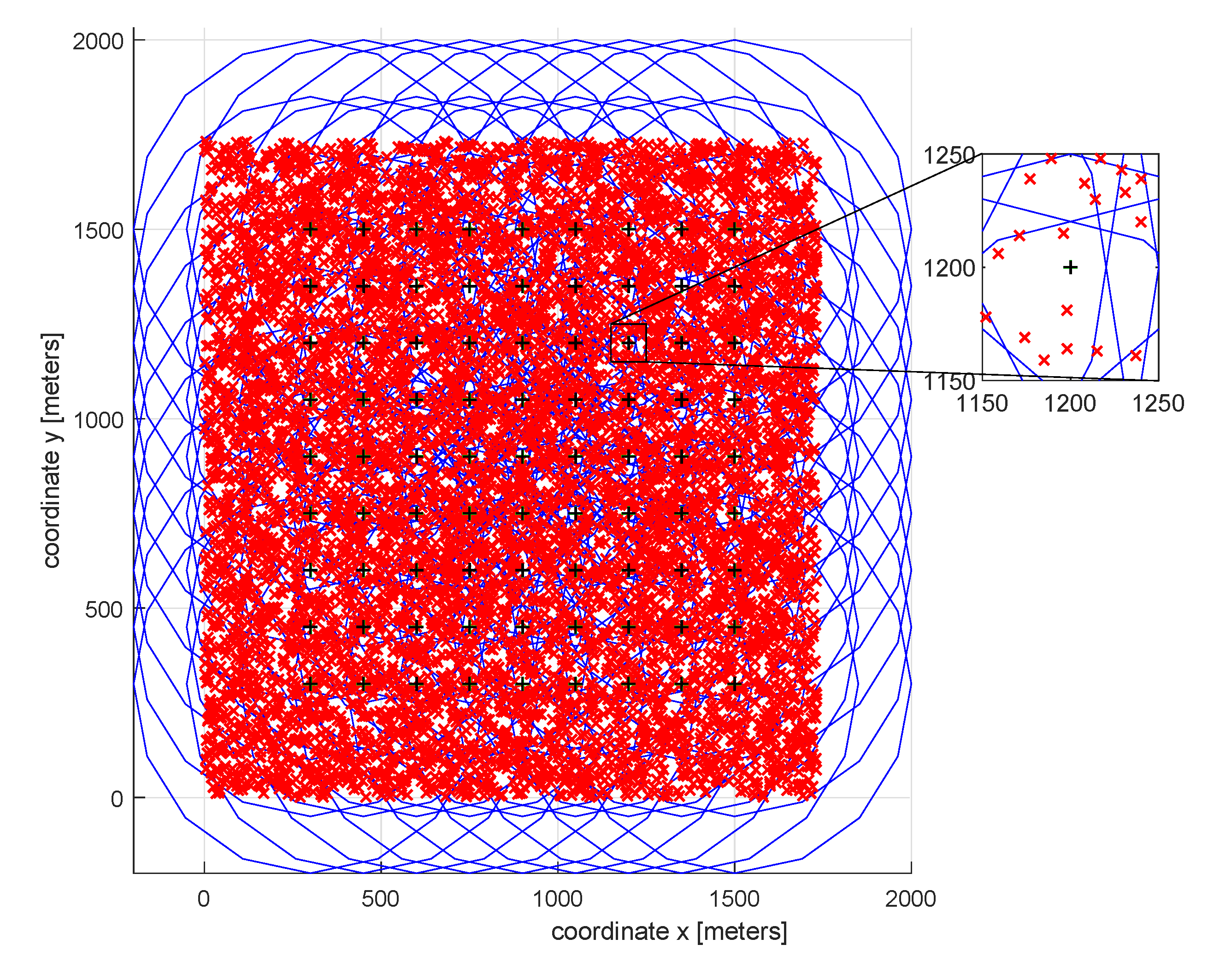
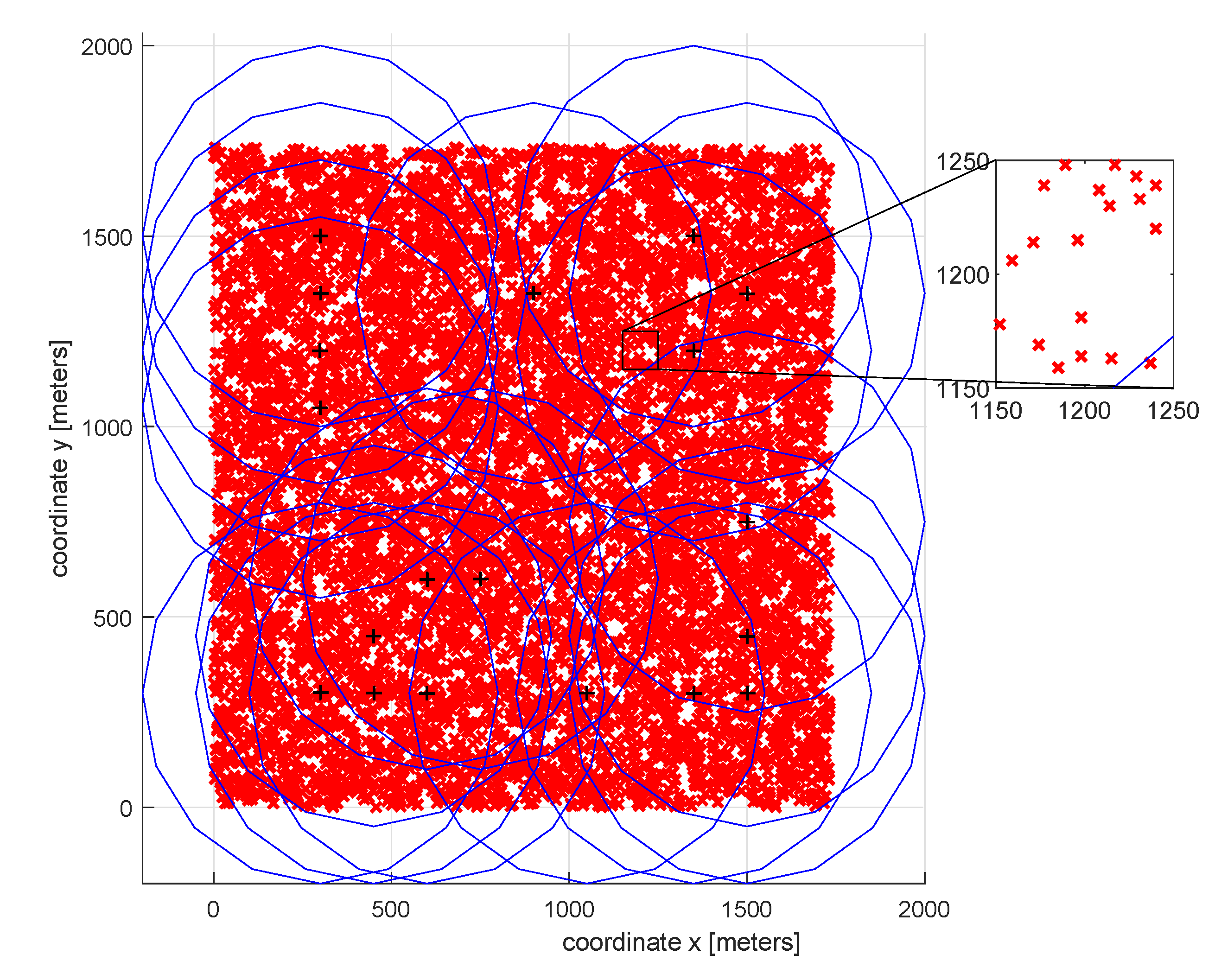

| Mathematical Terminology | Wireless Networks Terminology |
|---|---|
| Service centre | gNodeB node |
| Customer location | a location to cover |
| Capacity | throughput that is requested by sum of user requirements in a given location to cover |
| Existing service | gNodeB that already exists in the area to cover and should remain after the reconfiguration or deployment phase |
| Authors | Model | Description | Published |
|---|---|---|---|
| Berge [27] | SCP | The base covering model for all other models. Finding the minimal number of services to cover all the demands. | 1957 |
| Toregas [13] | Location Set Covering Problem (LSCP) | Extension of SCP considering services and demands locations. | 1970 |
| Church et al. [28] | Maximal Covering Location Problem (MLCP) | Describes the situation of a restricted number of services with the best coverage sought. | 1974 |
| Plane and Hendrick [29] | Existing Service System Location Set Covering Problem (ESS-LSCP) | Extension of LSCP addressing the need to consider the existing services. | 1977 |
| Schilling [30] | Location Set Covering Problem with Facility Types (LSCP-FT) | Extension of LSCP addressing the need of specific demand to be covered by specific services. | 1979 |
| Margules [31] | Site Quality Maximal Covering Location Problem (SQ-MCLP) | Takes into account the quality of the service provided for each demand. | 1986 |
| Current and Storbeck [32] | Capacitated Location Set Covering Problem (CLSCP) | The first article proposing capacities in LSCP. This model could not be used in network deployment since it does not force the entire demand at a particular node being assigned to the same facility. It assumes that the demand is split among facilities (see Equation (13)). | 1988 |
| Revelle and Hogan [33] | Maximal Availability Location Problem (MALP) | This model is characterized by an intention to maximize the availability provided by -reliable coverage | 1989 |
| Gerrard and Church [34] | Capacitated Location Set Covering Problem with Closest Assignment (CLSCP-CA) | Models considering services and capacities to satisfy the demands using the closest service. | 1996 |
| Berman and Krass [35] | Generalized Maximal Covering Location Problem (GMCLP) | Generalized variant of MLCP distinguishing the value of benefits received over a series of coverage ranges. | 2002 |
| Dembski and Marks [12] | CLSCP-EA | Models considering services and capacities to equally satisfy the demands. | 2009 |
| Hong and Kuby [36] | LSCP and MLCP with Threshold | This model considers a threshold meaning that each service needs some portion of demand to be viable for each type of service. | 2016 |
| Authors | Description | Published |
|---|---|---|
| Mattos, David Issa, et al. [46] | This paper proposes a gNodeB parameters optimization with regret minimization and a low number of iterations in the presence of uncertainties due to the stochastic response of KPI metrics | 2019 |
| Teague, Kory, Mohammad J. Abdel-Rahman and Allen B. MacKenzie [62] | Authors propose a two-stage stochastic optimization model to investigate the problem of gNodeB selection. They found that the genetic algorithms may be an adequate avenue for a solution. | 2019 |
| Tayal, Shikha and Garg, PK and Vijay, Sandip [63] | The paper provides a case study in Uttarakhand to develop a new model for placement of the optimal number of base stations. The paper compares different models and concludes them with their pros and cons. | 2019 |
| Afuzagani, Dzakyta and Suyanto, Suyanto [64] | The paper presents an evolutionary firefly algorithm and compares it to the standard firefly algorithm and uses it to deploy gNodeB stations. The authors conclude that enhanced algorithm can provide slightly better solutions in terms of the final coverage. | 2019 |
| Lingcheng and Hongtao [47] | This paper is mainly focused on the deployment of algorithms with the focus on the research of optimal machine learning (ML) model to deploy gNodeB nodes. It has found that multi-layer perceptron outperforms other ML algorithms. | 2020 |
| RSRP [dBm] | Signal Strength | Description |
|---|---|---|
| ≥−80 | Excellent | Strong signal with maximum data speeds |
| −80 to−90 | Good | Strong signal with good data speeds |
| −90 to−100 | Fair to poor | Reliable data speeds may be attained, but marginal data with drop-outs is possible. When this value gets close to −100, performance will drop drastically |
| ≤−100 | No signal | Disconnection |
| Use-Case | Combined gNodeB Capacity (DL + UL) [Gbit/s] | Single Cell Radius [km] | Demanded User Throughput (DL + UL) [Mbit/s] | Number of Connections/km [106] |
|---|---|---|---|---|
| urban | 30 | 0.5 | 43.9 | 2500 |
| suburban | 30 | 1 | 43.9 | 400 |
| rural | 30 | 8 | 43.9 | 100 |
| Scenarios | Theoretical Number of Candidate Locations to Deploy gNodeB | Number of Users | Total Coverage Area [km] | Resulting Number of gNodeB Nodes to Be Deployed |
|---|---|---|---|---|
| urban | 81 | 7500 | 3 | 19 |
| suburban | 421 | 7500 | 18.75 | 22 |
| rural | 484 | 7500 | 75 | 18 |
| Deployment Scenario | gNodeB Capacity [Gbit/s] | Single Cell Radius [km] | Demanded User Throughput (DL+UL) [Mbit/s] | N. of Existing gNodeB Nodes | N. of Users | Area [km] |
|---|---|---|---|---|---|---|
| Prague 11 (suburban) | 30 | 1 | 43.9 | 75 | 68,839 | 9.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seda, P.; Seda, M.; Hosek, J. On Mathematical Modelling of Automated Coverage Optimization in Wireless 5G and beyond Deployments. Appl. Sci. 2020, 10, 8853. https://doi.org/10.3390/app10248853
Seda P, Seda M, Hosek J. On Mathematical Modelling of Automated Coverage Optimization in Wireless 5G and beyond Deployments. Applied Sciences. 2020; 10(24):8853. https://doi.org/10.3390/app10248853
Chicago/Turabian StyleSeda, Pavel, Milos Seda, and Jiri Hosek. 2020. "On Mathematical Modelling of Automated Coverage Optimization in Wireless 5G and beyond Deployments" Applied Sciences 10, no. 24: 8853. https://doi.org/10.3390/app10248853
APA StyleSeda, P., Seda, M., & Hosek, J. (2020). On Mathematical Modelling of Automated Coverage Optimization in Wireless 5G and beyond Deployments. Applied Sciences, 10(24), 8853. https://doi.org/10.3390/app10248853






