A Parametric Study of Wind Pressure Distribution on Façades Using Computational Fluid Dynamics
Abstract
Featured Application
Abstract
1. Introduction
2. Description of the CFD Model
2.1. Geometry
2.2. Computational Domain
2.3. Boundary Conditions
2.4. Turbulence Model
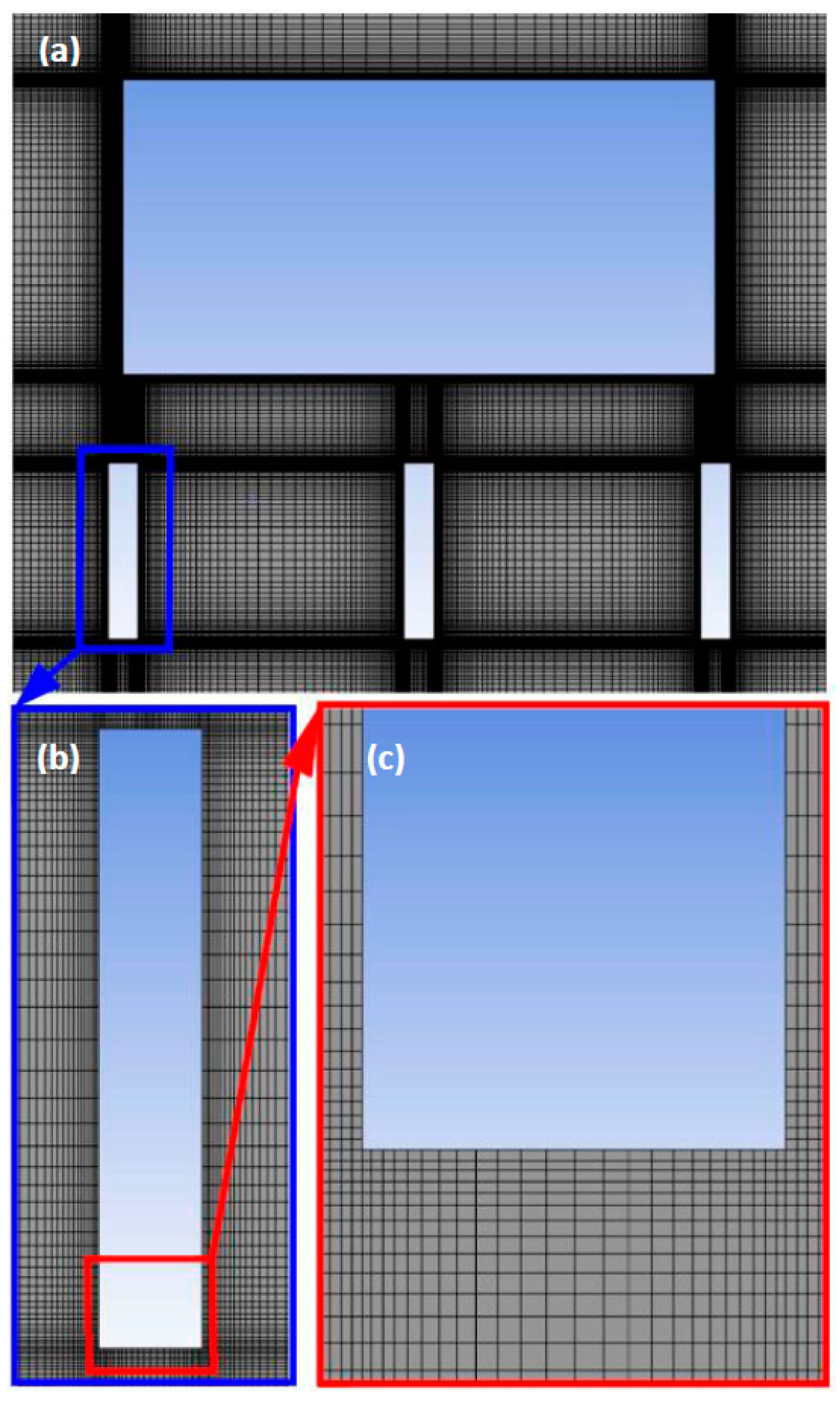
2.5. Mesh
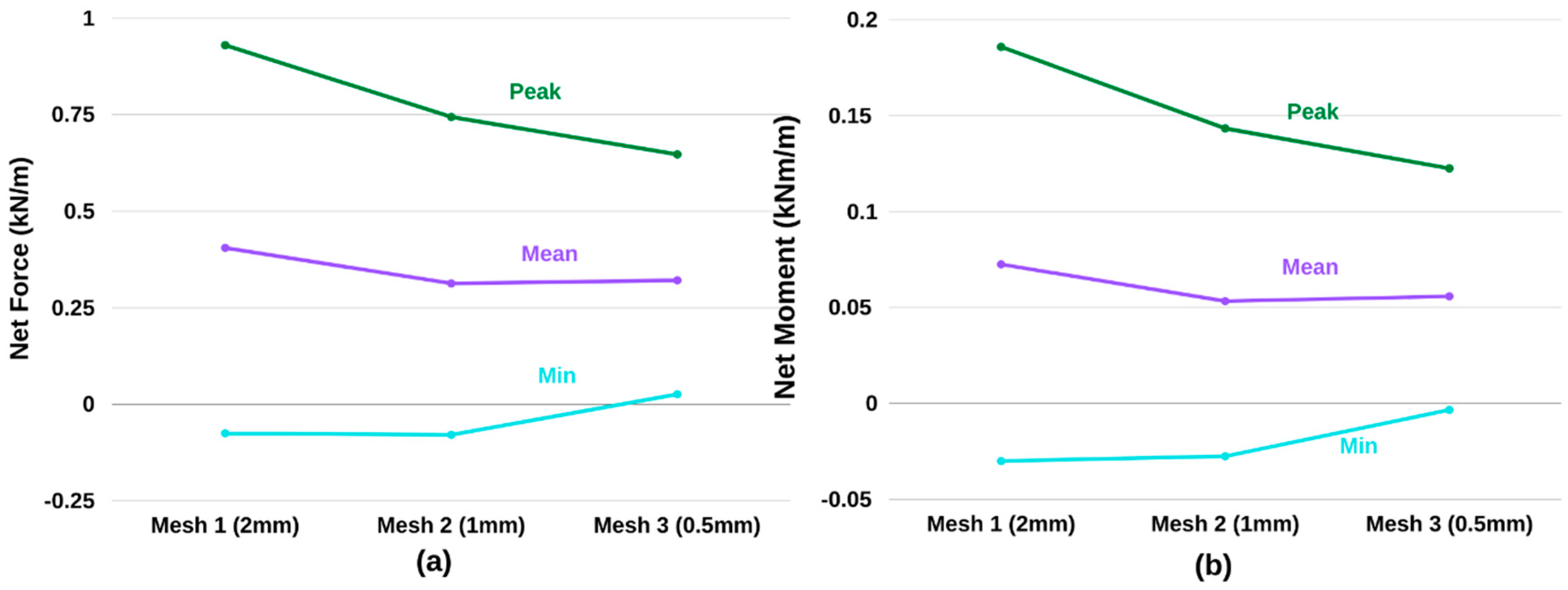
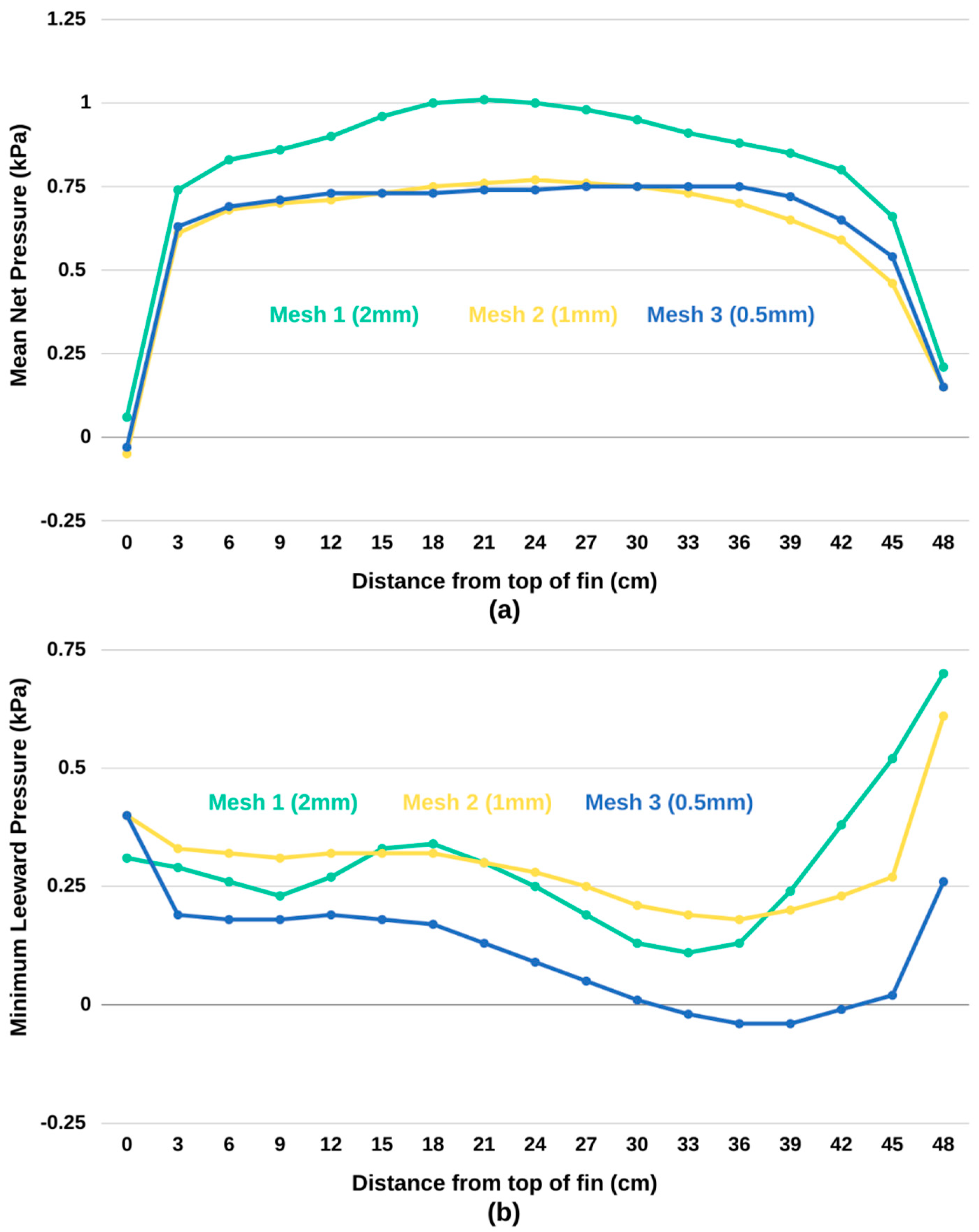
3. Model Convergence
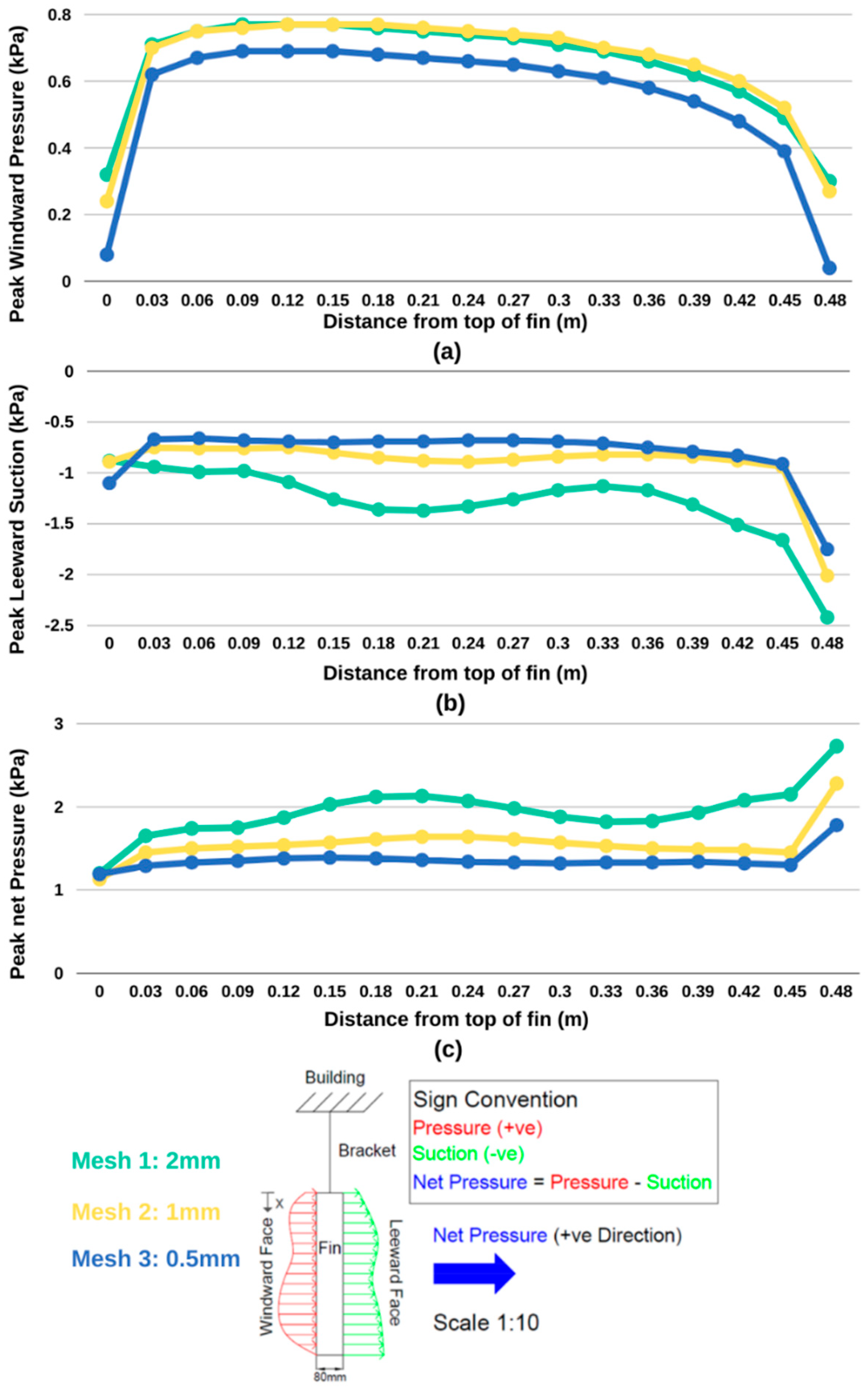
3.1. Mesh Sensitivuty Study
3.2. Convergence of Peak Pressures
4. Results
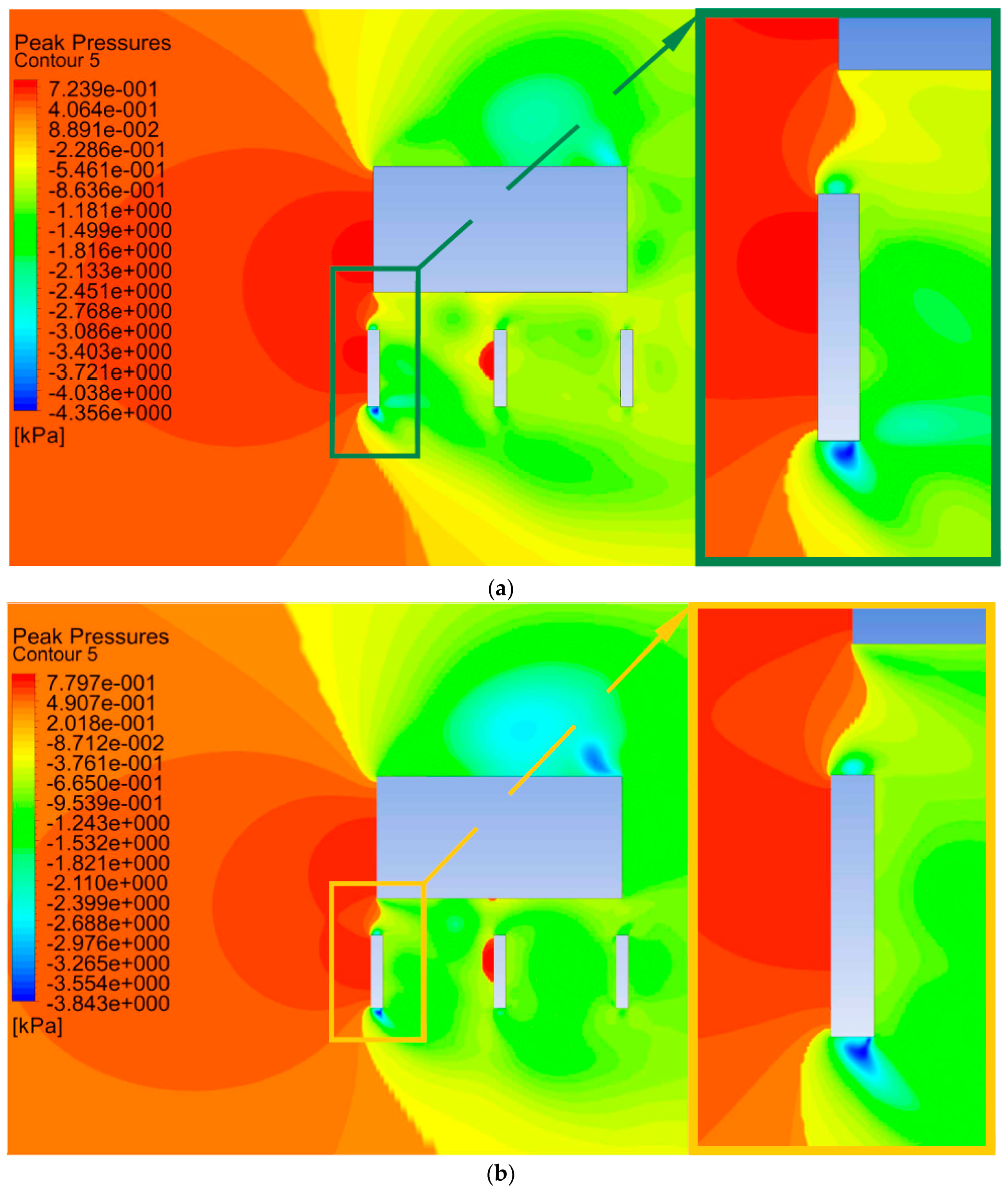
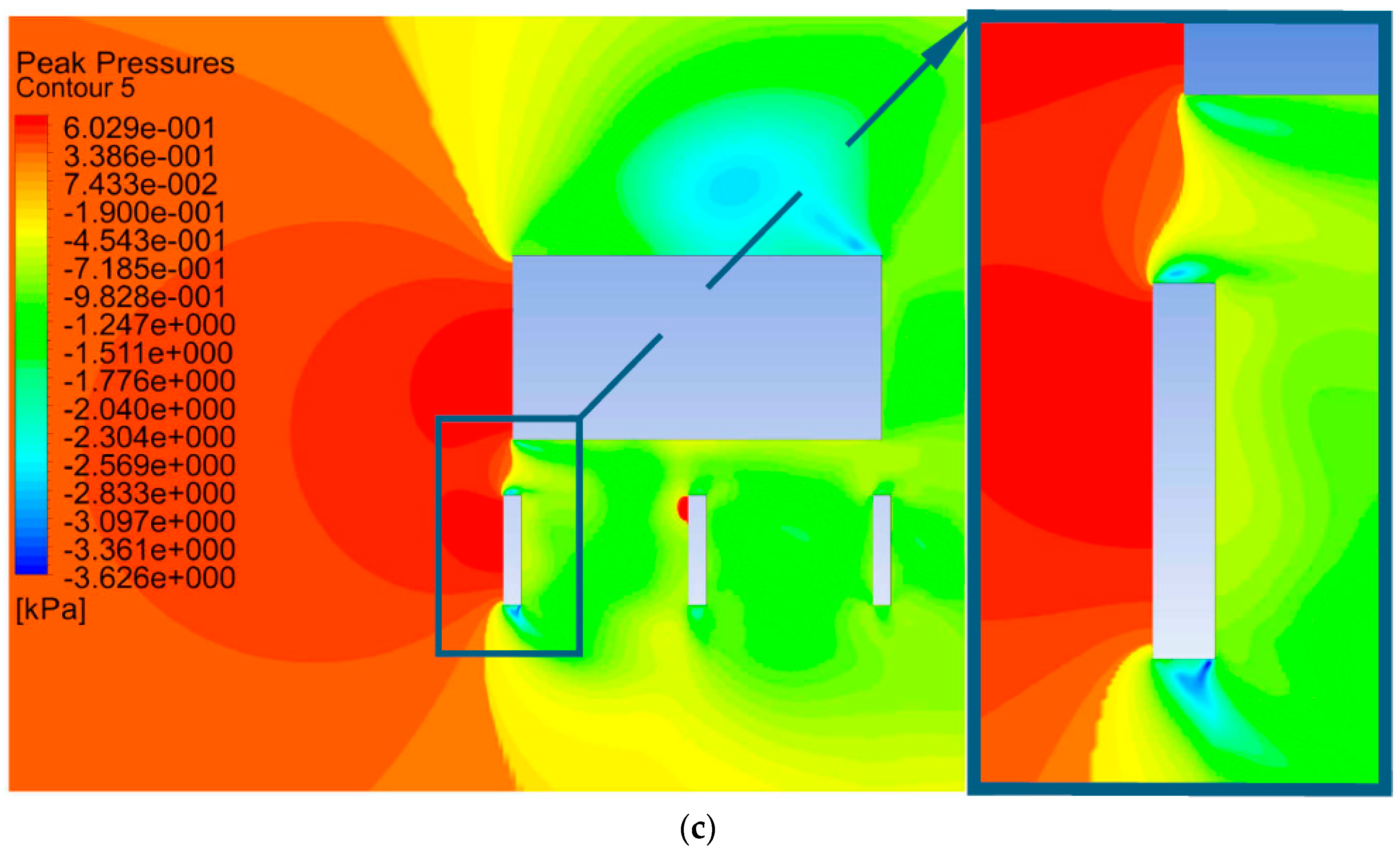
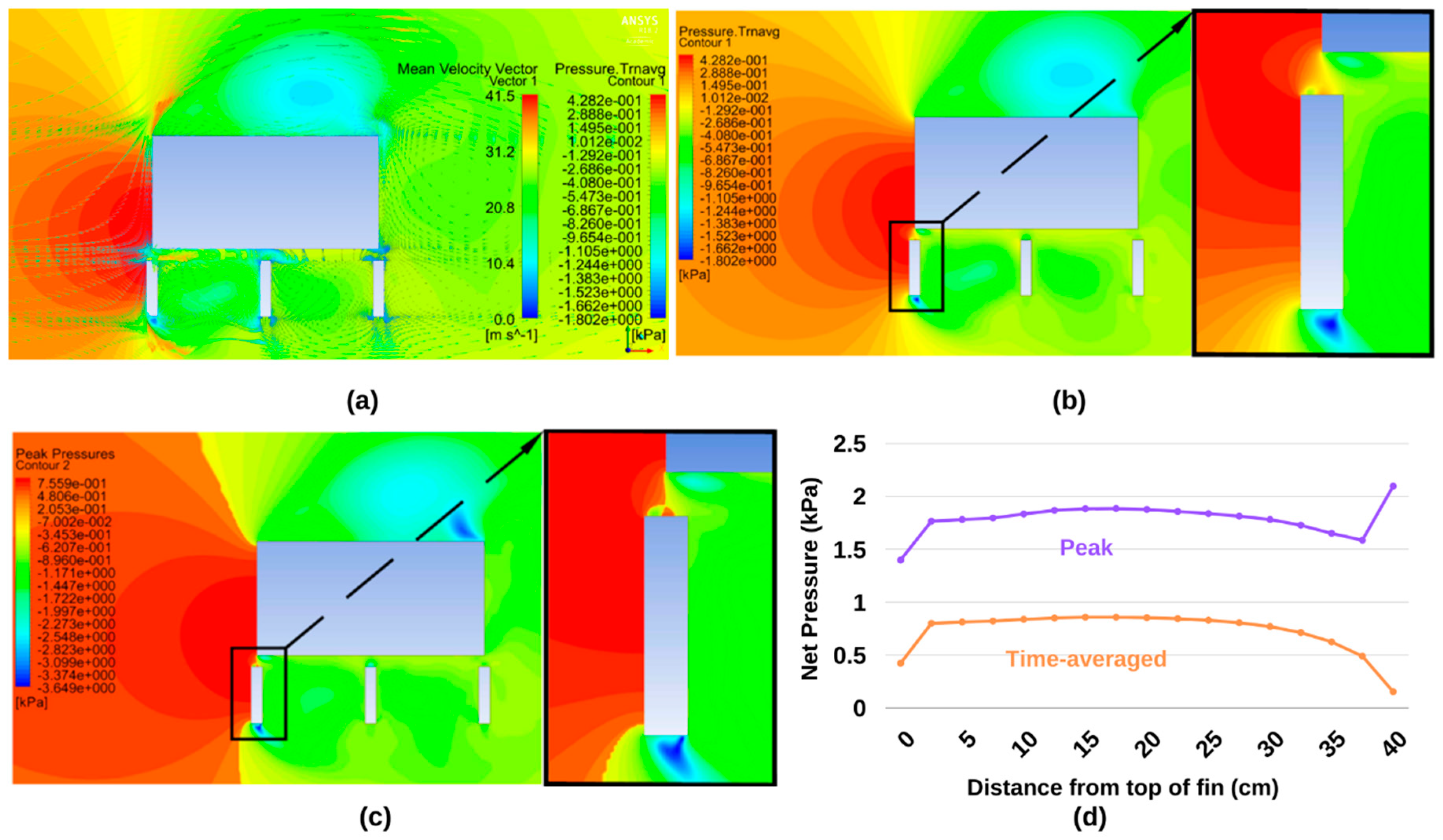
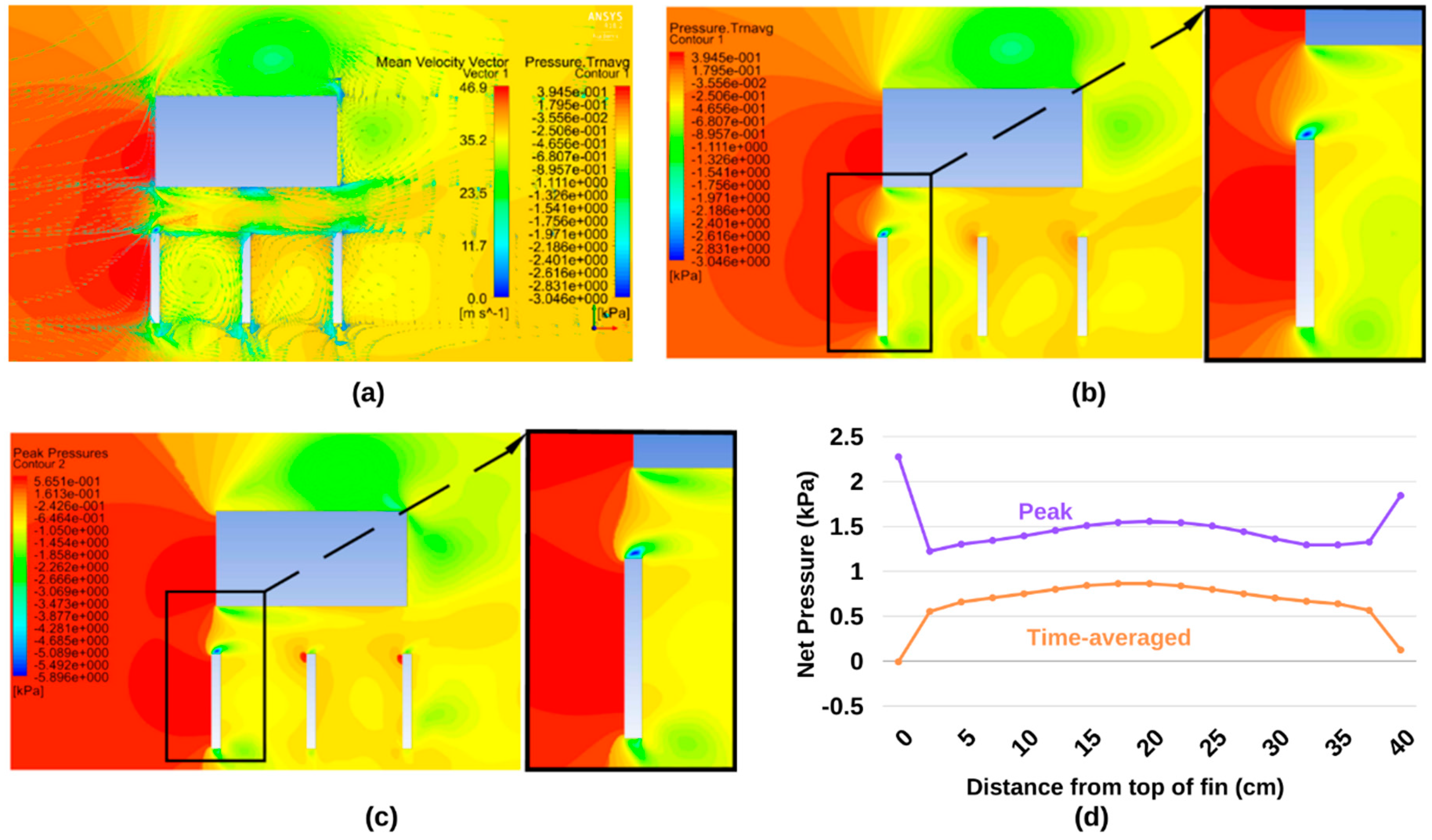
4.1. Results for Geometry No. 1 (g = 80 mm d = 400 mm)
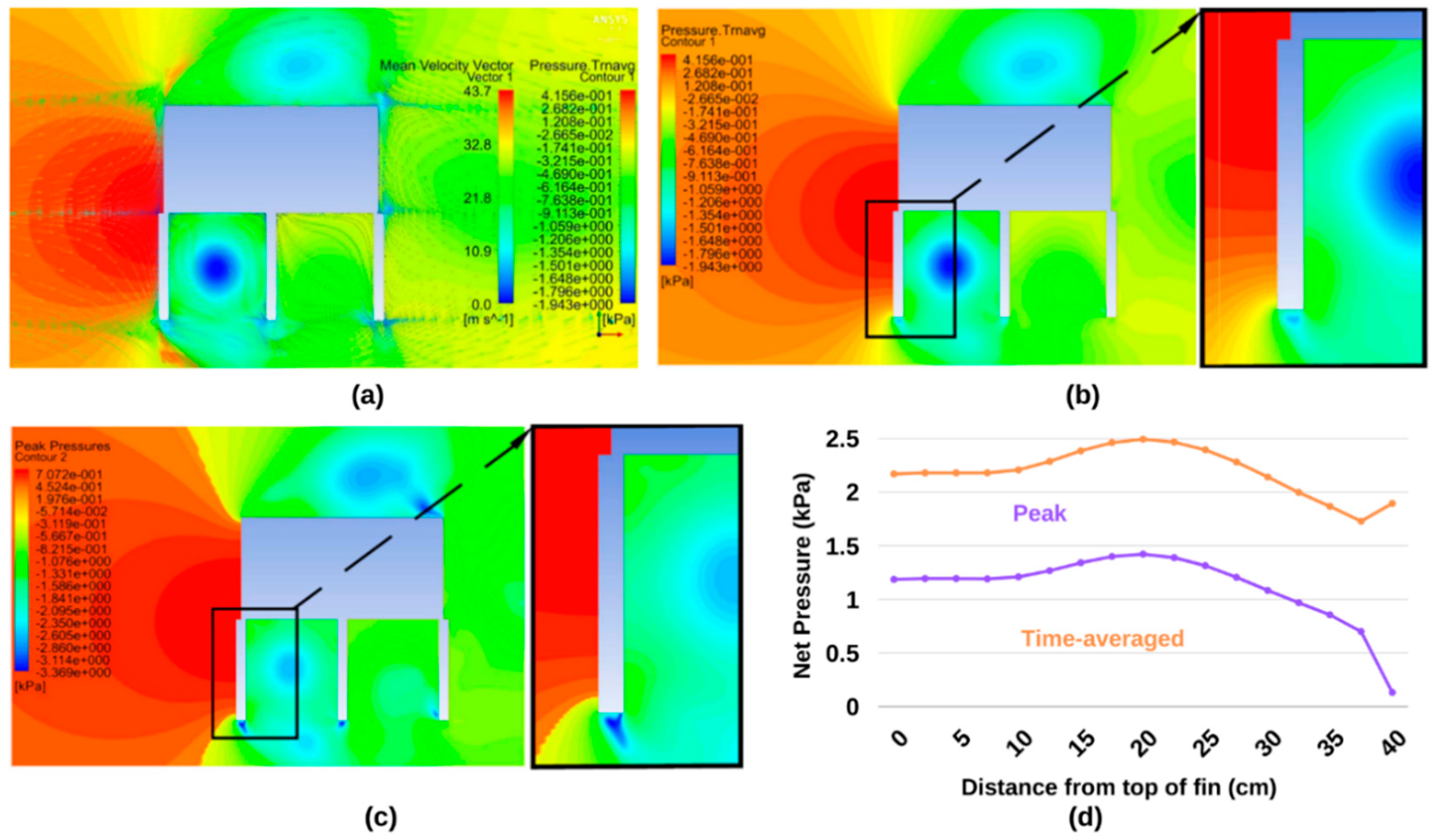
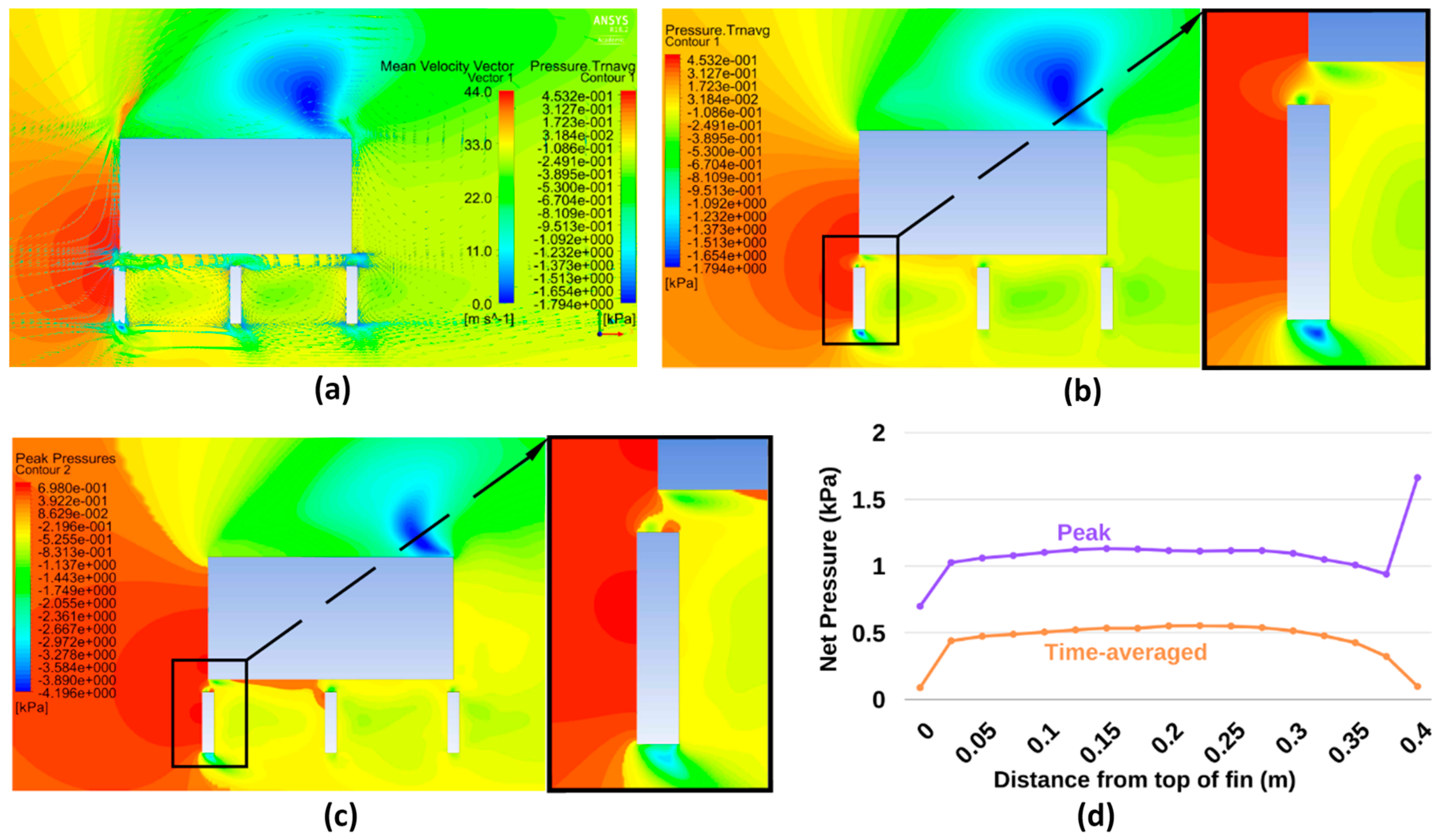
4.2. Results for Geometry No. 5 (g = 160 mm d = 560 mm)
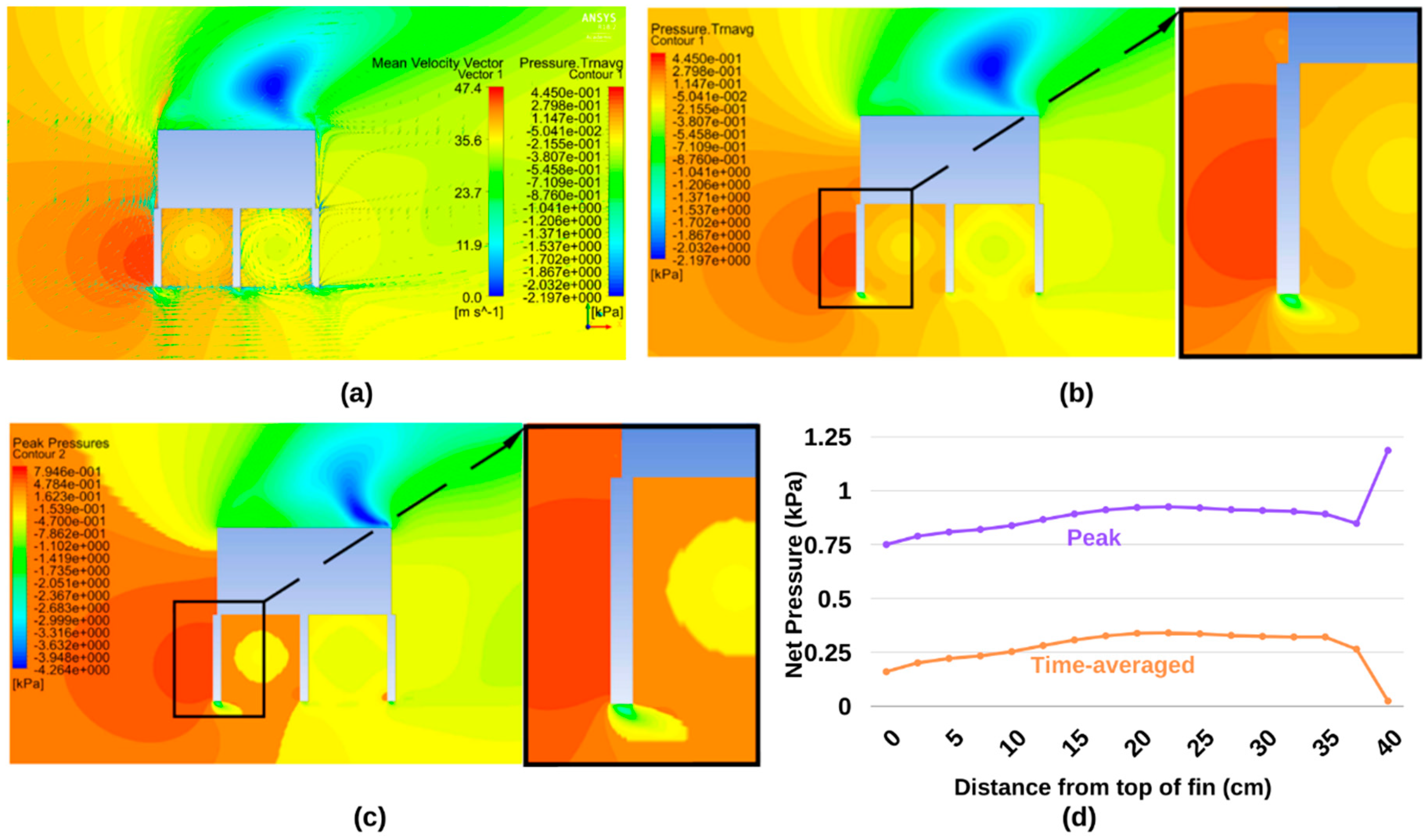
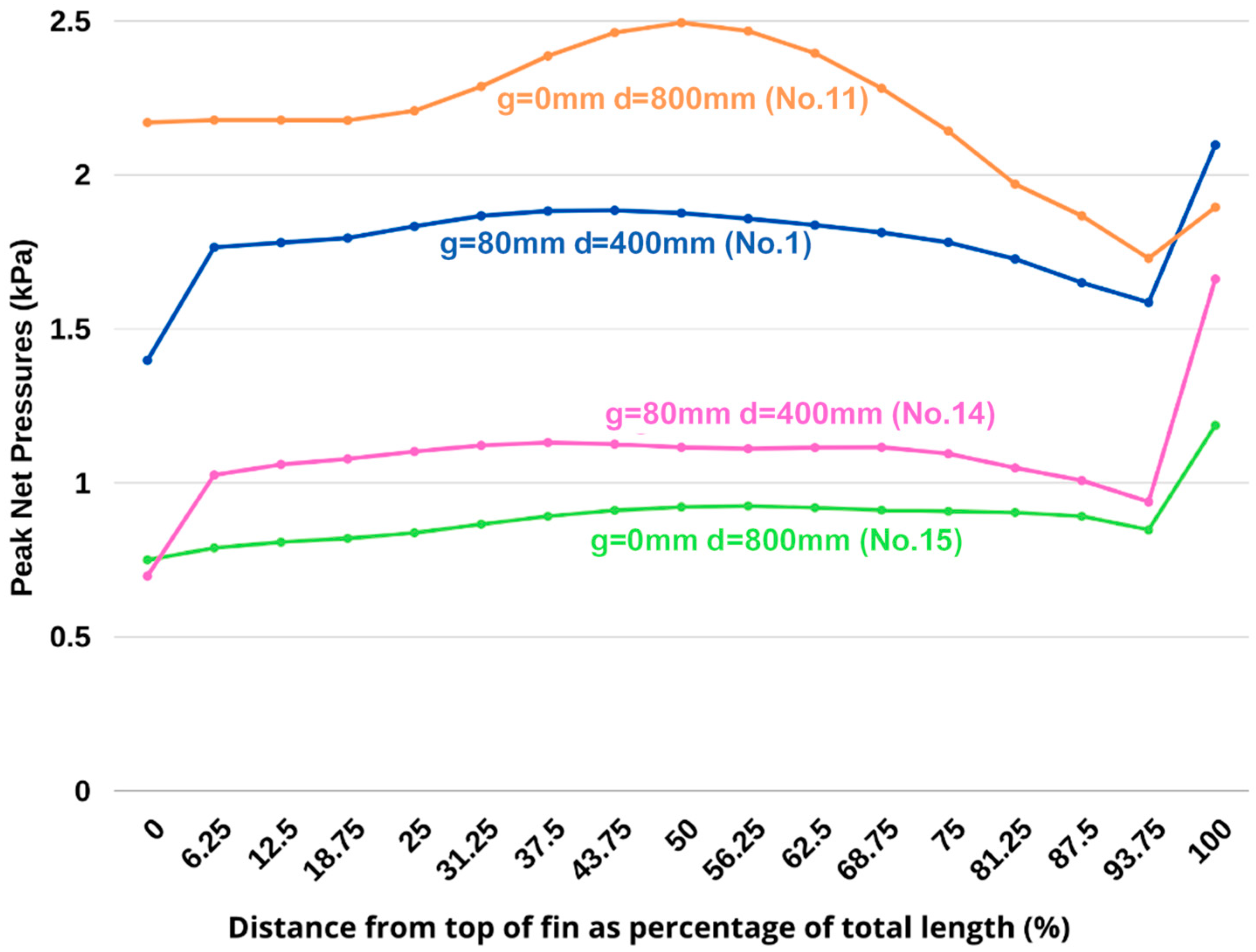
4.3. Results for Geometry No. 11 (g = 0 mm d = 800 mm)
4.4. Results for Geometry No. 13 (g = 400 mm d = 800 mm)
4.5. Results for Geometry No. 14 (g = 80 mm d = 400 mm)
4.6. Results for Geometry No. 15 (g = 0 mm d = 800 mm)
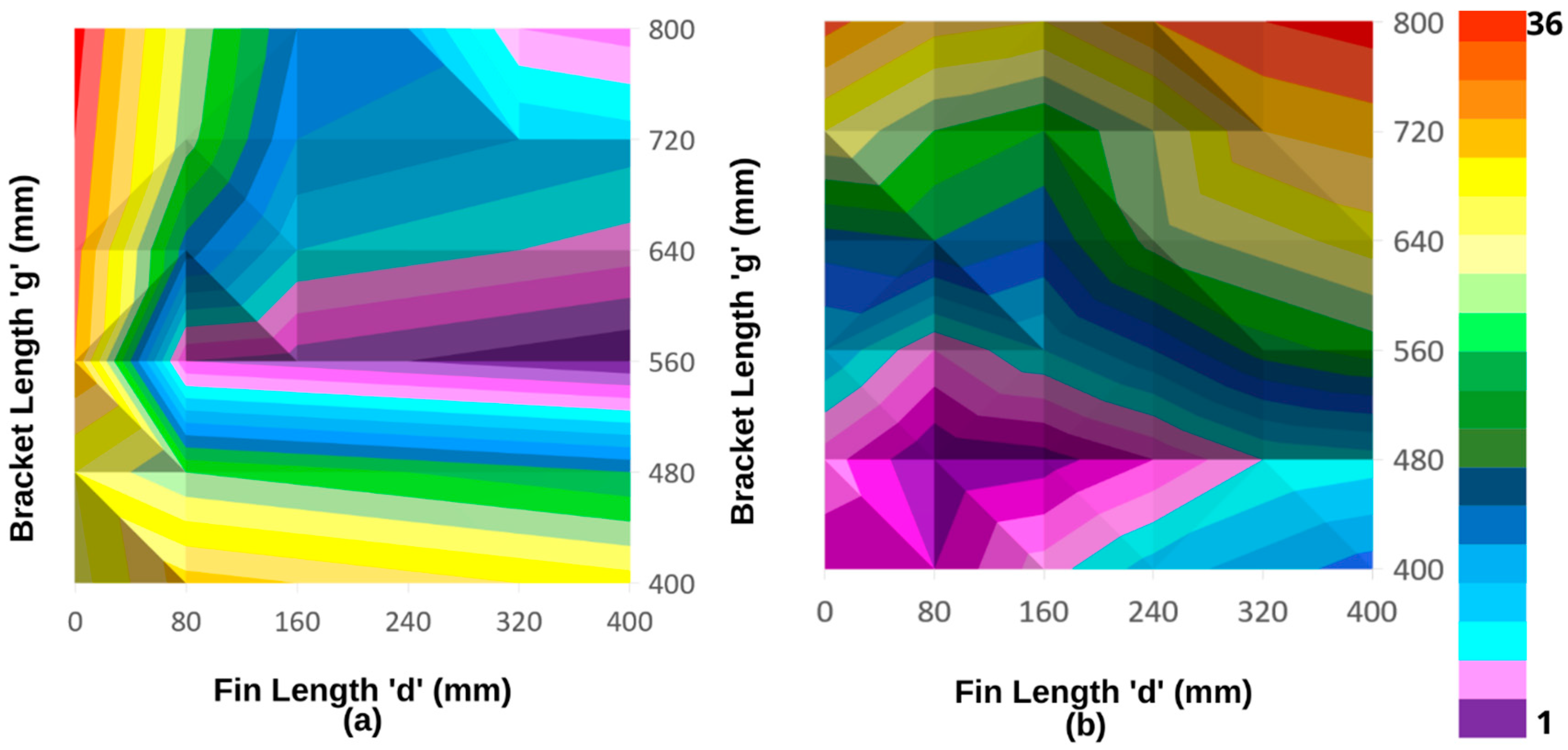
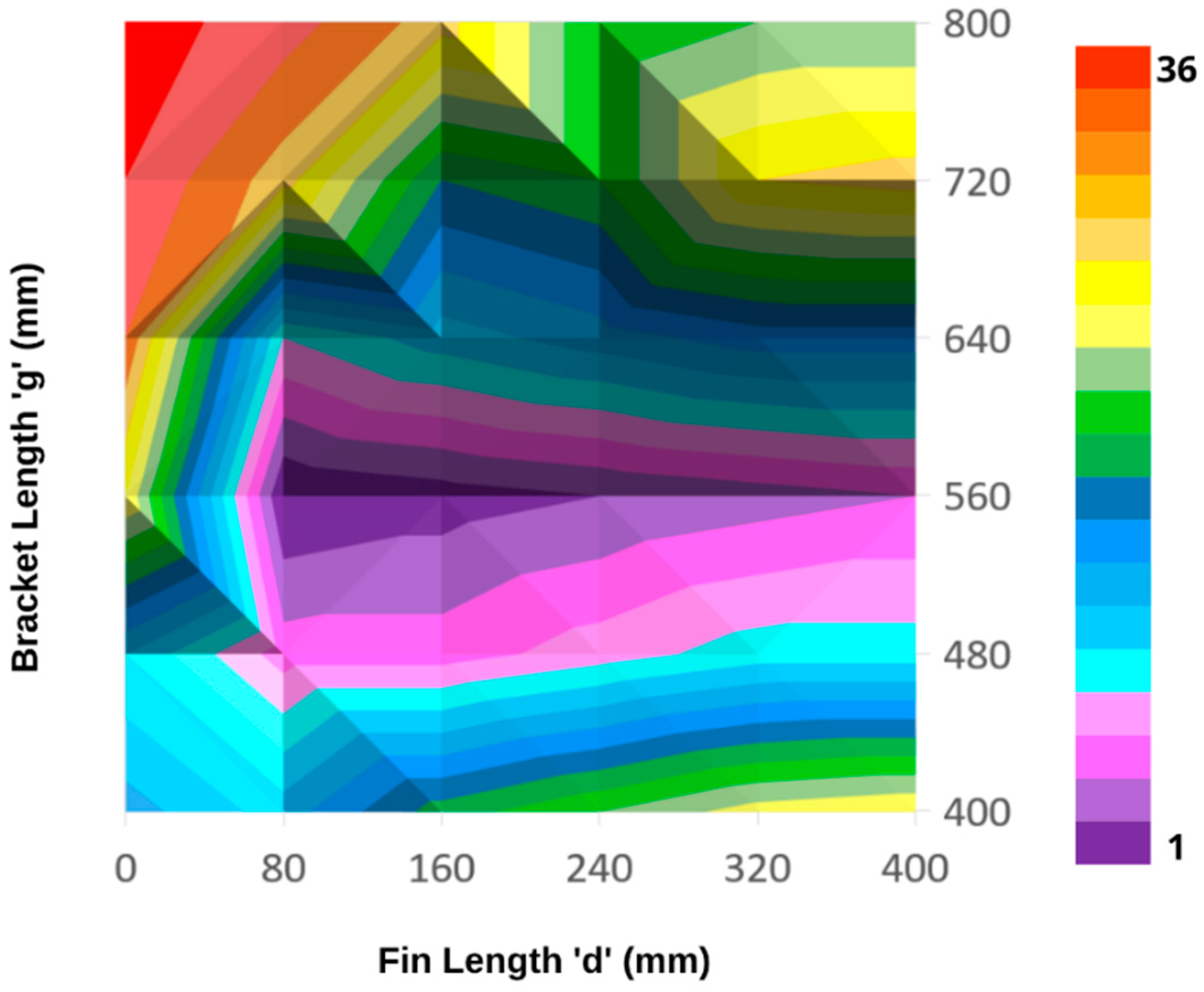
5. Discussion and Interpretation
5.1. Sheltered Case
5.2. Unsheltered Case
6. Conclusions
- The Venturi Effect tends to reduce the magnitude of pressures at the end of the fin nearest the building. The narrower the gap for airflow, the smaller the net pressure at this location.
- The more the flow is constricted towards the building, the greater the suction on the leeward side of the critical fin.
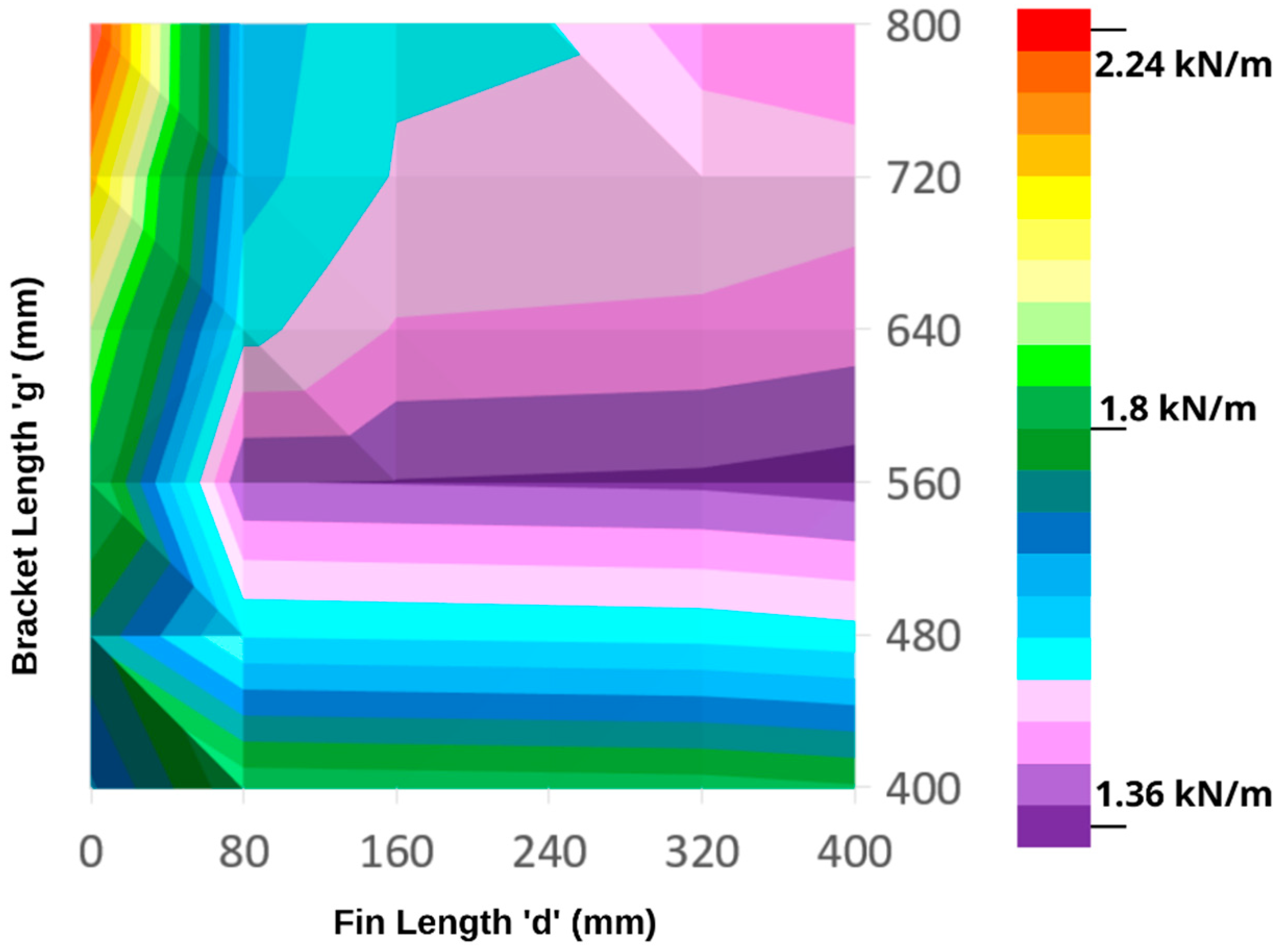
- Increasing the bracket length for a given fin length, achieves efficient distribution of load.
- Wind load is spread more evenly in cases where fin length is aerodynamically more efficient by utilizing the benefits of the Venturi Effect without the relative impact on continuity of the flow that occurs for less efficient fins.
- Reducing both fin length and bracket length tends to reduce moments.
- With these effects taken into account, the most efficient fin, as a combination of forces and moments has a length of 560 mm due to its ability to distribute stress through its aerodynamic efficiency, with a bracket of 80 mm recommended to minimize moments.
- The least efficient design is where the fins are directly attached to the building and with the longest fin length (800 mm).
Author Contributions
Funding
Conflicts of Interest
References
- Costola, D.; Blocken, B.; Hensen, J.L.M. Overview of pressure coefficient data in building energy simulation and airflow network programs. Build. Environ. 2009, 44, 2027–2036. [Google Scholar] [CrossRef]
- Aylanc, N.; Kasperski, M. Design wind loads for cladding elements, in 5th European and African Conference on Wind Engineering. In Proceedings of the 5th European and African Conference on Wind Engineering, Florence, Italy, 19–23 July 2009; Firenze University Press: Florence, Italy, 2009; pp. 379–391. [Google Scholar]
- Blocken, B. 50 years of computational wind engineering: Past, present and future. J. Wind Eng. Ind. Aerodyn. 2014, 129, 69–102. [Google Scholar] [CrossRef]
- Montazeri, H.; Blocken, B. CFD simulation of wind-induced pressure coefficients on buildings with and without balconies: Validation and sensitivity analysis. Build. Environ. 2013, 60, 137–149. [Google Scholar] [CrossRef]
- Casey, M.; Wintergerste, T. Best Practice Guidelines, ERCOFTAC Special Interest Group on “Quality and Trust in Industrial CFD”; European Research Community on Flow; Turbulence and Combustion: London, UK, 2000. [Google Scholar]
- Franke, J.; Baklanov, A. Best Practice Guideline for the CFD Simulation of Flows in the Urban Environment: COST Action 732 Quality Assurance and Improvement of Microscale Meteorological Models; Meteorological Inst: Hamburg, Germany, 2007. [Google Scholar]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Blocken, B.B.; Carmeliet, J.J. Pedestrian Wind Environment around Buildings: Literature Review and Practical Examples. J. Therm. Envel. Build. Sci. 2004, 28, 107–159. [Google Scholar] [CrossRef]
- Delaunay, D.; Lakehal, D.; Pierrat, D. Numerical approach for wind loads prediction on buildings and structures. J. Wind Eng. Ind. Aerodyn. 1995, 57, 307–321. [Google Scholar] [CrossRef]
- Selvam, R.P. Computation of pressures on Texas Tech University building using large eddy simulation. J. Wind Eng. Ind. Aerodyn. 1997, 67, 647–657. [Google Scholar] [CrossRef]
- Cochran, L.; Derickson, R. A physical modeler’s view of computational wind engineering. J. Wind Eng. Ind. Aerodyn. 2011, 99, 139–153. [Google Scholar] [CrossRef]
- Haque, N.; Katsuchi, H.; Yamada, H.; Nishio, M. Strategy to develop efficient grid system for flow analysis around two-dimensional bluff bodies. KSCE J. Civ. Eng. 2015, 20, 1913–1924. [Google Scholar] [CrossRef]
- Liu, J.; Niu, J.; Du, Y.; Mak, C. Large Eddy Simulation on the Pedestrian Level Wind around a Building Community: Evaluation of Influencing Factors. In Proceedings of the 4th International Conference on Building Energy, Environment, Melbourne, Australia, 5–9 February 2018; pp. 390–395. [Google Scholar]
- Li, W.-W.; Meroney, R.N. Gas dispersion near a cubical model building. Part I. Mean concentration measurements. J. Wind Eng. Ind. Aerodyn. 1983, 12, 15–33. [Google Scholar] [CrossRef]
- Gousseau, P.; Blocken, B.B.; Van Heijst, G.J.F. Quality assessment of Large-Eddy Simulation of wind flow around a high-rise building: Validation and solution verification. Comput. Fluids 2013, 79, 120–133. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Murakami, S.; Sawaki, S. Comparison of various revised k-ε models and LES applied to flow around a high-rise building model with 1:1:2 shape placed within the surface boundary layer. J. Wind Eng. Ind. Aerodyn. 2008, 96, 389–411. [Google Scholar] [CrossRef]
- O’Rourke, M. Fundamental Concepts, Fluid Properties, Inviscid Flow, Internal Flow [Lecture to BE and BSc Engineering], (MEEN20010: Mechanis of Fluids I); University College Dublin: Belfield, Dublin, 2011. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Argyropoulos, C.D.; Markatos, N.C. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Piomelli, U.; Balaras, E. Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Tamura, T.; Nozawa, K.; Kondo, K. AIJ guide for numerical prediction of wind loads on buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1974–1984. [Google Scholar] [CrossRef]
- Syrakos, A.; Varchanis, S.; Dimakopoulos, Y.; Goulas, A.; Fraggedakis, D. A critical analysis of some popular methods for the discretisation of the gradient operator in finite volume methods. Phys. Fluids 2017, 29, 127103. [Google Scholar] [CrossRef]
- Cardiff, P. Lecture 5–7: Finite Volume Method and Fluid Dynamics with Ansys Fluent [Lecture to Mechanical Engineering Stage 4], (MEEN40150: Computational Continuum Mechanics II); University College Dublin: Belfield, Dublin, Ireland, 2016. [Google Scholar]
- Fluent, A. Ansys Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2011; Volume 15317, pp. 724–746. [Google Scholar]






| Y+ (Max) | Y+ (Mean) | Y+ (Variance) | Co (Max) | Co (Mean) | Co (Variance) | |
|---|---|---|---|---|---|---|
| Mesh 1 (2 mm) | 290.1 | 212.3 | 830.6 | 38.1 | 27.7 | 12.4 |
| Mesh 2 (1 mm) | 157.2 | 112.0 | 276.6 | 38.4 | 19.2 | 12.8 |
| Mesh 3 (0.5 mm) | 78.8 | 58.3 | 63.1 | 33.4 | 24.2 | 8.1 |
| Cells | Ratio | Refinement (r) | |||
|---|---|---|---|---|---|
| Mesh 1 (2 mm) | 78,962 | Mesh1–2 | 1.414 | Mesh1–2 | 1.189 |
| Mesh 2 (1 mm) | 111,688 | Mesh2–3 | 1.376 | Mesh2–3 | 1.173 |
| Mesh 3 (0.5 mm) | 153,652 | -- | -- | -- | -- |
| Peak (m) | Mean (m) | Min (m) | |
|---|---|---|---|
| Mesh 1 (2 mm) | 0.250 | 0.239 | 0.347 |
| Mesh 2 (1 mm) | 0.244 | 0.237 | 0.286 |
| Mesh 3 (0.5 mm) | 0.242 | 0.239 | 0.225 |
| Net Forces | Lever Arm Lengths | Net Moments | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Peak | Mean | Min | Peak | Mean | Min | Peak | Mean | Min | |
| e12 | 19.9% | 22.8% | 5.1% | 2.4% | 0.9% | 17.5% | 21.8% | 23.4% | 13.3% |
| e23 | 13.1% | 2.7% | 133.5% | 0.9% | 1.2% | 21.4% | 13.9% | 3.9% | 123.6% |
| Model No | g (mm) | d (mm) | D (m) | 5D (m) | 10D (m) | 6D (m) | Domain Length (m) | Domain Height (m) |
|---|---|---|---|---|---|---|---|---|
| 1/14 | 80 | 400 | 1.28 | 6.4 | 12.8 | 7.68 | 20.88 | 16.64 |
| 2 | 320 | 400 | 1.52 | 7.6 | 15.2 | 9.12 | 24.48 | 19.76 |
| 3 | 0 | 480 | 1.28 | 6.4 | 12.8 | 7.68 | 20.88 | 16.64 |
| 4 | 240 | 480 | 1.52 | 7.6 | 15.2 | 9.12 | 24.48 | 19.76 |
| 5 | 160 | 560 | 1.52 | 7.6 | 15.2 | 9.12 | 24.48 | 19.76 |
| 6 | 400 | 560 | 1.76 | 8.8 | 17.6 | 10.56 | 28.08 | 22.88 |
| 7 | 0 | 640 | 1.44 | 7.2 | 14.4 | 8.64 | 23.28 | 18.72 |
| 8 | 240 | 640 | 1.68 | 8.4 | 16.8 | 10.08 | 26.88 | 21.84 |
| 9 | 80 | 720 | 1.60 | 8.0 | 16.0 | 9.6 | 25.68 | 20.8 |
| 10 | 320 | 720 | 1.84 | 9.2 | 18.4 | 11.04 | 29.28 | 23.92 |
| 11/15 | 0 | 800 | 1.60 | 8.0 | 16.0 | 9.6 | 25.68 | 20.8 |
| 12 | 160 | 800 | 1.76 | 8.8 | 17.6 | 10.56 | 28.08 | 22.88 |
| 13 | 400 | 800 | 2.00 | 10.0 | 20.0 | 12.0 | 31.68 | 26.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McGuill, C.; Keenahan, J. A Parametric Study of Wind Pressure Distribution on Façades Using Computational Fluid Dynamics. Appl. Sci. 2020, 10, 8627. https://doi.org/10.3390/app10238627
McGuill C, Keenahan J. A Parametric Study of Wind Pressure Distribution on Façades Using Computational Fluid Dynamics. Applied Sciences. 2020; 10(23):8627. https://doi.org/10.3390/app10238627
Chicago/Turabian StyleMcGuill, Christopher, and Jennifer Keenahan. 2020. "A Parametric Study of Wind Pressure Distribution on Façades Using Computational Fluid Dynamics" Applied Sciences 10, no. 23: 8627. https://doi.org/10.3390/app10238627
APA StyleMcGuill, C., & Keenahan, J. (2020). A Parametric Study of Wind Pressure Distribution on Façades Using Computational Fluid Dynamics. Applied Sciences, 10(23), 8627. https://doi.org/10.3390/app10238627






