1. Introduction
COVID-19 was declared a pandemic public health menace on 11 March 2020, by the World Health Organization (WHO) [
1]. This supposed the assumption of this severe acute respiratory syndrome (SARS-CoV-2) as a challenge for humanity to deal with a virus with the potential to condition our normal coexistence. In this pandemic, more than 190 countries have been affected by this outbreak and more than 1.23 M deaths have been cumulated globally according to the John Hopkins University as of 5 November 2020 [
2].
People with COVID-19 commonly show fever, cough, musculoskeletal symptoms, gastrointestinal symptoms, dyspnea or anosmia/dysgeusia even causing, in the most severe infections, death [
3,
4,
5]. These symptoms can even persist months after overcoming the infection and present novel evidence such as hair loss or cutaneous spots [
6]. These symptomatic patients have been treated in hospitals or isolated at home with their close contacts in order to control the propagation of COVID-19 [
7]. However, the challenge arises in the asymptomatic coronavirus patients not diagnosed, which propagate the virus without restricting their mobility [
8]. Even the symptomatic patients have an initial asymptomatic phase since alveolar macrophages, which are likely the first immune cells to encounter SARS-CoV-2 during the infection, are incapable of sensing the virus in the first stages [
9].
As a consequence, countries around the world have opted for severe lockdowns, frontier restrictions or contact tracing for controlling the virus propagation [
10] but causing severe impacts on the economy [
11] or other different health problems such as mental health or sleep disturbances [
12,
13].
In this context, education has been severely affected by the effects of the lockdowns that have forced new educational models in which online learning has taken special relevance [
14]. These efforts have partially mitigated the school closure and home confinement. However, especially for young children, traditional evidence of studies performed during school holidays have shown that children during these periods are physically less active, modify their sleep patterns, increment their screen time or follow less favorable diets [
15]. These effects have been even more pronounced during this outbreak due to the impossibility of the children of socializing with their classmates or playing outside their homes [
16].
Therefore, the reopening of schools has been a priority for many governments worldwide [
17]. Furthermore, schools are called to remain open during the second national lockdowns in some countries such as France, the United Kingdom, Germany and Italy [
18]. However, there are some studies that argue that a strict control on precautionary measures must be done in order to control possible COVID-19 outbreaks at school [
19]. Therefore, several restrictions and rules have been imposed for preserving the safe return to school such as the imposition of social distancing, wearing facemasks, reducing the students in the classrooms or hydroalcoholic gels for hand cleaning in every classroom.
In Spain, schools reopened in September facing all these measures described and fixing a social distancing of 1.5 m for reducing the exposition of the children to the virus in the school centers. This led to reorganizing the student desks for guaranteeing the social distancing inside the classrooms.
However, this is a complex problem to be addressed, which forces the reduction of the number of students in traditional classrooms. Many schools tried to find the most appropriate distribution of the tables for fulfilling the government social distancing requirements but they found problems in particularly irregular classrooms where regular patterns in the table disposition (i.e., rectangular or zig-zag grids) do not reach the best achievable results. Even, the beneficial effect of the social distancing for reducing the contagion probability in the COVID-19 pandemic [
20] recommends the finding of the table organization that maximizes the distance among the student desks even in classrooms in which the attainment of a valid table disposition can be more easily found.
However, the finding of the optimal table disposition is a combinatorial problem, which is similar to the technological Node Location Problem (NLP) [
21], which has been assigned as NP-Hard [
22,
23]. Therefore, a heuristic solution to this problem is recommended. Simulated annealing [
24], the firefly algorithm [
25] or the elephant herding optimization [
26] have been traditionally used for the NLP even though Genetic Algorithms (GA) [
27,
28,
29] and memetic algorithms [
30] are the most recommended for this problem for their trade-off among diversification and intensification of the space of solutions, which is essential for finding optimal results.
As a consequence, in this paper, we propose for the first time, in the authors’ best knowledge a GA optimization for the Table Location Problem (TLP) for finding optimal table dispositions at school that maximizes the distance among the student desks for increasing the social distancing in the classrooms thus reducing the children exposure to COVID-19 in their daily lessons.
The remainder of the paper is organized as follows: we analyze the TLP and its similarities to the NLP together with a complexity analysis in
Section 2, the problem definition and the real scenarios in which we applied our algorithm are described in
Section 3, the GA for the TLP is introduced in
Section 4, the results achieved are presented in
Section 5,
Section 6 presents the discussion for the TLP and we conclude the manuscript in
Section 7.
2. Analysis and Complexity Studies on the Table Location Problem
The TLP entails the definition of the two-dimensional Cartesian coordinates for the location of each student in the classroom. This supposes the associated table distribution in the plane for ensuring the follow-up of the classroom keeping the necessary social distancing by reducing the probability for the students of being infected from the coronavirus during the pandemic.
Therefore, the TLP is a combinatorial problem in which the number of possible table distributions (P) is factorial [
30]:
where
is the number of possible locations where a table can be located in the optimization process and
the number of students.
This analysis shows the dimensions of the space of solutions in which the size is incremented when considering a larger number of students and when a larger number of possible table locations is defined.
Since the number of students is commonly predetermined, an adequate selection of the
must be performed in order to achieve optimal results. This number should be, on the one hand, high enough for granting sufficient resolution in the table location and on the other hand, reduced for performing time-effective optimizations [
29]. In this paper, we have proved different configurations selecting the final hyperparameter based on the achievement of slight modifications in the principal statistical variables when reducing the spatial resolution.
Each one of these considerations makes the TLP factorial in complexity [
31] and very similar to the technological NLP, which has been assigned as NP-Hard [
22,
23]. As a consequence, the finding of an optimal solution for the TLP recommends a heuristic approach similarly to the NLP and can also be categorized as NP-Hard.
Many different metaheuristics have been used for the NLP, which could be applied to the TLP such as simulated annealing [
24], the firefly algorithm [
25], the elephant herding optimization [
26], the dolphin swarm [
32], the bat algorithm [
33], the grey wolf optimization [
34], the bacterial foraging algorithm [
35] or diversified local search [
36]. However, GA have been the most extended in the literature [
27,
28,
29,
37] since they provide an optimal balance between diversification and intensification of the space of solutions for the NLP [
38]. In addition, their flexibility and adaptation to any problem makes the GA the best candidate to address the TLP.
3. Problem Definition and Scenario of Application
A mathematical characterization of this problem is required for correctly defining the methods followed for its solution. In this section, we define the problem and the characteristics of the real-world scenarios in which we perform the table localization optimizations.
3.1. Problem Definition
Let
be the spatial coordinates of the table
i considered during the optimization process,
the number of students in the classroom and consequently the number of tables to be located,
T the set including every possible combination of tables in the classroom,
a subset containing a possible disposition of the tables in the classroom,
the subset containing every possible combination of
T except
,
the evaluation of the quality of the location of the table
i belonging to the set
, the TLP is defined as finding the optimal
fulfilling the following relation:
Consequently, the TLP is defined as the finding of the optimal table disposition in the classroom for maximizing a fitness function of which the main purpose is the maximization of the distances among tables but preserving the legislation of each country, which restricts the table disposition to having a minimum required distance among every table.
3.2. Scenario of Application
The TLP is a real-application problem that has been addressed in collaboration with the Marist Brothers School San José in the city of León, Spain. The government of the autonomous country of Castilla and León has promoted the disposition of the students in two kinds of grids for addressing the TLP (i.e., a rectangular and a zig-zag grid) in order to satisfy the 1.5 m separation defined by the Spanish legislation. However, this kind of table disposition is suboptimal and the regular patterns do not necessarily obtain the best results in this type of combinatorial problem [
39] since better results can be achieved by using metaheuristics for solving this complex problem.
Therefore, we have analyzed two different classrooms of this school (i.e., Class A and Class B) with different characteristics, which forces different optimization goals. The first class consists of 16 tables while the second scenario needs to allocate 21 students, although the first scenario is smaller, its student density is considerably lower than the second class. Therefore, the Class A scenario is less restrictive than the second classroom in respect to the 1.5 minimum separation protocol.
In order to model these classes and the table allocation area, we have defined three different regions for each class. The first area, the bigger one, represents the class limits, both classes were approximately rectangular; thus, both scenarios are considered to be of such shape.
The second area is defined as the Table Location Environment (TLE) and it is the region within the class limits where the tables can be positioned. For this optimization, the positions of the tables are referenced from the students coordinates; thus, each point of the TLE is a possible location for a student. Therefore, a series of table measurements, shown in
Table 1, have been considered in order to properly define the TLE region.
Moreover, although major obstacles of the classrooms were considered into the TLE limit definition, some prohibited areas remained inside the TLE region, thus the codification of these areas is required. The third region in the scenario is the prohibited areas or obstacles, which are defined as areas where a student cannot be allocated. In the simulations presented in this paper, we have displayed the limits of these obstacles with respect to the student’s table for visual clarification. Thus, in the following figures, neither the student nor the table can be positioned inside these obstacle regions.
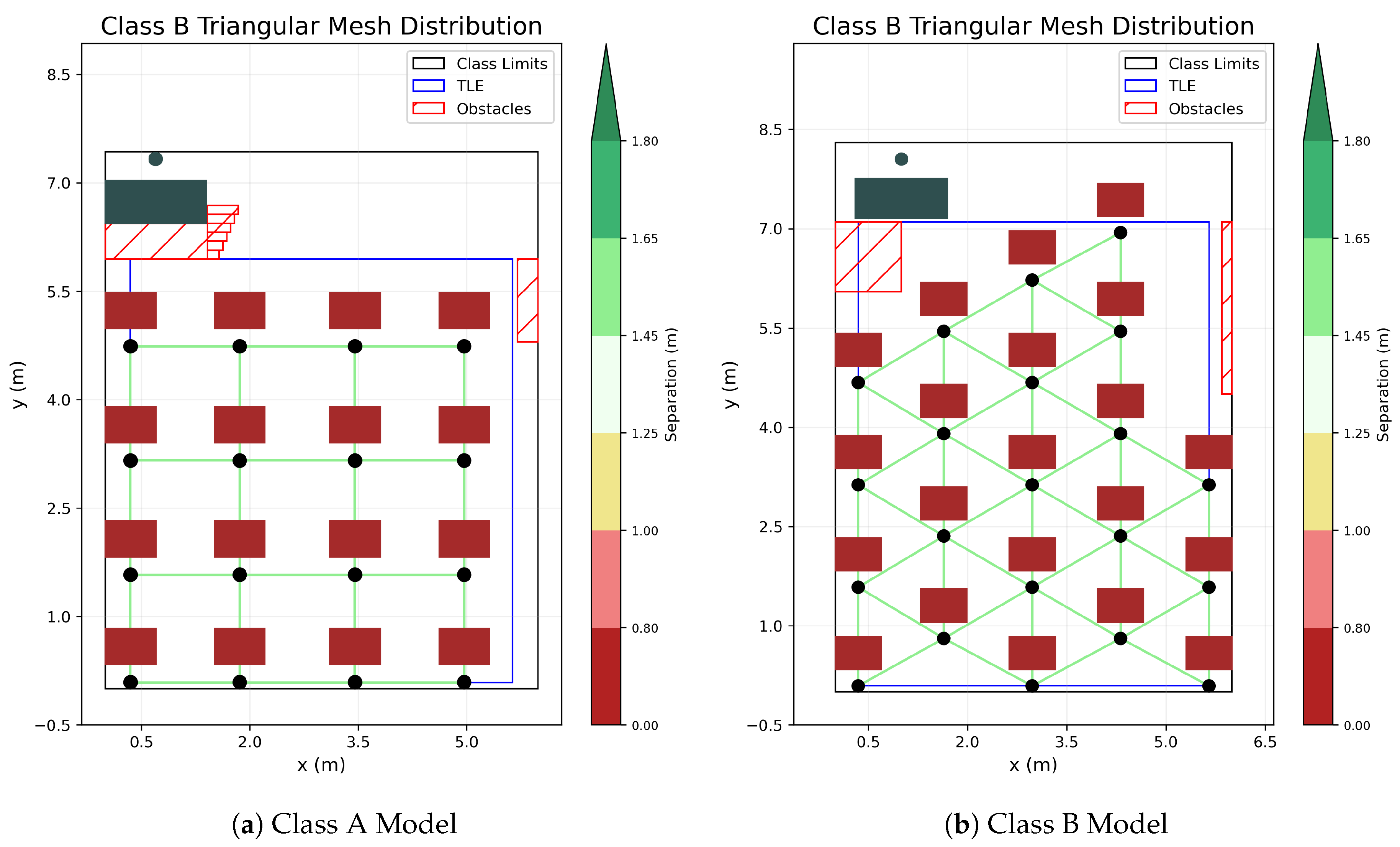
As for the original student distribution, the first class, shown in
Figure 1a, displays an orthogonal mesh distribution of tables, with this scenario being less restrictive in terms of student allocation. On the other hand, Class B, shown in
Figure 1b, requires a greater density of students, thus utilizing a triangular mesh distribution, which generally produces more efficient results in the table optimization.
Figure 2a,b shows the classroom models used in this study.
4. Genetic Algorithm Optimization for the TLP
Genetic Algorithms have proven to be among other metaheuristic techniques an excellent trade-off between diversification and intensification of the space of solutions in the optimization procedure. GA were initially proposed by Holland [
40] and refined by Goldberg [
41] afterward. These algorithms are based on the theory of evolution and rely on the fitness adaptation of a population of individuals to the problem specific scenario.
These individuals contain the problem’s distinct variables, from which the solution is dependent of. Through the optimization, our population is exposed to a certain pressure selection, so that the most adapted individuals prevail and pass out their remarkable genes to the following generation of individuals. This cycle of evolution, carried out through a sufficient amount of iterations, may achieve a state where an individual or a group of individuals contains an optimal enough solution to the problem, thus concluding the optimization.
In the following section we discuss the codification and implementation of the GA proposed for the TLP.
4.1. Codification of the Individuals
The population of a GA must be coded in a way so that it contains all the essential information for the optimization procedure. For this particular case, the main variable of the optimization is the spatial distribution of the tables among the specified region (i.e., the coordinates of each table). Therefore, each individual of the population contains a particular table distribution, carrying the coordinates of each table along the TLE.
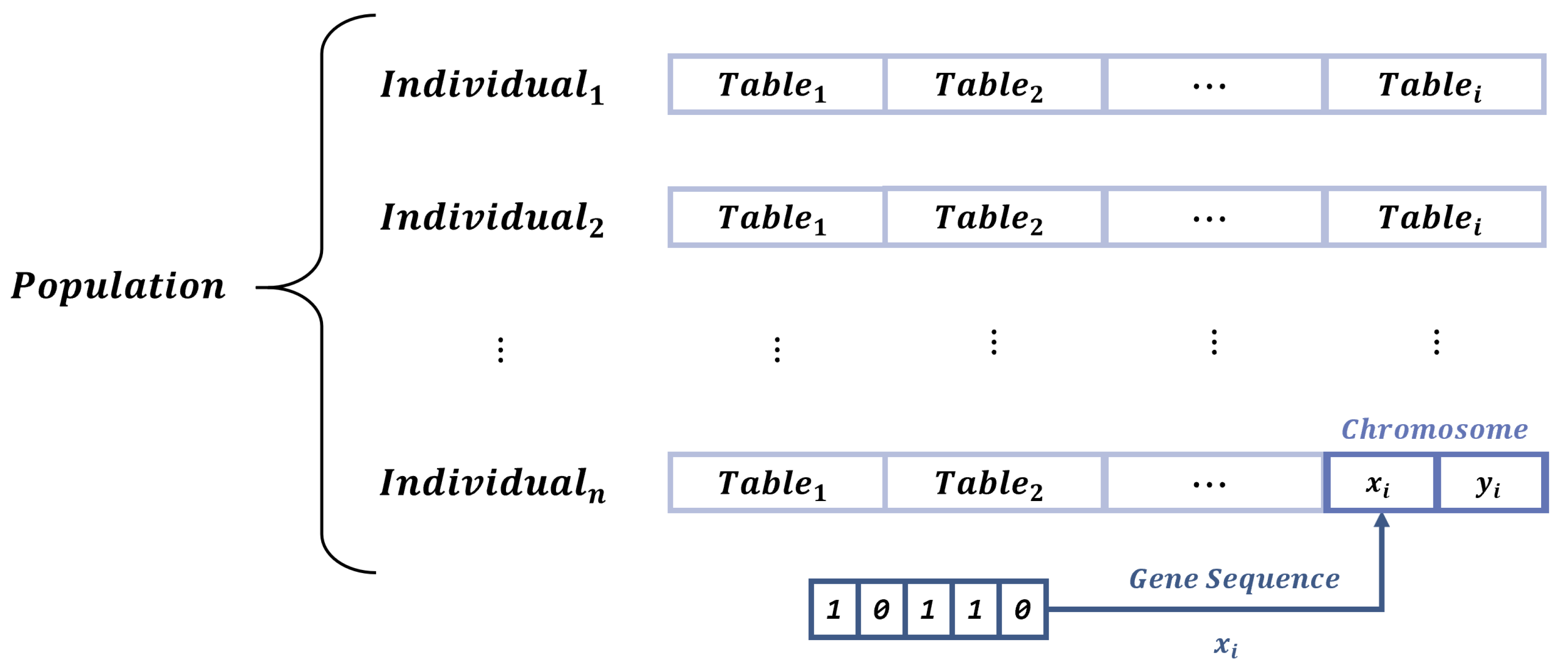
Figure 3 shows the codification scheme followed in this paper, executed in the Python programming language, where we create a population list composed of
n individuals. Each individual represents a distinct table distribution, carrying
i lists for coordinates of each specified table. Every table array carries the two spatial coordinates required for the table positioning, both coded into binary arrays.
The binary codification is particularly useful when undergoing the genetic operators, such as crossover or mutation. Moreover, the binary structure grants a superior degree of flexibility when facing irregular scenarios, through the application of a binary scaling [
29].
4.2. Evaluation of the Individuals
Once the population is coded and generated, the next step in the GA structure is to determine the value of each individual, through a specially designed fitness function.
For our particular case of study, the objective of the optimization is the distributions of the student’s tables in a way so that a minimum separation of 1.5 m is obtained, thus fulfilling the Spanish legislation. However, it is desirable in multiple ways for the distance between each pair of tables to be maximized, thus reducing contagion probability and increasing student and professor mobility through the class. Hence, the fitness function proposed must guarantee the minimum separation among every table while also seeking to enhance even beyond the 1.5 m separation distance.
Although it is possible to compute both elements of the optimization simultaneously (i.e., 1.5 minimum separation and mean distance maximization), we have concluded that it is more fruitful to implement a two-step fitness function evaluation that foremost aims to guarantee the safety distance, being this an imperative requisite for the optimization. Once the 1.5 has been obtained, the second phase of the fitness function takes place, seeking to optimize the mean distance between tables. This is similar to the process of predefining an initial population of the GA not randomized containing optimal potential solutions in particularly difficult evolutionary optimization scenarios [
42].
For the first phase of the evaluation, we have considered the severity of the 1.5 m infraction into the evaluation of the individuals. In GA optimizations, it is crucial to preserve the convergence through the generations to the final solution. By introducing some progression into the evaluation, even though the individuals may not have achieved the minimum separation, we assure a rewarding mechanism for those individuals that represent a more scattered distribution.
Therefore, the following fitness function equations have been implemented for the first phase of the evaluation:
where
is the sum of all the distances between pairs of tables that are under 1.5 m;
l is the number of distances that satisfy this statement;
L is the number of tables and the number of distances previously measured that are under 1.5 m; and
is a penalization applied to those individuals in which some of the tables have been located in a banned region, where
values
if a table is positioned in a prohibited region and
values 0; otherwise,
is a stated hyperparameter.
This fitness function evaluation may vary between , being the first value obtained when every table is positioned in the same coordinates, and 0 if all the tables maintain a minimum separation of 1.5 m.
This progressing evaluation grants a steadier convergence of the population to a state where most individuals respect the 1.5 m separation.
Once this evaluation has taken place, only if a certain individual or group of individuals have achieved a value of 0, the evaluation proceeds to the following phase.
In this second phase we seek to optimize the mean distance between tables; thus, the following fitness function is proposed:
where
is the mean distance between pairs of tables;
is the standard deviation of the distribution of the distances;
is a weight hyperparameter; and
is the hyperparameter that determines whether or not a pair of tables is considered to be close to each other.
In this second phase of the fitness evaluation, we measure both the mean distance and the standard deviation of the table distancing. The introduction of the standard deviation into the optimization aims to obtain a more uniform table distribution. The uniformity of the table distancing plays a vital role in the contagion probability, being undesirable the scenario where some tables are considerably closer than the mean distance. Moreover, we have encountered experimentally that this scenario (i.e., where a reduced number of tables are rather separated from the rest while the rest are substantially close to each other) to be particularly common in the different optimization stages. Therefore, the implementation of the standard deviation in our fitness evaluation addresses this phenomena by penalizing these imbalanced distributions.
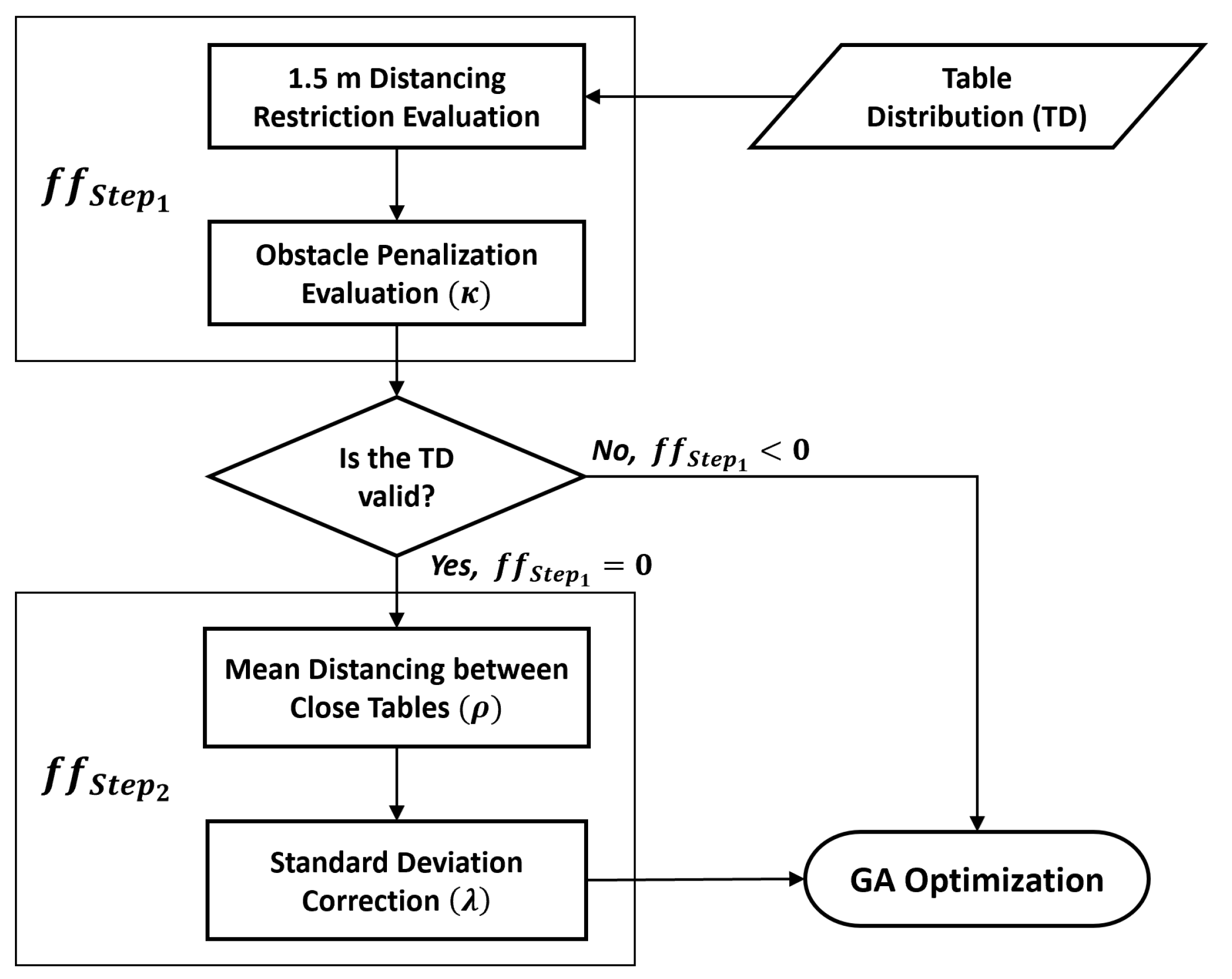
Figure 4 shows the two-step fitness evaluation procedure proposed for the TLP.
Furthermore, the main goal in this paper is to obtain a table distribution that minimizes the COVID-19 contagion probability, thus, maximizing the separation for every pair of tables is crucial. The implementation of the mean distance between tables as the primary value estimator results in the introduction of the selection pressure required for the GA convergence to the desired solution.
4.3. Selection and Elitism
The selection operator aims to arrange the individuals of the population in a way that enhances the optimization performance. This criterion is based on the fitness value given by the fitness function of each individual in the previous step.
However, we can encounter multiple selection methodologies throughout the literature. These methodologies differ in the pressure selection that they introduce into the optimization. GA optimization is mainly driven by two core aspects, the intensification and the diversification of the solution [
43].
The diversification phenomena introduce entropy into the optimization process, this randomness slows the convergence to the final solution, allowing a greater exploration of the solution environment, enhancing the quality of the solutions obtained.
On the other hand, the intensification boosts the convergence to a solution, thus directing the genetic evolution to the optimal path in a reduced space of solutions [
44].
The balance between these two factors is key in any GA optimization. An excessive approach to intensification may conclude in premature convergence of the problem into a local maximum due to the lack of exploration, while a heavy intensification focus may compromise the convergence to any solution.
Moreover, this balance depends not only on the problem studied but also may differ from different initial conditions or scenarios of applications. Therefore, we must study the performance of different genetic operators for each particular case of study [
45].
Thence, we will analyze the performance of the selection techniques of Tournament 2 (T2), Tournament 3 (T3) and Roulette (R) selection, being these methodologies among the most expanded selection techniques throughout the literature [
46].
Furthermore, in addition to the selection methodologies, we can introduce selection pressure into the optimization through the use of elitism. This technique aims to preserve the better adapted individuals throughout the generations, seeking to influence the optimization convergence into the optimal path.
Therefore, through elitism we preserve a certain percentage of individuals along with omitting those with a lesser fitness value [
43]. The percentage used is another hyperparameter that needs to be adjusted for each particular application. An excessive value may incur in a premature convergence while an insufficient percentage may not achieve the desired results.
4.4. Crossover and Mutation
The crossover operator seeks to create the new generation of individuals, based on the genetic characteristics of their predecessors. Being the pairing arrangement decided in the selection operator, by combining parents with different genetic properties, it is possible for their offspring to better both of their parents.
However, there coexist multiple crossover techniques, and likewise to the selection operators, their performance depends on the characteristics of the problem’s scenario. Therefore, we must study the behavior of multiple crossover methodologies in search of the most appropriate for every particular problem [
47].
Therefore, we analyze the implementation of the Single-Point crossover (SP), MultiPoint crossover for 2 and 3 cross-points (MP2 and MP3, respectively) and Uniform crossover (U), being these techniques among the most expanded methodologies throughout the literature [
48].
Moreover, it is possible to introduce a higher degree of entropy into the optimization through the application of mutation. In this operator, we randomly modify certain genes of a specific number of individuals. The purpose of this alteration is to perform a further exploration of the solution environment, since it is possible for a random mutation to induce a rather superior performance of the individual, influencing the optimization direction [
43,
49].
This operator plays a key role in the GA optimization, and although its implementation might appear less favorable, its adequate application allows the achievement of a greater solution in the whole GA optimization.
However, it is vital to balance the degree of entropy generated, being an excessive amount of mutation detrimental for the convergence; thus, we must study the appropriate amount for the desired scenario of application [
43,
50].
4.5. Stop Criteria
Once the new generation is created, the iteration of the GA ends, giving way to the successor generation to be evaluated in the following iteration. This cycle of evaluation, selection and crossover continues throughout multiple iterations, until the stop criteria of the GA is fulfilled.
Heuristic methodologies like GA are frequently applied in optimization problems where the optimal solution cannot be easily obtained. Furthermore, in these problems it is common that any solution obtained cannot be verified to be optimal.
For this particular problem, although we can evaluate a certain distribution by measuring its mean distance and verifying the 1.5 m separation accomplishment, we are unable to define if a certain distribution of tables is optimal. Therefore, it is necessary to define a stop criterion in the GA optimization.
In this paper, a double stop condition based on two logic parameters is proposed. Firstly, the GA optimization shall stop if a certain percentage of the population is identical, thus concluding the optimization when the algorithm has converged to a certain solution. In this state, any deviation from this solution presents a lower fitness value than the previous value; however, this phenomena is not limited to the optimal solution, being possible for this solution to be a local maximum [
51].
Secondly, the GA optimization shall also stop if a certain number of iterations have been completed. The addition of this parameter is crucial in any GA optimization, since it is possible that the GA does not achieve a convergence to any solution, thus entering the GA into an infinite loop.
5. Results
In this section, we present the results of the previously detailed GA in both classroom scenarios. All algorithms were coded and executed in the Python software environment, performing every test with an Intel(R) i7 2.4 GHz of CPU and 16 GB f RAM.
Previously, we have studied the significant impact of different genetic operators into the GA global performance. Their effect on the balance between intensification and diversification of the solution is key in order to obtain an adequate solution through the GA optimization.
Therefore, in order to obtain the most appropriate genetic operators for each particular scenario, firstly, we must study the performance of each individual combination of genetic operators through multiple simulations. All simulations were executed with the following parameters, as shown in
Table 2.
Hence, in search of the optimal combination of genetic operators, we have analyzed the performance of each possible individual combination among these functions, resulting in the comparison shown in
Table 3.
Table 3 shows the difference in the optimization performance of the GA depending on the combination of genetic operators selected and the scenario of application.
The first classroom presents a great opportunity for table location optimization; however, the results of the optimization differs from each combination of selection and crossover techniques utilized.
The second scenario is far more restrictive than the previous one, and in some combinations, the GA did not achieve a valid solution, proving the importance of testing the performance of multiple operators.
For both scenarios, the roulette selection and the uniform crossover showed inferior performance than the other studied techniques. Generally, R. selection and U. crossover are particularly heavy focused techniques on intensification and diversification, respectively, thus their introduction to this problem may result inadequate.
On the other hand, from the other combinations, tournament-2 with three-point crossover (T2-MP3) and two-point crossover (T2-MP2) showed satisfying results for the first and second scenario analyzed, respectively. These combinations of selection and crossover methodologies exhibiting an adequate balance between diversification and intensification in the maximum and mean fitness values obtained throughout the simulations.
Furthermore, once we selected both methodologies, we evaluated the most advantageous elitism and mutation values for each scenario of application, as shown in
Table 4.
The resulting configurations of the GA proposed in
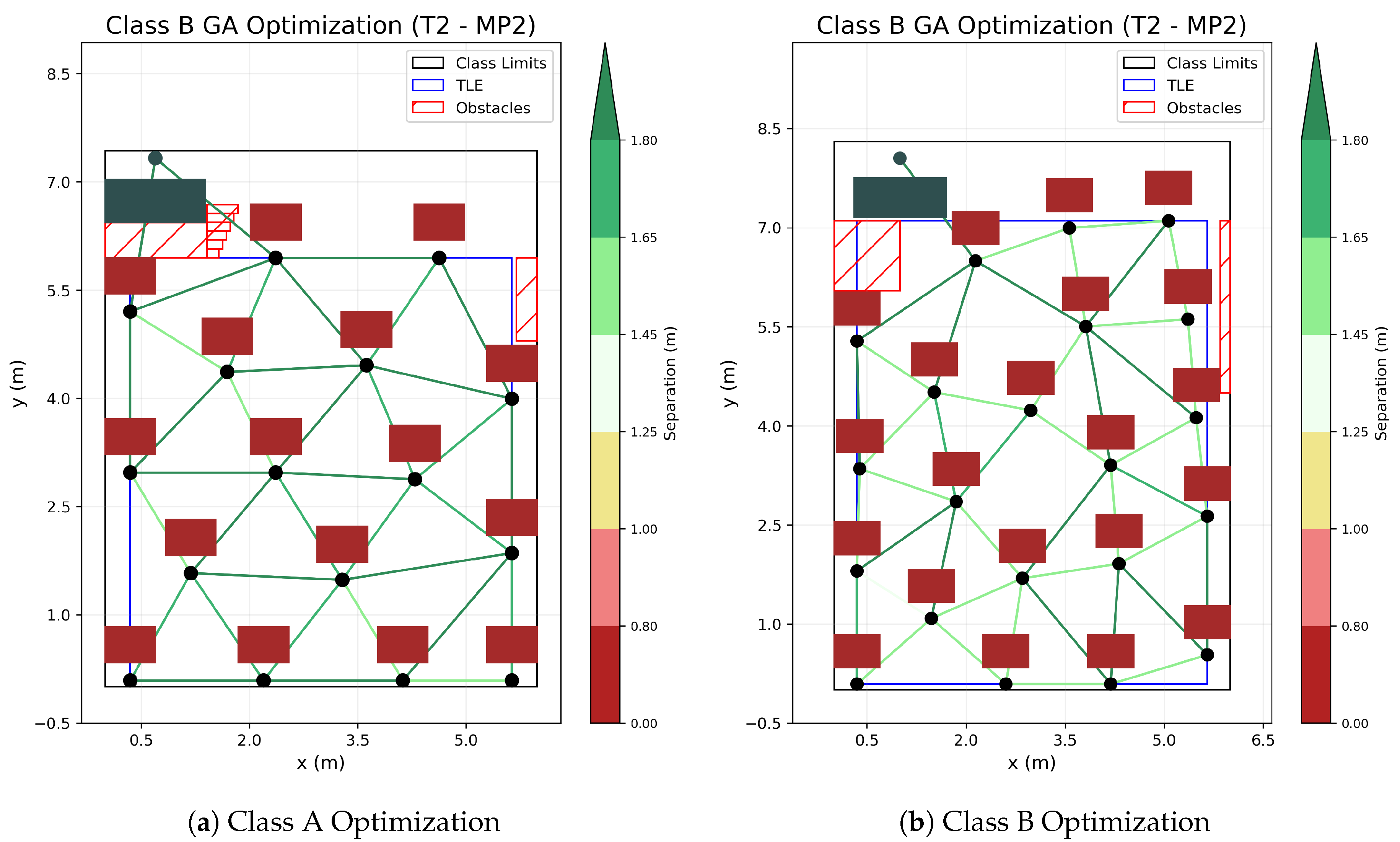
Table 4, executed for both scenarios obtaining the following table distribution, as shown in
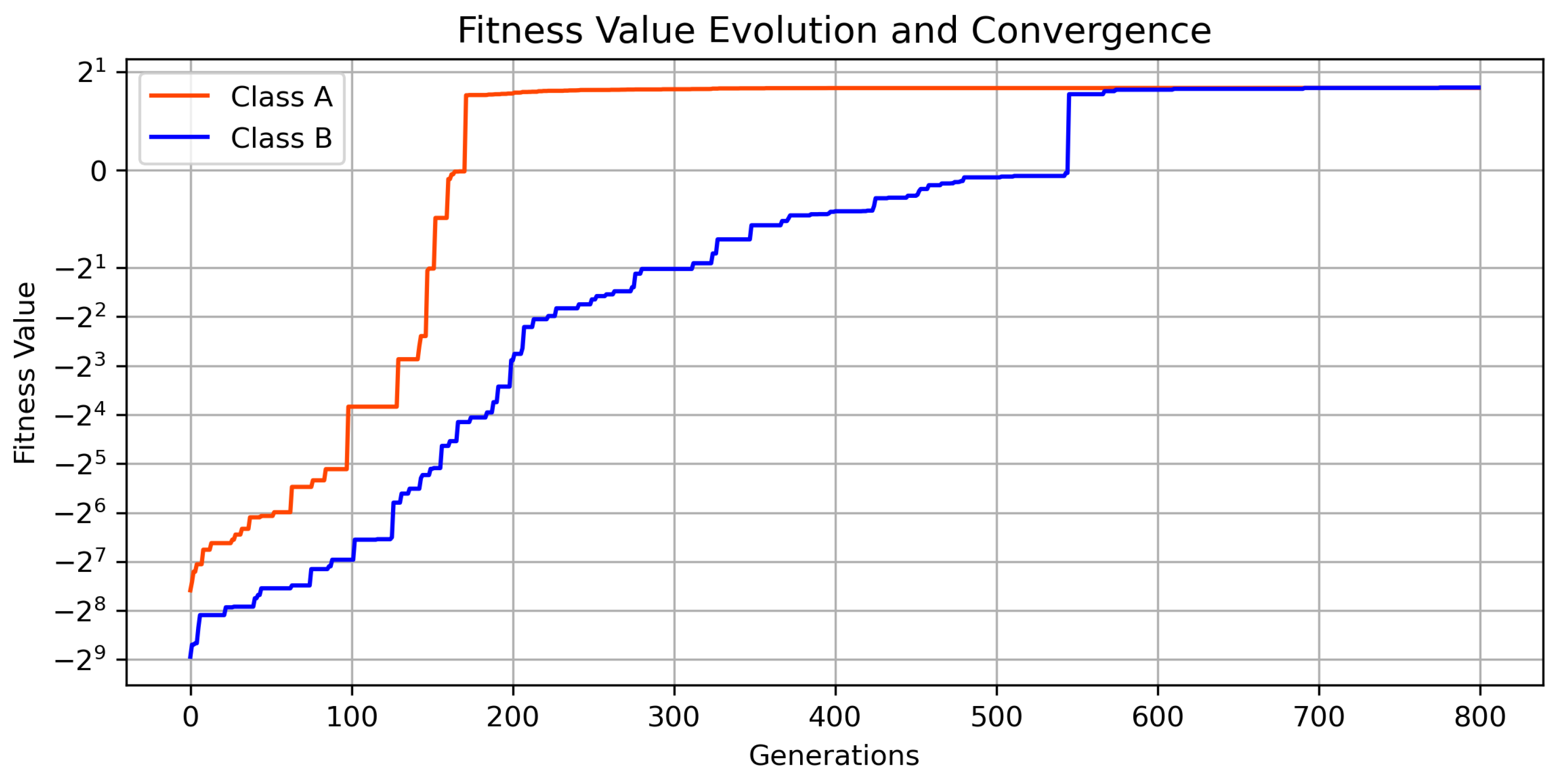
Figure 5. The evolution of the algorithms and convergence to the final solution is also shown in
Figure 6.
These resulting distributions obtained by the GA in both scenarios thrive at optimizing the available space, achieving a mean separation, shown in
Table 5, unreachable for regular meshes.
Furthermore, due to the introduction of the standard deviation into the fitness evaluation, the resulting distributions, although presenting irregular patterns, exhibit some degree of uniformity. This fact proves essential when minimizing Covid-19 contagion in our scenarios.
Results in
Table 5 show an improvement up to 19.33% in the mean distance between tables from the GA optimization. This statement proves the viability of these algorithms for any scenario of application, also achieving a 10% increase in mean distance in the second, most restrictive scenario.
Moreover, the obtained distribution for the first scenario was later implemented into the original classroom studied, proving the viability of this methodology, resulting in the distribution shown in
Figure 7.
Therefore, the GA proposed in this paper successfully enhances the table distribution for multiple scenarios with respect to the Covid-19 contagion probability, thus fulfilling the main objective of this research.
6. Discussion
This paper presents a technological solution for the TLP in the schools during the COVID-19 pandemic. The distance achieved among the students’ desks allows the reduction of the probability of contagion of this emerging infection, which collaborates with other rules such as wearing facemasks or using hydroalcoholic gels for creating safe places for the children to follow their daily lessons.
Our approach addresses a novel problem, which is firstly introduced in this paper. The location of the tables has been proved in the manuscript to be a combinatorial NP-Hard problem, which recommends a heuristic solution to find acceptable results. The huge dimension of the space of solutions dependent on the resolution of the TLE and the number of tables to be located introduces difficulties during the optimization process, which requires the definition of a two-step optimization procedure in which we first ensure a combination of the tables in a space that meets the government 1.5 m minimum separation among all the tables and we later expand this distance to minimize the contagion risks in the classrooms.
We have implemented a GA optimization for this purpose due to the flexibility of adaptation of this metaheuristic to different similar technological problems [
27,
28,
29,
37,
52,
53,
54] and the trade-off achieved between diversification and intensification of the space of solutions. The results obtained in the manuscript have demonstrated the suitability of the application of metaheuristics to solve this kind of problem that emerged during the pandemic, improving the government solutions proposed.
In our future works, we will extend the analysis of the TLP to other different metaheuristics such as simulated annealing, diversified local search or the combination of the GA with a local search procedure to explore improvements in the optimization results. Furthermore, we will consider novel optimization scenarios such as the school canteen, restaurants, or pubs in which novel challenges for the optimization can arise. Such as multi-objective optimization for different criteria leading to algorithms such as NSGA-II, NSGA-III or MOEA.
7. Conclusions
The COVID-19 pandemic has supposed a challenge for humanity to deal with a virus that has changed the normal coexistence. As a consequence, many restrictions have been imposed globally for reducing the probability of contagion of a virus that can even cause, in the most severe cases, death. Therefore, social distancing, wearing facemasks, hydroalcoholic gels for hand cleaning or reducing the capacity allowed in indoor spaces have been some of the rules adopted for containing the virus propagation.
Education has been one of the most affected sectors. Most of the countries decided to move to online learning during the first lockdowns promoted for facing the emergency of the initial coronavirus outbreak. This has complicated the normal learning of children, their social relationships and their physical health activity. Consequently, most of the countries have considered the reopening of the schools as a priority, even keeping the schools opened during the second coronavirus outbreak that it is nowadays facing Europe. This has promoted the implementation of restrictions and rules at schools for reducing the infectious potential of the virus.
One of them has consisted of smart dispositions of the tables in the classrooms for maintaining the social distancing. In Spain, the government has fixed a minimum of 1.5 m among the students’ desks, which has led to reducing the number of children in each classroom and designing regular patterns in the disposition of the tables such as orthogonal or triangular mesh configurations.
However, the problem of the disposition of the tables is NP-Hard and a metaheuristic solution is recommended for obtaining improved results through irregular table disposition patterns that maximize the distances among the tables thus minimizing the probability of getting the coronavirus at schools.
In this paper, we introduce for the first time to the authors’ best knowledge a Genetic Algorithm optimization for the Table Location Problem for addressing the table disposition during the COVID-19 pandemic. We analyze the definition and complexity of the problem and we propose a methodology for its resolution. This methodology is applied in two different real-application scenarios (i.e., Class A and Class B) in which we prove the suitability of the optimization of the table disposition for obtaining improved results. Results show that an increase of the mean distance among tables of 19.33% in Class A and 10% in Class B can be attained following the proposed methodology thus fulfilling the main objectives of this paper.