Abstract
Aerial twisting techniques are preferred by trampoline coaches for their balanced landings. As these techniques are not intuitive, computer simulation has been a relevant tool to explore a variety of techniques. Up to now, twisting somersaults were mainly simulated using arm abduction/adduction only (2D). Our objective was to explore more complex (3D) but still anatomically feasible arm techniques to find innovative and robust twisting techniques. The twist rotation was maximized in a straight backward somersault performed by a model including arm abduction/adduction with and without changes in the plane of elevation. A multi-start approach was used to find a series of locally optimal performances. Six of them were retained and their robustness was assessed by adding noise to the first half of the arm kinematics and then reoptimizing the second half of the skill. We found that aerial twist performance linearly correlates with the complexity of arm trajectory. Optimal techniques share a common strategy consisting of moving the arm in a plane formed by the twisting and angular momentum axes, termed as the best tilting plane. Overall, 3D techniques are simpler and require less effort than 2D techniques for similar twist performances. Three techniques which generate ∼3 aerial twists could be used by athletes because kinematic perturbations do not compromise the performance and the landing.
1. Introduction
To get higher scores in competitions, trampolinists enhance their 10-skill routines by increasing the number of somersaults and/or twist rotations. There exist three strategies to create twist rotation during a somersault, namely, contact, cat and aerial strategies [1]. Contact twists are generated when the athlete is in contact with the trampoline bed, by inducing initial twisting angular momentum along the longitudinal axis (termed as the twisting axis). It will be conserved throughout the aerial phase of the skill, until the landing. While twist velocity is desired during the skill, it is not recommended when landing onto the trampoline bed, as it leads to less balanced landings [2]. Cat twists are generated by rotating segments opposite to the desired twist rotation [3], such as hula-hoop motions. This strategy gets more efficient as the radii of rotation of the segments increase. However, in straight somersaults, such hip and trunk postures are penalized by judges through a stylistic score, discarding their extensive use among athletes. Aerial twists are created after take-off by segment asymmetries aiming to bring the twisting and the angular momentum axes closer together by tilting the body [4]. This strategy often involves asymmetrical arm motions [3]. While trampolinists can use a combination of these three strategies, the greatest contribution to twist usually comes from aerial strategies [5].
In pure aerial strategies, there is no twisting rotation velocity at take-off. Before landing, it is possible to stop twisting by untilting the body, i.e., bringing the twist and angular momentum axes perpendicular to each other [6]. Consequently, and in contrast to contact twists, this strategy has the advantage of allowing athletes to land with more balance [2]—an advantage which has led trampoline coaches to promote aerial twisting. However, the mechanics of aerial twisting are complex because it is subject to non-linear effects (i.e., Coriolis and centrifugal forces) leading to non-trivial control strategies, which require precise timing of the sequences of actions. Coaches usually teach aerial twisting in backward somersaults by means of basic sequences of arm raising/lowering in the frontal plane (i.e., abduction/adduction: further referred to as 2D techniques), leaving room for improvement [7]. With practice and experience, athletes manage to refine their techniques by adding 3D deviations from the technique they were taught.
Athletes also learn to make in-flight adjustments based on visual and vestibular feedback to land successfully [8]. This ability is crucial, since even elite athletes experience variations in the execution of their skills from one trial to another [9]. It is hypothesized that trampolinists use feedforward and feedback controls to modify their motor patterns [10] to cope with perturbations. Indeed, athletes’ responses to the sensory information are too complex to be reflexes [11,12]. Therefore, it can be hypothesized that the internal processes aiming to determine the best response to perturbations can be modeled by optimization. It is necessary to consider this process in the analysis of optimal techniques, since optimal simulations have an unfair advantage over athletes regarding accuracy. Therefore, to make sure that the proposed optimal techniques can be performed by athletes, it is necessary to guarantee their robustness. For this purpose, robustness can be part of the optimal control problem (OCP) [13] or can be evaluated after optimization [14].
Computer simulations are relevant tools for seeking innovative techniques in sports. They are particularly useful in acrobatic sports—in which trials of new techniques increase the risk of injury—by discarding dangerous techniques before experimentation. Numerical optimization has been shown to be particularly useful for analyzing athletes’ motion and for discovering innovative techniques [15,16,17]. Studies in which numerical optimization was used to investigate twist rotation in acrobatic sports using arm techniques [4,18,19,20] relied only on arm abduction/adduction actions. These aerial 2D arm techniques have been described in detail, leading to practical advice for coaches on efficient strategies to create twist rotations [21]. No similar advice has been provided for 3D arm techniques. However, new techniques combining abduction/adduction with changes in plane of elevation, referred to as 3D techniques, can increase the number of twists achievable [7].
We hypothesized that for similar twist performance in 2D and 3D, 3D techniques would require less complex arm motions, since the arms can reach for a longer period of time a novel reference plane called the “best tilting plane” (BTP). We also hypothesized that the number of twists achieved is correlated to arm motion complexity. The first aim of this study was to find innovative and robust twisting techniques. A secondary objective was to provide a biomechanical explanation of the underlying strategies to explain why 3D techniques outperform 2D techniques. These findings, combined with a robustness analysis and a thorough discussion of hand-picked salient solutions, will be of interest for acrobatic sport athletes and coaches.
2. Methods
The present study constitutes a secondary use of the data generated in [7]. Here, we present a deeper analysis of aerial twist strategies by introducing the BTP of cat twist strategies by considering their contributions to the final twists and of the robustness by introducing a novel method involving reoptimization.
2.1. Skeletal Model
To assess the improvements brought by 3D motions of the arms, two models were created with Spatial Vector and Rigid-Body Dynamics Software [22] to represent the body of the trampolinist. In accordance with the literature, the first one included a free floating base and one degree-of-freedom (DoF) at each arm for abduction/adduction movements, whereas the second one included two DoFs at each arm to add the possibility to change the plane of elevation (Figure 1). Both models were composed of three rigid bodies connected with inelastic joints: the root segment (including the head, trunk and lower limbs), and the right and left upper limbs with extended elbows.
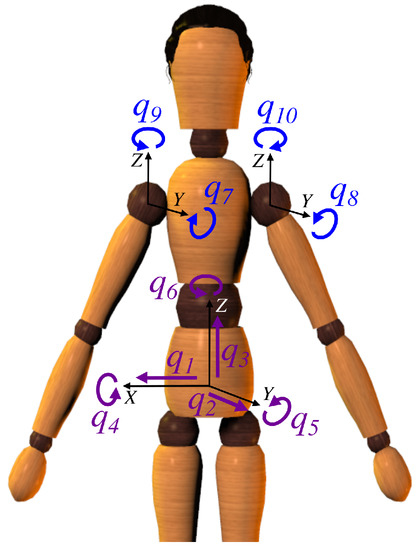
Figure 1.
Model definition with 10 DoFs: translations of the root (), rotations of the root (), right arm and left arm abduction/adduction (), right arm and left arm change in plane of elevation (). Arm rotation sequence: change in plane of elevation, elevation.
Both models were torque driven at the shoulders, i.e., two controls for the 2D model and four controls for the 3D one. Inertial parameters of the body segments were estimated from 95 anthropometric measurements of one subject (female, 21 years old, 65 kg, 158 cm) in line with Yeadon’s anthropometric model [23].
2.2. Formulation of the Optimization Problem
The main objective of the optimization problem was to maximize the number of twists generated by the arm technique (first term in Equation (1)). Some penalties were added to generate realistic techniques, namely, minimizing the effort required to execute the movement (second term in Equation (1)), minimizing the somersault rotation velocity at take-off (third term in Equation (1)) and minimizing the lengths of the hands’ trajectories (fourth term in Equation (1)). The cost function to be minimized was:
where T is the duration of the flight time (take-off to landing), and are weighting coefficients, is the control of the DoF and is the hand path in space. For the 2D model (resp. the 3D one) (resp. 4). The symbol in the last term of Equation (1) denotes a line integral along a path, which, in our case, represents the distance traveled by each hand. We looked for suitable compromises between the four objective terms by manually tuning to obtain highly twisting yet realistic techniques. Four types of problems (termed 2D-PHP, 2D-UHP, 3D-PHP and 3D-UHP) were solved using the 2D or 3D model and by penalizing (PHP) or not (UHP) the hand path. The following coefficients were used depending on the type of problem: 100,000, , and for the 3D model; and was receptively set to 1, 0, 100,000 and 0 for 2D-PHP, 2D-UHP, 3D-PHP and 3D-UHP.
2.3. Practical Implementation
During the flight, arm positions were bound (Table 1) to an anatomically feasible range of motion [24]. Since a term in the cost function (Equation (1)) was dedicated to torque minimization, it was assumed that velocities and torques should not end up at non-physiological values, and were thus bounded to arbitrary high values. Moreover, the initial and final states of the skill were constrained in line with the requirements of trampoline practice, i.e., in an upward position with the arms above the head. Additionally, the constraints on the initial state ensured that the avatar took-off with minimal horizontal speed and no tilt nor twist velocity.

Table 1.
Constraints applied to the model through the simulation.
A direct multiple-shooting formulation combined with the interior point non-linear solver IPOPT [25] and algorithmic differentiation from CasADI [26] were used to solve this problem.
2.4. Multi-Start Approach
Since the OCP was solved using a gradient-based algorithm, the optimal solution is a local minimum which satisfies the exit criterion. Therefore, optimal techniques are likely to differ depending on the initial solution provided [27]. In the scope of the present study, local minima were an opportunity to explore efficient techniques which were not globally optimal, but still interesting compromises from the sport’s perspective. A multi-start strategy was used to generate several solutions, as in [9]. Each OCP (2D-PHP, 2D-UHP, 3D-PHP and 3D-UHP) was given 440 initial solutions using combinations of the following parameters:
- Twist time history () linearly increasing from 0 to rotations.
- Number of shooting nodes .
- Random arm elevation ().
- Random arm torques ().
The best solutions of 2D-UHP and 3D-UHP (hand path unpenalized, thereby exhibiting the highest complexity) were selected for further analysis. The locally optimal solutions of 2D-PHP () and locally optimal solutions of 3D-PHP (twist ) were reviewed separately. Among them, we selected one 2D-PHP solution for its similarity with currently used strategies in trampoline and three 3D-PHP solutions for their innovation potential. The latest were chosen because of their minimal complexity and effort, which are relevant for athletes and coaches. In total, six techniques are further analyzed in Section 3.2.
2.5. Robustness Analysis of the Optimal Solutions
To simulate intra-athlete technique variability, noise was added to right and left arm kinematics as in [13]. Specifically, Gaussian noise (centered on zero with standard deviation of ) was added to the shoulder joint angles at a randomly chosen node of the first half of the skill. For the first half of the movement, the body’s kinematics were simulated consistently with these noisy arm trajectories. The second half of the movement was then optimized to match the optimal performance, i.e., the number of twist rotations. Bounds on the second half of the skill were kept unchanged from Section 2.3. Each technique was perturbed 100 times; the convergence rate, the kinematics and the number of twists generated were compared between techniques to assess robustness.
The robustness was first characterized by the differences in the number of twists between the optimal solutions and the perturbed ones; the mean and standard deviation are reported (). Robust techniques should still generate the same number of twists. To assess the magnitude of the arm kinematic changes required from the original technique, the root mean square (RMS) values were computed for the second half of the optimal technique and the reoptimized ones; the median and the median absolute deviation are reported (). The score adds some perspective to the robustness score, as when gets smaller, becomes more reliable. Robustness score should also be mitigated by the convergence rate, as a low convergence rate indicates that other local minima are hard to find in the region of the optimal solution, leading to important drops in performance in cases of kinematic variability. Techniques with small , and and a high convergence rate were considered robust, because they can be executed by athletes with different deviations from the optimal solution and still yield approximately the same outcome in terms of twist rotation, with minimal changes in arm kinematics.
2.6. Biomechanical Analysis of the Aerial Twist Strategies
To evaluate the effect of a technique’s complexity on performance, least mean square error was evaluated for a linear correlation between the number of twists generated and the length of the hand path. To analyze arm movements generating aerial twists, we introduce the “best tilting plane” (BTP) which is the plane formed by the twisting axis and by the angular momentum vector (constant in aerial phase). In a frame fixed to the body, this plane is rotating (consequently to the twist rotation). The angle () between the BTP and the plane of arm motions was calculated at each node for all optimal techniques. The orientation of the BTP was obtained from the cross product between the twisting and the angular momentum axes, and arm movement directions were evaluated with finite differences from their kinematics expressed in the frame of the body.
To discriminate parts of the skill including aerial twist strategies, the following criteria were used:
- The arm is moving ().
- The arm is not aligned with the body (the angle between the arm and the body is in the range ).
2.7. Biomechanical Analysis of the Cat Twist Strategies
To quantify the contributions of cat twist strategies to the final body twist, the body’s orientation was computed as a consequence of the arm kinematics. The kinematics of the body was simulated in a gravity-free condition from an initial state without somersault velocity as in [28].
To discriminate parts of the skill, including cat twist strategies, the following criteria were used:
- The twist (i.e., z-axis) component of the arm’s angular momentum in the global frame is non-null ( kg m s).
- The twist (i.e., z-axis) components of the arm’s and body’s angular momenta are of opposite signs ().
- The twist velocity resulting from the gravity-free simulation is significant (/s).
3. Results
3.1. Distribution of Optimal Solutions
Out of the 1760 optimizations, 1542 converged. For all converging solutions, the correlation between the achieved number of twists and the hand path (i.e., technique complexity) was: (Figure 2).
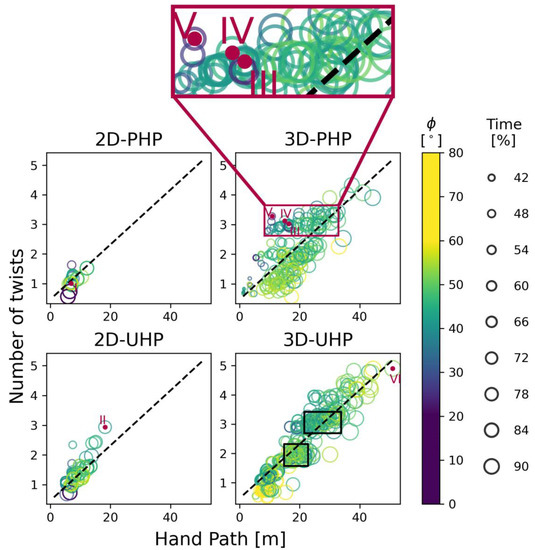
Figure 2.
Number of twists generated by optimal techniques as a function of the hand path length. The color code represents the mean angle from the arm movement to the best tilting plane (BTP). The size of each circle represents the time ratio wherein the arms are moving. Magenta points represent the selected solutions. Black boxes delimit the most dense areas of solutions. The magenta box delimits a cluster of solutions which seem to be greatly affected by the use of the BTP; an enlargement of this area is presented above the graph. The black dashed line presents the linear regression over all four types of problem.
3.2. Analysis of Locally Optimal Selected Solutions
Six techniques (Figure 3a and Figure 4d) were selected and further analyzed (Table 2). In what follows, a lowering of one arm occurring at the same time as a raising of the other arm is referred to as “arm inversion” (e.g., see Figure 3b). An adduction (resp. abduction) immediately followed by an abduction (resp. adduction) is referred to as add-abduction (resp. abd-adduction). Finally, some motions obtained with the 3D model are combinations of complex non-planar arm motions, hard to accurately describe with words. We refer the reader to the Supplementary Multimedia Material available online at http://www.mdpi.com/2076-3417/1/1/5/s1 to get deeper insights into these 3D arm techniques.
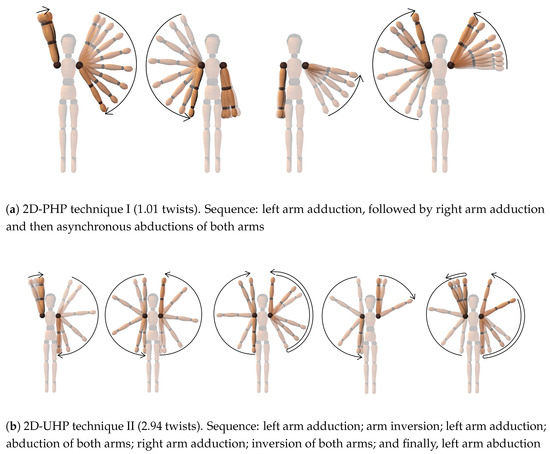
Figure 3.
Animations of 2D techniques presented in a frame attached to the root segment in order to emphasize the motions of the arms. All arm motions occur in the frontal plane.
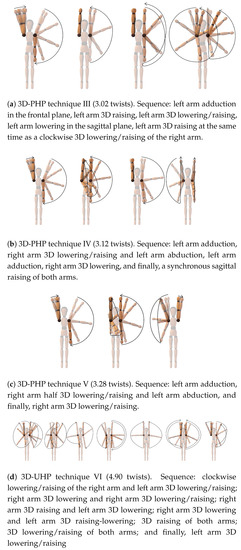
Figure 4.
Animations of 3D techniques presented in a frame attached to the root segment in order to emphasize the motion of the arms.

Table 2.
Characteristics of selected locally optimal arm techniques, including the number of twists, the mean angle between the BTP and the plane of motion of the arms (column ), the length of the hand path (column Complexity), the sum of the joint torques (column Effort), the robustness (column ), the reliability of the robustness (column ) and the convergence rate of the reoptimization (column Convergence).
Technique I (2D-PHP) is a 2D technique close to the one widely used by athletes to execute a backward somersault with one twist. Technique II (2D-UHP) is the 2D technique generating the most twists without a penalty for the hand path. Techniques III, IV and V (3D-PHP) are different 3D techniques which appear to yield more than three twists, while preserving a reasonable complexity. Techniques IV and V begin similarly. Even though technique IV is more complex than V at the end of the skill, it terminates in a more usual way with the arm raising in the sagittal plane just before landing on the trampoline bed. Technique III is different from IV and V, illustrating the richness of the set of locally optimal solutions. To support this last point, other solutions could have been presented, but for the sake of conciseness, the size of the selection was kept small. Technique VI (3D-UHP) is the 3D technique generating the most twists (∼5 twists); however, it is unrealistic to hope that athletes could reproduce it due to its high complexity. Still, it is presented here for the purpose of comparison and to explore optimal biomechanical principles.
3.3. Robustness of Selected Techniques
Regarding the robustness of the solutions (Table 2), technique I has a big score (compared to its number of twists) with a low , a high convergence rate and a small . Both UHP techniques (II and VI) have low convergence rates. All three 3D-PHP techniques (III, IV and V) have acceptable values of , and convergence rate.
3.4. Best Tilting Plane
The mean of the angle (between the BTP and the plane of arm motions) when arms are moving with an elevation between and is depicted in Figure 2 Techniques that generate more twists tend to include arm movements closer to the BTP than worse performing techniques. Another result from Figure 2 is that the arms are not always in the BTP, even when the arm path is not penalized.
3.5. Cat Twist Strategies
Sections of technique V involving cat and aerial twist strategies are presented in Figure 5. Sometimes, regions are overlapping, meaning that the arm movement yields both aerial and cat strategies at the same time (see Appendix B for an example of detailed analysis).
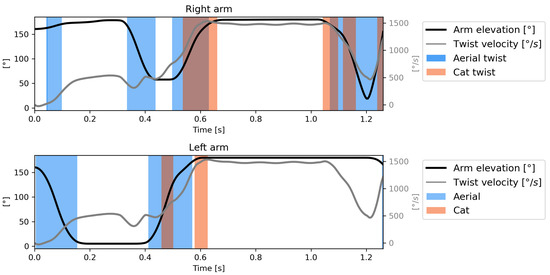
Figure 5.
Sections of technique V involving cat (orange shaded) and aerial (blue shaded) twist strategies according to previously mentioned criteria superimposed to the arm elevation and the twist rate.
Cat twist strategies are used in most 3D optimal techniques; however, they are only responsible for a minor part of the twist rotation (<2.5% as presented in Appendix D).
4. Discussion
The main objective of this study was to generate and analyze innovative and robust twisting techniques to highlight arm strategies that trampolinists could integrate into their practice. The main findings are that (i) aerial twist performance is linearly correlated with the complexity of arm trajectories, (ii) moving the arms in the so-called “best tilting plane” is an efficient strategy to generate twist rotation and (iii) 3D techniques are simpler and require less effort than 2D techniques for similar twist performances.
4.1. A Wide Range of Techniques
In the literature, most optimizations of twisting somersault techniques relied on a small number of actions using parametric curves of arm kinematics, such as series of quintic functions [6,20]. This has led to refinements in timing and range of motion, but has limited the possibility of generating innovative techniques that get off the beaten track. The 3D torque-driven model combined with a multi-start approach allowed us to explore more complex and performative techniques. Techniques with a wide range of complexity were exposed (up to 4.90 twists with hand path length ranging from 0.05 m to 50.96 m). Some of them were similar to beginners’ techniques (e.g., technique I), while others were too complex to be attempted in real conditions (e.g., technique VI). Due to our problem formulation, one should notice that a compromise is required between moving the arm in the BTP to maximize twist rotation and keeping a small hand path to minimize the complexity of the technique. For example, when arms are moving during a smaller proportion of the skill, arm motion tend to be closer to the BTP, as it is more efficient. This can be seen in the magenta box of Figure 2 where a gradient (left to right) of size and color is present for similar twist rotations. These techniques expose the relevance of including penalties on the hand path length, as it enabled us to find a set of high-in-twisting and yet realistic techniques.
4.2. Robustness of Optimal Techniques
The robustness of acrobatic movements has been mainly studied by simulating movements with perturbations on kinematics and timing [8], or by maximizing the robustness of motions in a narrow search region [29]. The present study offers an alternative approach to assess the robustness of optimal acrobatic techniques by perturbing the kinematics of the first half of the movement and reoptimizing the second half. Since the twist deviation at landing was small for all selected techniques (), no technique could be excluded based on this single criterion. In this regard, the score and the convergence rate were more informative.
In the best techniques, the avatar untilts rapidly just before landing. This allows one to benefit longer from the higher twisting rate created by the large tilt angle. However, this late untilting is highly affected by the kinematic perturbations that occur in the first half of the skill (Appendix C). Therefore, reoptimization is needed to satisfy the final tilt constraint (tilt ). The optimization is more likely to converge if multiple similar solutions are present in a neighboring search region (e.g., black boxes in Figure 2). Techniques with low convergence rate due to the difficulty to satisfy the landing constraint could lead to hazardous landings. Therefore they should not be attempted by athletes [30].
Modeling mid-skill replanning by means of optimization might be appropriate if this process leads to techniques similar to the optimal (original) technique, (i.e., small score). Indeed, a high score means that arm kinematics must undergo a large change to reach a good final performance. In this case, the new technique might belong to a different family of techniques than the optimal version; athletes might not be able to re-plan their kinematics with modifications of this magnitude. In contrast, it is expected that athletes can find their way through techniques with high convergence rates and small , such as techniques I, III and IV. Technique I (Table 2) respects these criteria, but has a high score, meaning that the number of twists will be reduced while adapting to kinematic perturbations, but that landing should not be problematic. Reoptimization was more relevant than a simulation on its own to identify techniques with challenging landings (see Appendix C for an example).
4.3. Best Tilting Plane
In the literature, asymmetrical arm movements in the frontal plane have been presented as the best way to create aerial twists in straight somersaults [1]. Arm motions near the sagittal plane were even disapproved of [3], which is refuted by our optimal solutions. At the beginning and at the end of the skill, optimal 3D solutions consist of arm motions in the frontal plane, but at some points they clearly include arm movements in the sagittal plane. Escaping from the frontal plane enabled 3D-PHP techniques (III, IV and V) to outperform 2D-UHP technique (II) in terms of the number of twists, complexity and effort, reinforcing the superiority of 3D motion over 2D. Of all 3D-PHP techniques, technique IV (composed of two lowering/raising per arm, the last raising being synchronous and in the sagittal plane) has the best potential for teachability due to the least effort being involved, and the and the . A mechanical explanation of this gain in performance is further provided thanks to the BTP, introduced in this paper (Section 2.6).
The angular momentum is coincident with the athlete’s mediolateral axis at take-off and is constant throughout the skill. Aerial twist strategies aim to decrease (resp. increase) the tilt angle between the angular momentum and the twist axes to increase (resp. decrease) the twist velocity [1]. According to the equation of motion, the most direct way to transfer angular momentum from the somersault axis to the twist axis is to incline the body strictly around the tilting axis by rotating a segment in a plane parallel to the BTP in the opposite direction. Since the BTP rotates with the somersault rotation, most efficient arm trajectories must be 3D and sometimes get closer to the sagittal plane of the body (see Appendix A for more details). The concept of moving the arms in 3D to twist efficiently is a generalization of the usual advice for 2D arm strategies. Indeed, coaches are already aware of the timing importance in the execution of 2D techniques in the frontal plane [21]; it turns out that these particular instants correspond to the alignment of the BTP and of the frontal plane. As a consequence, 2D strategies usually include portions without motion between these precise instants. Our mechanical analysis thus corroborates usual 2D techniques, but 3D arm motions offer new possibilities as the BTP is always reachable, aside from the unphysiological range of arm motions. Moving segments (arms or other body segments) in the BTP is an efficient motor strategy to generate twists.
4.4. Limitations
The content of the objective function (and constraints) for generating realistic human motions remains a research challenge [31,32]. Other objective terms and weighting could be tested to better fit athletes’ maximal capacities since performance should be maximized, but the techniques should be simple enough to be executed by athletes. While coaches aim to constantly push their athletes to the limits of their capacities, the absolute ceiling of technical complexity that can be achieved by athletes remains unknown. It is especially difficult to determine complexity limits since twisting somersaults vary a lot between acrobatic sports (divers bend an elbow behind the head, skiers keep arms wider, tumblers arch their back, etc.).
In the present study, a single model morphology was tested. In future work, the sensitivity of the optimal techniques to a model’s anthropometric parameters should be assessed. Besides, the model could include other joints, such as the chest and hips [23] to provide more realistic optimal techniques. These joints could improve landing balance and the amount of twisting created. It is anticipated that a small range of motion for the hips and chest may significantly simplify the arm kinematics for similar twist rotations and slightly increase the contribution in cat twist. In the present study, the effects of cat twist strategies from arm motions were investigated as in [28] by simulating movements without initial velocity. Due to the small number of joints of our model, cat twist strategies were responsible for a very small portion of the twisting. It is still biomechanically relevant to consider cat twist strategies to understand some behaviors that are not explained by the BTP, even though they are of no relevance for the sports community.
The kinematic perturbations used in the present study were consistent with the literature [13]. Nevertheless, future work could include perturbations on the controls (i.e., joint torque) to consider both kinematic and dynamic variability, since both are interdependent sources of variability in rotational environment [33]. Finally, our robustness analysis was conducted after the optimization, keeping the optimization computation time acceptable. However, the extent to which athletes can adapt by reoptimizing the end of their movement is unknown and should be further investigated. Including perturbations into the optimization, such as in [13], might be challenging for big scale OCP (approximately 7200 variables in the present study in comparison with less than 50 in [13]).
5. Conclusions
This research shows that athletes could gain in performance by incorporating 3D motions to their techniques, especially by moving their segments in the best tilting plane (i.e., plane formed by the twist and angular momentum axes). We provided three innovative and realistic 3D arm techniques for a triple twist backward somersault that are robust to kinematic perturbations. The selected 3D arm techniques were less complex, required less effort and had better potential for landing than the equivalent 2D technique, establishing the superiority of 3D arm techniques. With the comprehension brought by this work, coaches could better guide their future athletes throughout the learning of 3D arm techniques.
Supplementary Materials
The following are available online at https://www.mdpi.com/2076-3417/10/23/8363/s1, Video S1: Technique I, Video S2: Technique II, Video S3: Technique III, Video S4: Technique IV, Video S5: Technique V, Video S6: Technique VI.
Author Contributions
Conceptualization, E.C., F.B., L.D. and M.B.; Data curation, E.C., F.B. and M.B.; Formal analysis, E.C. and F.B.; Funding acquisition, M.B.; Investigation, E.C., F.B., L.D. and M.B.; Methodology, E.C., F.B., L.D. and M.B.; Software, E.C., F.B. and L.D.; Supervision, M.B.; Visualization, E.C.; Writing–original draft, E.C., F.B. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Mitacs Acceleration grant number IT11976 and Institut National du Sport du Québec.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| OCP | Optimal control problem |
| BTP | Best tilting plane |
| DoF | Degree-of-freedom |
| PHP | penalized hand path |
| UHP | unpenalized hand path |
| RMS | root mean square |
Appendix A. The Best Tilting Plane
A backward twisting somersault is displayed in Figure A1 at different instants ( and 3). This representation allows getting better geometrical insights into the concept of BTP. As explained before, the BTP is spanned by the somersault and the twisting axes (i.e., rotating only with the somersault rotation of the avatar). During the backward somersault, the BTP is rotating around the somersault axis, the twist axis is changing inclination inside the BTP and the body is rotating around the twist axis (Figure A1a). To understand the notion of BTP, it is easier to look at Figure A1b, which is a representation of the same motion but in a frame fixed to the BTP, thereby rotating around the somersault axis.
The avatar twisting while adducting its arm is depicted in Figure A2. The snapshots are depicted in a plane perpendicular to the somersault axis, so that the BTP is orthogonal to the page. In the middle of the 2D adduction, the arm is moving in the BTP only for a short instant, when the frontal plane and the BTP are parallel. As a consequence, every other time they do not coincide, only a fraction of the rotation induced by the raising/lowering of the arms in the frontal plane will be converted into tilt rotation. In the most extreme case, when the frontal plane and the BTP are orthogonal (first and last frame of the top kinogram of Figure A2), raising/lowering the arms yields a rotation around the somersault axis without any rotation around the global tilt axis. In contrast, 3D adduction allows the arm’s movement in the BTP during the whole movement to be fully converted into tilt. This explains why it is more challenging to generate twisting with 2D techniques than with 3D techniques. Indeed, 2D techniques lack efficiency for bringing the twisting and the somersault axes closer together, which is the condition for creating twisting in pure aerial techniques.
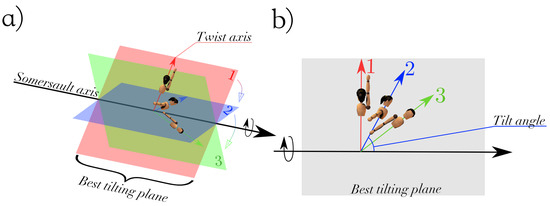
Figure A1.
Illustration of the BTP. (a) 3D representation, with the somersault axis (in black), fixed in an inertial frame and the twist axis (red, blue and green) at different instants ( and 3), rotating due to the somersaulting and tilting. At each instant, the BTP is spanned by the somersault and the twisting axes. (b) 2D representation, in a frame fixed to the BTP (rotating around the somersault axis). The twist axis rotates in this plane, due to the tilting of the body.
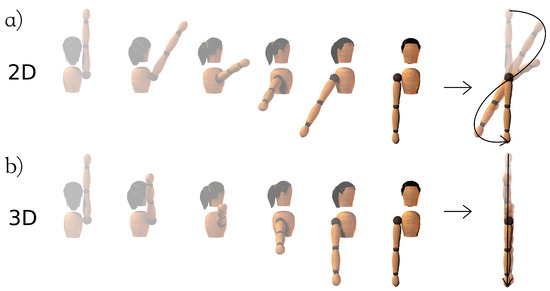
Figure A2.
Kinograms of a 2D adduction of the arm (a) and the best-case possible of a 3D adduction of the arm happening in the BTP (b). Both kinograms are presented from the BTP point of view. To the right-hand side of the arrows, the snapshots from the kinograms are superimposed to show arm trajectory.
Appendix B. Cat and Aerial Contributions
An example of the subdivision into aerial and cat twist sections for technique V is presented in Figure A3. Due to the absence of twist velocity at the beginning of the skill, the first adduction of the left arm can be executed at the same time in the frontal plane and close to the BTP. The left arm stays adducted until the frontal plane gets close to the BTP again; then it is abducted close to the frontal plane. The adduction/abduction of the left arm is executed close to the BTP (blue line on the graph is close to zero in blue shaded regions) to maximize its tilt potential. Simultaneously, the right arm executes a 3D add-abduction which is far from the BTP, but has a small hand path and generates a small number of cat twist rotations (bold orange line is of opposite sign to thin orange line in the orange shaded region). Then, the avatar stays still to minimize its inertia, twisting for an important portion of the skill. At last, the right arm is 3D add-abducted close to the BTP to decrease tilt in preparation for landing. An attentive reader would notice that during the 3D adduction of the right arm, cat twist is generated in the opposite direction to the twist rotation (thin orange line below zero while being of opposite sign to bold orange line); however, it is counterbalanced by cat twist in the proper direction, so that at the end of the simulation, the cat twist rotation is small but positive.
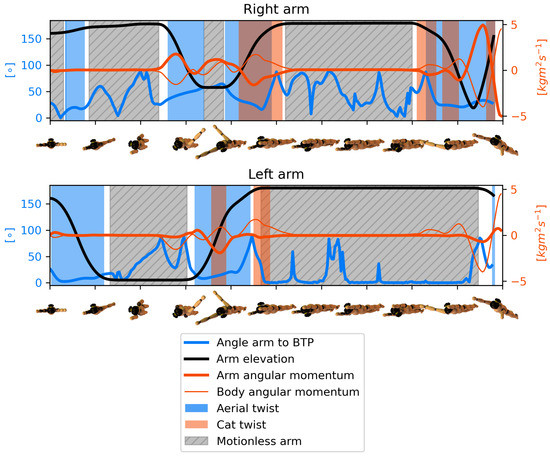
Figure A3.
Sections of technique V involving cat (orange shaded) and aerial (blue shaded) twist strategies according to criteria previously mentioned in Section 3.3. Regions where arms are not moving are gray shaded and hatched. Arm’s (bold orange line) and body’s (thin orange line) angular momentum expressed in the body’s reference frame, the angle of deviation of the arm movement from the BTP (blue line) and the angle between the body and the arm (black line) as functions of time are also presented. Under the graphs are snapshots of the body configuration seen from the top of the head at corresponding instants.
Appendix C. Reoptimization vs. Simulation
To illustrate the need for reoptimization of the last part of the skill, the difference in final body orientation between the perturbed simulations and the reoptimizations of technique III is presented in Figure A4. Kinematic perturbations in the first half of the skill result in up to in tilt at landing and only a deviation in twist angle of . After reoptimization of the second half of the performance, tilt angle with respect to the landing constraints () and twist deviation is .
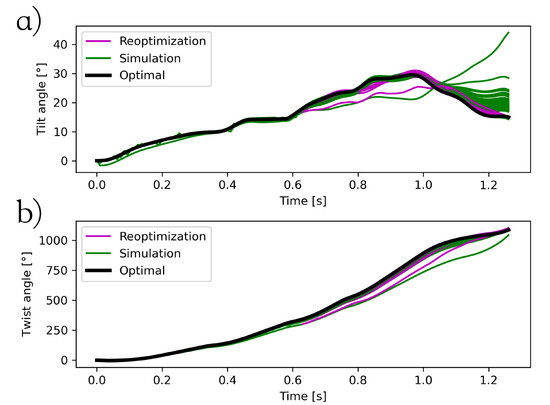
Figure A4.
Time histories of the tilt (a) and twist (b) angles for 100 simulations in perturbed conditions for the first half of technique III with (pink lines) and without (green lines) reoptimization of the second half of the skill. The optimal (original technique III) is presented (black line) for reference.
Appendix D. Performance of Cat Twist Strategies

Table A1.
Number of twists generated using cat twist strategies.
Table A1.
Number of twists generated using cat twist strategies.
| Technique | I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|
| Cat twist | − | − | ||||
| Total twist |
References
- Frohlich, C. The physics of somersaulting and twisting. Sci. Am. 1980, 242, 154–165. [Google Scholar] [CrossRef] [PubMed]
- Sanders, R.H. Effect of ability on twisting techniques in forward somersaults on the trampoline. J. Appl. Biomech. 1995, 11, 267–287. [Google Scholar] [CrossRef]
- Yeadon, M.F. Learning how to twist fast. In Applied Proceedings of the XVIIth International Symposium on Biomechanics in Sports–Acrobatics; School of Biomedical and Sport Sciences, Edith Cowan University: Perth, Australia, 1999; pp. 37–47. [Google Scholar]
- Dullin, H.R.; Tong, W. Twisting somersault. SIAM J. Appl. Dyn. Syst. 2016, 15, 1806–1822. [Google Scholar] [CrossRef]
- Yeadon, M.R. The biomechanics of twisting somersaults Part IV: Partitioning performances using the tilt angle. J. Sports Sci. 1993, 11, 219–225. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yeadon, M.R. The limits of aerial twisting techniques in the aerials event of freestyle skiing. J. Biomech. 2013, 46, 1008–1013. [Google Scholar] [CrossRef]
- Bailly, F.; Charbonneau, E.; Danès, L.; Begon, M. Optimal 3D arm strategies for maximizing twist rotation during somersault of a rigid-body model. Multibody Syst. Dyn. 2020, 1–17. [Google Scholar] [CrossRef]
- Yeadon, M.R.; Mikulcik, E. The control of non-twisting somersaults using configuration changes. J. Biomech. 1996, 29, 1341–1348. [Google Scholar] [CrossRef][Green Version]
- Huchez, A.; Haering, D.; Holvoet, P.; Barbier, F.; Begon, M. Differences Between Expert and Novice Gymnasts Performance of a Counter Movement Forward in Flight on Uneven Bars. Sci. Gymnast. J. 2016, 8, 31–41. [Google Scholar]
- Sayyah, M.; Yeadon, M.; Hiley, M.J.; King, M.A. Adjustment in the Flight Phase of 1m Springboard Forward Pike Dives. ISBS Proc. Arch. 2017, 35, 16. [Google Scholar]
- Heinen, T.; Walter, N.; Hennig, L.; Jeraj, D. Spatial Perception of Whole-body Orientation Depends on Gymnasts’ Expertise. Sci. Gymnast. J. 2018, 10, 5–15. [Google Scholar]
- Balter, S.G.; Stokroos, R.J.; Akkermans, E.; Kingma, H. Habituation to galvanic vestibular stimulation for analysis of postural control abilities in gymnasts. Neurosci. Lett. 2004, 366, 71–75. [Google Scholar] [CrossRef]
- Hiley, M.J.; Yeadon, M.R. Investigating optimal technique in a noisy environment: Application to the upstart on uneven bars. Hum. Mov. Sci. 2013, 32, 181–191. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Mombaur, K. Performing Open-Loop Stable Flip-Flops—An Example for Stability Optimization and Robustness Analysis of Fast Periodic Motions. In Fast Motions in Biomechanics and Robotics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 253–275. [Google Scholar]
- Ashby, B.M.; Delp, S.L. Optimal control simulations reveal mechanisms by which arm movement improves standing long jump performance. J. Biomech. 2006, 39, 1726–1734. [Google Scholar] [CrossRef] [PubMed]
- Spägele, T.; Kistner, A.; Gollhofer, A. A multi-phase optimal control technique for the simulation of a human vertical jump. J. Biomech. 1999, 32, 87–91. [Google Scholar] [CrossRef]
- Yeadon, M.R.; Hiley, M.J. The mechanics of the backward giant circle on the high bar. Hum. Mov. Sci. 2000, 19, 153–173. [Google Scholar] [CrossRef]
- Bharadwaj, S.; Duignan, N.; Dullin, H.R.; Leung, K.; Tong, W. The diver with a rotor. Indag. Math. 2016, 27, 1147–1161. [Google Scholar] [CrossRef][Green Version]
- Yeadon, M.R. Airborne Movements: Somersaults and Twists. In Handbook of Human Motion; Springer: Cham, Switzerland, 2017; pp. 1–19. [Google Scholar]
- Yeadon, M.R.; Hiley, M.J. Twist limits for late twisting double somersaults on trampoline. J. Biomech. 2017, 58, 174–178. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yeadon, M.R. Twisting Somersaults; SB & MC: Loughborough, UK, 2015. [Google Scholar]
- Featherstone, R. Rigid Body Dynamics Algorithms; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Yeadon, M.R. The simulation of aerial movement—II. A mathematical inertia model of the human body. J. Biomech. 1990, 23, 67–74. [Google Scholar] [CrossRef]
- Namdari, S.; Yagnik, G.; Ebaugh, D.D.; Nagda, S.; Ramsey, M.L.; Williams, G.R., Jr.; Mehta, S. Defining functional shoulder range of motion for activities of daily living. J. Shoulder Elb. Surg. 2012, 21, 1177–1183. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Huchez, A.; Haering, D.; Holvoët, P.; Barbier, F.; Begon, M. Local versus global optimal sports techniques in a group of athletes. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 829–838. [Google Scholar] [CrossRef] [PubMed]
- Decatoire, A. Analyse Tri-Dimensionnelle de La Gestion des Mouvements Vrillés en Gymnastique: La Simulation: Vers un Outil de Formation des Entraîneurs en Activités Acrobatiques. Ph.D. Thesis, Université de Poitiers, Poitiers, France, 2004. [Google Scholar]
- Hiley, M.J.; Yeadon, M.R. Optimisation of high bar circling technique for consistent performance of a triple piked somersault dismount. J. Biomech. 2008, 41, 1730–1735. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Grapton, X.; Lion, A.; Gauchard, G.C.; Barrault, D.; Perrin, P.P. Specific injuries induced by the practice of trampoline, tumbling and acrobatic gymnastics. Knee Surg. Sports Traumatol. Arthrosc. 2013, 21, 494–499. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Gu, Y.; Fan, X.; Cheng, H. Multi-Objective Optimization of Virtual Human Motion Posture for Assembly Operation Simulation. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016; American Society of Mechanical Engineers: New York, NY, USA; Volume 50077, p. V01AT02A056. [Google Scholar]
- Mombaur, K.; Clever, D. Inverse optimal control as a tool to understand human movement. In Geometric and Numerical Foundations of Movements; Springer: Cham, Switzerland, 2017; pp. 163–186. [Google Scholar]
- Tong, C.; Wolpert, D.M.; Flanagan, J.R. Kinematics and dynamics are not represented independently in motor working memory: Evidence from an interference study. J. Neurosci. 2002, 22, 1108–1113. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).