A Posteriori Detection of Numerical Locking in hpq-Adaptive Finite Element Analysis
Abstract
1. Introduction
1.1. State-of-the-Art Issues
1.1.1. Theoretical and Numerical Research of Locking Phenomena
1.1.2. Overcoming the Locking Phenomena
1.1.3. Detection and Assessment of the Locking
1.2. The Applied Methodology
1.3. Novelty of the Paper
2. Preliminaries
2.1. Model Problems
2.2. Locking Phenomena
3. Locking Detection, Assessment, and Resolution
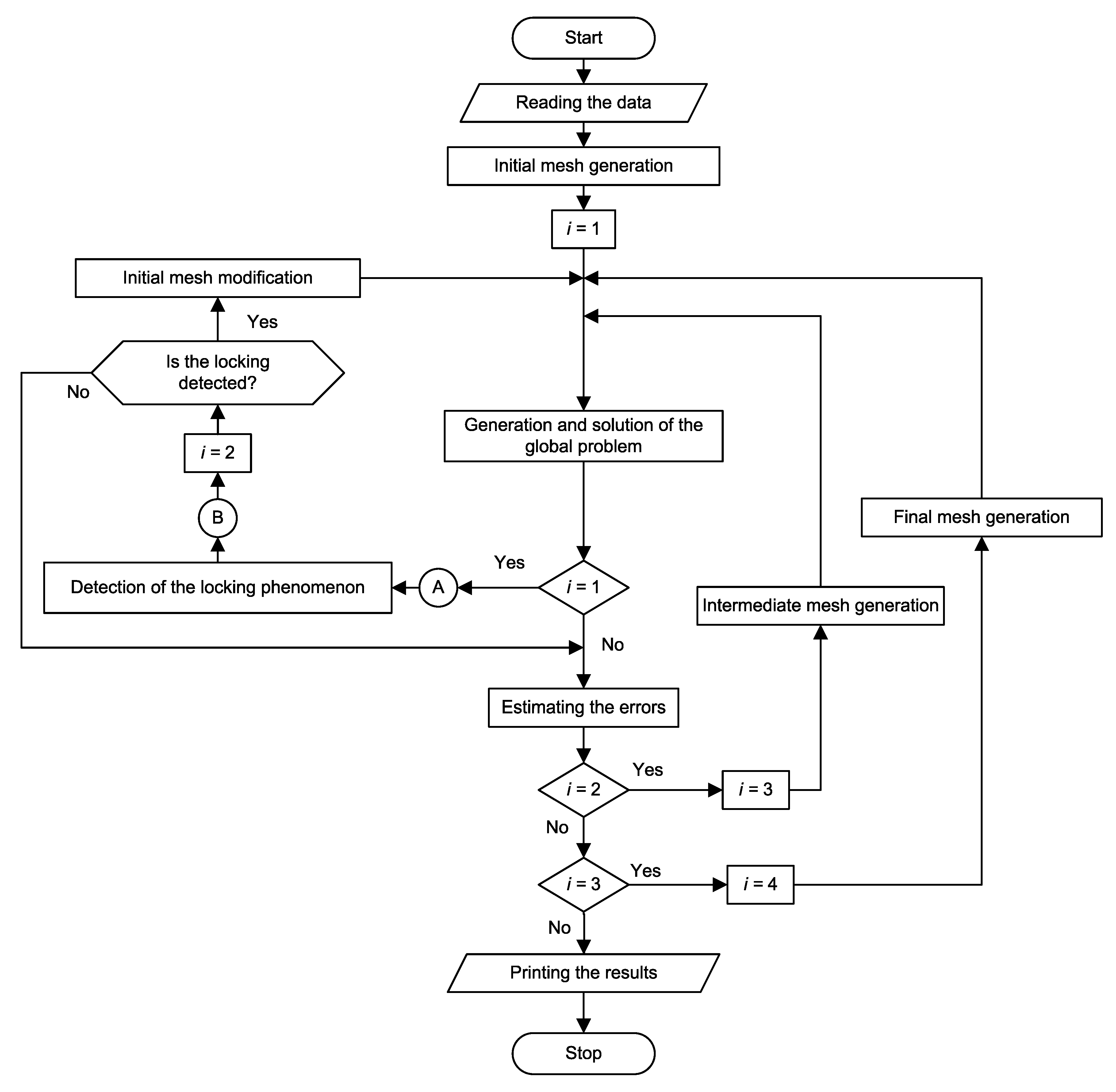
3.1. The Idea and Algorithm of a Posteriori Phenomenon Detection
3.1.1. Solutions from the Equilibrated Residual Method
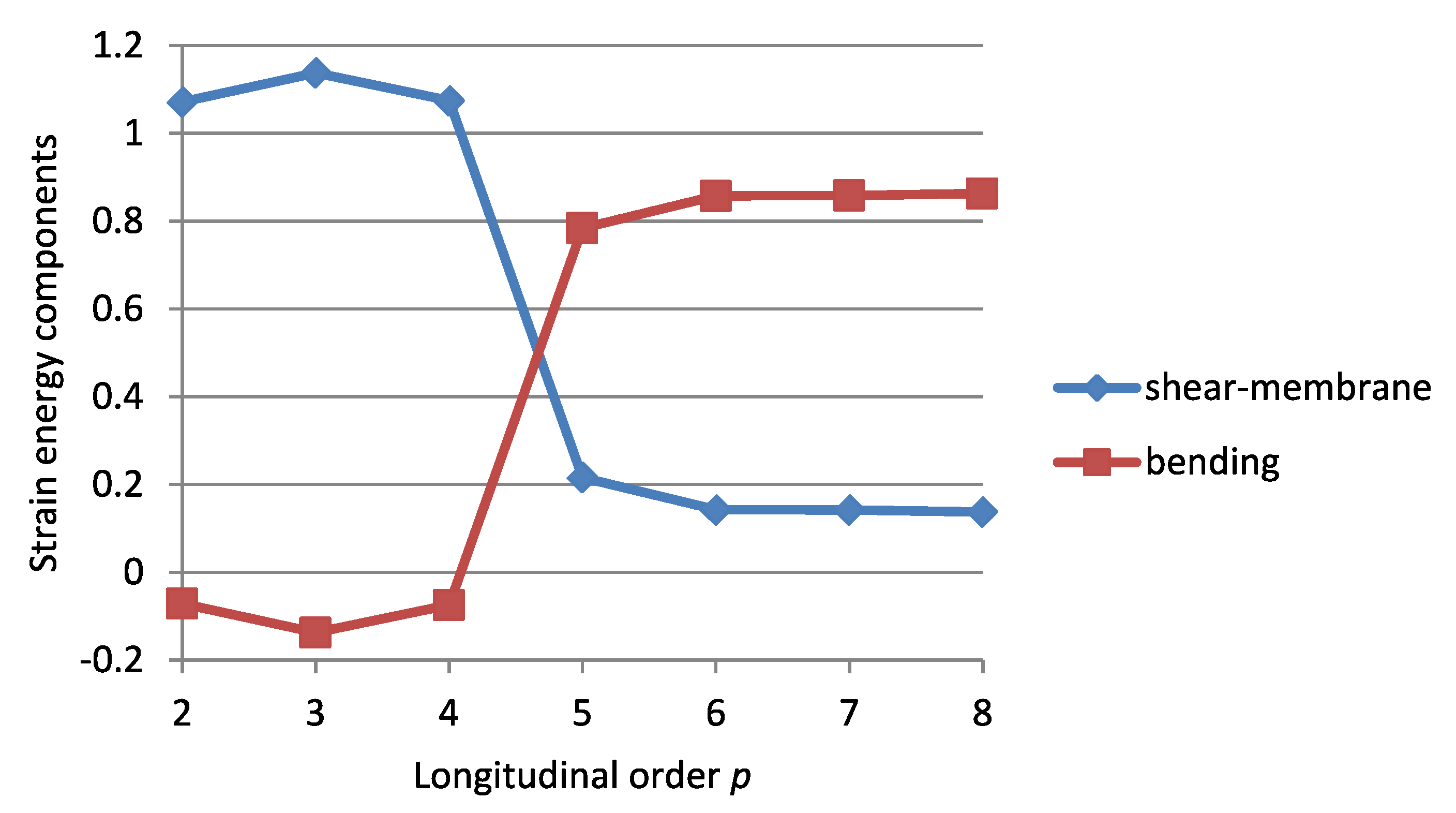
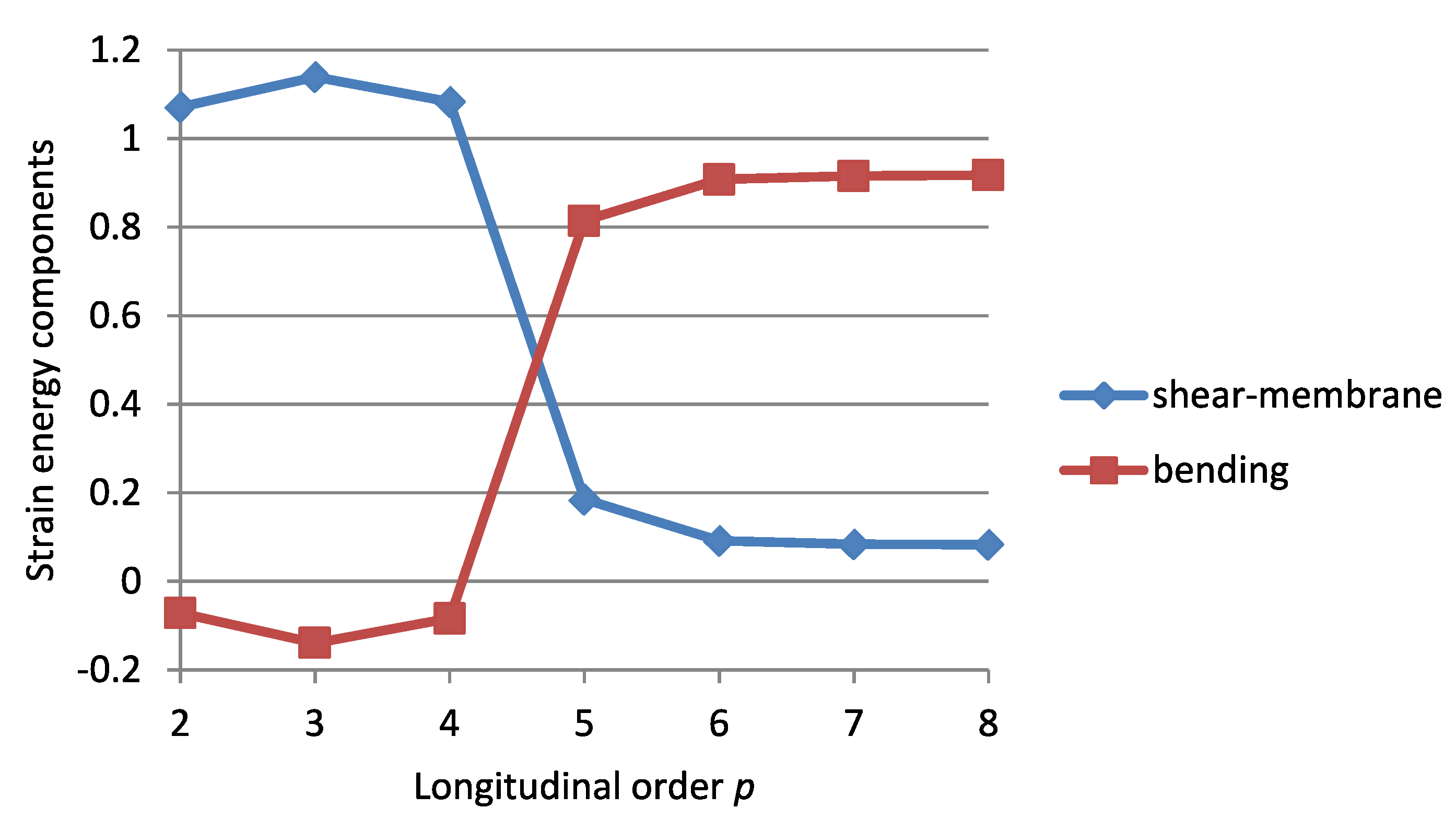
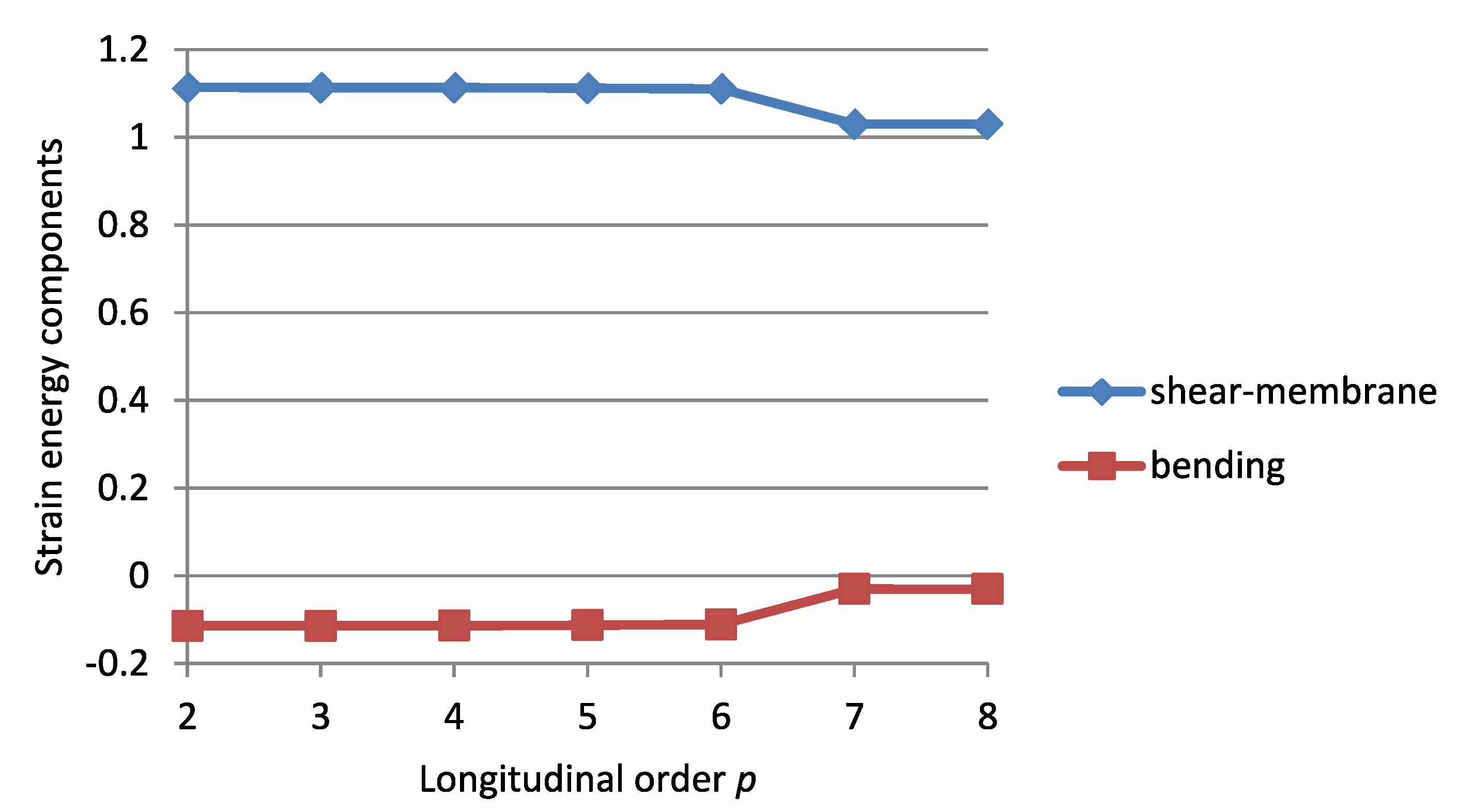
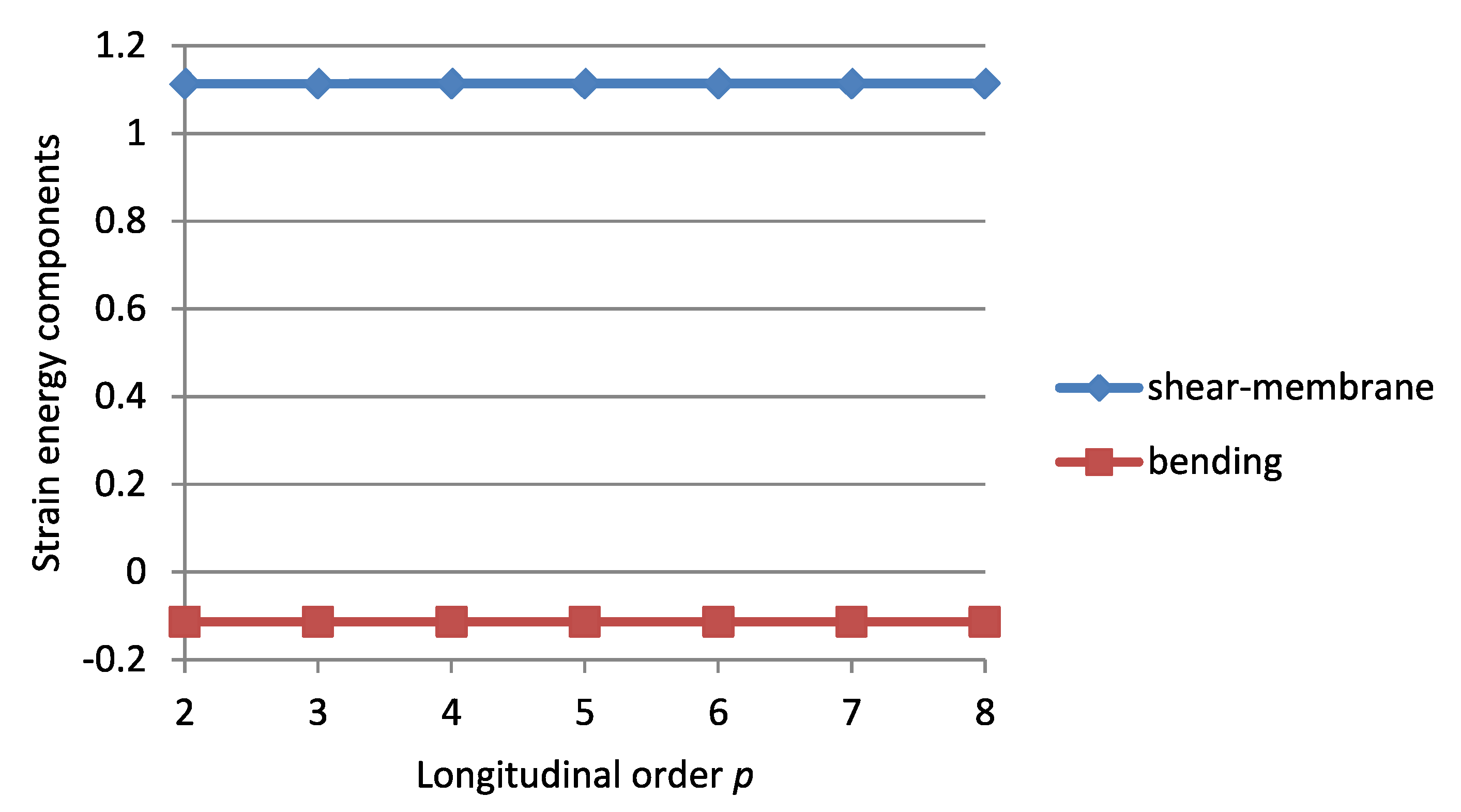
3.1.2. Check on Bending-Dominance of the Solution
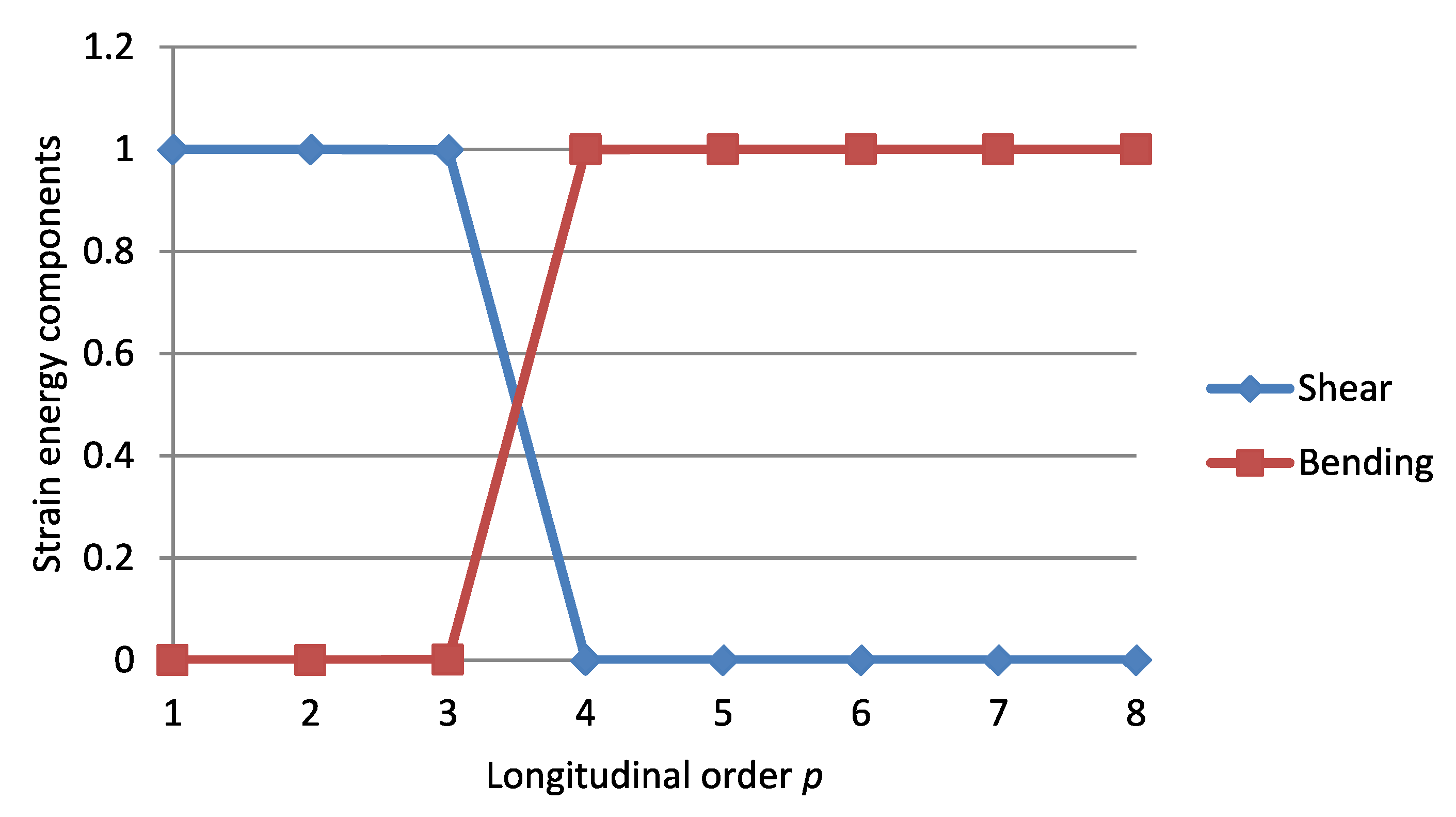
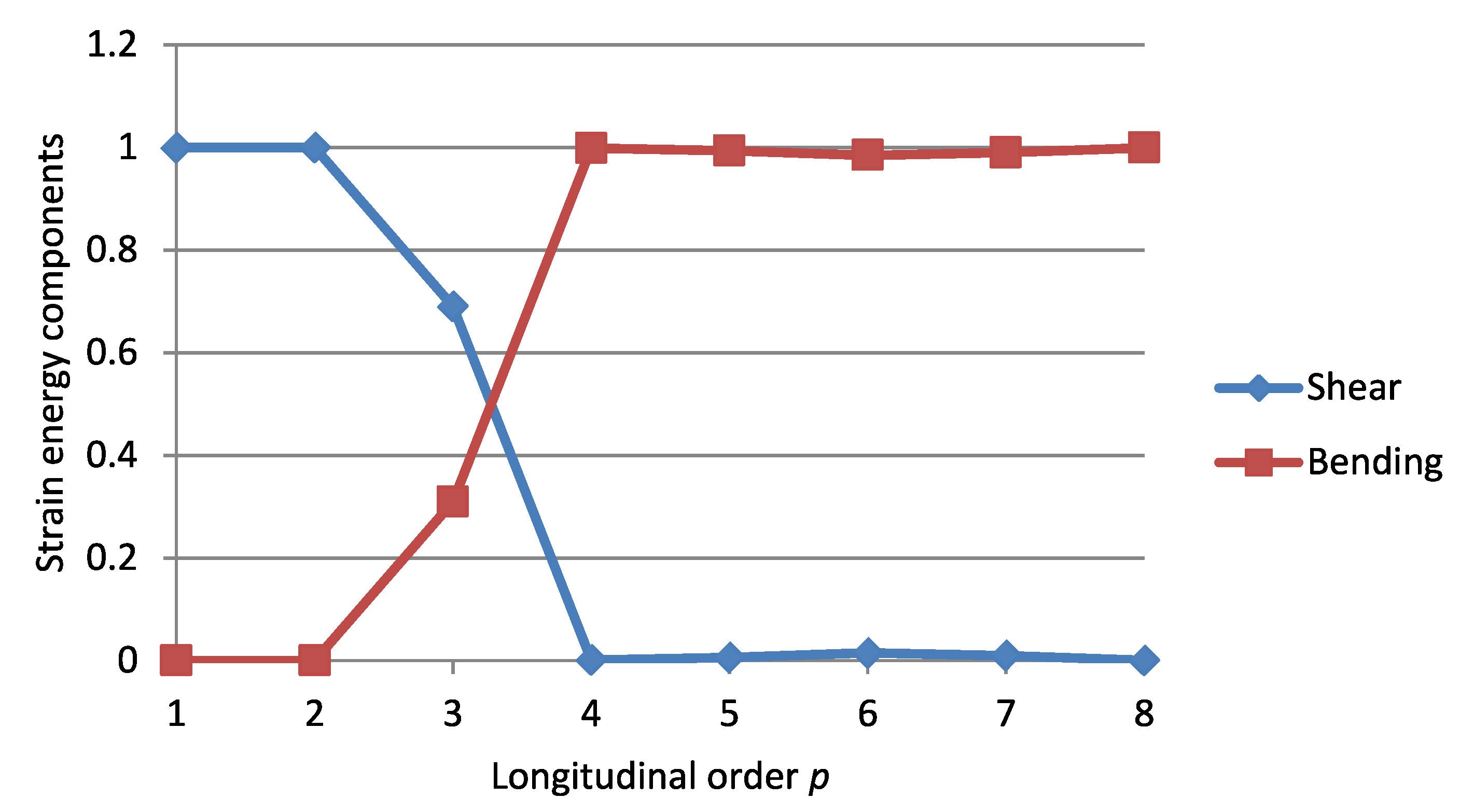
Strain Energy Components
The Criterion
3.1.3. Sensitivity Analysis of the Local Solutions
3.1.4. The Detection Algorithm
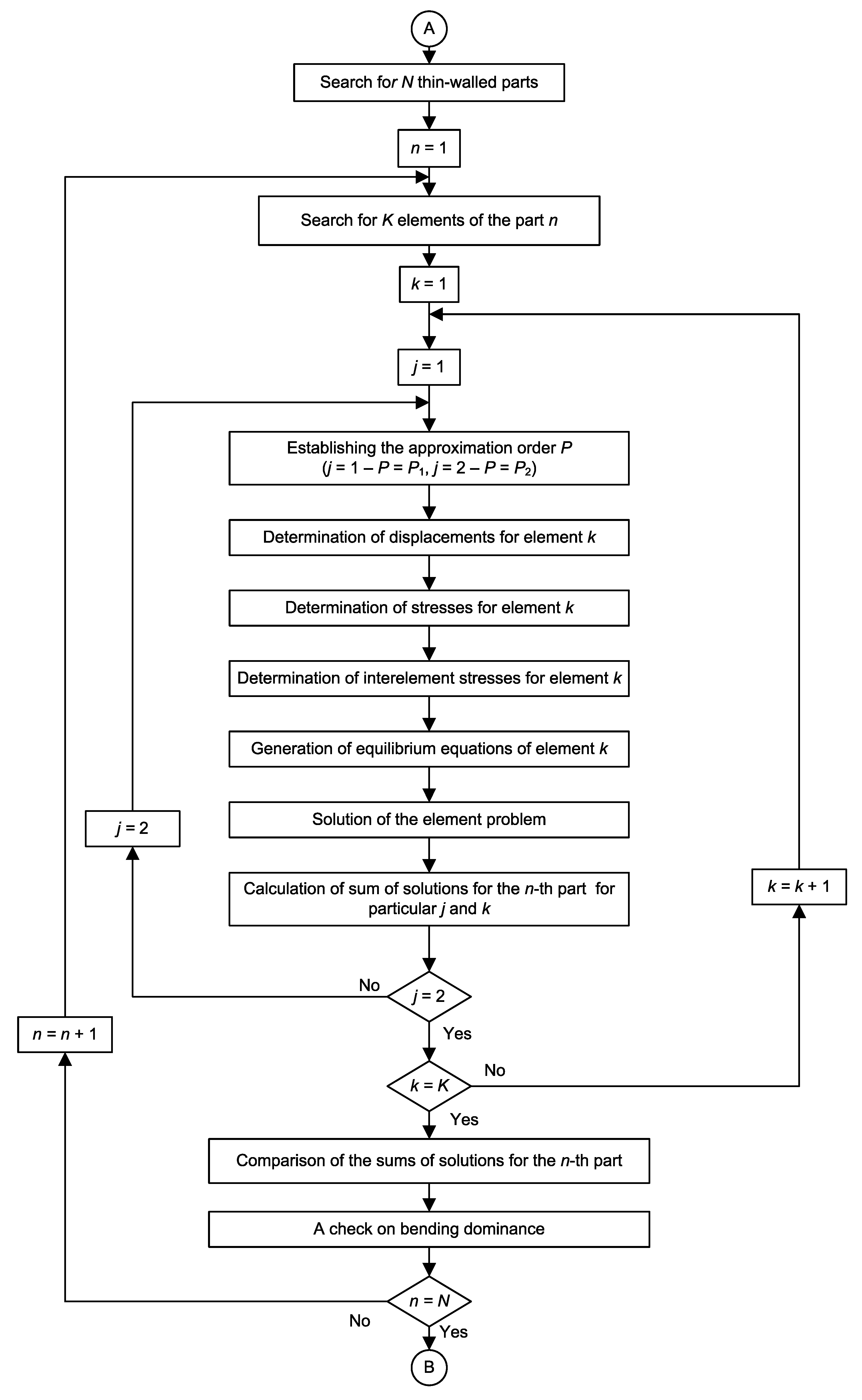
3.2. Calculation of the Optimized Value of p
3.2.1. The Idea
3.2.2. The Algorithm
4. Verification and Utilization of the Proposed Tools
4.1. Model Problems
4.2. Local Problems Solutions Versus Global Solutions
5. Effectivity of the Method in Model Problems
5.1. Problems and Methodology
5.2. Numerical Examples
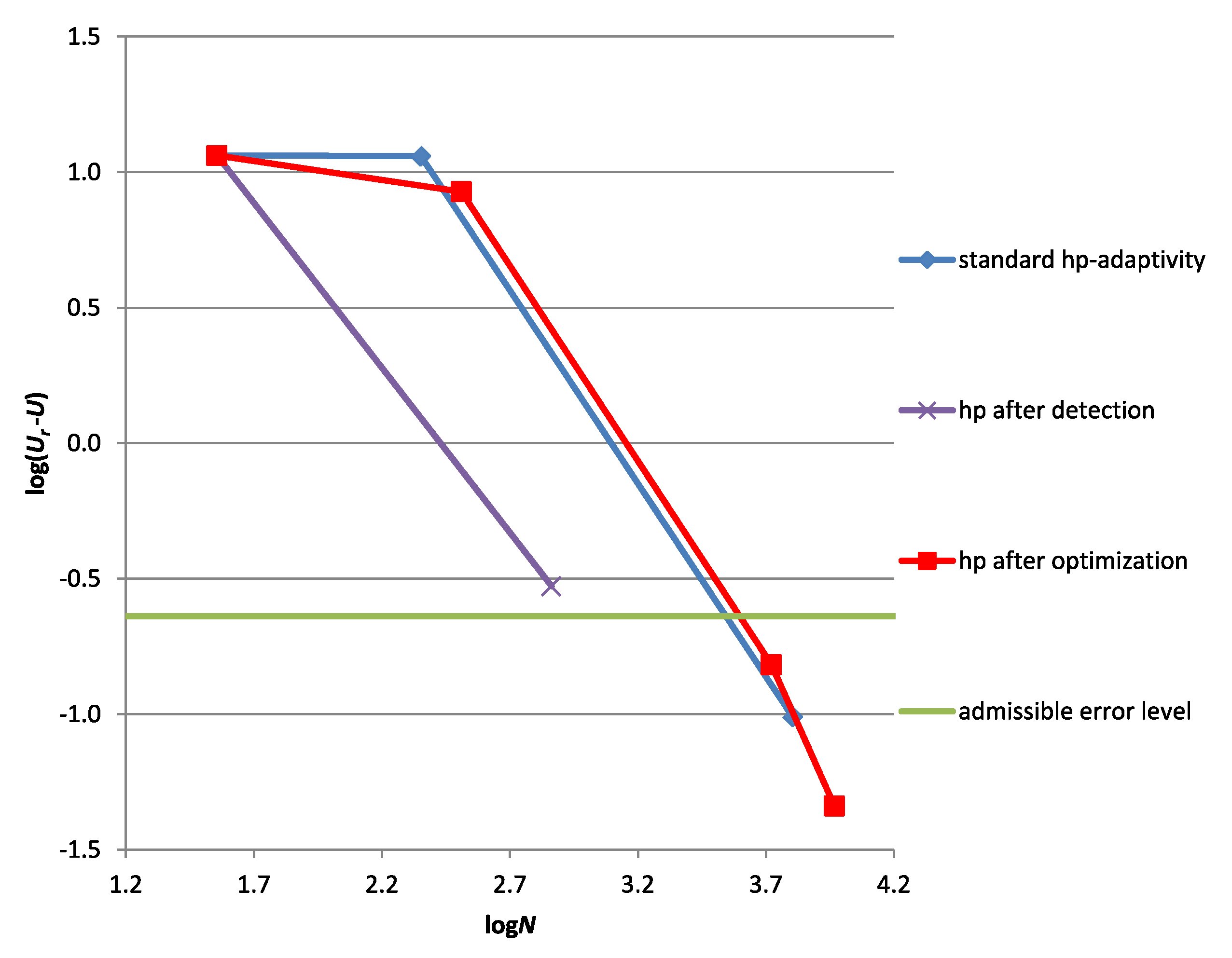
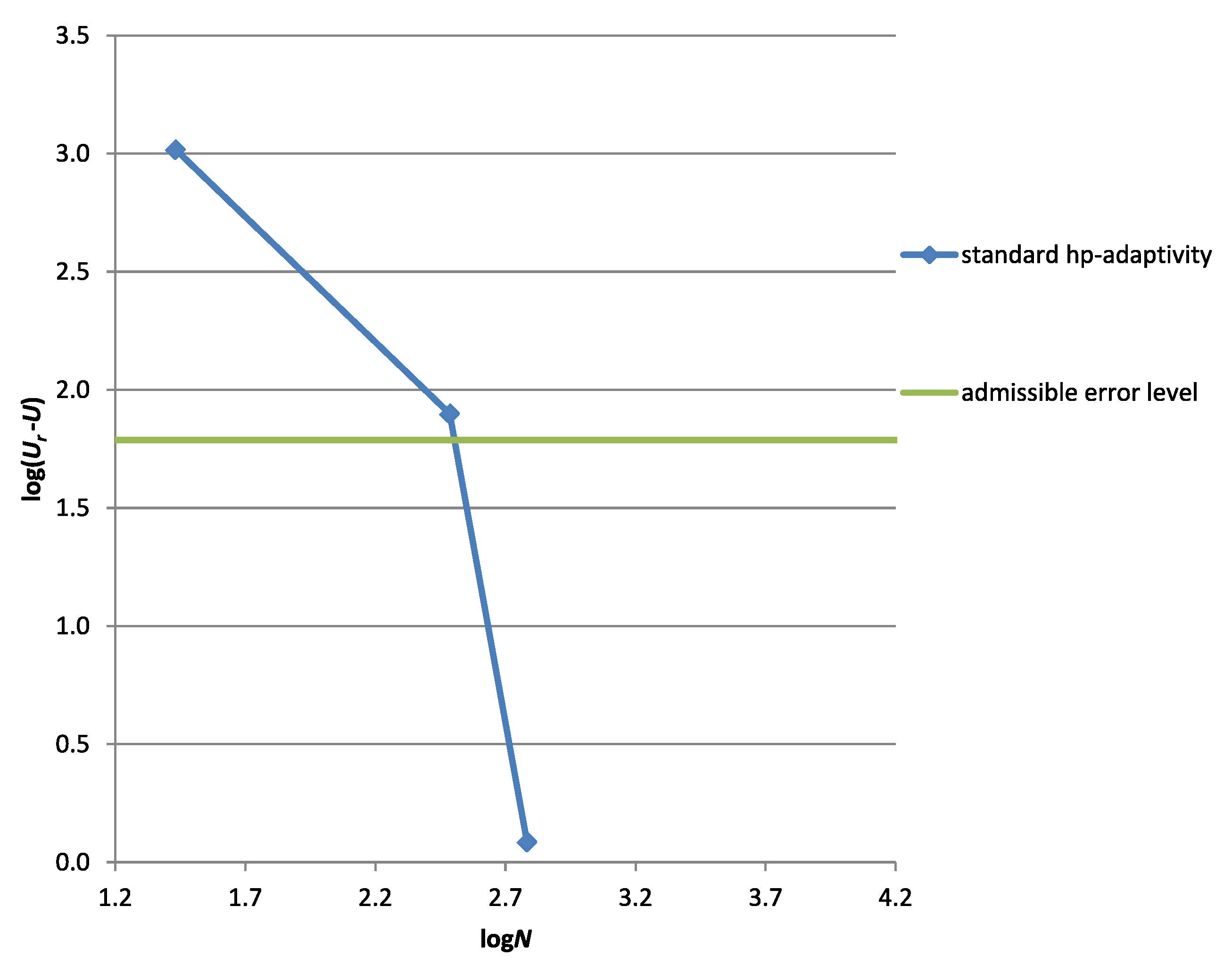
5.2.1. A Quarter of a Bending Dominated Plate
Data
Results
Discussion
5.2.2. A Bending-Dominated Plate
Data
Results
Discussion
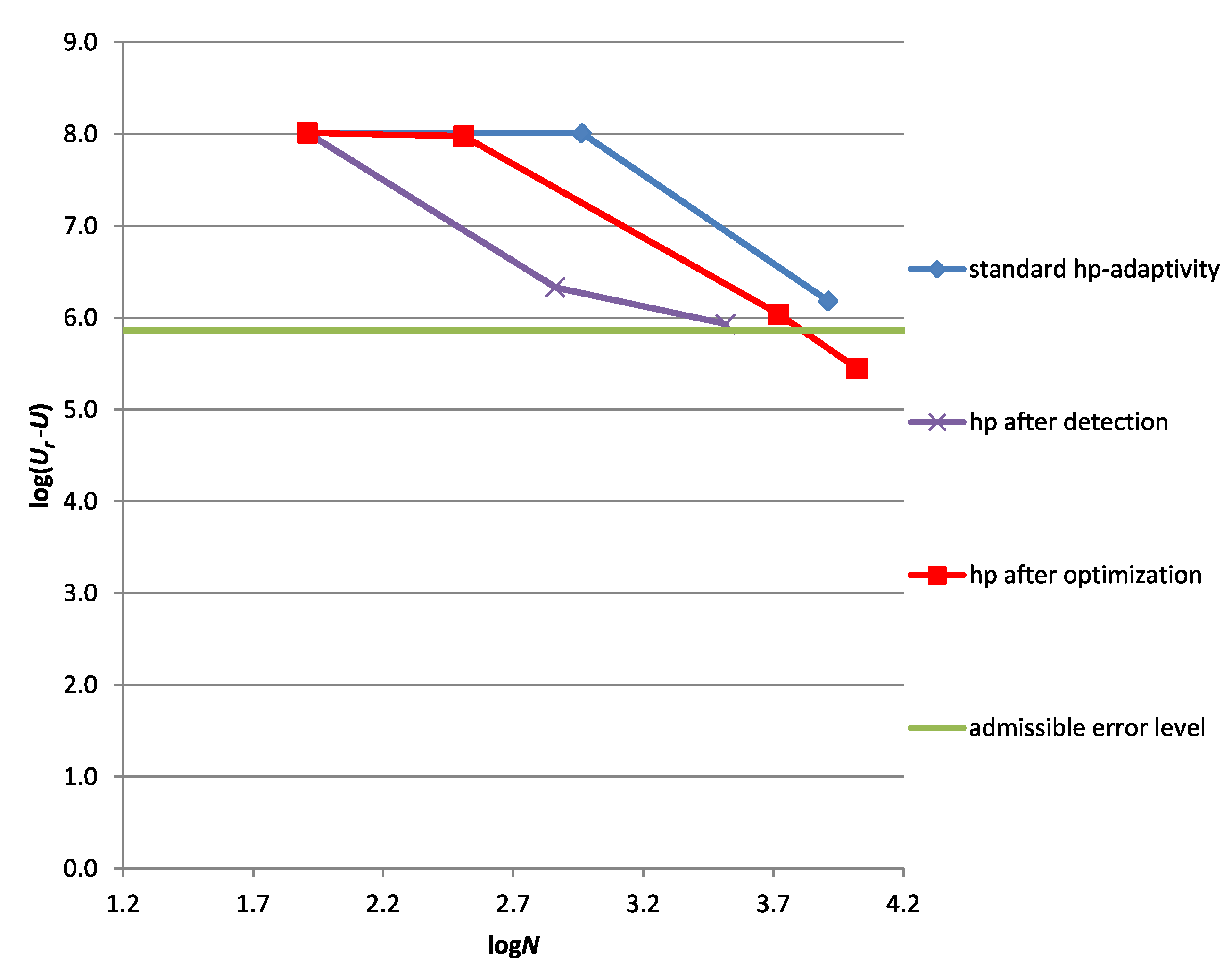
5.2.3. A Quarter of a Bending-Dominated Shell
Data
Results
Discussion
5.2.4. An Octant of a Membrane-Dominated Shell
Data
Results
Discussion
5.2.5. Generalizations
- The adaptation mode based on standard -adaptivity may fail when applied to the problems where the locking phenomena are present.
- The adaptation mode which allows modification of the initial mesh with the maximum possible longitudinal order of approximation may lead to underestimation of the final error value.
- The course of adaptation with the modification of the initial mesh by means of the optimized value of the longitudinal order of approximation is more effective in achieving the admissible error value than the previous two courses of adaptation.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Babuška, I.; Suri, M. Locking effects in finite element approximation of elasticity problems. Numer. Math. 1992, 62, 439–463. [Google Scholar] [CrossRef]
- Suri, M. Analytical and computational assessment of locking in the hp finite element method. Comput. Methods Appl. Mech. Eng. 1996, 133, 347–371. [Google Scholar] [CrossRef]
- Schwab, C.; Suri, M. Locking and boundary layer effects in the finite element approximation of the Reissner-Mindlin plate model. Proc. Symp. Appl. Math. 1994, 48, 367–371. [Google Scholar]
- Pitkäranta, J. The problem of membrane locking in finite element analysis of cylindrical shells. Numer. Math. 1992, 61, 523–542. [Google Scholar] [CrossRef]
- Cho, J.R.; Oden, J.T. Locking and boundary layer in hierarchical models for thin elastic structures. Comput. Methods Appl. Mech. Eng. 1997, 149, 33–48. [Google Scholar] [CrossRef]
- Stolarski, H.; Belytschko, T. Shear and membrane locking in curved C0 elements. Comput. Methods Appl. Mech. Eng. 1983, 41, 279–296. [Google Scholar] [CrossRef]
- Pinsky, P.M.; Jasti, R.V. A mixed finite element formulation for Reissner-Mindlin plates based on the use of bubble function. Int. J. Numer. Methods Eng. 1989, 28, 1677–1702. [Google Scholar] [CrossRef]
- Kang, D.S.; Pian, T.H.H. A 20-dof hybrid stress general shell element. Comput. Struct. 1988, 30, 789–794. [Google Scholar] [CrossRef]
- Ayad, R.; Dhatt, G.; Batoz, J.L. A new hybrid-mixed variational approach for Reissner-Mindlin plates. The MiSP model. Int. J. Numer. Methods Eng. 1998, 42, 1149–1179. [Google Scholar] [CrossRef]
- Cohen, G.; Grob, P. Mixed Higher Order Spectral Finite Elements for Reissner-Mindlin Equations. SIAM J. Sci. Comput. 2007, 29, 986–1005. [Google Scholar] [CrossRef]
- Guo, Y.H.; Yu, G.Z.; Xie, X.P. Uniform analysis of a stabilized hybrid finite element method for Reissner-Mindlin plates. Sci. China Math. 2013, 56, 1727–1742. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Too, J.; Taylor, R.L. Reduced integration technique in general analysis of plates and shells. Int. J. Numer. Methods Eng. 1971, 3, 275–290. [Google Scholar] [CrossRef]
- Jacquotte, O.P.; Oden, J.T. Analysis of hourglass instabilities and control in underintegrated finite element methods. Comput. Methods Appl. Mech. Eng. 1984, 44, 339–363. [Google Scholar] [CrossRef]
- Reese, S.; Wriggers, P. A stabilization technique to avoid hourglassing in finite elasticity. Int. J. Numer. Methods Eng. 2000, 48, 79–109. [Google Scholar] [CrossRef]
- Adam, C.; Bouabdallah, S.; Zarroug, M.; Maitournam, H. Improved numerical integration for locking treatment in isogeometric structural elements. Part II: Plates and shells. Comput. Methods Appl. Mech. Eng. 2015, 284, 106–137. [Google Scholar] [CrossRef]
- Abed-Meraim, F.; Combescure, A. A physically stabilized and locking-free formulation of the (SHB8PS) solid-shell element. Eur. J. Comput. Mech. 2007, 16, 1037–1072. [Google Scholar] [CrossRef]
- Wempner, G.; Oden, J.T.; Kross, D.A. Finite element analysis of thin shells. J. Engrg. Mech. Div. (ASCE) 1968, 94, 1273–1294. [Google Scholar]
- Crisfield, M.A. A four-noded thin-plate bending element using shear constraints–A modified version of Lyon’s element. Comput. Methods Appl. Mech. Eng. 1983, 38, 93–120. [Google Scholar] [CrossRef]
- Areias, P.M.A.; Song, J.H.; Belytschko, T. A finite strain quadrilateral shell element based on discrete Kirchhoff-Love constraints. Int. J. Numer. Methods Eng. 2005, 64, 1166–1206. [Google Scholar] [CrossRef]
- Kapuria, S.; Kulkarni, S.D. An improved discrete Kirchhoff quadrilateral element based on third order zigzag theory for static analysis of composite and sandwich plates. Int. J. Numer. Methods Eng. 2007, 69, 1948–1981. [Google Scholar] [CrossRef]
- Carpenter, N.; Belytschko, T.; Stolarski, H. Improvements in 3-node triangular shell element. Int. J. Numer. Methods Eng. 1986, 23, 1643–1667. [Google Scholar] [CrossRef]
- Naganarayana, B.P.; Prathap, G.; Dattaguru, B.; Ramamurty, T.S. A field-consistent and variationally correct representation of transverse shear strains in the nine-noded plate element. Comput. Methods Appl. Mech. Eng. 1992, 97, 355–374. [Google Scholar] [CrossRef]
- MacNeal, R.H. Derivation of element stiffness matrices by assumed strain distribution. Nuclear Eng. Des. 1982, 70, 3–12. [Google Scholar] [CrossRef]
- Stolarski, H.; Chiang, M.Y.M. Assumed strain formulation for triangular C0 plate elements based on a weak form of the Kirchhoff constraints. Int. J. Numer. Methods Eng. 1989, 28, 2323–2338. [Google Scholar] [CrossRef]
- Militello, C.; Felippa, C.A. A variational justification of the assumed natural strain formulation of finite elements–II. The C0 four node plate element. Comput. Struct. 1990, 34, 438–444. [Google Scholar] [CrossRef]
- Bui, Q.V.; Papeleux, L.; Ponthot, J.P. Numerical simulation of springback using enhanced assumed strain elements. J. Mater. Process. Technol. 2004, 153–154, 314–318. [Google Scholar] [CrossRef]
- Reinoso, J.; Paggi, M.; Linder, C. Phase field modeling of brittle fracture for enhanced assumed strain shells at large deformations: Formulation and finite element implementation. Comput. Mech. 2017, 59, 981–1001. [Google Scholar] [CrossRef]
- Dasgupta, S.; Sengupta, D. A high-order triangular plate bending element revisited. Int. J. Numer. Methods Eng. 1990, 30, 419–430. [Google Scholar] [CrossRef]
- Scapolla, T.; Della Croche, L. On robustness of hierarchic finite elements for Reissner-Mindlin plates. Comp. Methods Appl. Mech. Eng. 1992, 101, 43–60. [Google Scholar] [CrossRef]
- Oden, J.T.; Cho, J.R. Adaptive hpq finite element methods of hierarchical models for plate- and shell-like structures. Comput. Methods Appl. Mech. Eng. 1996, 136, 317–345. [Google Scholar] [CrossRef]
- Szabó, B.A.; Sahrmann, G.J. Hierarchic plate and shell models based on p-extension. Int. J. Numer. Methods Eng. 1988, 26, 1855–1881. [Google Scholar] [CrossRef]
- Zboiński, G. Application of the three-dimensional triangular-prism hpq adaptive finite element to plate and shell analysis. Comput. Struct. 1997, 65, 497–514. [Google Scholar] [CrossRef]
- Echter, R.; Bischoff, M. Numerical efficiency, locking and unlocking of NURBS finite elements. Comput. Methods Appl. Mech. Eng. 2010, 199, 374–382. [Google Scholar] [CrossRef]
- Özdemir, Y.I. Development of a higher order finite element on a Winkler foundation. Finite Elem. Anal. Des. 2012, 48, 1400–1408. [Google Scholar] [CrossRef]
- Rakowski, J. A critical analysis of quadratic beam finite elements. Int. J. Numer. Methods Eng. 1991, 31, 949–966. [Google Scholar] [CrossRef]
- Rakowski, J. A new methodology of evaluation of C0 bending finite elements. Comput. Methods Appl. Mech. Eng. 1991, 91, 1327–1338. [Google Scholar] [CrossRef]
- Zboiński, G.; Ostachowicz, W.; Krawczuk, M. Modifications of Adaptive Procedures for Analysis of Complex Structures in the Case of the Improper Solution Limit, Locking and Boundary Layer; Report No. 204/2000; Institute of Fluid Flow Machinery: Gdańsk, Poland, 2000. (In Polish) [Google Scholar]
- Zboiński, G. Hierarchical Modeling and Finite Element Approximation for Adaptive Analysis of Complex Structures. D.Sc. Thesis, Institute of Fluid Flow Machinery, Gdańsk, Poland, 2001. (In Polish). [Google Scholar]
- Zboiński, G. Numerical tools for a posteriori detection and assessment of the improper solution limit, locking and boundary layers in analysis of thin walled structures. In Adaptive Modeling and Simulation 2005, Proceeding of the Second International Conference on Adaptive Modeling and Simulation; Wiberg, N.-E., Diez, P., Eds.; CIMNE: Barcelona, Spain, 2005; pp. 321–330. [Google Scholar]
- Oden, J.T. Error estimation and control in computational fluid dynamics. The O. C. Zienkiewicz Lecture. In Proc. Math. of Finite Elements–MAFELAP VIII; Brunnel Univ.: Uxbridge, UK, 1993; pp. 1–36. [Google Scholar]
- Demkowicz, L. Computing with hp-Adaptive Finite Elements. Vol. 1. One- and Two-Dimensional Elliptic and Maxwell problems; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Demkowicz, L.; Kurtz, J.; Pardo, D.; Paszyński, M.; Rachowicz, W.; Zdunek, A. Computing with hp-Adaptive Finite Elements. Vol. 2. Three-Dimensional Elliptic and Maxwell Problems with Applications; Chapman & Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Ainsworth, M.; Oden, J.T. A Posteriori Error Estimation in Finite Element Analysis; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Ainsworth, M.; Oden, J.T.; Wu, W. A posteriori error estimation for hp approximation in elastostatics. Appl. Numer. Math. 1994, 14, 23–55. [Google Scholar] [CrossRef]
- Zboiński, G. Adaptive hpq finite element methods for the analysis of 3D-based models of complex structures. Part 1. Hierarchical modeling and approximation. Comput. Methods Appl. Mech. Eng. 2010, 199, 2913–2940. [Google Scholar] [CrossRef]
- Zboiński, G. Adaptive hpq finite element methods for the analysis of 3D-based models of complex structures. Part 2. A posteriori error estimation. Comput. Methods Appl. Mech. Eng. 2013, 267, 531–565. [Google Scholar] [CrossRef]
- Cho, J.R.; Oden, J.T. A priori error estimations of hp-finite element approximations for hierarchical models of plate- and shell-like structures. Comput. Methods Appl. Mech. Eng.. 1996, 132, 135–177. [Google Scholar] [CrossRef]
- Zboiński, G. 3D-based hierarchical models and hpq-approximations for adaptive finite element method of Laplace problems as exemplified by linear dielectricity. Comput. Math. Appl. 2019, 78, 2468–2511. [Google Scholar] [CrossRef]
- Pietraszkiewicz, W. Finite Rotations and Lagrangean Description in the Non-Linear Theory of Shells; Polish Scientific Publishers: Warsaw, Poland, 1979. [Google Scholar]
- Ciarlet, P.G. Plates and Junctions in Elastic Multi-Structures; Springer: Berlin, Germany, 1990. [Google Scholar]
- Rachowicz, W.; Oden, J.T.; Demkowicz, L. Towards a universal hp adaptive finite element strategy. Part 3. Design of h-p meshes. Comp. Methods Appl. Mech. Eng. 1989, 77, 181–212. [Google Scholar] [CrossRef]
- Oden, J.T. The best FEM. Finite Elem. Anal. Des. 1990, 7, 103–114. [Google Scholar] [CrossRef]
- Rachowicz, W.; Pardo, D.; Demkowicz, L. Fully automatic hp-adaptivity in three dimensions. Comput. Methods Appl. Mech. Eng. 2006, 195, 4816–4842. [Google Scholar] [CrossRef]
- Ainsworth, M.; Oden, J.T. A posteriori error estimators for second order elliptic systems: Part 1. Theoretical foundations and a posteriori error analysis. Comput. Math. Appl. 1993, 25, 101–113. [Google Scholar] [CrossRef]
- Ainsworth, M.; Oden, J.T. A posteriori error estimators for second order elliptic systems: Part 2. An optimal order process for calculating self-equilibrating fluxes. Comput. Math. Appl. 1993, 26, 75–87. [Google Scholar] [CrossRef]

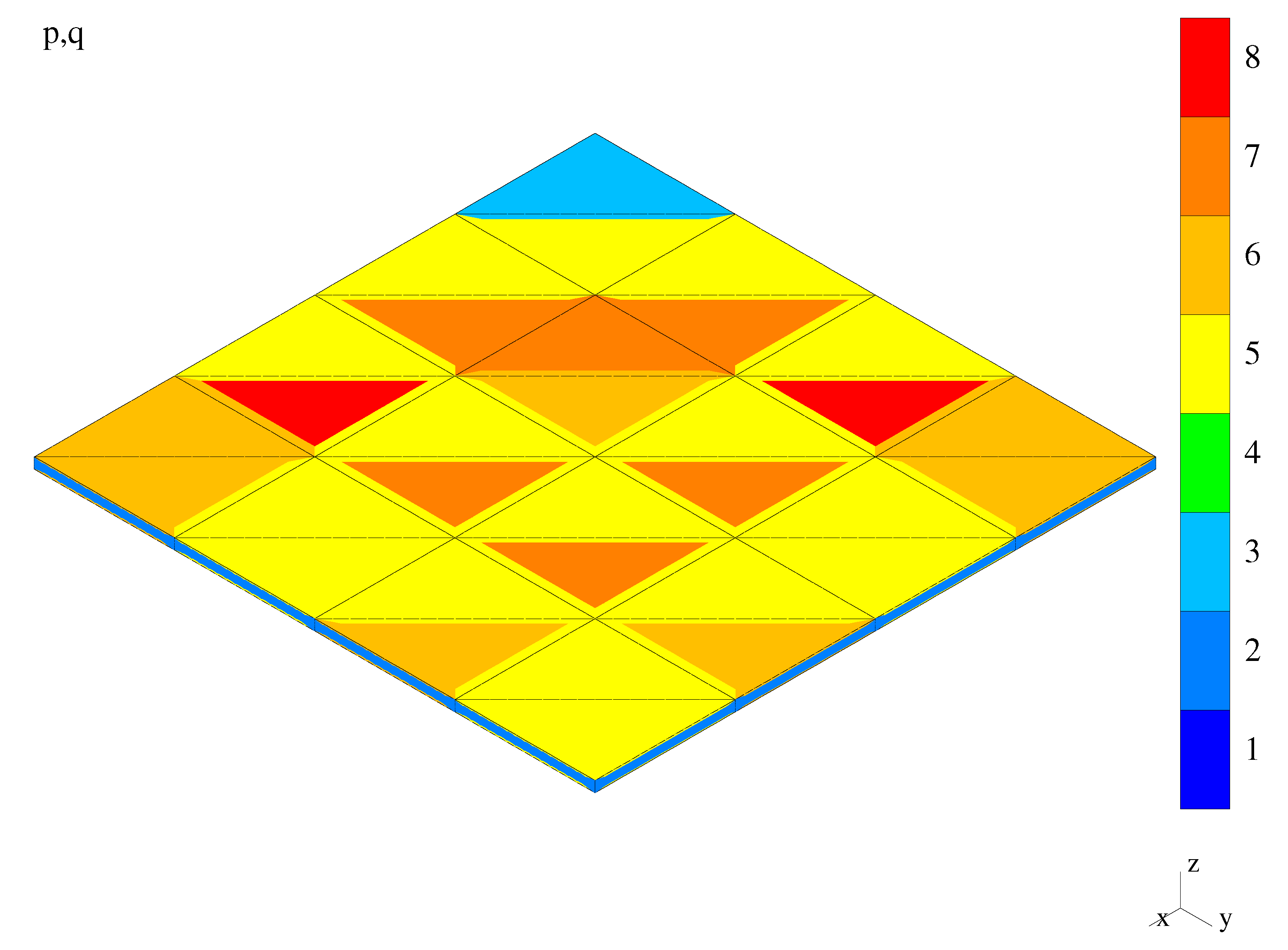


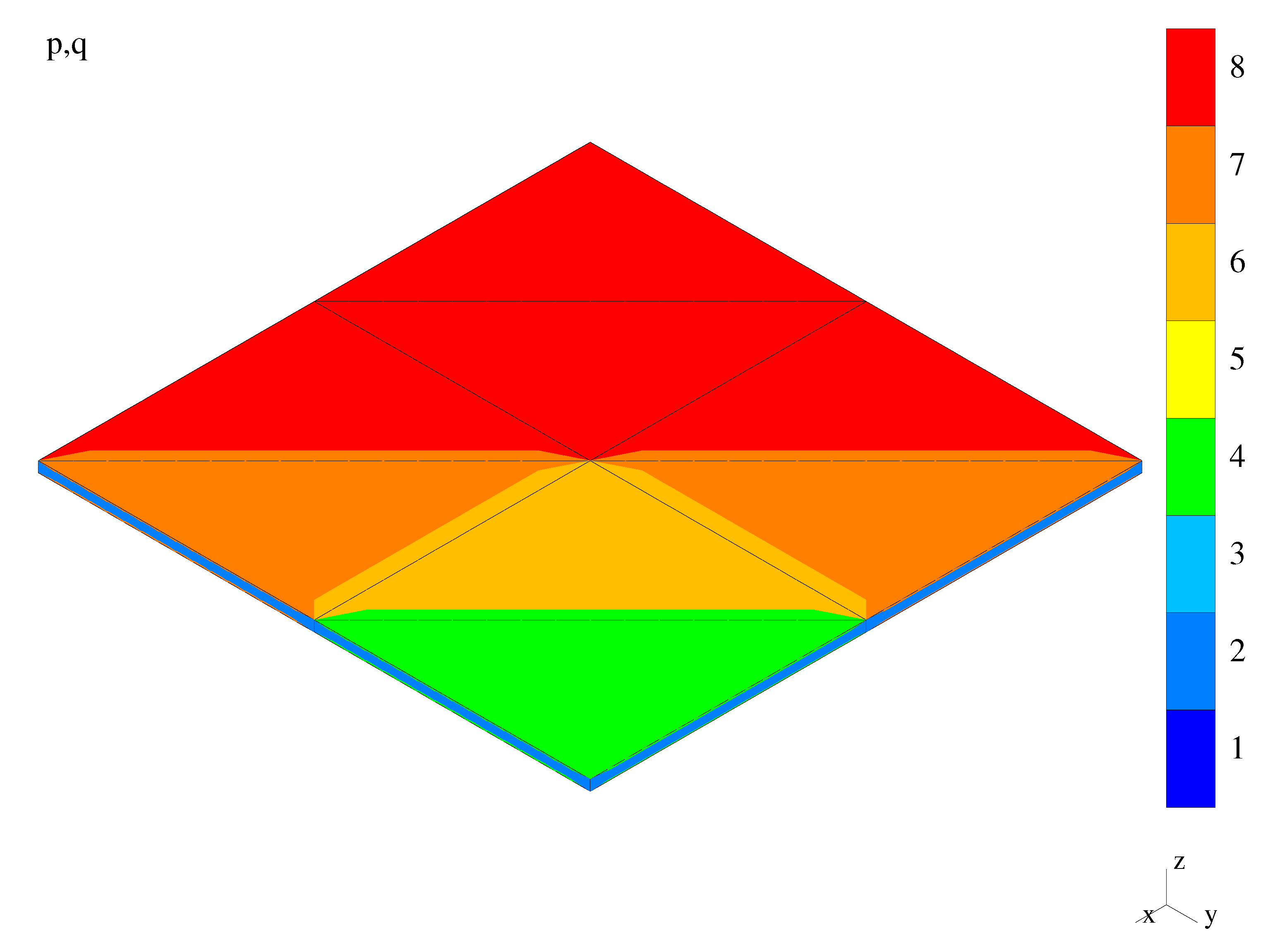
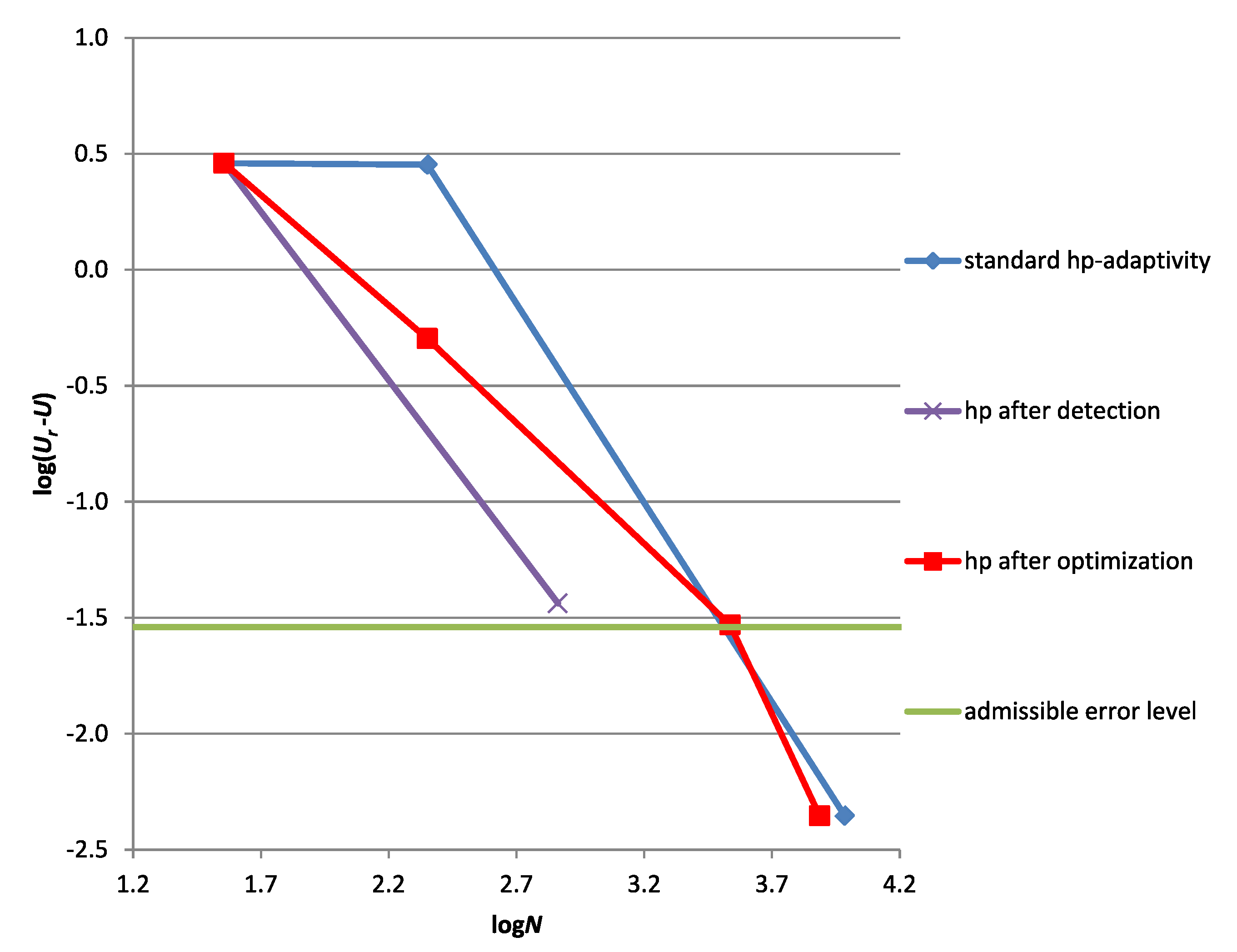

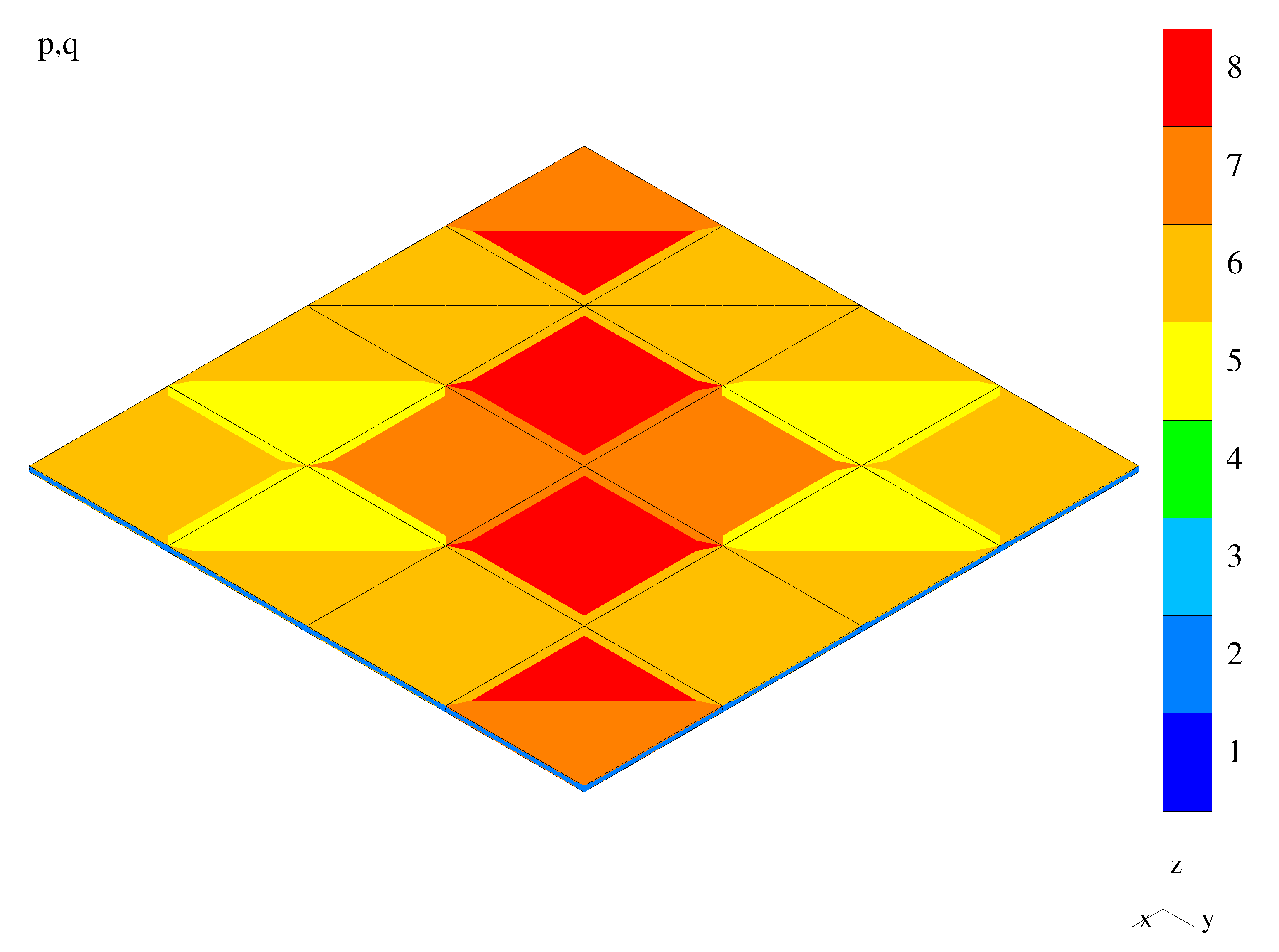






| Adaptive Method | Result Quantity | Mesh Type | |||
|---|---|---|---|---|---|
| Initial | Modified | Intermediate | Final | ||
| mesh figure no. | Figure 9 | – | – | Figure 10 | |
| standard | dofs number N [1] | 36 | – | 225 | 9648 |
| -adaptivity | log [N/m] | – | |||
| [%] * | 99.9 | – | 98.4 | 0.15 | |
| mesh figure no. | Figure 9 | Figure 11 | – | – | |
| standard | dofs number N [1] | 36 | 729 | – | – |
| after detection | log [N/m] | 0.459481 | −1.43770 | – | – |
| [%] * | 99.9 | 1.27 | – | – | |
| mesh figure no. | Figure 9 | Figure 12 | – | Figure 13 | |
| standard | dofs number N [1] | 36 | 531 | 3438 | 7704 |
| after optimization | log [N/m] | 0.459481 | −0.297250 | −1.531051 | −2.354113 |
| [%] * | 99.9 | 17.5 | 1.02 | 0.15 | |
| Adaptive Method | Result Quantity | Mesh Type | |||
|---|---|---|---|---|---|
| Initial | Modified | Intermediate | Final | ||
| mesh figure no. | Figure 15 | – | – | Figure 16 | |
| standard | dofs number N [1] | 36 | – | 225 | 6381 |
| -adaptivity | log [N/m] | – | |||
| [%] * | 100. | – | 99.6 | 0.85 | |
| mesh figure no. | Figure 15 | Figure 17 | – | – | |
| standard | dofs number N [1] | 36 | 729 | – | – |
| after detection | log [N/m] | 1.060969 | −0.527871 | – | – |
| [%] * | 100. | 2.58 | – | – | |
| mesh figure no. | Figure 15 | Figure 18 | – | Figure 19 | |
| standard | dofs number N [1] | 36 | 324 | 5265 | 9279 |
| after optimization | log [N/m] | 1.060969 | 0.927962 | −0.817269 | −1.338752 |
| [%] * | 100. | 73.6 | 1.32 | 0.40 | |
| Adaptive Method | Result Quantity | Mesh Type | |||
|---|---|---|---|---|---|
| Initial | Modified | Intermediate | Final | ||
| mesh figure no. | Figure 21 | – | – | Figure 22 | |
| standard | dofs number N [1] | 81 | – | 918 | 8145 |
| -adaptivity | log [N/m] | – | |||
| [%] * | 99.9 | – | 99.5 | 1.47 | |
| mesh figure no. | Figure 21 | – | Figure 23 | – | |
| standard | dofs number N [1] | 81 | 729 | 3294 | – |
| after detection | log [N/m] | 8.015996 | 6.330842 | 5.930839 | – |
| [%] * | 99.9 | 2.06 | 0.82 | – | |
| mesh figure no. | Figure 21 | Figure 24 | – | Figure 25 | |
| standard | dofs number N [1] | 81 | 324 | 5265 | 10,512 |
| after optimization | log [N/m] | 8.015996 | 7.978775 | 6.039104 | 5.449802 |
| [%] * | 99.9 | 91.73 | 1.05 | 0.27 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miazio, Ł.; Zboiński, G. A Posteriori Detection of Numerical Locking in hpq-Adaptive Finite Element Analysis. Appl. Sci. 2020, 10, 8247. https://doi.org/10.3390/app10228247
Miazio Ł, Zboiński G. A Posteriori Detection of Numerical Locking in hpq-Adaptive Finite Element Analysis. Applied Sciences. 2020; 10(22):8247. https://doi.org/10.3390/app10228247
Chicago/Turabian StyleMiazio, Łukasz, and Grzegorz Zboiński. 2020. "A Posteriori Detection of Numerical Locking in hpq-Adaptive Finite Element Analysis" Applied Sciences 10, no. 22: 8247. https://doi.org/10.3390/app10228247
APA StyleMiazio, Ł., & Zboiński, G. (2020). A Posteriori Detection of Numerical Locking in hpq-Adaptive Finite Element Analysis. Applied Sciences, 10(22), 8247. https://doi.org/10.3390/app10228247





