A Proposed Extended Version of the Hadi-Vencheh Model to Improve Multiple-Criteria ABC Inventory Classification

Featured Application

Inventory Management.

Abstract

The ABC classification problem is approached as a ranking problem by the most current classification models; that is, a group of inventory items is expressed according to its overall weighted score of criteria in descending order. In this paper, we present an extended version of the Hadi-Vencheh model for multiple-criteria ABC inventory classification. The proposed model is one based on the nonlinear weighted product method (WPM), which determines a common set of weights for all items. Our proposed nonlinear WPM incorporates multiple criteria with different measured units without converting the performance of each inventory item, in terms of converting each criterion into a normalized attribute value, thereby providing an improvement over the model proposed by Hadi-Vencheh. Our study mainly includes various criteria for ABC classification and demonstrates an efficient algorithm for solving nonlinear programming problems, in which the feasible solution set does not have to be convex. The algorithm presented in this study substantially improves the solution efficiency of the canonical coordinates method (CCM) algorithm when applied to large-scale, nonlinear programming problems. The modified algorithm was tested to compare our proposed model results to the results derived using the Hadi-Vencheh model and demonstrate the algorithm’s efficacy. The practical objectives of the study were to develop an efficient nonlinear optimization solver by optimizing the quality of existing solutions, thus improving time and space efficiency.

1. Introduction

To facilitate the successful management of a growing number of stock-keeping units (SKUs), inventory managers have found that inventory classification systems provide essential context for evaluating inventory management. ABC analysis is one of the most frequently used inventory classification techniques. Raw materials, subassemblies, intermediate products, parts, and end products can be divided into three classes: A (very important items), B (moderately important items), and C (relatively unimportant items). The ABC classification problem is presented as a ranking problem by the most current classification models [1,2,3]; that is, a group of inventory items is represented according to its overall weighted score of criteria in descending order. The idea of ABC analysis was applied to the inventory management at General Electric during the 1950s. This approach is based on Pareto’s famous theory of inequality in the distribution of incomes. A conventional ABC study is conducted on the basis of one criterion: the annual dollar usage (value of an item times its annual usage) of SKUs.

Under Pareto’s theory, all items are ranked based on a single criterion; within inventory management, dollar usage is the only criterion for managers to classify items into the A, B, and C categories. However, managers sometimes want to consider more attributes of an item when classifying goods. Many item characteristics could influence inventory control policy and must be considered. Flores [2] noted that other vital criteria can be adopted in addition to dollar usage, such as commonality, reparability, substitutability, lead time, and commonality. For instance, an enterprise must pursue efficient operations that can both minimize total costs and maximize satisfaction brought to their internal or external customers. If SKUs are only classified based on the single criterion of dollar usage, an item with a lower dollar usage, but a long lead time and high criticality, would be misclassified into the C category, resulting in serious damage to the company if the item were to run out of stock.

Detailed literary research has been carried out on multi-choice programming (MCP) theories and applications. MCP is a branch of multi-objective programming that stems from multiple-criteria decision-making (MCDM). MCDM tests several overlapping criteria of decision-making in various areas [4,5]. Multi-criteria inventory classification (MCIC) can be viewed as an application of multi-criteria decision analysis [6,7]. To solve the MCIC problem, the joint criteria matrix [8] is a simple and easy-to-understand tool, but it is not practical for more than two criteria and involves too much subjectivity. The analytic hierarchy process (AHP) is a popular methodology, but it involves subjectivity as well. Methods for solving the ABC inventory classification problem have been systematically and thoroughly reviewed and discussed in the relevant literature [9,10,11,12]. A number of methods were suggested in order to achieve multi-criteria classification of SKUs. These methods contribute much to the classification of items and help improve the efficiency and performance of a firm through better inventory management. However, these approaches contain some shortcomings, such as involving too much subjectivity or being overly complicated.

To facilitate better allocation of the priorities of items and further classification, it is worth developing a model that can accommodate multiple criteria to create guidelines for inventory control. This study builds a proper model for categorizing SKUs and demonstrates an efficient algorithm for solving the nonlinear programming model, in which the feasible solution set does not have to be convex. The rest of this paper is structured as follows. Section 2 provides the details of the model’s development. The solution algorithm and its improvement are presented in Section 3. Section 4 details the results of the model constructed herein, with comparisons to previous studies using a benchmark data set. Conclusions and recommendations for future research are offered in the final section.

2. Literature Review on the HV Model and the WPM

Hadi-Vencheh [13] proposed a multi-criteria weighted nonlinear model for ABC inventory classification. The proposed model (hereafter the HV model) is an extension of the Ng model [1]. The Ng model transforms the inventory object to a scalar value. The grouping, according to the measured values, is then applied according to the ABC theory. Hadi-Vencheh also extended the Ng model to resolve the condition in which the score is independent of the weights from the model for each item. Despite the improvement in maintaining the influences of weights in the final score, one notable problem remains: the HV model calculates the scores assigned to each item using the weighted sum method (WSM) for criteria with different measurement units, which therefore requires converting the performance of individual inventory items into a normalized attribute value, expressed in terms of every criterion. Triantaphyllou [14] contended that if the problem involved criteria with different measurement units, the weighted product method (WPM) would be a more suitable tool to calculate the scores given to each item. To avoid an erroneous extreme value leading to inventory item misclassification, we propose the following nonlinear WPM to model the classification problem involving criteria with different measurement units. This study presents a broader version of the HV model, taking weight values into account in the ABC inventory classification for multiple criteria by using the WPM, which applies multiplication weights and forms a nonlinear optimization problem. To solve the nonlinear optimization problem efficiently, the canonical coordinates method (CCM) algorithm is used to calculate the weights of the criteria for each inventory item.

Suppose that $I$ inventory items are present, and that the items must be graded as A, B, or C based on their results, according to $J$ criteria. In particular, let the output of the $i$th inventory item be referred to as $y_{i,j}$ with respect to each criterion. For simplicity, all parameters are beneficial; in other words, they are positively connected with the degree of value of an item. The goal is to combine many performance scores in the subsequent ABC inventory classification, in regard to different parameters, into a single score. In both the Ng and HV models, a nonnegative weight $w_{i,j}$ is the weight of performance contribution of the $i$th item under the $j$th criteria to the score of the item. The parameters are supposed to be listed in descending order such that $w_{i,1}\ge w_{i,2}\ge \cdots \ge w_{i,J}$ for all items $i$. The proposed model by Hadi-Vencheh [13] is as follows:

$$\begin{array}{cc}\max \hspace{1em}{S}_i=& {\displaystyle \sum _{j=1}^J{y}_{i,j}{w}_{i,j}}\hfill \\ \mathrm{s}.\mathrm{t}.& {\displaystyle \sum _{j=1}^J{w}_{i,j}{}^2}=1\hfill \\ & w_{i,j}-w_{i,j+1}\ge 0, j=1,2,\dots ,J-1\hfill \\ & w_{i,j}\ge 0, j=1,2,\dots ,J\hfill \end{array}$$

(1)

In the HV model, the performance in each criterion of the $i$th inventory item $y_{i,j}$ is further normalized to $s_{i,j}$, and the objective function of the nonlinear programming (NLP) model from Equation (1) is found to be

$$\begin{array}{cc}\max & S_i={\displaystyle \sum _{j=1}^J{s}_{i,j}{w}_{i,j}}\end{array}$$

Ng [1] indicated that normalization scaling involves extreme measurement values and would thus have an effect on all normalized measurements if the extremes changed. To avoid an invalid extreme value leading to inventory item misclassification, we propose the following nonlinear WPM to model the classification problem involving criteria with different measure units:

$$\begin{array}{cc}\max \hspace{1em}{S}_i=& \underset{j=1}{\overset{J}{\Pi }}{y}_{i,j}{}^{w_{i,j}}\hfill \\ \mathrm{s}.\mathrm{t}.& {\displaystyle \sum _{j=1}^J{w}_{i,j}{}^2}=1\hfill \\ & w_{i,j}-w_{i,j+1}\ge 0, j=1,2,\dots ,J-1\hfill \\ & w_{i,j}\ge 0, j=1,2,\dots ,J\hfill \end{array}$$

(2)

3. The Solution Algorithm

3.1. Nomenclature

3.1.1. Notation of the Weighted Product Method for ABC Classification

• $I$: set of inventory items;
• $J$: set of evaluation criteria;
• $y_{i,j}$: the $i$th inventory item in terms of the $j$th criteria;
• $w_{i,j}$: the weight of performance contribution of the $i$th item under the $j$th criteria;
• $S_i$: score of the item $i$.

3.1.2. Notation of the CCM Algorithm

• $\Re$: the set of all real numbers;
• $\xi$: decision variables;
• ${\xi }^0$: feasible initial solution;
• ${\varphi }_i\left(\xi \right)$: set of constraints, $i=1,\dots ,m$;
• $f\left(\xi \right)$: the objective function;
• ${\xi }^{*}$: the optimal solution.

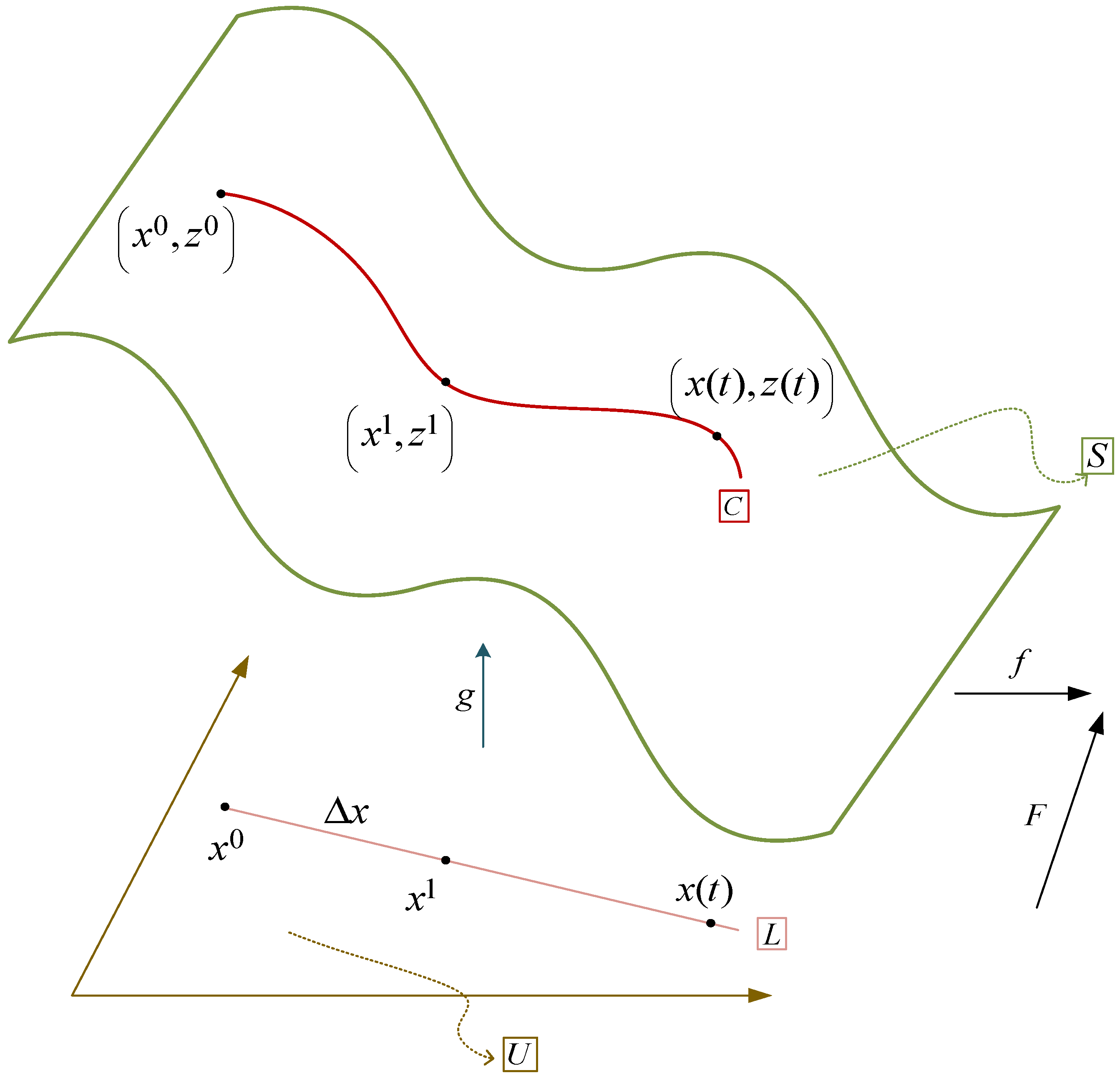
3.2. The CCM Algorithm

This section presents the canonical coordinates method (CCM) algorithm [15,16], which is applied to solve nonlinear programming problems in which the feasible solution set does not have to be convex. Convexity is a strong property that often replaces differentiability as a desirable property in most constrained optimization problems. However, the CCM efficiently addresses continuous search spaces and benefits from the low computational cost for solving constrained optimization. A set containing nonlinear constraints may or may not be convex. This study mainly demonstrates an efficient algorithm for solving nonlinear programming problems in which the feasible solution set does not have to be convex. The main difference between linear and nonlinear programming is that linear programming helps find the best solution from a set of parameters or requirements that have a linear relationship, whereas nonlinear programming helps find the best solution from a set of parameters or requirements that have a nonlinear relationship. The prerequisite for applying the CCM algorithm is that the implicit function theorem can be used in any feasible set. That is, at any point in the feasible set, one can find $m$ variables, such as $z=\left(z_1,\dots ,z_m\right)$, in such a way that the Jacobian matrix of the constraint functions $\varphi =\left({\varphi }_1,\dots ,{\varphi }_m\right)$, with respect to $z$, are nonsingular. In the implicit function theorem, there exist functions $g_j$ such that $z_j=g_j\left(x_1,\dots ,x_n\right)$, $j=1,\dots ,m$. We describe the Algorithm 1 below:

Algorithm 1. CCM Algorithm

Input: The nonlinear program: $$\max \left\{f\left(\xi \right)|{\varphi }_i\left(\xi \right)=0, i=1,\dots ,m\right\}$$ with given differentiable functions $f, {\varphi }_i:{\Re }^{m+n}\to \Re , i=1,\dots ,m$, and a feasible point ${\xi }^0\in {\Re }^{m+n}$ satisfying ${\varphi }_i\left({\xi }^0\right)=0, i=1,\dots ,m$. Output: A critical point ${\xi }^{*}$ of $f$ satisfying $\varphi \left({\xi }^{*}\right)=0$. Steps: ${\xi }^0$ is partitioned into ${\xi }^0=\left(x^0,z^0\right)$, where $x^0\in {\Re }^n$ and $z^0\in {\Re }^m$ are such that $\det \left(J\left(\varphi ,z\right)|{}_{\left(x^0,z^0\right)}\right)\ne 0$. For $i,j=1,\dots ,m$ and $k=1,\dots ,n$, we calculate the following partial derivatives at point ${\xi }^0=\left(x^0,z^0\right)$: $\partial f/\partial x_k$, $\partial f/\partial z_j$, $\partial {\varphi }_i/\partial x_k$, and $\partial {\varphi }_i/\partial z_j$. We then calculate the $m\times n$ matrix for the implicit function $g$ (i.e., $\left(\partial g/\partial x\right)=-{\left(\partial \varphi /\partial z\right)}^{-1}\left(\partial \varphi /\partial x\right)$) and then find the direction $D^0:=\left(\partial f/\partial x\right)=\left(\partial f/\partial x_1,\dots ,\partial f/\partial x_n\right)$ and $D^0={\left(\partial f/\partial x\right)}^T+\left(\partial f/\partial z\right)\left(\partial g/\partial x\right)$. We perform a line search along the ray through $x^0$ with the direction $D^0=D\left(x^0\right)$; that is to say, we find a one-dimensional local optimal $t^{*}$ of $\widehat{F}(t):=f\left(x^0+t{D}^0,z\left(t\right)\right), t\ge 0$. To do so, we need to solve for $z\left(t\right)$, which is done by solving the following system of ordinary differential equations: $$\{\begin{array}{l}z\left(0\right)=z^0\\ \left(\partial \varphi /\partial x\right){\left(\partial F/\partial x\right)}^T+\left(\partial \varphi /\partial z\right){\left(dz/dt\right)}^T=0\end{array}$$ where we set $x^{*}\leftarrow x^0+t^{*}{D}^0$. We compute $z_j^{*}=g_j\left(x^{*}\right)$, $j=1,\dots ,m$ using Taylor polynomial approximation and then apply Newton’s method to solve the system of ordinary differential equations at $t=t^{*}$ above. If $\nabla f\left(x^{*},z^{*}\right)\approx 0$, then we have found a local optimal point. Otherwise, we replace $\left(x^0,z^0\right)$ with $\left(x^{*},z^{*}\right)$ and repeat the procedure.

The CCM algorithm helped us identify the local optimal points of NLP so that the feasible set fulfilled the requirements of the implicit function theorem. The problem could then be turned into an NLP problem on a subspace ${\Re }^n$ of the original space ${\Re }^{m+n}$.

3.3. Improvement of the Algorithm Using Efficient Selection of Bases

Step 1 in the CCM algorithm is to find a subset of $m$ variables among the $\left(m+n\right)$ variables so that a resulting Jacobian matrix is non-singular [8]. This is equivalent to finding a subset of column vectors in the original $m\times \left(m+n\right)$ matrix that is linearly independent. Let ${\varphi }_1,\cdots ,{\varphi }_m$ be differentiable functions in $\left(m+n\right)$ variables:

$$A=\left[\begin{array}{cccc}\partial {\varphi }_1/\partial x_1& \partial {\varphi }_1/\partial x_2& \cdots & \partial {\varphi }_1/\partial x_{m+n}\\ \partial {\varphi }_2/\partial x_1& \partial {\varphi }_2/\partial x_2& \cdots & \partial {\varphi }_2/\partial x_{m+n}\\ ⋮& ⋮& ⋮& ⋮\\ \partial {\varphi }_m/\partial x_1& \partial {\varphi }_m/\partial x_2& \cdots & \partial {\varphi }_m/\partial x_{m+n}\end{array}\right]$$

In order to find a subset of $m$ columns of $A$ that is linearly independent, the original method by Chang and Prabhu [15] was to choose any $m$ subset of the $\left(m+n\right)$ columns to check if it qualified. There are two drawbacks to doing this. First, there are $C_m^{m+n}$ choices of such subsets, and second, each choice will require a calculation of the determinant of an $m\times m$ matrix, which has the same complexity as a Gaussian elimination process. We will show that, by using Gaussian elimination on $A$ to reach its reduced row echelon form, we can find one subset of columns of $A$ that is linearly independent. The process of Gaussian elimination involves performing a sequence of row operations to a given matrix to reach its reduced row echelon form. Each type of row operation corresponds to a type of elementary matrix, all of which are nonsingular. Each time a row operation is performed, it is equivalent to multiplying the original matrix by an elementary matrix on the left. We can also see that in an $m\times \left(m+n\right)$ matrix with rank $m$, there is a subset of column vectors that is linearly independent. Now, let us state the proposition that yields the discovery of the desired linearly independent subset of columns of $A$.

Proposition 1.

Let$m$and$n$be positive integers,$A$be an$m\times \left(m+n\right)$matrix with rank$m$, and$u_1,\dots ,u_{m+n}$be the column vectors of$A$. Suppose$B$is the reduced row echelon form of$A$, and that$v_1,\dots ,v_{m+n}$are the columns of$B$. Then, there exist integers$1\le j_1<j_2<\cdots <j_m\le \left(m+n\right)$such that$\left[v_{j_1},\cdots ,v_{j_m}\right]=I_{m\times m}$forms the$m\times m$identity matrix. Moreover, the corresponding subset of columns of$A$,$\left[u_{j_1},\cdots ,u_{j_m}\right]$, is non-singular.

Proof. 

Matrix $B$ must also have a rank of $m$ because it is the reduced row echelon form of $A$, whose rank is $m$. Thus, there are $m$ columns of $B$ that form the $m\times m$ identity matrix. That is, there exist integers $1\le j_1<j_2<\cdots <j_m\le \left(m+n\right)$ such that $\left[v_{j_1},\cdots ,v_{j_m}\right]=I_{m\times m}$. During the process of Gaussian elimination, performed to obtain the reduced row echelon form of $A$, we can find elementary matrices $E_1,E_2,\cdots ,E_p$ such that

$$B=E_p\cdots E_2{E}_{1}A$$

Note that the $k$th column of $B$ is also obtained from performing the same row operations on the $k$th column of $A$. Thus, we can say

$$v_{j_k}=E_p\cdots E_2{E}_1{u}_{j_k}, k=1,2,\cdots ,m$$

Additionally, we can say

$$E_p\cdots E_2{E}_1\left[u_{j_1},\cdots ,u_{j_m}\right]=\left[v_{j_1},\cdots ,v_{j_m}\right]=I$$

Since all the elementary matrices $E_1,E_2,\cdots ,E_p$ and the identity matrix $I$ are nonsingular, then $\left[u_{j_1},\cdots ,u_{j_m}\right]$ must also be nonsingular. Now, we can simply apply Gaussian elimination to the matrix and find a linearly independent subset of column vectors that allows the implicit function theorem and the CCM algorithm to be applied. □

3.4. Accuracy Improvement

A line search in the fourth step, whereby a system of nonlinear ordinary differential equations with initial values is resolved [15], must be carried out in the implementation of the CCM algorithm. The desired unidimensional direction can be approximated numerically from any line search, but its explicit functional expression cannot be calculated. This drawback impedes the output of the points found in any line search system. We present a modification of the CCM algorithm used by Chang and Prabhu [15], which adopted the gradient method to determine the next point without any line searching.

Suppose the feasible set $S=\left\{u\in R^{m+n}|{\varphi }_i\left(u\right)=0, i=1,\cdots ,m\right\}$ satisfies the condition of the implicit function theorem. That is, ${\varphi }_i\left(u\right)$ is a holomorphic function in the $m+n$ variables, if one treats the $m+n$ variables as complex variables such that one of its Jacobians is nonsingular. Therefore, one can find an m subset of the $m+n$ variables, such as $z_1,\cdots ,z_m$, so that the corresponding Jacobian matrix $\left(\partial \varphi /\partial z\right)$ is nonsingular. Furthermore, there exist implicit functions $g_j$, $j=1,\cdots ,m$ in terms of the remaining $n$ variables, $x_1,\cdots ,x_n$ for example, such that $z_j=g_j\left(x_1,\dots ,x_n\right)$, $j=1,\cdots ,m$. The original NLP can now be viewed as the following induced NLP:

$$\begin{array}{ll}\mathrm{Maximize}& F\left(x\right)\\ \mathrm{Subject} \mathrm{to}& x\in U\end{array}$$

where $F\left(x\right)=f\left(x,g_1\left(x\right),\cdots ,g_m\left(x\right)\right)$ and $U$ is a neighborhood of the point $x^0\in R^n$ that the implicit function theorem holds. Because $U$ contains an open subset of $R^n$, the induced NLP can be viewed as a locally non-constrained NLP model. One important benefit is that moving along the induced gradient direction $D=\left(\partial F/\partial x\right)$ will stay in $U$ if the distance is small enough.

One common issue with solving an NLP model using the gradient method is that it is likely to leave $S$ by traveling along the gradient direction of a feasible point. This causes a big problem in keeping the NLP model’s feasibility. Applying the CCM algorithm does not present such a problem, as every iteration remains within the feasible region. This is because the gradient of the inducted objective function $F$, with regard to the selected value $x_1,\cdots ,x_n$, will locally move inside the feasible set $U$ if selected carefully. When using the CCM algorithm in a small-scale NLP model, one can conduct a line search along the gradient direction of the induced objective function. The relation between the induced line search and the movement along the original feasible set is illustrated in Figure 1.

Because there is one-to-one mapping between U and a neighborhood of $\left(x^0,z^0\right)$ in $S$, there is a one-dimensional curve $C$ in $S$, corresponding to the line $L=\left\{x\left(t\right)|t\ge 0\right\}$ in $U$ such that

$$C=\left\{x\left(t\right),z\left(t\right)|x\left(t\right)\in L,z\left(t\right)=g\left(x\left(t\right)\right)\right\}$$

The problem can be viewed as lifting a straight line in $R^n$ to a curve in $R^{m+n}$. In performing a line search, one has to find a one-dimensional, local, optimal point on such a curve with only the knowledge of the projection of the curve, while the other coordinates are unknown. Fortunately, we also know the explicit objective and constraint functions, so we can approximate the change of the unknown coordinates $\Delta z$ with the derivatives $dz/dt$. That is, we can approximate $\Delta z$ by

$$\Delta z~\left(\frac{dz}{dt}\right)\Delta t$$

Let $D^0=D\left(x^0\right)=\left(d_1,\cdots ,d_n\right)$, in which case

$$\frac{d{z}_j}{dt}=\frac{\partial g_j}{\partial x_1}\frac{d{x}_1}{dt}+\cdots +\frac{\partial g_j}{\partial x_n}\frac{d{x}_n}{dt}$$

In addition,

$$\left(\frac{dz}{dt}\right)=\left(\frac{\partial g}{\partial x}\right)\left(\begin{array}{c}{d}_1\\ ⋮\\ d_n\end{array}\right)=-{\left(\frac{\partial \varphi }{\partial z}\right)}^{-1}\left(\frac{\partial \varphi }{\partial x}\right)\left(\begin{array}{c}{d}_1\\ ⋮\\ d_n\end{array}\right)$$

We can now move the previous point along its gradient direction $\left(\Delta x,\Delta z\right)$ where $\Delta x=D^0\Delta t$, in which $D^0$ is the exact induced gradient of the induced objective function in the projection space and $\Delta z$ is the change in $z$ by the above approximation. We can choose $\Delta t$ carefully to avoid any line searching. There are two reasons to avoid a line search.

First, it requires the knowledge of the lifted curve for any $z>0$. When an NLP model is a small-scale problem and the corresponding system of ordinary differential equations is possible to solve, the CCM algorithm can locate or approximate the exact lifted curve $C$ at any $t>0$. To do so, we may need to apply some Ordinary Differential Equation methods, such as the Euler and Runge–Kutta methods. As $t$ gets larger, the feasibility of the point $\left(x\left(t\right),z\left(t\right)\right)$ is likely disappearing.

Second, we use numerical data to approximate the partial derivatives at all the points involved. The ODE problem in the fourth step is a point-by-point case without an explicit global expression for the coefficients $\left(\partial \varphi /\partial x\right){\left(\partial F/\partial x\right)}^T$ and $\partial \varphi /\partial z$ in it. Thus, it might be impossible to solve for it in practice. We have chosen to avoid any line searching. Instead, as mentioned above, we move a point to the next one in its gradient direction $\left(\Delta x,\Delta z\right)$ with a chosen $\Delta t$. This way, we have control over staying as close to the feasible set as we need. Not only is the feasibility better kept, but the calculation is also reduced, since we are not solving for the system of ordinary differential equations globally.

4. Illustrative Example

We applied the WPM to the same problem of the multi-criteria inventory classification problem as reported in the referenced literature [1,6,7,13,17]. Following Ng [1] and Hadi-Vencheh [13], we considered three criteria for inventory classification: annual dollar usage (ADU), average unit cost (AUC), and lead time (LT). We also assumed the importance of the criteria to be ADU, AUC, and LT, in descending order. All of the criteria held positive inventory item scores.

4.1. Quality of Solutions

The 47 inventory items’ optimal scores and weights are shown in

Table 1. Measures of inventory items, including their optimal scores and weights.

Item Parameter				LINGO				CCM
				Objective Value	Decision Variable			Objective Value	Decision Variable
	ADU	AUC	LT	Score	ADU Weight	AUC Weight	LT Weight	Score	ADU Weight	AUC Weight	LT Weight
1	5840.64	49.92	2	8.92	7.050 × 10−1	7.050 × 10−1	7.770 × 10−2	8.92	7.050 × 10−1	7.049 × 10−1	7.790 × 10−2
2	5670	210	5	10.02	6.979 × 10−1	6.979 × 10−1	1.606 × 10−1	10.02	6.980 × 10−1	6.978 × 10−1	1.608 × 10−1
3	5037.12	23.76	4	8.38	6.974 × 10−1	6.974 × 10−1	1.654 × 10−1	8.38	6.974 × 10−1	6.973 × 10−1	1.658 × 10−1
4	4769.56	27.73	1	8.34	7.071 × 10−1	7.071 × 10−1	0.000 × 100	8.34	7.072 × 10−1	7.071 × 10−1	2.360 × 10−4
5	3478.8	57.98	3	8.71	7.015 × 10−1	7.015 × 10−1	1.262 × 10−1	8.71	7.015 × 10−1	7.014 × 10−1	1.264 × 10−1
6	2936.67	31.24	3	8.15	7.007 × 10−1	7.007 × 10−1	1.347 × 10−1	8.15	7.007 × 10−1	7.006 × 10−1	1.350 × 10−1
7	2820	28.2	3	8.05	7.005 × 10−1	7.005 × 10−1	1.364 × 10−1	8.05	7.005 × 10−1	7.004 × 10−1	1.367 × 10−1
8	2640	55	4	8.52	6.977 × 10−1	6.977 × 10−1	1.627 × 10−1	8.52	6.977 × 10−1	6.976 × 10−1	1.630 × 10−1
9	2423.52	73.44	6	8.73	6.921 × 10−1	6.921 × 10−1	2.051 × 10−1	8.73	6.921 × 10−1	6.920 × 10−1	2.053 × 10−1
10	2407.5	160.5	4	9.20	6.990 × 10−1	6.990 × 10−1	1.507 × 10−1	9.20	6.991 × 10−1	6.989 × 10−1	1.509 × 10−1
11	1057.2	5.12	2	6.12	7.026 × 10−1	7.026 × 10−1	1.133 × 10−1	6.12	7.025 × 10−1	7.024 × 10−1	1.145 × 10−1
12	1043.5	20.87	5	7.24	6.894 × 10−1	6.894 × 10−1	2.222 × 10−1	7.24	6.894 × 10−1	6.893 × 10−1	2.226 × 10−1
13	1038	86.5	7	8.30	6.874 × 10−1	6.874 × 10−1	2.346 × 10−1	8.30	6.875 × 10−1	6.873 × 10−1	2.347 × 10−1
14	883.2	110.4	5	8.28	6.936 × 10−1	6.936 × 10−1	1.944 × 10−1	8.28	6.938 × 10−1	6.934 × 10−1	1.945 × 10−1
15	854.4	71.2	3	7.87	7.002 × 10−1	7.002 × 10−1	1.397 × 10−1	7.87	7.003 × 10−1	7.000 × 10−1	1.399 × 10−1
16	810	45	3	7.51	6.995 × 10−1	6.995 × 10−1	1.463 × 10−1	7.51	6.996 × 10−1	6.994 × 10−1	1.465 × 10−1
17	703.68	14.66	4	6.68	6.917 × 10−1	6.917 × 10−1	2.075 × 10−1	6.68	6.917 × 10−1	6.916 × 10−1	2.081 × 10−1
18	594	49.5	6	7.49	6.866 × 10−1	6.866 × 10−1	2.391 × 10−1	7.49	6.867 × 10−1	6.865 × 10−1	2.393 × 10−1
19	570	47.5	5	7.39	6.902 × 10−1	6.902 × 10−1	2.177 × 10−1	7.39	6.902 × 10−1	6.900 × 10−1	2.178 × 10−1
20	467.6	58.45	4	7.36	6.944 × 10−1	6.944 × 10−1	1.885 × 10−1	7.36	6.946 × 10−1	6.942 × 10−1	1.887 × 10−1
21	463.6	24.4	4	6.74	6.920 × 10−1	6.920 × 10−1	2.056 × 10−1	6.74	6.920 × 10−1	6.919 × 10−1	2.058 × 10−1
22	455	65	4	7.41	6.946 × 10−1	6.946 × 10−1	1.871 × 10−1	7.41	6.948 × 10−1	6.944 × 10−1	1.873 × 10−1
23	432.5	86.5	4	7.57	6.952 × 10−1	6.952 × 10−1	1.830 × 10−1	7.57	6.954 × 10−1	6.949 × 10−1	1.832 × 10−1
24	398.4	33.2	3	6.80	6.978 × 10−1	6.978 × 10−1	1.616 × 10−1	6.80	6.979 × 10−1	6.977 × 10−1	1.618 × 10−1
25	370.5	37.05	1	6.74	7.071 × 10−1	7.071 × 10−1	0.000 × 10−0	6.74	7.071 × 10−1	7.071 × 10−1	2.570 × 10−4
26	338.4	33.84	3	6.70	6.975 × 10−1	6.975 × 10−1	1.640 × 10−1	6.70	6.975 × 10−1	6.975 × 10−1	1.642 × 10−1
27	336.12	84.03	1	7.25	7.071 × 10−1	7.071 × 10−1	0.000 × 100	7.25	7.071 × 10−1	7.071 × 10−1	2.860 × 10−4
28	313.6	78.4	6	7.37	6.859 × 10−1	6.859 × 10−1	2.431 × 10−1	7.37	6.859 × 10−1	6.859 × 10−1	2.433 × 10−1
29	268.68	134.34	7	7.67	6.840 × 10−1	6.840 × 10−1	2.537 × 10−1	7.67	6.840 × 10−1	6.840 × 10−1	2.539 × 10−1
30	224	56	1	6.67	7.071 × 10−1	7.071 × 10−1	0.000 × 100	6.67	7.071 × 10−1	7.071 × 10−1	2.880 × 10−4
31	216	72	5	7.01	6.882 × 10−1	6.882 × 10−1	2.295 × 10−1	7.01	6.882 × 10−1	6.882 × 10−1	2.297 × 10−1
32	212.08	53.02	2	6.63	7.032 × 10−1	7.032 × 10−1	1.045 × 10−1	6.63	7.032 × 10−1	7.032 × 10−1	1.048 × 10−1
33	197.92	49.48	5	6.69	6.864 × 10−1	6.864 × 10−1	2.404 × 10−1	6.69	6.864 × 10−1	6.864 × 10−1	2.406 × 10−1
34	190.89	7.07	7	5.46	6.606 × 10−1	6.606 × 10−1	3.567 × 10−1	5.46	6.606 × 10−1	6.606 × 10−1	3.595 × 10−1
35	181.8	60.6	3	6.67	6.975 × 10−1	6.975 × 10−1	1.647 × 10−1	6.67	6.975 × 10−1	6.975 × 10−1	1.649 × 10−1
36	163.28	40.82	3	6.32	6.963 × 10−1	6.963 × 10−1	1.738 × 10−1	6.32	6.963 × 10−1	6.963 × 10−1	1.740 × 10−1
37	150	30	5	6.16	6.826 × 10−1	6.826 × 10−1	2.612 × 10−1	6.16	6.826 × 10−1	6.826 × 10−1	2.613 × 10−1
38	134.8	67.4	3	6.54	6.971 × 10−1	6.971 × 10−1	1.680 × 10−1	6.54	6.971 × 10−1	6.971 × 10−1	1.683 × 10−1
39	119.2	59.6	5	6.47	6.849 × 10−1	6.849 × 10−1	2.486 × 10−1	6.47	6.849 × 10−1	6.849 × 10−1	2.488 × 10−1
40	103.36	51.68	6	6.33	6.782 × 10−1	6.782 × 10−1	2.831 × 10−1	6.33	6.782 × 10−1	6.782 × 10−1	2.833 × 10−1
41	79.2	19.8	2	5.25	7.009 × 10−1	7.009 × 10−1	1.321 × 10−1	5.25	7.009 × 10−1	7.009 × 10−1	1.323 × 10−1
42	75.4	37.7	2	5.67	7.018 × 10−1	7.018 × 10−1	1.223 × 10−1	5.66	7.018 × 10−1	7.018 × 10−1	1.227 × 10−1
43	59.78	29.89	5	5.53	6.765 × 10−1	6.765 × 10−1	2.908 × 10−1	5.53	6.765 × 10−1	6.765 × 10−1	2.910 × 10−1
44	48.3	48.3	3	5.59	6.933 × 10−1	6.933 × 10−1	1.964 × 10−1	5.59	6.933 × 10−1	6.933 × 10−1	2.000 × 10−1
45	34.4	34.4	7	5.37	6.590 × 10−1	6.590 × 10−1	3.625 × 10−1	5.37	6.590 × 10−1	6.590 × 10−1	3.639 × 10−1
46	28.8	28.8	3	4.88	6.889 × 10−1	6.889 × 10−1	2.252 × 10−1	4.88	6.889 × 10−1	6.889 × 10−1	2.291 × 10−1
47	25.38	8.46	5	4.12	6.510 × 10−1	6.510 × 10−1	3.903 × 10−1	4.12	6.510 × 10−1	6.510 × 10−1	3.931 × 10−1

. As demonstrated, the optimal scores derived by using the CCM algorithm to solve the WPM of multicriteria ABC classification were as good as those derived using LINGO [18], the off-the-shelf optimization software. If we look carefully at the weights derived using LINGO, it is obvious that most item weights for ADU and AUC were identical, and that some item weights (4, 25, 27, and 30) for LT were zero. This is because the primary underlying technique used by LINGO’s nonlinear solver is to reach a feasible solution for nonlinear models quickly. The weight values derived by using the CCM better fit the assumption that the criteria were graded in descending order, such that $w_{i,1}\ge w_{i,2}\ge \cdots \ge w_{i,J}$ for all items $i$. Therefore, the CCM is superior to LINGO in terms of solution quality in this illustrative example.

Next, the maximal overall scores were sorted in descending order, and inventory classification was conducted based on the WPM (shown in

Table 2. Comparison of ABC classifications using the optimal weighted product model (WPM), Zhou and Fan (ZF) model, Ng model, and Hadi-Vencheh (HV) model inventory scores.

Item	Optimal Score (CCM)	ADU	AUC	LT	WPM Model (CCM)	WPM Model (LINGO)	HV model	Ng Model	ZF Model
2	10.0222	5670	210	5	A	A	A	A	A
10	9.20134	2407.5	160.5	4	A	A	A	A	A
1	8.92424	5840.64	49.92	2	A	A	A	A	A
9	8.73406	2423.52	73.44	6	A	A	A	A	A
5	8.70633	3478.8	57.98	3	A	A	A	A	B
8	8.51791	2640	55	4	A	A	B	B	B
3	8.38316	5037.12	23.76	4	A	A	A	A	A
4	8.33829	4769.56	27.73	1	A	A	A	A	C
13	8.29587	1038	86.5	7	A	A	A	A	A
14	8.28055	883.2	110.4	5	A	A	A	B	A
6	8.15406	2936.67	31.24	3	B	B	B	A	C
7	8.05394	2820	28.2	3	B	B	B	B	C
15	7.86615	854.4	71.2	3	B	B	C	C	C
29	7.67051	268.68	134.34	7	B	B	A	A	A
23	7.57315	432.5	86.5	4	B	B	B	B	B
16	7.50776	810	45	3	B	B	C	C	C
18	7.49247	594	49.5	6	B	B	B	B	A
22	7.40991	455	65	4	B	B	C	C	B
19	7.39402	570	47.5	5	B	B	B	B	B
28	7.36954	313.6	78.4	6	B	B	B	B	A
20	7.35514	467.6	58.45	4	B	B	C	C	B
27	7.24598	336.12	84.03	1	B	B	C	C	C
12	7.24393	1043.5	20.87	5	B	B	B	B	B
31	7.01167	216	72	5	B	B	B	B	B
24	6.79949	398.4	33.2	3	C	C	C	C	C
21	6.74367	463.6	24.4	4	C	C	C	C	C
25	6.73618	370.5	37.05	1	C	C	C	C	C
26	6.69892	338.4	33.84	3	C	C	C	C	C
33	6.69389	197.92	49.48	5	C	C	B	B	B
17	6.67996	703.68	14.66	4	C	C	C	C	C
30	6.67213	224	56	1	C	C	C	C	C
35	6.67164	181.8	60.6	3	C	C	C	C	C
32	6.63135	212.08	53.02	2	C	C	C	C	C
38	6.53696	134.8	67.4	3	C	C	C	C	C
39	6.47356	119.2	59.6	5	C	C	B	B	B
40	6.32774	103.36	51.68	6	C	C	B	B	B
36	6.32156	163.28	40.82	3	C	C	C	C	C
37	6.16169	150	30	5	C	C	C	C	B
11	6.11791	1057.2	5.12	2	C	C	C	C	C
42	5.66488	75.4	37.7	2	C	C	C	C	C
44	5.59151	48.3	48.3	3	C	C	C	C	C
43	5.5337	59.78	29.89	5	C	C	C	C	C
34	5.45517	190.89	7.07	7	C	C	B	B	B
45	5.36813	34.4	34.4	7	C	C	B	B	B
41	5.24818	79.2	19.8	2	C	C	C	C	C
46	4.87682	28.8	28.8	3	C	C	C	C	C
47	4.12265	25.38	8.46	5	C	C	C	C	C

). For comparison purposes, we maintained the same distribution of items in the A, B, and C classes as in studies within the cited literature [1,13,17]; that is, there were 10 class A items, 14 class B items, and 23 class C items. The ABC analysis using the Ng [1], Hadi-Vencheh [13], and Zhou and Fan (ZF) models [17] are also shown in Table 2. There were ten items (8, 29, 15, 16, 27, 33, 39, 40, 34, and 45) that did not have the same classifications in the WPM model as in the Ng, HV, and ZF models. The difference in classification was due to the difference in score computation schemes. Of the 10 class A items identified in the WPM, only item 8 was recognized as a class B item in the Ng, ZF, and HV models. Moreover, in these models, item 29 was classified as a class A item, while the WPM reclassified it as a class B item. A comparison of items 8 and 29 revealed that item 8 was superior to item 29 in terms of ADU value ($y_{8,1}=2640$ > $y_{29,1}=268.68$). Although item 29 outperformed item 8 in AUC ($y_{8,2}=55$ < $y_{29,2}=134.34$) and LT ($y_{8,3}=4$ < $y_{29,3}=7$), the differences were not significant. Therefore, based on the most important consideration, the value of the annual consumption of inventory items (ADU) in a year, the WPM provided a more reasonable classification.

Regarding the 14 class B items in the HV model, eight items (6, 7, 23, 18, 19, 28, 12, and 31) were retained in class B when the WPM was adopted, five of the class B items (33, 39, 40, 34, and 45) were reclassified as C, and the remaining one (item 8) was moved up to class A. Out of the 23 class C items, 18 items were retained as such, whereas the remaining five (15, 16, 22, 20, and 27) were moved up to class B. Items 33, 39, 40, 34, and 45, classified as class B items in the Ng, HV, and ZF models, were reclassified as class C items when using the WPM (see

Table 3. The 10 items reclassified using the WPM.

Item	ADU	AUC	LT	WPM	HV Model	Ng Model	ZF Model
8	2640	55	4	A	B	B	B
29	268.68	134.34	7	B	A	A	A
15	854.4	71.2	3	B	C	C	C
16	810	45	3	B	C	C	C
27	336.12	84.03	1	B	C	C	C
33	197.92	49.48	5	C	B	B	B
39	119.2	59.6	5	C	B	B	B
40	103.36	51.68	6	C	B	B	B
34	190.89	7.07	7	C	B	B	B
45	34.4	34.4	7	C	B	B	B

) and had relatively higher LT measurements (more than 4), but lower performance in terms of AUC and ADU, which were the two more important criteria. However, the maximum ADU value (197.92) of these five items was much less than the minimum ADU value (336.12) of items 15, 16 and 27, which were reclassified as class C items by the WPM, while their AUC values were about even. Therefore, the WPM provided a more reasonable ranking of items.

4.2. Elapsed Runtime and Iterations

The efficiency of solving a problem is also an important criterion for algorithm comparisons; a good algorithm should solve problems within an acceptable time. This section compares the number of iterations of implementations of the CCM and LINGO to solve the WPM of multi-criteria ABC classification. The main difference between implementing the CCM algorithm and the LINGO solver was that we did not need to specify a starting point or moving step size. When the solution region is a polyhedron, determining the first basic solution (the starting point) would be vital, as the local optimal solution is usually located near the basic feasible solution (BFS); the quality of the solution is highly related to the location of the BFS. An unsuitable starting point could lead to a worse local optimal solution. The search region of an algorithm is related to the step size of the line search, and the search region decides whether a feasible solution can be found. The step size also determines the quality of the final solution. A large step size within a line search could jump over the optimal solution, whereas smaller search distances could trap in and require a significant amount of time to reach the local optimal solution. A good starting point and step size for a search can help researchers find acceptable solutions in less time.

Table 4. Tuning the step size to reach a feasible solution.

Item 4	Step size	${\displaystyle \sum _{j=1}^J{w}_j^2}$	Item 5	Step size	${\displaystyle \sum _{j=1}^J{w}_j^2}$
	0.0003	1.000009		0.00045	1.000062
	0.000295	0.999993		0.000448	1.000059
	0.000298	1.000003		0.00044	1.000046
	0.000297	1		0.00041	0.999997
				0.000413	1.000002
				0.000412	1

illustrates the process of tuning the step size in order to reach a feasible solution. The CCM algorithm provides more flexibility than other solvers from commercial package software, which presents a higher probability of finding better solutions. In this study, using CCM to solve the problem required more time to achieve the local optimal solution than using LINGO because the step size of the line search determined whether the CCM could find feasible solutions. In this study, LINGO took mere seconds to find a feasible solution, whereas CCM took more time—sometimes nearly a minute—to find a solution.

When looking at the number of iterations each algorithm needs, CCM requires more iterations to solve the problem, even with a larger step size. As presented in

Table 5. The number of iteration for LINGO and the canonical coordinates method (CCM) to find the local optimal solution.

Item	LINGO	CCM	Item	LINGO	CCM	Item	LINGO	CCM	Item	LINGO	CCM
1	60	1720	13	60	1505	25	35	2482	37	60	1367
2	60	1866	14	55	1852	26	60	1646	38	50	2369
3	60	1207	15	60	1911	27	35	3213	39	50	1888
4	35	1867	16	59	1673	28	55	1741	40	50	1657
5	60	1627	17	60	1090	29	50	2024	41	58	1903
6	60	1419	18	59	1377	30	35	3045	42	50	2452
7	60	1388	19	57	1456	31	55	1900	43	55	1496
8	60	1495	20	60	1729	32	55	2397	44	75	555
9	58	1428	21	60	1287	33	55	1645	45	55	215
10	57	1995	22	55	1802	34	60	1158	46	75	492
11	60	1086	23	55	2009	35	50	2223	47	60	2712
12	60	1105	24	60	1612	36	55	1932

, LINGO can solve most problems in only 60 iterations, whereas CCM might need approximately one thousand iterations. In conclusion, LINGO is more efficient than CCM in this study, which contradicts the results of the previous study, which stated that CCM can solve nonlinear problems more quickly than other software packages. The result of the current study might stem from the fact that the problem in this study is too simple to demonstrate the power of CCM.

5. Conclusions

In this paper, we presented an extended version of the HV model to improve multi-criteria ABC inventory classification. Our proposed nonlinear weighted product model (WPM) incorporates multiple criteria with different measurement units without converting the performance of each inventory item in terms of each criterion into a normalized attribute value. This represents an improvement over the model proposed by Hadi-Vencheh. The WPM could also be viewed as providing a more reasonable classification for inventory items from the illustrated example, presented and used to compare our model with the HV model. In this paper, we also presented the improved CCM algorithm for solving the WPM, in which nonconvex nonlinearity was present in both the objective function and the constraints. The strategy presented here involved greatly reducing the steps in choosing m variables among $(m+n)$ variables, such that the corresponding $m\times m$ Jacobian matrix was nonsingular. Using the improved algorithm, we applied Gaussian elimination to the original matrix to determine which m variables to choose. Our second improvement was to remove solving the nonlinear differential equations system, which occurs in the line search method of the CCM algorithm. This paper demonstrates an efficient algorithm for solving nonlinear programming problems, in which the feasible solution set does not have to be convex. The practical implication of this study is to further improve the efficient nonlinear optimization solver based on the CCM by optimizing the quality of existing solutions, thus improving time and space efficiency.

Future research should continue to investigate the feasibility of implementing this proposed CCM algorithm in discrete domain issues for engineering applications in order to decide if the algorithm could be superior to off-the-shelf software. Future studies could apply the CCM to other nonlinear programs that arise in practice. For instance, autonomous vehicles represent one of many developments that will influence future mobility needs and planning needs. Traffic assignment models seek the same objective as route guidance strategies and provide turning points with information for implementing route guidance control strategies. Faster algorithms developed specifically for traffic assignment can be adapted and used in vehicle route guidance systems. The minimization of total travel time is a common goal, both globally and from a traffic administration perspective. The current road network manages more traffic by achieving system optimization. Some researchers have focused their efforts on dynamic traffic assignment because of the unrealistic assumptions of static traffic assignment. Difficulties encountered by the dynamic model result from route calculation being related to travel time on an arc, which is also dependent on the traffic along the route. It is difficult to solve such relationships analytically under a dynamic circumstance. In response to the difficulties of dynamic traffic modeling, Jahn et al. [19] therefore developed a model in which flow represents the traffic patterns in a steady state, and the results are the boundary for the total travel time. However, the algorithm by Jahn et al. [19] only solves problems with convex, nonlinear objective functions and linear constraints. To avoid this restriction, future studies could adopt the CCM to solve nonlinear optimization models and provide strategies for route guidance.