4.3. Comparison Study
The comparison study between the analytical and CFD models was set to validate the CFD model used to develop the aerodynamic study. To do so, a CFD case with the aircraft geometry of
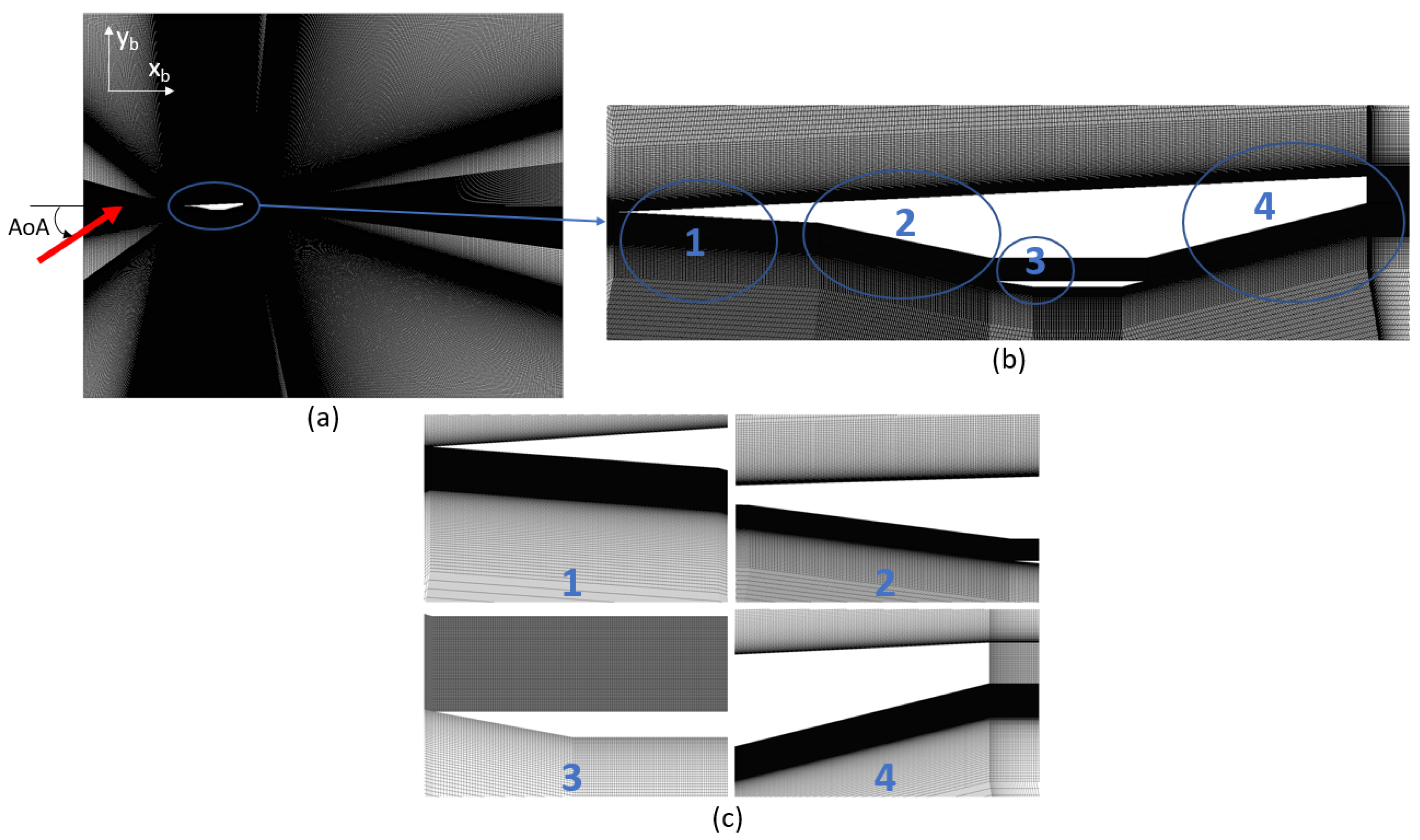
Figure 1 was developed. Since the scramjet was neglected, few changes in the CFD domain were carried out: only the quadrilateral regions around the intrados of the aircraft were slightly modified, see
Section 3. The structure of the mesh was maintained and its discretization was identical to that from Mesh 2 since it was the optimal one according to
Section 4.1. All the other parameters such as the height of the cell in contact with the contours of the aircraft or the boundary conditions remained exactly the same. Furthermore, this case incorporated the same design angles as those from the analytical case and one single simulation per angle of attack was run, composing a total of 10 simulations.
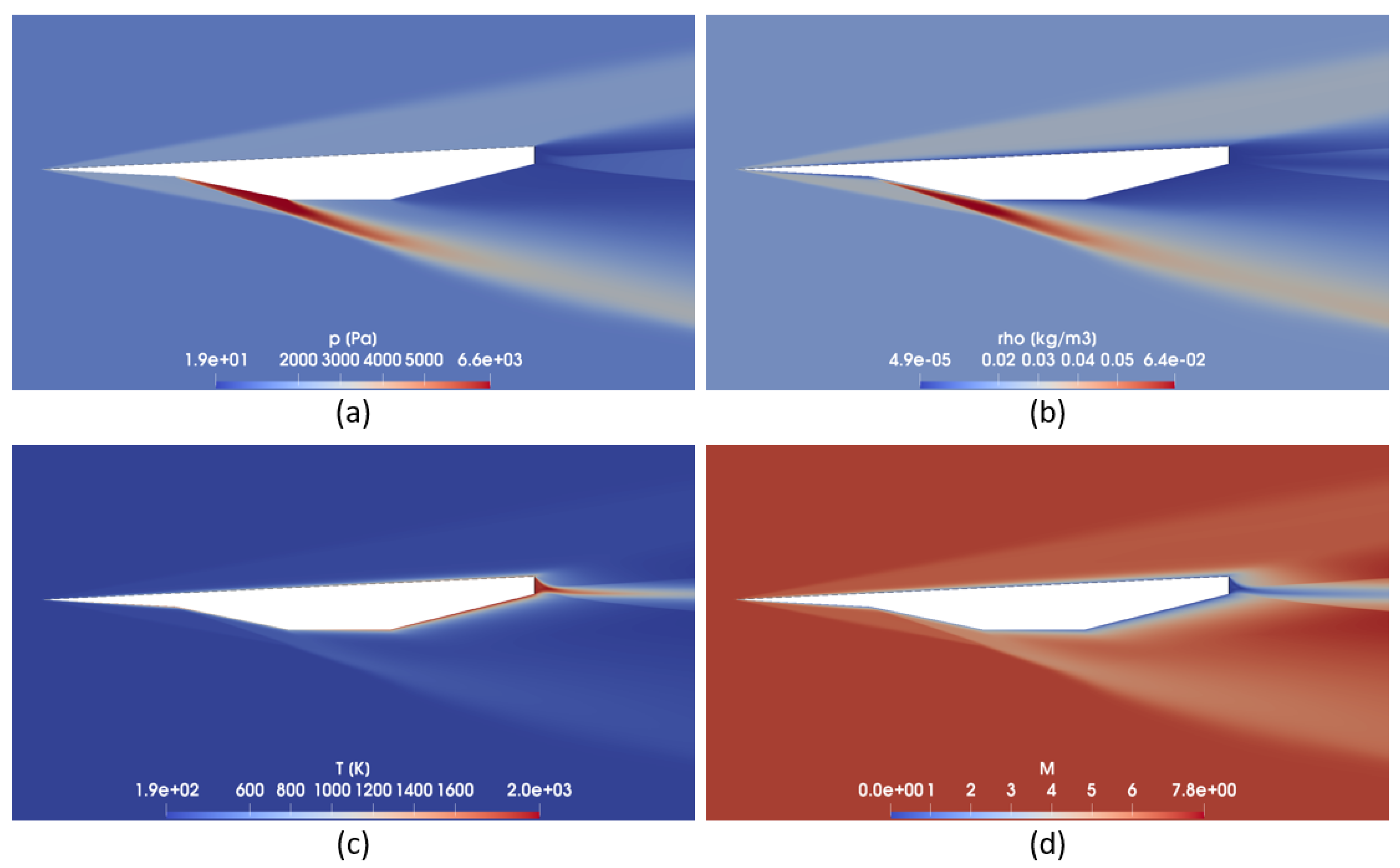
The pressure, density, temperature and Mach fields for
of the CFD case with the scramjet neglected are depicted in
Figure 3. The different discontinuities due to the oblique shock and Prandtl–Meyer expansion waves are clearly visible as well as the drastic expansion at the trailing edge. These physical phenomena are precisely explained in
Section 4.5.
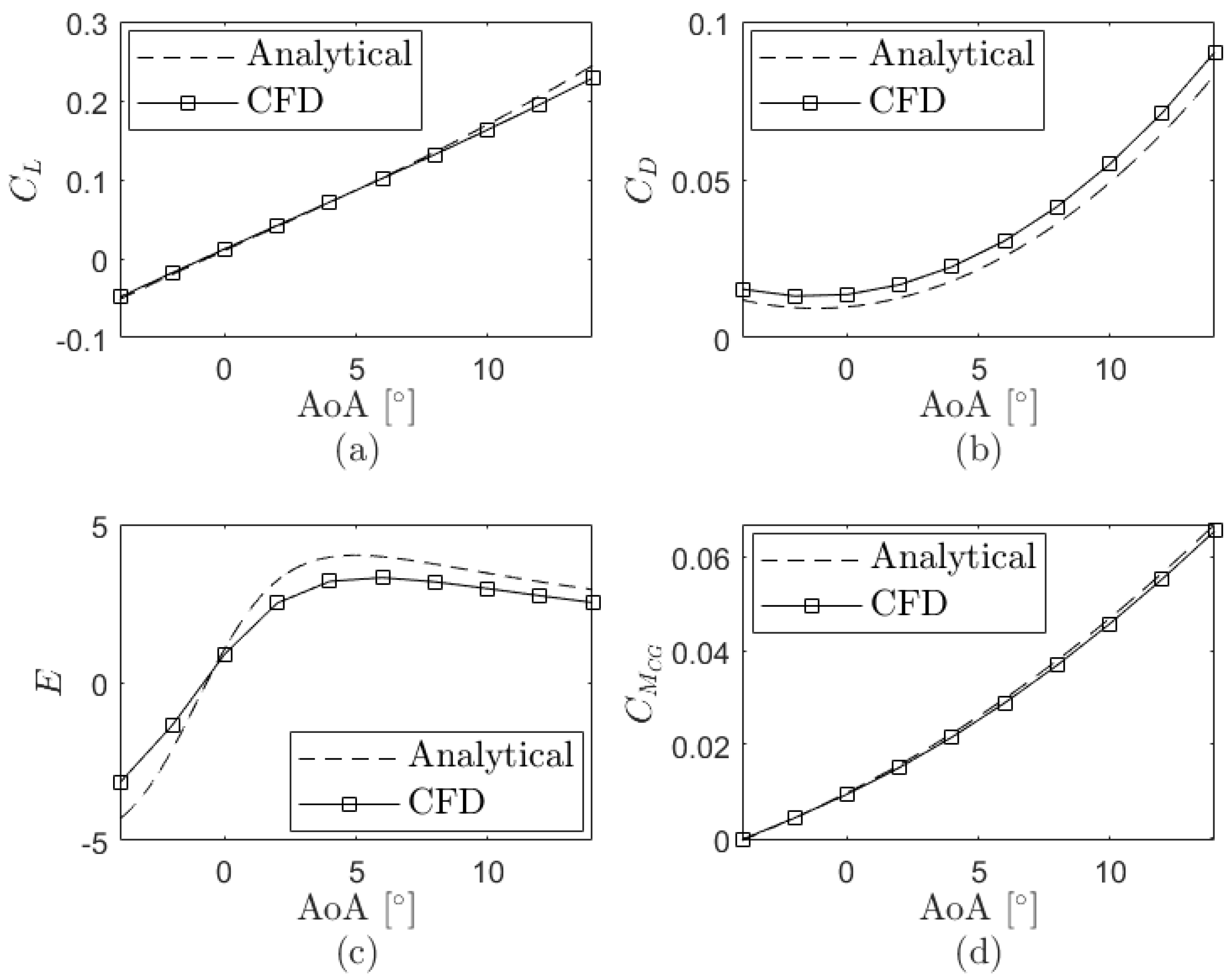
The comparison of the aerodynamic parameters is represented in
Figure 4.
Figure 4a shows that the CFD lift coefficient is lower than the analytical one in terms of absolute value; from
to
, the maximum deviation is under 1%, while from
to
, a maximum deviation of 5% is observed, approximately. The CFD drag coefficient is around 22% higher (
Figure 4b). These differences are mainly caused by the viscous stresses considered in the CFD model since the analytical model did not include them. The aerodynamic efficiency is plotted in
Figure 4c where, in terms of absolute value, the analytical aerodynamic efficiency is larger than the CFD for all the presented angles of attack since its drag coefficient is lower. In this case, the maximum efficiency in the analytical case is 18% higher than that of the CFD case (maximum deviation); such discrepancy is due to the viscous forces evaluated in the CFD simulations. Finally, according to
Figure 4d, the pitching moment coefficient is similar in both types of studies and regardless of the angle of attack evaluated; only a maximum deviation of around 1% is observed.
Table 5 shows the analysis of the zero pitching moment and Vertical Force Balance conditions of the CFD case with the scramjet neglected. For the analytical case studied, the same analysis is presented in the following section,
Table 6. The characteristic angles of attack
and
are almost the same as those calculated in the analytical study, compare
Table 5 and
Table 6. The CFD angle of attack that allows a zero pitching moment condition,
, which is
, is 0.5% higher than that of the analytical case, shown in
Table 6. For the CFD angle of attack in which the aircraft flies with the Vertical Force Balance condition, which is
, it is exactly the same as the analytical one, shown in
Table 6. As a result, for this last condition, the CFD lift coefficient is exactly the same as the analytical one and the CFD pitching moment coefficient
only differs by 3%. The CFD drag coefficient and CFD aerodynamic efficiency, however, differ by 21% and 17%, respectively, due to the consideration of the viscous effects in the CFD model.
This study shows that the analytical and CFD implementations generate very similar results. Only the drag coefficient and aerodynamic efficiency show some deviations, around 20% between both models.
In order to further validate the CFD model, the results of the CFD case 1 presented in
Section 4.5 were compared by those presented in [
2,
3,
8], where full three-dimensional CFD models and experimental tests at Mach number 6 were analysed. The parameters involved in the comparison study were the lift and drag coefficients for
,
,
and
. It is particularly remarkable to see that the experimental data presented in [
2,
8] is almost identical. In each of these two studies, there is also a good agreement between the experimental and CFD results. In addition to that, it is seen that the drag coefficients presented in the current paper are slightly smaller than those presented in the other studies. This fact is understandable since the wings, stabilizers and the lateral side of the aircraft are not considered in the present approach. It is also remarkable to see that the lift coefficients of the present paper are very close to the experimental and simulated ones obtained by [
2,
8]. For the drag coefficient, a maximum deviation of 37% between the experimental results from [
2] and the results from the 2D CFD case 1 is obtained for an angle of attack of 2
. For the rest of the angles of attack evaluated, the
average deviation is 17%. The maximum deviation for the lift coefficient is observed to be 20% for an angle of attack of 2
. The average
deviation for the other angles of attack is 10%. Perhaps one positive conclusion extracted from the comparisons presented is that simple 2D simulations are capable of showing a trend in the same direction as full 3D experimental tests and CFD approaches. Furthermore, they show that the main body of the aircraft is responsible for most of the lift and drag exerted on the body.
4.4. Analytical Case and Geometric Modifications
The dependence of the lift coefficient, drag coefficient, aerodynamic efficiency and pitching moment coefficient on the angle of attack of the analytical case studied at Mach 7 and an altitude of 30 km are depicted in
Figure 5. In the analytical study, it was verified that the aerodynamic coefficients did not depend on the altitude, but the main parameters in which the aircraft flew with the Vertical Force Balance condition did. Within the angles of attack from −4
to 14
, the lift coefficient increases almost linearly with the angle of attack (
Figure 5a), while the drag coefficient does it in a parabolic way (
Figure 5b). The stall in
vs.
is not contemplated since the effects of the boundary layer detachment were not considered. Efficiency
E increases with the increase in the angle of attack, reaches its maximum value of 4.02 at
, and then decreases (
Figure 5c). Finally, the pitching moment coefficient, which was considered to be positive in the pitch up of the aircraft, also increases approximately in a linear way with the
(
Figure 5d). As its gradient, known as the longitudinal static stability index, is positive, the aircraft is unstable with regard to any disturbance in the angle of attack; when
, then
and the aircraft tends to raise its nose.
Table 6 shows these coefficients in addition to the shock wave angles
and
for the zero pitching moment and Vertical Force Balance conditions as well as the corresponding
and
. Both parameters
and
are the shock wave angles of stages 2 and 3, respectively, in which the aircraft would fly with the nose optimised configuration according to the defined angles of attack. This configuration can be considered if the deviations between them and
and
are under 10%. The zero pitching moment condition is achieved for
, which leads to a negative lift coefficient and aerodynamic efficiency, and a Prandtl–Meyer expansion wave is originated at the beginning of stage 2. Moreover, since
is very close to
, the aircraft can be considered to fly with the nose optimised configuration. In case of the Vertical Force Balance condition, since
, the lift coefficient is positive and the aerodynamic efficiency is almost maximum, but
. As
differs by 5% from
and
by 8% from
, the aircraft can also be considered to fly with the shock waves of stages 2 and 3 focusing on the tip of the lower edge of the scramjet.
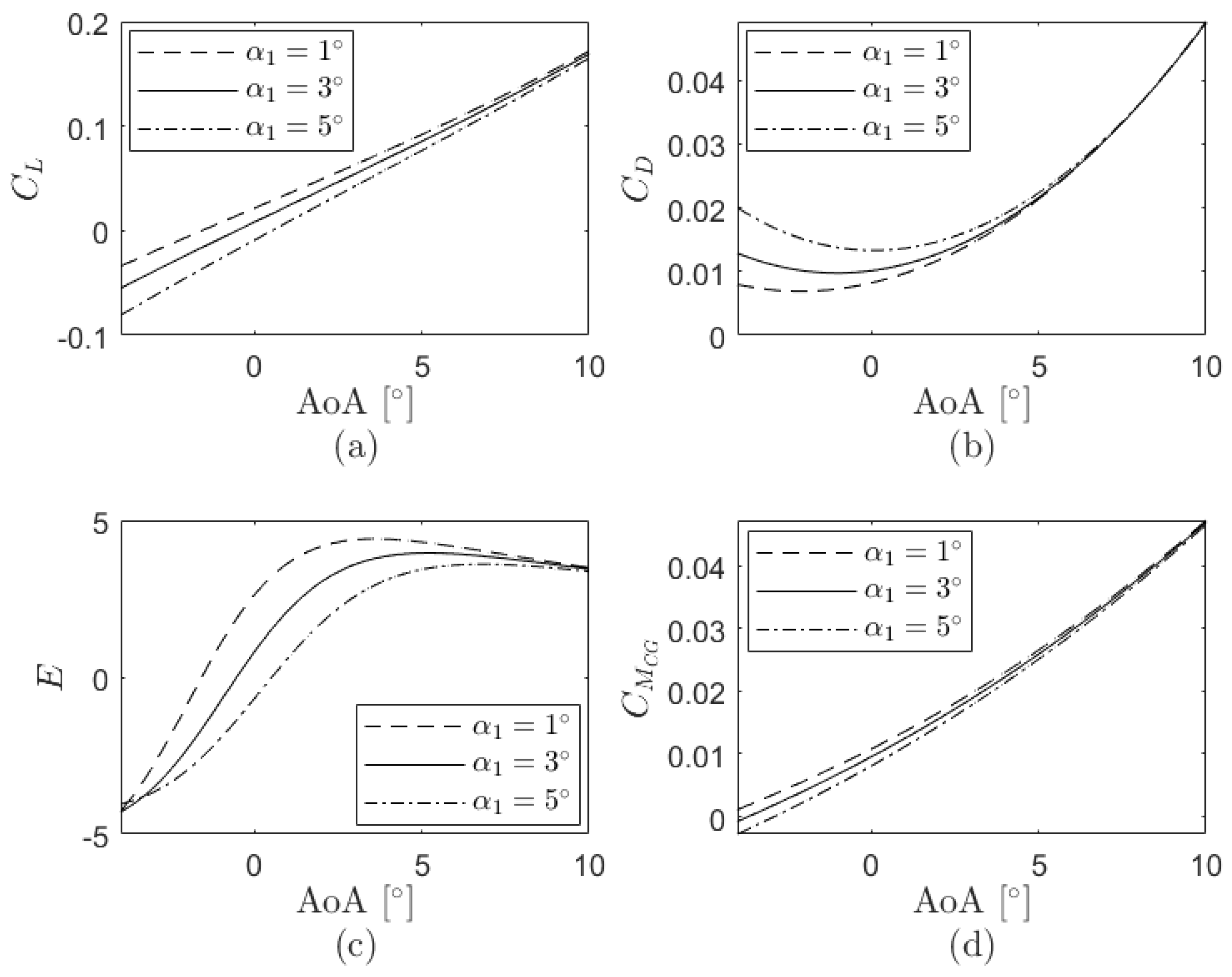
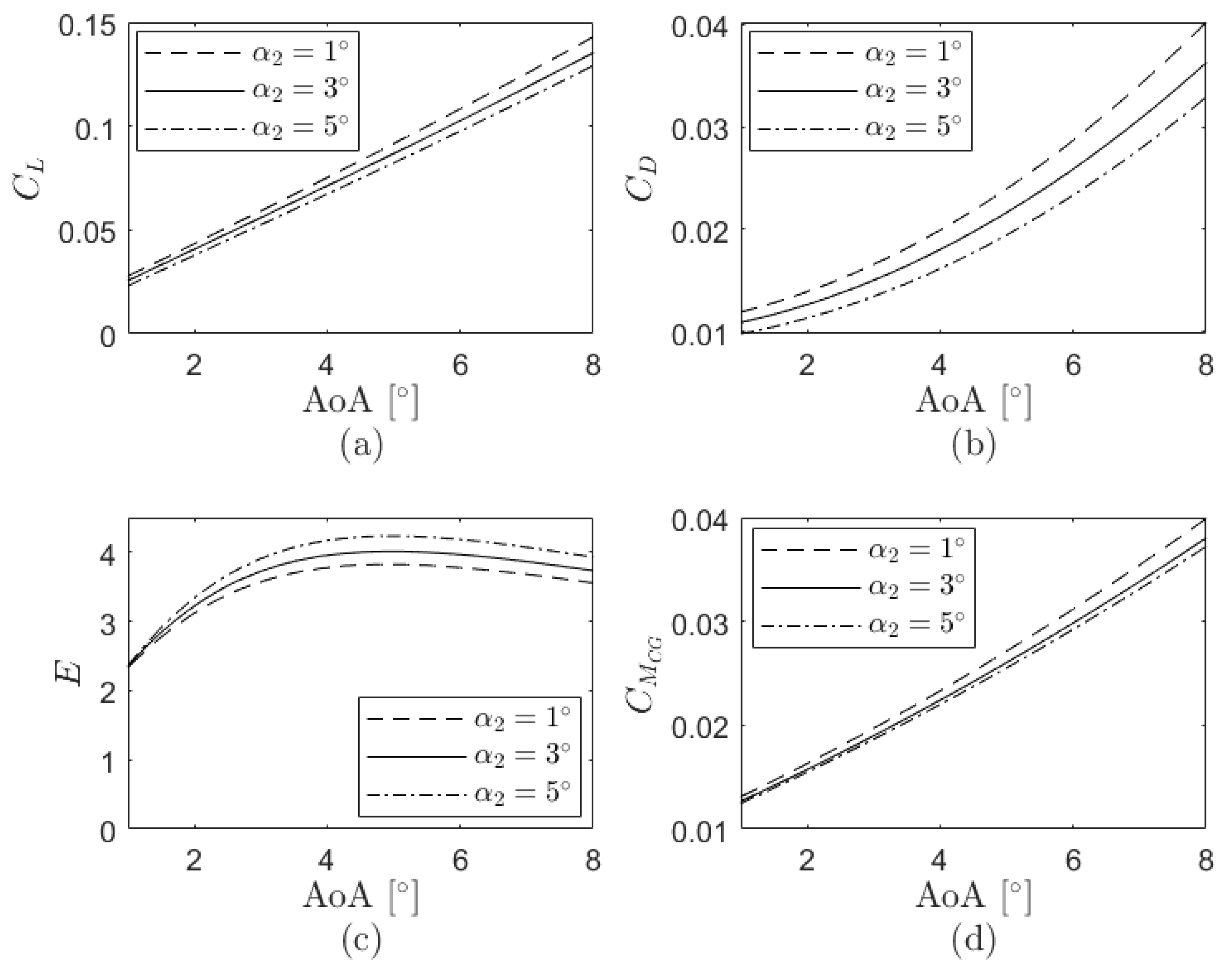
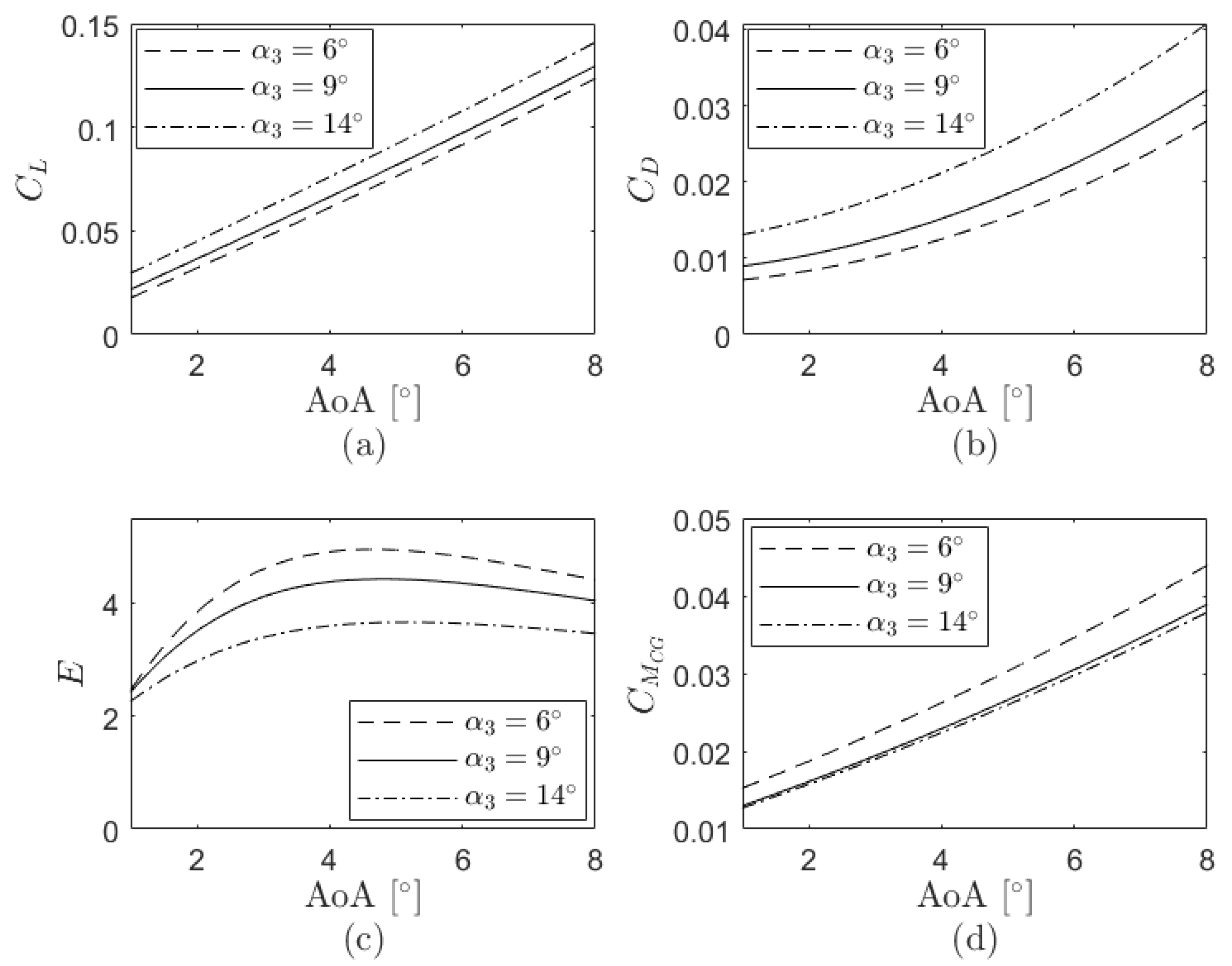
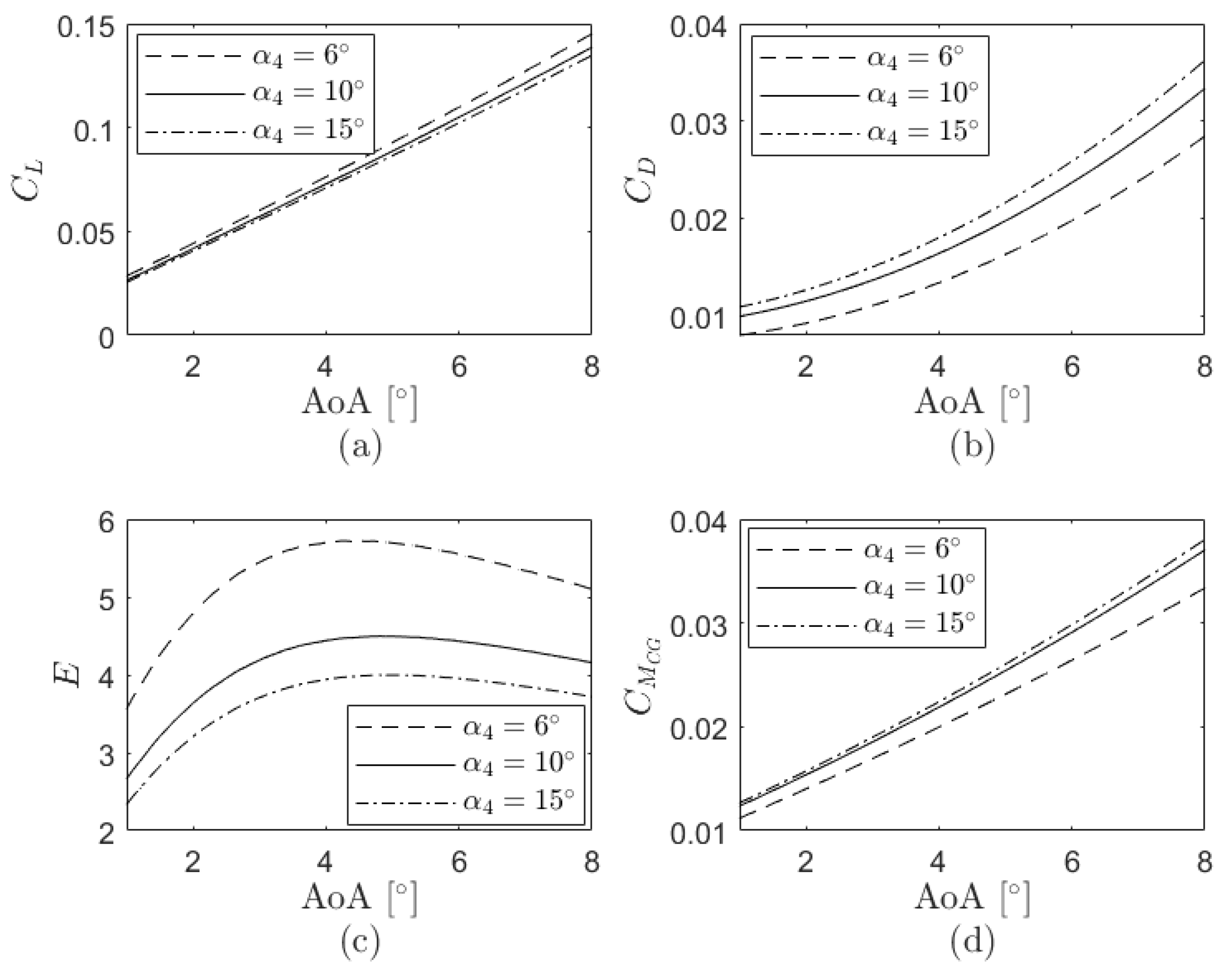
The variations of the lift coefficient, drag coefficient, aerodynamic efficiency and pitching moment coefficient as a consequence of the changes in the design angles are evaluated next. These parameters in terms of the angle of attack for different
and maintaining constant the remaining design angles (
,
and
) as those from the analytical case are presented in
Figure 6, where a reduction of
brings an increase of the lift coefficient, aerodynamic efficiency and pitching moment coefficient and a decrease of the drag coefficient. As seen in
Figure 7, decreasing
increases the lift, drag and pitching moment coefficients while the aerodynamic efficiency decreases. According to
Figure 8, a reduction of
implies an increase of the pitching moment coefficient and aerodynamic efficiency and a decrease of the lift and drag coefficients.
Figure 9 finally shows the modifications of the aerodynamic coefficients due to the changes in
where, in this particular case, a decrease of this design angle comes with an increase of the lift coefficient and aerodynamic efficiency and a decrease of the drag and pitching moment coefficients. Overall, since the surface of stage 1 is far bigger than that of the other stages, the variations of the aerodynamic parameters are more significant when
is manipulated than when the other design angles are modified. Although modifications on
are smaller than those on the other angles, the differences of the aerodynamic coefficients are more notorious in the first case.
4.5. CFD Cases
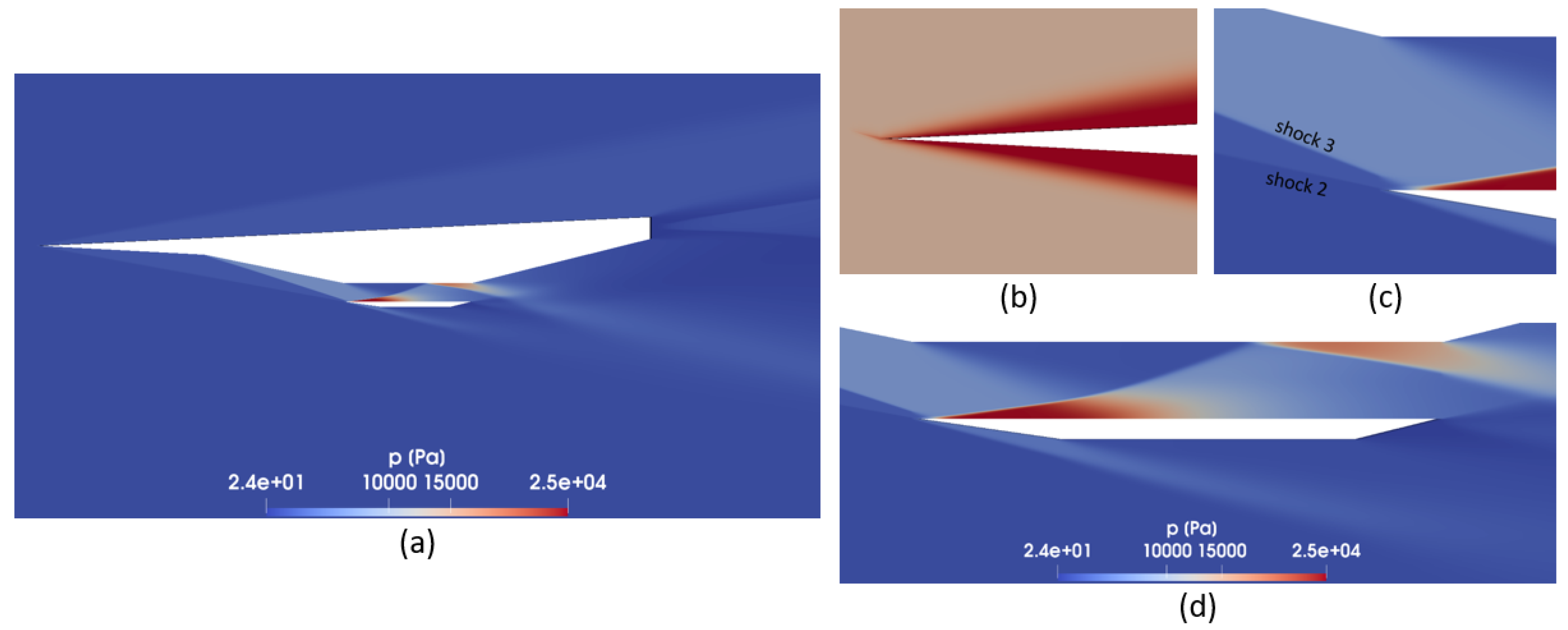
Case 1 is initially presented with the variation of the pressure field throughout the aircraft at a zero angle of attack in
Figure 10a. Since
, a shock wave is produced at the beginning of the extrados where, consequently, the pressure is increased and remains approximately constant along the surface. This phenomenon is also present in the aircraft nose (stages 2 and 3); in case of stage 3, the increase of pressure is more significant due to the difference in the design angles (
, see
Table 3).
Figure 10b shows that shock waves of stages 1 and 2 are completely attached to the sharp leading edge of the wedge. This fact is given because of the high Mach number where X-43A flies and the small wedge angle that presents at the leading edge. X-43A uses the fuselage nose part to form the shock in front of the intake. Theoretically (according to the analytical model), the aircraft should fly with the nose optimised configuration under those conditions of design angles and
. Notice that in this case a different colour scale has been used to represent this phenomenon. Focusing on
Figure 10c, shock 2 (which is the one formed at the beginning of stage 2) is focused on the tip of the lower edge, while shock 3 (the one that corresponds to the shock wave created at the beginning of stage 3) is slightly deflected into the entrance of the throat.
Inside the scramjet, different things occur together (see
Figure 10d for more detail). On the one hand, the flow expands as a Prandtl–Meyer expansion wave being produced at the end of stage 3. As a result, there is a small region situated in the upper left side in which the pressure decreases from that of the previous stage. On the other hand, shock 3 reflects from the lower edge generating a new shock, which, in turn, reflects from the upper edge forming, once again, another shock wave. In other words, two regular reflections in steady flow inside the engine are created. The first reflection leads to a high pressure region downstream at about 25 kPa, while the pressure after the second reflection is 15 kPa approximately. These differences are caused by the incident pressure of each reflection shock (the one of the first reflection shock is bigger than that of the second reflection shock) which, overall, translates into an energy dissipation of these reflection shock waves along the scramjet. In addition to that, after the first reflection, the flow is theoretically parallel to both wedges. This phenomenon is known as the shock diamond and provides some regions with strong adverse pressure gradients which induce flow separation. Finally, at the end of the upper right side of the scramjet, a Prandtl–Meyer expansion wave is originated. The pressure decreases and remains constant along the surface all the way to the trailing edge; there, the expansion process is so drastically that the pressure goes down to 20 Pa approximately, which enables the creation of some vortex.
Overall, all the waves originating along the aircraft are dissipated slowly downstream until the outlet boundary section.
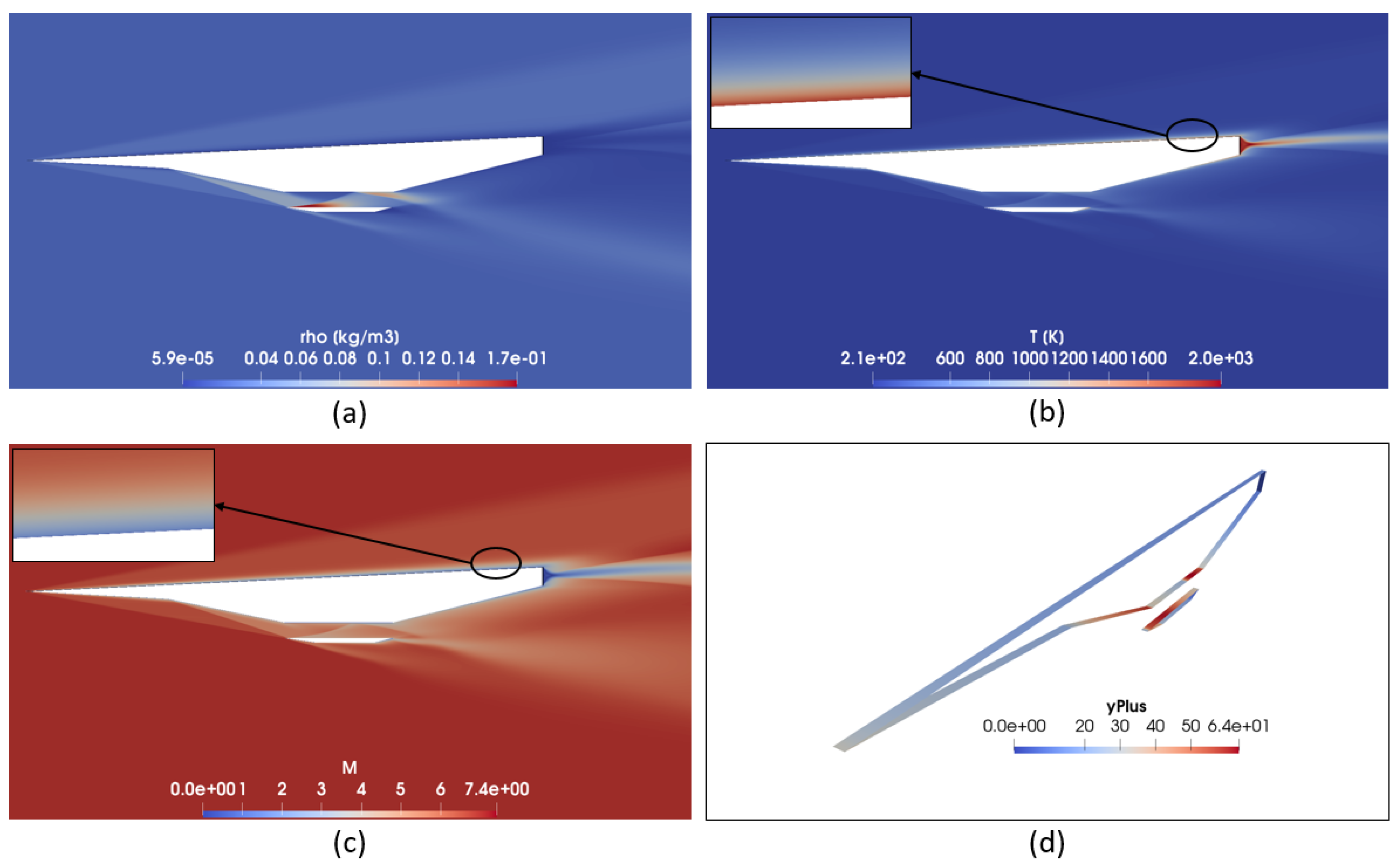
The density, temperature and Mach fields of the domain for the same angle of attack are depicted in
Figure 11 in addition to the
distribution along the walls of the aircraft. The density behaviour (
Figure 11a) is almost the same as the pressures: a high density in some regions inside the scramjet and an almost zero one along the trailing edge. In addition, as the flight altitude is high, the density values are relatively small as well as those from pressure. Since the air was considered to be a perfect gas, the density along the surfaces is reduced due to the high temperatures there. In case of the temperature field (
Figure 11b), two remarkable things are given in addition to the discontinuities caused by the oblique shock and Prandtl–Meyer expansion waves. Firstly, some aircraft contours are illuminated or, equivalently, the temperature is higher. This means that these regions capture the thermal boundary layer; the surface temperature is higher and decreases with the normal direction until arriving to the freestream temperature, which it keeps constant. From a theoretical point of view, this high temperature is caused by the viscous stresses, which, in turn, are caused by the enormous velocity gradients along the boundary layer. According to
Figure 11d, these regions are the same as those with low
values, which, evidently, translates into a more precise capture of the boundary layer. Contrary to that, other regions where the pressure is relatively high (e.g., some parts of the walls inside the scramjet or the wall of stage 3), the maximum
values are around 50 or, in other words, are relatively high and, consequently, the temperature gradients can not be properly visualised. In fact, the
of the different surfaces of the aircraft are extremely different due to the drastic changes of the air properties that are caused by the shock and Prandtl–Meyer expansion waves phenomena. Secondly, the temperature around the trailing edge is extremely high and decreases gradually downstream producing two lines around it. These lines represent discontinuities such as expansion waves, forming a triangle that dissipates with the distance. Finally, for the Mach field (
Figure 11c), a zero Mach number is found in some aircraft contours, which translates into a zero flow velocity. In fact, these regions are also the same as those with low
, meaning that some part of the boundary layer is captured. The Mach number starts being zero on the surface and increases gradually along its normal direction until arriving to the Mach number downstream the wave. Overall, the Mach field has the same behaviour as the pressure and temperature fields. The oblique and Prandtl–Meyer expansion waves are clearly delimited, and the regions where the pressure increases, the Mach number decreases and vice versa. As well as in the temperature field, a large fluid expansion occurs at the trailing edge; the Mach number falls to zero and increases progressively downstream.
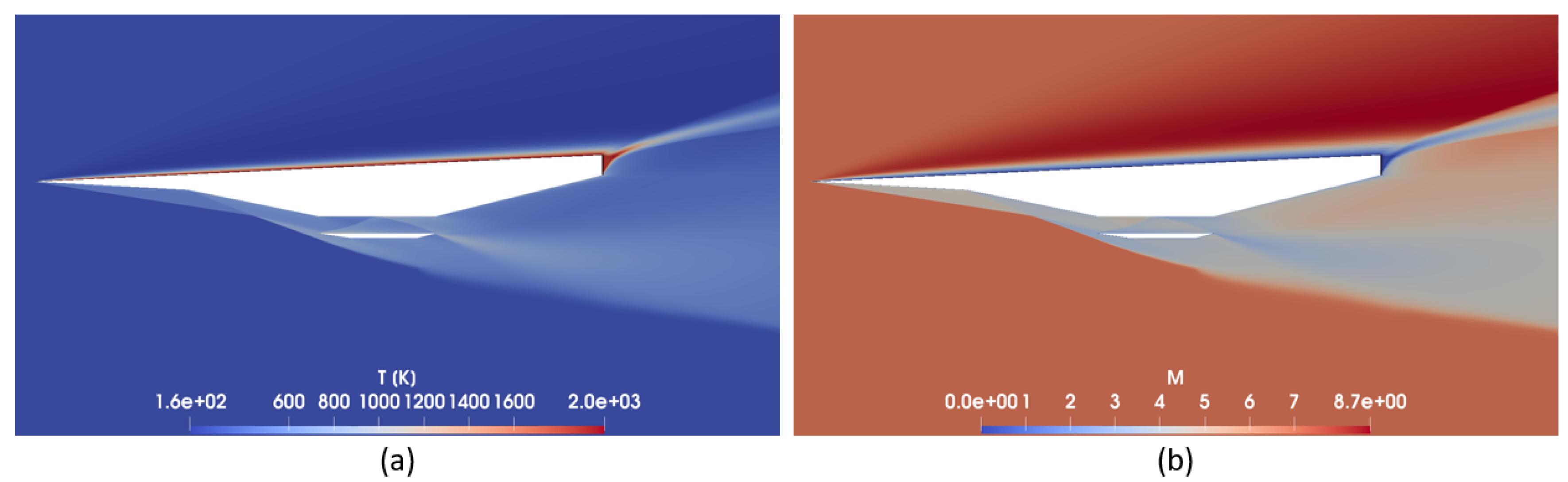
The main fields for
of case 1 are also evaluated, see
Figure 12 and
Figure 13. Under these conditions, a Prandtl–Meyer expansion wave is originated at the beginning of extrados, thus the pressure (
Figure 12a), density (
Figure 12b) and temperature (
Figure 13a) decrease and the Mach number (
Figure 13b) increases. The increase of the angle of attack causes a displacement to the left side of shock 3, which cuts the one coming from stage 2 due to its superiority in pressure strength and incapacitates it to reach the scramjet. A third reflection takes place at the end of the tip of the scramjet, which is almost imperceptible due to its weakness. Finally, the increase of the
also produces an increase of the pressure gradients inside the scramjet in addition to a higher curvature of shock 3 and the waves created at the trailing edge.
For
(
Figure 14), the aircraft can be considered to fly with the nose optimised configuration since the oblique shock wave formed at the beginning of stage 3 is focused on the tip of the lower edge of the scramjet.
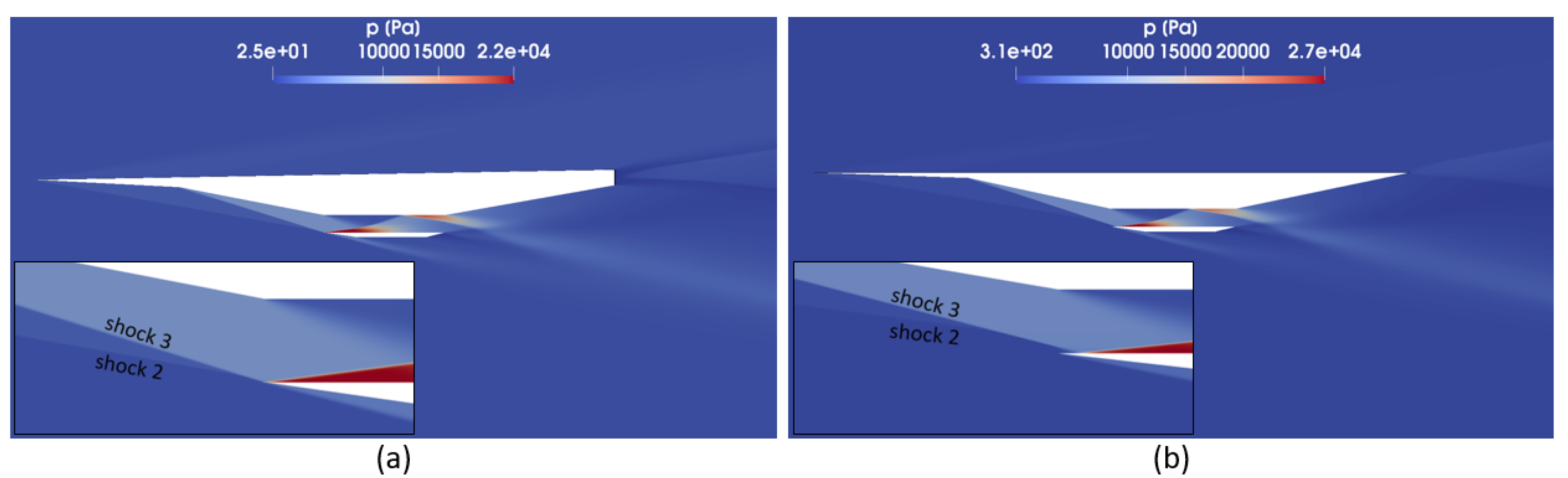
The pressure field of the other two CFD cases studied, case 2 and case 3 defined in
Table 3 for
, is presented in
Figure 15. Case 2 was designed to fly with the nose optimised configuration for
as seen in
Figure 15a. In addition to that, the design angles
and
were slightly reduced from case 1 in order to have a better aerodynamic performance according to the results obtained of the analytical model, see
Figure 6 and
Figure 9; the maximum reached pressure (situated in the lower edge of the scramjet) is about 22 kPa instead of the 25 kPa observed in case 1 which, in the end, translates into a higher lift. Case 3 was not only created to improve the aerodynamics of the aircraft by reducing
and
from case 1, but also to avoid the drastic expansion and, consequently, an extremely low pressure and velocity and a high temperature at the trailing edge by eliminating its surface. In this case, for
, shock 3 is slightly deflected into the entrance of the throat as seen in
Figure 15b. Furthermore, it was seen that the aircraft flew with the nose optimised configuration for
(this corresponding simulation is not presented in the study). The maximum pressure is focused along the scramjet and is about 27 kPa. Furthermore, as the surface of the trailing edge is eliminated, the drastic expansion is not observed as in the other cases.
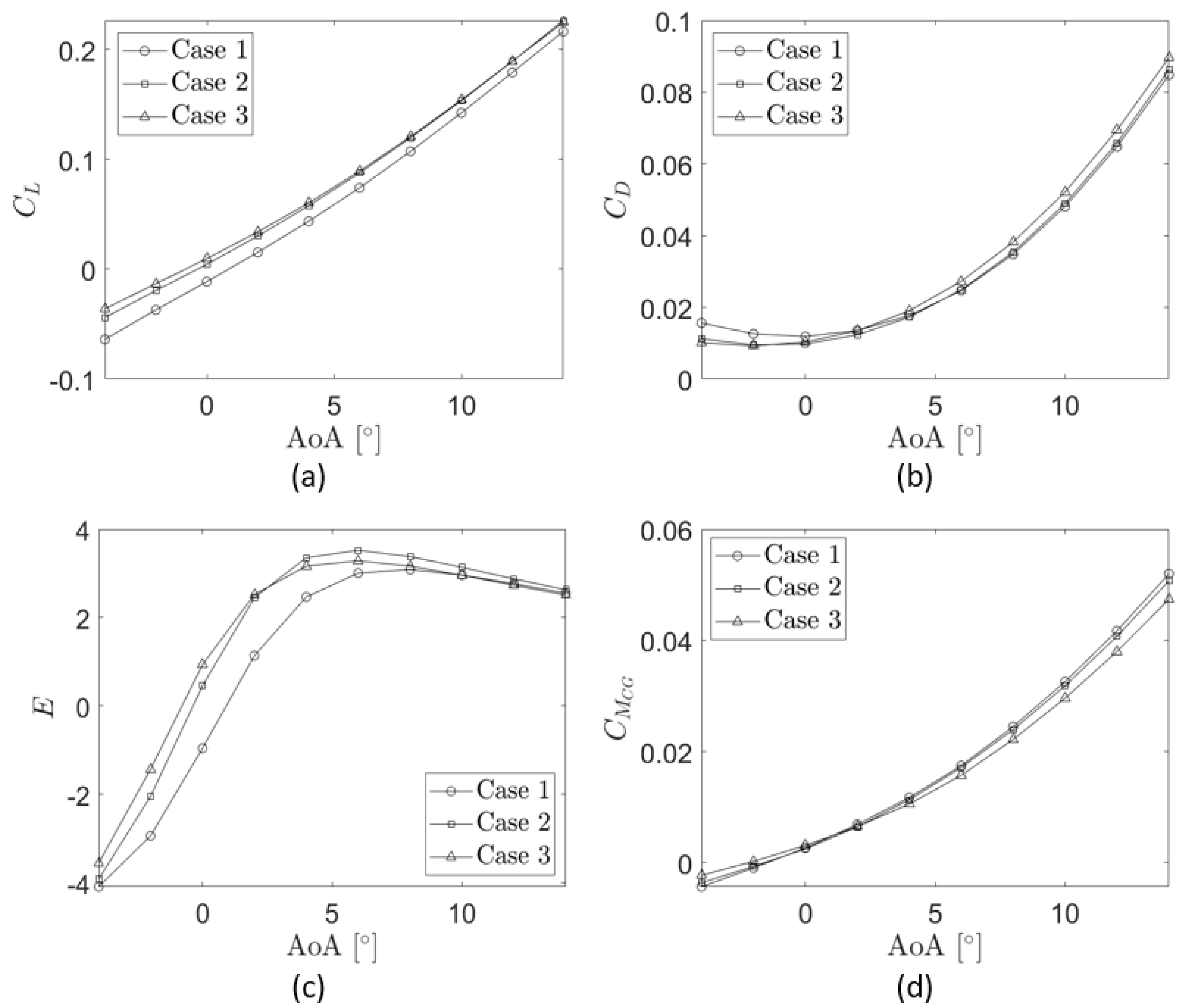
The integral aerodynamic characteristics
,
,
E and
in terms of the angle of attack for the three CFD cases are shown in
Figure 16. As seen in
Figure 16a, case 3 has the highest lift coefficient until
, where it is approximately the same as that of case 2. Case 1, however, has the lowest lift coefficient with a negative lift coefficient for
. According to
Figure 16b, case 1 has the highest drag coefficient up to
, where the first place is replaced by case 3, and case 1 has a very similar drag coefficient as case 2. The combination between the lift and drag coefficients leads to the aerodynamic efficiency in terms of the
(
Figure 16c). Both cases 2 and 3 have a similar
E; the aerodynamic efficiency of case 3 is higher for
and lower for the other angles of attack. Therefore, according to this graph, the maximum aerodynamic efficiency of case 2 is the highest one (
for
), followed by the one in case 3 (
for
) and finally case 1 (
for
). In addition, from
, all cases seem to converge to a certain value. Finally, the behaviour of the pitching moment coefficient through the different angles indicates a longitudinal instability condition with regard to any perturbation of the
(
Figure 16d); cases 1 and 2 are mostly similar according to this graph, while case 3 has the highest pitching moment coefficient for
and the lowest one for the other angles of attack. Therefore, as stated before, cases 2 and 3, which are very similar from an aerodynamic point of view, offer, in general, a better aerodynamic performance than the one from case 1.
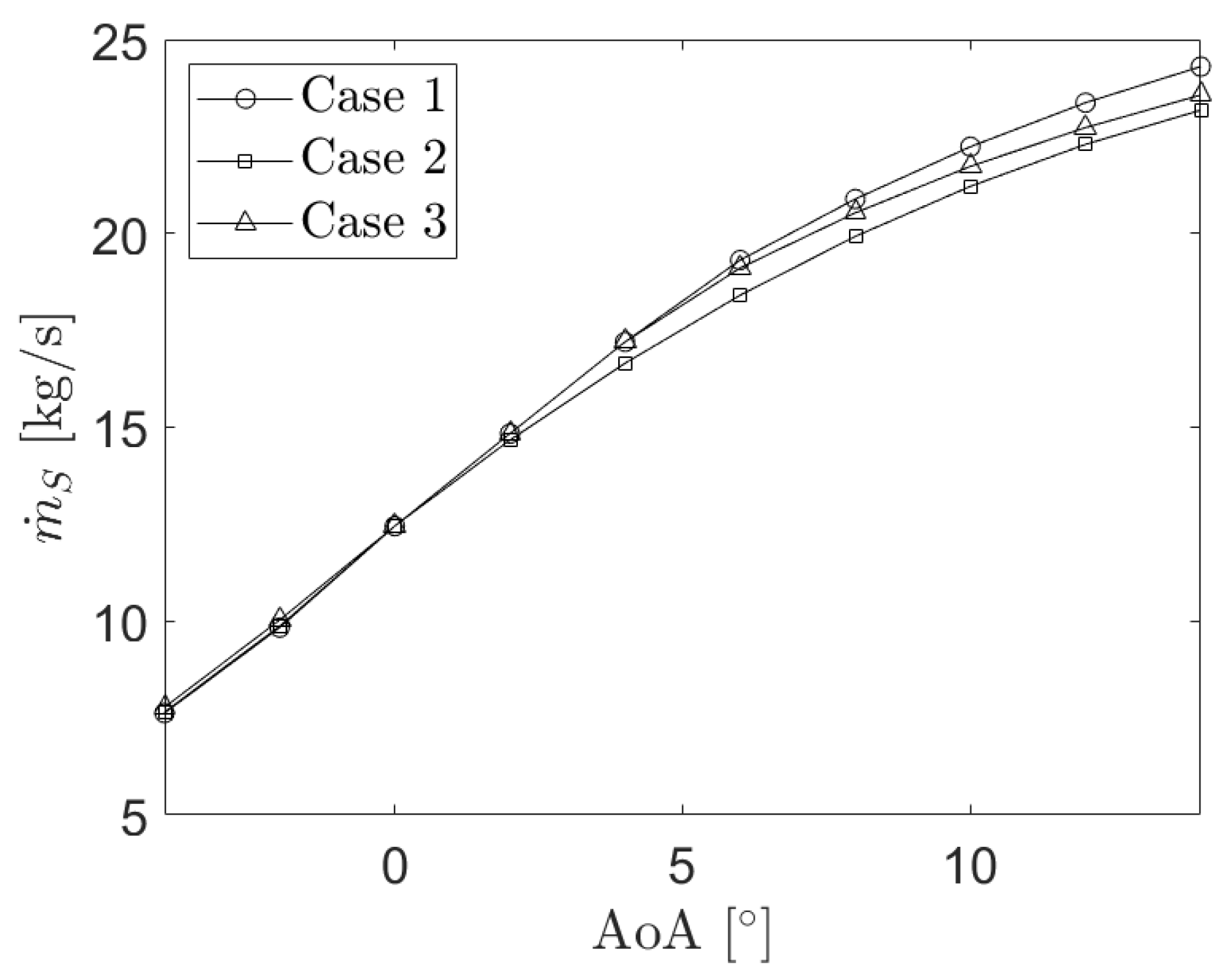
The mass flow rate throughout the scramjet in terms of the angle of attack of the three CFD cases is presented in
Figure 17 where, for the three cases, increases with it. In addition to that, all cases have approximately the same mass flow rate for
; at higher angle of attack, the mass flow rate of case 1 is the highest one, followed by the one from case 2 and finally case 3. For
, the mass flow rate of cases 1 and 3 are higher than that of case 2 as the aircraft flies with the nose optimised configuration.
All of the presented parameters of the three CFD cases are shown in
Table 7 and
Table 8 for the zero pitching moment and Vertical Force Balance conditions, respectively. For the first condition, all cases have a negative lift coefficient and aerodynamic efficiency since the angle of attack is negative; case 2 presents a lift coefficient slightly least negative than the rest, while case 3 has the lowest drag coefficient. This leads case 2 to reach the least negative aerodynamic efficiency and case 3 to have the lowest
. It is important to highlight that the negative lift coefficient obtained in the present study is caused by the non consideration of the stabilizers. These elements would be able to compensate this coefficient allowing the aircraft to fly. For the second condition, case 2 also gets the highest aerodynamic efficiency and the lowest drag coefficient. However, case 3 achieves this condition with a lower
, which translates into a better aerodynamic performance from a “lift point of view”. In addition to that, when the Vertical Force Balance condition is achieved, all cases present their corresponding maximum aerodynamic efficiency. Despite case 1 being the worst case in all aerodynamic aspects, it has the highest mass flow rate for both conditions.