1. Introduction
Damage can be defined as a change in the state of a material that disrupts the functioning of the structural element currently or may cause it in the future and which can lead to the destruction of this element or, in the worst-case scenario, the entire structure. Defects usually have the form of delamination, cracks or local destruction of the material due to corrosion or fatigue. They may also be in the form of voids or undesirable inclusions. Their cause may be external factors, such as exceeding the structure working time and various types of errors: service, maintenance, renovation, assembly and technological.
The issue of early detection, location and estimation of the structural damage is one of the most important engineering problems because it is closely related to the safety and durability of the facility. Non-destructive defect identification methods are a relatively young, continually developing field, e.g., a contactless method implementing the thermovision camera [
1]. New directions of research are indicated, different approaches are used, and many advanced methods are developed. Many of these are based on the analysis of structural response signals. A very promising tool for signal analysis, based on mathematical theory, is a wavelet transform (WT), which allows non-stationary signals to be effectively analyzed. Due to the possibility of multiresolution decomposition/analysis (MRA), it manages to extract even small, local signal disturbances from the global structural response, which often requires taking into account a considerable number of data. Moreover, if the wavelet analysis is used to identify the defect, it is enough to process the data obtained from the damaged structure without the need to compare it with the signal of the undamaged system. This is the main advantage of the method because in real experiments, the undamaged structure response signal is usually unavailable, and the numerical model may not be a precise representation of reality.
Wavelet transform was first used to detect defects in the mid-1990s, in which [
2] the vibration signal obtained in a computer-simulated experiment for a beam with a crack was analyzed. Numerically simulated experiments were also presented in [
3,
4,
5], in which the effectiveness of the WT in detecting damages in plates, beams and trusses, based on the analysis of static or dynamic structural response signals, was demonstrated. Experimental verification, conducted with the use of a laser scanning vibrometer, of numerical tests for eight vibration modes of the cantilever beam with cuts of 5, 10 and 20% of the beam height is presented in [
6]. The effectiveness of the discrete wavelet transform (DWT) for detecting damage and the influence of the wavelet order on the reliability of the obtained results was tested in real dynamic tests of concrete slabs in [
7].
Another non-destructive diagnostic method is the acoustic emission method (AE). In this method, elastic waves generated during physical, chemical or biological processes are analyzed. The analysis of the parameters of the recorded signals allows locating the emission source, which may be, for example, partial discharges occurring in the insulation of electrical power devices [
8,
9]. Online acoustic emission monitoring in order to observe damage progression in the filler-loaded glass/epoxy samples and characterize different fracture mechanisms associated with loading was presented in [
10].
The literature provides information on the use of wavelet analysis of acoustic signals concerning, for example, the identification of micro damages in composite materials [
11], analysis of changes in the structure of glass fiber under load [
12] and the location of AE sources based on the amplitudes of wavelet transform [
13]. Moreover, in the areas of interest of researchers, there are issues similar to those presented in this article, i.e., locating the AE source based on the wavelet analysis of the signal using the minimum number of sensors [
14] or searching for the wavelet coefficients of AE signals that can predict material damage [
15]. In addition, the analysis of AE signals may concern the monitoring of technological processes: aluminum welding [
16] or quality assessment of the chemical mechanical polishing (CMP) process [
17]. In addition, it is worth mentioning scientific research with the improvement of ultrasound methods [
18] or references such as wireless technologies [
19] or IoT [
20].
This paper is devoted to the problem of detecting and locating one or more defects in a steel plate while using the acoustic emission method in conjunction with a discrete wavelet transform.
Apart from the introduction, the paper is organized as follows: The second part of the article describes the AE method and wavelet transform. Then, in the third part, the construction of the test setup and test method are presented. The next part includes the results of the measurements. The article ends with conclusions from the research, and this part also includes plans for future research.
2. Acoustic Emission Method and Wavelet Transform
The AE method has many advantages, of which the possibility of using the device during regular operation deserves particular attention, as well as the minimal, often a total lack of influence of the measuring system on the working signals. However, when constructing a measuring system, the conditions in which it will work should be taken into account.
These conditions refer mainly to the registering device exposed to the environmental impact. This aspect is particularly important for recorded signals, i.e., special attention should be given to the possible recording of signals coming from outside the measurement system (disturbances) and the noise generated by the apparatus. In some cases, there may be a situation in which the signal-to-noise ratio is very low, and then an effective method of filtering the noise from the signal should be applied. The wider bandwidth signal further complicates the task or if this band is not known. Then a method is sought, which could be considered universal, i.e., effective in the whole band of the registered signal. The solution may be to use a wavelet transform that meets these requirements [
21,
22].
Wavelets are functions that, by meeting specific mathematical requirements, create a representation of signals or data. Wavelet analysis divides input data into components at different frequencies, analyzing each element with a resolution matched to its scale. To illustrate the situation, one can say that due to its ability to adjust the scale, wavelet analysis allows simultaneous observation of both the whole picture and the smallest details. That is why wavelets are very useful for approximating functions (signal processing) with discontinuities or sharp peaks.
In the presented work, the wavelet transform will be implemented as a tool to detect defects in engineering structures. A linear combination of wavelet functions is used to represent the signal (where it is any variable). A discussion on the mathematical foundations of wavelet transform can be found in extensive literature, e.g., [
23,
24,
25].
Continuous wavelet transform of the signal f(t) is defined as:
wherein the overbar denotes the complex conjugate of the function under it. The function (t) belongs to the space of measurable, square-integrable one-dimensional functions L
2(
R) and is an admissible basic (mother) wavelet if it fulfills the condition:
where Ψ(ω) is the Fourier transform of function ψ(t):
The average value of the wavelet function is zero, which can be expressed by the relation:
For signal decomposition, copies of the wavelet function, representing the family of wavelets, are used. They are obtained by scaling and translating the function (t):
where t is a time or space coordinate, a is a scaling parameter, b means a wavelet shift in the time/space domain. Parameters a and b belong to the set of real numbers (a, b ∈
R) and a ≠ 0. The number |a|
−1/2 is a normalizing factor, ensuring constant wavelet energy, independent of the scale which means that the norm ||ψ
a,b|| = ||ψ|| = 1 [
26].
In the analyses presented in this paper, the leading role plays the discrete wavelet transform (DWT). By entering a = 1/2
j and b = k/2
j (k, j ∈ C) into Formula (5) the wavelet family is created:
where j and k are scale and translation parameters, respectively.
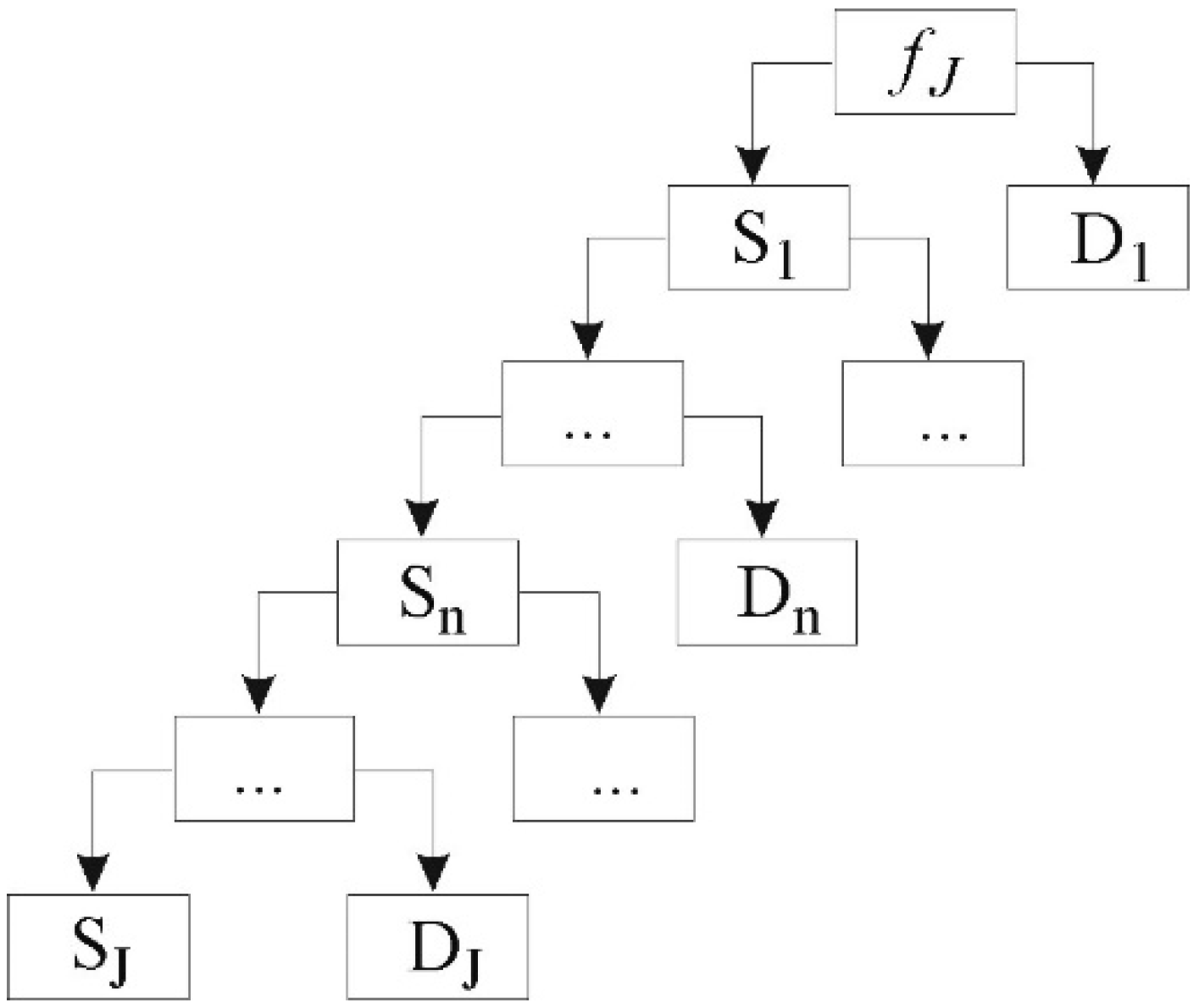
The multiresolution analysis of the discrete signal f
J(t) can be written according to the Mallat pyramid algorithm [
11]:
Each component in the signal representation (7) is associated with a specific frequency range and provides information at different levels of decomposition j = 1, …, J. The level of multiresolution analysis (MRA) is determined by the discrete parameter J, S
J is the approximation of the signal, D
n and S
n are, respectively, details and rough parts at different decomposition levels, and D
1 corresponds to the most detailed representation of the signal. To satisfy the dyadic requirements of DWT, the function f
J must be approximated by N = 2 J discrete values. The multiresolution analysis, while using the Mallat pyramid algorithm, is presented schematically in
Figure 1.
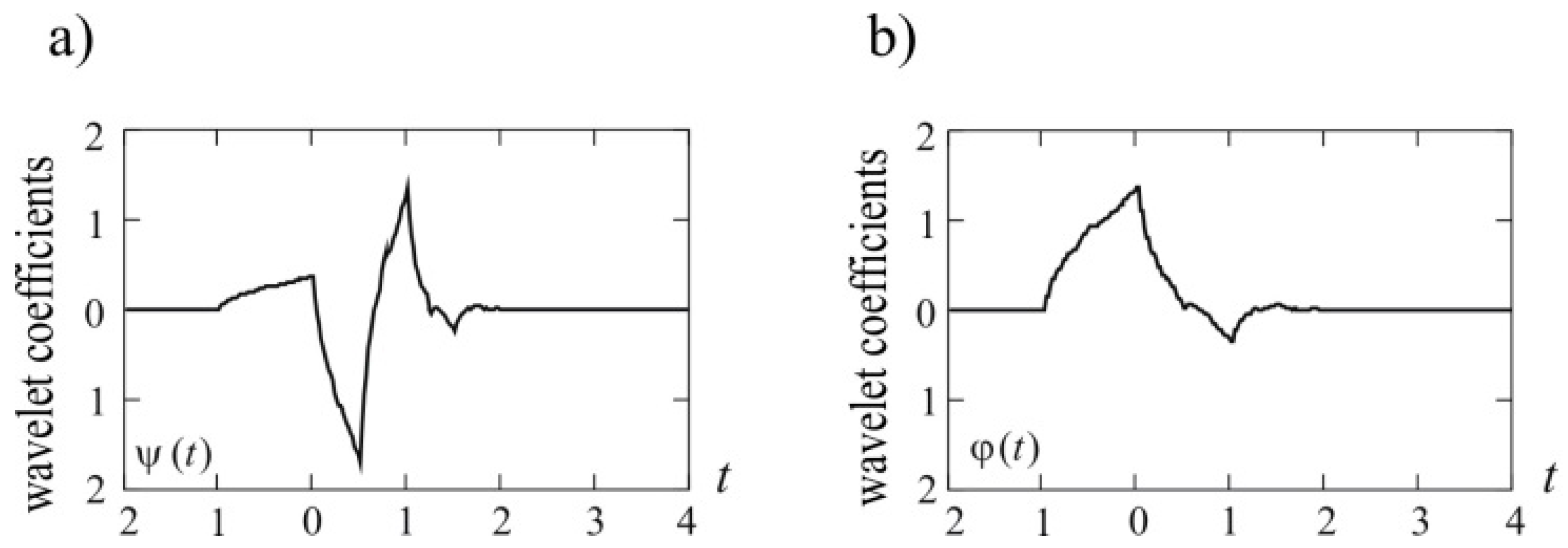
In the considerations regarding damage detection in steel structures, the Daubechies wavelet was applied. This is a family of orthogonal wavelets with compact support, asymmetrical with sharp edges. It requires a relatively small number of wavelet coefficients, and its order is between 2 and 20, always even numbers.
The selection of this wavelet results from the authors’ previous experience in detecting damages in various types of structures [
4,
5,
7]. The basic Daubechies wavelet (mother) and scaling wavelet (father) are shown in
Figure 2.
3. Concept of Tests
3.1. Assumptions of the Developed Method
Modal analysis is used in structural evaluation studies. It involves an analysis of accelerations generated in the facility by hitting with a modal hammer and registering the vibrations of the structure with an accelerometer. It seems that such an analysis may not give full information about the object condition due to its limitations regarding the use of measurement sets capable of recording signals in narrow, precisely defined frequency bands.
The purpose of the conducted research is to build an exciting-recording system, allowing for full observation of signals coming both from the excitation and the measuring transducer. Enforcement of the tests will allow indicating the characteristic parameters of the time course of the excitation signal, and the use of the wavelet transformation will enable to indicate the parameters (details), allowing to find the presence of damage in a given structure.
Considering the above, it is assumed that the method will be effective regardless of the value of force applied during the excitation of the structure. In this assumption, the hammer is to hit by any person (operator), the type of surface on which the construction is resting (to which it is attached), and, to a certain extent, resistant to imperfections of the test (to meet the conditions of the field test) which cannot affect the current state of the structure.
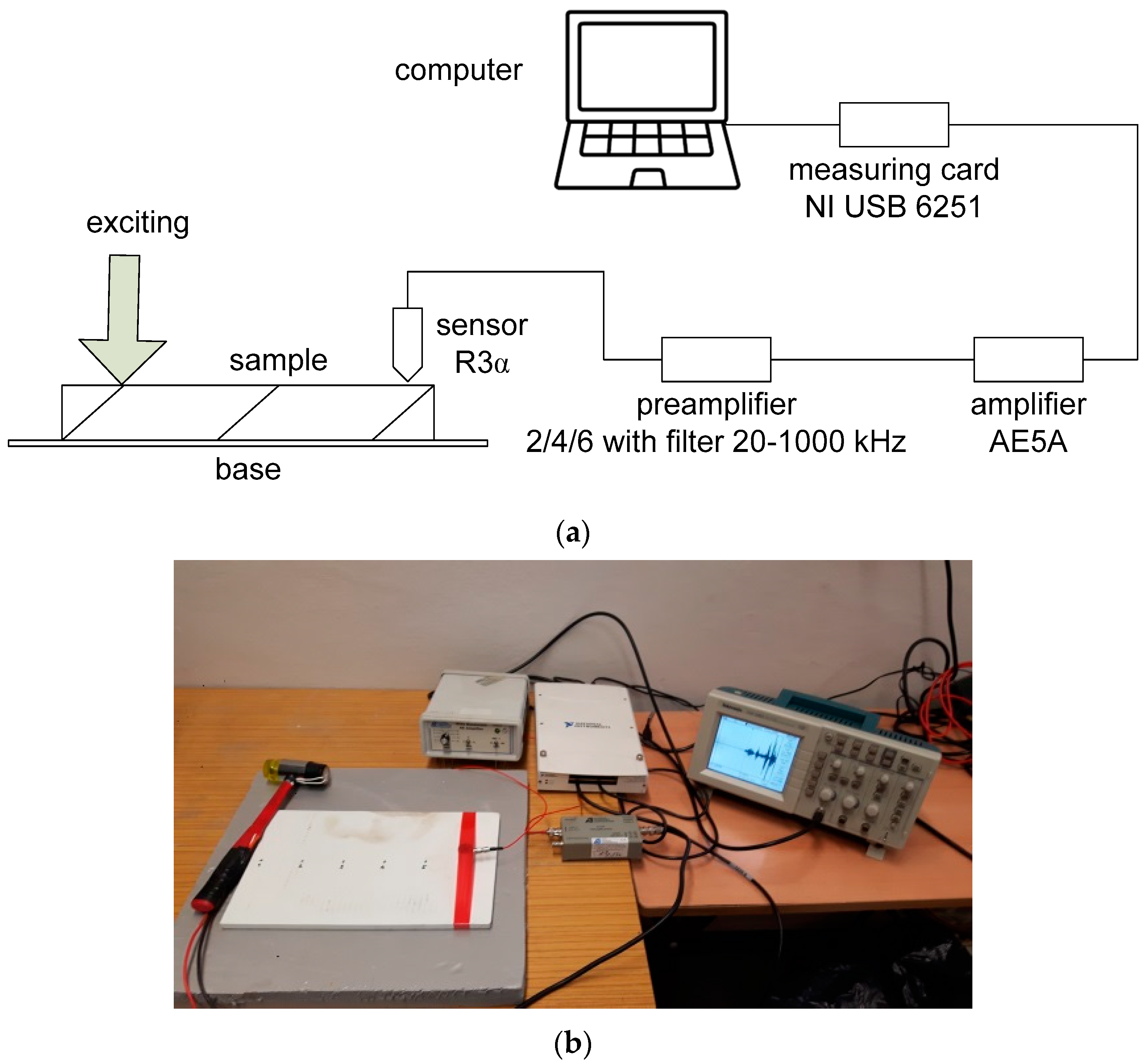
3.2. Description of the Experiment
For the purpose of conducting the experiment, a measurement stand was built, the diagram and view of which is shown in
Figure 3.
The test sample (plate) was excited using a modified hammer tinsmith. The modification consisted of attaching a piezoelectric plate and a polymer tip to its flexible boom. This treatment allowed recording the signals generated by the piezoelectric while hitting the sample with the hammer and minimizing the possible recontacts of the excitation with the sample. The precise knowledge of the moment of impact and the identification of the presence of possible, unintentional repetitions allows the starting point of the observation to indicate the signal coming from the transducer. The signals generated by the transducer were amplified and filtered in the preamplifier. The preamplifier has a built-in bandpass filter with a frequency range of 20 ÷ 1000 kHz. Then the signal was amplified in the amplifier and recorded with a resolution of 16 bits and a sampling rate of 1 MS/s in a binary form using a measuring card in the memory of the computer.
Before each test, the calibration of the recording circuit with the use of the Hsu–Nielsen method was performed. The measurements were carried out in three series of five excitations for different distances from the transducer. This number of attempts was considered sufficient to indicate the characteristics of the signal-dependent on the distance and type of damage. These tests were carried out first for the undamaged panel and then repeated for each type of damage: a small cavity, a large cavity, a hole and two holes.
The mutual location of the defects, the transducer, and the impact points in the case with two holes are shown in
Figure 4. The remaining defects were modeled in the upper half-plane (above a line drawn through the points of excitation).
Before the analysis, the recorded signals were denoised using the wavelet transform with a discrimination threshold equal to 10 mV to prevent the impact of equipment noise on the calculation results.
Based on catalog data and preliminary research, it was estimated that the noise of the measuring equipment was at the level of 6 mV. Hence, it was assumed, with some margin, that signals with amplitudes less than 10 mV should be rejected. At the same time, in order not to lose the information contained in the signal, it was decided to use the most effective noise reduction mechanism.
As shown in work [
21], the use of the wavelet transform is an effective method of noise removal and guarantees minimal information loss. The assumption of the algorithm is to minimize the mean square error. The procedure algorithm includes three main steps:
The appropriate selection of the wavelet used for filtration requires comparing the noise reduction results obtained for different wavelets.
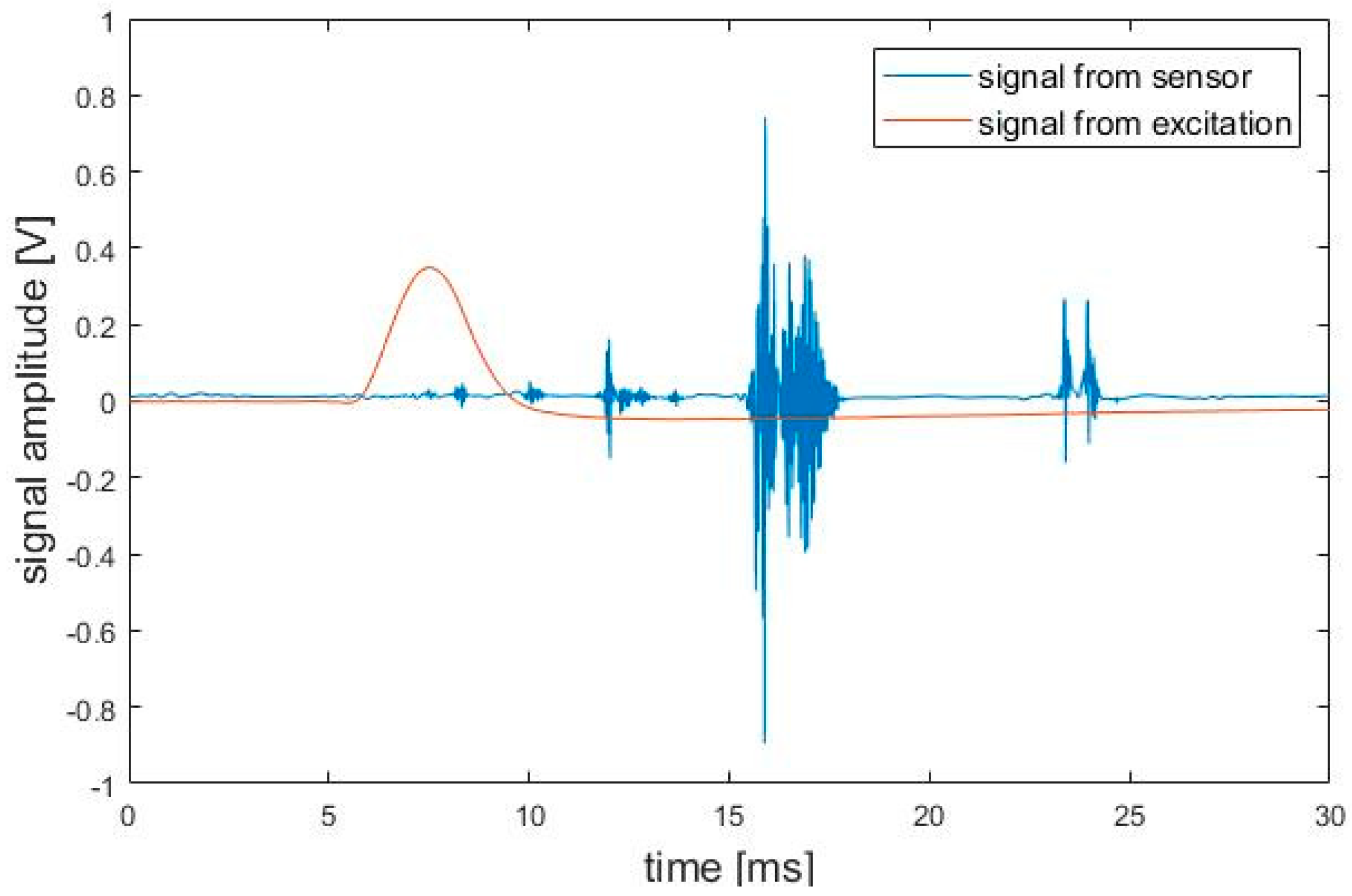
Exemplary signals coming from both excitation and measuring transducer are shown in
Figure 5.
4. Experimental Results
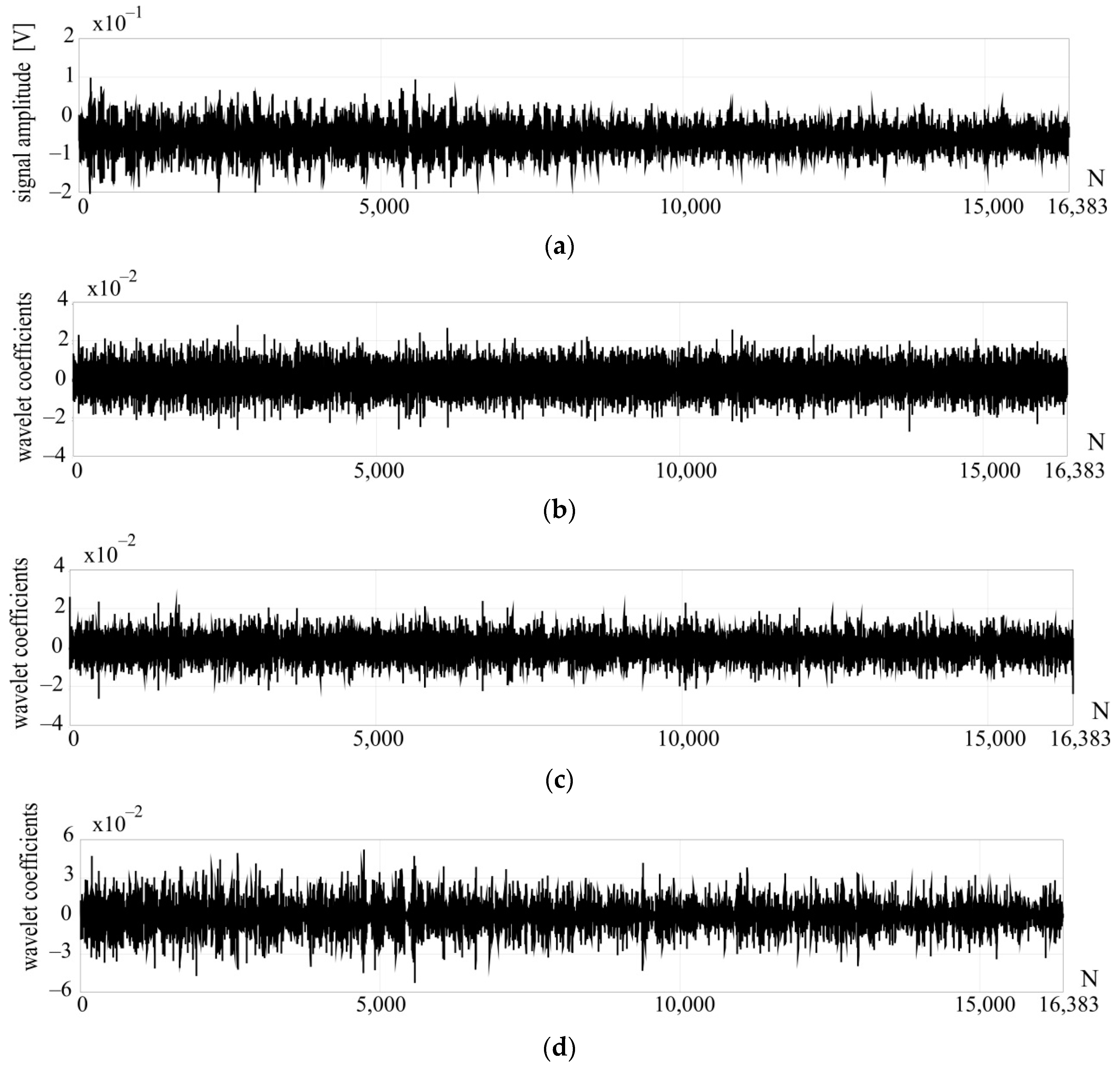
Experimental research was carried out for several simulated lesions, ranging from a small change on the surface of the plate (simulated as the tile’s bore), through a change in the structure (hole in the plate), up to two damages in the form of holes. The obtained results were compared with the case of no damage.
Examples of signals recorded for particular types of damage are presented as follows:
Figure 6a for the undamaged board; a case with minor damage (bore) in
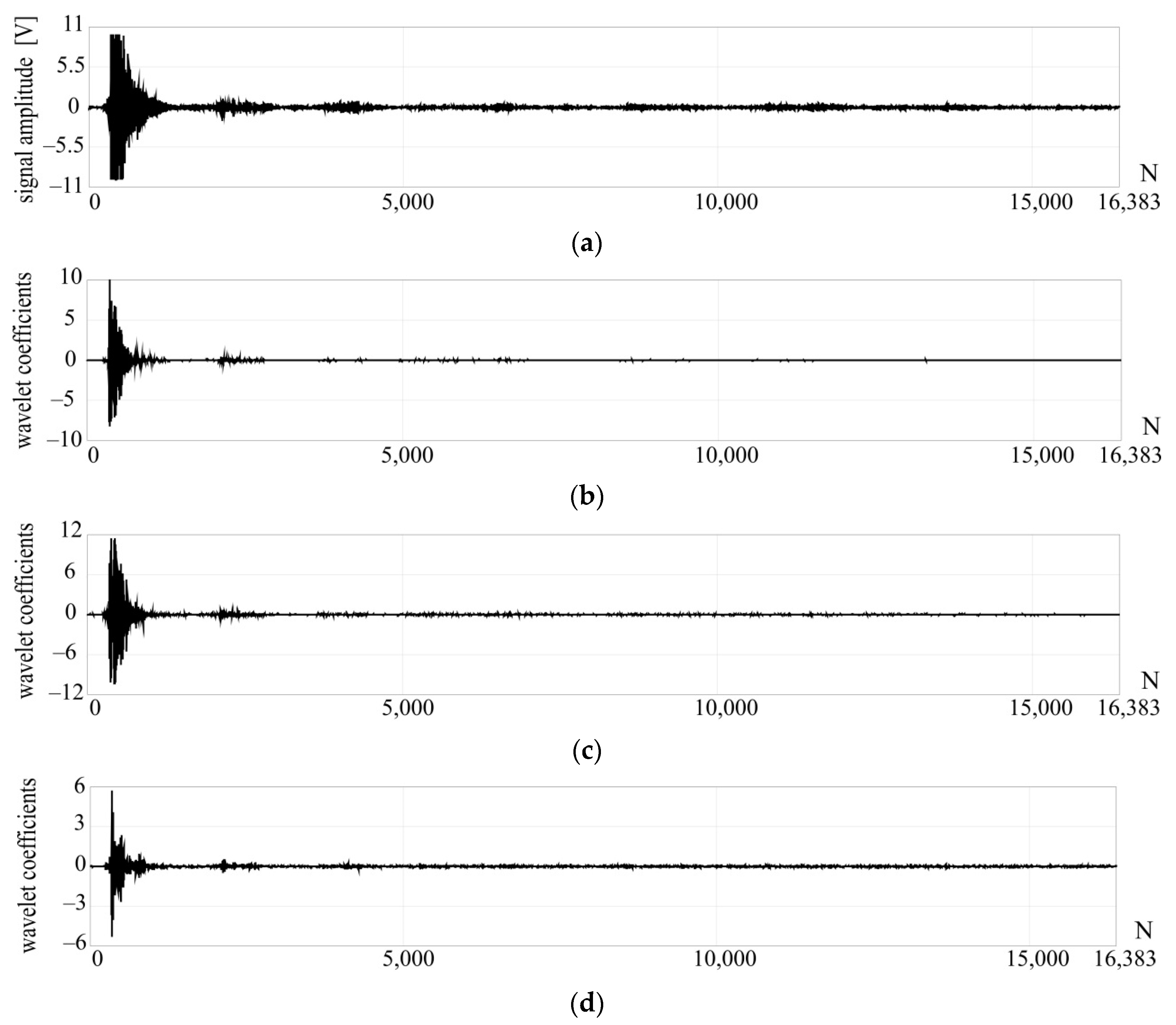
Figure 7a; plate significantly damaged (two holes) in
Figure 8a. The comparison of such extreme cases makes it possible to assess the validity of the adopted assumptions regarding both the possibility of using the proposed method and its eventual usefulness in field conditions.
At the present stage of research, the quantitative assessment concerns the differences in the number of single pulses visible in the signal and the wavelet coefficients. It can be observed that for single, minor damage, there is one impulse, and for a larger number of damages, more impulses were registered. Hence, the recorded number of pulses or peaks in the details of the wavelet transform are quantitative indicators in the proposed method. Moreover, indicators independent of the mechanical wave excitation force in the analyzed element are sought; therefore, a direct comparison of, e.g., signal amplitudes is not a reliable indicator.
Analyzing the above examples of waveforms, one can notice some regularities in the signals or details of the wavelet transform. While the absolute values, from the point of assumption of the method, are not the most important, the differences in the signal waveforms, and especially the details, allow indicating characteristic features related to the state of the sample. Thus, for the state without damage in the details of the wavelet transform, and even in the signal at the excitation with a small amplitude, no characteristic features were characterizing this state. The waveforms were similar to the noise (as in the example) or to the distribution corresponding to the typical, relaxing course of the AE impulse.
On the other hand, in the case of a damaged board, it is important to determine the beginning of the signal analysis properly—there is a difference in the initial phase of the details for different types of damage, as well as during the signal.
These differences may be related to the presence of a different number of points of reflection of waves propagating in the metal, i.e., the presence of holes may cause additional multiple reflections of the wave; and the overlap of waves reflected on each other. This may result in changes in the amplitude and fall time of the signal. It has been observed that increasing the number and size of damage causes an increase in the amplitude and duration of the signal
Evident disturbances of the transformed signal characterized by high peaks in the transformation window for particular DWT details can be considered as tangible information about the presence of damage in the structure. The signals obtained from excitation of the undamaged panel and with the defect in the form of a cavity were analyzed over 16,384 time-intervals, whereas in the case of a plate with two holes for 65,536 intervals. It was necessary to fulfill the condition of dyadic discrete wavelet transform and provide 2N data for decomposition. During the analysis of the obtained signal, the authors tested different ranges (4, 6, 8, 10) of Daubechies wavelet. Growth of the wavelet order increases the number of wavelet coefficients (which is equal to the wavelet order) and smoothens the wavelet and scaling function, which can result in better defect detection. Ultimately, Daubechies 8 wavelet was applied. This range of Daubechies wavelet best indicated the presence of the damage.
The main goal of the experiment was to find local discontinuities contained in a registered signal caused by deterioration(s) of the plate. However, the global response of the structure may not indicate the presence of damage in the element. For this purpose, the wavelet transform for signal decomposition was applied. In the case of the undamaged plate analysis, no obvious disturbances were observed in the transformation windows in
Figure 6b–d for the first three DWT details. One peak visible in
Figure 7b–d suggests the presence of one defect, which fully coincides with the reality, i.e., the hollow in the tested plate. Two obvious peaks observed in
Figure 8b–d indicate the occurrence of two defects in the analyzed steel element—two holes.
It should also be noted that no influence of the excitation site was observed on the details of the wavelet transform., i.e., regardless of the excitation site (A, B, C, D, E), the results of the wavelet transform were similar. This confirms the assumption that the type of damage only influences the results (details of transformation). Similarities of individual elements (
Figure 6,
Figure 7 and
Figure 8b–d) to the signal from the transmitter (
Figure 6,
Figure 7 and
Figure 8a) shows that they are wideband signals.
It should be noted that the analysis was subjected to not denoised signals, i.e., no measurement errors were removed from them, which is a good prognosis for using the proposed method in field tests.
5. Conclusions
The motivation to carry out the experiment was to verify the concept of using the wavelet transform to identify the presence of damage in structural elements. The main assumption was to use the properties of a wavelet transform, i.e., to obtain similar conclusions regardless of the applied force inducing the plate, in contrast to the classic transient ultrasonic method [
27]. In the classical ultrasonic method, there is a signal emission source with specific parameters (amplitude, frequency) and a receiver. The work aims to simplify the signal source while maintaining the possibility of identifying the damage. The analyzed object is mechanically excited, and the appropriate analysis of the recorded signal is to identify the damage. The current stage of work included the identification of the failure type based on the details of the wavelet transform. The correctness of the concept of the adopted method is confirmed by the differences in the course of individual details. In particular, for a single fault, there is one local signal maximum, and for two holes, there are more. This is the basis for the recognition that the presence of discontinuities in the material structure affects the wavelength coefficients of the signal generated by the plate excitation, as it would affect the signal generated from the source. For us, this is a sufficient confirmation of the correctness of the assumptions made. Further research should focus on a more precise assessment of the size of the damage and its location.
The conducted tests confirm the validity of the adopted assumptions.
As a result of the experiment, differences in the details of the transformations were observed, depending on the type of damage. These waves were not affected by the force of hammering the plate– the only limitation is the sensitivity of the transducer and the measuring range of the recording system. Too weak impact insufficiently deformed the applied acoustic–electric transducer, in turn too strong caused the “clipping” of the amplitude of the recorded signal. However, it was noticed that in the latter case, the shapes of the details were similar to the case when the signal amplitude was within the measuring range. This means that such a signal was also useful. In addition, previous studies [
21] have shown that in the case of measurement signals with amplitudes at the noise level, the application of wavelet transform allows for the “extraction of information” from the signal.
At this stage of the study, the main goal of the authors was to prove that the damage exists in the examined plate and that the proposed approach allows obtaining information about the number of deteriorations. There was no attempt to assess the damage intensity nor its shape. During excitation, a mechanical wave propagating in all directions is generated. The wave arrives at the transducer directly from the excitation point (if it does not encounter obstacles), or the wave is reflected from the discontinuity in the sample structure. These waves can travel in different ways, which has a direct impact on the course of the recorded signal.
This influence is the presence of successive pulses for subsequent damage. The number of damage can be related to the number of pulses. It is a response to the search for a correlation between the number of failures and the courses of individual details of the wavelet transform of the observed signals.
Among the advantages of the proposed, novel method, the possibility of using standard measuring elements to construct a test bench should be indicated. This solution, however, requires initial calibration, and the key parameter is the selection of the frequency range of the transducer. During the measurements, calculations were made to determine the time that the sound wave needs to travel from the point of excitation to the transducer. This was the basis for choosing the minimum sampling frequency of the A/D converter of the measuring card. The proper selection of this frequency is shown in
Figure 5, i.e., the recording starts at the moment of impact, the moment of reaching the signal to the transducer is known. All secondary signals are derived from reflections, either from the edge of the damage or from the edge of the test sample.
Bearing in mind the above conclusions, it seems that under field conditions, two approaches are possible: preparation of standard signals for undamaged elements or development of intelligent fault identification algorithms. According to the authors, the first solution is justified in the case of the analysis of the condition of elements with a repeatable structure—for example, on a production warehouse. In this case, the comparison of one measurement with the standard may be sufficient. The second approach is justified with unknown or complicated geometry of the object being diagnosed and, according to the authors, requires the evaluation of a series of wavelet transform details for different source—sensor distances. The development of such universal algorithms should be a further goal of work on the proposed solution. Therefore, the authors plan to undertake work related to the use of artificial intelligence methods. These works would concern the search for such parameters of transformation details that will be universal. This universality is based on the insensitivity of the type of material and geometry of the tested object to the ability to detect damage.