Abstract
The measurement of the cesium (Cs) 5p67d 2D5/2 excited state’s hyperfine splitting intervals and hyperfine interaction constants was experimentally investigated using a ladder-type (852 nm + 698 nm) three-level Cs system (5p66s 2S1/2–5p66p 2P3/2–5p67d 2D5/2) with a room-temperature Cs atomic vapor cell. By scanning the 698 nm coupling laser’s frequency, the Doppler-free high-resolution electromagnetically-induced transparency (EIT)-assisted double-resonance optical pumping (DROP) spectra were demonstrated via transmission enhancement of the locked 852 nm probe laser. The EIT-assisted DROP spectra were employed to study the hyperfine splitting intervals for the Cs 5p67d 2D5/2 excited state with a room-temperature Cs atomic vapor cell, and the radio-frequency modulation sideband of a waveguide-type electro-optic phase modulator (EOPM) was introduced for frequency calibration to improve the accuracy of frequency interval measurement. The existence of EIT makes the DROP spectral linewidth much narrower, and it is very helpful to significantly improve the spectroscopic resolution. Benefiting from the higher signal-to-noise ratio (SNR) and much better resolution of the EIT-assisted DROP spectra, the hyperfine splitting intervals between the hyperfine folds of (F” = 6), (F” = 5), and (F” = 4) of the Cs 5p67d 2D5/2 state (HFS6″–5″ = −10.60(17) MHz and HFS5″–4″ = −8.54(15) MHz) were measured and, therefore, the magnetic dipole hyperfine interaction constant (A = −1.70(03) MHz) and the electrical quadrupole hyperfine interaction constant (B = −0.77(58) MHz) were derived for the Cs 5p67d 2D5/2 state. These constants constitute an important reference value for an improvement of the precise measurement and determination of basic physical constants.
1. Introduction
In recent years, with the maturity and development of high-precision spectroscopic technology, the precise measurement of the hyperfine structure (HFS) of alkali metal atoms and related physical constants has been a topic of concern in the fields of atomic physics, laser spectroscopy, and precision measurement [1,2]. To reduce the Doppler broadening effect, two-photon Doppler-free spectroscopy [3] and electromagnetically-induced transparency (EIT) [4] have been used for precise measurements. The hyperfine splitting interval of the excited state of alkali metal atoms can be measured and the corresponding hyperfine interaction constants can be further derived with high precision. The hyperfine structure of atoms resulting from electron-nuclear interactions provides structural information about the nuclear and electronic structure of the atoms [5]. There is a further problem with parity nonconservation (PNC) [6,7]. PNC is sensitively dependent on the overlap of the nuclear and electronic wave functions [8], which is related to an accurate atomic structure. As the hyperfine structure can be accurately measured, we can improve the accuracy of measurements to explain the relevant physical measurements and calculations [9,10]. Sahoo et al. [11] recently studied the calculation of the nuclear spin-independent parity violating the electric dipole transition amplitude and constraints on new physics from an improved calculation of parity violation in Cs. On the other hand, another challenging problem which arises in this domain, as highlighted by Safronova et al. [12], is that the polarizability of the 6p state is consistent with the experimental values, but the lifetime is inconsistent with the experimental values of the 5d state. The polarizability and the lifetime are also closely related to the calculation of the dipole matrix element [10,13]. In order to analyze the origin of this inconsistency, it is necessary to continue studying the structural properties of nd states. Dzuba et al. [14], who studied the feasibility of measuring PNC amplitudes in the dipole-forbidden transitions of cesium (Cs) atoms, was hampered by the difficulty of the strong correlation effects. Therefore, research related to the nd state and the precise measurement of hyperfine structures play an important role in fundamental physics, such as atomic frequency calibration, construction of quantum theoretical models, laser cooling and trapping, and isotope identification [15,16,17,18,19].
Although many groups carried out theoretical and experimental studies on the atomic hyperfine structure, there were few precise measurements of the hyperfine interaction constants, especially for the nd state. Considering the complexity of their internal electronic cloud’s structure and strong correlation effects [14], the calculation results of different theoretical models differ greatly. In order to verify the theoretical model of the nd state, it is urgent to accurately measure the hyperfine-level structure of the nd state experimentally. In 1995, Grove et al. [20] measured the hyperfine interaction constant of the 85Rb 4p65d 2D5/2 state by using optical double resonance spectroscopy and performed frequency calibration using an acousto-optic modulator (AOM). Auzinsh et al. [21] conducted experimental and theoretical research on the polarizability and hyperfine interaction constants of Cs atoms in the d state, and the experimental values of the hyperfine interaction constants were obtained from the energy-level crossover signal of the nd state. On the basis of the atomic coherence effect of a 5p66s 2S1/2–5p66p 2P3/2–5p68s 2S1/2 system in a Cs atomic cell at room temperature, Wang et al. [22] proposed a new high-resolution technique for measuring the hyperfine splitting of the excited state and developed a method to eliminate the error arising from nonlinear frequency scanning by employing an optical waveguide-type electro-optic phase modulator (EOPM) and a confocal Fabry-Perot cavity [23]. Using this technique, Yang et al. [24] measured the hyperfine interaction constants of the 4p65d 2D5/2 state of 85Rb atoms. Recently, He et al. [25] presented the measurement of the hyperfine structure of the Cs 5p67s 2S1/2 excited state by using electromagnetically-induced transparency (EIT) spectroscopy with a Cs three-level cascade system. Yuan et al. [3] studied the electromagnetically induced grating diffraction controllability in a ladder-type (4p65s 2S1/2–4p65p 2P3/2–4p65d 2D5/2) rubidium atomic system and the nonlinear dependence of the first-order diffraction efficiency on the coupling laser power.
As for Cs 5p67d 2D5/2 state, only a few studies showed a relevant measurement of its structure. Bulos et al. [26] determined the A value of the Cs 5p67d 2D5/2 state from the optical double-resonance transition spectra. Lee et al. [27] used the Cs 5p66s 2S1/2–5p67d 2D5/2 two-photon transition method by introducing an EOPM to determine the corresponding hyperfine splitting intervals and hyperfine interaction constants of the Cs 5p67d 2D5/2 state. Stalnaker et al. [28] measured the absolute transition frequency and the hyperfine interaction constants of the Cs 5p67d 2D5/2 states by using the frequency comb method in a two-photon excitation system. Recently, Wang et al. [29] used a single laser with a wavelength of 767 nm driving the dipole forbidden transition 5p66s 2S1/2–5p67d 2D3/2, 5/2 in a thermal Cs vapor. The magnetic dipole coupling constant A and the electric quadrupole coupling constant B for the Cs 5p67d 2D3/2, 5/2 states were precisely determined by using the hyperfine splitting intervals.
Due to the fact that its adjacent splitting intervals are less than ~10 MHz, the main practical problem confronting us is how to improve the spectroscopic resolution and signal-to-noise ratio (SNR) of the Cs 5p67d 2D5/2 state. Unlike previous experiments and theoretical studies, we employed ladder-type EIT spectroscopy to improve the spectroscopic resolution and SNR. We used a 698 nm coupling laser and 852 nm probe laser in opposite directions to realize the Cs cascade two-photon excitation in a Cs atomic vapor cell at room temperature. The effect of the 852 nm probe beam’s linewidth and the optical intensity of the 852 nm probe beam and 698 nm coupling beam as a function of the spectroscopic SNR were investigated. After studying the effect of the spectroscopic scheme and the optimization of experimental parameters, the EIT-assisted double-resonance optical pumping (DROP) spectra with a higher SNR and better resolution were observed, and the hyperfine splitting intervals of the Cs 5p67d 2D5/2 state were measured. The sideband of an optical waveguide-type EOPM was introduced as a frequency calibration to improve the accuracy of the frequency measurement. The hyperfine splitting intervals between the hyperfine folds of (F” = 6), (F” = 5), and (F” = 4) of the Cs 5p67d 2D5/2 state (HFS6″–5″ = −10.60(17) MHz and HFS5″–4″ = −8.54(15) MHz) were measured and, therefore, the magnetic dipole hyperfine interaction constant (A = −1.70(03) MHz) and the electrical quadrupole hyperfine interaction constant (B = −0.77(58) MHz) for the Cs 5p67d 2D5/2 state were derived.
This paper is organized into five sections. In Section 2 we introduce relevant principles, including the relation between the hyperfine splitting and the momentum quantum number, the relation between the hyperfine splitting and the hyperfine interaction constants, and the spectroscopic schemes we chose in this work. In Section 3 we describe the experimental setup and conditions under which we performed the measurements. In Section 4 we present the optimization of experimental parameters in order to achieve a higher SNR and better resolution of the EIT-assisted DROP spectra. In Section 5 we more precisely measure the hyperfine splitting intervals and the hyperfine interaction constants of the Cs 5p67d 2D5/2 state by analyzing the experimental data and discussing the related techniques. Finally, we outline the main points in Section 6.
2. Relevant Principles
2.1. Hyperfine Splitting, Momentum Quantum Number, and Hyperfine Interaction Constants
The hyperfine interaction includes the magnetic dipole hyperfine interaction and the electrical quadrupole hyperfine interaction. In general, the hyperfine splitting is mainly considered from the following two aspects: The interaction of the nuclear magnetic dipole moment with the magnetic flux density created by electrons, and the interaction of the electric quadrupole moment with the gradient of the electric field at the nucleus [30]. Therefore, the total shift in energy level can be expressed as follows [24]:
where , I is the total angular momentum quantum number of the nucleus, J is the total angular momentum quantum number of electron, F = I + J is the total angular momentum quantum number of the atoms, and A and B are the magnetic dipole hyperfine interaction constants and the electrical quadrupole hyperfine interaction constants, respectively.
For the s state, owing to the orbital angular momentum L = 0, the electron distribution has a spherical symmetry. Therefore, A is the only term of concern. The magnetic dipole hyperfine constant can be directly calculated using Equation (1). However, for the d state, the calculation of A, B can be obtained from Equation (1) [31].
2.2. Spectroscopic Schemes
High-resolution and high-SNR spectroscopic schemes are very helpful to achieve a higher accuracy of the hyperfine splitting measurement, so as to deduce accurate hyperfine interaction constants. (here, the magnetic dipole hyperfine interaction constant A and the electrical quadrupole hyperfine interaction constant B for the Cs 5p67d 2D5/2 excited state).
A DROP spectroscopic scheme using the ladder-type three-level system (5p66s 2S1/2–5p66p 2P3/2–5p67d 2D5/2) was employed to measure the hyperfine splitting in the Cs 5p67d 2D5/2 excited state. An 852 nm laser was used as the probe laser to detect the population change of the ground state, reflecting the hyperfine spectrum between excited states. At the same time, we also studied the optical-optical double-resonance (OODR) absorption spectroscopic scheme and used a 698 nm probe laser to detect the population change of intermediate state to reflect the hyperfine spectrum between excited states. The OODR spectroscopic signal was related to the population between 5p66p 2P3/2 (F’ = 5) and 5p67d 2D5/2 (F” = 4, 5, 6), while 5p66p 2P3/2 (F’ = 5) had a large spontaneous decay rate (Г = 2π × 5.22 MHz); thus, atoms were not easy to inhabit in the 5p66p 2P3/2 (F’ = 5) state. On the contrary, this accelerated the DROP process, which rapidly reduced the population of atoms in the ground state (F = 4), thereby leading to a relatively higher SNR, which was helpful to more accurately measure the hyperfine splitting interval.
In the three-level system shown in Figure 1, when the coupling laser and the probe laser were in resonance, under the weak laser approximation, the polarizability of the medium could be expressed as follows [32]:
where is the frequency of the probe laser, is the frequency of the coupling laser, is the detuning of the probe laser corresponding to the frequency of the 5p66s 2S1/2 (F = 4)–5p66p 2P3/2 (F′ = 5) transition, is the detuning of the coupling laser corresponding to the frequency of the 5p66p 2P3/2 (F′ = 5)–5p67d 2D5/2 (F″ = 6) transition, the decay rate is , g21 is the dipole moment matrix element for the 5p66s 2S1/2 (F = 4)–5p66p 2P3/2 (F′ = 5) transition, is the Rabi frequency of the coupling laser, Гi is the natural linewidth of level i, N is the density of Cs atoms, v is the velocity of Cs atoms, represents the amplitude of the coupling laser field, and c is the speed of the laser [32]. For the counter-propagating (CTP) configuration, the difference of narrow linewidth is attributed to the atomic coherence between the ground and upper states driven by the two coherent laser fields via a common intermediate state, resulting in an EIT effect. In Equation (2), the term corresponds to CTP configuration, making it easy to achieve EIT signals in the two-photon Doppler-free configuration, as the linewidth of the signal is narrow due to the atomic coherence effect. On the contrary, for the co-propagating (CP) configuration, the term cannot be ignored. The Doppler background basically overwhelms the EIT signals [33].
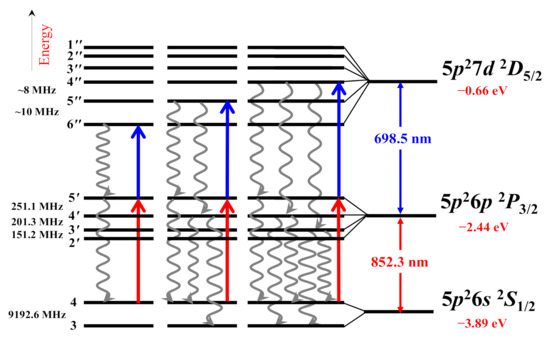
Figure 1.
The relevant hyperfine energy levels of cesium (Cs) atoms. A double-resonance optical pumping (DROP) spectroscopic scheme using the ladder-type three-level system (5p66s 2S1/2–5p66p 2P3/2–5p67d 2D5/2) was employed to measure the hyperfine splitting of the Cs 5p67d 2D5/2 excited state. The 852 nm probe laser drives the 5p66s 2S1/2 (F = 4)–5p66p 2P3/2 (F’ = 5) transition, as indicated by the red arrows, while the 698 nm coupling laser drives the 5p66p 2P3/2 (F’ = 5)–5p67d 2D5/2 (F” = 6), (F” = 5), and (F” = 4) transitions, as indicated by the three blue arrows. The wavy arrows indicate the spontaneous decay channels. The energy at infinity is zero (the energy axis is not to scale).
In order to obtain a spectral signal with high resolution, we adopted a scheme where the probe and coupling beams counter-propagated through the Cs atomic vapor and scanning coupling laser’s frequency to obtain signals without the Doppler background in the experiment.
3. Experimental Setup
The experimental setup is shown in Figure 2. The 852 nm probe beam was provided by a tunable diode laser (external-cavity diode laser (ECDL) (Toptica, Munich, Germany) or distributed Bragg reflector (DBR) diode laser). Part of the laser output was used to lock the laser frequency to the Cs 5p66s 2S1/2 (F = 4)–5p66p 2P3/2 (F′ = 5) transition using polarization spectroscopy (PS). The main beam of the 852 nm laser overlapped with the 698 nm beam provided by an ECDL with a typical linewidth of ~200 kHz. The two beams were transmitted through the Cs atomic vapor cell in the opposite direction (CTP configuration). The 852 nm probe beam had a 1/e2 Gaussian diameter of ~600 μm and the 698 nm coupling beam had a 1/e2 Gaussian diameter of ~840 μm. The Cs vapor cell was placed in a μ-metal box in order to decrease the influence of the background magnetic field. A wavelength meter (Advantest, TQ-8325, Japan) was employed to monitor the wavelength of the 698 nm laser in real-time.
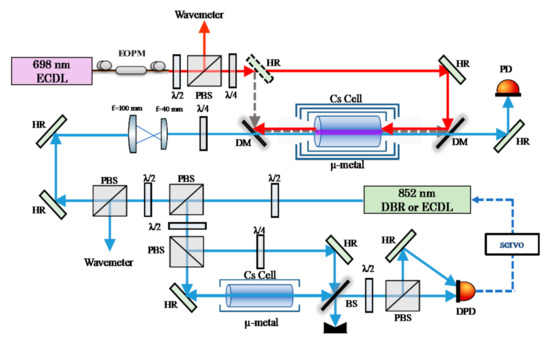
Figure 2.
Experimental setup for hyperfine splitting measurement. Red solid arrows represent the counter-propagating (CTP) configuration with the probe and coupling laser beams, whereas the gray dashed arrows represent the co-propagating (CP) configuration. µ-metal, magnetic shielding device; EOPM, waveguide-type electro-optic phase modulator; PBS, polarization beam splitter cube; BS, beam splitter plate; λ/2, half-wave plate; λ/4, quarter-wave plate; PD, photodetector; DPD, differential photodiode; DM, dichroic mirror; HR, high-reflectivity mirror; servo, frequency-locking servo system.
4. Optimization of Experimental Parameters
4.1. Comparison of Optical-optical Double Resonance (OODR) and Double-resonance Optical Pumping (DROP) Spectroscopic Schemes
In the experiment, we compared two spectroscopic signals by detecting different beams corresponding to the OODR and DROP spectra. We used the 852 nm laser as the probe beam, and its frequency was locked by the polarization spectrum, through which atoms were distributed from the ground state of 5p66s 2S1/2 to the intermediate state of 5p66p 2P3/2. The 698 nm laser served as the coupling beam, and, when it was scanned over the range of 5p66p 2P3/2 to 5p67d 2D5/2 transitions, the absorption spectrum was obtained. The 852 nm probe laser transmitted the atoms from the ground state 5p66s 2S1/2 (F = 4) to the intermediate state 5p66p 2P3/2 (F’ = 5). The 698 nm coupling beam excited atoms into the 5p67d 2D5/2 (F” = 4, 5, 6) state. However, some atoms in the 5p67d 2D5/2 (F” = 4, 5, 6) state could be pumped into another ground 5p66s 2S1/2 (F = 3) state via other intermediate states, as shown in Figure 1, which led to a change in the population due to DROP. It can be seen in Figure 3 that the resolution of the DROP spectra were better than that of the OODR spectra, and there was basically no coincidence among the three peaks, which was helpful for measuring the hyperfine splitting interval.
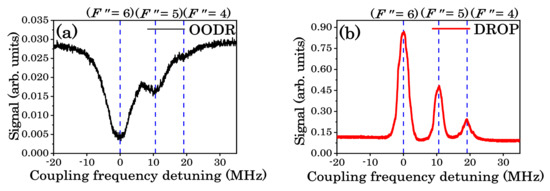
Figure 3.
Comparison of optical-optical double-resonance (OODR) and double-resonance optical pumping (DROP) spectra for the Cs 5p66p 2P3/2 (F’ = 5)–5p67d 2D5/2 (F” = 4, 5, 6) transitions. (a) OODR spectra; (b) DROP spectra.
4.2. Effect of the Probe Laser’s Linewidth
Two 852 nm lasers with different linewidths were used in the experiment, and the measured full-text data were based on the ECDL with a typical linewidth of ~200 kHz (except Figure 4a). Similarly, we also compared a DBR diode laser with a typical linewidth of ~2 MHz, and the spectra obtained is shown in Figure 4a. The difficulty in separating the three peaks suggests that a laser with a narrower linewidth would be very helpful in gaining the spectra with a higher spectroscopic resolution.
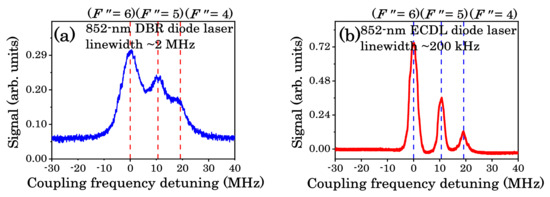
Figure 4.
The two-photon transition spectra with no Doppler background were measured with two different 852 nm probe lasers: (a) an 852 nm distributed Bragg reflector (DBR)-type diode laser with a typical linewidth of ~2 MHz; (b) an 852 nm external-cavity diode laser (ECDL) with a typical linewidth of ~200 kHz.
4.3. Electromagnetically-induced Transparency (EIT)-assisted DROP Spectra
We compared the two transmission methods in the CP and CTP configurations. Two different scanning methods were used to obtain the spectral signals, as shown in Figure 5; keeping the 698 nm coupling laser in free running mode, we obtained the two-photon transition spectra with the Doppler background shown in Figure 5a,c by scanning the 852 nm probe laser. Compared with the spectra obtained by scanning the 698 nm coupling laser, the spectra had a large Doppler background. Furthermore, when we locked the weak 852 nm probe laser to the 5p66s 2S1/2 (F = 4)–5p66p 2P3/2 (F′ = 5) hyperfine transition, we scanned the 698 nm laser over the 5p66p 2P3/2 (F′ = 5)–5p67d 2D5/2 transition to obtain the spectra without a Doppler background, as shown in Figure 5b,d.
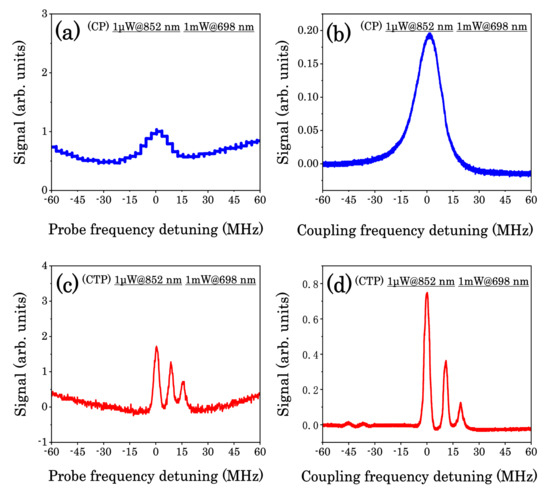
Figure 5.
Spectral signals under different transmission modes and scanning modes: (a,b) the CP configuration; (c,d) the CTP configuration. (a,c) The 698 nm laser was adjusted to the 5p66p 2P3/2 (F’ = 5)–5p67d 2D5/2 (F” = 6) transition, while the 852 nm laser was scanned to obtain the two-photon transition spectra with a Doppler background. (b,d) The 852 nm laser was locked to the 5p66s 2S1/2 (F = 4)–5p66p 2P3/2 (F’ = 5) transition, while the 698 nm laser was scanned over the Cs 5p66p 2P3/2 (F′ = 5)–5p67d 2D5/2 (F” = 6, 5, 4) transitions to obtain the two-photon transition spectra without a Doppler background.
Figure 5 shows that the linewidth in the CP configuration was wider than that in the CTP configuration. There was an atomic coherence effect, e.g., EIT, and incoherence effects, e.g., spontaneous emission and DROP. The narrow part of the spectra due to the coherent process of atoms in the CTP configuration was caused by the EIT. The wider part was a result of the DROP process. In the CP configuration, DROP, accompanied by spontaneous emission, was the two-photon optical pumping process caused by the incoherence effect [33].
4.4. Effect of the Laser Beam’s Intensity
As shown in Figure 6, there were three enhanced transmission signals in the spectra, and the three peaks from left to right corresponded to the Cs atom 5p66p 2P3/2 (F′ = 5)–5p67d 2D5/2 (F” = 6), (F” = 5), and (F” = 4) hyperfine transitions, respectively. The evolution of signals with different probe laser power and coupling laser power was studied. In Figure 6a–e, when the coupling power was set to 1.0 mW, upon increasing the power of the probe beam, the amplitude of the EIT-assisted DROP signals increased. When the power of the probe beam was set to ~1.0 μW, upon increasing the power of the coupling beam, the amplitude of the EIT-assisted DROP signals also increased, as shown in Figure 6f–j, whereas the SNR of the spectral line obviously decreased when the power of the coupling laser was too weak and was gradually submerged in the noise. Upon increasing the power of the coupling or probe beam, the EIT effect strengthened. Since the DROP effect mainly depended on the power of the 852 nm beam, the optical double-resonance effect widened the spectral linewidth and hindered the separation of hyperfine-level intervals. In order to clearly distinguish the intervals among the three peaks, appropriate powers were chosen for measurement in the experiment.
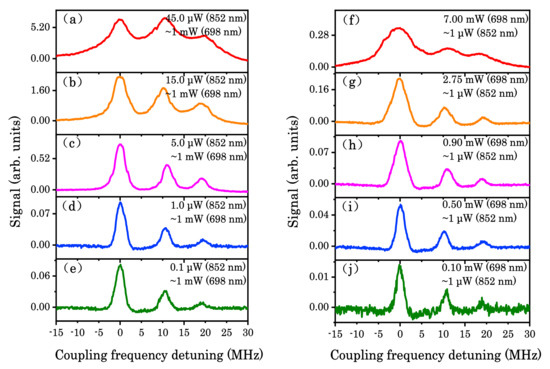
Figure 6.
Evolution of the electromagnetically induced transparency (EIT) signals in the CTP configuration with (a–e) increasing probe laser power and (f–j) increasing coupling laser power. (a–e) The 698 nm laser power was ~1.0 mW, and the evolution of the signals with increasing probe laser power is shown. (f–j) The 852 nm laser power was ~1.0 µW, and the evolution of the signals with increasing coupling laser power is shown.
We studied the evolution of signal amplitude and SNR of the EIT-assisted DROP spectra versus the laser power. It can be seen from Figure 7 that the power we chose allowed obtaining the spectra with relatively high SNR and a narrow linewidth, thereby facilitating splitting of the 5p67d 2D5/2 (F” = 6, 5, 4) three-peak intervals. We can see that the amplitude linearly increases with the power. As the ratio (f5″–6″/FWHM6″) can describe the relation of spectral linewidth with power, this also means the overlap of the peaks. In fact, when the ratio is 1, it means that the two peaks are indistinguishable. In summary, we chose the EIT-assisted DROP spectra with an appropriate power range. When the probe power was increased from ~0.1 μW to ~5.0 μW and the coupling power was increased from ~0.5 mW to ~1.0 mW, the three peaks did not overlap with each other. These advantages were particularly valuable for measuring the hyperfine splitting intervals and the hyperfine interaction constants.
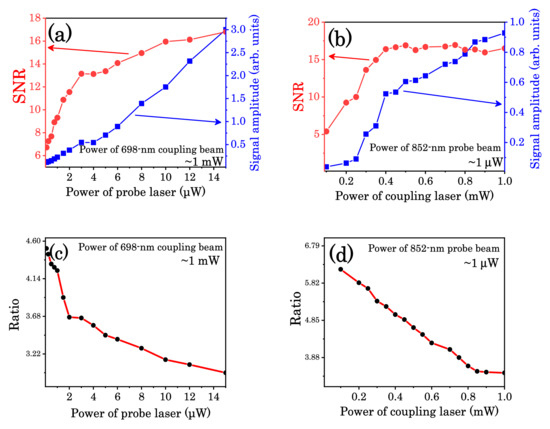
Figure 7.
The signal-to-noise ratio (SNR), amplitude and ratio (f5″–6″/FWHM6″) of the cesium 5p67d 2D5/2 (F” = 6) spectroscopic signals versus. (a,c) the 852 nm probe beam’s power; (b,d) the 698 nm coupling beam’s power.
5. Experimental Results and Discussion
In Figure 8, under the conditions of P852 nm = 1.0 μW and P698 nm = 1.0 mW, the frequency calibration was performed by using an EOPM with a 30 MHz modulation sideband for 698 nm coupling beam. The EOPM was driven by a frequency synthesizer (Agilent Technologies E8257C, CA, USA) with a stability of 1 × 10−10 s−1. The transmission peak of 5p67d 2D5/2 (F” = 6) served as the reference position for detecting zero detuning of the frequency.
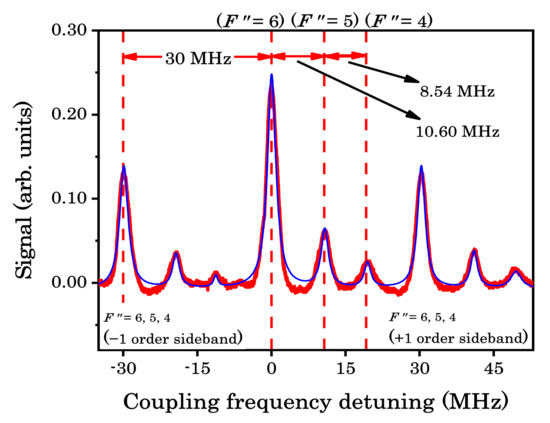
Figure 8.
Calibration of the frequency interval with a 30 MHz radio-frequency phase modulation applied to the coupling laser beam via the waveguide-type electro-optic phase modulator (EOPM). The frequency interval between the carrier (reasonably indicated zero detuning) and the −1-order sideband (or the +1-order sideband) should be 30 MHz. The blue line displays multi-peak Lorentz fitting, while the red curve displays the experimental spectra. The three peaks at the left side belong to the −1-order modulation side band, corresponding to the (F” = 6, 5, and 4) hyperfine folds. The three peaks at the right side belong to the +1-order modulation side band, corresponding to the (F” = 6, 5, and 4) hyperfine folds.
In this work, we used the EIT-assisted DROP spectra with high SNR and narrow linewidth, thereby facilitating splitting of the Cs 5p67d 2D5/2 (F” = 6, 5, 4) three-peak intervals. These advantages were valuable for measuring the hyperfine interval and the hyperfine interaction constants. In reference [27,29], the Cs 5p66s 2S1/2–5p67d 2D3/2, 5/2 electric quadrupole transitions were used to couple the ground state and the excited state, representing a monochromatic two-photon transition. The probability was low and the power of the laser beam was much higher. The hyperfine splitting intervals of the corresponding states were measured, and the experimental results showed that the SNRs of the obtained spectra were high due to the large splitting intervals of the Cs 5p67d 2D3/2 states. However, for the Cs 5p67d 2D5/2 state, the resolution was so poor that it was difficult to separate the peaks for the (F” = 6), (F” = 5), and (F” = 4) hyperfine folds in Cs 5p67d 2D5/2 state.
The frequency interval between the carrier frequency and the −1-order sideband served as the frequency calibration to measure the Cs 5p67d 2D5/2 (F” = 6, 5, 4) frequency intervals. We used the interval between the −1-order sideband peak and Cs 5p67d 2D5/2 (F” = 6) peak to calibrate the horizontal axis frequency in Figure 8, thus allowing the frequency intervals between states 5p67d 2D5/2 (F” = 6, 5, 4) to be calculated. Due to the nonlinear frequency scanning of grating external cavity, a larger scanning range resulted in a greater influence of the nonlinear effect. The frequency of the selected radio-frequency signal was 30 MHz, which was close to the measured interval value of the 5p67d 2D5/2 state, in order to minimize the influence of the nonlinear effect for scanning the laser frequency. The hyperfine splitting intervals of the 5p67d 2D5/2 (F” = 6, 5, 4) state were measured and calibrated several times. Therefore, we used a convolution of a Lorentzian profile to fit the width of these peaks and to locate their central position. Each simulated peak had three fitting parameters corresponding to the amplitude of the signal, the central position of each signal, and the Lorentzian width. The linewidth of these transitions was about ~3 MHz, which was a combination of the two-photon natural linewidth, laser linewidth, and power and collision broadening effects. The mean frequency splitting intervals between the Cs 5p67d 2D5/2 (F” = 6, 5, 4) hyperfine levels were 10.60(17) MHz (5″–6″) and 8.54(15) MHz (4″–5″), respectively. Table 1 and Figure 9 show the mean values and errors of the energy-level intervals obtained through multiple fitting.

Table 1.
Measured values of hyperfine splitting of the Cs 5p67d 2D5/2 state.
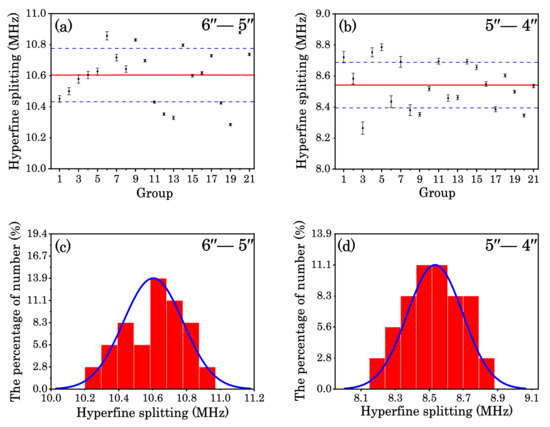
Figure 9.
The measured values of the hyperfine splitting intervals for the Cs 5p67d 2D5/2 excited state. The horizontal red lines represent the mean values of the hyperfine splitting. The ranges between the two horizontal blue dashed lines donate the statistical errors. (a) Hyperfine splitting between (F” = 6) and (F” = 5) levels of the Cs 5p67d 2D5/2 state; (b) Hyperfine splitting between (F” = 5) and (F” = 4) levels of the Cs 5p67d 2D5/2 state. The histograms of the hyperfine splitting intervals are shown in (c,d).
The magnetic dipole hyperfine interaction constant A and the electrical quadrupole hyperfine interaction constant B for the Cs 5p67d 2D5/2 excited state were determined as a function of the splitting interval of the spectra, expressed as follows:
According to Equations (3) and (4), the magnetic dipole hyperfine interaction constant A was calculated to be −1.70(03) MHz and the electrical quadrupole hyperfine interaction constant B was calculated to be −0.77(58) MHz for the Cs 5p67d 2D5/2 excited state. These results are in good agreement with the previous reported results [27,28,29,34], as shown in Table 2. The A coupling constant agrees well with previous measurements (e.g., reference [34], which demonstrated an experiment using direct frequency-comb spectroscopy). In reference [27], a positive value was also obtained for the constant B for the Cs 5p67d 2D5/2 state. This discrepancy could have arisen from the overlap of multiple peaks in that study. The hyperfine splitting intervals of the Cs 5p67d 2D5/2 state were too small and could only be barely resolved. In reference [29], a study of the Cs 5p66s 2S1/2–5p67d 2D3/2, 5/2 electric quadrupole transition in a thermal Cs vapor was reported using a single laser with a wavelength of 767 nm, also giving a positive value for the constant B. The exact determination of the constant B using laser absorption spectroscopy is very difficult and subject to high uncertainty.

Table 2.
Magnetic dipole (A) and the electrical quadrupole (B) hyperfine interaction constants of the Cs 5p67d 2D5/2 state.
The experimental error mainly resulted from the spectral resolution limitation caused by the wide linewidth of the obtained spectra and the accuracy of the function generator driving the EOPM. Considering the error of the system, the frequency locking accuracy of the 852 nm laser needs to be improved. The nonlinear frequency scanning of the 698 nm coupling laser also affected the experimental results. A larger scanning range led to an obvious nonlinear effect. The spectral signal asymmetry also affected the zero-point determined by fitting and resulted in fluctuation of the measurement results. The phenomena of non-overlapping beams and the fluctuation of atomic number density caused by the temperature fluctuation of Cs atomic vapor due to the absence of temperature stabilization, thereby affecting the accuracy of hyperfine splitting intervals, need to be further improved. Although a µ-metal magnetic shied was used to minimize the stray magnetic field, the Zeeman shift also influenced the results. The AC-Stark displacement constitutes the frequency shift of the atomic energy level due to the dipole interaction between the gradient light field and the induced electric dipole moment of atoms. The energy-level frequency shift causes a measurement error which is proportional to the laser intensity. These uncertainties all contribute to the errors of the obtained hyperfine spectra.
6. Summery and Outlook
In conclusion, we measured the hyperfine splitting intervals and derived the hyperfine interaction constants of the Cs 5p67d 2D5/2 excited state. Cs atoms were excited from the ground state 5p66s 2S1/2 to the excited state 5p67d 2D5/2 (F” = 6, 5, 4) through the ladder-type 5p66s 2S1/2–5p66p 2P3/2–5p67d 2D5/2 three-level system. The EIT-assisted DROP and OODR spectroscopic schemes were compared, and EIT was employed to obtain improved SNR and higher resolution. The effects of the 852 nm probe beam’s linewidth and of the optical intensity of the 852 nm probe beam and 698 nm coupling beam on the spectroscopic amplitude were investigated. After choice of the spectroscopic scheme and optimization of the experimental parameters, the Cs 5p67d 2D5/2 state’s hyperfine splitting intervals between (F” = 6), (F” = 5), and (F” = 4) hyperfine folds were measured (HFS6″–5″ = −10.60(17) MHz and HFS5″–4″ = −8.54(15) MHz) by introducing EOPM to provide modulation sidebands for frequency calibration. Furthermore, the hyperfine interaction constants (A = −1.70(03) MHz, the magnetic dipole constant; B = −0.77(58) MHz, the electrical quadrupole constant) were derived for the Cs 5p67d 2D5/2 state. The measurement results were found to be consistent with previous measurement results, thereby providing an improved foundation for further relevant theoretical and experimental studies.
The combination of atomic coherence and optical pumping spectroscopy allowed the EIT-assisted DROP spectroscopic scheme to achieve improved SNR and a higher frequency resolution, which is of great significance for the precise measurement. On the other hand, it provides an important reference value for measuring the internal structure of atoms to deal with PNC and other related studies.
Author Contributions
J.W. proposed and supervised the project. Z.W. and J.B. set up the ladder-type EIT system. Z.W. measured and collected the experimental data. Z.W. and X.H. fitted the experimental data. Z.W. and J.W. analyzed all the experimental data, then wrote and revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially supported by The National Key R&D Program of China, [grant number 2017YFA0304502], the National Natural Science Foundation of China, [grant numbers 11774210, 11974226, 61875111, and 61905133], and the Shanxi Provincial 1331 Projects for Key Subjects Construction.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, R.; Wu, Y.; Rui, Y.; Li, B.; Jiang, Y.; Ma, L.; Wu, H. Absolute frequency measurement of 6Li D lines with kHz-level uncertainty. Phys. Rev. Lett. 2020, 124, 063002. [Google Scholar] [CrossRef] [PubMed]
- Ray, T.; Gupta, R.K.; Gokhroo, V.; Everett, J.L.; Nieddu, T.; Rajasree, K.S.; Chormaic, S.N. Observation of the 87Rb 5S1/2 to 4D3/2 electric quadrupole transition at 516.6 nm mediated via an optical nanofiber. New J. Phys. 2020, 22, 062001. [Google Scholar] [CrossRef]
- Yuan, J.P.; Wu, C.H.; Li, Y.H.; Wang, L.R.; Zhang, Y.; Xiao, L.T.; Jia, S.T. Controllable electromagnetically induced grating in a cascade-type atomic system. Front. Phys. 2019, 14, 52603. [Google Scholar] [CrossRef]
- Zheng, X.; Sun, Y.; Chen, J.; Jiang, W.; Pachucki, K.; Hu, S. Measurement of the frequency of the 23S–23P transition of 4He. Phys. Rev. Lett. 2017, 119, 263002. [Google Scholar] [CrossRef]
- Gerginov, V.; Derevianko, A.; Tanner, C.E. Observation of the nuclear magnetic octupole moment of Cs 133. Phys. Rev. Lett. 2003, 91, 072501. [Google Scholar] [CrossRef]
- Wood, C.S.; Bennett, S.C.; Cho, D.; Masterson, B.P.; Roberts, J.L.; Tanner, C.E.; Wieman, C.E. Measurement of parity nonconservation and an anapole moment in cesium. Science 1997, 275, 1759–1763. [Google Scholar] [CrossRef]
- Porsev, S.G.; Beloy, K.; Derevianko, A. Precision determination of electroweak coupling from atomic parity violation and implications for particle physics. Phys. Rev. Lett. 2009, 102, 181601. [Google Scholar] [CrossRef] [PubMed]
- Kuchiev, M.Y.; Flambaum, V.V. Influence of perturbations on the electron wave function inside the nucleus. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 4101. [Google Scholar] [CrossRef][Green Version]
- Kozlov, M.G.; Porsev, S.G.; Tupitsyn, I.I. High accuracy calculation of 6S-7S parity nonconserving amplitude in Cs. Phys. Rev. Lett. 2001, 86, 3253–3260. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, B.K.; Gopakumar, G.; Chaudhuri, R.K.; Das, B.P.; Merlitz, H.; Mahapatra, U.S.; Mukherjee, D. Hyperfine interactions in 137Ba+ and the accuracies of the neutral weak interaction matrix elements. Phys. Rev. A 2003, 68, 040501. [Google Scholar] [CrossRef]
- Sahoo, B.K.; Das, B.P. Constraints on new physics from an improved calculation of parity violation in 133Cs. arXiv 2020, arXiv:2008.08941v1. [Google Scholar]
- Safronova, M.S.; Clark, C.W. Inconsistencies between lifetime and polarizability measurements in Cs. Phys. Rev. A 2004, 69, 361. [Google Scholar] [CrossRef]
- Safronova, M.S.; Safronova, U.I.; Clark, C.W. Magicwavelengths, matrix elements, polarizabilities, and lifetimes of Cs. Phys. Rev. A 2016, 94, 012505. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V.; Ginges, J.S. Calculations of parity-nonconserving s-d amplitudes in Cs, Fr, Ba+, and Ra+. Phys. Rev. A 2001, 63, 062101. [Google Scholar] [CrossRef]
- Heshamia, K.; Englanda, D.G.; Humphreysb, P.C.; Bustarda, P.J.; Acostac, V.M.; Nunnb, J.; Sussmana, B.J. Quantum memories: Emerging applications and recent advances. J. Mod. Opt. 2016, 63, 2005–2028. [Google Scholar] [CrossRef]
- Yang, B.D.; Liang, Q.B.; He, J.; Zhang, T.C.; Wang, J.M. Narrow-linewidth double-resonance optical pumping spectrum due to electromagnetically induced transparency in ladder-type inhomogeneously broadened media. Phys. Rev. A 2010, 81, 043803. [Google Scholar] [CrossRef]
- Sinclair, A.G.; Mcdonald, B.D.; Riis, E.; Duxbury, G. Double resonance spectroscopy of laser-cooled Rb atoms. Opt. Commun. 1994, 106, 207–212. [Google Scholar] [CrossRef]
- Fendel, P.; Bergeson, S.D.; Udem, T.; Hänsch, T.W. Two-photon frequency comb spectroscopy of the 6S-8S transition in cesium. Opt. Lett. 2007, 32, 701–703. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.P.; Dong, S.C.; Wu, C.H.; Wang, L.R.; Xiao, L.T.; Jia, S.T. Optically tunable grating in a V + Ξ conguration involving a Rydberg state. Opt. Express 2020, 28, 23820–23838. [Google Scholar] [CrossRef]
- Grove, T.T.; Sanchez-Villicana, V.; Duncan, B.C.; Maleki, S.; Gould, P.L. Two-photon two-color diode laser spectroscopy of the Rb 5D5/2 state. Phys. Scr. 1995, 52, 271–276. [Google Scholar] [CrossRef]
- Auzinsh, M.; Blushs, K.; Ferber, R.; Gahbauer, F.; Jarmola, A.; Tamanis, M. Electric field induced hyperfine level-crossings in (nD) Cs at two-step laser excitation: Experiment and theory. Opt. Commun. 2006, 264, 333. [Google Scholar] [CrossRef][Green Version]
- Wang, J.; Liu, H.F.; Yang, G.; Yang, B.D.; Wang, J.M. Determination of the hyperfine structure constants of the 87Rb and 85Rb 4D5/2 state and the isotope hyperfine anomaly. Phys. Rev. A 2014, 90, 052505. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.F.; Yang, B.D.; He, J.; Wang, J.M. Determining the hyperfine structure constants of cesium 8S1/2 state aided by atomic coherence. Meas. Sci. Technol. 2014, 25, 035501. [Google Scholar] [CrossRef][Green Version]
- Yang, G.; Wang, J.; Wang, J.M. Determination of the hyperfine coupling constants of the 5D5/2 state of 85Rb atoms by using high signal-to-noise ratio electromagnetically-induced transparency spectra. Acta Phys. Sin. 2017, 66, 103201. (In Chinese) [Google Scholar]
- He, Y.H.; Fan, J.B.; Hao, L.P.; Jiao, Y.C.; Zhao, J.M. Precise measurement of hyperfine structure of cesium 7S1/2 excited state. Appl. Sci. 2020, 10, 525. [Google Scholar] [CrossRef]
- Bulos, B.R.; Gupta, R.; Moe, G.; Tsekeris, P. Hyperfine structure determination of the 7D5/2 state of 133Cs. Phys. Rev. A 1967, 55, 407–408. [Google Scholar]
- Lee, Y.C.; Chang, Y.H.; Chang, Y.Y.; Chen, Y.Y.; Tsai, C.C.; Chui, H.C. Hyperfine coupling constants of cesium 7D states using two-photon spectroscopy. Appl. Phys. B 2011, 105, 391–397. [Google Scholar] [CrossRef]
- Stalnaker, J.E.; Mbele, V.; Gerginov, V.; Fortier, T.M.; Tanner, C.E. Femto-second frequency comb measurement of absolute frequencies and hyperfine coupling constants in cesium vapor. Phys. Rev. A 2010, 81, 043840. [Google Scholar] [CrossRef]
- Wang, S.D.; Yuan, J.P.; Wang, L.R.; Xiao, L.T.; Jia, S.T. Investigation on the Cs 6S1/2 to 7D electric quadrupole transition via monochromatic two-photon process at 767 nm. arXiv 2020, arXiv:2008.09739v1. [Google Scholar]
- Foot, C.J. Atomic Physics; Oxford University Press: New York, NY, USA, 2005; pp. 97–119. [Google Scholar]
- Yang, G.; Wang, J.; Yang, B.D.; Wang, J.M. Determination of the hyperfine coupling constant of the cesium 7S1/2 state. Laser Phys. Lett. 2016, 13, 085702. [Google Scholar] [CrossRef]
- Yang, B.D.; Gao, J.; Zhang, T.C.; Wang, J.M. Electromagnetically induced transparency without a Doppler background in a multilevel ladder-type cesium atomic system. Phys. Rev. A 2011, 83, 013818. [Google Scholar] [CrossRef]
- Gea-Banacloche, J.; Li, Y.Q.; Jin, S.Z.; Xiao, M. Electromagnetically induced transparency in ladder-type inhomogeneously broadened media: Theory and experiment. Phys. Rev. A 1995, 51, 576. [Google Scholar] [CrossRef] [PubMed]
- Auzinsh, M.; Blushs, K.; Ferber, R.; Gahbauer, F.; Jarmola, A.; Safronova, M.S. Level-crossing spectroscopy of the 7, 9, and 10D5/2 states of 133Cs and validation of relativistic many-body calculations of the polarizabilities and hyperfine constants. Phys. Rev. A 2007, 75, 22502. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).