Abstract
With the Clean Energy Package, the European Union introduced the concept of Renewable Energy Communities: groups of citizens, small and medium enterprises and local authorities that decide to join forces to equip themselves with systems to produce and share energy from renewable energy sources. The Italian legislation recently started an experimental phase in which renewable energy communities receive an incentivising tariff for the energy produced and shared within the community. This paper faces the problem of creating a new renewable energy community in two steps. First, a mathematical model of the energy flows among the members of the community is characterised according to the Italian schema. This model is used to find the optimal portfolio for the energy community, given energy requests and local source availability. Secondly, the Shapley value, a particular solution of cooperative games known to be the most fair method to allocate costs and profits of shared infrastructures, is proposed to distribute benefits among community members. The methodology has been applied to a case study based on a real low voltage network, and the economics for consumers and producers in participating to the project have been evaluated. The proposed solution, simulated adopting real economic parameters defined in the Italian regulatory framework, results to be economically viable from the point of view of the investors with a profitability index of 1.36 and, at the same time, aligned with the social purposes of the energy communities.
1. Introduction
The clean energy for all Europeans package (also known as Clean Energy Package—CEP) is a set of eight legislative acts defining the European Union’s legislative framework to achieve the energy transition. Among the many innovations provided in the CEP, an important novelty is the definition of the Renewable Energy Community (REC) provided by Directive 2018/2001 (For the sake of completeness, note that in the CEP two types of energy communities are defined: the REC in Directive 2018/2001 and the Citizen Energy Community (CEC) in Directive 2019/944. In this work we refer always to the REC.). According to the Directive, REC is a legal entity which is based on open and voluntary participation, is autonomous and is effectively controlled by shareholders or members that are located in the proximity of the community’s renewable energy projects. Moreover, shareholders must be natural persons, small medium enterprises or local authorities, including municipalities. Generally speaking, the primary purpose of REC is to provide environmental, economic or social benefits to the community of members or for the local area where it operates, rather than granting financial profits [1]. More details on the European legislative framework are reported in [2].
Energy communities (EC) are willing to bring closer Europeans to renewable energy projects and to make them actively participate to the clean energy transition [3]. Past experience in co-owned energy projects taught that the involvement of the population into the decision making process allowed to overcome their resistance (the so-called NIMBY syndrome) towards their implementation [4]. More local jobs are created and participants of the community feel more engaged in the promotion of renewable energy, making them more aware of their energy habits [5]. Most importantly, due to their non-profit nature, EC will tackle the issue of energy poverty, by performing energy efficiency measures to decrease consumption, reduce energy supply tariffs for vulnerable households or establish a fund within the community to help needing neighbourhoods [6].
In Italy, the evolution of collective energy project has not been straightforward [7], but it reached a milestone on first March 2020 when came into force the first Italian law that transposes Article 21 and Article 22 of the Directive 2018/2001 of the CEP, concerning self-consumption and REC [8]. EC members connected to the same low-voltage network (i.e., under the same Medium Voltage/Low Voltage transformer substation - MV/LV) can invest in new shared generators with a nominal power output of up to 200 kW, and they can share the energy produced consuming it immediately or by storing it in storage systems. This configuration has been defined also virtually since it does not require any physical change in the structure of the network: the users are connected to their Points Of Delivery (PODs) and the energy is shared using the public distribution network. The Italian Authority, adopting a cost-reflective approach, stated that some tariff components are not due for the energy shared and consequently are reimbursed to the community [9]. Furthermore, the policy maker has defined an incentivising tariff for the shared energy that will be recognized for 20 years.
From the legislative point of view, energy sharing is a new concept for many European countries, as in a few cases the legislative framework was already open to this option [10]. On the other hand, in academic literature, energy sharing mechanisms have been already analysed in detail, especially with a focus on the trading of energy surplus in P2P local markets [11,12,13,14,15]. Nevertheless, these approaches are not applicable for the optimal planning of collective and politically driven renewable energy projects [16]. On the contrary, when considering the planning of an energy community, two directions can be defined: from one side, a holistic view is required, modelling energy community as complex multi-energy system [17], from the other side, the focus is on the practical implementation of real-life REC projects, where the need is to formalize standard and reusable models [18,19]. To face this issue, this paper proposes a two-step methodology for the optimal implementation of the REC schema based on collective power plants. In Figure 1, the flowchart of the procedure is depicted. The first step is devoted to the definition of the optimal investment for the community (in terms of generators and storage) given the local source availability and energy needs. In the second step, the goal was to define a fair distribution of the generated value among the members of the community. The rest of paper is structured as follows. In Section 2, the model of the EC is detailed. It is based on the Italian case, but most of the equations can be generalized to a similar situation based on energy sharing. Based on this model, the optimal investment for the EC is identified. While in Section 2 the EC is evaluated as a unique entity, in Section 3 it is highlighted the fact that among the members different interests coexist and the possibility to apply a game theoretic approach is addressed. The optimization problem and the value redistribution is applied to the case study presented in Section 4, and the results are reported in Section 5. Finally, some conclusions about the proposed methodology are detailed in Section 6.
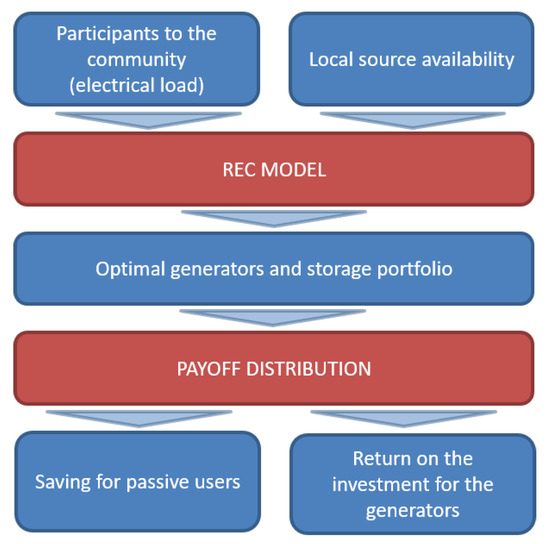
Figure 1.
Flowchart of the proposed methodology.
2. Proposed REC Model
The energy community is supposed to be composed by a set of users and a set of generators. Each passive user is connected to the grid by mean of a specific POD, while generators can be connected to a dedicated POD as well as to one of the POD of the passive users. Given this configuration, the energy consumed by each user can be categorised in three different ways:
- Self-consumed—It is produced and consumed under the same POD.
- Shared—It is produced by a generator of the community and it is consumed by users of the community connected to different PODs.
- Bought—It is bought from the market if the production of the generators is not enough to satisfy the request of passive users.
The methodology considers a base case in which there are no generators owned by the community and the overall energy is bought from the market. Starting from this, it is possible to consider costs, revenues and savings obtained with the installation of new generators. The self-consumed energy can generate a saving by buying less energy and at a reduced network tariff thanks to a minor usage of the grid. In addition, the shared energy can generate savings, but at a less convenient tariff reduction than self-consumption, as the distribution network is still affected by power fluxes. Nevertheless, given the high importance of energy sharing in the REC configuration, the model considers the possibility to introduce an economical incentive based on the quantity of energy shared. Finally, the energy produced but not consumed can be sold on the market, generating additional revenues. It is clear that the value of the savings, incentive and revenues depend on the regulation in place. Even if the application has been tested only in the Italian context, it may be possible, adapting these values, to apply it for different countries.
The energy balances are evaluated hourly to quantify the energy produced, self-consumed, shared, bought and sold from the single users’ and the community’s perspectives. The installation of new generators for the community is evaluated, and the relative economical revenues will provide different incomes for the community. Since the benefits are mainly given by the energy shared and self-consumed, there will be an optimal choice for the type and size of the power plants, given the local availability. Operational cost of the generators are considered, and also some administration cost are taken into account. The complete model of the renewable energy community and the investment in new power plants is detailed in the following paragraphs.
2.1. Sets
- M: Members of the community (element i);
- G: Available generators (element j);
- T: Time steps within each single year for which the energy balances are computed (element t);
- Y: Years in the expected lifetime for which the yearly balance is repeated, and the economical flows are evaluated (element y).
2.2. Parameters—Data to Be Provided by the User
- : Reference yearly load profile for user i [kWh];
- : Energy produced by plant j normalized for the rated power [kWh/kW];
- : Relationship between users and generators. 1: user i and generator j are under the same POD. 0: user i and generator j are under different PODs;
- : Reference yearly price profile for the energy sold to the market [€/kWh];
- : Reference yearly price profile for the energy bought from the market [€/kWh];
- : Maximum rated power for generator j;
- : Investment cost for generator j [€/kW];
- : Operational cost for generator j [€/kW/year];
- : Maximum storage capacity [kWh];
- : Minimum Energy to Power Ratio [h];
- : Minimum state of charge of the ESS;
- : Maximum number of cycle for the ESS;
- : Investment cost of the energy storage system [€/kWh] ;
- : Operational cost of the energy storage system [€/kWh];
- : Replacement cost of the energy storage system [€/kWh];
- : Administrative cost for the energy community [€/year];
- : Charge efficiency;
- : Discharge efficiency;
- : Actualization factor;
- : Incentive on shared energy [€/kWh];
- : Expected life of the investments [year];
- : Discount rate or return that could be earned in alternative investments [%];
- : Shared Energy saving index. Saving achieved thanks to energy sharing [€/kWh];
- : Self-Consumption saving index. Saving achieved thanks to self-consumption [€/kWh];
- : Yearly growth of the load [%/year];
- : Yearly growth of the price [%/year];
- : Percentage of the investment expense that can be deduced;
- : Number of years in which the deduction has to be split.
2.3. Variables—Unknown or Changing Parts of the Model
- : Rated power of generator j [kW];
- : Capacity of the centralized energy storage system [kWh];
- : Energy consumed by member i for each year y [kWh]
- : Energy produced by the sum of generators of user i [kWh];
- : Energy self-consumed by user i [kWh];
- : Energy surplus of user i [kWh];
- : Energy deficit of user i [kWh];
- : Energy offered from the members of the community that have a surplus [kWh];
- : Energy required from the members of the community that have a deficit [kWh];
- : Energy shared in real time within the community [kWh];
- : Energy shared within the REC considering also energy provided by the ESS [kWh];
- : Energy bought from the market [kWh];
- : Energy sold to the market [kWh];
- : Energy stored in the ESS at time t (initial instant of the time window) [kWh];
- : Energy withdrawn from the ESS [kWh];
- : Energy injected into the ESS [kWh];
- : Price of the energy sold to the market for each year y [€/kWh];
- : Price of the energy bought from the market for each year y [€/kWh];
- : Investment cost [€];
- : Operational cost [€];
- : Equivalent cost for the energy storage replacement [€];
- : Saving obtained self-consuming/sharing energy [€];
- : Revenues obtained selling the surplus to the market or by mean of the incentives [€];
- : Financial incentives for the community [€].
2.4. Constrains: Single Users Energy Balances
Energy consumed by each user i in the expected lifetime:
Energy produced by the generators in the availability of user i:
Energy that is self-consumed by user i:
Energy surplus for user i:
Energy deficit for user i:
In some conditions it may be forbidden to selfconsume energy produced by community plants (Allowing members’ self-consumptions could increase the revenue of the community, but at the same time it requires a more complex way to redistribute the economical benefits, that may be unfairly concentrated on the users that self-consume the energy.). In this case, it could not be possible to self-consume the energy produced and Equation (3) is substituted with:
2.5. Constrains: Energy Community Energy Balance
The amount of energy that is offered to the energy community from the members that have a surplus at time t can be evaluated as:
The amount of energy that is requested to the energy community from the members that have a deficit at time t can be evaluated as:
In general, these two values are different and it is not possible for the community to manage all the energy required and offered by the users at each time step.
The amount of energy the community can collect and redistribute in the same hour is equal to the minimum for each instant between the energy offered to the community and the energy request to the community. We define this quantity as energy shared in real time.
Energy Storage System
In the case the community does not have an energy storage system, the energy offered to the community but not requested by other users is sold to the market.
The energy requested to the community but not provided from other users is bought from the market.
The shared energy is equal to energy shared in real time.
In the case when a centralized energy storage system (ESS) is considered, the amount of energy managed by the community can increase because the system can store the energy instead of selling it. Other than the shared energy in real time, a more general definition of shared energy can be specified as the energy consumed by the users coming from the community generation or from the ESS. The model of the ESS is technologically neutral and, depending on the value assigned to the parameters, can represent different types of storage (e.g., electrochemical, hydroelectric, compressed air, etc.).
The maximum capacity of the ESS is:
The maximum charging power for the energy storage system is:
The maximum discharging power for the energy storage system is:
The amount of energy stored into the system is defined with the following constrains:
Furthermore, the energy stored within the battery has to respect SOC limits.
The energy sold to the market is the energy offered to the community that is not shared in real time and not stored.
The energy bought from the market is the energy request to the community not provided from other users in real time nor from the storage system.
The energy that is evaluated as shared is equal to the energy shared in real time plus the extra energy provided from the storage.
2.6. Constrains: Cash Flow Evaluation
The investment is equal to:
For each year y the net cash flow is evaluated as:
The net present value of the investment is then calculated as:
The savings for each year y are the sum of the instantaneous savings due to self-consumption (SC) of each member i and the saving due to shared energy (SE) in the considered year.
The revenues at year y come from the energy sold to the market in each time step or from the incentive.
The market price profiles used in Equations (27) and (28) are evaluated for the entire lifetime depending on the expected growth or decrease.
In some particular cases of the Italian context there is the possibility to deduct a part of the investments in photovoltaic power plants from the taxes of the years following the investment. This financial incentive can be treated as a yearly revenue from year 1 to and can be evaluated as:
The total cost at year y is:
where the replacement cost of the battery is:
2.7. Blocks of Years
The evaluation of more than one year is useful to take into account the variation of load, production and prices over time. Nevertheless, it increases the computational effort required to evaluate the variables of the model. For this reason, a simplified approach is used to represent blocks of years with common characteristics, instead of single years y with unique values. To apply these change, all the variables that are function of y are converted in function of . The expected lifetime (i.e., the number of yearly energy balances to be computed) becomes . The ratio has to be an integer number, and it represents the number of years for each considered block.
The load profiles of each user (Equation (1)) have to be updated as follows:
where is computed in order to keep the same overall consumption over the entire lifetime. It can be demonstrated that this happens when:
The same approach is adopted to define the value of the market prices as defined in Equations (29) and (30) according to their growing trend. The price trend has to be updated as:
Finally, the evaluation of the net present value of the investment has to be updated as:
2.8. Optimization
The optimization provides to the community the indication of the generators and storage to install to maximise the economical value of the investment. To achieve this, the maximisation of the net present value of the investment is the selected objective function. In this way, the overall cash flow of the energy community is evaluated. By the way, in real life, this economical balance is not referred to a single entity, since many actors are involved in a community project (different users and at least one producer). It is thus essential to investigate whether the return on investment of each stakeholder justifies its participation in the community.
3. Game Theoretic Approach for Value Redistribution
The model presented in Section 2 is capable to define an overall cash flow, in which costs and revenues are considered as they were monetary flows of a single entity. Nevertheless, considering the nature of the energy communities, it is clear that multiple stakeholders are involved and the interest of each one has to be taken into account. As a matter of fact, an investment that can be theoretically profitable when considering the cumulative profits, can be halted by insufficient returns from individual investors.
Taking this challenge into consideration, game theory is an effective tool to address the interactive nature of energy sharing, since it provides general mathematical techniques for analysing situations in which two or more individuals make decisions that will influence one another’s welfare [20]. The game, that can also be referred as conflict or interaction, describes any situation in which the decision-making processes of the players, i.e., the game participants, are interrelated. The players are said to be rational, as their decisions are guided solely by the desire to complete their own objectives, that are assumed to be the maximization of their expected payoff, mathematically described by an utility function. The players are also said to be intelligent, and it is assumed that any player is aware about the rules of the game and can think of consistent assumptions to make his decisions. The game theory is generally divided into two classes defining the level of constraint of the agreements taken among the players. Cooperative games analyse situations in which commitments are fully binding and enforceable. On the other hand, in non-cooperative (or strategic) games there is no obligation to fulfil such commitments.
3.1. Non-Cooperative Game
In non-cooperative games the players are independent and choose their strategy, the maximization of their utility function, with no communication or exchange of information with the other players. The outcome of the decisions will lead to conflicting interests in reaching the desired objectives. A classical representation of static non-cooperative games is given by a set of players N, a set of possible actions and the utility functions of the players . The players have to select an appropriate action in the set so that its utility function will be maximised. Nevertheless, the utility function does not only depend on the individual action of the player , but also on the array of actions of the other players. One important solution in non-cooperative games is the Nash equilibrium, a stable state in which the players cannot improve their utility function by changing their action , if the other players keep the same array of decisions .
Non-cooperative game theory is often used to model those situations in microgrids or small power systems in which users act individually and aim to optimize their own benefit. In [21], a framework to regulate the percentage of domestic users owning a storage device is presented. The problem is modelled as a non-cooperative game in which players act to minimise their costs. A Nash equilibrium that maximises social welfare is found as the number of battery owners with respect to the considered population. The authors of [22] provide a methodology to enhance the stability and the efficiency of a microgrid, using an algorithm based on non-cooperative game theory. A Nash equilibrium is found as a solution of this dynamic game, that optimises the power regulation of the load and the sources within the system. Moreover, it is studied how loads and sources can react by adjusting their power to the actions of the other players. Some specific declinations of non-cooperative game theory are also considered in literature, in order to better analyse some particular situations. As an example, [23] studies an isolated microgrid with users benefiting of PV electricity generation and batteries. The system is analysed using two concepts from non-cooperative game theory: the Potluck problem and an auction game. The interaction between consumers and producers is modelled as a Potluck problem, a dynamic non-cooperative problem in which players have no communication but act rationally. The problem is known in literature for not possessing a Nash equilibrium. As game theory predicts, due to the rational thinking of the players, the system oscillates between a state in which there is excess demand or excess production. As a consequence, a non-rational thinking is adopted for the users to find an equilibrium in which the system can work. An auction game is then implemented to simulate the internal market under different conditions of market clearing strategies. For every condition, a different Nash equilibrium is found. Another example of non-cooperative game is reported in [24], where a mechanism to encourage users in a smart grid to actively participate in energy trading with a central power station is proposed. The system is modelled as a single-leader multiple-follower Stackelberg game (a theory first developed in economics in which a leader has the advantage of a first move and the follower plays the best response to optimize its utility) in which the aggregator is the leader that sets the internal price of energy within the microgrid and the users of such microgrid have to decide the amount of energy to sell in response to the determined price. The objective of the aggregator is to set a price that incentivises active users to sell electricity during peak hours in order to meet the demand of the microgrid, while maximizing the overall benefit (generalized Nash equilibrium).
3.2. Cooperative Game
Cooperative (or coalitional) games are characterized by the possibility of communication between the players. In particular, the players decide to form coalitions between each other in order to improve their payoff from the game. This alliance represent an agreement that binds the players to act collectively. Cooperative games comprehend two categories of games. Nash bargaining deals with the analysis of the possible conditions and terms that players stipulate in order to form coalitions. Nash bargaining is used to find if a payoff for the players exists, whose value exceeds one of the so-called disagreement points, that is the value that the players receive if the negotiation does not go through. On the other hand, coalition games study the architecture of formed coalitions and the interaction between the players. Another possible division of cooperative games is based on the nature of the utility function. In games with Transferable Utility (TU) the utility function assumes a numerical (monetary) value that can be distributed among the players of the coalition following a fairness rule. The payoff of each player is represented by the share of the coalition’s utility received.
The coalitional game is uniquely defined by the pair , where N denotes again the set of players and is the value of the coalition . The payoff of the player , part of the coalition, is determined by an allocation criterion. This allocation should be fair and accepted from all the players, that otherwise would prefer to leave the community.
3.2.1. The Core
The core is a classical solution of the stability of a canonical game and delineates a space of solutions (i.e., payoffs) x for the members of the grand coalition N, for which no player can receive any greater payoff in any other subset of the grand coalition . Indeed, it could happen that, given a payoff vector, a subset of actors would prefer to form a smaller coalition instead to form the gran coalition. In mathematical terms, a payoff vector x is in the core of a coalitional game if and only if:
3.2.2. The Shapley Value
All things considered, a solution based on the core may comprehend many possible values for each player and this payoff may not reflect the most fair way to allocate the grand coalition’s value. In order to fairly allocate the coalition’s value among the players of the game, the Shapley value takes into account the added value that each player brings to the coalition. In other words, it reflects the most fair payoff for the players in the grand coalition, taking into account the marginal contribution of each player. Shapley value for user i is expressed as:
in which the marginal contribution of the player i in the coalition S is weighted on the factor that takes into account the possible orders in which player i can join the coalition S. The Shapley value definition is bounded to four axioms:
- Pareto efficiency: , the total value of the grand coalition is redistributed among the players.
- Symmetry: if then , if two players contribute equally to the coalition, they receive the same payoff.
- Additivity: being v and u value functions of two games, it holds
- Null player: if then , a player that does not contribute to the coalition, receives no payoff.
One of the major drawbacks of the Shapley value is its computational burden as the number of players inside the coalition increases. It is not possible to evaluate the Shapley value for a set of hundreds of users like it could be the one of an energy community. Furthermore, it has to be noted that the Shapley value does not necessary lie in the core.
When considering academic literature in the domain of cooperative games, Nash bargaining is employed to provide incentives to individual users to share their excess energy. In [25], a Nash bargaining problem is set up to stimulate two users to share an energy storage device. The Nash Bargaining solution is used to determine a fair compensation that a user should receive, if the other user has discharged the battery that he had first charged. In a similar fashion, in [26] the authors design an incentive mechanism based on Nash bargaining to develop energy trading between interconnected microgrids. The Nash bargaining solution finds a price of electricity at which the microgrids can trade electricity that minimises the individual costs of electricity demand. As all the microgrids act as rational layers with the objective of minimizing their cost, the Nash bargaining solution also delineates the subset of microgrids willing to participate in active energy trading. On the other hand, coalition formation game theory can analyse which size of micro-grid is more convenient for the participants. As an example, the purpose of [27] is to form coalitions of microgrids comprising energy producers and energy buyers whose objective is to optimize the payoff of each participant. Users’ costs are reduced by trading the power within the distribution and avoiding much power flowing through the macro station and the subsequent power losses. An algorithm based on coalition formation game theory is set up, that creates coalitions within a selected area bringing together in the same coalition buyers and producers whose production and demand curves are as similar as possible and whose distance does not create too many power losses. The algorithm iterates the creation of coalitions until the game becomes stable, so no user has an advantage to leave its coalition. Within canonical coalitional games, the Shapley value proves to be the most effective method applied in the literature to fairly divide the benefit resulted by forming a microgrid in which energy is shared. [28] relates to a community microgrid in which active users, equipped also with a storage system, can share their excess energy. In the paper, different methods are used to allocate the energy bill among the community participants. When the problem is modelled as a cooperative game, allocating the costs with Shapley value, the users receive a more fair treatment with respect to other P2P trading mechanisms such as bill sharing, mid-market rate and supply demand ratio. [29] introduces instead a payment calculation scheme to compensate the users of a joint microgrid based on the Shapley value. In particular, the energy producers within the microgrid are fairly compensated taking into account the difference between the Shapley values and the generation costs of each technology. The authors in [30] optimize the energy fluxes in an energy community in order to minimise the overall costs of the system. Some participants are provided with a renewable energy source, some participants with a storage systems. A coalitional game framework is used to model the energy trading inside the community. Shapley value is then used to fairly distribute the savings among the participants.
3.3. Energy Community as a Coalitional Game
The model of energy community presented in this paper can be seen as a cooperative game. The players are the producers (i.e., the financers of the generation plants) and the consumers. The economical value generated hour by hour depends on the presence and the interaction between load and production, in particular on the quantities of energy produced and shared. The players can decide to take part to the community or not. Both producers and consumers want to take advantage from the participation to the community. Producers can be generically considered as external actors that can invest in the installation of new generators and wants to get a return from the investment. In real applications, they can be external financers or the community itself (with the financial participation of the community members). In any case, even if external and internal financers could require different rates of return, it is important to notice that they are both expecting a positive return of the investment. From the methodological side, who the financier does not impact. On the other hand, when considering consumers, they have a certain contractual power as they are necessary to generate the profit (mainly based on the incentive for shared energy). As a consequence, they can require an appropriate return for their participation in the energy community. The objective of studying this game is to find a stable and fair allocation rule that gives an adequate payoff to the players, so that each one is encouraged to take part to the EC.
3.3.1. The Game
The game is defined as follows:
- N is the set of players , where and are respectively the number of generators and passive users participating to the energy community.
- The possible actions for each player are to take part to the community or not (In this planning phase we consider the worst case in which users are not changing their loads to increase the amount of energy shared. In real operation, the same game could become dynamic and users could also apply some demand response schema to maximise their payoff.).
- associates with each coalition a real-valued payoff that the coalition’s members can distribute among themselves. The value generated by coalition S at hour t is defined as:where the energy sold to the market and the energy shared depends on the members of the coalitions S and are obtained from Equations (21) and (23). The presence of each player in the community affects the quantity of energy produced and shared, and consequently the economical value produced. The value should be redistributed among the players depending on their contribution. For convenience, the value function could be evaluated yearly, keeping the results immediately comparable with the cash flow analysis. The yearly value is simply the summation over time of .
3.3.2. Stability and Fairness
The study of the stability of the coalition, that is the confirmation that everybody wants to form the gran coalition instead of smaller ones, is trivial. The reason is that the rules of the game state that the participation to the energy community has to be open and voluntary. This means that, even if some coalition could be preferred from a subset of players, they are not allowed to exclude others from the coalition. From their side, all the users want to take part to the community, since they can only gain from this participation. From the producers side, since the optimal portfolio for the community as a whole has already been evaluated in the optimization phase, the community will constrain its generation portfolio to that one. In other words, it is not the single investor that decides which generator is more profitable, but is the community that defines the set of generators that have to be installed. The choice of the producer is to invest or not in that specific portfolio. Given this consideration, the study of the game is reduced to the research of a fair way of dividing the grand coalition’s payment amongst its members.
When dealing with fairness, two issues are of particular importance. The first concerns the division of the value produced between consumers and producers. It is important for those who invest in community facilities to know that they are getting a fair return for their financial intervention. At the same time, value should be distributed among consumers according to their contribution to value generation, because not everyone contributes in the same way. The contribution of a passive user will be zero if his energy demand occurs at a time when the total load already exceeds the current production. On the contrary, a user will produce a greater value if he consumes the energy produced by the facilities of the community when there are no other users who require it. The calculation of the Shapley value can solve both issues.
For the application into this field, we propose a two-level payoff distribution. In the first level, the payoff is distributed with the Shapley value between producers and groups of consumers. The distribution based on group of consumers instead of each single consumer introduces an approximation, since the marginal contribution of the group of costumers can be different from the sum of marginal contributions of each single user. Nevertheless, in the planning phase, this can be accepted in exchange of a computational feasibility. The second level of distribution concerns the division amongst each single consumer within each group with a proportional distribution.
3.4. Implementation
The model of the energy community has been written in Python’s pyomo environment and the optimization has been solved with the solver Gurobi. The value redistribution for the optimal solution has been evaluated computing the Shapley value in a Python environment.
4. Case Study
The model of the renewable energy community has been applied to a real case study, to test it on a practical usage and to evaluate its potential. The case study is related to the low voltage grid of Chiou, a fraction of the village Porossan (710 m), in the municipality of Aosta (Figure 2). Given the great presence of renewable energy sources and the mountainous morphology of the area, Valle d’Aosta Region has always been a producer of renewable energy. The Distribution System Operator (DSO) of Porossan is the Electric Cooperative of Gignod (CEG), a pioneer in the field of energy communities [31]. Policy makers in the area are particularly willing to improve the environmental sustainability; in [32], it is reported a study devoted to identifying the optimal portfolio for maximising local self-sufficiency.

Figure 2.
The village of Porossan and its location in Italy. The red circle indicates the area feeder by the substation Chiou.
4.1. Users Consumption
The power profile of each user (active and passive) under the MV/LV substation has been obtained from real measurements collected by the DSO. The selected LV network has already some PV power plants connected, but for the goal of this application, they have been removed in order to consider a more generic greenfield project. In Porossan there are two MV/LV substations: Chapelle and Chiou. The nominal power of each transformer is 250 kVA. The power profile of the transformer in the substations is available from the local DSO. Their data have been elaborated assuming realistic assumptions, as detailed in the following.
To evaluate the feasibility of a REC in the area fed by Chiou, the number of users connected and their consumption needs to be known. The information about number and type of users connected is obtained from public dataset (ISTAT). Specifically, in Porossan there are 245 buildings, some of them are divided in more than one internal unit, for a total number of 324 units. We suppose that each unit has its own POD. According to the Italian regulation, LV users can be of three different types: domestic (that can be resident or not resident), for “other usages” and for public lighting.
The number of families living in Porossan according to ISTAT data is 247, for a total number of 565 people. The number of people in each family is reported in the Table 1. Since we are supposing that the grid of Chiou feeds 40% of the village of Porossan, the number of families is then adapted to this quote. Each family has its own POD of residential type Domestico residente. The consumption of each type of family is supposed to increase with the number of people in the family, with the following formula:

Table 1.
Number and consumption of users in the energy community grouped by types.
The yearly consumption for each type of family is reported in Table 1. Giving this hypothesis, the mean yearly consumption results to be 1862 kWh. This value is comparable with the average value for domestic residential users for the entire Valle d’Aosta Region (2018 kWh/year according to DSO data).
From ISTAT data, we also know that 38 building units in Porossan are for not domestic usages, it means they are used for economic activities, business and other services. From the electrical point of view, they are all labelled as other usages (Altri usi). Keeping the hypothesis that 40% of the load is under Chiou substation, we consider 16 users of this type. We suppose that the users of this type have a yearly consumption equal to 1356 kWh, that is the average value in the entire Valle d’Aosta Region.
The units that are not residential or for other usages are domestic users not resident (Domestico non residente). These are not related to people living in the area and, giving the tourist interest of the place, they could be holiday houses. According to the hypothesis that 40% of Porossan’s users are under the grid of Chiou, we obtain that there are 15 users of this type. We suppose that yearly consumption for LV domestic but non residential users is equal to the mean value for the Valle d’Aosta Region, that is equal to 642 kWh.
Finally, we suppose also that the total consumption for public lighting is equal to 2000 kWh/year. The total consumption of the LV grid results to be equal to 217.2 MWh/year.
To compute energy balances, a specific hourly profile has to be assigned to each type of user.
Users Power Profiles
The hourly power transit in the substation is measured by the DSO and reported in Figure 3. It is clear that many PV power plants are installed and, especially in spring and summer, there is an important inverse flow from the LV to the MV level. This reverse flow appears for 20.0% of the hours of the year. Indeed, 18 PV power plants are connected to the LV feeders, for a rated power of 80.6 kWp. The average size of each plant is 4.48 kWp.

Figure 3.
Power transit in the MV/LV transformer of Chiou.
To evaluate the profile of load consumption, it is necessary to quantify the effect of local generators. Not all of these plants are monitored, so the total production from the PV generators has been estimated. A standard PV production profile is computed from the production profile of the monitored plant, and it is multiplied by the total rated power of the 18 plants. The standard profile is computed, hour by hour, as the 90th percentile of the measured profiles. This choice is due the fact that the measurement available are for the injected powers and not for the produced ones. Evaluating the standard profile in this way avoids to consider values that are particularly low due to high self-consumption. The obtained profile is depicted in Figure 4. The number of yearly equivalent hours for such profile is 1072 (the value is reasonable considering that for the optimal oriented panels in the same location, the tool PVgis [33] indicates a number of equivalent hours equal to 1210).

Figure 4.
Power production of plants connected to LV grid of Chiou.
The total load profile due to LV users has been evaluated as the difference between the transit in the substation and the local production. The profile obtained is shown in Figure 5. Simple machine learning techniques based on regression trees (specifically, random forest) have been used to remove outliers. It is interesting to notice that the total consumption of the area has been estimated equal to 215.5 MWh. This value is quite close to the value obtained from the mean consumption for each category of users as detailed in Table 1 (217 MWh).
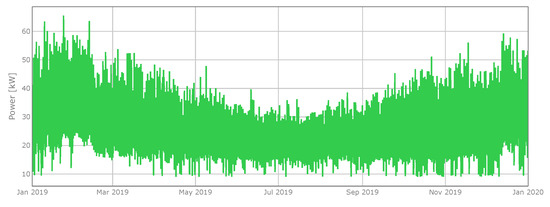
Figure 5.
Estimated power consumption of LV users of Chiou.
Once the total load profile has been obtained, it has been divided among the LV users, according to their estimated yearly consumption and hypotheses about the hourly distribution. In total, 9 different power profiles have been defined, clustered into the following groups:
- Profile for public lighting. There is only one user to which this profile is assigned. The yearly energy consumption has been spread over the hours of darkness, supposing the public lighting work in an ON/OFF mode.
- Profile for other usages. Sixteen users have been defined. We suppose that these users are mainly offices, small artisans and commercial activities. The profile has been created supposing energy consumption in the working hours of the year. In addition, in this case, an ON/OFF mode is considered, with energy consumption concentrated in the peak time windows of the Italian tariff schema (Fascia 1: from 8 a.m. to 7 p.m. from Monday to Friday, national holidays excluded).
- Profile for not residential usage. Fifteen users have been defined. The profile for public lighting and other usages is subtracted to the power transit in primary substation and the resulting profile is the total consumption of domestic users. This is divided between residential and not residential users. The consumption of non residential users is supposed to the be concentrated on weekends.
- Profiles for residential usage. The remaining part of the consumption profile is distributed among 6 types of families, according to the number of family members and their consumption.
4.2. Sources Availability
With respect to the generation side, two technologies have been investigated: photovoltaic and hydroelectric. More in detail, we consider the possibility to install a single hydro power plant and several PV power plants. The main data about the availability of these sources are reported in Table 2.

Table 2.
Potential generator availability for the energy community.
Theoretically, each rooftop could host a PV plant, nevertheless it is trivial to exclude some of them due to their particular shape, orientation and shadows. For this reason, the number of considered rooftops in the optimization has been reduced to 20. This represents the number of surfaces for which the installation of a PV plant is supposed to be reasonable. The area and the orientation of the surfaces have been evaluated with GIS software, while the slopes have been defined with realistic values from 10 to 40. The installation cost for each plant is considered different, going from the lowest value equal to 1400 €/kWh to the highest value equal to 2000 €/kWh.
The production profiles for each of these plants are automatically requested via API to the PVgis tool “Performance of grid-connected PV” [33], in order to properly take into account the shadows from high horizon. Since the location of all the surfaces is almost the same, this type of shadow does not introduce big differences among the plants, and each power profile is mainly characterised by the orientation and the slope of the single surface. The profile is requested to PVgis for a PV plant with a rated power of 1 kW based on crystalline silicon cells, and the sum of the system losses is set to 14%. In Figure 6, the profiles obtained for each of the 20 surfaces are reported for four days. From this zoom, it is possible to see the effect of the different orientation on the daily production profiles. The heatmap in Figure 7 reports the average profile with time divided into two axis: the day of the year and the hour of the day. In this way, it is easy to see the daily and seasonal trends. This specific profile is not used in the model, but it is useful to see the seasonal behaviour of this type of generators.

Figure 6.
Daily differences among PV power profiles.

Figure 7.
Average photovoltaic power production.
The production profile of the hydroelectric power plant is a standard profile, built from the production profiles of similar power plants in the area. Since the maximum allowed size of a generator connected to the Italian LV network is 200 kW, only power plants with a nominal power lower than 200 kW are used to build the standard profile. In the area under evaluation, there are 6 monitored hydroelectric power plants with the following rated power: 40 kW, 6.4 kW, 72 kW, 45 kW, 45 kW. Looking to their production profiles, it is clear there is a common path defined by the seasonal water availability. In Figure 8, the standard production profile of the hydroelectric power plant is depicted compared with the five measured profiles of the real plants currently in place. They are all normalized by their maximum power and the reference profile is obtained as the median value for each hour of the year. It is also shown in Figure 9, where it is possible to see the seasonal trend and the absence of a daily trend. The number of the equivalent working hours per year for the profile obtained is equal to 4205.

Figure 8.
Hydroelectric power profiles.

Figure 9.
Hydroelectric power profiles.
4.3. Economical Data
The lifetime of the investment is supposed to be equal to 20 years, the actualization factor is equal to 4%. The possibility to install an energy storage system up to 200 kWh is considered. In Table 3, the values of the economical parameters are detailed, while in Table 4 the values used to detail the battery model are reported. They refer to an electrochemical storage, based on lithium-ion cells.

Table 3.
Economical data.

Table 4.
Storage data.
5. Results
5.1. Optimization Results
Solving the model presented in Section 2, the optimal energy community configuration has been calculated. It is based on 2 PV power plants and 1 hydroelectric plant. In Figure 10, the optimal power is compared with the theoretically available one. This production portfolio includes 14.4 kWp of photovoltaic generators and 20 kW of hydroelectric. With this configuration, the energy community is expected to produce on average 102.2 MWh/year, sharing 95.2% of it amongst the members (97.4 MWh/year) and selling the other 4.8% to the market (4.9 MWh/year). Thanks to the incentive on shared energy, and considering the actualization of these values, shared energy provides an average income equal to 7230.5 €/year, while producing savings of 3397 €/year. The energy sold to the market contributes with 173.7 €/year to the yearly income. The result is that the incentive of shared energy contributes to 66.9% of the total revenues over the lifetime of the investment (Figure 11), the second driver for the investment is the saving due to the not bought energy (31.5%). The smallest part of the income is due to the energy not shared within the community but sold to the market. Considering that this is not the main goal of the energy community, it contributes only for 1.61% of the total. The net present value of the investment is equal to 85,866 €. The profitability index is equal to 1.84 and the payback time is less than 9 years. It is interesting to notice that the energy storage system does not result in the optimal solution, due to the high cost of investment.

Figure 10.
Optimal installed power for each generator’s availability.
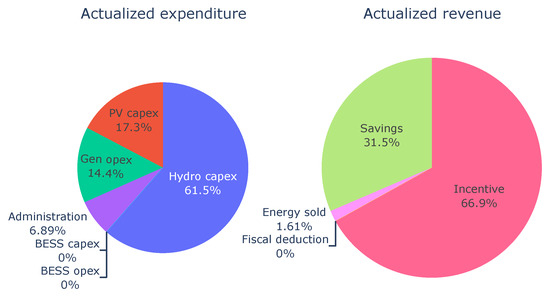
Figure 11.
Cash flow contributions.
5.2. Value Distribution
The Shapley value has been evaluated considering the producers and the group of consumers as actors. The producers receive only a part of the profit of the investment, since part of it goes to the consumers. In Figure 12, the global value of the investment for the community is depicted in blue, while the cash flow of the producers is shown in red. It is possible to see that the initial investment of the community is exactly the investment of the producers, but then the community obtains higher profits that are only partially shared with the producers. This means the payback time is higher than the one that could be achieved allocating to the producers the entire value generated by the community (+44.4%). In a similar way, the net present value of the investment for the producers is lower than the global one achieved by the community (37,204 €, −56.7%), with a profitability index equal to 1.36 (−0.48). The difference between the value of the community and the value allocated to the producers is distributed to the consumers. The distribution amongst the group of users is obtained via the Shapley value, then it is divided proportionally between the number of users within the group. In Figure 13, the yearly revenue obtained by each consumer that is taking part to the community is depicted. The revenues depend on the amount of energy consumed but also on the way to consume it and, on average, each user achieves a saving of 32.1 € per year. It is important to notice that users can obtain this value without any economical effort (not considering the yearly contribution to cover administrative expenses, set in this case to 5 €). This is aligned with one of the primary purposes of the energy community as characterised in the aforementioned REC definition; that is “to provide economic or social community benefits for its shareholders or members or for the local areas where it operates”. Furthermore, this could be a way to fight energy poverty “assessing the possibility to enable participation by households that might otherwise not be able to participate, including vulnerable consumers and tenants” [1].

Figure 12.
Investment cash flows obtained by the producers applying redistribution rules.

Figure 13.
Yearly revenue obtained by each consumer applying redistribution rules.
6. Conclusions
Renewable Energy Communities are an important tool for citizens’ involvement in the energy transition process. In some cases, as in the current Italian scenario, renewable energy communities have clear and simple regulations and incentives in place. Nevertheless, the presence of many stakeholders can make it difficult to create new energy communities. The risk is that only projects based on profit and far from the original economic, social and environmental principles of EC will be developed. The methodology proposed in this article searches for the configuration that maximizes the value that the community is able to generate with the installation of new generators and, afterwards, divides it between the participants in the community according to a logic of fairness. In this way, all participants in the project can obtain an economic advantage, and at the same time the sustainability of the investments is verified from the financers’ point of view. The application to a real life case study based on the actual Italian scenario has confirmed the effectiveness of the methodology and the possibility to be easily applied to real life problems. The application of the proposed payoff distribution schema causes a 44.4% increase of the payback time and a 56.7% decrease of the net present value, in exchange for an average yearly saving for the passive users equal to 32.1 €.
Author Contributions
Conceptualization, M.M. (Matteo Moncecchi) and M.M. (Marco Merlo); methodology, M.M. (Matteo Moncecchi) and S.M.; validation, M.M. (Matteo Moncecchi) and M.M. (Marco Merlo); writing—original draft preparation, M.M. (Matteo Moncecchi) and S.M.; writing—review and editing, M.M. (Marco Merlo); supervision, M.M. (Marco Merlo). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Società Cooperativa Elettrica di Gignod (CEG) for providing measured data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- EU. Directive (EU) 2018/2001 of the European Parliament and of the Council on the promotion of the use of energy from renewable sources. Off. J. Eur. Union 2018, 2018, 82–209. [Google Scholar]
- Moncecchi, M.; Meneghello, S.; Merlo, M. Energy Sharing in Renewable Energy Communities: The Italian Case. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Torino, Italy, 1–4 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Kunze, C.; Becker, S. Energy Democracy in Europe—A Survey and Outlook; Rosa Luxemburg Foundation Brussels Office: Bruxelles, Belgium, 2014; p. 68. [Google Scholar]
- Wüstenhagen, R.; Wolsink, M.; Bürer, M.J. Social acceptance of renewable energy innovation: An introduction to the concept. Energy Policy 2007, 35, 2683–2691. [Google Scholar] [CrossRef]
- Bauwens, T. What Roles for Energy Cooperatives in the Diffusion of Distributed Generation Technologies? 2013. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2382596 (accessed on 19 October 2020).
- Koirala, B.P.; Koliou, E.; Friege, J.; Hakvoort, R.A.; Herder, P.M. Energetic communities for community energy: A review of key issues and trends shaping integrated community energy systems. Renew. Sustain. Energy Rev. 2016, 56, 722–744. [Google Scholar] [CrossRef]
- Candelise, C.; Ruggieri, G. Status and evolution of the community energy sector in Italy. Energies 2020, 13, 1888. [Google Scholar] [CrossRef]
- Repubblica Italiana. LEGGE 28 Febbraio 2020, n. 8. Gazzetta Ufficiale Della Repubblica Italiana. 2020, pp. 32–33. Available online: https://www.gazzettaufficiale.it/eli/id/2020/02/29/20G00021/sg (accessed on 19 October 2020).
- ARERA. Deliberazione 4 Agosto 2020—318/2020/R/EEL. 2020. Available online: https://www.arera.it/it/docs/20/318-20.htm (accessed on 19 October 2020).
- Inês, C.; Guilherme, P.L.; Esther, M.G.; Swantje, G.; Stephen, H.; Lars, H. Regulatory challenges and opportunities for collective renewable energy prosumers in the EU. Energy Policy 2020, 138, 111212. [Google Scholar] [CrossRef]
- Reihani, E.; Siano, P.; Genova, M. A new method for peer-to-peer energy exchange in distribution grids. Energies 2020, 13, 799. [Google Scholar] [CrossRef]
- Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy-Sharing Model with Price-Based Demand Response for Microgrids of Peer-to-Peer Prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
- Jiang, A.; Yuan, H.; Li, D. A two-stage optimization approach on the decisions for prosumers and consumers within a community in the Peer-to-peer energy sharing trading. Int. J. Electr. Power Energy Syst. 2021, 125, 106527. [Google Scholar] [CrossRef]
- Cui, S.; Wang, Y.W.; Shi, Y.; Xiao, J.W. An Efficient Peer-to-Peer Energy-Sharing Framework for Numerous Community Prosumers. IEEE Trans. Ind. Inform. 2020, 16, 7402–7412. [Google Scholar] [CrossRef]
- Zafar, R.; Mahmood, A.; Razzaq, S.; Ali, W.; Naeem, U.; Shehzad, K. Prosumer based energy management and sharing in smart grid. Renew. Sustain. Energy Rev. 2018, 82, 1675–1684. [Google Scholar] [CrossRef]
- Kunze, C.; Becker, S. Collective ownership in renewable energy and opportunities for sustainable degrowth. Sustain. Sci. 2015, 10, 425–437. [Google Scholar] [CrossRef]
- Fleischhacker, A.; Lettner, G.; Schwabeneder, D.; Auer, H. Portfolio optimization of energy communities to meet reductions in costs and emissions. Energy 2019, 173, 1092–1105. [Google Scholar] [CrossRef]
- Ghiani, E.; Giordano, A.; Nieddu, A.; Rosetti, L.; Pilo, F. Planning of a Smart Local Energy Community: The Case of Berchidda Municipality (Italy). Energies 2019, 12, 4629. [Google Scholar] [CrossRef]
- Mutani, G.; Todeschi, V.; Tartaglia, A.; Nuvoli, G. Energy Communities in Piedmont Region (IT). The case study in Pinerolo territory. In Proceedings of the 2018 IEEE International Telecommunications Energy Conference (INTELEC), Turin, Italy, 7–11 October 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Myerson, R.B. Game Theory: Analysis of Conflict; Harvard University Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Vytelingum, P.; Voice, T.D.; Ramchurn, S.D.; Rogers, A.; Jennings, N.R. Agent-based micro-storage management for the smart grid. Proc. Int. Jt. Conf. Auton. Agents Multiagent Syst. AAMAS 2010, 1, 39–46. [Google Scholar]
- Weaver, W.W.; Krein, P.T. Game-theoretic control of small-scale power systems. IEEE Trans. Power Deliv. 2009, 24, 1560–1567. [Google Scholar] [CrossRef]
- Maity, I.; Rao, S. Simulation and pricing mechanism analysis of a solar-powered electrical microgrid. IEEE Syst. J. 2010, 4, 275–284. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Smith, D.B.; Poor, H.V. Price Discrimination for Energy Trading in Smart Grid: A Game Theoretic Approach. IEEE Trans. Smart Grid 2017, 8, 1790–1801. [Google Scholar] [CrossRef]
- Dai, R.; Charkhgard, H.; Chen, Y.; Kuang, Y. Balancing Benefit Distribution for Energy Storage Sharing based on Nash Bargaining Solution. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Incentivizing Energy Trading for Interconnected Microgrids. IEEE Trans. Smart Grid 2018, 9, 2647–2657. [Google Scholar] [CrossRef]
- Saad, W.; Han, Z.; Poor, H.V. Coalitional game theory for cooperative micro-grid distribution networks. In Proceedings of the 2011 IEEE International Conference on Communications Workshops (ICC), Kyoto, Japan, 5–9 June 2011. [Google Scholar] [CrossRef]
- Long, C.; Zhou, Y.; Wu, J. A game theoretic approach for peer to peer energy trading. Energy Procedia 2019, 159, 454–459. [Google Scholar] [CrossRef]
- Pilling, R.; Chang, S.C.; Luh, P.B. Shapley value-based payment calculation for energy exchange between micro- and utility grids. Games 2017, 8, 45. [Google Scholar] [CrossRef]
- Chis, A.; Koivunen, V. Coalitional game-based cost optimization of energy portfolio in smart grid communities. IEEE Trans. Smart Grid 2019, 10, 1960–1970. [Google Scholar] [CrossRef]
- REScoop 20-20-20 Consortium. REScoop Best Practices Report I. 2013. Available online: https://www.rescoop.eu/toolbox/best-practices-report-part-1-and-2 (accessed on 18 November 2020).
- Moncecchi, M.; Falabretti, D.; Merlo, M. Regional energy planning based on distribution grid hosting capacity. AIMS Energy 2019, 7, 264–284. [Google Scholar] [CrossRef]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).