Abstract
The paper addresses path planning and path-following problems in an unknown complex environment for an underactuated autonomous underwater vehicle (AUV). The AUV is required to follow a given reference path represented as a sequence of smoothly joined lines and arcs, bypassing obstacles encountered on the path. A two-level control system is proposed with an upper level for event-driven path planning and a lower level for path-following. A discrete event system is designed to identify situations that require planning a new path. An improved waypoint guidance algorithm and a Dubins curves based algorithm are proposed to build paths that allow the AUV to avoid collision with obstacles and to return to the reference path respectively. Both algorithms generate paths that meet the minimum turning radius constraint. A robust parameter-varying controller is designed using sublinear vector Lyapunov functions to solve the path-following problem. The performance of the developed event-based control system is demonstrated in three different simulation scenarios: with a sharp-edged obstacle, with a U-shaped obstacle, and with densely scattered obstacles. The proposed scheme does not require significant computing resources and allows for easy implementation on board.
1. Introduction
The rapid development of unmanned technologies in recent decades has resulted in significant growth in commercial, environmental, and military underwater applications [1]. Most underwater operations, especially those that involve risk to humans, are supported by autonomous underwater vehicles (AUV). Enhancing the autonomy and reliability of AUVs and expanding their range of applications is not possible without efficiently solving two underlying problems: path planning and path-following.
Path planning is a challenging problem has attracted the considerable attention of specialists in robotics. Insight into state of the art in path-planning methods for AUVs can be obtained from recent survey papers [1,2,3]. Path planning can be divided [4,5] into static and dynamic planning. Static planning is usually done offline and ensures the construction of an optimal global path in a known environment (see, for example, [6,7]). On the contrary, dynamic planning is aimed at building a safe path online based on local information about the environment, which is usually considered to be unknown or partially known.
The emphasis in the contemporary studies on dynamic (local) path planning is made on developing effective algorithms with low computational costs that are applicable for real-time implementation. Real-time path planning can be achieved while using artificial potential field method [8], rapidly-exploring random trees [9,10], Voronoi diagrams [11], bioinspired meta-heuristics [12], method based on interfered fluid dynamical system [13], and waypoint guidance method [4,14,15]. Additionally, AI-based optimization algorithms are actively applied to path-planning of AUVs in an unknown environment. Among them are particle swarm optimization (PSO) algorithm [5,16,17], ant colony algorithm [18], and differential evolution algorithm [19]. Many approaches are combined in order to provide the best solution. For example, in [4], PSO determines the best direction to avoid obstacles, and the waypoint guidance algorithm generates a sequence of points that provide a way around the obstacle in the selected direction.
Almost all of the mentioned methods indirectly or directly use iterative procedures in order to obtain a locally optimal path. However, when dealing with an unknown environment, extensive optimization requiring significant computing resources is meaningless in many cases, since the resulting local path may not be optimal in the global sense. It should be noted that optimization-based methods do not always guarantee obtaining a near-optimal solution in a reasonable time. Thus, approaches that generate feasible paths in a short time are still in demand.
It is known that AUVs operate in fairly harsh underwater environments and they are designed to be underactuated to reduce their costs. All of this imposes additional requirements to path planning algorithms; the planner must produce paths that meet the kinematic and dynamic constraints of the vehicle. In order not to take the AUV model explicitly into account when planning the path, kinematic constraints are often set by the minimum turning radius [4,5,14,16]. In this case, the obtained path, which usually consists of straight lines and circular arcs, is only first-order differentiable or smooth. The degree of smoothness of the path can be increased with the help of splines [12], but their use makes the planning process more complicated due to the need to meet the geometrical constraints of obstacles. Another common approach for satisfying kinematic constraints consists in building a path of minimum curvature via solving a nonlinear programming problem [20].
The path planning problem can be considered in three different contexts, depending on the global goal pursued by the AUV. The variety of possible goals includes achieving a target point, navigating through a sequence of waypoints, and following a predefined reference path, in particular a path that connects waypoints by line and arc segments. Most of the studies mentioned above focus on path-planning within the first setting. Despite the great applied value, the path planning problem in which the AUV has to pass through a bunch of waypoints in a given order is practically not investigated. In this context, we can only refer to paper [21]. The main difficulties in handling multiple waypoints arise when some of them are located on obstacles. In this case, an additional mechanism for managing the activity of waypoints are required. The need for the AUV to follow the desired path makes the problem more complicated, since it is necessary to provide the return of the AUV to the reference path after completing obstacle avoidance manoeuvres.
Once a path is generated, one needs to make the AUV follow the path accurately, when considiering its dynamic model, control constraints, and kinematics. A wide diversity of methods have been developed in order to solve the path-following problem, among which are backstepping method [22,23,24], observer-based method [25], nonlinear PID control [26], adaptive control [27], model predictive control [21,28], sliding mode control [5,29], and fuzzy control [30]. In the context of the simultaneous solution of path-planning and path-following problems, we note the studies presented in [5,20,21,31]. The majority of these studies are aimed at combating uncertainties, disturbances, and control constraints. However, in addition to taking into account these negative factors, a path-following controller should allow for its simple implementation in the on-board control system, which is usually designed as a digital one, and for the fast calculation of control signals. Tuning control parameters in path-following controllers to ensure desired or optimal tracking performance is an important step in designing path-following controllers.
The contributions of this paper are as follows. We propose a new formulation of the path planning problem, in which the AUV’s primary goal is to sail along a given path passing through a sequence of waypoints. To the best of the authors’ knowledge, such a path planning formulation has not been considered before. To solve the problem, we develop an event-based framework that includes two levels: the upper one for real-time path planning and the lower one for path-following. A discrete-event system, which is a basis of the upper level, is designed in order to detect situations that require building a new path and changing the active waypoint. Two path-planning algorithms are proposed. The first one, based on refined data from forward-looking sonar (FLS), plans a path that ensures safe obstacle avoidance, and the second one generates a path that returns the AUV to the reference path. Paths that are built by these algorithms meet the minimum turning radius constraint. A robust path-following controller is designed using the gain scheduling control methodology and sublinear vector Lyapunov functions. When synthesizing the controller gains, in contrast to most known studies, we aim to minimize the AUV’s positioning errors on the path and take into account the control saturation, measurement errors, and variability of the path curvature. The designed controller can be easily implemented in digital control platforms, which are traditional for AUVs.
The remainder of this paper is organized, as follows. The problem statement is presented in Section 2. The main results of the work are presented in Section 3. In particular, Section 3.1 presents the architecture of the overall control system. The path-following controller design is discussed in Section 3.2. Section 3.3 presents an event-based approach for path-planning in an unknown environment, including path planning algorithms and a discrete event system in order to determine the moments to run them. In Section 4, the simulation results are provided in order to illustrate the performance of the proposed approach. Finally, Section 5 discusses the obtained results.
2. Problem Formulation
2.1. AUV Model
A wide variety of underwater applications require the AUV to operate at a constant depth. Following [23], we consider an underactuated AUV with two identical back thrusters mounted symmetrically with respect to its longitudinal axis in order to steer the AUV in the horizontal plane. Using the common and differential modes, the thrusters can generate a force along the AUV’s longitudinal axis and a torque about its yaw axis, respectively.
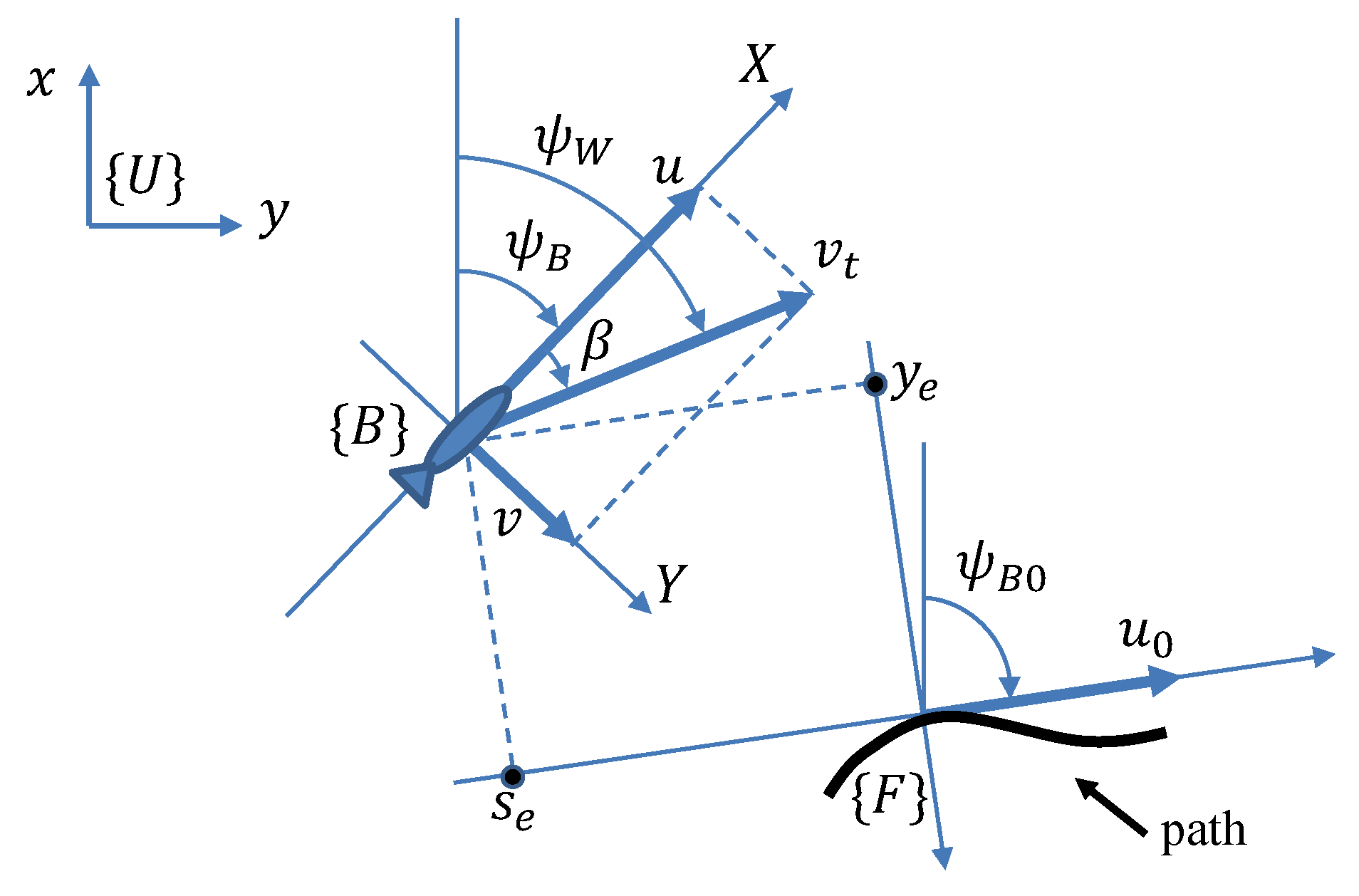
According to [23], the dynamics of such an AUV in 3DOF can be described while using a global coordinate frame and a body-fixed coordinate frame (see Figure 1) by three kinematic equations
and three dynamic equations (for surge, sway and yaw)
where are the global coordinates of the AUV, denotes the yaw angle, u and v are, respectively, the surge and sway speeds expressed in , r is the yaw rate;
m is the nominal mass of the AUV, is its moment of inertia around Z-axis (as adopted in marine navigation, Z-axis or the yaw axis of the AUV is directed towards the bottom), , , are the classical hydrodynamic derivatives that define added mass forces and moments as well as hydrodynamic damping. The interested reader is referred to [32,33] for complete details.
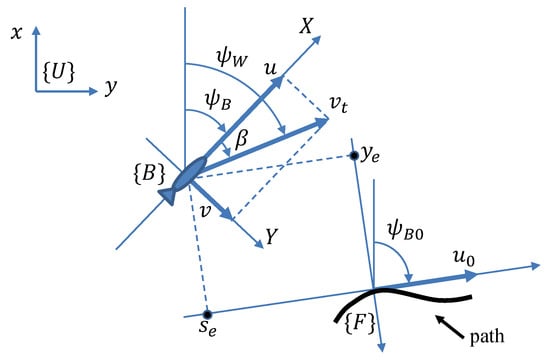
Figure 1.
Reference frames.
We use the following assumptions and physical constraints on the dynamics of the AUV to solve the problem under study.
- The model considered in the paper corresponds to the INFANTE AUV [33], which is a large-sized vehicle with a length of 4.22 m and a mass of 2234.5 kg.
- The motion in roll, pitch, and heave is ignored in the model.
- No waves, currents, or other disturbances are taken into account.
- The AUV is fully submerged in water and away from the surface and seabed, which allows us to consider the hydrodynamic derivatives constant.
- The back thrusters can generate force and torque constrained by and , respectively.
- The desired surge speed of the AUV is constant: u = 1 m/s.
Assuming that u is always nonzero, we define side-slip angle and a reference frame , which is obtained by rotating around the yaw axis through angle . Subsequently, the kinematic Equation (1) can be rewritten as
where , is the absolute value of the total velocity vector . Straightforward calculations give the equation for , as
2.2. Relative Dynamics
In order to solve the path-following problem, we use the virtual target-based method [23]. In this method, the virtual target (VT) as a point moves along a given path, and the AUV must pursue it, trying to match its position with the position of the VT.
Denote the course angle of the VT by , its forward and angular speeds by and , respectively. Define the coordinates of the AUV in a Serret–Frenet reference frame that is associated with the VT (see Figure 1), as
are the coordinates of the VT in the reference frame . As shown in [23], the error dynamics of the AUV in can be described by
where .
2.3. Sonar Model
We assume that the AUV is equipped with a multi-beam forward looking sonar (FLS) installed onboard the AUV in the XOY plane in order to detect obstacles in the heading direction. The data produced by the FLS can be presented as a set of pairs , where is the signed angle counted from the AUV’s heading direction to the beam direction, is the distance to an obstacle in the beam direction, , is the number of beams. Here and further, a signed angle is assumed to be positive if it is counted clockwise (when viewed from above), and negative in the other case. If no obstacles are detected in the direction i or is greater than the detection range then . For certainty, we take for the left beams (beams that are on the left from the AUV’s heading direction) and for the right beams. For further purposes, define the following subsets of beams: , , , . They indicate the presence of obstacles on the left, right, and ahead of the AUV. Based on the FLS data, one can form a situational (local) model of underwater environment as a sequence of 2D points .
2.4. Path Representation
Throughout the paper, a path is represented as a sequence of line and arc segments as
where , are the start and end points of the segment, is the radius of the segment connecting these points (for line segments ), and is the number of segments. We assume that corresponds to the left turn and to the right one. It is natural to require that every two adjacent segments of a path are mutually agreed to be smooth. Moreover, all paths, it does not matter whether they are predefined or constructed using path-planning algorithms, should satisfy the kinematic constraints that are given by the minimum turning radius , .
2.5. Problem Formulation
The problem that is addressed in the paper consists in designing a control scheme that allows for the AUV governed by Equations (1) and (2) to follow a given reference path , bypassing encountered obstacles detected by FLS.
The designed system must meet the following requirements.
- The path-following controller (control laws for and ) should be designed in such a way that the virtual target tracking errors satisfywhere , , , and are positive constants that characterize the tracking accuracy.
- The paths generated by path-planning algorithms for detouring obstacles and returning to the reference path should be at least first-order differentiable ( continuous), lie no closer than safe distance from obstacles, and satisfy kinematic constraints that are given by minimum turning radius .
- Whenever possible, the AUV must follow the reference path , which means that after leaving to detour an obstacle or a group of obstacles the AUV must return, if possible, to at the point closest to the leaving point.
- The system must be efficient for various environments, regardless of the number and location of obstacles.
Note that most path planning studies focus on generating a safe path that leads the AUV to a static target point. In contrast, we consider a setting where the AUV should, as far as possible, follow a given reference path that passes through a sequence of waypoints. This requirement entails the need to change the active segment of the reference path carefully. We assume that the reference path, which is constructed by a global planner [6,7] or received from the operator, does not change during the mission. Focusing on the path planning problem, we believe, for simplicity, that the desired speed of the AUV while travelling along the path is constant and chosen in such a way that the AUV can follow it accurately.
3. Two-Level Control System
3.1. Control System Architecture
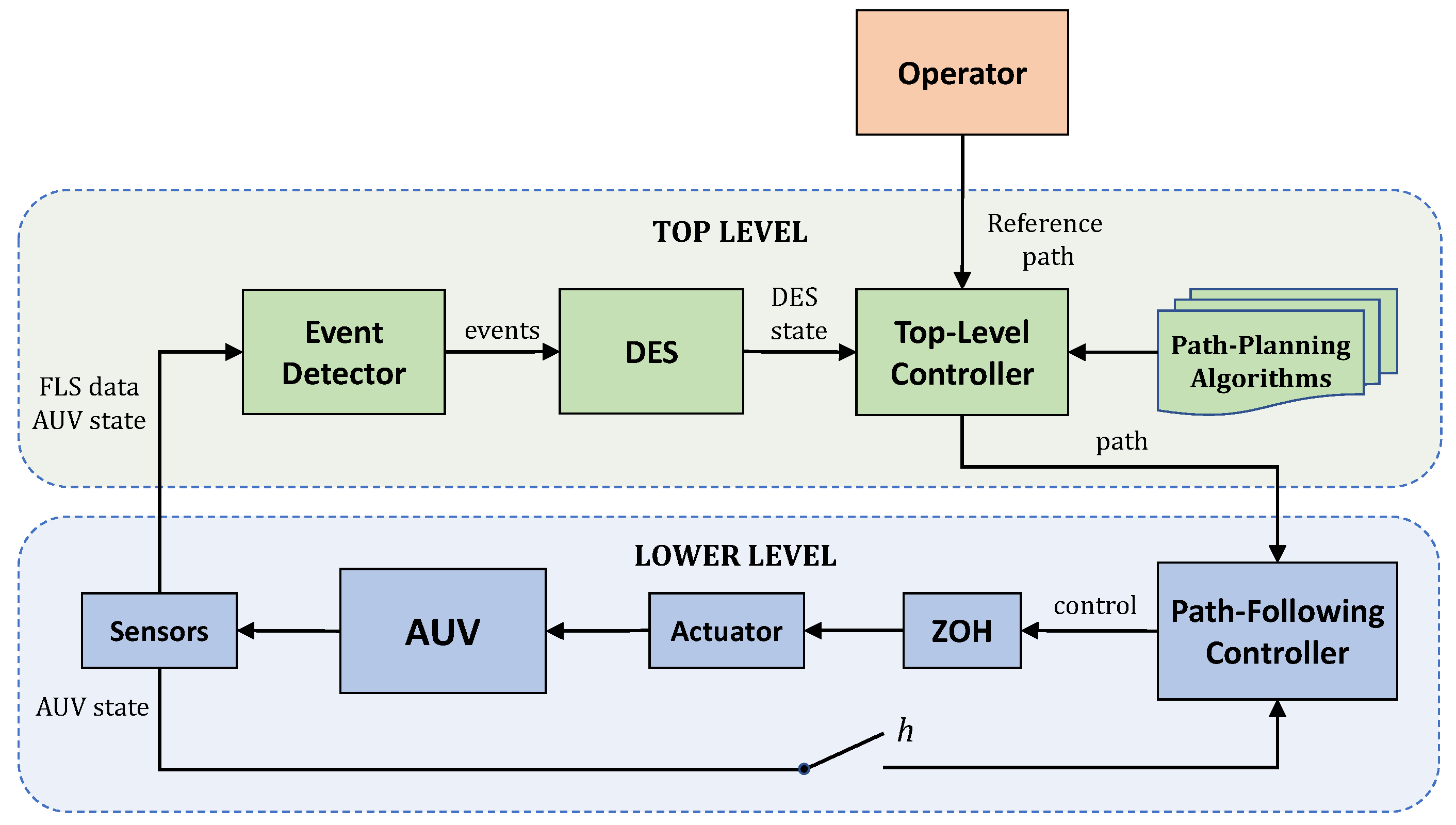
A two-level control system (see Figure 2) is developed in order to provide the AUV with both the path-planning and path-following capabilities. The path-following controller at the lower level is designed to drive the AUV along the path that is generated by the top level. In order to be closer to practice, the controller is implemented as a digital one with a sample time h.
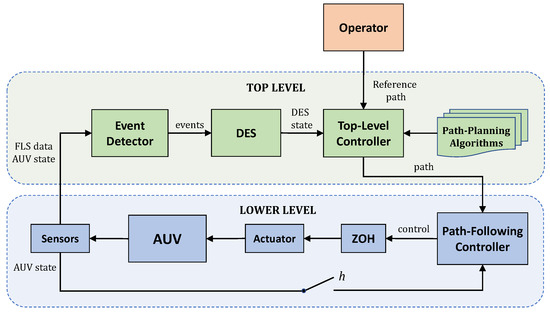
Figure 2.
Control system architecture.
The main component of the top level is a discrete-event system (DES). We consider a class of logical discrete-event systems that can be modelled by finite state machines. Based on the detected events, the DES changes its state, thus starting a sequence of actions performed by the top-level controller to build a new path. Therefore, the main goal of the DES is to identify situations that require updating the current path. For each monitored event, we assign a time interval at which the event-triggering condition is checked. In order to reduce the load on the on-board computer, this interval for most events is assigned to be much larger than h. For simplicity of implementation, we will assume that this interval is the same for all events and equals .
In general, the path-planning process includes the following steps:
- detect events by processing data from FLS and other sensors;
- change the DES state; and,
- perform a suitable sequence of actions to rebuild the current path or change the active segment of the reference path.
Path-planning algorithms proposed in the paper can generate two types of paths: to avoid obstacles and return to the reference path.
3.2. Path-Following Controller
The path-following control laws for tracking the VT’s motion is designed, as follows (cf. [34]):
where , are the feedforward control terms aimed to cancel disturbances and to track the VT’s heading direction; , are the feedback control terms that were calculated on the basis of discrete measurements of variables , , , and to stabilize the AUV’s position along the path, , are the control resources in force and torque aimed at stabilization; and, is the saturation function. The acceleration is evaluated using the direct measurement of u, v and their derivatives [23].
In order to reduce the negative effect of discontinuity of on the performance of the closed-loop system, we use discrete observers for variables and , defined as
The parameter-varying feedback controllers are built using the gain-scheduling methodology [35]. The feedback gains are scheduled as functions of the VT’s angular speed , as
where are operation regions that form an operation envelope, is the number of regions. As the speed is assumed to be constant and there is a constraint on the turning radius, we have ; therefore, we can take and when obtaining operation regions .
In order to synthesize feedback gains for each operation region , we transform the closed-loop system given by (4) and (6)–(8) to a sampled-data representation with uncertainties and then apply control design algorithms that are based on the sublinear vector Lyapunov functions [36,37] to determine feedback gains. The synthesis objective is to minimize the weighted sum of estimates of steady-state tracking errors , , and . When designing gains, we took measurement errors, control saturation, and the size of operation regions into account. The design steps are described in detail in [34], where a cooperative path-following controller for multiple AUV is synthesized. Section 4 provides feedback gains determined for the path-following controller considered in the paper.
3.3. Event-Based Path-Planning
3.3.1. Discrete-Event System
A discrete-event system (DES) is designed in this section in order to identify situations when a new path needs to be built. Before describing the designed DES, we will introduce some definitions and notations.
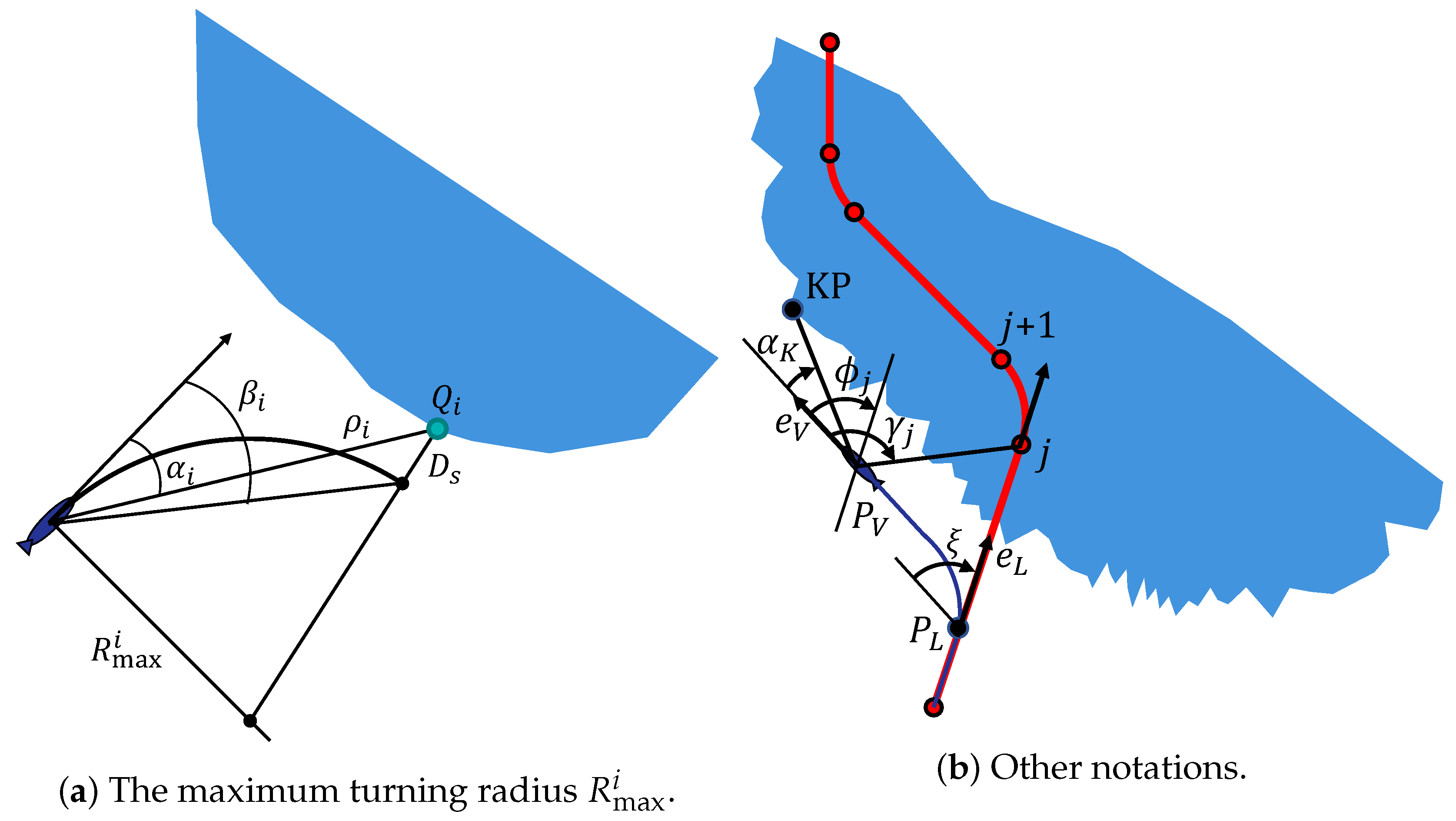
For each obstacle point , , define the maximum turning radius , which allows for the AUV to bypass the point at a safe distance (see Figure 3a). It can be calculated (cf. [14]) as
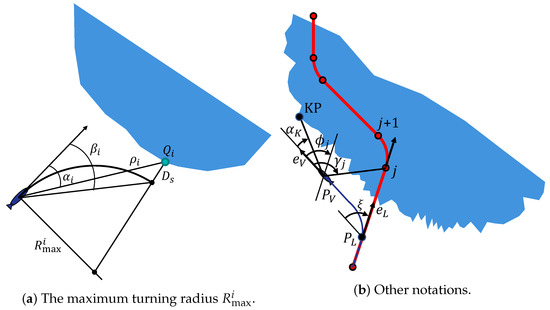
Figure 3.
Introduced notations.
Note that, when evaluating the proximity of the AUV to obstacles, the maximum radius is preferable to the distance , since using ensures safe bypassing of an obstacle point, when considering the turning radius constraint .
Define , , is a logical condition that narrows the set . For example, set contains all for which . Define also
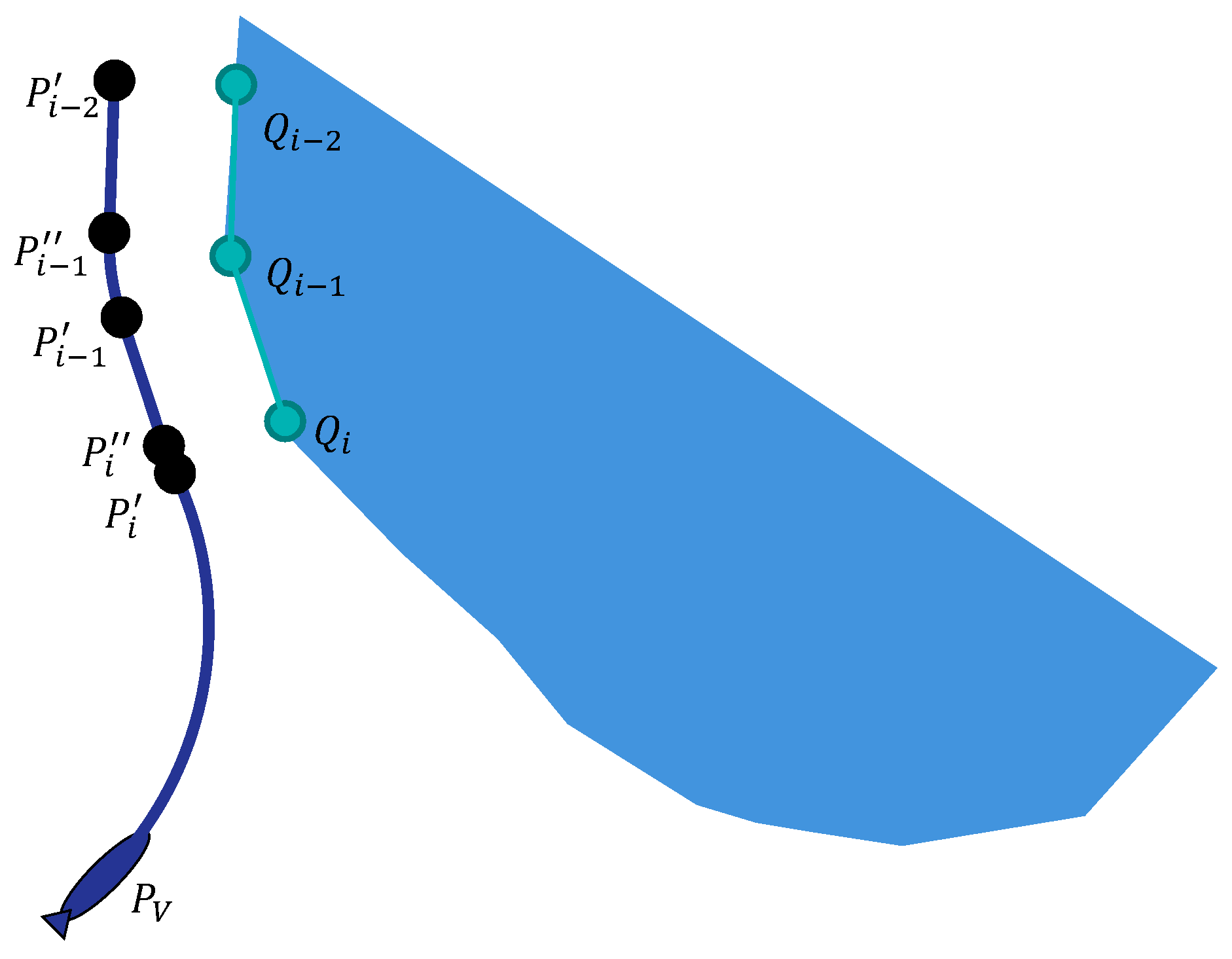
Denote the current position of the AUV by , its orientation vector by , the angle measured from the AUV forward direction to the location of waypoint j (the waypoint bearing angle) by , the angle between the forward direction and the direction of the reference path at waypoint j by , and the distance to the reference path in the travel direction by . When leaving the reference path to avoid an obstacle, the AUV saves the leaving time and its orientation vector , and then monitors the change in angle measured from vector to vector . Denote, by (), the time when angle changes its sign from minus to plus (plus to minus). If no change occurs, then the corresponding time is assumed to be equal to . The last point processed by the path-planning algorithm described in Section 3.3.2, we will call the key point (KP). Denote, by , the bearing angle to the KP. Let be the active segment (or the active waypoint) of the reference path. The most relevant notations are explained in Figure 3a,b.
We employ a class of discrete-event systems modeled by a finite automaton (FA) [38]. A FA is represented by the tuple
where X is the finite set of states, is the finite set of events, is the transition function, is the initial state, and is the set of marked states.
For the designed DES, set X consists of states that are given in Table 1, , . For the sake of simplification, we assume that the events of the set consist of atomic events that are presented in Table 2. In this table, in addition to the previously introduced entries, we use the following abbreviations: WP for the waypoint and RP for the reference path. A composite event is triggered when all of its atomic events , is triggered simultaneously. Table 3 summarizes the transition rules implementing the function f.

Table 1.
States of the discrete-event system (DES).

Table 2.
Events of the DES.

Table 3.
Transition rules of the DES.
The AUV behavior strategy that is provided by the DES can be expressed, as follows.
- Try not to get to a place where it is impossible to get out using standard obstacle avoidance algorithms.
- Do not change once chosen obstacle avoidance direction until the AUV returns to the reference path (left or right-hand rule).
- Rebuild the path only if it is vital.
In the DES states that are associated with obstacle avoidance (mDOL, mSOR, mDOR, and mSOL), monitoring atomic events eRRPL and eRRPR (see Table 3) prevents the AUV from prematurely returning to the reference path, which may happen when the obstacle has a U-shape.
Changing the state of the DES entails the execution of a sequence of actions, which can be regarded as a program that consists of a sequence of self-contained functions. As a result of these actions, a new path is built and/or the active segment is changed.
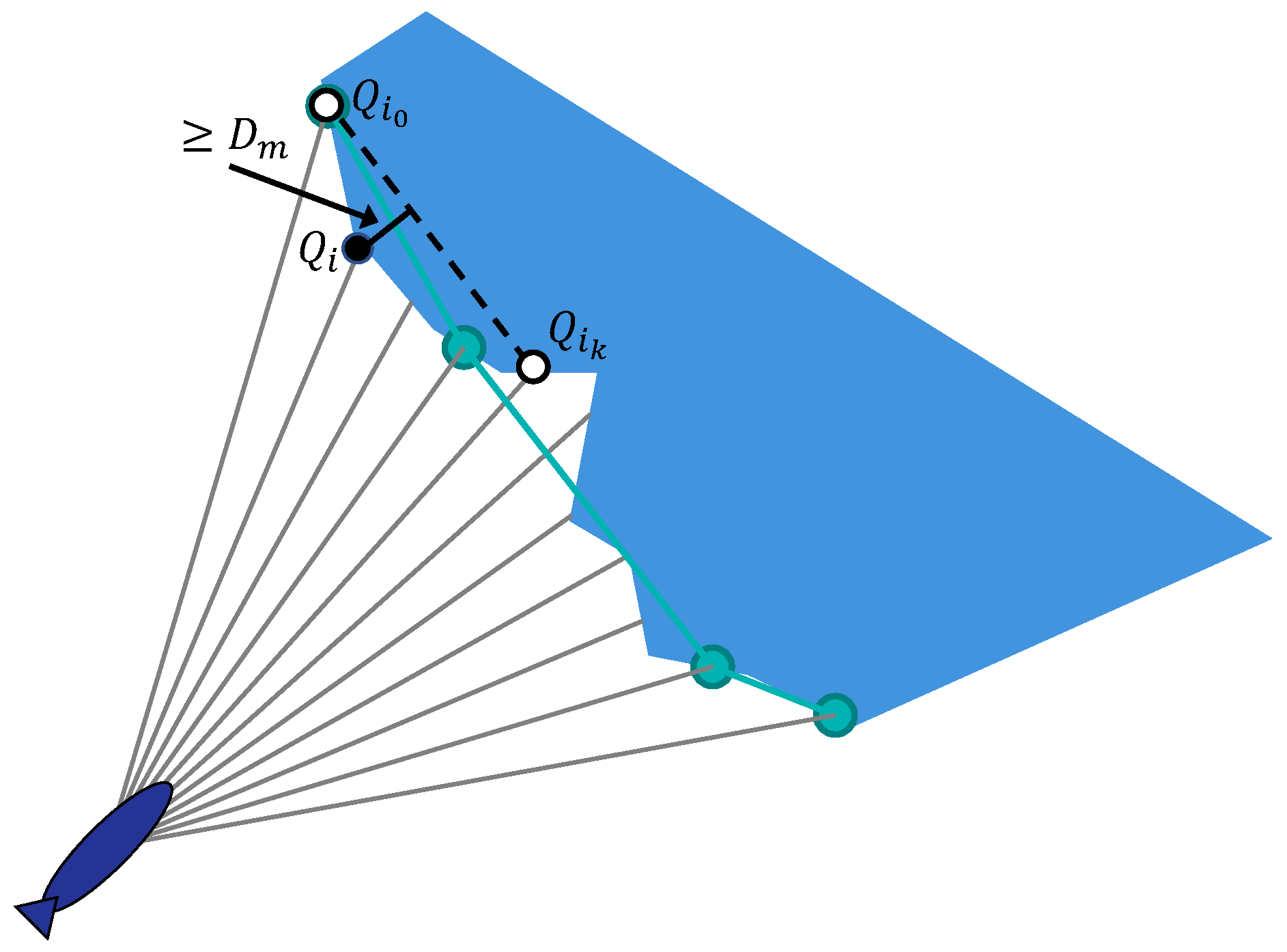
Function = SelectObstacleLeftP generates an obstacle from a set of points that are produced by FLS by adding all points from that meet two conditions:
provided that or the point also meets these conditions. The order in which the points are added to is preserved. Similarly, the function = SelectObstacleLeftP is defined, with the only difference that the added points should satisfy
Unlike function SelectObstacleLeftP, which forms an obstacle by starting from the point i and including this point in the output sequence, function = SelectObstacleLeftP determines the obstacle to detour it from its left side. The function chooses from all of the obstacles identified based on FLS data the one for which the direction to its leftmost point deviates least from the heading direction of the AUV. When identifying a set of obstacles, two adjacent points and of are considered to belong to the same obstacle if they satisfy.
Similarly, function SelectObstacleRight selects an obstacle for detouring it from its right side.
Function InitVTState initializes the state of the VT after performing a bypass manoeuvre and returning to the reference path. The VT state includes the segment on which the VT is located as well as its curvilinear coordinate, forward speed, and acceleration.
Function = AvoidPath builds a path to detour a selected obstacle on the left () or on the right (). The path is planned in two steps. First, the convex outline of the obstacle is built while using the RCOA algorithm presented in Section 3.3.2, and then the obtained outline is used to construct an avoidance path by applying a path-planning algorithm that is presented in Section 3.3.3.
Finally, function [, ] = DubinsPath(, , , ) constructs a Dubins path that connects the AUV’s current position to the part of the path that begins with segment . The constructed path consists of three segments, each of which corresponds a left-turn arc (L), a right-turn arc (R), or a straight line (S). The function can build the following paths: LSL, LSR, RSL, or RSR. In Figure 7, one can find examples of RSL (red line) and RSR (blue line) paths. Arguments define the allowable motion primitives for the first and third segments of the path.
Function DubinsPath works, as follows. First, it tries to find the path to segment . If the attempt is unsuccessful, it takes the next segment and searches for the path to it. This action is sequentially repeated for all segments of the selected path fragment until a path is found. The function returns the found path and the index of the segment to which the path is built. A path-planning algorithm that builds a path to a segment is described in detail in Section 3.3.4.
Because it is not possible to implement continuous checking of event-triggering conditions, we cannot prevent situations when . When such situations happen, the AUV must activate a special emergency mode in which it slows down the forward speed and starts turning in one of two possible directions, which is selected based on the last state of the DES. For example, if the last state of the DES is mDOL, which corresponds to avoiding an obstacle on the left, the AUV should turn in the left direction. Once is valid for all i, the AUV returns to the last normal operating mode with planning a new path if necessary. The emergency mode is not desirable, and the AUV should avoid it. The use of this mode can be restricted and, in many cases, eliminated, by temporarily relaxing the requirements for safe distance when planning a path to bypass an obstacle, or increasing the frequency of checking the triggering condition for composite events requiring the calculation of , or increasing the value of parameter included in some event-triggering conditions. The AUV should act in a similar way when it is too close to an obstacle. In this article, we do not investigate the implementation of the emergency mode and apply the above mechanisms to exclude its use.
3.3.2. Robust Convex Outline Algorithm
For efficient path-planning, we propose a simple algorithm that transforms a sequence of obstacle points that are produced by the FLS into another sequence of points that forms a convex outline of the obstacle. Usually, the sequence contains a relatively small number of points. The algorithm implies the following steps.
- Step 1:
- If sequence consists of less than 3 points, mark these points for further inclusion in the output sequence and go to Step 5.
- Step 2:
- Mark the start and end points of . Assign .
- Step 3:
- By going through the points, starting from point , find the first point that satisfies the following condition: there exists a point between and such that the shortest distance from it to the line passing through the points and is greater than a predetermined value and it lies on the same side of the line as the AUV (see Figure 4). If such a point does not exist, go to Step 5.
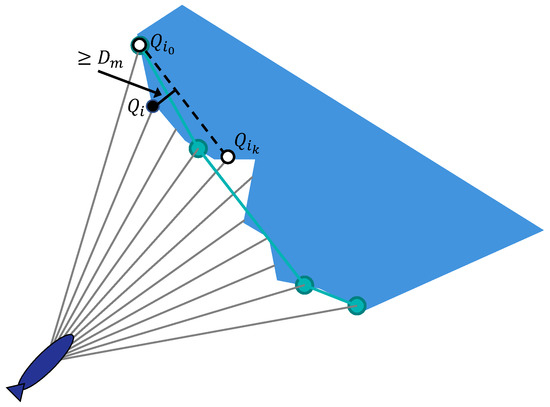 Figure 4. Building a convex obstacle outline.
Figure 4. Building a convex obstacle outline. - Step 4:
- Mark the point immediately preceding point . If is not the end point of , then and go to Step 3.
- Step 5:
- Form the sequence from all marked points of keeping the order.
Note that the proposed algorithm is robust in the sense that small measurement errors and the irregularity of the obstacle do not significantly increase the number of generated points. When using the resulting convex outline in the path-planning algorithm presented in the next section, the safe distance parameter should be increased by .
3.3.3. Path-Planning Algorithm for Detouring Obstacles
This section proposes a path-planning algorithm for detouring a single obstacle or a group of obstacles considered as a single one. Given a sequence of points that represents a convex outline of an obstacle, the algorithm finds a collision-free path , which consists of line and arc segments, which satisfies the turning radius constraint and passes no closer than the safe distance from the obstacle. We restrict ourselves to the case when the AUV detours the obstacle on the left side. Without a loss of generality, we assume that the last point of is the point with minimum , i.e., .
- Step 1:
- Take . Construct the arc segment of radius that connects the AUV’s current position with the point located at the distance (or after applying the RCOA algorithm) from the obstacle point (see Figure 5). Add this segment to the avoidance path .
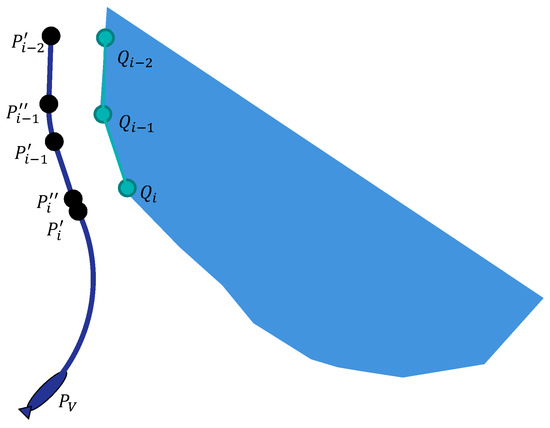 Figure 5. Building a path that detours obstacle from its left side.
Figure 5. Building a path that detours obstacle from its left side. - Step 2:
- Construct an arc segment that rotates the AUV around its vertical axis until its longitudinal axis is directed along vector that is drawn from point to point . The direction of the rotation is selected depending on the sign of the angle between vector and the tangent vector of the constructed segment at point . Add the constructed segment to the avoidance path .
- Step 3:
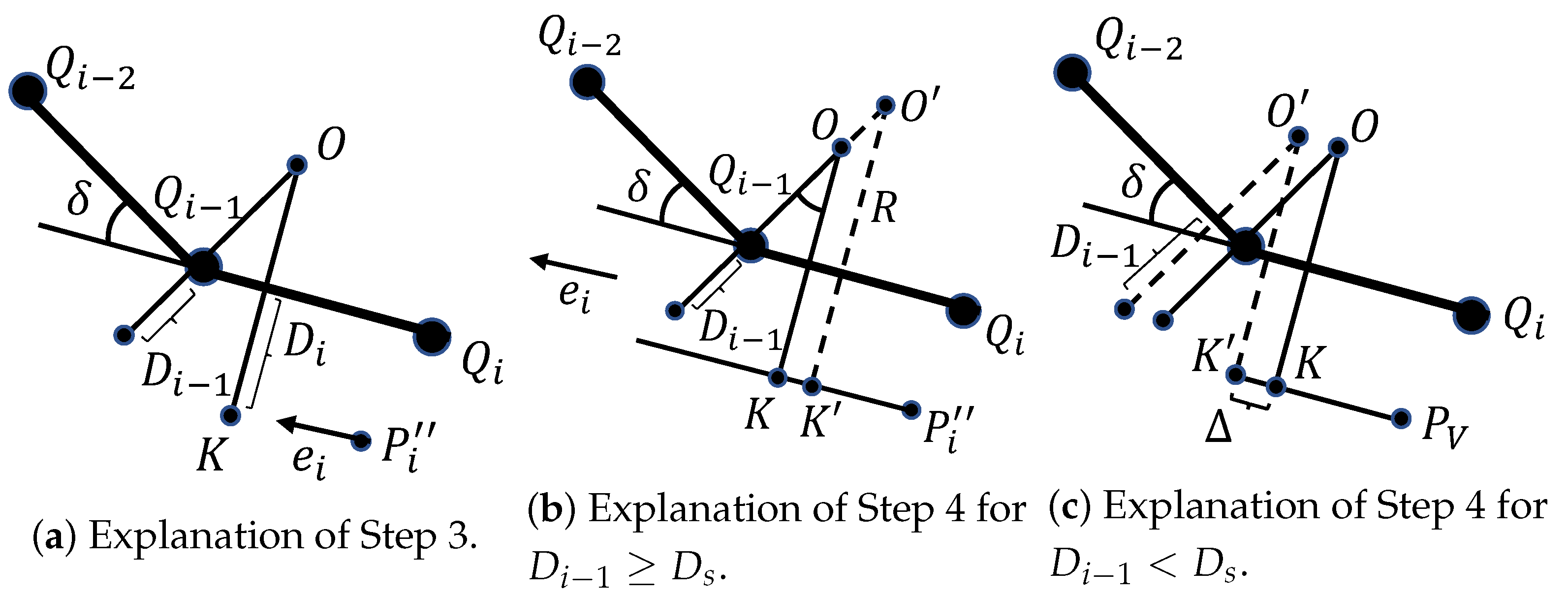
- Take and calculatewhere is the distance from point to line and is the angle between vectors and . The specified R and uniquely define the arc with center O and start point K that wraps around the point , as shown in Figure 6a.
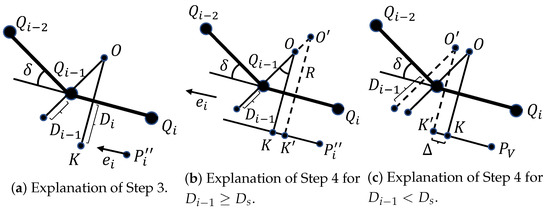 Figure 6. Building a path that wraps around a middle obstacle point.
Figure 6. Building a path that wraps around a middle obstacle point. - Step 4:
- Step 5:
- Construct a line segment with and an arc segment with center and radius R. Add both segments to path .
- Step 6:
- If (point is not the first in ) then and go to Step 3.
- Step 7:
- Supplement path with the line segment , which is parallel to vector , where is the point on a line passing through the point and parallel to the line , which is closest to the point .
3.3.4. Path-Planning Algorithm for Building a Path to a Given Segment
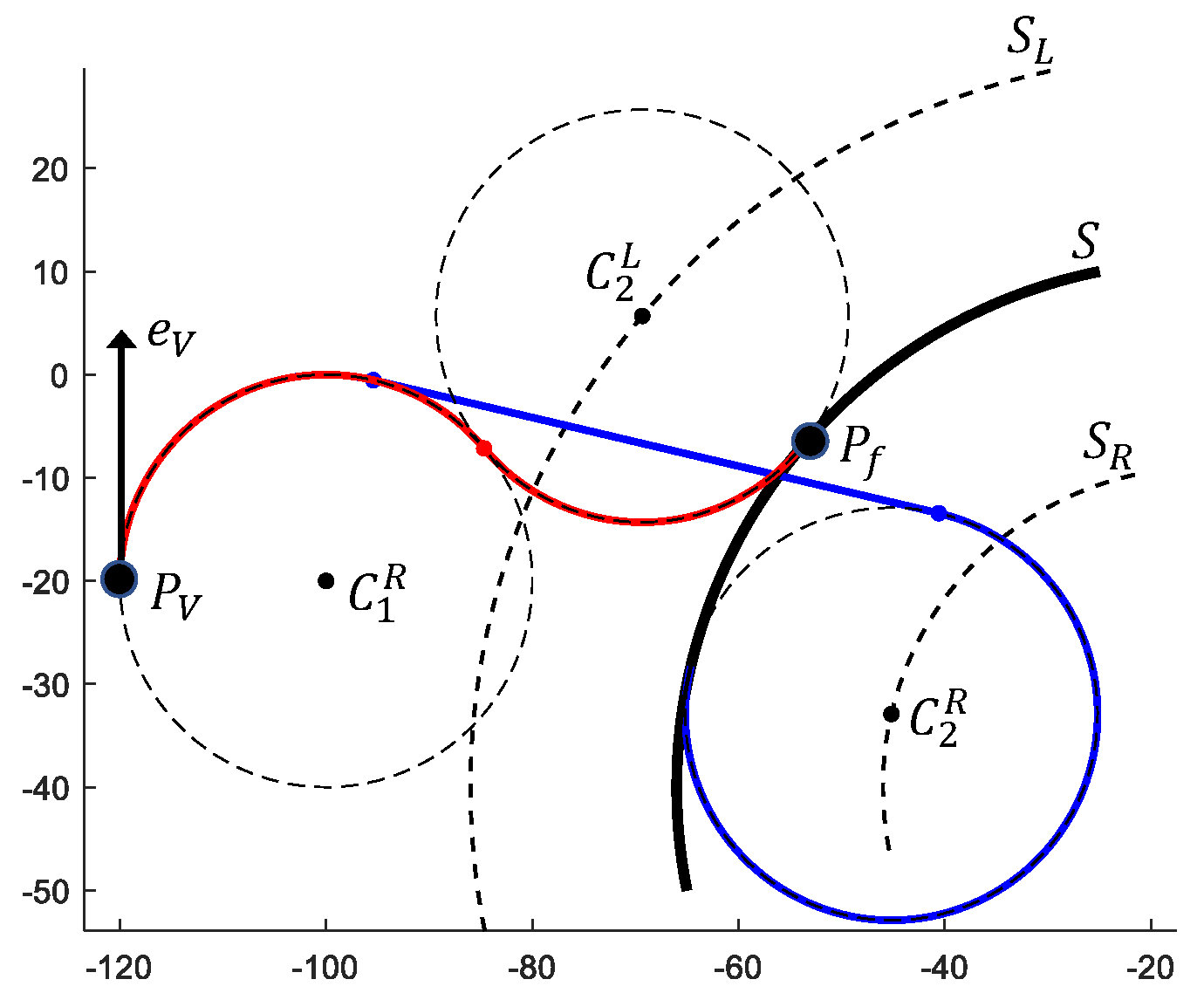
The path-planning algorithm that is proposed in this section generates a path that connects the current position of the AUV oriented along the vector with a segment S, thus solving the problem of returning the AUV to the reference path . It is based on Dubins curves [39]. The generic Dubins algorithms generate the shortest path that connects two points with a constraint on the curvature of the path. However, in our case, it is also necessary to determine the final path point, which is on a line or arc segment of , as well as to limit the set of allowable types for the path, specifying allowable motion primitives for the start and final segments of the path respectively. Here, as before, the symbol ‘L’ corresponds to a left-arc turn and the symbol ‘R’ to a right-arc turn. Note that there are algorithms that build a Dubins path to a circle [40,41], but they cannot be directly adapted for our purposes.
- Step 1:
- Set and .
- Step 2:
- For each start turning direction and final turning direction perform Steps 3–8.
- Step 3:
- Find the center of the arc S for start turning direction .
- Step 4:
- Shift segment S in direction by , resulting in a new segment .
- Step 5:
- Find a point on segment which is closest to point . If the distance between points and is greater than , then build a Dubins path of type that connects points and and go to step 8.
- Step 6:
- Find the point of intersection of the circle with the center and radius with the segment . If there are no such points, go to Step 2 and continue with the next .
- Step 7:
- Build a path of type connecting point with point , which is obtained by projecting point onto segment S.
- Step 8:
- If the path is successfully built () and the length of the path is less than L, then and .
The described algorithm is illustrated in Figure 7.
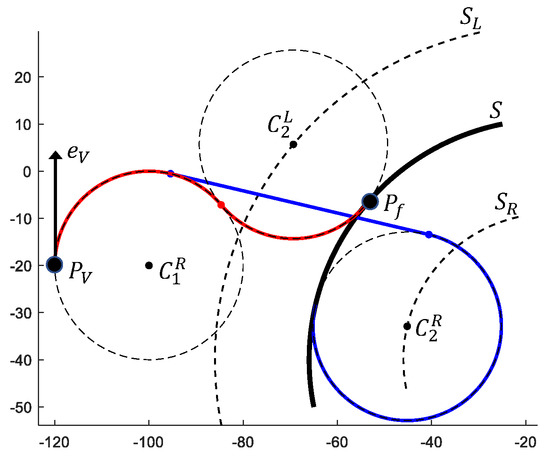
Figure 7.
An example of building a Dubins path that connects point with arc S. For this example, and . The red line indicates the shortest path.
4. Simulation Results
We conducted numerical simulations using three scenarios in order to validate the performance of the designed control system: with a sharp-edged obstacle, with a U-shaped obstacle, and with densely scattered obstacles. Scenario 1 aims to test the ability of the path planner to cope with obstacles having complex shapes. Scenario 2 demonstrates how the planner can drive the AUV out of a trap made by a U-shaped obstacle. The last scenario shows whether the algorithm is effective in a cluttered environment.
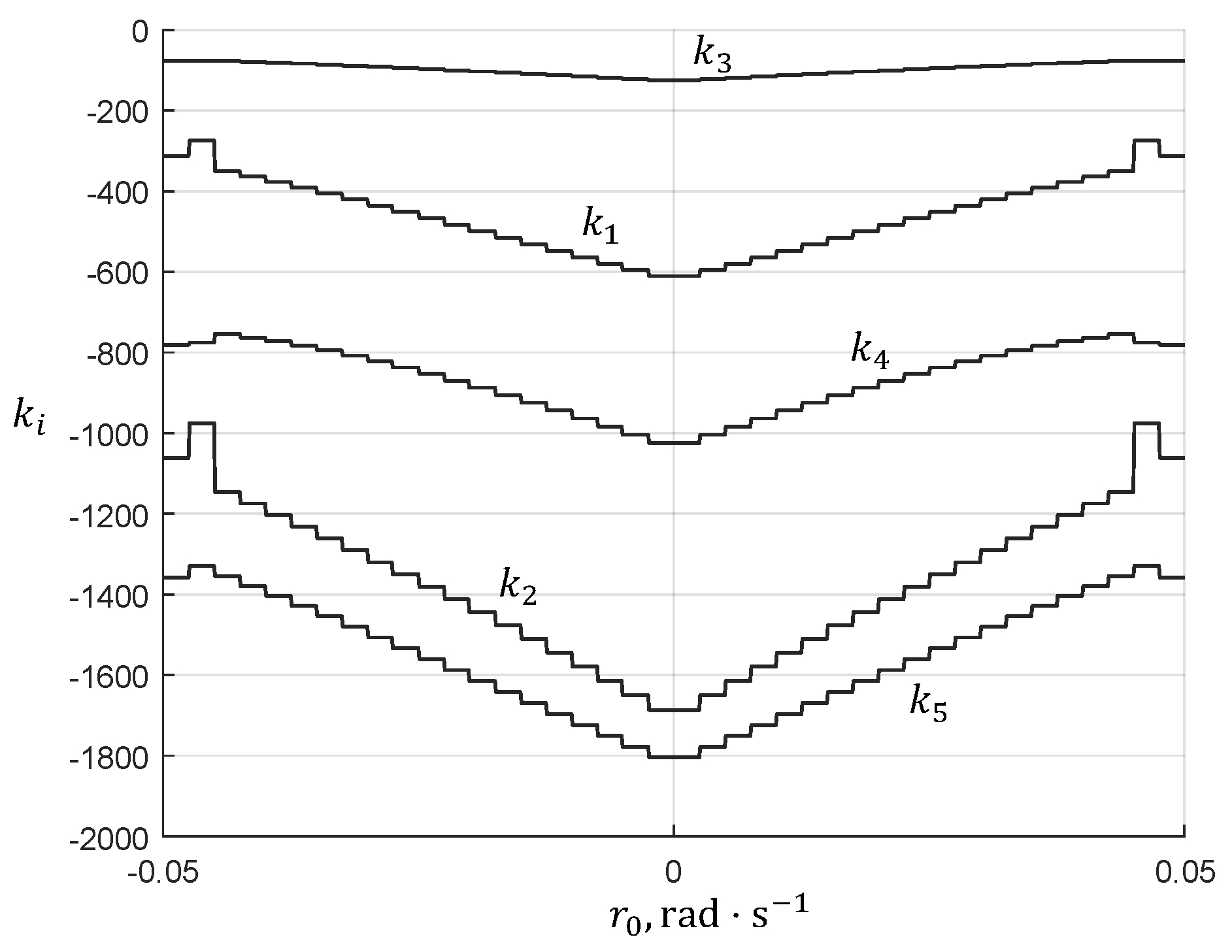
In the simulations, we adopted parameters of the model (1) and (2) that correspond to the INFANTE AUV [23]: the nominal mass and moment of inertia . The rest of the model parameters can be found in [23]. The path-following controller was designed with the following parameters: sampling time , control constraints and , and maximum path curvature . Figure 8 shows the feedback gains , of the path-following controller (7), (8) as functions of the VT’s angular speed .
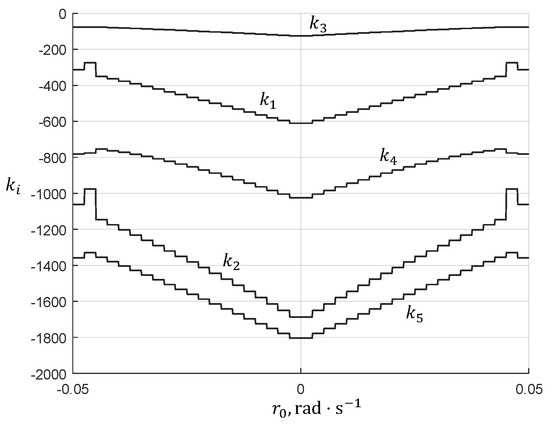
Figure 8.
Feedback coefficients () synthesized for the path-following controller (7) as functions of the VT’s angular speed .
Path-planning parameters are specified, as follows: m, m, m, m, m, m, m, m, m. Also, for the FLS we specify the number of beams , the detection range m, and the field of view . The triggering conditions for all events, excluding eEP (the VT has reached the end of the current path) and eES (the VT has reached the end of the current segment), which are monitored with period , are checked with interval .
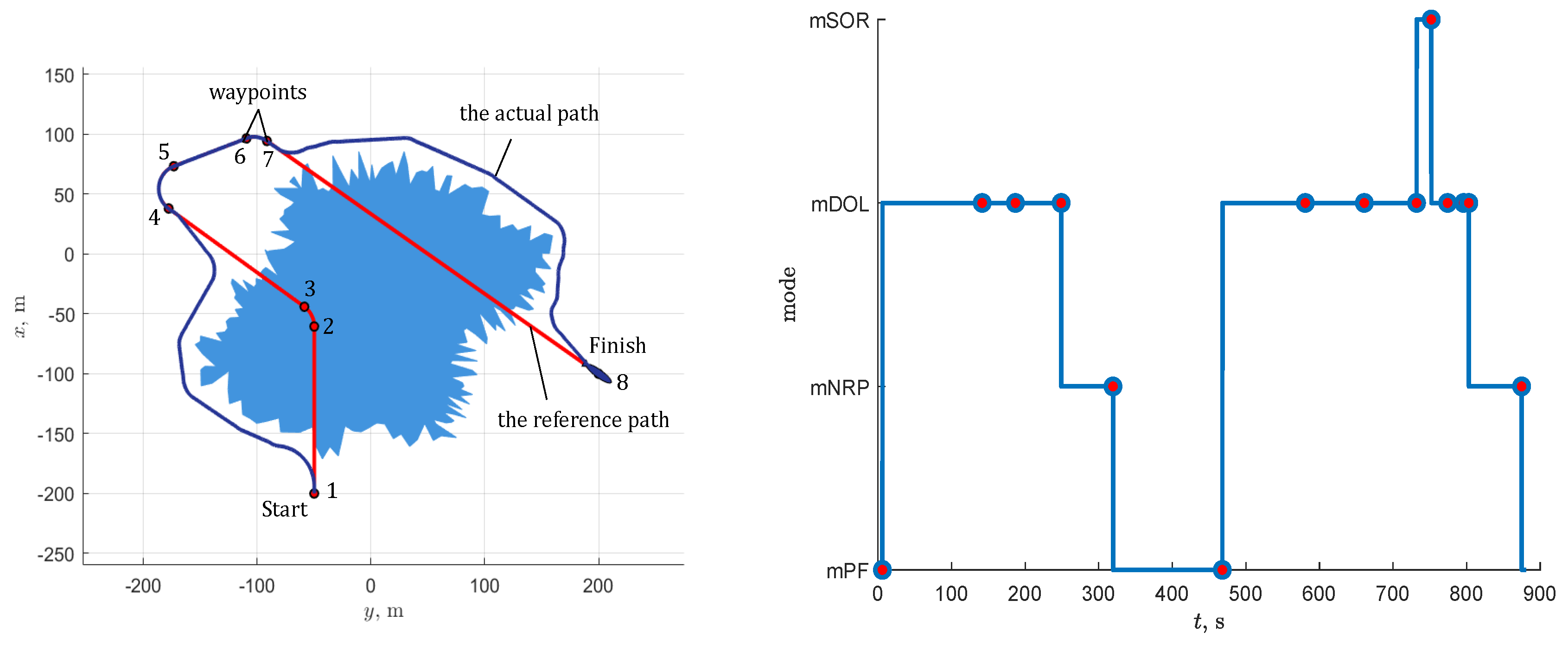
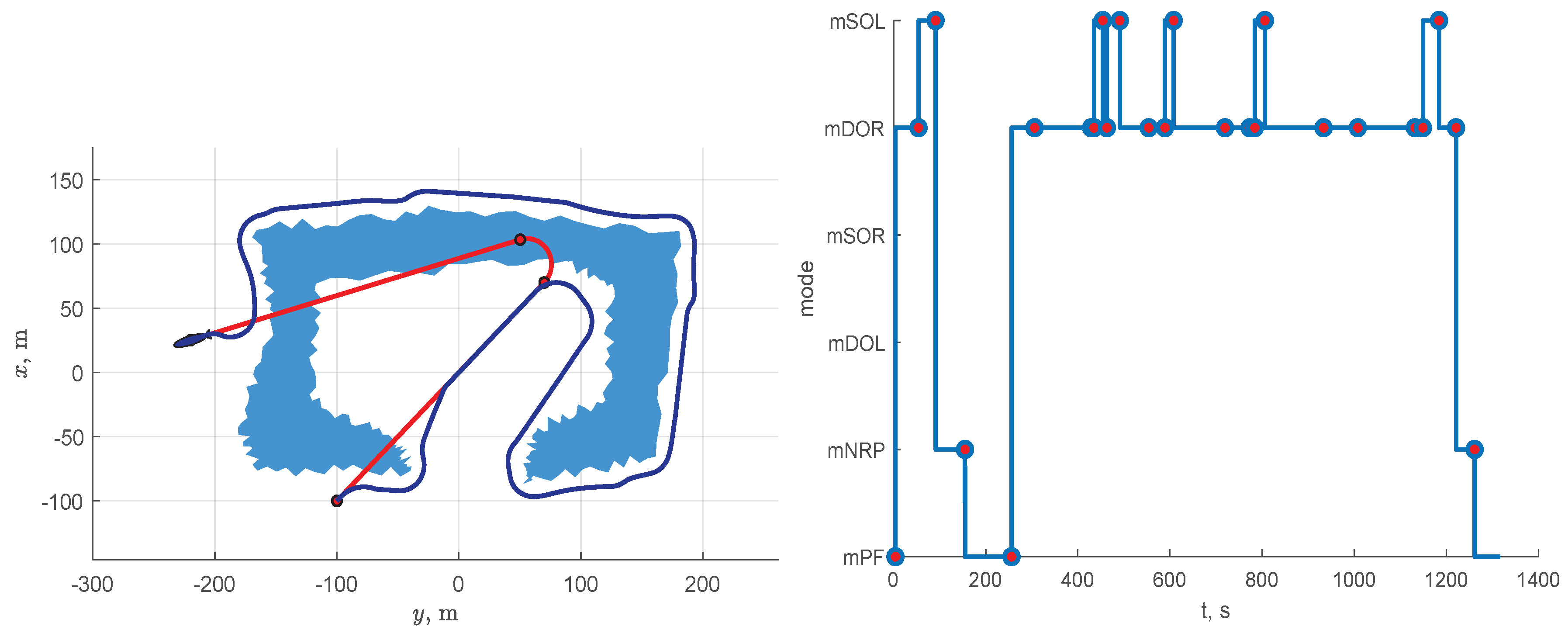
Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show the results of the simulation for Scenario 1. From Figure 1, we can conclude that the AUV successfully avoids collisions with the obstacle by keeping a safe distance from it. In this scenario, which lasts approximately 900 s, the AUV rarely corrects the path. The left-hand part of Figure 9 demonstrates that the designed DES changes its state only 14 times and, therefore, the path is corrected the same number of times. Between corrections, the upper control level only checks the event triggering conditions at an interval of 2 s. Obviously, the less the DES changes its state, the less the path is updated, and the less load on the on-board computing device.
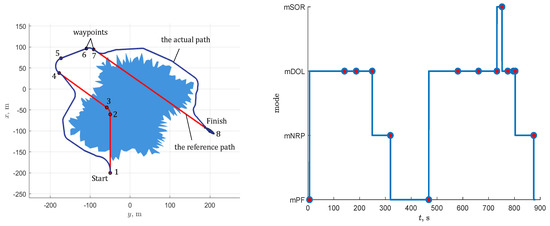
Figure 9.
Simulation results for Scenario 1: sharp-edged obstacle environment. On the left, the blue area corresponds to the obstacle on the plane, the red line represents the AUV’s reference path, and the blue line represents the actual trajectory obtained by the simulation; marks on the red line are points connecting two adjacent segments of the reference path. On the right, the blue line shows the change in the state of the designed discrete event system and red marks on the line indicate moments when a new path is generated.
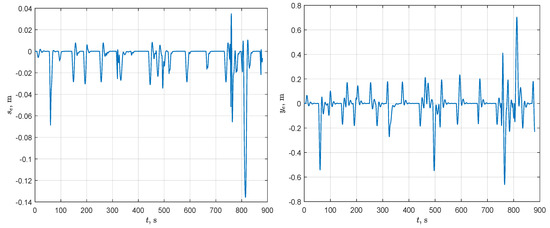
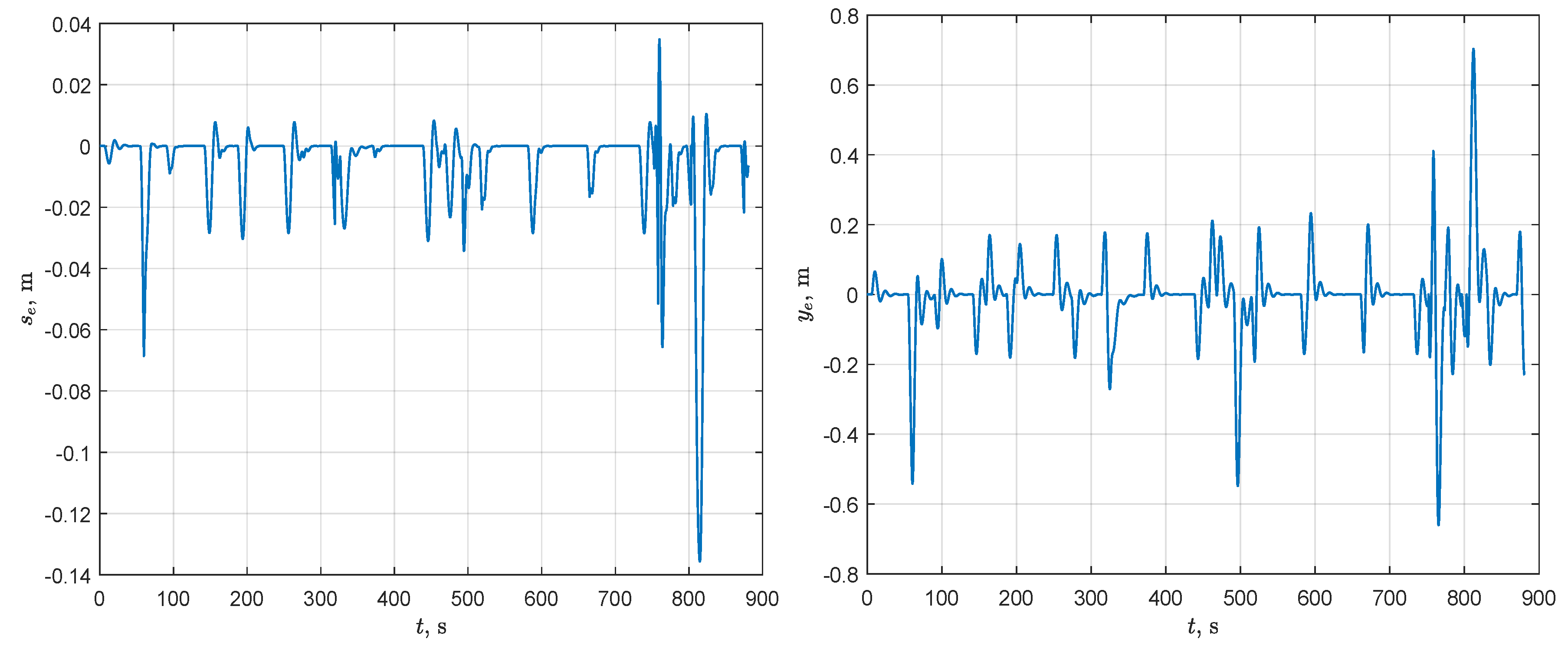
Figure 10.
Path-following errors for Scenario 1: along path error (left-hand part) and across path error (right-hand part).
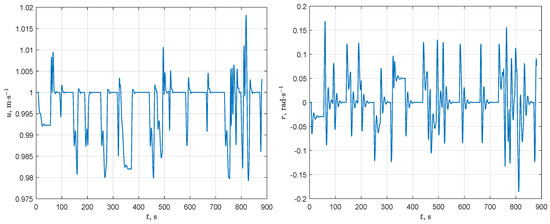
Figure 11.
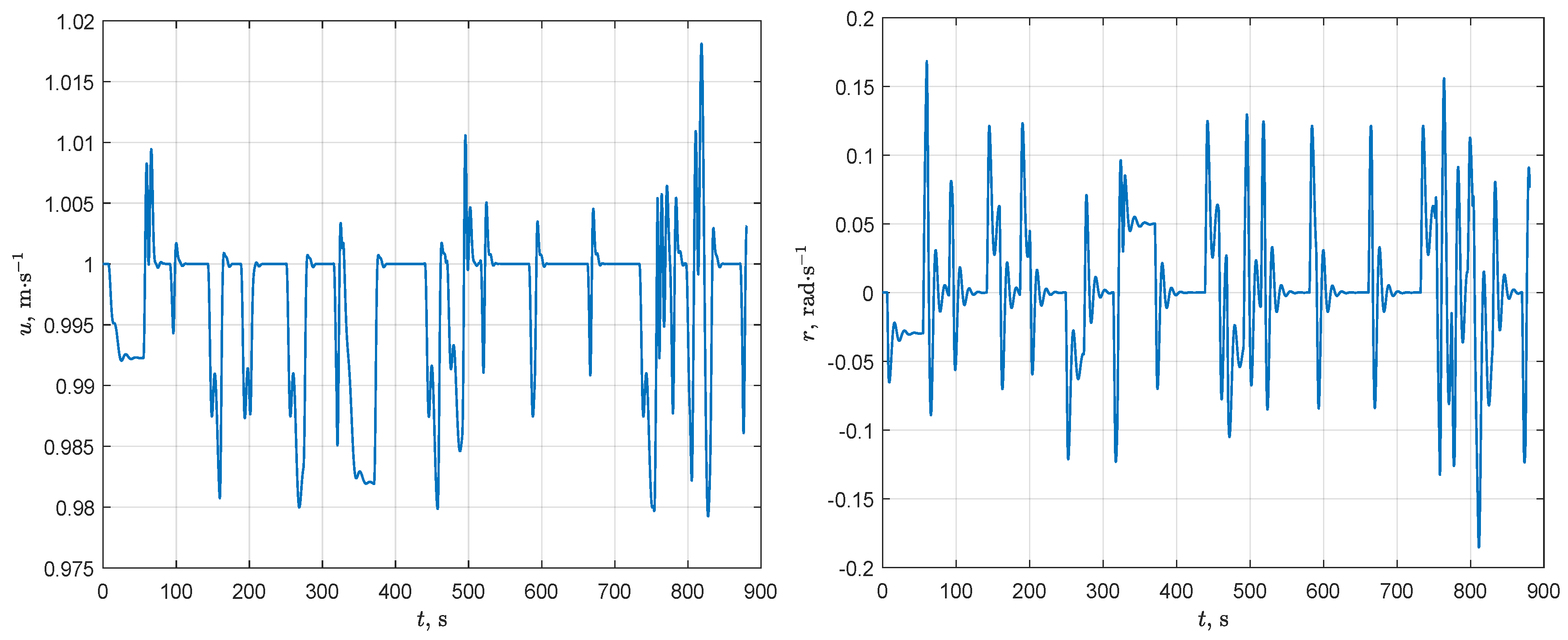
AUV velocities for Scenario 1: forward velocity (left-hand part) and yaw velocity (right-hand part).
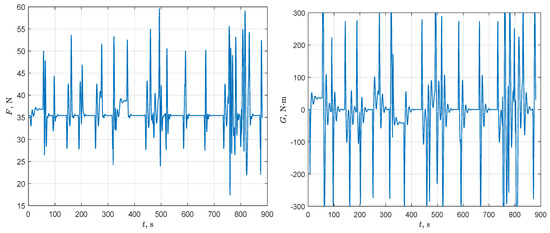
Figure 12.
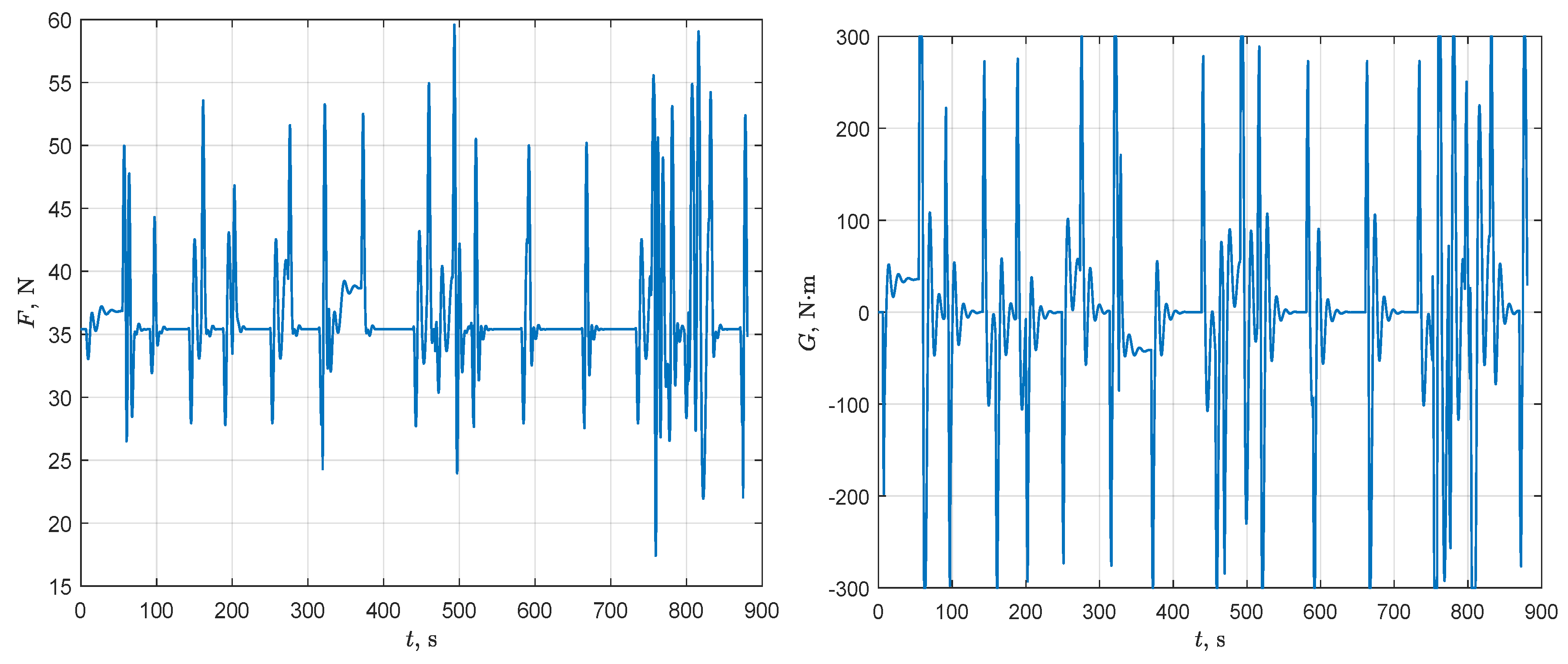
Control activity for Scenario 1: force (left-hand part) and torque (right-hand part).
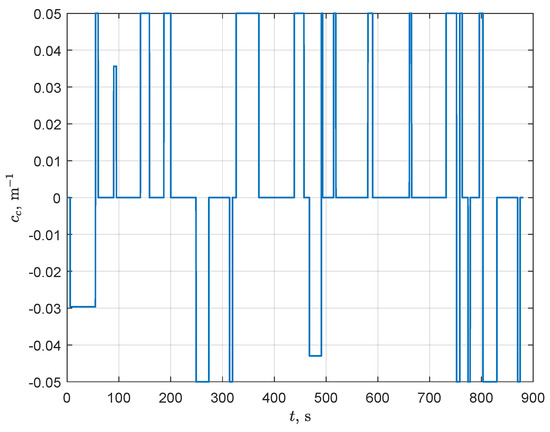
Figure 13.
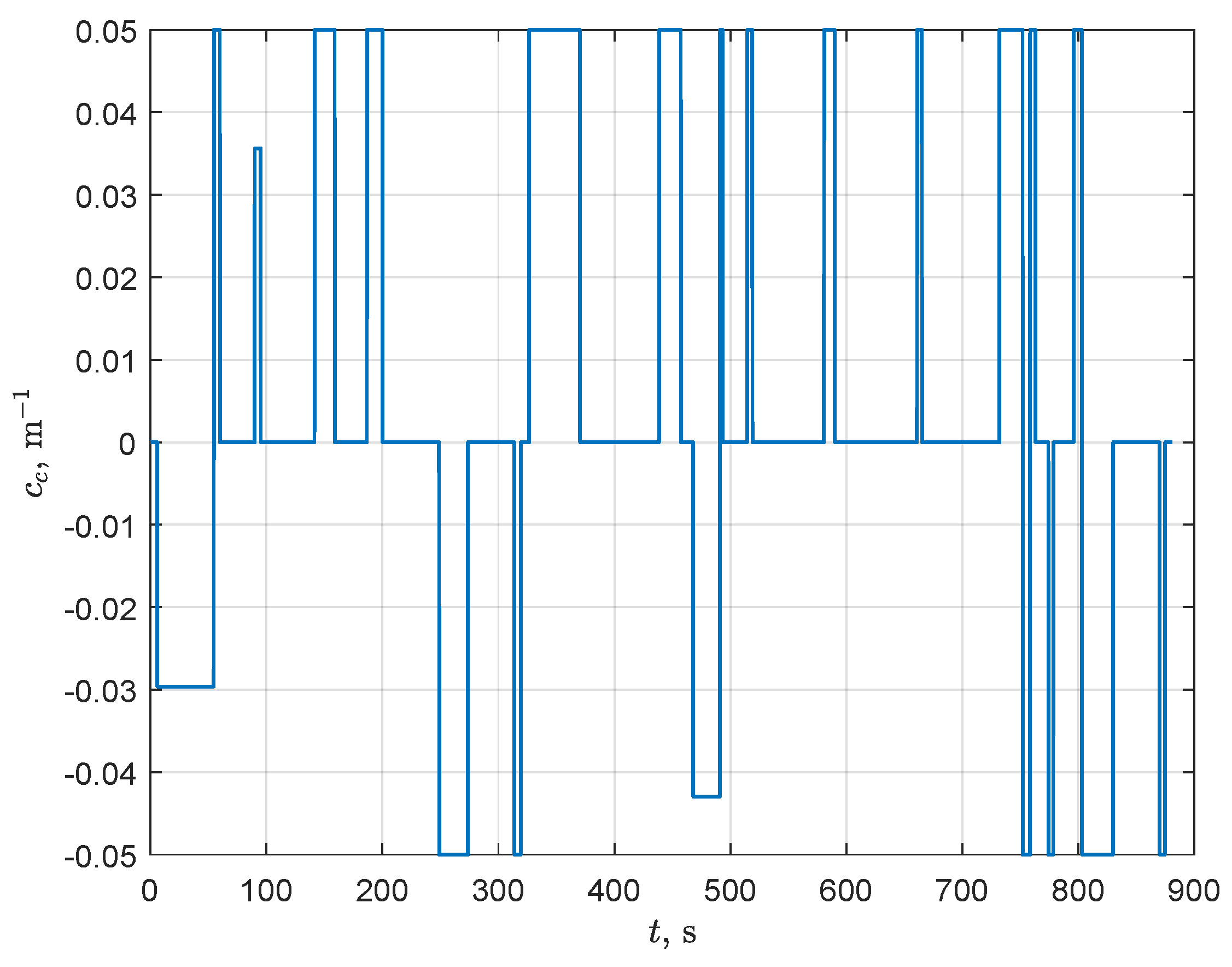
Evolution of the path curvature in Scenario 1.
Note that DES detects not only situations when it is necessary to generate a new path, but also situations when the active waypoint should be changed. For example, during the first 250 s of scenario 1, the active waypoint is changed twice, due to the simultaneous occurrence of elementary events eWPB, eWPR, and eWPDN (rule 1 of the mDOL block in Table 3). As a result of these changes, waypoint 4 of the reference path becomes active before the AUV approaches the line segment between waypoints 3 and 4, and events that triggers the return to the reference path (rule 5 of the mDOL block in Table 3) can be detected.
Figure 13 shows that the proposed path-planning algorithms generate paths that have a constrained curvature , and, consequently, meets the turning radius constraint m.
The analysis of Figure 10, Figure 11, and Figure 13 allows for drawing a conclusion that the main source of disturbances causing the growth of path-following errors , and velocity discrepancies is jumps in the path curvature. Without these disturbances, the errors asymptotically tend to zero as well as velocities u and r tend to the desired values and . The horizontal sections of lines that are shown in Figure 10 and Figure 11 correspond to a motion without disturbances.
Figure 12 shows that the developed path-following controller, combating the curvature-induced disturbances, may cause saturation of the torque (maximum torque ). The reason for this is that the feedback gains of the controller were synthesized in order to minimize the steady-state errors for and . It should be noted that other requirements to the lower level controller, specified in terms of direct indicators of dynamic quality, can be satisfied using the VLF-based tool employed in this paper for tuning feedback gains. For example, the aim of synthesis may be to maximize the size of the region of attraction. Note also that the path-following errors can be reduced by regulating the forward speed of the VT, or transforming the generated path into a smoother one, or reducing the control interval h.
Figure 14 and Figure 15 show the simulation results for Scenarios 2 and 3, respectively. We do not display all results for these scenarios because the missed data do not provide new information about the performance of the designed path-following controller and are quite similar to the simulation results of Scenario 1. In particular, the path curvature is bounded by constant ; the path-following errors and increase significantly when the path curvature changes with a jump, and then, passing through a transient phase, tend to the neighbourhood of zero; u and r behave similarly, with the only difference being that they tend to and respectively; force and torque do not exceed the maximum allowed limits and , respectively.
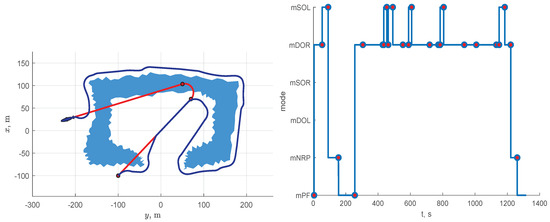
Figure 14.
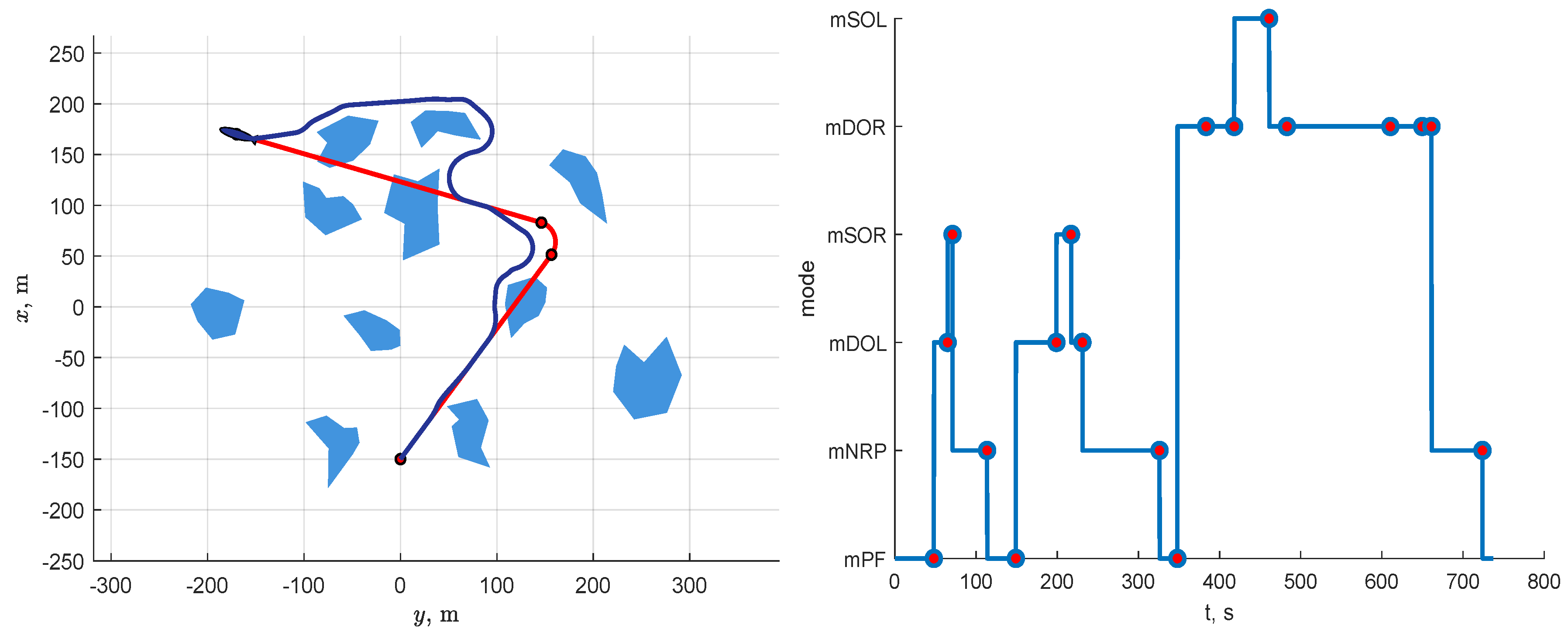
Simulation results for Scenario 2: U-shaped obstacle environment. The explanation of the figure is the same as that of Figure 9.
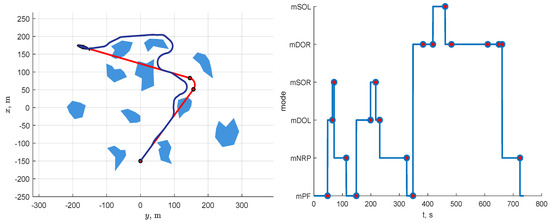
Figure 15.
Simulation results for Scenario 3: cluttered environment. The explanation of the figure is the same as that of Figure 9.
As shown in Figure 14, being in path-following mode mPF, the AUV activates obstacle avoidance mode mDOR twice: at the very beginning and on the 250th s of Scenario 2. Following the right-hand rule that was implemented in the developed DES, the AUV does not change the chosen avoidance direction until it returns to the reference path. During the obstacle bypass, mode mDOR alternates with mode mSOL. The last is activated when the AUV reaches the end of the avoidance path, and no obstacles are detected on the left. Elementary event eRRPR, which is monitored in mode mDOR, determines whether the AUV is ready to return to the reference path: the AUV is ready if event eRRPR can be detected. This event is introduced to exclude situations when the AUV repeatedly travel along the same reference path segment. In Scenario 2, when the AUV gets out of the U-shaped obstacle trap, the fact that event eRRPR does not occur prevents the AUV from returning to the part of the reference path that it has already passed.
The left-hand part of Figure 15 shows that the AUV freely passes between obstacles at the bottom part of the scene because they are located far enough away from each other (the distance between obstacles is more than 70 m). In turn, the AUV does not try to squeeze between the tightly placed obstacles at the top of the scene and detours them by turning to the right. Such behavior allows for the vehicle not to be caught in a potential trap and to use only standard path planning algorithms.
5. Discussion
The simulation experiments have shown that the developed event-based approach to real-time path planning is practical in most possible situations. However, we are far from the opinion that it provides rational behavior for the AUV in all circumstances. An example of the irrational behavior of the AUV is the simulation scenario 2 (see Figure 14), in which it is more advantageous for the AUV, after getting out of the U-shaped trap, to turn to the right and move along the obstacle, holding it on the right. The irrational behavior arises from the fact that an essential characteristic of the proposed approach is the reactivity of decision making without using global information about the environment, for example, in the form of a map incrementally built during the motion. The application of such models in path planning procedures will be studied further.
In general, it is not easy to evaluate a path planning algorithm from a real-time perspective without conducting experimental work on real AUVs. However, extensive simulations can also be used in order to evaluate the algorithm for real-time applicability indirectly. For example, it takes less than 100 s on a computer with the Intel Core i7-8550U 1.8 GHz processor to run the simulation scenario 1 (with a sharp-edged obstacle) of 900 s from Section 4. Computations for this scenario, in addition to integrating the motion equation, generating paths, and updating control signals, also include rendering the scene. The computation time indicates that the proposed method has high potential for working in real-time. The efficiency of path planning is achieved due to some features of the proposed event-based approach. First, the path update regulated by the designed DES occurs when it is vital. Second, the developed path planning algorithms do not rely on in-depth optimization: the algorithm based on the waypoint guidance method uses only a simple model of the environment built on raw data that were obtained from FLS and is not optimizing in its essence; the algorithm based on Dubins curves moves through only up to four path alternatives to choose the best one. Third, to determine the direction of bypassing detected obstacles, an in-depth analysis of the local environment is not performed: if two obstacle avoidance directions are equal, then the designed DES chooses one of them based on the analysis of forthcoming waypoints of the reference path. Finally, checking all of the triggering conditions does not require significant computing efforts.
The developed approach to path planning is ideologically close to (and in many ways inspired by) [4,14]. However, in contrast to these studies, we consider a more elaborate formulation of the path planning problem, in which the AUV has to move along a reference path, instead of trying to reach a static target point. Besides, we do not divide obstacles into classes and do not use separate planning algorithms for each class. Additionally, the robust convex outline algorithm proposed in the paper produces fewer points compared to the largest polar angle algorithm from [14], which reduces the number of path segments generated by the waypoint guidance method used in both studies.
In the proposed event-based approach, a DES determines the obstacle avoidance behavior of the AUV. We designed the DES in such a way as to avoid situations that require the use of energy inefficient emergency modes [14]. These situations arise when any path generated by path-planning algorithms leads to a collision with an obstacle or dangerously approaches it. The logic of the AUV’s behavior is described using concepts accepted in the theory of discrete event systems. In the future, this will allow for us to apply formal methods and software tools to analysis of DESs intended for path planning. Besides, we plan to develop a convenient tool for specifying DES with the possibility to integrate new rules and actions in the path planning process.
Although the focus of the paper is on path planning in an unknown environment, it also concerns the path-following problem. The designed path-following controller demonstrates acceptable performance: the steady-state tracking errors in the along path direction and in the across path direction do not exceed 1 m (see Figure 10). Analysis of the simulation results showed that the tracking errors are primarily affected by jump changes in the path curvature. At the same time, such jumps occur quite rarely at junction points of two adjacent path segments, so the AUV has time to reduce errors before reaching the next junction point. It should be noted that increasing in the RCOA algorithm can reduce the number of path segments that are generated by the waypoint guidance algorithm and, therefore, the number of jumps. In turn, a path generated by Dubins curve-based algorithm consists only of three segments.
6. Conclusions
In the paper, we developed a two-level control system that allows for the AUV to move along a given reference path in a two-dimensional (2D) environment with obstacles. The key idea behind the developed approach is to use a discrete event system at the top level as a mechanism for detecting situations that require path updates and waypoint management. Two path planning algorithms were developed in order to ensure safe obstacle avoidance and return to the reference path after completing the avoidance maneuver. A digital path-following controller was designed while using the vector Lyapunov function method by minimizing the steady-state positioning errors of the AUV with respect to the moving VT. The simulation results illustrated the performance of the control system proposed.
The developed approach demonstrates promising results on the plane. In our opinion, the approach has the potential to be extended to the 3D case. Additionally, there is a particular interest in its application to multiple AUVs. We plan to work on these directions in the future.
Author Contributions
S.U., I.B., and N.M. proposed the main idea; I.B. supervised the research work; S.U. designed the algorithms and conducted simulation; S.U. and N.M. analyzed the data; S.U. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
The event-triggered control system architecture has been developed under support of the Russian Foundation for Basic Research (Projects No. 20-07-00397). The work related to the development of the event-based path planning algorithm for AUVs is supported by the Ministry of Science and Higher Education of the Russian Federation (Grant No. 075-15-2020-787, large scientific project “Fundamentals, methods and technologies for digital monitoring and forecasting of the environmental situation on the Baikal natural territory”). The path-following controller has been designed using algorithms and software tools developed under support of the Russian Science Foundation (Project No. 16-11-00053).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sahoo, A.; Dwivedy, S.K.; Robi, P. Advancements in the field of autonomous underwater vehicle. Ocean. Eng. 2019, 181, 145–160. [Google Scholar] [CrossRef]
- Li, D.; Wang, P.; Du, L. Path Planning Technologies for Autonomous Underwater Vehicles-A Review. IEEE Access 2019, 7, 9745–9768. [Google Scholar] [CrossRef]
- Panda, M.; Das, B.; Subudhi, B.; Pati, B.B. A Comprehensive Review of Path Planning Algorithms for Autonomous Underwater Vehicles. Int. J. Autom. Comput. 2020, 17, 321–352. [Google Scholar] [CrossRef]
- Yan, Z.; Li, J.; Wu, Y.; Zhang, G. A Real-Time Path Planning Algorithm for AUV in Unknown Underwater Environment Based on Combining PSO and Waypoint Guidance. Sensors 2019, 19, 20. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yao, X.; Zhang, L. Path Planning under Constraints and Path Following Control of Autonomous Underwater Vehicle with Dynamical Uncertainties and Wave Disturbances. J. Intell. Robot. Syst. 2020. [Google Scholar] [CrossRef]
- Ataei, M.; Yousefi-Koma, A. Three-Dimensional Optimal Path Planning for Waypoint Guidance of an Autonomous Underwater Vehicle. Robot. Auton. Syst. 2015, 67, 23–32. [Google Scholar] [CrossRef]
- Sun, B.; Zhu, D.; Tian, C.; Luo, C. Complete Coverage Autonomous Underwater Vehicles Path Planning Based on Glasius Bio-Inspired Neural Network Algorithm for Discrete and Centralized Programming. IEEE Trans. Cogn. Dev. Syst. 2019, 11, 73–84. [Google Scholar] [CrossRef]
- Fan, X.; Guo, Y.; Liu, H.; Wei, B.; Lyu, W. Improved Artificial Potential Field Method Applied for AUV Path Planning. Math. Probl. Eng. 2020, 2020, 6523158. [Google Scholar] [CrossRef]
- Hernández, J.D.; Vidal, E.; Moll, M.; Palomeras, N.; Carreras, M.; Kavraki, L.E. Online motion planning for unexplored underwater environments using autonomous underwater vehicles. J. Field Robot. 2019, 36, 370–396. [Google Scholar] [CrossRef]
- Xiong, C.; Zhou, H.; Lu, D.; Zeng, Z.; Lian, L.; Yu, C. Rapidly-Exploring Adaptive Sampling Tree*: A Sample-Based Path-Planning Algorithm for Unmanned Marine Vehicles Information Gathering in Variable Ocean Environments. Sensors 2020, 20, 2515. [Google Scholar] [CrossRef]
- Candeloro, M.; Lekkas, A.M.; Sorensen, A.J. A Voronoi-diagram-based dynamic path-planning system for underactuated marine vessels. Control. Eng. Pract. 2017, 61, 41–54. [Google Scholar] [CrossRef]
- Wei, D.; Wang, F.; Ma, H. Autonomous Path Planning of AUV in Large-Scale Complex Marine Environment Based on Swarm Hyper-Heuristic Algorithm. Appl. Sci. 2019, 9, 2654. [Google Scholar] [CrossRef]
- Yao, P.; Zhao, S. Three-Dimensional Path Planning for AUV Based on Interfered Fluid Dynamical System Under Ocean Current (June 2018). IEEE Access 2018, 6, 42904–42916. [Google Scholar] [CrossRef]
- Yan, Z.; Li, J.; Zhang, G.; Wu, Y. A Real-Time Reaction Obstacle Avoidance Algorithm for Autonomous Underwater Vehicles in Unknown Environments. Sensors 2018, 18, 438. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, J.; Zhang, H.; Yan, Z. A Predictive Guidance Obstacle Avoidance Algorithm for AUV in Unknown Environments. Sensors 2019, 19, 2862. [Google Scholar] [CrossRef] [PubMed]
- Lim, H.S.; Fan, S.; Chin, C.K.; Chai, S.; Bose, N.; Kim, E. Constrained path planning of autonomous underwater vehicle using selectively-hybridized particle swarm optimization algorithms. In Proceedings of the 12th IFAC Conference on Control Applications in Marine Systems, Robotics, and Vehicles CAMS, Daejeon, Korea, 18–20 September 2019. [Google Scholar] [CrossRef]
- Yan, Z.; Li, J.; Wu, Y.; Yang, Z. A Novel Path Planning for AUV Based on Objects’ Motion Parameters Predication. IEEE Access 2018, 6, 69304–69320. [Google Scholar] [CrossRef]
- Ma, Y.; Gong, Y.; Xiao, C.; Gao, Y.; Zhang, J. Path Planning for Autonomous Underwater Vehicles: An Ant Colony Algorithm Incorporating Alarm Pheromone. IEEE Trans. Veh. Technol. 2019, 68, 141–154. [Google Scholar] [CrossRef]
- MahmoudZadeh, S.; Powers, D.M.W.; Yazdani, A.M.; Sammut, K.; Atyabi, A. Efficient AUV Path Planning in Time-Variant Underwater Environment Using Differential Evolution Algorithm. J. Mar. Sci. Appl. 2018, 17, 585–591. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y.; Buckham, B. Integrated Path Planning and Tracking Control of an AUV: A Unified Receding Horizon Optimization Approach. IEEE/ASME Trans. Mechatron. 2017, 22, 1163–1173. [Google Scholar] [CrossRef]
- Yao, X.; Wang, X.; Wang, F.; Zhang, L. Path Following Based on Waypoints and Real-Time Obstacle Avoidance Control of an Autonomous Underwater Vehicle. Sensors 2020, 20, 795. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Hou, Y.; Zhang, J. Three-dimensional path following control of underactuated autonomous underwater vehicle based on damping backstepping. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417724179. [Google Scholar] [CrossRef]
- Lapierre, L.; Soetanto, D. Nonlinear path-following control of an {AUV}. Ocean. Eng. 2007, 34, 1734–1744. [Google Scholar] [CrossRef]
- Lapierre, L.; Jouvencel, B. Robust Nonlinear Path-Following Control of an AUV. IEEE J. Ocean. Eng. 2008, 33, 89–102. [Google Scholar] [CrossRef]
- Kim, E.; Fan, S.; Bose, N.; Nguyen, H. Current Estimation and Path Following for an Autonomous Underwater Vehicle (AUV) by Using a High-gain Observer Based on an AUV Dynamic Model. Int. J. Control. Autom. Syst. 2020. [Google Scholar] [CrossRef]
- Guerrero, J.; Torres, J.; Creuze, V.; Chemori, A.; Campos, E. Saturation based nonlinear PID control for underwater vehicles: Design, stability analysis and experiments. Mechatronics 2019, 61, 96–105. [Google Scholar] [CrossRef]
- Zeng, J.; Wan, L.; Li, Y.; Dong, Z.; Zhang, Y. Adaptive line-of-sight path following control for underactuated autonomous underwater vehicles in the presence of ocean currents. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417748127. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y.; Buckham, B. Path-Following Control of an AUV: A Multiobjective Model Predictive Control Approach. IEEE Trans. Control. Syst. Technol. 2019, 27, 1334–1342. [Google Scholar] [CrossRef]
- Guo, C.; Han, Y.; Yu, H.; Qin, J. Spatial Path-Following Control of Underactuated AUV With Multiple Uncertainties and Input Saturation. IEEE Access 2019, 7, 98014–98022. [Google Scholar] [CrossRef]
- Xiang, X.; Yu, C.; Zhang, Q. Robust Fuzzy 3D Path Following for Autonomous Underwater Vehicle Subject to Uncertainties. Comput. Oper. Res. 2017, 84, 165–177. [Google Scholar] [CrossRef]
- Sgorbissa, A. Integrated robot planning, path following, and obstacle avoidance in two and three dimensions: Wheeled robots, underwater vehicles, and multicopters. Int. J. Robot. Res. 2019, 38, 853–876. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Silvestre, C.; Pascoal, A. Control of the INFANTE AUV using gain scheduled static output feedback. Control. Eng. Pract. 2004, 12, 1501–1509. [Google Scholar] [CrossRef]
- Ulyanov, S.; Maksimkin, N. Formation path-following control of multi-AUV systems with adaptation of reference speed. Math. Eng. Sci. Aerosp. (MESA) 2019, 10, 487–500. [Google Scholar]
- Leith, D.J.; Leithead, W. Survey of Gain-Scheduling Analysis & Design. Int. J. Control. 2000, 73, 1001–1025. [Google Scholar]
- Kozlov, R.I.; Kozlova, O.R. Investigation of stability of nonlinear continuous-discrete models of economic dynamics using vector Lyapunov function. J. Comput. Syst. Sci. Int. 2009, 48, 262–271. [Google Scholar] [CrossRef]
- Vassilyev, S.; Ulyanov, S.; Maksimkin, N. A VLF-Based Technique in Applications to Digital Control of Nonlinear Hybrid Multirate Systems; AIP Publishing LLC: Melville, NY, USA, 2017; pp. 020170(1)–020170(10). [Google Scholar] [CrossRef]
- Cassandras, C.G.; Lafortune, S. Introduction to Discrete Event Systems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Dubins, E.L. On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents. Am. J. Math. 1957, 79, 497. [Google Scholar] [CrossRef]
- Manyam, S.G.; Casbeer, D.W.; Moll, A.V.; Fuchs, Z. Shortest Dubins Path to a Circle. arXiv 2018, arXiv:1804.07238v1. [Google Scholar]
- Chen, Z. On Dubins paths to a circle. Automatica 2020, 117, 108996. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).