Abstract
Data type abstraction plays a crucial role in software verification. In this paper, we introduce a domain for abstracting strings in the C programming language, where strings are managed as null-terminated arrays of characters. The new domain M-String is parametrized on an index (bound) domain and a character domain. By means of these different constituent domains, M-Strings captures shape information on the array structure as well as value information on the characters occurring in the string. By tuning these two parameters, M-String can be easily tailored for specific verification tasks, balancing precision against complexity. The concrete and the abstract semantics of basic operations on strings are carefully formalized, and soundness proofs are fully detailed. Moreover, for a selection of functions contained in the standard C library, we provide the semantics for character access and update, enabling an automatic lifting of arbitrary string-manipulating code into our new domain. An implementation of abstract operations is provided within a tool that automatically lifts existing programs into the M-String domain along with an explicit-state model checker. The accuracy of the proposed domain is experimentally evaluated on real-case test programs, showing that M-String can efficiently detect real-world bugs as well as to prove that program does not contain them after they are fixed.
1. Introduction
C is still one of the mainly used programming languages [1], and a large portion of systems of critical relevance are written in this language, such as server-side software and embedded systems. Unfortunately, C programs suffer of bugs, due to the way they are laid out in memory, which malicious parties may exploit to drive security attacks. Ensuring the correctness of such software is of great concern. Our main interest is guaranteeing the correctness of C programs that manage strings, because the incorrect string manipulation may lead to several catastrophic events, ranging from loss or exposure of sensitive data to crashes in critical software components.
Strings in C are not a basic data type. As a matter of facts, strings in C are represented by zero-terminated arrays of characters and there are libraries that provide functions which allow operating on them [2]. C programs that manipulate strings can suffer from buffer overflows and related issues due to the possible discrepancy between the size of the string and the size of the array (buffer). A buffer overflow is a bug that affects C code when a buffer is accessed out of its bounds. In particular, an out-of-bounds write is a particular (and very dangerous) case of buffer overflow. Out-of-bounds read is less critical as a bug. It is important to design methods supporting the automatic correctness verification of string management in C programs for the previously mentioned reasons and also because buffer overflows are usually exploitable and can easily lead to arbitrary code execution [3]. Existing bugs can be identified by enhancing tools for code analysis, which can also reduce the risk of introducing new bugs and limit the occurrence of costly security incidents.
1.1. Paper Contribution
This paper is a revised and extended version of [4,5]. We introduce M-String, a new abstract domain tailored for the analysis of strings in C, whose elements:
- approximate sets of C character arrays;
- allow the abstraction of both shape information on the array structure and value information on the contained characters;
- highlight the presence of well-formed strings in the approximated character arrays.
M-String refines the segmentation approach to array representation introduced in [6]. M-String’s goal is to detect the presence of common string management errors that may lead to undefined behaviours or, more specifically, which may result in buffer overflows. Moreover, keeping track of the content of the characters occurring after the first null character allows us to reduce the number of false positives. In fact, rewriting the first null character in the array is not always an error, as further occurrences of the null character may follow. M-String, such as the array segmentation-based representation introduced in [6], is parametric in two ways: both with respect to the representation of the indices of the array and with respect to the abstraction of the element values.
To provide evidence of the effectiveness of M-String, we extend LART [7], a tool which performs automatic abstraction on programs, making it supporting also sophisticated (non-scalar) domains such as M-String.
We extend LART along with DIVINE 4 [8], an explicit state model checker based on LLVM. This way, we can verify the correctness of operations on strings in C programs automatically. The experimental evaluation is performed by analyzing several C programs, ranging from quite simple to moderately complex, including parsers generated by bison, a tool which translates context-free grammars into C parsers. The results show the actual impact of an ad-hoc segmentation-based abstract domain on model checking of C programs.
1.2. Paper Structure
In the following Section 2 we give basics in abstract interpretation and we introduce the array segmentation abstract domain [6] on which M-String is based. Furthermore, Section 3 introduces the syntax of some operations of interest. Section 4 defines the concrete domain and semantics. Section 5 presents the M-String abstract domain for C character arrays and its semantics, whose soundness is formally proved. In the Section 6, we present a general approach to abstraction as a program transformation and extend it to abstraction of program strings. Section 7 and Section 8 present implementation and evaluation details of M-String abstraction. In Section 9 we discuss related work. Finally, Section 10 concludes.
2. Prerequisites
We assume the reader is familiar with order theory.
2.1. Abstract Interpretation
Abstract Interpretation [9,10] is a theory about sound approximation or abstraction of semantics of computer programs, focusing on some run-time properties of interest. Formally, the concrete semantics is based on a concrete domain D. Likewise, the abstract semantics is based on an abstract domain . Both the concrete and the abstract domains form a complete lattice, such that: and . Please note that we use the same notation interchangeably to denote a domain and its set of elements. The concrete and the abstract domains are related by a pair of monotonic functions: the concretization and the abstraction functions. In order to obtain a sound analysis, and have to form a Galois Connection (GC) [11]. is a GC if and only if for every d ∈ D and
∈ ; we have that . Notice that, one function univocally identifies the other. Consequently, we can infer a Galois Connection by proving that is a complete meet morphism (resp. is a complete join morphism) (Proposition 7 of [12]). Please note that these conditions can be relaxed, performing abstract interpretation over non-lattice abstract domains [12]. Abstract domains that do not respect the Ascending Chain Condition (ACC) need to be equipped with a widening and a narrowing operator, in order to get fast convergence and to improve the accuracy of the resulting analysis, respectively [13]. An abstract domain functor is a function from the parameter abstract domains to a new abstract domain . The abstract domain functor composes abstract domain properties of the parameter abstract domains to build a new class of abstract properties and operations [6].
2.2. Fun Array
In the following we recall the array segmentation analysis presented in [6]. Notice that we slightly modified the notation to be consistent with the whole work. For more details, we invite the reader to refer directly to the original paper.
2.2.1. Array Concrete Semantics
Let be the set of concrete array environments. A concrete array environment maps array variables to their values , such that:
- and,
where
- is the set of concrete variable environments. A concrete variable environment maps variables (of basic types) to their values .
- is the set of program expressions made up of constants, variables, mathematical unary and binary operators. In the following, for simplicity, expressions are evaluated to integers. are expressions whose value, given by and , respectively represents the lower bound and the upper bound of an array a, i.e., the lower and the upper bound of its indexes range. According to the denotational semantics approach, in [6] the value of an arithmetic expression e is denoted by , where: (1) the double square brackets notation denotes the semantic evaluation function and, (2) is an environment mapping program variables (which also may appear in e) to their value. Typically, is equivalent to , with , and , where n is a constant, is equivalent to n itself. Thus, for example, if e is the expression , its semantics is defined as , which corresponds to . Notice that the value of an upper bound of an array concrete value corresponds to the index immediately after the one that points to the last memory block allocated to the array when it has been initialized. As usual, array indexes are 0-based.
- is the set of integer numbers and is the set of values. Let be the set of indexes i of an array a, i.e., and, let be the set of pairs such that v is the value of the element indexed by i in an array a, i.e., . Thus, is a function mapping the indexes of an array a to their corresponding pairs (index, indexed array value).
Example 1.
Letabe aCinteger array initialized as follows:a[5] = {5,7,9,11,13}. The concrete value ofais given by the tuple , where the value of the lower and the upper bound ofaare clear from the context and the codomain of the function is the set . Moreover, letbdenote the sub-array ofafrom position 2 to 3 included, its concrete value is given by such that .
Observe that this array representation allows reasoning about the correspondence between shape components of an array and actual values of the array elements.
2.2.2. Array Segmentation Abstract Domain Functor
According to [6], the FunArray abstract domain (shortcut for ) allows representing a sequence of consecutive, non-overlapping and possibly empty segments that over-approximate a set of concrete array values in , i.e., the powerset of . Each segment represents a sub-array whose elements share the same property (e.g., being positive integer values) and is surrounded by the so-called segment bounds, i.e., abstractions on its lower and upper bound.
Example 2.
Consider the integer arraya[5] = {5,7,9,10,12}. As an abstraction ofawe may consider odd even saying that the array contains odd numbers in the first three elements (indexed from 0 to 2) and two even elements (indexed from 3 to 4).
The elements of FunArray belong to the set , which have the form where
- is the segment bound abstract domain, approximating array indexes, with abstract properties such that and .We denote by the set of expressions of canonical form , where and . The segment bounds are sets of expressions , such that . The variable abstract domain encodes program variables, i.e., , where is a special variable whose value is assumed to be zero. Moreover, denotes unreachability; if , the expressions appearing in a segment bound are all equivalent symbolic denotations of some concrete value (generally unknown in the abstract representation except when one of the is a constant). Thus, depends on the expression abstract domain which, in turn, depends on the variable abstract domain .
- is the array element abstract domain, with abstract properties . It denotes possible values of pairs (index, indexed array element) in a segment, for relational abstractions, array elements otherwise.
- is the variable environment abstract domain, which depends on the variable abstract domain , with abstract properties .
- the question mark, if present, expresses the possibility that the segment that precedes it may be empty. The question mark can never precede . The space symbol ␣ in represents a non-empty segment.
Example 3.
Let be the classical sign abstraction of numerical values. The segmentation abstract predicate represents arrays of length 5, with either 0 or 3 positive elements followed by either 5 or 2 negative elements, respectively. For instance, it represents: , and . Please note that in the last case, the lack of positive values is justified by the presence of the question mark that says that the first segment is optional.
Two segmentations, and , are compatible if and . The unification algorithm, in [6], modifies two compatible segmentations in order to align them with respect to the same list of bounds. The unification algorithm does not guarantee the maximality of the result, but it is always well-defined, it does terminates and it is deterministic. The partial order over is defined over unified segmentations as well as the join and the meet operators. Please note that is not necessarily a lattice [14]. Moreover, does not respect the Ascending Chain Condition, therefore, in order to ensure the convergence of the analysis, it is equipped with a widening operator . A narrowing operator which improves the precision of the widening result, is also defined. Widening and narrowing operators are applied on unified segmentations.
Such an abstract array representation is effective for analyzing the content of arrays, but in the case of the C programming language where a string is defined as a null-terminating character array, it is not powerful enough to detect common string manipulation errors.
3. Syntax
Strings in the programming language C are arrays of characters, whose length is determined by a terminating null character ‘\0’. Thus, for example, the string literal “bee” has four characters: ‘b’, ‘e’, ‘e’, ‘\0’. Moreover, C supports several string handling functions defined in the standard library string.h.
We focus on the most significant functions in the string.h header (see Table 1), manipulating null-terminated sequences of characters, plus the array elements access and update operations. Recall that char, int and size_t are data types in C, const is a qualifier applied to the declaration of any variable which specifies the immutability of its value, and *str denotes that str is a pointer variable.

Table 1.
String functions syntax in C.
- strcat appends the null-terminated string pointed to by str2 to the null-terminated string pointed to by str1. The first character of str2 overwrites the null-terminator of str1 and str2 should not overlap str1. The string concatenation returns the pointer str1.
- strchr locates the first occurrence of c (converted to a char) in the string pointed to by str. The terminating null character is considered to be part of the string. The string character function returns a pointer to the located character, or a null pointer if the character does not occur in the string.
- strcmp lexicographically compares the string pointed to by str1 to the string pointed to by str2. The string compare function returns an integer greater than, equal to, or less than zero, accordingly as the string pointed to by str1 is greater than, equal to, or less than the string pointed to by str2.
- strcpy copies the null-terminated string pointed to by str2 to the memory pointed to by str1. str2 should not overlap str1. The string copy function returns the pointer str1.
- strlen computes the number of bytes in the string to which str points, not including the terminating null byte. The string length function returns the length of str.
Accessing an array element is possible indexing the array name. Let i be an index, the i-th element of the character array str is accessed by str[i]. On the other hand, a character array element is updated (or an assignment is performed to a character array element) by str[i] = ‘x’, where ‘x’ denotes a character literal.
As mentioned in Section 1, C does not guarantee bounds checking on array accesses and, in case of strings, the language does not ensure that the latter are null-terminated. As a consequence, improper string manipulation leads to several vulnerabilities and exploits [15]. For instance, if non null-terminated strings are passed to the functions above, the latter may return misleading results or read out of the array bound. Moreover, since strcat and strcpy do not allow the size of the destination array str1 to be specified, they are frequent sources of buffer overflows.
4. Concrete Domain and Semantics
Our aim is to capture the presence of well-formed strings in C character arrays, to avoid undesired execution behaviours that may be security relevant. To reach our goal, we propose a character array concrete value which highlights the occurrence of null characters in it and we introduce the notion of string of interest of an array of chars. The concrete semantics relative to the operations presented in Section 3 is also given.
4.1. Character Array Concrete Semantics
Let be a finite set of characters representable by the character encoding in use equipped with a top element representing an unknown value and let
be the set of character array variables, such that (with being the set of array variables - of any type - presented in Section 2.2). Then, the operational semantics of character array variables are concrete array environments mapping character arrays to their values . Precisely:
- and,
so that is a map from to , where and are the concrete variable environment and the expression domain defined in Section 2.2 respectively, is the integer domain and is the character set introduced above. Notice that with respect to the concrete array environment introduced in Section 2.2, the function returns as a last component the set of indexes which map to the string terminating characters , with being the domain of the function . On the other hand, behaves exactly as in , mapping each index i of the considered array to the pair of the index i and the indexed array element v.
Thus, extends (c.f., Section 2.2) by adding a parameter that takes into account the presence of null characters in a character array. For well-formed strings, cannot be empty. Moreover, character array elements which have not been initialized are mapped to the top value as they may be values already present in the memory assigned to the locations array itself.
Example 4.
Letmbe aCcharacter array initialized as follows: m[6] = {‘b’,‘e’,‘e’,‘\0’,‘b’}.The concrete value ofmis given by the tuple , where the codomain of the function is the set and is the singleton , being the array cell of index the only one certainly containing a null character.
4.1.1. String of Interest
We formally define the string of interest of a character array as the sequence of its elements up to the first terminating one (included).
Definition 1 (string of interest).
Let be an array of characters with concrete value and let z be the minimum element of (if it is non-empty). The string of interest of the character array described by is defined as follows:
with denoting the character value which occurs in the pair .
Example 5.
Consider the concrete character array value of Example 4. Its string of interest is the sequence of characters‘‘bee\0’’.
Our definition of string of interest of character arrays allows us to distinguish well-formed strings and avoid bad usage of arrays of characters. If the null character appears at the first index of a character array, then we refer to its string of interest as null (null). In general, we refer to character arrays which contain a well-defined or null string of interest as character arrays which contain a well-formed string.
Moreover, when allocated memory capacity is not sufficient for a declared character array, the system writes a null character outside the array, occupying memory that is not destined for it and causing a buffer overflow. We do not represent this system behaviour, since it leads to an undefined one, so we simply consider the string of interest of such character arrays as undefined (undef).
4.2. Concrete Domain
As a concrete domain for array of characters we refer to the complete lattice defined as where: is the powerset of concrete character array values, the set inclusion corresponds to the partial order, the bottom element is the emptyset ∅, the top element is the superset of any subset of (i.e., itself), the set union denotes the least upper bound and, the set intersection denotes the greatest lower bound.
We stress the fact that the concrete domain we introduce is used as a framework that helps us in creating the abstract representation, and it is not how the (concrete) character array values are actually represented in C programs.
4.3. Concrete Semantics
To formalize the concrete semantics of the C standard library functions from string.h introduced in Section 3, the following auxiliary functions embedding, extraction, comparison and substitution over single concrete character array values need to be introduced.
Definition 2 (embedding).
Letbe two concrete character array values and ,be two indexes ranges of the same length. The function embeddingembeds the sequence of characters ofwhich occurs from the indexto the index into from the index to the index . Formally, embedding such that:
- and
- ∗
- :s.t.and
- ∗
- : s.t. and
- ∗
- : s.t. and
Example 6.
Let and be two concrete character array values such that:
Moreover, consider the intervals of equal length:
The function embedding where:
- and
| Algorithm 1 Lexicographic comparison of concrete character array values. |
| Function: |
| Input: two concrete character array values such that: |
| • both are different from the emptyset and, |
| • for |
| Output: an integer value n. |
| 1: |
| 2: while do |
| 3: |
| 4: if then |
| 5: return n |
| 6: else |
| 7: |
| 8: |
| 9: return n |
- ‘a’‘a’‘b’‘b’‘\0’‘a’‘a’
Definition 3 (extraction).
Let be a concrete character array value and be an indexes range. The function extracts the sequence of characters which occurs in from the index l to the index u. Formally, such that:
- and
- : s.t. and
Example 7.
Let be the character array concrete value of Example 6 and be an indexes range of . The function such that:
- and
- ‘a’‘a’‘\0’
Definition 4 (comparison).
Let , be two concrete character array values which contain a fully initialized well-formed string of interest, i.e., no occurs. The function (c.f. Algorithm 1) lexicographically compares the strings of interest of and and it returns an integer value n which denotes the lexicographic distance between them.
Notice that n will be strictly smaller than zero if string precedes string in lexicographic order, equal to zero if string and string are lexicographically equivalent, and strictly greater than zero if string follows string in lexicographic order.
Example 8.
Let and be the character array concrete values of Example 6. Both of them contain a fully initialized well-formed string of interest and the function comparison computes the lexicographic distance between them. Precisely, the procedure stops after the first iteration of the for loop (c.f. Algorithm 1) and, assuming ASCII as the character encoding set, it returns the value , i.e., , which means that string lexicographically precedes string.
Definition 5 (substitution).
Let be a concrete character array value, be an index and be a character. The function substitution substitutes the character which appears in at the index z with the character c. Formally, substitution such that:
- and
- ∗
- : s.t. and
- ∗
- for :
- ∗
- : s.t. and
Example 9.
Let be the character array concrete value of Example 6, the index z be equal to 4 and the character c be the null termination ‘\0’. The function sub ‘\0’ such that:
- and
- ‘a’‘a’‘a’‘\0’‘\0’‘a’‘a’
4.3.1. Array Access
The semantics operator , given the statement and a set of concrete character array values in as parameter, returns a value in . In particular, returns the character v which occurs at position j if all the character array values in contain v at index j and the latter is well-defined (i.e., it ranges in the array bounds) for all the character array values in ; otherwise it returns . Formally,
4.3.2. String Concatenation
The semantics operator , given a statement and some sets of concrete character array values in as parameters, returns a set of concrete character array values. When applied to , it returns all the possible embeddings in of a string of interest taken from if all the character array values (which belong to both and ) contain a well-formed string and the condition on the size of the destination character array values is fulfilled; otherwise it returns . Please note that the size condition ensures to perform the string concatenation only if the destination character array value is big enough to contain the string of interest of the source character array value, thus preventing undefined behaviours. Formally,
The size.condition is true if:
Moreover, is the set of embedding (c.f. Definition 2), such that:
- , and
- , and
4.3.3. String Character
The semantics operator , when applied to , returns the set of string of interest suffixes in from the index corresponding to the first occurrence of the character v if all the character array values in contain a well-formed string containing v. Otherwise, if all the character array values in contain a well-formed string in which does not occur the character v, it returns the emptyset (denoted by ); otherwise it returns . Formally,
In particular, is the set of extraction (c.f. Definition 3), such that:
- , and
4.3.4. String Compare
The semantics operator , given the statement and two sets of concrete character array values in as parameters, returns a value in the set of integers equipped with a top element, i.e., . In particular, returns an integer value n which denotes the lexicographic distance between strings of interest in and if for all and the procedure comparison (c.f. Definition 4) returns n; otherwise it returns . Formally,
4.3.5. String Copy
The semantics operator , when applied to , behaves similarly to the string concatenation function above. Formally,
The size.condition is true if:
Moreover, is the set of embedding, such that:
- , and
- , and
4.3.6. String Length
The semantics operator , given the statement and a set of concrete character array values in as parameter, returns a value in the set of integers equipped with a top element, i.e., . In particular, returns an integer value n which corresponds to the length of the sequence of characters before the first null one of the character arrays values in if all the character array values in contain a well-formed string of the same length; otherwise it returns . Formally,
4.3.7. Array Update
The semantics operator , when applied to , returns the set of character array values in where the character that occurs at position j has been substituted with the character v if the index j is well-defined for all the character array values in ; otherwise it returns . Formally,
In particular, is the set of substitution (c.f. Definition 2).
5. M-String
In the previous section we defined the concrete value of a character array, which highlights the presence of a well-formed string in it. Moreover, we presented our concrete domain , made of sets of character array values, and its concrete semantics of some operations of interest. In the following we formalize the M-String abstract domain, which approximates elements in , and its semantics for which soundness is proved.
5.1. Character Array Abstract Domain
The M-String () abstract domain approximates sets of concrete character array values with a pair of segmentations that highlights the nature of their strings of interest. The elements of the domain are split segmentation abstract predicates. As for FunArray (recalled in Section 2.2), segments represent sequences of characters which share the same property and are delimited by the so-called segment bounds. More precisely, the M-String abstract domain is a functor given by where
- denotes the abstraction of segment bounds, equipped with the addition and subtraction operations.
- is the abstraction of the character array elements, it is signed, it contains the value 0, and it is equipped with is_null, a special monotonic function lifting abstract elements in to a value in the set {true, false, maybe} and with subtraction .
- denotes the abstraction of scalar variable environments (cf. Section 2.2). Namely, the constant propagation domain on the set of variables .
Elements of M-String belong to the set such that:
- corresponds to and it represents the segmentation of the strings of interest of a set of character arrays.
- corresponds to and it represents the segmentation of the content of character arrays after their string of interests, or character arrays that do not contain the null terminating character.
- , are special elements denoting the bottom/top element of .
The elements in are split segmentation abstract predicates of the form . For instance, when is equal to , it abstracts concrete character array values of length 1 and containing a null string of interest (c.f. Section 4.1.1). On the other hand, when is equal to , it approximates concrete character array values of length greater than or equal to 1 containing a null string of interest. In particular:
- ∈ denotes the segment bounds, chosen in abstract domain , such that and . A segment bound approximates a set of indexes (i.e., positive integers ), but contrary to what defined for the FunArray abstraction, the choice of is let free.For the sake of readability, we apply arithmetic operators on directly. For instance, should be read as or as , where and are respectively the abstraction and concretization functions over the bounds abstract domain.Please note that and respectively represent the segmentation lower and upper bound and in the case in which corresponds to the split segmentation the segmentation upper bound is hidden, due to a representative choice, and equal to . Moreover, in a segmentation we always assume that .
- are abstract predicates, chosen in an abstract domain , denoting possible values of pairs (index, character array element value) in a segment, for relational abstraction, character array elements otherwise.
- the question mark ?, if present, indicates that the preceding segment might be empty, while ␣ indicates a non-empty segment and, as for [6], non-empty segments are not marked.
Example 10.
Consider the split segmentation abstract predicate ‘a’ where is the constant propagation domain for characters and the interval domain. approximates character arrays certainly containing a string of interest which is actually a sequence of ‘a’, whose length goes from 2 to 5, followed by a null character, e.g., “aa\0” and “aaaaa\0”.
In the rest of the paper we will refer to the s and to the ns parameters of a given split segmentation abstract predicate by and respectively.
M-String, like FunArray, is equipped with join , meet , widening and narrowing operators (c.f. Section 2.2.2). We highlight the fact that the choice of is let free, so the segmentation unification algorithm presented in [6] needs to be modified accordingly, while preserving its original requirements. The unify procedure behaves as follows: given , results into the pair and , where and (resp. and ) are compatible, leading to two abstract predicates and , respectively. Given two split segmentations and , let and (resp. and ) denote the lower and upper bounds of (resp. ). and are compatible if and . The same apply to and . Definitions 6 and 7 present how the join and the meet operators over are computed. The widening and narrowing can be easily derived.
Example 11.
Consider the following split segmentations: odd even and odd even . Their unification leads to the abstract elements odd even and odd . Observe that the unify yields to a pair of segmentations with the same number of segments and that is not always optimal.
Definition 6 (M-String join).
represents the join operator that defines a minimal upper bound between two abstract elements. Let , then such that:
if and (resp. and ) are compatible; otherwise.
Please note that , and ⋎ denote the join operator of , and , respectively. In particular, and .
Definition 7 (M-String meet).
represents the meet operator that defines a maximal lower bound between abstract elements.
Let , then such that:
if and (resp. and ) are compatible; otherwise.
Please note that , and ⋏ denote the meet operator of , and , respectively. In particular, and .
5.1.1. Abstraction
Let be a set of concrete character array values. The abstraction function on the M-String abstract domain maps to in the case in which is empty, otherwise to the pair of segmentations that optimally over-approximates values in .
5.1.2. Concretization
The concretization function on the M-String abstract domain maps an abstract element to a set of concrete character array values as follows: , otherwise is the set of all possible character array values represented by a split segmentation abstract predicate .
Formally, we firstly define the concretization function of a generic segment (regardless of what part of the split it is part of) , following [6], which corresponds to the set of character array values whose elements in the segment satisfy the predicate .
where is the concretization function for the variable environment abstract domain, is the concretization function for the segment bounds abstract domain, and is the concretization function for the array characters abstract domain.
We remind that the upper bound of is not followed by a segment abstract predicate. Let be the upper bound of (which may coincide with the lower bound of in the case in which approximates characters arrays containing null strings of interest). is equivalent to the segment such that and is null.
An abstract element in the M-String domain is a pair of segmentations. Thus, we define the concretization function of the possible and belonging to a character array abstract predicate , i.e., . Let denote the concatenation of several concrete values.
Finally, the concretization function of a split segmentation abstract predicate is as follows:
Definition 8 (invalid segment).
Given a generic segment , it is considered invalid if its segment abstract predicate is equal to and its upper bound is not followed by a question mark.
Theorem 1.
Let such that all elements in are compatible and their meet does not result in split segmentation abstract predicates which contain invalid abstract elements. The following inference chain holds:
where is the result of the meet operation over as defined in Definition 7
by definition of
by definition of
Observe that if the hypotheses of Theorem 1 are not satisfied, i.e., if either the abstract predicates in are not compatible or their meet leads to invalid segmentations, then , and .
In the implementation we will make use of two functions lift and lower that relate single strings to their abstraction in M-String.
Definition 9 (lift).
Let be a set of concrete character array values. Given the abstraction function on M-String, we define the lift operation of as follows:
Definition 10 (lower).
Let denote (c.f. Definition 9). Given the concretization function on M-String, we define the lower operation of as follows:
5.2. Abstract Semantics
Let us now formalize the abstract semantics of the concrete operations defined in Section 4.3, over the M-String domain. In doing so, we will take advantage of the auxiliary function minlen which computes the minimum length of an element
∈ , as the upper bound of a split segmentation is possibly followed by a question mark.
Definition 11 ( minimum length).
Let ∈ different from and let , ∈ denote the lower and the upper bound of , respectively. We define the minimum length of a split segmentation abstract predicate , denoted by , as follows:
Please note that in the second case of Definition 11, the minimum length of a split segmentation corresponds to its length, denoted by . The len operation can be also applied over the parameters of
themselves, when they are different from the emptyset and their upper bound is not question marked, which is always the case with .
Example 12.
Consider the split segmentation abstract predicate where is the constant propagation domain for characters and the interval domain. The minimum length of is given by as its upper bound is followed by a question mark. Logically speaking, the maximum length of is . The length of is given by .
5.2.1. Abstract Array Access
The semantics operator is the abstract counterpart of (c.f. Section 4.3.1). In particular, returns, if is valid for (i.e., there exist, and it is unique, a segment bounds interval in to which belongs), the segment abstract predicate ; otherwise it returns . Formally,
where iff .
5.2.2. Abstract String Concatenation
The semantics operator is the abstract counterpart of . When applied to , it returns that is into which has been embedded starting from the upper bound of , if both the input split segmentations approximate character arrays which contain a well-formed string and the condition on the size of the destination split segmentation is fulfilled; otherwise it returns . Formally,
The is if . Let:
Then, such that denotes the immediately preceding adapted segment bound. On the other hand, is the result of removing from the sub-segmentation that goes from the lower bound of to the upper bound of included.
Example 13.
Let and be two abstract elements in , such that is the interval domain over array indexes and is the prefix domain over string values. Precisely, approximates all the characters arrays with as string of interest any string starting with the character a whose length goes from 5 to 7, followed by the null character and any string starting with br whose length goes from 5 to 8. On the other hand, abstracts all the array of chars with string of interest equal to a string, of length 3, starting with a. Consider now the concatenation between them,
The size condition is satisfied: the minimum length of the destination split segmentation is equal to 13, which is strictly greater than , i.e., the maximum length of the destination abstract array plus the maximum length of the source segmentation plus one (the null character). Their concatenation results in the following abstract element:
which is equivalent to .
5.2.3. Abstract String Character
The semantics operator , when applied to , returns a split segmentation abstract predicate with the left hand side parameter equal to the suffix segmentation of the input from the first segment in which certainly occurs and the right hand side parameter equal to the emptyset, if
approximates character arrays which contain a well-formed string and the character appears in at least one segment whose bounds are not question marked. Otherwise, if approximates character arrays which contain a well-formed string of interest and the abstract character does not occur in , it returns ; otherwise it returns . Formally,
where such that .
5.2.4. Abstract String Compare
The semantics is the abstract counterpart of . In particular, returns a value denoting the lexicographic distance between and if both the input split segmentations approximate character arrays which contain a well-formed string and they can be unified; otherwise it returns .
Notice that if is negative, this means that the strings of interest approximated by precede those represented by in lexicographic order. Conversely, if is positive, this means that the strings of interest approximated by follows those represented by in lexicographic order, and if is equal to zero they are lexicographically equal. Formally,
where (c.f. Algorithm 2).
| Algorithm 2 Lexicographic comparison of split segmentation abstract predicates. |
| Function: |
| Input: two compatible split segmentation abstract predicates . |
| Output: an integer value . |
| 1: |
| 2: |
| 3: if then |
| 4: return |
| 5: else if then |
| 6: |
| 7: return |
| 8: else if then |
| 9: |
| 10: return |
| 11: else |
| 12: while do |
| 13: |
| 14: if then |
| 15: return |
| 16: else |
| 17: |
| 18: return |
5.2.5. Abstract String Copy
The semantics , when applied to , it returns that is into which has been embedded starting from the lower bound of , if both the input split segmentations approximate character arrays which contain a well-formed string and the condition on the size of the destination split segmentation is fulfilled; otherwise it returns . Formally,
The is if . Let:
Then, such that denotes the immediately preceding adapted segment bound. On the other hand is the sub-segmentation of that goes from the upper bound of plus one to the upper bound of .
5.2.6. Abstract String Length
The semantics is the abstract counterpart of . In particular, returns a value , if approximates character arrays which contain a well-formed string, the upper bound of is not followed by a question mark and in do not occur possibly null segment abstract predicates; otherwise it returns . Formally,
where .
5.2.7. Abstract Array Update
The semantics , when applied to , returns, if corresponds to the singleton and is valid for (i.e., there exists - and it is unique - a segment bounds interval in to which belongs), that is where the segment is split so that the segment abstract predicate at position is substituted with ; otherwise it returns . Formally,
5.3. Soundness
Theorem 2.
is a sound over-approximation of . Formally,
Proof.
Consider the unary operator and let be a split segmentation abstract predicate. We have to prove that:
accessj of returns, by definition of , the character array value v that occurs at position j, if j belongs to ; otherwise. Let . Then, v belongs to because of , by definition of , is equal to the segment abstract predicate , if there exists - and it unique - a segment bounds interval to which belongs; otherwise. □
Theorem 3.
is is a sound over-approximation of . Formally,
Proof.
- Consider the binary operator strcat and let and be two split segmentation abstract predicates. We have to prove that:strcat of and returns, by definition of , where the first null-terminating memory block of (including the null terminator), i.e., its string of interest, is embedded into starting from the index to which occurs the first null character in , if both and contain a well-formed string and the size condition on the destination character array value is fulfilled; otherwise. Then, belongs to because of and , by definition of , is equal to that is into which has been embedded starting from the upper bound of , if both and approximate character arrays which contain a well-formed string and the size condition on the destination segmentation abstract predicate is fulfilled; otherwise.
- Consider the unary operator , and let be a split segmentation abstract predicate. We have to prove that:of returns, by definition of , that corresponds to the suffix of the string of interest of starting from the index to which appears the first occurrence of v, if contains a well-formed string and v occurs in ; the emptyset (i.e., ), if contains a well-formed string and v does not occur in ; otherwise. Let . Then, belongs to because of , by definition of , is equal to that is the split segmentation abstract predicate with equal to the sub-segmentation of starting from the first segment to which certainly occurs and equal to the emptyset if approximates character arrays which contain a well-defined string and appears in at least one segment whose bounds are not question marked; if approximates character arrays which contain a well-formed string and does not appear in ; otherwise.
- Consider the binary operator strcpy and let and be two split segmentation abstract predicates. We have to prove that:strcpy of and returns, by definition of , where the first null-terminating memory block of (including the null terminator), i.e., its string of interest, is embedded into starting from the lower bound of , if both and contain a well-formed string and the size condition on the destination character array value is fulfilled, otherwise. Then, belongs to because of and , by definition of , is equal to that is into which has been embedded starting from the lower bound of , if both and approximate character arrays which contain a well-formed string and the size condition on the destination segmentation abstract predicate is fulfilled; otherwise.
- Consider the unary operator and let be a split segmentation abstract predicate. We have to prove that:of returns, by definition of , that is where the character at position j has been substituted with the character v, if j is a valid index for ; otherwise. Let and . Then, belongs to because of , by definition of , is equal to that is where the segment that is valid for is split so that the segment abstract predicate which occurs at position is substituted with , if is equal to the singleton and is valid for ; otherwise.
□
Theorem 4.
is a sound over-approximation of . Formally,
Proof.
Consider the binary operator strcmp and let and be two split segmentation abstract predicates. We have to prove that:
strcmp of and returns an integer value n, resulting from the difference between corresponding character array elements, denoting the lexicographic distance between the strings of interest of and , if both contain a well-formed string, otherwise, by definition of . Then n belongs to because strcmp of and , by definition of , is equal to that is the difference between corresponding segment abstract predicates, denoting the lexicographic distance between and , if and are comparable, both approximate character arrays which contain a well-formed string where does not occur; otherwise. □
Theorem 5.
is a sound over-approximation of . Formally,
Proof.
Consider the unary operator strlen and let be a split segmentation abstract predicate. We have to prove that:
strlen of returns, by definition of , an integer value n which denotes the length of the sequence of character before the first null one in , if contains a well-formed string; otherwise. Then n belongs to because of , by definition of is equal to the difference between the lower and the upper bound of if approximates character arrays which contain a well-formed string of interest; otherwise. □
6. Program Abstraction
Adapting M-String to the analysis of real-world C programs requires, first of all, a procedure that identifies string operations automatically. A subset of such operations then has to be performed using abstract operations, carried out on a suitable abstract representation. The technique that captures this approach is known as abstract interpretation. A typical implementation is based on an interpreter in the programming language sense: it executes the program by directly performing the operations written down in the source code. However, rather than using concrete values and concrete operations on those values, part (or the entirety) of the computation is performed in an abstract domain, which over-approximates the semantics of the concrete program.
In this paper, we mainly focus on string abstraction. Therefore we will interpret the portions of the program that do not make use of strings without abstracting values. We only apply abstraction to strings that within the program are manipulated by string operations: when the program deals with string variables that exhibit minimal variation, e.g., string literals, the M-String representation would provide no benefit, and instead it could either hurt performance or it may introduce spurious counterexamples.
Based on the considerations above, it is clear that it is beneficial to reuse and refactor existing tools that implement abstract verification in a modular way on explicit programs. A compilation-based abstraction design that follows this approach was introduced and implemented in [7]. However, such a tool is designed to abstract scalar values only. This is why we need to extend it to operate with more sophisticated domains that represent more complex objects, such as strings.
In the rest of this section, we will first summarize the general approach to abstraction as a program transformation. In Section 6.3, we explore the implications of aggregate (as opposed to scalar) domains within this framework. Section 6.4 and Section 6.5 then go on to discuss the semantic (run-time) aspects of the abstraction and which operations we consider as primitives of the abstraction.
6.1. Compilation-Based Approach
Instead of (re-)interpreting instructions abstractly, in a compilation-based approach, abstract instructions are transformed into an equivalent explicit code that implements the abstract computation. The transformation takes place before the analysis of the program (e.g., model checking) during the compilation process.
Consequently, the analysis processes the program without needing special knowledge of the abstract domains in use, as the abstraction is encoded directly in the program. Figure 1 depicts a comparison of the compilation-based approach with respect the interpretation-based approach adopted by more conventional abstract interpreters.
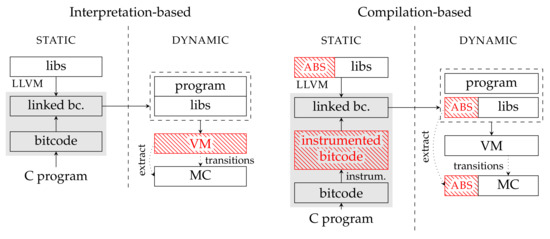
Figure 1.
In the figure, we compare an abstract interpretation with a compilation-based approach. In the interpretation-based approach, the whole abstract interpretation is performed at runtime. The bitecode operations are interpreted abstractely by a virtual machine (VM) which maintains an abstract state. In this way, an abstract state-space is generated for a model-checking algorithm (MC). The compilation-based approach is different. The abstract operations are instrumented into the compiled program and their implementation is provided as a library. Then, the virtual machine executes the instrumented program as a regular bitcode [7].
In a compilation-based approach, two different abstraction perspectives are considered:
- static, referencing to the syntax and the type system,
- dynamic, or semantic, referencing to execution and values.
The LART tool performs syntactic (static) abstraction on LLVM bitcode [16]. Syntactic abstraction replaces some of the LLVM instructions that occur in the program with their abstract counterparts, as depicted in Figure 2.

Figure 2.
Syntactic abstraction.
6.2. Syntactic Abstraction
The first step of program abstraction performed by LART is a syntactic abstraction. Syntactic abstraction replaces LLVM instructions or whole functions with their abstract counterparts. Since we do not want to perform all operations abstractly, we need to classify only those operations that might obtain abstract values as their arguments. The abstract values emerge in the program as input values. From these values, LART computes all operations that might come into contact with abstract values using a combination of data flow and alias analyses. Finally, as a result of analyses, LART obtains a set of possibly abstract operations that are replaced by their abstract equivalents, e.g., strcat, strlen are replaced by abstract_strcat and abstract_strlen. Abstract operations then implement the manipulation with abstract values, in our case with M-Strings as described in Section 4, in other words the specific meaning of abstract instructions and abstract values then defines the semantic abstraction.
For the precise formulation of syntactic abstraction, we take advantage of the static type system of LLVM. We leverage the fact that we can assign to each variable its type, which is either concrete or abstract. In this way, we can precisely set a boundary between concrete and abstract values.
Let us consider a simplified version of LLVM. It defines a set of concrete scalar types S. The set of all possible types is given by a map that inductively defines all finite (non-recursive) algebraic types over the set of given scalars. To be precise, the set of all possible types derived from a set of scalars T is defined as follows:
- , meaning each scalar type is included in ,
- if then also the product type is in : ,
- if then also disjoint union is in : ,
- if then , where denotes pointer type.
In a concrete LLVM program, the set of admissible types comprise those derived from concrete scalars S, i.e., . In syntactic abstraction, we need to extend admissible types by abstract types. From these, we generate all possible types using . Depending on the type of abstraction, we use a different set of basic abstract types. In the case of scalar abstraction, a set of basic abstract types contains abstract scalar types . Correspondence between abstract and concrete scalars is given by a bijective map . Finally, each value, which exists in the abstracted program, has an assigned type of . Specifically, this implies that the abstraction works with mixed types—products and unions might contain both concrete and abstract fields. Moreover, it is possible to create pointers to both abstract or mixed values.
6.3. Aggregate Domains
In addition to scalar values that cannot be further decomposed, programs typically operate with more complex data which can be seen as compositions—aggregates—of multiple scalar values. Depending on aggregates’ nature, we can classify them as aggregates which contain a variable number of items (arrays), records that contain a fixed number of items in a fixed layout, where each of these can be of a different type. The items in such aggregates can be (and often are) scalars. However, more complex aggregates are also possible: arrays of records, records which in turn contain other records, and so on.
While scalar domains only dealt with simple values, in aggregate abstraction, we consider composite data in the spirit of the above definition. Similarly to scalar domains, abstract aggregate domains approximate concrete aggregate values by describing a particular set of aggregate properties. For example, we can describe a set of aggregates by their length or a set of values that appear in the aggregate. In the M-String, the kept properties are in the form of segmentation, where segments are further abstracted by bounds and characters. Values in an aggregate domain then keep the representation of chosen properties and operations updates them. For instance, consider an array length property domain—the domain operations in such a case operate only with lengths of arrays, e.g., abstract concat of arrays adds together lengths of its arguments (abstract arrays).
In general, aggregate domains can provide arbitrary operations. However, two operations are, in some sense, universal, being elementary memory manipulation operations, namely: byte-wise access and update of the aggregate. The universality of these operations originates from the fact that all aggregate operations can be represented as accesses and updates. In a low-level representation of a program (assembly), they usually are presented in this form. LLVM allows a slightly higher level of manipulation to access and update individual scalars present in the aggregates (as opposed to bytes). For M-String, though, this distinction is not essential because the scalars stored in C strings are individual bytes (characters). All other operations are present in the form of sequences of elementary instructions—possibly encapsulated in functions. Moreover, as in concrete programs, the access and update represents an interface between scalars and memory, in the abstraction, they form an interface between scalar and aggregate domains (even in the case of byte-oriented access since bytes are also scalars). We refer the reader to the Section 4.3.1 for abstract semantics of access, respectively to the Section 4.3.7 for the abstract semantics of update.
In comparison to scalar abstraction, the syntactic abstraction of aggregates does not operate directly with aggregate types. In LLVM, aggregate values are usually represented by a pointer to the underlying aggregate type. Therefore all the accesses and updates are made through the pointers to the aggregates. For instance, strings are represented as a pointer to a character array. We need to take this fact into account when we perform the syntactic abstraction. In the analysis, we consider the pointers to aggregates as base types for the abstraction. In the case of arrays, the base types are concrete pointers to those arrays: let us call them , where . A set of abstract pointers types then describes types of abstracted aggregates (arrays). As for scalar domains, we define a natural correspondence between pointers to concrete values and abstract aggregates as a bijective map . For instance, in the case of M-String abstraction, the map assigns to char* a type of M-String value. Finally, we allow all the mixed types generated from scalars and abstract aggregates: .
Observe that pointers, in general, also in LLVM maintain two pieces of information about memory location: they represent both the memory object and an offset into that object. In particular, our implementation treats the first 32-bits of the pointer as an object identifier and the last 32-bits as its offset. This distinction is not very relevant in explicit programs because those two components are represented in a uniform way in a single value and often they cannot be distinguished at all. However, the distinction becomes relevant when dealing with abstract aggregate values. In fact, in this case, the object component of the pointer is concrete as it determines a single specific abstract object. On the other side, the offset component may or may not be concrete. The choice depends on the specific abstract aggregate domain: it may be more advantageous representing the offset in an abstract way, i.e., by a 32-bit abstract scalar value. Observe that a memory access through such a pointer needs to be treated in both cases as an abstract access or update operation.
In LLVM, two basic memory access operations are defined—load and store, corresponding to the access and update operations. It is important to notice that memory access is always explicit: memory is never used in a computation directly. This observation is used in the design of aggregate abstraction, where we can assume that the access to the content of an aggregate will always go through a pointer associated with the abstract object.
6.4. Semantic Abstraction
In syntactic abstraction, we dealt with operations’ syntax, their types, and the types of values and variables. It described how LART performs a source-to-source transformation. In contrast, semantic abstraction concerns with the values computed at runtime by a program. It defines how abstract operations modify values and how to transfer between concrete and abstract values. Therefore, similarly to syntactic abstraction that defined the maps and to transfer between concrete and abstract types, the semantic abstraction makes use of lift and lower (cf. Definitions 9 and 10): operations (instructions) converting values between their concrete and abstract representations. They realize a runtime implementation of domain functions: abstraction ( in the case of M-String) and concretization ().
The lift operation implements abstraction of concrete values by a single over-approximating abstract value. For example, in Figure 2 on line 3 of the abstracted program, a concrete string b is lifted to the abstract domain. This allows performing abstract_strcat in a single abstract domain. In other words, operations do not need to consider concrete values because all their arguments are lifted to the abstract domain. This simplifies the implementation of a domain and reduces the number of possible domain interactions. In comparison to , which was a purely syntactic construct, lift and lower accomplish actual conversion of values between domains during program runtime. During program execution, lowering an abstract value into multiple concrete values can be seen as nondeterministic branching in the program and the lower operator is indeed based on a non-deterministic choice operator. In a model checker, the non-deterministic choice would be typically implemented as branching in the state space and the consequences of all possible outcomes would be explored. In a testing context, however, the choice might implemented as random, by choosing one particular path. For further details of the program transformation performed by LART, we kindly refer the reader to [7].
6.5. Abstract Operations
As a result of syntactic abstraction, we obtain a program that temporarily contains abstract operations. These operations take abstract values as operands and return abstract values as a result. Though, after the program transformation, the resulting program is required to be a semantically valid LLVM bitcode. Therefore, we demand that each abstract operation can be realized as a sequence of concrete instructions. This allows us to obtain an abstract program that does not contain any abstract operations and executes it using standard (concrete, explicit) methods.
Thoroughly, syntactic abstraction substitutes concrete operations with their abstract counterparts: an operation with type is substituted by an abstract operation of type . Furthermore, transformation inserts lift and lower operations as needed, e.g., in places where concrete values are operands of abstract operations. The implementation is free to select the operations to be abstracted and where value lifting and lowering be inserted, so long type constraints are satisfied. However, it tends to minimize the number of abstracted operations.
In addition to LLVM instructions, the M-String abstraction requires the transformation to abstract function calls to standard library functions such as strcmp, strcat. From the perspective of syntactic abstraction, we can treat function calls as single atomic operations that take abstract values and produce abstract results. Hence, the transformation substitutes them in the same way as instructions: for instance strcmp operation of type is replaced by abstract_strcmp of type where m is a concrete character array and s is a concrete scalar result of the string comparison. Afterwards, all abstract operations are implemented by using concrete subroutines (implementation of abstract semantics). For details, see [7].
Observe that, as an alternative approach, the standard library functions strcat, strcmp, etc. could have been transformed instruction by instruction, by using abstract access and update of a content only. However, the price to pay would have been loosing a certain degree of accuracy in the abstraction, the exact amount depending on the single operation.
7. Instantiating M-String
As an aggregate domain, M-String is a parametrizable by scalar domains of characters and indices (bounds). This allows us to tailor the abstraction to the needs of the analysis of string values. Depending on the precision of chosen domains, the instance of the M-String domain will inherit their properties. With more precise domains, the M-String values will maintain higher granularity of segmentation. On the other hand, simpler character representation will decrease the segmentation granularity for the cost of a higher rate of false alarms.
A particular instance of M-String is automatically derived from a parametric description given in Section 5, provided a suitable scalar domain for characters and scalar domain to represent segment bounds. The instantiation demands that both scalar domains and are equipped with operations that appear in the operations with the segmentation. These are mainly elementary arithmetic and relational operations. In the implementation, we provide an M-String domain template that automatically derives all the operations from provided scalar domains.
7.1. Symbolic Scalar Values
In program verification, it is common practice to represent certain values symbolically (for instance, inputs from the environment). The symbolic representation allows the verifier to consider all admissible values with a reasonably small overhead. In DIVINE, symbolic verification is implemented using a similar abstraction to one described in the previous section: symbolic scalar values represent their content by SMT formula expressions (terms) in form of abstract syntax trees. The input values are represented as unconstrained variables in the bit vector logic. Operations then build formulae trees from their arguments. In addition to these so-called data definitions, symbolic representation also maintains one global formula of constraints (path-condition), which is derived from the control flow of the program. A more detailed description of this symbolic representation is presented in [7].
The domain of symbolic values (we call it a term domain) requires DIVINE to be augmented with an SMT solver form a suitable theory. For scalars in C programs, we use the bitvector theory. DIVINE uses the solver to detect computations that have reached the bottom of the term domain (those are the infeasible paths through the program). Furthermore, as a model checker, it needs to identify equal states or whether the state subsumes another one. This is achieved by the equivalence check of corresponding formulae. With these prerequisites, the symbolic representation in joint with the bit-vector theory is a precise abstraction (i.e., it is not an approximation but models the program state faithfully).
7.2. Concrete Characters, Symbolic Bounds
In the evaluation, we instantiate the M-String domain in two ways. The first simpler instantiation sets the domain of characters to be the concrete domain (i.e., we let the characters be represented by themselves). We let the domain of segment bounds to be a symbolic 32b integers. This instantiation balances between simplicity on the one hand (both domains we used for parameters were already present in DIVINE) and the ability to describe strings with undetermined length and structure.
At the implementation level (as described in more detail in the following section), the domain remains generic: the particular domains we picked can be easily substituted by other domains. Compared to the theoretical description of M-String, the implementation uses a slightly simplified representation of segmentation by a pair of arrays (cf. Figure 3). The elements of these arrays are characters and bounds, whose type is derived from parametrization, i.e., from the scalar domains and . The modification of the representation is just optimization for the implementation and does not affect the operations’ semantics. The analysis with this representation is presented in Example 14.

Figure 3.
M-String value with symbolic bounds, where string of interest is from to .
This instantiation of M-String is particularly suitable for representing strings with sequences of a single character of variable length, i.e., the strings of the form where relationships between can be specified using standard arithmetic and relational operators and each of is a concrete letter. This, in turn, allows M-String to be used for the analysis of program behavior on broad classes of input strings described this way. A more detailed description of this approach can be found in Section 8.
Example 14. 
Simple program analysis with symbolic bounds and concrete characters:

Imagine we are given symbolic bounds , then the first line of the transformed program createsmstringvalue with characters and bounds . In the following, we describe mstring values as pairs of these two arrays. The second line creates a symbolic index of arbitrary value. On line 3, the program constraints the index to be smaller than mstring maximal length. Otherwise, the update on the next line would yield an error. Next the program assigns to the position of abstract index a charactery. The assignment is implemented as update operation on mstring value. Depending on the value of the , the operations results in the following strings , as result we join all possibilities:
- if falls to the first segment: and creates a new segment between and containing character . Notice that if the first segment is empty, similarly the third segment for . The string of interest for is of form .
- if than , with string of interest as join of following forms:
- if the update is performed right after the first segment, i.e., :
- -
- if and , i.e., the segment of zeros contains more elements, then the string has form ,
- -
- otherwise the update overwrites the single zero character, hence extends the string of interest by segment of characters: .
- otherwise between first segment and is a terminating zero, hence the string of interest remains unchanged: .
- if than , because update stores the same character as is already present in the segment.
- if than update creates a new segment inside of sequence of last zeros: .
Consequently, the operation on the last line of the program computes the join of all possible lengths of strings of interest, i.e., .
7.3. Symbolic Characters, Symbolic Bounds
The second instantiation is used in benchmarks, where the computation with M-String values encountered abstract scalars (characters). This occurs when the program obtains some character as input from the environment and tries to store it into the M-String value. Therefore, we instantiated the M-String domain with an abstract representation of characters by setting the domain to be the term domain, which keeps track of symbolic 8b bitvectors (characters in C language). In this way, we do not need to lower abstract characters before storing them to the M-Strings, what was needed for the concrete domain used in the previous instantiation. However, we pay the price for more expensive computation with symbolic characters.
7.4. Implementation
Finally, we implemented the M-String abstraction as a LART domain. The implementation, with examples and documentation of domain usage, can be found online on the supplementary page https://divine.fi.muni.cz/2020/mstring. The LART domain is a C++ library that implements abstract semantics of M-String operations presented in Section 5. Such a library is then linked to the transformed program allowing the program to perform abstract analysis with model-checker DIVINE. An abstract domain definition in LART consists of a C++ class that describes both the representation (in terms of data) and the operations (in terms of code) of the abstract domain.
In the case of M-String domain, this class contains 2 attributes: an array of bounds and an array of characters, as outlined in Section 7.2 and depicted in Figure 3. The class has two type parameters: the domain to use for representing segment bounds and the domain to represent individual characters (i.e., the content of segments). A specific instantiation is then automatically derived by the C++ compiler from the classes which represent the type parameters and the parametric class which represents M-String values.
As a minimal set of operations, the M-String domain implements all requisite aggregate operations: these are lift, update and access. Furthermore, the implementation provides an optimized version of string operations described in Section 5: strlen, strcpy, strcat, strcmp and strchr. These operations reduce the loss of abstraction precision that would arise if only the abstraction of accesses and updates from strings were used.
Since C strings are stored, in fact, as shared, mutable character arrays, the implementation of the M-String domain needs to reflect the sharing semantics of such arrays. If multiple pointers exist into the same abstract string, modifications through one such pointer must be also visible when the string is accessed through another pointer. Moreover, the pointers do not have to be equal: they may point to different suffixes of the same string. Therefore, the representation of pointers to abstract strings must treat the object and the offset components separately (see also Section 6.3), and the representation of the offset component must be compatible with the bound domain .
8. Experimental Evaluation
In the evaluation, we chose a few scenarios to demonstrate the properties of the abstraction. In the first scenario, we show that using abstract versions of standard functions is more efficient than if concrete versions were transformed using only abstract string accesses and updates. The second scenario investigates several implementations of standard library functions: we transform them automatically in the means of accesses and updates, and we show that their results agree with results generated by M-String library operations. In the third scenario, we evaluate M-String instantiation with symbolic characters on the set of benchmarks from real software that contain buffer-overflow errors. Here we show that M-String can efficiently detect real-world bugs as well as to prove that program does not contain them after they are fixed. The last benchmark shows the use of abstractions on more complex C programs. As an example, we analyze automatically generated parsers from bison and flex tools on abstract (M-String) inputs. The resource limits for all scenarios were the same: each verification run was limited to 4 processing units (cores), 80 GB of memory, and 1 hour of CPU time. The processor used to run benchmarks was AMD EPYC 7371 clocked at 2.60GHz.
8.1. M-String Operations
The first group of benchmarks focuses on the use of resources by abstraction. Benchmarks compare the effectiveness of abstract domain operations with the automatically abstracted implementation of standard library functions from PDCLib, a public-domain libc implementation, using only essential abstract operations: lift, update and access. The results depicted in Table 2 were measured with parametrized M-String inputs of two kinds (l is a parametric length of the input):

Table 2.
Measurements of M-String operations on two types of inputs: Word and Sequence described in Section 8.1. Each benchmark measures a size of state space and verification time for input M-Strings of a given length. Lastly, the table shows an average transformation time (LART). All measurements of time are in seconds. The size of state space does not change for different lengths of input—for more details, see discussion in Section 8.1.
- Word w is a string of the form: where and is an arbitrary character from domain .
- Sequence w is a string of the form , where and c is a character from domain .
For each standard library function and input type, we created an isolated benchmark in two variants: one using an abstract semantics of M-String operations (see Table 2) and the other variant (Table 3) only with an automatic abstraction of essential aggregate operations.

Table 3.
Benchmark of standard library functions abstracted using only the M-String definitions of access and update operations for Sequence inputs of size 8, 64 and 1024 characters. Verification for Word strings times out in most of the instances.
The first notable difference between automatically abstracted implementations of library functions and M-String operations is that the analysis of the former timeouts for input strings longer than 64 characters. The main cause of the lifted implementation’s inefficiency is that it has to iterate over all characters, while M-String operations leverage iteration over larger segments. This difference also causes a blow-up of the model checker’s state space for the lifted implementations while the state space size does not change for M-String operations. The reason for this is the fact that the number of segments does not change with the length of the input. Therefore M-String operations always perform the same computation independently of the M-String length.
8.2. C Standard Libraries
In the second set of benchmarks (see Table 4), we investigate whether the implementation from several standard libraries matches the expected results of abstract implementation. In other words, we perform an equivalence check of results obtained from M-String operations with the results of the automatically abstracted (originally concrete) standard library functions. We expect that both give the same results. For the evaluation, we picked three open-source libraries: PDClib, musl-libc and CLibc. Since results for the libraries are rather similar, we present here only an evaluation of PDClib functions. The remaining results are provided in the Supplementary Material. All benchmarks showed that our implementation matches the standard one.

Table 4.
Verification results of functions from PDCLib with timeout of 1 h. Measurements show the size of state space and verification time for the parametric length of the input.
Similarly, as in the previous case, these benchmarks suffer from the state space blow up caused by an exponential number of possible character combinations. For this reason, we decreased the size of the input strings. In addition to large state space, many string accesses and updates of concrete implementations result in a large smt formulae, causing a long time spent in solvers.
Furthermore, notice that the computation analysis with Word input, which has more segments, results in longer execution times than the analysis with Sequence. The reason is that the more segments naturally also causes overhead for the analyses. For example, The M-String needs to consider cases when some segments have zero length: this causes a hard smt queries because, in the worst case, it needs to check all possible strings for given segment bounds and characters.
8.3. Veriabs Overflow Benchmarks
In this scenario (see Table 5), we show that the domain is capable of efficient overflow bug finding. Veriabs benchmarks exhibit overflow errors and fixed variants of real-world software. To soundly prove correctness of these benchmarks, we instantiate M-string with term domain also for characters. Hence we can reason about arbitrary strings of a symbolic length. However, as a drawback of this instantiation is that whenever the length of the string bounds a loop, we might have to unroll the loop infinitely in the analysis—these cases timeouts in the correct benchmarks.

Table 5.
Veriabs overflow benchmarks depict a few categories of programs exhibiting an overflow error and their fixed variants. The table shows the number of solved benchmarks (tests) and accumulated time for each category. For each category, the table depicts correctly verified benchmarks, benchmarks where the verifier was able to find an error and number of timeouts.
8.4. Parsers
Lastly, we evaluate our implementation on more complex programs: automatically generated parsers. For the generation, we use a tool Bison. It reads a language specification in the form of context-free grammar and produces a C parser that accepts the language. In the benchmarks, we generate two such parsers. The first one accepts a language of numerical expressions (mathematical expressions that consist of numbers and binary operators). The second parser is of a simple programming language with variables and branching. We present a evaluation for both parsers in Table 6. As with the previous benchmark sets, the M-String inputs with a smaller number of segments outperformed other analyses. In these benchmarks, we use specifically hand-crafted M-String inputs for parsers. For parsing of mathematical expressions, it was: addition input had a form of two arbitrary numbers with a plus sign between them, ones was a simple input of a single digit sequence, and lastly, alternation was input that produced complicated M-Strings by alternating digits inside of expressions. The other parser of simple programming language was evaluated on: value was in input that created a variable and assigned a constant to it, loop was a short program with some control flow and wrong was a program that contained a syntax error.

Table 6.
Measurements of time and size of state space for analyses of automatically generated parsers.
9. Related Work
Static methods tailored to automatically identify buffer overflows have been extensively studied in the literature and several inference techniques were proposed and implemented: tainted data-flow analysis, constraint solvers for various theories (including string theories) and techniques based on them (e.g., symbolic execution), annotation analysis or string pattern matching analysis [17]. Furthermore, the above mentioned techniques and a large number of bug hunting tools based on static analysis have been implemented [18,19,20,21,22,23].
For instance, in [24] authors introduced a backward compatible method of bounds checking of C programs, which leaves the representation of pointers unchanged, allowing inter-operation between checked and unchecked code, with recompilation confined to the modules where problems might occur. The just mentioned feature differentiates the proposed schema from previously existing techniques. In [20] the static verifier of C strings CSSV is introduced. Contracts are supplied to the tool, which acts in 4 stages, reducing the problem of checking code that manipulates string to checking code that manipulates integers. Finally, Splat, described in [25], is a tool that automatically generates test inputs, symbolically reasoning about lengths of input buffers.
Static code analysis aims at approximating possible behaviours of a program without examining all of its (possibly infinite) actual executions. By a proper abstraction of data and operations, static analysis results into an over-approximation of all the possible runs of a program, and its effectiveness heavily depends on degree of precision of such an abstraction. In particular, the framework of abstract interpretation [9] can be adopted also to approximate semantics of string operations. The basic, well-known domain is a string set domain, which simply keeps track of a set of strings and it is a specific instance of the general (bounded) set domain. Others are the prefix-suffix domain (which captures the first and the last letter of a string) and the character inclusion domain (which only tracks the characters that surely or maybe appear in a string). Another general-purpose string domain is the string hash domain proposed in [26], based on a distributive hash function. More complete reviews of general-purpose string domains can be found in [11,27].
Most general-purpose domains focus on the generic aspects of strings, without accounting for the specifics of string handling by the different programming languages. However, it is often beneficial to consider specific aspects of string representation when designing abstract domains for program analysis. Referring to the C programming language, [28] has proposed an abstract domain for C strings which tracks both their length and the buffer allocated size into which they are contained. Combining it with the cell abstraction [29], such domain is able to describe relations between length of variables and offsets of pointers. Amadini et al. [27] have evaluated several abstract string domains (and their combinations) for analysis of JavaScript programs. In [30] was defined the simplified regular expression domain for JavaScript analysis too. In addition to theoretical work, a number of tools based on the above mentioned abstract domains and their combinations have been designed and implemented [30,31,32,33]. While dynamic languages heavily rely on strings and their analysis benefits greatly from tailored abstract domains, the specifics of the C approach to strings also earns attention.
10. Conclusions
A new segmentation-based abstract domain for approximating C strings has been introduced, whose main novelty lies in abstracting both index bounds and substrings while managing strings as a pair of two string buffers: the string of interest itself, and a tail of allocated and possibly initialized but unused memory.
The presented approach enables a more precise modelling of the functions in the standard C library for strings, considering also the known weaknesses for the management of terminating null characters and buffer bounds. The M-string domain results effective for identifying security leaks caused by string manipulation errors, e.g., buffer overflows.
After theoretically describing the domain and the basic operations on strings, we implemented (using C++ language) the abstract semantics combining them with a tool that starting from string-manipulating C codes lifts them to the M-String domain. Our experimental results also focused on tuning the parameters of M-String (the domains for both segment content and segment bounds ) by instantiating them by both concrete and symbolic characters and by symbolic (bitvector) bounds.
As a future work, we plan to further enhance the effectiveness of the M-String domains by combining it by reduced product with other either numerical or symbolic domains.
yes
Supplementary Materials
The supplementary materials at https://divine.fi.muni.cz/2020/mstring contain binary distribution and sources of extended model-checker DIVINE, which is open source software distributed under the ISC license.
Author Contributions
All authors contributed substantially to the work reported. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been partially supported by the Czech Science Foundation grant No. 18-02177S.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cass, S. The Top Programming Languages 2019. IEEE Spectr. Mag. 2019. Available online: https://spectrum.ieee.org/computing/software/the-top-programming-languages-2019 (accessed on 10 February 2020).
- Bultan, T.; Yu, F.; Alkhalaf, M.; Aydin, A. String Analysis for Software Verification and Security; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- One, A. Smashing the Stack for Fun and Profit. Phrack Magazine, 8 November 1996. [Google Scholar]
- Cortesi, A.; Olliaro, M. M-String Segmentation: A Refined Abstract Domain for String Analysis in C Programs. In Proceedings of the Theoretical Aspects of Software Engineering—12th International Symposium (TASE 2018), Guangzhou, China, 29–31 August 2018. [Google Scholar] [CrossRef]
- Cortesi, A.; Lauko, H.; Olliaro, M.; Rockai, P. String Abstraction for Model Checking of C Programs. In Proceedings of the Model Checking Software—26th International Symposium (SPIN 2019), Beijing, China, 15–16 July 2019; pp. 74–93. [Google Scholar] [CrossRef]
- Cousot, P.; Cousot, R.; Logozzo, F. A Parametric Segmentation Functor for Fully Automatic and Scalable Array Content Analysis. In Proceedings of the 38th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL 2011), Austin, TX, USA, 26–28 January 2011; pp. 105–118. [Google Scholar] [CrossRef]
- Lauko, H.; Rockai, P.; Barnat, J. Symbolic Computation via Program Transformation. In Proceedings of the Theoretical Aspects of Computing—15th International Colloquium (ICTAC 2018), Stellenbosch, South Africa, 16–19 October 2018; pp. 313–332. [Google Scholar] [CrossRef]
- Baranová, Z.; Barnat, J.; Kejstová, K.; Kucera, T.; Lauko, H.; Mrázek, J.; Rockai, P.; Still, V. Model Checking of C and C++ with DIVINE 4. In Proceedings of the Automated Technology for Verification and Analysis–15th International Symposium (ATVA 2017), Pune, India, 3–6 October 2017; pp. 201–207. [Google Scholar] [CrossRef]
- Cousot, P.; Cousot, R. Abstract Interpretation: A Unified Lattice Model for Static Analysis of Programs by Construction or Approximation of Fixpoints. In Proceedings of the Conference Record of the Fourth ACM Symposium on Principles of Programming Languages, Los Angeles, CA, USA, 17–19 January 1977; pp. 238–252. [Google Scholar] [CrossRef]
- Cousot, P.; Cousot, R. Systematic Design of Program Analysis Frameworks. In Proceedings of the Conference Record of the Sixth Annual ACM Symposium on Principles of Programming Languages, San Antonio, TX, USA, 29–31 January 1979; pp. 269–282. [Google Scholar] [CrossRef]
- Costantini, G.; Ferrara, P.; Cortesi, A. A Suite of Abstract Domains for Static Analysis of String Values. Softw. Pract. Exper. 2015, 45, 245–287. [Google Scholar] [CrossRef]
- Cousot, P.; Cousot, R. Abstract Interpretation Frameworks. J. Log. Comput. 1992, 2, 511–547. [Google Scholar] [CrossRef]
- Cortesi, A.; Zanioli, M. Widening and Narrowing Operators for Abstract Interpretation. Comput. Lang. Syst. Struct. 2011, 37, 24–42. [Google Scholar] [CrossRef]
- Gange, G.; Navas, J.A.; Schachte, P.; Søndergaard, H.; Stuckey, P.J. Abstract Interpretation over Non-lattice Abstract Domains. In Proceedings of the Static Analysis—20th International Symposium (SAS 2013), Seattle, WA, USA, 20–22 June 2013; Logozzo, F., Fähndrich, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7935, pp. 6–24. [Google Scholar] [CrossRef]
- Seacord, R.C. Secure Coding in C and C++, 2nd ed.; Addison-Wesley Professional: Boston, MA, USA, 2013. [Google Scholar]
- Lattner, C.; Adve, V. LLVM: A Compilation Framework for Lifelong Program Analysis & Transformation. In Proceedings of the International Symposium on Code Generation and Optimization (CGO’04), San Jose, CA, USA, 20–24 March 2004. [Google Scholar] [CrossRef]
- Shahriar, H.; Zulkernine, M. Classification of Static Analysis-Based Buffer Overflow Detectors. In Proceedings of the Fourth International Conference on Secure Software Integration and Reliability Improvement (SSIRI 2010), Singapore, 9–11 June 2010; pp. 94–101. [Google Scholar] [CrossRef]
- Xie, Y.; Chou, A.; Engler, D.R. ARCHER: Using symbolic, path-sensitive analysis to detect memory access errors. In Proceedings of the 11th ACM SIGSOFT Symposium on Foundations of Software Engineering 2003 Held Jointly with 9th European Software Engineering Conference, Helsinki, Finland, 1–5 September 2003; pp. 327–336. [Google Scholar] [CrossRef]
- Wagner, D.A.; Foster, J.S.; Brewer, E.A.; Aiken, A. A First Step Towards Automated Detection of Buffer Overrun Vulnerabilities. In Proceedings of the Network and Distributed System Security Symposium, San Diego, CA, USA, 23–26 February 2020. [Google Scholar]
- Dor, N.; Rodeh, M.; Sagiv, S. CSSV: Towards a Realistic Tool for Statically Detecting All Buffer Overflows in C. In Proceedings of the ACM SIGPLAN 2003 Conference on Programming Language Design and Implementation 2003, San Diego, CA, USA, 9–11 June 2003; pp. 155–167. [Google Scholar] [CrossRef]
- Evans, D.; Larochelle, D. Improving Security Using Extensible Lightweight Static Analysis. IEEE Softw. 2002, 19, 42–51. [Google Scholar] [CrossRef]
- Holzmann, G.J. UNO: Static Source Code Checking for UserDefined Properties. In Proceedings of the 6th World Conference on Integrated Design and Process Technology, IDPT’02, Pasadena, CA, USA, 23–28 June 2002. [Google Scholar]
- MathWorks. Polyspace. 2001. Available online: https://www.mathworks.com/products/polyspace.html (accessed on 10 February 2020).
- Jones, R.W.M.; Kelly, P.H.J. Backwards-Compatible Bounds Checking for Arrays and Pointers in C Programs. Presented at AADEBUG, Linkoping, Sweden, 26–27 May 1997; pp. 13–26. [Google Scholar]
- Xu, R.; Godefroid, P.; Majumdar, R. Testing for Buffer Overflows with Length Abstraction. In Proceedings of the ACM/SIGSOFT International Symposium on Software Testing and Analysis, Seattle, WA, USA, 20–24 July 2008; pp. 27–38. [Google Scholar] [CrossRef]
- Madsen, M.; Andreasen, E. String Analysis for Dynamic Field Access. In Proceedings of the Compiler Construction—23rd International Conference, CC 2014, Held as Part of the European Joint Conferences on Theory and Practice of Software, Grenoble, France, 5–13 April 2014; pp. 197–217. [Google Scholar] [CrossRef]
- Amadini, R.; Jordan, A.; Gange, G.; Gauthier, F.; Schachte, P.; Søndergaard, H.; Stuckey, P.J.; Zhang, C. Combining String Abstract Domains for JavaScript Analysis: An Evaluation. In Proceedings of the European Joint Conferences on Theory and Practice of Software, Uppsala, Sweden, 22–29 April 2017; pp. 41–57. [Google Scholar] [CrossRef]
- Journault, M.; Miné, A.; Ouadjaout, A. Modular Static Analysis of String Manipulations in C Programs. In Proceedings of the Static Analysis—25th International Symposium, Freiburg, Germany, 29–31 August 2018; pp. 243–262. [Google Scholar] [CrossRef]
- Miné, A. Field-sensitive value analysis of embedded C programs with union types and pointer arithmetics. In Proceedings of the 2006 ACM SIGPLAN/SIGBED Conference on Languages, Compilers, and Tools for Embedded Systems (LCTES’06), Ottawa, ON, Canada, 14–16 June 2006; pp. 54–63. [Google Scholar] [CrossRef]
- Park, C.; Im, H.; Ryu, S. Precise and Scalable Static Analysis of jQuery Using a Regular Expression Domain. In Proceedings of the 12th Symposium on Dynamic Languages, Amsterdam, The Netherlands, 1 November 2016; pp. 25–36. [Google Scholar] [CrossRef]
- Spoto, F. The Julia Static Analyzer for Java. In Proceedings of the Static Analysis—23rd International Symposium, Edinburgh, UK, 8–10 September 2016; pp. 39–57. [Google Scholar] [CrossRef]
- Jensen, S.H.; Møller, A.; Thiemann, P. Type Analysis for JavaScript. In Proceedings of the 16th International Static Analysis Symposium, Los Angeles, CA, USA, 9–11 August 2009; pp. 238–255. [Google Scholar] [CrossRef]
- Kashyap, V.; Dewey, K.; Kuefner, E.A.; Wagner, J.; Gibbons, K.; Sarracino, J.; Wiedermann, B.; Hardekopf, B. JSAI: A Static Analysis Platform for JavaScript. In Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering, (FSE-22), Hong Kong, China, 16–22 November 2014; pp. 121–132. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).