An Abstraction Technique for Verifying Shared-Memory Concurrency ^†

Abstract

Modern concurrent and distributed software is highly complex. Techniques to reason about the correct behaviour of such software are essential to ensure its reliability. To be able to reason about realistic programs, these techniques must be modular and compositional as well as practical by being supported by automated tools. However, many existing approaches for concurrency verification are theoretical and focus primarily on expressivity and generality. This paper contributes a technique for verifying behavioural properties of concurrent and distributed programs that balances expressivity and usability. The key idea of the approach is that program behaviour is abstractly modelled using process algebra, and analysed separately. The main difficulty is presented by the typical abstraction gap between program implementations and their models. Our approach bridges this gap by providing a deductive technique for formally linking programs with their process-algebraic models. Our verification technique is modular and compositional, is proven sound with Coq, and has been implemented in the automated concurrency verifier VerCors. Moreover, our technique is demonstrated on multiple case studies, including the verification of a leader election protocol.

1. Introduction

Modern software is typically composed of multiple concurrent components that communicate via shared or distributed interfaces, for example via shared-memory or via message passing. The concurrent nature of the interactions between (sub)components makes such software highly complex as well as notoriously difficult to develop correctly. To ensure the reliability of modern software, verification techniques are much-needed to aid software developers to comprehend all possible concurrent system behaviours. To be able to reason about realistic programs these techniques must be modular and compositional, as well as be supported by automated verification tools.

Even though verification of concurrent and distributed software is a very active research field [1,2,3,4,5,6], most work in this line of research is essentially theoretical, and tends to focus primarily on contributing expressive program logics specialised in reasoning about advanced concurrency features like relaxed or weak memory, fine-grained concurrency, message passing interaction, etc. Even though expressive, it is very challenging for these logics to be integrated into SMT-based automated verifiers like for example VeriFast  [7], VerCors  [8] and Viper  [9,10]. Instead, most of these works have to be applied in pen-and-paper style, or at best semi-automatically in the context of an interactive theorem prover like Coq  [11,12] or Isabelle/HOL [13].

This article contributes a concurrency verification technique that applies directly on the level of program code and is supported by automated verifiers. However, rather than doing the verification fully on the level of program code, our approach allows soundly abstracting program behaviour into abstract models which can be reasoned about externally, on a higher level in which irrelevant implementation details are hidden, to (indirectly) prove properties about the program behaviour. The presented verification technique (1) has been implemented in VerCors—an automated SMT-based concurrency verifier; (2) is demonstrated on various (real-world) examples, including a leader election protocol (presented in Section 5); and (3) the metatheory of the technique has been fully formalised and proven sound with the Coq proof assistant. With respect to (2); apart from the examples given in this article, more examples of our approach are given in [14], including the verification of a (reentrant) lock as well as a concurrent parallel GCD algorithm. Our technique has also been used in a real-world industrial case study [15]—on the formal verification of a safety-critical traffic tunnel control system.

This article extends our earlier VMCAI’20 article [16]. Elaborating on the contributions with respect to this earlier article; we contribute a generalisation of the theory in [16] by combining it with the techniques proposed in [17] and [18] into a single logical framework that is more general than the original. This combined unified framework is proven sound with Coq and is available online at [19].

1.1. Motivation

Reasoning about complex concurrent program behaviours is only practical if conducted at a suitable level of abstraction that hides implementation details that are irrelevant for the properties to prove. Furthermore, any real concurrent programming language with shared memory, threads and locks, has only very little algebraic behaviour. In contrast, process algebras offer an abstract, mathematically elegant way of expressing program behaviour. Process algebras have been used widely in the past for modelling and analysing the behaviour of concurrent programs at an adequate level of abstraction [20,21]. Our approach therefore uses a process algebra as a language for specifying program behaviour. Such a specification can be seen as a model, the properties of which can additionally be checked (say by interactive theorem proving, or by model checking against temporal logic formulas, which can be seen as even more abstract behavioural specifications). The main difficulty of this approach is dealing with the typical abstraction gap between program implementations and their abstract models. The unique contribution of our approach is that it bridges this gap by providing a deductive technique for formally linking programs with their process-algebraic models. These formal links preserve safety properties [22]; we leave the preservation of liveness properties for future work.

The key idea of the approach rests in the use of concurrent separation logic (CSL) to reason not only about data races and memory safety, which is standard [23,24], but also about process-algebraic models (that is, specified program behaviours), viewing the latter as resources that can be split and consumed. This results in a modular and compositional approach to establish that a program behaves as specified by its abstract model. Our approach is formally justified by (mechanically proven) correctness results stating that any verified program is a refinement of its abstract, process-algebraic model.

Process-algebraic models are composed out of individual actions that abstract atomic behaviours of program components. Our approach allows specifying program components to follow a particular sequence/pattern of actions—a protocol. One can then reason about the interaction behaviour of different program components by reasoning about the composition of their models, for example by using a model checker for process algebra, like mCRL2  [25]. This approach of specifying the interactions of program components is different from classical Hoare logic, which is purely transformational in the sense that it considers verified (terminating) program components essentially as transformers from states satisfying the specified precondition to states satisfying the specified postcondition.

A benefit of our combined approach compared to model checking is that it allows reasoning soundly about both data and control-oriented properties in a single framework. Model checkers typically specialise in reasoning about temporal, control-oriented specifications (e.g., send actions must always be matched by a recv), and generally have limited support for handling data due to the risk of state-space explosions. Hoare logic based techniques, on the other hand, tend to specialise in reasoning about data specifications (e.g., a sorting function should yield a sorted permutation of its input), and are typically limited in their capabilities to reason about control-flow properties. Since realistic concurrent systems often deal with both data and control-flow, it is beneficial to be able to reason about both in a single framework. Additionally, our technique addresses the typical “abstraction gap” problem of model checking: is the model actually a faithful abstraction of the modelled system? We propose techniques to formally link programs to their abstract models, allowing one to prove that all program behaviours that should be captured by the abstract model are indeed soundly abstracted.

1.2. Contributions

The main contributions of this extended article are:

• A verification technique to reason about the behaviour of shared-memory concurrent programs that is modular, compositional, and proven sound. This article extends [16] by generalising its verification technique and combining it with the core ideas of [17,18]. In particular, it extends the process algebra specification language with summations, support for input parameters, and the assertional processes of [17], which shall all be introduced later, in Section 3.
• A full Coq development of the formalisation as presented in Section 3, together with a soundness proof of the approach. The Coq sources and their documentation are available at [19].
• Several examples that demonstrate this new (unified) verification approach, including a leader election protocol case study discussed in Section 5.

1.3. Outline

The remainder of this article is organised as follows. First Section 2 illustrates our technique on a small Owicki–Gries example program, before Section 3 gives theoretical justification of the verification technique. In particular, Section 3.1 introduces the process algebra specification language, after which Section 3.2 introduces the programming language on which the approach is formalised on. Section 3.3 defines and discusses the syntax and semantics of the assertion language, which is a concurrent separation logic with special constructs to to handle process-algebraic models. Section 3.4 discusses the proof system and Section 3.4 its soundness. Section 4 gives details on how the verification technique is implemented in the concurrency verified VerCors, and briefly elaborates on the Coq development. Section 5 demonstrates the approach on a larger case study: the verification of a classical leader election protocol. Finally, Section 6 discusses related work and Section 7 concludes.

2. Approach

Before going into the formal details of the approach, let us first illustrate it on a simple example. Our approach allows abstractly specifying concurrent program behaviour as process-algebraic models. Processes are composed of atomic, indivisible actions. In our approach the actions are logical descriptions of shared-memory modifications: they describe what changes the program is allowed to make to a specified region of shared memory—the program heap. These actions are then linked to the concrete instructions in the program code that perform the memory updates. These links between program components and their abstract models are established deductively, using a concurrent separation logic that is presented later. Well-known techniques for process-algebraic reasoning can then be applied to guarantee safety properties over all possible state changes, as described by their compositions of actions. The novelty of the approach is that these safety properties can then be relied upon in the program logic due to the established formal connection between program components and their process-algebraic models.

2.1. Example Program

Consider the following example program, which is a simple variant of the classical concurrent Owicki–Gries program [26].

$$\mathtt{atomic}\left\{X:=\left[E\right];\left[E\right]:=X+4\right\}\left|\right|\mathtt{atomic}\left\{Y:=\left[E\right];\left[E\right]:=Y\ast 4\right\}$$

This program consists of two threads: one that atomically increments the value at heap location E by four, while the other atomically multiplies the value at E by four. The notation $\left[E\right]$ denotes heap dereferencing, with E an expression whose evaluation determines the heap location to dereference.

The challenge is to modularly deduce the classical Owicki-Gries postcondition: after termination the value at heap location E is either $4\ast ({\mathit{old}}_{\mathit{E}}+4)$ or $(4\ast {\mathit{old}}_{\mathit{E}})+4$ (depending on the interleaving of threads), where ${\mathit{old}}_{\mathit{E}}$ is the “old value at E”—the value of E at the pre-state of the computation.

Well-known existing classical approaches and techniques to deal with such concurrent programs [27] include auxiliary state [26] and interference abstraction via rely-guarantee reasoning [28]. Modern program logics employ more intricate constructs, like atomic Hoare triples [5] in the context of TaDa, or higher-order ghost state [29] in the context of Iris. However, the mentioned classical approaches typically do not scale well, whereas such modern, theoretical approaches are hard to integrate into (semi-)automated SMT-based verifiers like for example VeriFast or VerCors.

In contrast, our approach makes a balanced trade-off between expressivity and usability: it is scalable as well as implemented in an automated deductive verifier.

The approach consists of the following three steps:

Step 1.

Define a process-algebraic model $\mathtt{OG}=(\mathtt{incr}\left(4\right)\Vert \mathtt{mult}\left(4\right))·?\left(b_{\mathtt{post}}\right)$ that is composed out of two actions, $\mathtt{incr}$ and $\mathtt{mult}$, that abstract the two atomic sub-programs;

Step 2.

Verify that the $\mathtt{OG}$ process indeed satisfies the Owicki–Gries postcondition, $b_{\mathtt{post}}$; and

Step 3.

Deductively verify that $\mathtt{OG}$ is a correct behavioural specification of the program’s execution flow. That is, verify that every atomic state change that is executed by a run of the program has a corresponding action in OG.

The following paragraphs give more detail on these three steps.

2.1.1. Step 1: Specifying Program Behaviour

The first step is to construct a behavioural specification OG of the example program. The OG process is defined to be the parallel composition of the actions $\mathtt{incr}\left(4\right)$ and $\mathtt{mult}\left(4\right)$, which specify the behaviour of the atomic increment and multiplication in the program, respectively. In our approach, program behaviour is specified logically, by associating a contract to every action. For the example program, incr and mult would have the following contract:

$$\begin{array}{cc}\mathtt{guard}\mathtt{true};\hfill & \mathtt{guard}\mathtt{true};\\ \mathtt{effect}x=\backslash \mathtt{old}\left(x\right)+n;\hfill & \mathtt{effect}x=\backslash \mathtt{old}\left(x\right)\ast n;\\ \mathtt{action}\mathtt{incr}\left(\mathtt{int}n\right);\hfill & \mathtt{action}\mathtt{mult}\left(\mathtt{int}n\right);\end{array}$$

Any action contract consists of a guard and an effect. The guard of any action specifies the condition under which the action is allowed to be executed. In the above example, the guard of both incr and mult is specified to be true, meaning that both these actions may unconditionally be performed. The effect clause of any action specifies the way the action is allowed to change the (program) state. Observe that incr and mult are indeed abstractions of the two atomic sub-programs, and that the effect clauses of these actions are abstract specifications of how the program updates the heap. (Note that one could think of guards and effect of actions as pre- and postconditions, respectively. However, they are not strictly the same (hence the slightly different terminology). For the sake of process-algebraic analysis all action contracts can be assumed to hold, while on the program level one has to prove that sets of instructions that correspond to the action satisfy the action contract, as will be explained in a moment.) Note that both these abstract specifications contain a free variable x, which is a process-algebraic variable that is later linked to a concrete heap location in the program (this will be $\left[E\right]$). Moreover, the increment and multiplication of 4 has now been generalised to an arbitrary integer n.

These two actions may be composed into a full behavioural specification of the example program, by also assigning a top-level contract to OG:

requires$\mathtt{true}$;

process$\mathtt{OG}\left(\mathtt{int}n\right):=(\mathtt{incr}\left(n\right)\Vert \mathtt{mult}\left(n\right))·?\left(x=\left(\backslash \mathtt{old}\right(x)+n)\ast n\vee x=\backslash \mathtt{old}\left(x\right)\ast n+n\right)$;

Notice that the $\mathtt{OG}$ process has the form $(\mathtt{incr}\left(n\right)\Vert \mathtt{mult}\left(n\right))·?\left(b_{\mathit{post}}\right)$ with $b_{\mathit{post}}$ the Owicki–Gries postcondition. Here · denotes sequential composition, and $?\left(b_{\mathit{post}}\right)$ is an assertion process. These assertions are the main subject of process-algebraic reasoning: we verify that all asserted properties are never violated. Here we specify that $?\left(b_{\mathit{post}}\right)$ holds after executing $\mathtt{incr}\left(n\right)$ and $\mathtt{mult}\left(n\right)$ in any order.

The $\mathtt{OG}$ process also has a precondition that could potentially impose restrictions on the values of n. But for this Owicki–Gries example we do not have any such restrictions. Note that postconditions (that is, ensures clauses) are encoded as assertional processes, like done above.

2.1.2. Step 2: Process-Algebraic Reasoning

The next step is to verify that OG satisfies all properties b that are encoded as assertions $?\left(b\right)$, which can be reduced to standard process-algebraic analysis. Intuitively we say that $\mathtt{OG}$ is verified if, starting from any state satisfying $\mathtt{OG}$’s $\mathtt{requires}$ clause, the process can never reach an asserted property b that does not hold. We shall later give a more formal definition of what it means for a process to be verified with respect to its precondition, in Section 3.4.2.

The standard approach to analysing $\mathtt{OG}$ would be to first linearise it to the bisimilar process $\mathtt{incr}\left(n\right)·\mathtt{mult}\left(n\right)·?\left(b_{\mathit{post}}\right)+\mathtt{mult}\left(n\right)·\mathtt{incr}\left(n\right)·?\left(b_{\mathit{post}}\right)$, where + denotes non-deterministic choice and with $b_{\mathit{post}}$ again the Owicki–Gries postcondition, and then to reason about all branches of this linearised process. With “reasoning about all branches” we intuitively mean establishing that all assertions encountered during any execution of a process are a logical consequence of the series of effects preceding the assertion. A formal definition is provided later in Section 3.1. VerCors currently does the analysis by encoding the linearised process as input to the Viper verifier [10]. VerCors can indeed automatically prove that OG satisfies the asserted property.

2.1.3. Step 3: Deductively Linking Processes to Programs

The key idea of our approach is that, by analysing how contract-complying action sequences change the values of process-algebraic variables, we may indirectly reason about how the content at heap location $\left[E\right]$ evolves over time. So the final step is to project this process-algebraic reasoning onto program behaviour, by annotating the program.

Figure 1 shows the required program annotations. First, x is connected to $\left[E\right]$ by initialising a new model M on line 2 that executes according to $\mathtt{OG}\left(4\right)$. The actions $\mathtt{incr}$ and $\mathtt{mult}$ are then linked to the corresponding sub-programs on lines 5–7 and 11–13 by identifying action blocks in the code, using special program annotations. We use these $\mathtt{action}$ annotations to verify in a thread-modular way that the left thread performs the $\mathtt{incr}\left(4\right)$ action (on lines 5–7) and that the right thread performs $\mathtt{mult}\left(4\right)$ (lines 11–13). As a result, when the program reaches the $\mathtt{query}$ annotation on line 15, only the $?\left(b_{\mathit{post}}\right)$ process is left on the process level—the $\mathtt{incr}\left(4\right)\Vert \mathtt{mult}\left(4\right)$ part has already been executed alongside the program. Since the Owicki–Gries postcondition $b_{\mathit{post}}$ is already proven externally, by other means, in the previous step, the program logic may rely on its validity. But since we tracked the contents at heap location $\left[E\right]$ on the process level as the variable x, one may indirectly conclude that the heap at location $\left[E\right]$ has evolved as described by $\mathtt{OG}$. In other words, using program annotations we prove that the program is a refinement of $\mathtt{OG}$, meaning that we get the asserted property in the logic, on line 17.

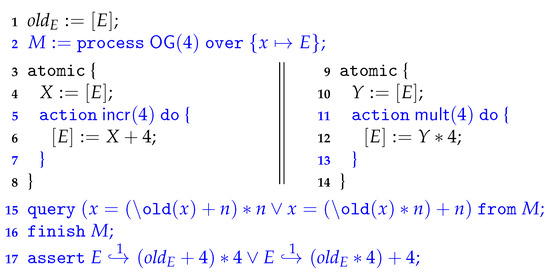
Figure 1. The annotated Owicki–Gries example (the annotations are coloured blue).

Finally, the $\mathtt{finish}$ annotation on line 16 indicates that the model has been fully reduced at that point, and thus may be disposed of. This is for technical reasons; the program logic will do some bookkeeping while dealing with process-algebraic abstractions, and $\mathtt{finish}$ will cause this bookkeeping to be cleaned up. This is later discussed in greater detail, in Section 3.4.2.

3. Formalisation

We now give theoretical justification of the verification approach and explains the underlying logical machinery. First, Section 3.1 and Section 3.2 briefly discuss the syntax and semantics of process algebraic models and programs, respectively. Then Section 3.3 presents the program logic as a  concurrent separation logic with assertions that allow to specify program behaviour as a process algebraic model. Section 3.4 formally introduces and discusses the proof rules. Finally, Section 3.5 discusses soundness of the approach. All these components have been fully formalised in Coq, including the soundness proof of the logic. Section 4 elaborates on the Coq development of the meta-theory, as well as on tool support, developed for the VerCors concurrency verifier.

3.1. Process-Algebraic Models

Program abstractions are defined using the following ACP-style [30] process-algebraic specification language, where $x,y,z,\cdots \in \mathit{ProcVar}$ are process-algebraic variables; $v,w,\cdots \in \mathit{Val}$ are values from an infinite domain $\mathit{Val}$; and $a,\cdots \in \mathit{Act}$ are (process-algebraic) actions.

Definition 1

(Processes).

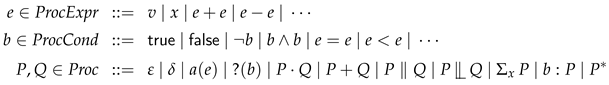
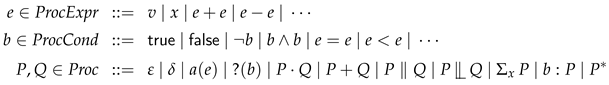
Clarifying the different connectives and constructs, $\epsilon$ is the empty process, which has no behaviour. The $\delta$ process is the deadlocked process which neither progresses nor terminates. Processes of the form $a\left(e\right)$ are actions, which model the basic, observable (shared-memory) system behaviours. Actions are parameterised by data, in the form of expressions e. The process $P·Q$ is the sequential composition of P and Q, whereas $P+Q$ is their non-deterministic choice. The parallel composition of processes P and Q is written $P\Vert Q$. The process P Q is the left-merge of P and Q, which is similar in spirit to parallel composition, however insists that the left-most process P proceeds first. The left-merge is an auxiliary connective commonly used to axiomatise parallel composition [31], by having $P\Vert Q=$PQ + QP. The process ${\Sigma }_{x}P$ is the infinite summation $P[x/v_0]+P[x/v_1]+\cdots$ over all values $v_0,v_1,\dots \in \mathit{Val}$. Any summation ${\Sigma }_{x}P$ is a binder for the summation variable x. In the remainder we assume without loss of generality that all variables bound by summation are unique (since any such variables can be renamed to unique ones if this is not yet the case). Sometimes ${\Sigma }_{x_0,\cdots ,x_n}P$ is written to abbreviate ${\Sigma }_{x_0}\cdots {\Sigma }_{x_n}P$. The conditional (guarded) process $b:P$ behaves as P if the Boolean condition b holds, and otherwise behaves as $\delta$. Finally, $P^{\ast }$ is the repetition, or iteration of P, and denotes a sequence of zero or more P’s. The infinite iteration of P is derived to be $P^{\omega }\triangleq P^{\ast }·\delta$. Finally, $?\left(b\right)$ is the assertive process, which is very similar to guarded processes: $?\left(b\right)$ is behaviourally equivalent to $\delta$ in case b does not hold. However, assertive processes have a special role in our approach: they are the main subject of process-algebraic analysis, as they encode the properties b to verify, as logical assertions. Moreover, they are a key component in connecting process-algebraic reasoning with deductive reasoning, as their properties can be relied upon in the deductive proofs of programs via the $\mathtt{query}b$ ghost command.

3.1.1. Action Contracts

The presented verification approach uses processes in the presence of data, which is implemented via action contracts. Action contracts consist of pre- and postconditions which we refer to as guards and effects, respectively, that logically describe the state changes that are imposed by the corresponding action. In the remainder of this article, each action is assumed to have an action contract assigned to it. Instead of defining syntax for writing these contracts, the following two functions are assumed for obtaining the pre- and postcondition of an action (from $\mathit{Act}$) and its data parameter (from $\mathit{ProcExpr}$), respectively.

$$\mathtt{guard}:\mathit{Act}\to \mathit{ProcExpr}\to \mathit{ProcCond}\hspace{1em}\mathtt{effect}:\mathit{Act}\to \mathit{ProcExpr}\to \mathit{ProcCond}$$

Both these conditions are of type $\mathit{ProcCond}$, which is the domain of Boolean expressions over process-algebraic variables. Note that, since actions are parameterised by data (see Definition 1), both $\mathtt{guard}$ and $\mathtt{effect}$ take a second argument to account for the input parameter, which is of type $\mathit{ProcExpr}$—the type of arithmetic expressions over process-algebraic variables.

Here $\mathit{Act}\to \mathit{ProcExpr}\to \mathit{ProcCond}$ should be read as $\mathit{Act}\to (\mathit{ProcExpr}\to \mathit{ProcCond})$ and interpreted as a function sequence (in the sense of currying). That is, it is the set of functions mapping $\mathit{Act}$ to the set of functions mapping $\mathit{ProcExpr}$ to $\mathit{ProcCond}$.

3.1.2. Free Variables and Substitution

A function ${\mathtt{fv}}_{\mathtt{e}}:\mathit{ProcExpr}\to 2^{\mathit{ProcVar}}$ is used to determine the set of free process-algebraic variables in expressions as usual, and likewise for ${\mathtt{fv}}_{\mathtt{e}}\left(b\right)$ and ${\mathtt{fv}}_{\mathtt{P}}\left(P\right)$ for Boolean expressions b and processes P. We often omit the subscripts and simply write $\mathtt{fv}(·)$ whenever the context allows it. The definitions of ${\mathtt{fv}}_{\mathtt{e}}$, ${\mathtt{fv}}_{\mathtt{b}}$ and ${\mathtt{fv}}_{\mathtt{P}}$ are mostly standard and thus deferred to [19]. Noteworthy however are:

$${\mathtt{fv}}_{\mathtt{P}}\left(a\left(e\right)\right)\triangleq {\mathtt{fv}}_{\mathtt{b}}\left(\mathtt{guard}ae\right)\cup {\mathtt{fv}}_{\mathtt{b}}\left(\mathtt{effect}ae\right)\hspace{1em}{\mathtt{fv}}_{\mathtt{P}}\left({\Sigma }_{x}P\right)\triangleq {\mathtt{fv}}_{\mathtt{P}}\left(P\right)\backslash \left\{x\right\}\hspace{1em}{\mathtt{fv}}_{\mathtt{P}}\left(?\left(b\right)\right)\triangleq {\mathtt{fv}}_{\mathtt{e}}\left(b\right)$$

Substitution is written $e^{\prime }[x/e]$ (and likewise for Boolean expressions and processes) and has a standard definition: replacing any occurrence of x inside $e^{\prime }$ by the expression e. Noteworthy is that substitutions inside action processes $a\left(e\right)$ do not affect the action contracts: $a\left(e^{\prime }\right)[x/e]\triangleq a\left(e^{\prime }[x/e]\right)$.

3.1.3. Operational Semantics

The denotational semantics of process-algebraic expressions ${\left[[·]\right]}_{\mathsf{e}}:\mathit{ProcExpr}\to \mathit{ProcStore}\to \mathit{Val}$ and conditions ${\left[[·]\right]}_{\mathsf{b}}:\mathit{ProcCond}\to \mathit{ProcStore}\to \mathit{Bool}$ is defined in the standard way, as total functions that evaluate to $\mathit{Val}$ and $\mathit{Bool}$, resp. The set $\sigma \in \mathit{ProcStore}\triangleq \mathit{ProcVar}\to \mathit{Val}$ is the domain of process stores, which are used to give an interpretation to all process-algebraic variables. The overloaded notations $\left[\right[e\left]\right]\sigma$ and $\left[\right[b\left]\right]\sigma$ are used instead of ${\left[\left[e\right]\right]}_{\mathsf{e}}\sigma$ and ${\left[\left[b\right]\right]}_{\mathsf{b}}\sigma$ wherever the context allows it. Moreover, $\left[\right[e\left]\right]$ is sometimes written instead of ${\left[\left[e\right]\right]}_{\mathsf{e}}\sigma$ when e is closed (i.e., when $\mathtt{fv}\left(e\right)=\varnothing$), and likewise for $\left[\right[b\left]\right]$.

The operational semantics of the process algebra language is expressed as a labelled binary small-step reduction relation $\stackrel{\alpha }{⟶}\subseteq \mathit{ProcConf}\times \mathit{ProcLabel}\times \mathit{ProcConf}$ over process configurations, defined as $\mathit{ProcConf}\triangleq \mathit{Proc}\times \mathit{ProcStore}$—pairs of processes and process stores. The labels $\alpha$ of the reduction rules are defined as follows: $\alpha \in \mathit{ProcLabel}::=a\left(v\right)|\mathit{assn}$. Transitions labelled $a\left(v\right)$ are reductions of actions, whereas $\mathtt{assn}$ indicates reductions of assertions.

Before giving the reduction rules we first define a notion of successful termination $P\downarrow$ of processes P. Successful termination is only defined for processes that are well-formed. Any process P is defined to be well-formed if any action parameters (the e’s in $a\left(e\right)$) and conditions (the b’s in $b:Q$) occurring inside P are closed.

Definition 2

(Successful termination).

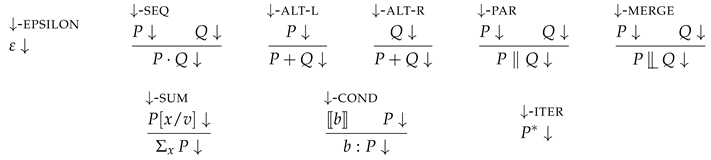
Intuitively, any process P can terminate successfully if P has the choice to have no further behaviour. This means that $\epsilon$ can always successfully terminate (↓-EPSILON), as it has no behaviour, while $\delta$ can never successfully terminate. Iteration $P^{\ast }$ can always successfully terminate (↓-ITER) as it may choose not to start iterating and thereby to behave as $\epsilon$.

The small-step reduction rules of process configurations are given below. Likewise to the definition of successful termination, also these reduction rules require processes to be well-formed.

Definition 3

(Reductions of process configurations).

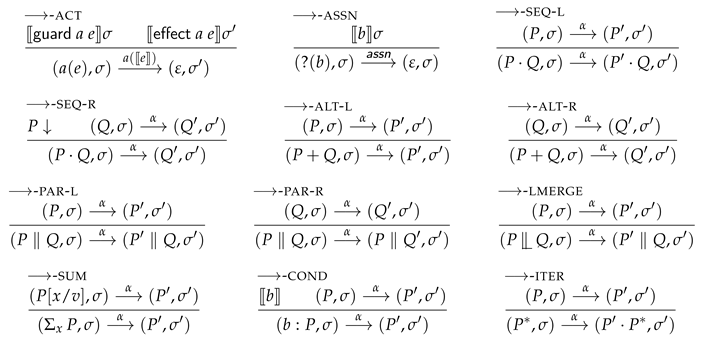
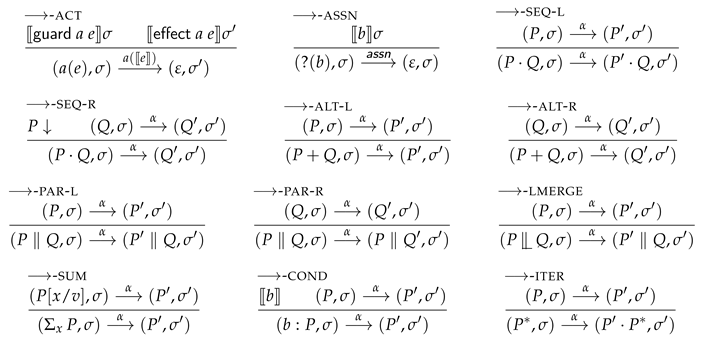
Most of the reduction rules are standard in spirit [32]. However, the handling of actions and their contracts make this process algebra language non-standard. More specifically, the non-standard ⟶-ACT reduction rule for action handling permits the state $\sigma$ to change in any way, as long as these changes comply with the action contract. We will later use the ⟶-ACT rule to connect shared-memory updates in programs, to action contract-complying state changes on the process level.

Moreover, the notion of successful termination is used to define the reduction rule for sequential composition, ⟶-SEQ-R, which is standard in process algebra languages with $\epsilon$ [33]. (An alternative on the explicit use of successful termination is to introduce internal ($\tau$-)transitions for the reductions of $\epsilon$. However, this might make the remaining formalisation less elegant, for example by requiring a notion of weak bisimilarity, instead of the notion of strong bisimilarity that is introduced later in this section.)

3.1.4. Process-Algebraic Verification

Process-algebraic verification in our approach amounts to verifying that all reachable assertional processes $?\left(b\right)$ are always satisfied, which we are interested in so that the program logic can rely on the b’s. Any process configuration $(P,\sigma )$ fails to verify, or exhibits a fault, which we write $↯\left(P,\sigma \right)$, if it can directly violate an assertion. Verifying a process, i.e., checking for fault absence, could for example be reduced to checking the $\mu$-calculus formula $[{\mathtt{true}}^{\ast }·↯]\mathtt{false}$, e.g., using the mCRL2 model checker, where ↯ is modelled as an explicit fault state, meaning “no faults are every reachable”.

Fault exhibition is defined inductively as follows.

Definition 4

(Faulting process configuration).

Any process configuration $(P,\sigma )$ is defined to be safe, denoted as $\left(P,\sigma \right)$, if it can never reach a faulting configuration. More formally:

Definition 5

(Safe process configurations). The $✓\subset \mathit{ProcConf}$ predicate is coinductively defined such that, whenever $✓\left(P,\sigma \right)$ holds, then(1)$\neg ↯\left(P,\sigma \right)$; and (2) for any $P^{\prime }$, ${\sigma }^{\prime }$ and α, if $(P,\sigma )\stackrel{\alpha }{⟶}(P^{\prime },{\sigma }^{\prime })$, then $✓\left(P,\sigma \right)$.

Definition 6

(Verified processes). Any well-formed process P is defined to be verified with respect to a (pre)condition b, which is written $\models \left\{b\right\}P$, if $\forall \sigma .\left[\right[b\left]\right]\sigma \Rightarrow ✓\left(P,\sigma \right)$.

3.1.5. Bisimulation

Our verification approach allows handling process-algebraic models up to (strong) bisimulation.

Definition 7

(Bisimulation). Any binary relation $\mathcal{R}\subseteq \mathit{Proc}\times \mathit{Proc}$ over processes is defined to be a  bisimulation relation if, whenever $P\mathcal{R}Q$, then:

(1) 

$P\downarrow$ if and only if $Q\downarrow$.

(2) 

$↯\left(P,\sigma \right)$ if and only if $↯\left(Q,\sigma \right)$, for any σ.

(3) 

For any σ, $P^{\prime }$, ${\sigma }^{\prime }$ and α, if $(P,\sigma )\stackrel{\alpha }{⟶}(P^{\prime },{\sigma }^{\prime })$, then there exists a $Q^{\prime }$ such that $(Q,\sigma )\stackrel{\alpha }{⟶}(Q^{\prime },{\sigma }^{\prime })$ and $P^{\prime }\mathcal{R}{Q}^{\prime }$.

(4) 

For any σ, $Q^{\prime }$, ${\sigma }^{\prime }$ and α, if $(Q,\sigma )\stackrel{\alpha }{⟶}(Q^{\prime },{\sigma }^{\prime })$, then there exists a $P^{\prime }$ such that $(P,\sigma )\stackrel{\alpha }{⟶}(P^{\prime },{\sigma }^{\prime })$ and $P^{\prime }\mathcal{R}{Q}^{\prime }$.

Any two processes P and Q are defined to be bisimilar, or bisimulation equivalent, written $P\cong Q$, if and only if there exists a bisimulation relation $\mathcal{R}$ such that $P\mathcal{R}Q$. Bisimilarity expresses that both processes exhibit the same behaviour, in the sense that their action sequences describe the same state changes. Any bisimulation relation constitutes an equivalence relation. Furthermore, bisimilarity is a congruence for all process algebraic connectives.

Successful termination $P\downarrow$ can intuitively be understood as P being bisimilar to the process $\epsilon +P$, that is, by having the choice to have no further behaviour.

Proposition 1.

If $P\downarrow$ then $P\cong \epsilon +P$.

Lemma 1.

If $P\cong Q$ and $✓\left(P,\sigma \right)$, then $✓\left(Q,\sigma \right)$.

Figure 2 gives a list of bisimulation equivalences that hold for our process algebra language. Note that the left-merge connective is not strictly needed, in the sense that our approach does not rely on it, but can be used to prove for example that $a\left(e\right)\Vert a^{\prime }\left(e^{\prime }\right)$ is bisimilar to $a\left(e\right)·a^{\prime }\left(e^{\prime }\right)+a^{\prime }\left(e^{\prime }\right)·a\left(e\right)$.

Figure 2. Standard bisimulation equivalences of the process algebra language.

3.2. Programs

Our verification approach is formalised on the following simple concurrent pointer language, where $X,Y,\cdots \in \mathit{Var}$ are (program) variables.

Definition 8

(Expressions, conditions, conditions, commands).

$$\begin{array}{cc}\hfill E\in \mathit{Expr}::=& v\left|X\right|E+E|E-E|\cdots \hfill \\ \hfill B\in \mathit{Cond}::=& \mathtt{true}\left|\mathtt{false}\right|\neg B|B\wedge B|E=E|E<E|\cdots \hfill \\ \hfill \mathsf{\Pi }\in \mathit{AbstrBinder}::=& \left\{x_0\mapsto E_0,\cdots ,x_n\mapsto E_n\right\}\hfill \\ \hfill C\in \mathit{Cmd}::=& \mathtt{skip}|X:=E|X:=\left[E\right]\left|\right[E]:=E|C;C|X:=\mathtt{alloc}E|\mathtt{dispose}E|\hfill \\ \hfill & \mathtt{if}B\mathtt{then}C\mathtt{else}C\left|\mathtt{while}B\mathtt{do}C\right|\mathtt{atomic}C\left|\mathtt{inatom}C\right|C\Vert C|\hfill \\ \hfill & X:=\mathtt{process}(\lambda x.P)\left(E\right)\mathtt{over}\mathsf{\Pi }\left|\mathtt{action}Ea\left(E\right)\mathtt{do}C\right|\mathtt{inact}C|\hfill \\ \hfill & \mathtt{finish}E|\mathtt{query}E\hfill \end{array}$$

This language is a variation of the language proposed by O’Hearn [24] and Brookes [23]. In particular, we extend their language with specification-only commands (code annotations) for handling process-algebraic models. These commands are coloured blue. Note that the blue colourings do not have any semantic meaning; they only indicate which language constructs are specification-only. Moreover, we interchangeably refer to commands also as programs.

3.2.1. Standard Language Constructs

The notation $\left[E\right]$ stands for heap dereferencing, where E is an expression whose evaluation determines the heap location to dereference. The commands $X:=\left[E\right]$ and $\left[E\right]:=E^{\prime }$ denote heap reading and writing: they read from, and write to, the heap at location E, respectively. Moreover, $X:=\mathtt{alloc}E$ allocates a free heap location and writes the value represented by E to it, whereas $\mathtt{dispose}E$ deallocates the heap location at E.

Regarding concurrency, the command $C_1\Vert C_2$ is the statically-scoped parallel composition of $C_1$ and $C_2$ and expresses their concurrent execution. In the sequel, we sometimes refer to commands that are put in parallel as different threads; for example $C_1$ and $C_2$ in the above. Moreover, $\mathtt{atomic}C$ expresses a statically-scoped lock: it represents the atomic execution of C, that is, without interference of other threads. The command $\mathtt{inatom}C$ represents partially executed atomic programs: ones that are currently being executed, where C is the remaining program that still has to be executed atomically. Such commands are sometimes referred to as “runtime syntax”, as they are not written by users of the language, but are instead an artefact of program execution.

3.2.2. Specification-Only Constructs

The instructions that are displayed in blue are the specification-only language constructs, for handling process-algebraic models in the logic. These instructions are ignored during regular program execution and are essentially handled as if they were code comments.

Specification-wise, $X:=\mathtt{process}(\lambda x.P)\left(E\right)\mathtt{over}\mathsf{\Pi }$ initialises a new process-algebraic model P in the proof system that takes a single input argument named x, namely (the evaluation of) the expression E. This model is used (1) as a specification of how a particular region of shared memory, specified by $\mathsf{\Pi }$, is allowed to evolve over time; and (2) to support reasoning over the model to indirectly prove properties of how the heap evolves. The $\mathsf{\Pi }$ component is an abstraction binder, which is also defined in Definition 8 and is used to connect process-algebraic variables to heap locations in the program. In particular, the abstraction binders make the connections/links between process-algebraic state and shared-memory program state (that is, heap locations). In the sequel, we often use abstraction binders as if they were finite partial mappings, $\mathsf{\Pi }:\mathit{ProcVar}{\rightharpoonup }_{\mathtt{fin}}\mathit{Expr}$, from process-algebraic variables to the expressions whose evaluation determine the corresponding heap location. Finally, the variable X identifies the process-algebraic model after initialisation.

The command $\mathtt{finish}E$ is used to finalise the process-algebraic model identified by E in the logic, given that it can successfully terminate. Finalisation is later explained in more detail, in Section 3.4.

The specification command $\mathtt{action}Ea\left(E^{\prime }\right)\mathtt{do}C$ is used to link the execution of programs with the execution of process-algebraic models. More specifically, it executes the program C in the context of the model identified by E, as the process-algebraic action a that takes (the evaluation of) $E^{\prime }$ as an input argument. The soundness argument of the program logic establishes a refinement relation between programs and their models, and this relation is established by synchronising program execution with process execution, with help of these action blocks.

The $\mathtt{inact}$C command denotes a partially executed action program; one that still has to execute C. Likewise to $\mathtt{inatom}$, this command can only occur during runtime and is not written by users.

Lastly, $\mathtt{query}$ E is used to connect process-algebraic reasoning to deductive reasoning: it allows the deductive proof of the program to rely on (or assume) properties that are proven to hold (or guaranteed) on the process-algebraic model identified by E, via process-algebraic analysis. These are the properties that are encoded as assertions $?(·)$ in this model. Of course, this would require linking process-algebraic state to program state, which we come to later, in Section 3.3 and Section 3.4.

3.2.3. Free Variables and Substitution

We use the standard (overloaded) notations $\mathtt{FV}\left(E\right)$, $\mathtt{FV}\left(B\right)$, $\mathtt{FV}\left(\mathsf{\Pi }\right)$ and $\mathtt{FV}\left(C\right)$ to refer to the set of free program variables in the given (Boolean) expression E and B, abstraction binder $\mathsf{\Pi }$, and command C, respectively. Moreover, the notation $E[X/E^{\prime }]$ denotes the substitution of the program variable X for the expression $E^{\prime }$ inside E; and likewise for Boolean expressions, abstraction binders, and commands. The full definitions of $\mathtt{FV}(·)$ and $(·)[X/E]$ are mostly standard, and therefore deferred to [19].

3.2.4. User Programs

As just discussed, our simple programming language contains runtime syntax—instructions that are not written by users but are only introduced during runtime. Commands that are free of such runtime constructs are called user commands.

Definition 9

(User commands). Any command C is defined to be a  user command, denoted $\mathtt{user}\left(C\right)$, if C does not contain sub-commands of the forms $\mathtt{inatom}{C}^{\prime }$ and $\mathtt{inact}$$C^{\prime }$, for any command $C^{\prime }$.

3.2.5. Wellformedness

Moreover, our verification approach only applies to well-formed commands. Notably, our technique requires that, for any program of the form $\mathtt{action}$$\_$$\mathtt{do}$$C$ and $\mathtt{inact}$ C, the inner action program C only contains a subcategory of commands, excluding atomic commands and specification-only constructs, in particular nested action blocks. The latter is needed since actions must be atomically observable by environmental threads. This restriction is captured by the following definition.

Definition 10

(Basic programs, well-formed programs). Any command C is defined to be basic, denoted $\mathsf{basic}\left(C\right)$, if C does not contain any atomic sub-programs, i.e., $\mathtt{atomic}$ or $\mathtt{inatom}$, nor specification-specific language constructs, i.e., $\mathtt{process}$, $\mathtt{action}$, $\mathtt{inact}$, $\mathtt{finish}$, or $\mathtt{query}$.

A command C is defined to be well-formed, denoted $\mathtt{wf}\left(C\right)$, if, for any command $\mathtt{action}$$\_$$\mathtt{do}$$C^{\prime }$ or $\mathtt{inact}$ C that occurs in C it holds that $\mathsf{basic}\left(C^{\prime }\right)$.

Lemma 2.

$\mathsf{basic}\left(C\right)$ implies $\mathtt{wf}\left(C\right)$ for any command C.

3.2.6. Operational Semantics

The denotational semantics of expressions $\left[\right[E\left]\right]s$ and conditions $\left[\right[B\left]\right]s$ are again defined in the standard way, and evaluate to $\mathit{Val}$ and $\mathit{Bool}$, respectively, where $s\in \mathit{Store}\triangleq \mathit{Var}\to \mathit{Val}$ is a (program) store that gives an interpretation to all program variables.

The operational semantics of programs is defined in terms of a binary small-step reduction relation $⇝\subseteq \mathit{Conf}\times \mathit{Conf}$ between program configurations. A program configuration $\mathfrak{C}=(C,h,s)\in \mathit{Conf}\triangleq \mathit{Cmd}\times \mathit{Heap}\times \mathit{Store}$ is a triple, consisting of a command C as well as a heap h that models shared memory, and a store $s\in \mathit{Store}$ that models thread-local memory. Any program configuration of the form $(\mathtt{skip},h,s)$ is defined to be final or terminated. Heaps $h\in \mathit{Heap}\triangleq \mathit{Val}{\rightharpoonup }_{\mathtt{fin}}\mathit{Val}$ are defined to be finite partial mappings from values to values. Heap locations are themselves values, so that they can be assigned to, and read from, local variables, and thus be handled as any value. The function $\mathtt{dom}:\mathit{Heap}\to 2^{\mathit{Val}}$ denotes the mapped domain of a given heap, so that $\mathtt{dom}\left(h\right)\triangleq \left\{v\left|h\right(v)\ne \mathit{undefined}\right\}$.

Definition 11

(Small-step operational semantics of programs).

Most of the transition rules are standard; see for example [34]. The update notation $s[X\mapsto v]$ defines a store that is equal to s, except that X is mapped to v. A similar notation is used for heaps, namely $h[v_1\mapsto v_2]$. Moreover, the notation $h\backslash v$ denotes the removal of the entry at v in h.

An interesting aspect of the operational semantics is that atomic programs are executed using a small-step reduction strategy (via $⇝$-INATOM-STEP and $⇝$-INATOM-SKIP), rather than a big-step execution, which is more customary. This is done for technical reasons: it simplifies the establishment of a simulation/refinement between programs and their models. Consequently, we use a notion of a locked program to define the transition rules for atomic programs. Any command C is said to be (globally) locked if C executes an atomic program, i.e., if C has $\mathtt{inatom}{C}^{\prime }$ as a subprogram for some $C^{\prime }$.

Definition 12

(Locked programs). Any command C is locked if $\mathsf{locked}\left(C\right)$ holds, where $\mathsf{locked}\subset \mathit{Cmd}$ is defined as follows, by structural recursion on C:

$$\mathtt{locked}\left(C\right)\triangleq \left\{\begin{array}{cc}\mathtt{true}\hfill & \mathit{if}C=\mathtt{inatom}{C}^{\prime }\hfill \\ \mathtt{locked}\left(C_1\right)\hfill & \mathit{if}C=C_1;C_2\hfill \\ \mathtt{locked}\left(C_1\right)\vee \mathtt{locked}\left(C_2\right)\hfill & \mathit{if}C=C_1\Vert C_2\hfill \\ \mathtt{locked}\left(C^{\prime }\right)\hfill & \mathit{if}C=\mathtt{inact}{C}^{\prime }\hfill \\ \mathtt{false}\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

The rules $⇝$-PAR-L and $⇝$-PAR-R for parallel composition allow a thread to make an execution step only if the other thread is not locked, thereby preventing thread interference while executing atomic programs. One might ask whether this handling of locks could not potentially lead to deadlock scenarios, for example by encountering configurations $(C_1\Vert C_2,h,s)$ during runtime for which both $\mathsf{locked}\left(C_1\right)$ and $\mathsf{locked}\left(C_2\right)$ hold. However, we will later see and prove that no such deadlocks can be reached, given that one starts with an initial configuration that contains a user program.

Furthermore, the specification-only language constructs do not affect the state of the program (not the heap nor the store) and are essentially handled as if they were comments. Notice however, that commands of the form $\mathtt{action}$$\_$$\mathtt{do}$$C$ are first reduced to $\mathtt{inact}$ C before C is being executed. This is done for technical reasons, as this makes it more convenient to later establish a simulation relation between execution steps of programs and processes.

The semantics of programs has the following preservation properties.

Lemma 3.

Program execution preserves basicality and wellformedness:

1. 

If $\mathtt{basic}\left(C\right)$ and $(C,h,s)⇝(C^{\prime },h^{\prime },s^{\prime })$, then $\mathtt{basic}\left(C^{\prime }\right)$.

2. 

If $\mathtt{wf}\left(C\right)$ and $(C,h,s)⇝(C^{\prime },h^{\prime },s^{\prime })$, then $\mathtt{wf}\left(C^{\prime }\right)$.

3.2.7. Fault Semantics

Apart from an operational semantics, we also define a fault semantics for programs [35] that classifies runtime errors that may occur during program execution. Its definition uses two auxiliary functions, $\mathtt{acc}(C,s)$ and $\mathtt{writes}(C,s)$, for obtaining the set of heap locations that can be accessed or written-to, respectively, in a next reduction step of C. Their definitions are deferred to [19] as well, as they are quite lengthy and not essential for understanding the definition of the fault semantics.

The fault semantics of program configurations $\mathfrak{C}$ is expressed as a predicate $↯\left(\mathfrak{C}\right)$ that is inductively defined as follows.

Definition 13

(Fault semantics of programs).

Intuitively, a program configuration exhibits a fault if it (1) accesses unallocated memory, or (2) is deadlocked, or (3) allows performing a data-race.

More specifically, ↯-READ expresses that heap reading $X:=\left[E\right]$ faults if the heap location at E is unoccupied. For the same reason, also heap writing (↯-WRITE) and heap deallocation (↯-DISPOSE) may fault. The ↯-PAR-L rule expresses that any parallel program $C_1\Vert C_2$ can fault if $C_1$ can fault, given that $C_2$ is not locked, or the other way around (↯-PAR-R covers the other direction). Program configurations that hold multiple global locks are also considered to be faulting, by ↯-DEADLOCK. Finally, the fault semantics encodes the definition of a data-race, via ↯-RACE-1 and ↯-RACE-2. To clarify, any configuration $(C,h,s)$ exhibits a data-race if C has (at least) two threads that can both access a common location in h in the next reduction step, where at least one of these accesses is a write.

We will later see that the soundness argument of our program logic covers that verified programs are free of faults. More specifically, we will prove that, for any program C for which a proof can be derived, we have that C is fault-free with respect to any heap h and store s that satisfy C’s precondition, and moreover, that every configuration that is reachable from $(C,h,s)$ is also fault-free.

Finally, to show that the operational semantics of programs is coherent with respect to faults, we prove that the operational semantics is progressive for all non-faulting program configurations.

Theorem 1

(Progress of $⇝$). For any program configuration $\mathfrak{C}$ for which $\neg ↯\left(\mathfrak{C}\right)$ holds, either $\mathfrak{C}$ is final, or there exists a configuration ${\mathfrak{C}}^{\prime }$ such that $\mathfrak{C}⇝{\mathfrak{C}}^{\prime }$.

3.3. Assertions

The assertion language of our verification approach is defined by the following grammar.

Definition 14

(Assertions).

$$\begin{array}{cc}\hfill t\in \mathit{PointsToType}::=& \mathtt{std}\left|\mathtt{proc}\right|\mathtt{act}\hfill \\ \hfill \mathcal{P},\mathcal{Q},\mathcal{R},\cdots \in \mathit{Assn}::=& B|\forall X.\mathcal{P}|\exists X.\mathcal{P}|\mathcal{P}\vee \mathcal{Q}|\mathcal{P}\ast \mathcal{Q}|{\ast }_{i\in I}{\mathcal{P}}_i\left|\mathcal{P}-\ast \mathcal{Q}\right|E{\stackrel{\pi }{\hookrightarrow }}_{t}E|\hfill \\ \hfill & {\mathtt{Proc}}_{\pi }(E,\tilde{P},\mathsf{\Pi })|\tilde{P}\approx \tilde{Q}\hfill \end{array}$$

Assertions can be built from plain Boolean expressions B, and may contain several standard connectives from predicate logic: universal and existential quantifiers, and disjunction. Moreover, logical conjunction (∧) is replaced by the separating conjunction * from Concurrent Separation Logic (CSL). The ${\ast }_{i\in I}{\mathcal{P}}_i$ connective is the iterated separating conjunction, with I a finite set that represents ${\mathcal{P}}_0\ast \cdots \ast {\mathcal{P}}_n$, given that $I=\left\{0,\cdots ,n\right\}$. The $-\ast$ connective is known as the magic wand and is used to describe hypothetical judgments, much like the logical implication from predicate logic.

Apart from these standard CSL connectives, the assertion language contains three different heap ownership predicates ${\stackrel{\pi }{\hookrightarrow }}_t$, with $\pi \in \mathbb{Q}$ a rational number that represents a fractional permission, and t the heap ownership type, as well as an ownership predicate ${\mathtt{Proc}}_{\pi }$ for program abstractions. Finally $\tilde{P}\approx \tilde{Q}$ intuitively means that $\tilde{P}$ and $\tilde{Q}$ are bisimilar processes with respect to the current state.

The definitions of free variables $\mathtt{FV}\left(\mathcal{P}\right)$ of assertions $\mathcal{P}$, and substitution $\mathcal{P}[X/E]$ in $\mathcal{P}$, are the standard ones and are therefore deferred to [19]. Assertions that are free of ${\stackrel{\pi }{\hookrightarrow }}_t$ and ${\mathtt{Proc}}_{\pi }$ predicates are called pure. Any assertion that is not pure is said to be spatial.

3.3.1. Heap Ownership

The assertion $E_1{\stackrel{\pi }{\hookrightarrow }}_t{E}_2$ is the heap ownership assertion and expresses that the heap contains the value represented by the expression $E_2$ at heap location $E_1$. Moreover, $\pi$ and t together determine the access rights to this heap location. In more detail, depending on the ownership type t, the ${\stackrel{\pi }{\hookrightarrow }}_t$ ownership predicates express different access rights to the associated heap location:

• Standard heap ownership.$E_1{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{std}}{E}_2$ is the standard heap ownership predicate from (intuitionistic) separation logic that provides read-access whenever $0<\pi <1$, and write-access in case $\pi =1$. Moreover, the subscript $\mathtt{std}$ indicates that the associated heap location $E_1$ is not bound to any process-algebraic model. We say that a heap location $v\in \mathit{Val}$ is bound by, or subject to, a program abstraction, if there is an active program abstraction with a binder $\mathsf{\Pi }$ that contains a mapping to v, that is, $v\in \mathtt{dom}\left(\mathsf{\Pi }\right)$.
• Process heap ownership.$E{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}{E}^{\prime }$ is the process heap ownership predicate, which indicates that the heap location at E is bound by an active process-algebraic abstraction, but in a purely read-only manner. More precisely, ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}$ assertions exclusively grant read-access, even in case $\pi =1$.
• Action heap ownership.$E{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{act}}{E}^{\prime }$ is the action heap ownership predicate, which indicates that the heap location E is bound by an active process-algebraic model, and is used in the context of an action block, in a read/write manner.

Observe that action points-to assertions ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{act}}$ essentially give the same access rights as ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{std}}$ assertions. Nevertheless, they are both needed, to be able to distinguish between bound and unbound heap locations in the logic. For example, the program logic must not allow to deallocate memory that is currently bound to (protected by) an active process-algebraic model, as this would be unsound.

Moreover, even though ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}$ predicates never grant write access, we will later see that the proof system allows ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}$ predicates to be upgraded to ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{act}}$ inside action blocks, and ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{act}}$ again provides write access when $\pi =1$. More precisely, $E{\stackrel{1}{\hookrightarrow }}_{\mathtt{proc}}{E}^{\prime }$ predicates grant the capability to regain write access to E, in the context of an action program. This system of upgrading enforces that all modifications to E happen in the context of $\mathtt{action}{E}_{\mathit{abstr}}a\left(E_{\mathit{abstr}}^{\prime }\right)\mathtt{do}C$ commands, so that the modifications are protected and can be recorded by the program abstraction identified by $E_{\mathit{abstr}}$, as the action a.

In addition to these three heap ownership predicates, we derive a fourth such predicate, called the process–action heap ownership predicate. This ownership predicate is equivalent to ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{act}}$ only if $\pi$ denotes write access, and otherwise it is equivalent to ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}$.

Definition 15

(Process–action heap ownership).

$$\begin{array}{c}{E}_1{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{procact}}{E}_2\triangleq \left\{\begin{array}{cc}{E}_1{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{act}}{E}_2\hfill & \mathit{if}\pi =1\hfill \\ E_1{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}{E}_2\hfill & \mathit{otherwise}\hfill \end{array}\right.\end{array}$$

This derived predicate is for later use, in the proof system of our program logic. Finally, the notation $E{\stackrel{\pi }{\hookrightarrow }}_t-$ is sometimes used as shorthand for $\exists X.E{\stackrel{\pi }{\hookrightarrow }}_{t}X$, where $X\notin \mathtt{FV}\left(E\right)$.

3.3.2. Process Ownership

The ${\mathtt{Proc}}_{\pi }(E,\tilde{P},\mathsf{\Pi })$ assertion expresses ownership of a program abstraction that is identified by E, where the abstraction is represented by the process $\tilde{P}$. Ownership in this sense means that the thread has knowledge of the existence of the process-algebraic model $\tilde{P}$, as well as the right to execute as prescribed by this model. The mapping $\mathsf{\Pi }$ connects the abstract model to the concrete program by mapping the process-algebraic variables in the abstraction to heap locations in the program, as discussed before. And last, the fractional permission $\pi$ is needed to implement the ownership system of program models. Fractional permissions are only used here to be able to reconstruct the full ${\mathtt{Proc}}_1$ predicate. We shall later see that ${\mathtt{Proc}}_{\pi }$ predicates can be split and merged along $\pi$ and parallel compositions inside $\tilde{P}$, and be consumed in the proof system by $\mathtt{action}$ programs.

Even though reasoning about process-algebraic models is done purely on the level of process-algebraic state, in the program logic it is allowed to mix program state with process-algebraic state. This is indicated by the tilde above the $\tilde{P}$, which means that P can have both program variables and process-algebraic variables. Such processes are called hybrid processes and are defined as follows.

Definition 16

(Hybrid expressions, conditions and processes).

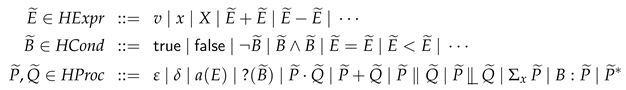
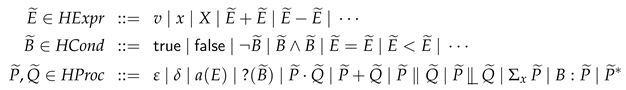
These hybrid processes thus allow mixing process-algebraic reasoning with deductive reasoning using our program logic. The function $\mathtt{fv}\left(\tilde{P}\right)$ is used for obtaining the set of free process-algebraic variables in $\tilde{P}$, and $\mathtt{FV}\left(\tilde{P}\right)$ for obtaining all free program variables in $\tilde{P}$ (and likewise for $\tilde{E}$ and $\tilde{B}$).

We shall later see that the program logic allows replaces processes $\tilde{P}$ inside ${\mathtt{Proc}}_{\pi }(E,\tilde{P},\mathsf{\Pi })$ predicates by bisimilar ones. However, note that one cannot use the standard notion of bisimilarity as defined in Definition 7 for this in case $\tilde{P}$ has any program variables occurring freely in it. To resolve this, we include a relation $\tilde{P}\approx \tilde{Q}$ in the assertion language, stating that $\tilde{P}$ and $\tilde{Q}$ are bisimilar while taking into account any (pure) information that is available from the context. This is further clarified in Section 3.3.7, after we discussed the models of the logic.

3.3.3. Models of the Program Logic

Before Section 3.3.7 discusses the semantics of assertions, this section first introduces permission heaps and process maps, that form the basis for the models of our concurrent separation logic. Permission heaps extend ordinary program heaps (i.e., $\mathit{Heap}$) to capture the three different types t of heap ownership, whereas process maps capture the state and ownership of process-algebraic abstractions.

Let us start by introducing fractional permissions, which are used in the definitions of both permission heaps and process maps.

3.3.4. Fractional Permissions

In the assertion language, all heap/process ownership predicates have an associated rational number $\pi \in \mathbb{Q}$. There are used to express the “amount” of ownership that is available to the corresponding heap location or program model.

We define a rational number $\pi$ to be a (Boyland) fractional permission in case $\pi \in {(0,1]}_{\mathbb{Q}}$ [36]. The original work of Boyland uses fractional permissions to distinguish between write access ($\pi =1$) and read access ($0<\pi <1$) to some shared resource. However, in our work this is slightly different, since the fractional access permissions $\pi$ annotated to ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}$ predicates never provide write access.

To conveniently handle fractional permissions, we define basic notions of validity (${\mathtt{valid}}_{\mathbb{Q}}$) and disjointness (${\perp }_{\mathbb{Q}}$) of rational numbers, as follows.

Definition 17

(Permission validity, Permission disjointness).

$${\mathtt{valid}}_{\mathbb{Q}}\left(\pi \right)\triangleq 0<\pi \le 1\hspace{1em}{\pi }_1{\perp }_{\mathbb{Q}}{\pi }_2\triangleq 0<{\pi }_1\wedge 0<{\pi }_2\wedge {\pi }_1+{\pi }_2\le 1$$

The predicate ${\mathtt{valid}}_{\mathbb{Q}}:\mathbb{Q}\to \mathit{Prop}$ determines whether the given rational number is within the range ${(0,1]}_{\mathbb{Q}}$, that is, is a valid Boyland fractional permission. (Here $\mathit{Prop}$ is the sort of propositions.) The binary relation ${\perp }_{\mathbb{Q}}:\mathbb{Q}\to \mathbb{Q}\to \mathit{Prop}$ determines disjointness of two rationals. Disjoint rational numbers do not overlap, in the sense that both operands are fractional permissions, as well as their addition.

Lemma 4.

${\mathtt{valid}}_{\mathbb{Q}}$ and ${\perp }_{\mathbb{Q}}$ satisfy the following properties.

1. 

If ${\pi }_1{\perp }_{\mathbb{Q}}{\pi }_2$, then ${\pi }_2{\perp }_{\mathbb{Q}}{\pi }_1$, ${\mathtt{valid}}_{\mathbb{Q}}\left({\pi }_1\right)$, and ${\mathtt{valid}}_{\mathbb{Q}}\left({\pi }_1+{\pi }_2\right)$.

2. 

If ${\pi }_1{\perp }_{\mathbb{Q}}{\pi }_2$ and $({\pi }_1+{\pi }_2){\perp }_{\mathbb{Q}}{\pi }_3$, then ${\pi }_2{\perp }_{\mathbb{Q}}{\pi }_3$ and ${\pi }_1{\perp }_{\mathbb{Q}}({\pi }_2+{\pi }_3)$.

3.3.5. Permission Heaps

The models of our program logic use permission heaps to give a  semantic meaning to heap ownership. Permission heaps and their heap cells are defined as follows, and are slightly richer than ordinary program heaps $\left(\mathit{Heap}\right)$ to be able to administer the access permissions and the different ownership types.

Definition 18

(Permission heap cells, Permission heaps).

$$\begin{array}{cc}\hfill \mathit{hc}\in \mathit{PermHeapCell}::=& {\mathtt{free}|⟨v⟩}_{\mathtt{std}}^{\pi }{|⟨v⟩}_{\mathtt{proc}}^{\pi }\left|{⟨v_1,v_2⟩}_{\mathtt{act}}^{\pi }\right|\mathtt{inv}\hfill \\ \hfill \mathit{ph}\in \mathit{PermHeap}\triangleq & \mathit{Val}\to \mathit{PermHeapCell}\hfill \end{array}$$

Permission heaps $\mathit{ph}$ are defined to be total functions from values (representing heap locations) to permission heap cells, $\mathit{hc}$, which in turn are inductively defined to be one of the following:

• $\mathtt{free}$, which is an unoccupied heap cell.
• ${⟨v⟩}_{\mathtt{std}}^{\pi }$, which is a standard heap cell that stores the value $v\in \mathit{Val}$. Standard heap cells are the models of the standard heap ownership predicates, ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{std}}$.
• ${⟨v⟩}_{\mathtt{proc}}^{\pi }$, which is a process heap cell that stores the value v. These are used as models of the ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}$ ownership predicates.
• ${⟨v_1,v_2⟩}_{\mathtt{act}}^{\pi }$, which is an action heap cell that stores the value $v_1$. Action heap cells are used as the models for the ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{act}}$ predicates. Moreover, action heap cells store a second value $v_2$. This extra value is maintained for technical reasons, to help in establishing soundness of the program logic. The value $v_2$ is referred to as a snapshot value: a copy of the original value stored by the heap cell, that is made when an action block was entered.
• $\mathtt{inv}$, which is an invalid, or corrupted, permission heap cell.

Note that, unlike program heaps, permission heaps are defined to be total functions, where the heap cells have an explicit notion of being $\mathtt{free}$. This is done to give permission heaps and their cells nicer algebraic properties. The unit permission heap is defined to be ${\mathrm{𝟙}}_{\mathtt{ph}}\triangleq \lambda v\in \mathit{Val}.\mathtt{free}$, containing $\mathtt{free}$ at every entry. Furthermore, permission heap cells also have an explicit notion of being invalid. Invalid heap cells $\mathtt{inv}$ represent the erroneous result of composing two incompatible heap cells.

We now define several operations on permission heaps.

Validity. Any permission heap $\mathit{ph}$ is defined to be valid if the permissions of all $\mathit{ph}$’s heap cells are valid, where $\mathtt{free}$ is always valid and $\mathtt{inv}$ is never valid.

Definition 19

(Validity of permission heaps). A permission heap $\mathit{ph}$ is defined to be valid, written ${\mathtt{valid}}_{\mathtt{ph}}\left(\mathit{ph}\right)$, if ${\mathtt{valid}}_{\mathtt{hc}}\left(ph\left(v\right)\right)$ holds for every $v\in \mathit{Val}$, where the ${\mathtt{valid}}_{\mathtt{hc}}$ predicate is defined as follows.

$${\mathtt{valid}}_{\mathtt{hc}}\left(\mathit{hc}\right)\triangleq \left\{\begin{array}{cc}\mathtt{true}\hfill & \mathit{if}\mathit{hc}=\mathtt{free}\hfill \\ {\mathtt{valid}}_{\mathbb{Q}}\left(\pi \right)\hfill & \mathit{if}\mathit{hc}={⟨v⟩}_{\mathtt{std}}^{\pi }\vee \mathit{hc}={⟨v⟩}_{\mathtt{proc}}^{\pi }\vee {⟨v,v^{\prime }⟩}_{\mathtt{act}}^{\pi }\mathit{for}\mathit{some}v,v^{\prime }\hfill \\ \mathtt{false}\hfill & \mathit{if}\mathit{hc}=\mathtt{inv}\hfill \end{array}\right.$$

Disjointness. Two permission heaps ${\mathit{ph}}_1$ and ${\mathit{ph}}_2$ are disjoint if all their heap cells are pairwise compatible and their underlying permissions are disjoint.

Definition 20

(Disjointness of permission heaps). Two permission heaps, ${\mathit{ph}}_1$ and ${\mathit{ph}}_2$, are disjoint, denoted ${\mathit{ph}}_1{\perp }_{\mathtt{ph}}{\mathit{ph}}_2$, if ${\mathit{ph}}_1\left(v\right){\perp }_{\mathtt{hc}}{\mathit{ph}}_2\left(v\right)$ holds for every $v\in \mathit{Val}$, where the ${\perp }_{\mathtt{hc}}$ relation is defined as follows.

$${\mathit{hc}}_1{\perp }_{\mathtt{hc}}{\mathit{hc}}_2\triangleq \left\{\begin{array}{cc}{\mathtt{valid}}_{\mathtt{hc}}\left({\mathit{hc}}_2\right)\hfill & \mathit{if}{\mathit{hc}}_1=\mathtt{free}\hfill \\ {\mathtt{valid}}_{\mathtt{hc}}\left({\mathit{hc}}_1\right)\hfill & \mathit{if}{\mathit{hc}}_2=\mathtt{free}\hfill \\ {\pi }_1{\perp }_{\mathbb{Q}}{\pi }_2\wedge v_1=v_2\hfill & \mathit{if}{\mathit{hc}}_1={⟨v_1⟩}_{\mathtt{std}}^{{\pi }_1}\wedge {\mathit{hc}}_2={⟨v_2⟩}_{\mathtt{std}}^{{\pi }_2}\hfill \\ {\pi }_1{\perp }_{\mathbb{Q}}{\pi }_2\wedge v_1=v_2\hfill & \mathit{if}{\mathit{hc}}_1={⟨v_1⟩}_{\mathtt{proc}}^{{\pi }_1}\wedge {\mathit{hc}}_2={⟨v_2⟩}_{\mathtt{proc}}^{{\pi }_2}\hfill \\ {\pi }_1{\perp }_{\mathbb{Q}}{\pi }_2\wedge v_1=v_2\wedge v_1^{\prime }=v_2^{\prime }\hfill & \mathit{if}{\mathit{hc}}_1={⟨v_1,v_1^{\prime }⟩}_{\mathtt{act}}^{{\pi }_1}\wedge {\mathit{hc}}_2={⟨v_2,v_2^{\prime }⟩}_{\mathtt{act}}^{{\pi }_2}\hfill \\ \mathtt{false}\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

Disjoint union. The following operation defines the disjoint union (i.e., the composition) of two permission heaps.

Definition 21

(Disjoint union of permission heaps). The disjoint union ${\mathit{ph}}_1{\uplus }_{\mathtt{ph}}{\mathit{ph}}_2$ of any two permission heaps ${\mathit{ph}}_1,{\mathit{ph}}_2$ is defined to be the permission heap $\lambda v\in \mathit{Val}.{\mathit{ph}}_1\left(v\right){\uplus }_{\mathtt{hc}}{\mathit{ph}}_2\left(v\right)$, with ${\uplus }_{\mathtt{hc}}$ defined as follows.

$${\mathit{hc}}_1{\uplus }_{\mathtt{hc}}{\mathit{hc}}_2\triangleq \left\{\begin{array}{cc}{\mathit{hc}}_1\hfill & \mathit{if}{\mathit{hc}}_2=\mathtt{free}\hfill \\ {\mathit{hc}}_2\hfill & \mathit{if}{\mathit{hc}}_1=\mathtt{free}\hfill \\ {⟨v_1⟩}_{\mathtt{std}}^{{\pi }_1+{\pi }_2}\hfill & \mathit{if}{\mathit{hc}}_1={⟨v_1⟩}_{\mathtt{std}}^{{\pi }_1}\wedge {\mathit{hc}}_2={⟨v_2⟩}_{\mathtt{std}}^{{\pi }_2}\wedge v_1=v_2\hfill \\ {⟨v_1⟩}_{\mathtt{proc}}^{{\pi }_1+{\pi }_2}\hfill & \mathit{if}{\mathit{hc}}_1={⟨v_1⟩}_{\mathtt{proc}}^{{\pi }_1}\wedge {\mathit{hc}}_2={⟨v_2⟩}_{\mathtt{proc}}^{{\pi }_2}\wedge v_1=v_2\hfill \\ {⟨v_1,v_1^{\prime }⟩}_{\mathtt{act}}^{{\pi }_1+{\pi }_2}\hfill & \mathit{if}{\mathit{hc}}_1={⟨v_1,v_1^{\prime }⟩}_{\mathtt{act}}^{{\pi }_1}\wedge {\mathit{hc}}_2={⟨v_2,v_2^{\prime }⟩}_{\mathtt{act}}^{{\pi }_2}\wedge v_1=v_2\wedge v_1^{\prime }=v_2^{\prime }\hfill \\ \mathtt{inv}\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

Note that ${\uplus }_{\mathtt{hc}}$ only gives a non-corrupted entry when applied to two compatible heap cells. Furthermore, $\mathtt{free}$ is neutral with respect to ${\uplus }_{\mathtt{hc}}$ while $\mathtt{inv}$ is absorbing.

Below are the most important properties of validity, disjointness and disjoint union.

Lemma 5.

(The analogous operations on permission heap cells have the exact same properties.)

1. 

${\mathit{ph}}_1{\uplus }_{\mathtt{ph}}\left({\mathit{ph}}_2{\uplus }_{\mathtt{ph}}{\mathit{ph}}_3\right)=\left({\mathit{ph}}_1{\uplus }_{\mathtt{ph}}{\mathit{ph}}_2\right){\uplus }_{\mathtt{ph}}{\mathit{ph}}_3$.

2. 

${\mathit{ph}}_1{\uplus }_{\mathtt{ph}}{\mathit{ph}}_2={\mathit{ph}}_2{\uplus }_{\mathtt{ph}}{\mathit{ph}}_1$.

3. 

If $\mathit{ph}{\uplus }_{\mathtt{ph}}{\mathrm{𝟙}}_{\mathtt{ph}}=\mathit{ph}$.

4. 

If ${\mathit{ph}}_1{\perp }_{\mathtt{ph}}{\mathit{ph}}_2$, then ${\mathtt{valid}}_{\mathtt{ph}}\left({\mathit{ph}}_1{\uplus }_{\mathtt{ph}}{\mathit{ph}}_2\right)$.

5. 

If ${\mathit{ph}}_1{\perp }_{\mathtt{ph}}{\mathit{ph}}_2$ and $\left({\mathit{ph}}_1{\uplus }_{\mathtt{ph}}{\mathit{ph}}_2\right){\perp }_{\mathtt{ph}}{\mathit{ph}}_3$, then also

(a) 

${\mathit{ph}}_2{\perp }_{\mathtt{ph}}{\mathit{ph}}_3$ and

(b) 

${\mathit{ph}}_1{\perp }_{\mathtt{ph}}\left({\mathit{ph}}_2{\uplus }_{\mathtt{ph}}{\mathit{ph}}_3\right)$.

3.3.6. Process Maps

The models of the logic also use process maps in addition to permission heaps, to give a semantic meaning to process ownership predicates ${\mathtt{Proc}}_{\pi }$ in the logic. Process maps and their entries are defined as follows, where binders $\mathsf{\Lambda }$ are finite partial mappings from process variables to heap locations (i.e., values). These binders are the models for the abstraction binders $\mathsf{\Pi }$ defined earlier in Definition 8.

Definition 22

(Process map entries, process maps, binders).

$$\begin{array}{cc}\hfill \mathit{me}\in \mathit{ProcMapEntry}::=& {\mathtt{free}|⟨P,\mathsf{\Lambda }⟩}^{\pi }|\mathtt{inv}\hfill \\ \hfill \mathit{pm}\in \mathit{ProcMap}\triangleq & \mathit{Val}\to \mathit{ProcMapEntry}\hfill \\ \hfill \mathsf{\Lambda }\in \mathit{Binder}\triangleq & \mathit{ProcVar}{\rightharpoonup }_{\mathtt{fin}}\mathit{Val}\hfill \end{array}$$

Process maps are total mappings from values (identifying program abstractions) to process map entries, which are, in turn, inductively defined to one of the following three elements:

• $\mathtt{free}$, which models unoccupied or free entries in $\mathit{pm}$.
• ${⟨P,\mathsf{\Lambda }⟩}^{\pi }$, which is an occupied process map entry. These are used as models for the ${\mathtt{Proc}}_{\pi }(E,\tilde{P},\mathsf{\Pi })$ assertions, where E identifies the process map entry in $\mathit{pm}$, and the binder $\mathsf{\Lambda }$ is a model for $\mathsf{\Pi }$.
• $\mathtt{inv}$, which denotes an invalid, or corrupted, process map entry.

Likewise to permission heaps, process maps are defined as total functions with entries that can explicitly be $\mathtt{free}$ or $\mathtt{invalid}$, as this provides desirable algebraic properties. Corrupted entries represent the erroneous result of taking the disjoint union of two incompatible, non-disjoint entries. The unit process map is defined to be ${\mathrm{𝟙}}_{\mathtt{pm}}\triangleq \lambda v\in \mathit{Val}.\mathtt{free}$, containing $\mathtt{free}$ at every entry.

We now define several operations and relations on process maps that are analogous to the operations defined earlier for permission heaps, starting with bisimilarity.

Bisimilarity. Any two process maps are said to be bisimilar, if all their entries are equal point-wise, or contain occupied entries with process components that are bisimilar.

Definition 23

(Process map bisimilarity). Two process maps ${\mathit{pm}}_1$ and ${\mathit{pm}}_2$ are defined to be bisimilar, denoted ${\mathit{pm}}_1{\cong }_{\mathtt{pm}}{\mathit{pm}}_2$, if ${\mathit{pm}}_1\left(v\right){\cong }_{\mathtt{mc}}{\mathit{pm}}_2\left(v\right)$ for every $v\in \mathit{Val}$, with the relation ${\cong }_{\mathtt{mc}}$ defined as follows.

$${\mathit{me}}_1{\cong }_{\mathtt{mc}}{\mathit{me}}_2\triangleq \left\{\begin{array}{cc}\mathtt{true}\hfill & \mathit{if}{\mathit{me}}_1=\mathtt{free}\wedge {\mathit{me}}_2=\mathtt{free}\hfill \\ P_1\cong P_2\wedge {\mathsf{\Lambda }}_1={\mathsf{\Lambda }}_2\wedge {\pi }_1={\pi }_2\hfill & \mathit{if}{\mathit{me}}_1={⟨P_1,{\mathsf{\Lambda }}_1⟩}^{{\pi }_1}\wedge {\mathit{me}}_2={⟨P_2,{\mathsf{\Lambda }}_2⟩}^{{\pi }_2}\hfill \\ \mathtt{true}\hfill & \mathit{if}{\mathit{me}}_1=\mathtt{inv}\wedge {\mathit{me}}_2=\mathtt{inv}\hfill \\ \mathtt{false}\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

Both ${\cong }_{\mathtt{pm}}$ and ${\cong }_{\mathtt{mc}}$ are equivalence relations. A notion of bisimilarity of process maps is needed in addition to ordinary equality, since for example disjoint union of process maps is not associative nor commutative with respect to ordinary equality, as opposed to bisimilarity. Moreover, we will later see that the program logic always allows replacing processes $\tilde{P}$ inside ${\mathtt{Proc}}_{\pi }(X,\tilde{P},\mathsf{\Pi })$ predicates by bisimilar ones, as discussed earlier. But to handle such replacements at the semantic level, we allow process maps and their entries to be handled up to ${\cong }_{\mathtt{pm}}$ and ${\cong }_{\mathtt{mc}}$, respectively.

Validity. Any process map $\mathit{pm}$ is said to be valid intuitively if none of $\mathit{pm}$’s entries are corrupt and all occupied entries of $\mathit{pm}$ hold a valid associated fractional permission.

Definition 24

(Process map validity). Any process map $\mathit{pm}$ is defined to be valid, denoted ${\mathtt{valid}}_{\mathtt{pm}}\left(\mathit{pm}\right)$, if ${\mathtt{valid}}_{\mathtt{mc}}\left(\mathit{pm}\left(v\right)\right)$ holds for every $v\in \mathit{Val}$, with the ${\mathtt{valid}}_{\mathtt{mc}}:\mathit{ProcMapEntry}\to \mathit{Prop}$ predicate defined as follows.

$${\mathtt{valid}}_{\mathtt{mc}}\left(\mathit{me}\right)\triangleq \left\{\begin{array}{cc}\mathtt{true}\hfill & \mathit{if}\mathit{me}=\mathtt{free}\hfill \\ {\mathtt{valid}}_{\mathbb{Q}}\left(\pi \right)\hfill & \mathit{if}\mathit{me}={⟨P,\mathsf{\Lambda }⟩}^{\pi }\mathit{for}\mathit{some}P\mathrm{and}\mathsf{\Lambda }\hfill \\ \mathtt{false}\hfill & \mathit{if}\mathit{me}=\mathtt{inv}\hfill \end{array}\right.$$

It is not difficult to see that ${\mathrm{𝟙}}_{\mathtt{pm}}$ is trivially valid, and that bisimilarity is validity-preserving, i.e., ${\mathtt{valid}}_{\mathtt{pm}}\left({\mathit{pm}}_1\right)$ and ${\mathit{pm}}_1{\cong }_{\mathtt{pm}}{\mathit{pm}}_2$ implies ${\mathtt{valid}}_{\mathtt{pm}}\left({\mathit{pm}}_2\right)$ for every ${\mathit{pm}}_1$ and ${\mathit{pm}}_2$; and likewise for ${\mathtt{valid}}_{\mathtt{mc}}$.

Disjointness. Two process maps are said to be disjoint if none of their entries are corrupt, and all fractional permissions of their entries are point-wise disjoint, as captured by the following definition.

Definition 25

(Process map disjointness). Any two process maps ${\mathit{pm}}_1$ and ${\mathit{pm}}_2$ are defined to be disjoint, denoted ${\mathit{pm}}_1{\perp }_{\mathtt{pm}}{\mathit{pm}}_2$, if ${\mathit{pm}}_1\left(v\right){\perp }_{\mathtt{mc}}{\mathit{pm}}_2\left(v\right)$ for every $v\in \mathit{Val}$, with the ${\perp }_{\mathtt{mc}}$ relation defined as follows.

$${\mathit{me}}_1{\perp }_{\mathtt{mc}}{\mathit{me}}_2\triangleq \left\{\begin{array}{cc}{\mathtt{valid}}_{\mathtt{mc}}\left({\mathit{me}}_1\right)\hfill & \mathit{if}{\mathit{me}}_2=\mathtt{free}\hfill \\ {\mathtt{valid}}_{\mathtt{mc}}\left({\mathit{me}}_2\right)\hfill & \mathit{if}{\mathit{me}}_1=\mathtt{free}\hfill \\ {\pi }_1{\perp }_{\mathbb{Q}}{\pi }_2\wedge {\mathsf{\Lambda }}_1={\mathsf{\Lambda }}_2\hfill & \mathit{if}{\mathit{me}}_1={⟨P_1,{\mathsf{\Lambda }}_1⟩}^{{\pi }_1}\wedge {\mathit{me}}_2={⟨P_2,{\mathsf{\Lambda }}_2⟩}^{{\pi }_2}\mathit{for}\mathit{some}{P}_1\mathrm{and}{P}_2\hfill \\ \mathtt{false}\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

The intuition of disjointness is that disjoint process maps can safely be composed without corrupting any of their entries. Disjointness is a symmetric relation and is a congruence with respect to bisimilarity, meaning that ${\mathit{pm}}_1{\perp }_{\mathtt{pm}}{\mathit{pm}}_2$ and ${\mathit{pm}}_1{\cong }_{\mathtt{pm}}{\mathit{pm}}_1^{\prime }$ and ${\mathit{pm}}_2{\cong }_{\mathtt{pm}}{\mathit{pm}}_2^{\prime }$ implies ${\mathit{pm}}_1^{\prime }{\perp }_{\mathtt{pm}}{\mathit{pm}}_2^{\prime }$.

Disjoint union. The following operation defines the disjoint union of two process map (entries).

Definition 26

(Disjoint union of process maps). The disjoint unionof two process maps ${\mathit{pm}}_1$ and ${\mathit{pm}}_2$ is defined as ${\mathit{pm}}_1{\uplus }_{\mathtt{pm}}{\mathit{pm}}_2\triangleq \forall v.{\mathit{pm}}_1\left(v\right){\uplus }_{\mathtt{mc}}{\mathit{pm}}_2\left(v\right)$, with ${\uplus }_{\mathtt{mc}}$ defined as follows.

$${\mathit{me}}_1{\uplus }_{\mathtt{mc}}{\mathit{me}}_2\triangleq \left\{\begin{array}{cc}{\mathit{me}}_1\hfill & \mathit{if}{\mathit{me}}_2=\mathtt{free}\hfill \\ {\mathit{me}}_2\hfill & \mathit{if}{\mathit{me}}_1=\mathtt{free}\hfill \\ {⟨P_1\Vert P_2,{\mathsf{\Lambda }}_1⟩}^{{\pi }_1+{\pi }_2}\hfill & \mathit{if}{\mathit{me}}_1={⟨P_1,{\mathsf{\Lambda }}_1⟩}^{{\pi }_1}\wedge {\mathit{me}}_2={⟨P_2,{\mathsf{\Lambda }}_2⟩}^{{\pi }_2}\wedge {\mathsf{\Lambda }}_1={\mathsf{\Lambda }}_2\hfill \\ \mathtt{inv}\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

Likewise to disjoint union of permission heaps, the composition of incompatible process map entries produces a corrupted $\mathtt{inv}$ entry. The $\mathtt{free}$ entry is again neutral, whereas $\mathtt{inv}$ is absorbing (that is, composing $\mathtt{inv}$ with any entry results in $\mathtt{inv}$). Disjoint union is a congruence with respect to bisimilarity, so that ${\mathit{pm}}_1{\cong }_{\mathtt{pm}}{\mathit{pm}}_2$ and ${\mathit{pm}}_1^{\prime }{\cong }_{\mathtt{pm}}{\mathit{pm}}_2^{\prime }$ implies ${\mathit{pm}}_1{\uplus }_{\mathtt{pm}}{\mathit{pm}}_1^{\prime }{\cong }_{\mathtt{pm}}{\mathit{pm}}_2{\uplus }_{\mathtt{pm}}{\mathit{pm}}_2^{\prime }$.

Lemma 6.

(The analogous operations on process map entries have the exact same properties.)

1. 

${\mathit{pm}}_1{\uplus }_{\mathtt{pm}}\left({\mathit{pm}}_2{\uplus }_{\mathtt{pm}}{\mathit{pm}}_3\right){\cong }_{\mathtt{pm}}\left({\mathit{pm}}_1{\uplus }_{\mathtt{pm}}{\mathit{pm}}_2\right){\uplus }_{\mathtt{pm}}{\mathit{pm}}_3$.

2. 

${\mathit{pm}}_1{\uplus }_{\mathtt{pm}}{\mathit{pm}}_2{\cong }_{\mathtt{pm}}{\mathit{pm}}_2{\uplus }_{\mathtt{pm}}{\mathit{pm}}_1$.

3. 

$\mathit{pm}{\uplus }_{\mathtt{pm}}{\mathrm{𝟙}}_{\mathtt{pm}}{\cong }_{\mathtt{pm}}\mathit{pm}$.

4. 

If ${\mathit{pm}}_1{\perp }_{\mathtt{pm}}{\mathit{pm}}_2$, then ${\mathtt{valid}}_{\mathtt{pm}}\left({\mathit{pm}}_1{\uplus }_{\mathtt{pm}}{\mathit{pm}}_2\right)$.

5. 

If ${\mathit{pm}}_1{\perp }_{\mathtt{pm}}{\mathit{pm}}_2$ and $\left({\mathit{pm}}_1{\uplus }_{\mathtt{pm}}{\mathit{pm}}_2\right){\perp }_{\mathtt{pm}}{\mathit{pm}}_3$, then also

(a) 

${\mathit{pm}}_2{\perp }_{\mathtt{pm}}{\mathit{pm}}_3$, and

(b) 

${\mathit{pm}}_1{\perp }_{\mathtt{pm}}\left({\mathit{pm}}_2{\uplus }_{\mathtt{pm}}{\mathit{pm}}_3\right)$.

3.3.7. Semantics of Assertions

Let us now define the semantic meaning of assertions. The semantics of assertions is defined in terms of a satisfaction relation $\mathit{ph},\mathit{pm},s,g\models \mathcal{P}$ stating that the assertion $\mathcal{P}$ is satisfied by the model $(\mathit{ph},\mathit{pm},s,g)$. Its definition depends on an operation $\left[\right[·\left]\right]:\mathit{AbstrBinder}\to \mathit{Store}\to \mathit{Binder}$ for evaluating abstraction binders $\mathsf{\Pi }=\left\{x_0\mapsto E_0,\cdots ,x_n\mapsto E_n\right\}$, that is defined as follows.

Definition 27

(Abstraction binder evaluation).

$$\begin{array}{c}\left[\left[\left\{x_0\mapsto E_0,\cdots ,x_n\mapsto E_n\right\}\right]\right]s\triangleq \lambda x.\left\{\begin{array}{cc}\left[\left[E_i\right]\right]s\hfill & \mathit{if}x=x_i\mathit{for}\mathit{some}0\le i\le n\hfill \\ \mathit{undefined}\hfill & \mathit{otherwise}\hfill \end{array}\right.\end{array}$$

Moreover, recall that hybrid processes may contain both program variables and process-algebraic variables. The semantics of assertions relies on a closure operation for “closing” processes with respect to any program variable occurring in it. More specifically, given any hybrid process $\tilde{P}$ and store s, the s-closure of $\tilde{P}$, written $\tilde{P}\left[s\right]$, is defined to be $\tilde{P}{[X/s\left(X\right)]}_{X\in \mathtt{FV}\left(\tilde{P}\right)}$, i.e., replacing every free program variable X in $\tilde{P}$ by $s\left(X\right)$. This operation is “closing” $\tilde{P}$ in the sense that $\mathtt{FV}\left(\tilde{P}\left[s\right]\right)=\varnothing$ and $\tilde{P}\left[s\right]\in \mathit{Proc}$.

Definition 28

(Semantics of assertions). The modelling relation $\mathit{ph},\mathit{pm},s,g\models \mathcal{P}$ is defined by structural recursion on $\mathcal{P}$ as follows.

$$\begin{array}{ccc}\hfill \mathit{ph},\mathit{pm},s,g\models B& \mathit{iff}& \left[\right[B\left]\right]s\hfill \\ \hfill \mathit{ph},\mathit{pm},s,g\models \forall X.\mathcal{P}& \mathit{iff}& \forall v.(\mathit{ph},\mathit{pm},s[X\mapsto v],g[X\mapsto v\left]\right)\models \mathcal{P}\hfill \\ \hfill \mathit{ph},\mathit{pm},s,g\models \exists X.\mathcal{P}& \mathit{iff}& \exists v.(\mathit{ph},\mathit{pm},s[X\mapsto v],g[X\mapsto v\left]\right)\models \mathcal{P}\hfill \\ \hfill \mathit{ph},\mathit{pm},s,g\models {\mathcal{P}}_1\vee {\mathcal{P}}_1& \mathit{iff}& \mathit{ph},\mathit{pm},s,g\models {\mathcal{P}}_1\vee \mathit{ph},\mathit{pm},s,g\models {\mathcal{P}}_2\hfill \\ \hfill \mathit{ph},\mathit{pm},s,g\models {\mathcal{P}}_1\ast {\mathcal{P}}_2& \mathit{iff}& \exists {\mathit{ph}}_1,{\mathit{ph}}_2.{\mathit{ph}}_1{\perp }_{\mathtt{ph}}{\mathit{ph}}_2\wedge {\mathit{ph}}_1{\uplus }_{\mathtt{ph}}{\mathit{ph}}_2=\mathit{ph}\wedge \hfill \\ & & \exists {\mathit{pm}}_1,{\mathit{pm}}_2.{\mathit{pm}}_1{\perp }_{\mathtt{pm}}{\mathit{pm}}_2\wedge {\mathit{pm}}_1{\uplus }_{\mathtt{pm}}{\mathit{pm}}_2{\cong }_{\mathtt{pm}}\mathit{pm}\wedge \hfill \\ & & {\mathit{ph}}_1,{\mathit{pm}}_1,s,g\models {\mathcal{P}}_1\wedge {\mathit{ph}}_2,{\mathit{pm}}_2,s,g\models {\mathcal{P}}_2\hfill \\ \hfill \mathit{ph},\mathit{pm},s,g\models {\ast }_{i\in I}{\mathcal{P}}_i& \mathit{iff}& \mathit{ph},\mathit{pm},s,g\models {\mathcal{P}}_{i_0}\ast \cdots \ast {\mathcal{P}}_{i_n}\mathit{for}I=\left\{i_0,\cdots ,i_n\right\}\hfill \\ \hfill \mathit{ph},\mathit{pm},s,g\models {\mathcal{P}}_1-\ast {\mathcal{P}}_2& \mathit{iff}& \forall {\mathit{ph}}^{\prime },{\mathit{pm}}^{\prime }.(\mathit{ph}{\perp }_{\mathtt{ph}}{\mathit{ph}}^{\prime }\wedge \mathit{pm}{\perp }_{\mathtt{pm}}{\mathit{pm}}^{\prime }\wedge {\mathit{ph}}^{\prime },{\mathit{pm}}^{\prime },s,g\models {\mathcal{P}}_1)\Rightarrow \hfill \\ \hfill \mathit{ph}{\uplus }_{\mathtt{ph}}{\mathit{ph}}^{\prime },\mathit{pm}{\uplus }_{\mathtt{pm}}{\mathit{pm}}^{\prime },s,g\models {\mathcal{P}}_2\\ \hfill \mathit{ph},\mathit{pm},s,g\models E_1{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{std}}{E}_2& \mathit{iff}& {\mathtt{valid}}_{\mathbb{Q}}\left(\pi \right)\wedge \exists {\pi }^{\prime }.\mathit{ph}\left(\left[\left[E_1\right]\right]s\right)={⟨\left[\left[E_2\right]\right]s⟩}_{\mathtt{std}}^{{\pi }^{\prime }}\wedge \pi \le {\pi }^{\prime }\hfill \\ \hfill \mathit{ph},\mathit{pm},s,g\models E_1{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}{E}_2& \mathit{iff}& {\mathtt{valid}}_{\mathbb{Q}}\left(\pi \right)\wedge \exists {\pi }^{\prime }.\mathit{ph}\left(\left[\left[E_1\right]\right]s\right)={⟨\left[\left[E_2\right]\right]s⟩}_{\mathtt{proc}}^{{\pi }^{\prime }}\wedge \pi \le {\pi }^{\prime }\hfill \\ \hfill \mathit{ph},\mathit{pm},s,g\models E_1{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{act}}{E}_2& \mathit{iff}& {\mathtt{valid}}_{\mathbb{Q}}\left(\pi \right)\wedge \exists \pi ,v.\mathit{ph}\left(\left[\left[E_1\right]\right]s\right)={⟨\left[\left[E_2\right]\right]s,v⟩}_{\mathtt{act}}^{{\pi }^{\prime }}\wedge \pi \le {\pi }^{\prime }\hfill \\ \hfill \mathit{ph},\mathit{pm},s,g\models {\mathtt{Proc}}_{\pi }(E,\tilde{P},\mathsf{\Pi })& \mathit{iff}& \exists {\mathit{me}}^{\prime }.\mathit{me}{\perp }_{\mathtt{mc}}{\mathit{me}}^{\prime }\wedge \mathit{pm}\left(\left[\left[E\right]\right]g\right){\cong }_{\mathtt{pm}}\mathit{me}{\uplus }_{\mathtt{mc}}{\mathit{me}}^{\prime }\hfill \\ \hfill \mathrm{where}\mathit{me}={⟨\tilde{P}\left[s\right],\left[\right[\mathsf{\Pi }\left]\right]s⟩}^{\pi }\\ \hfill \mathit{ph},\mathit{pm},s,g\models \tilde{P}\approx \tilde{Q}& \mathit{iff}& \tilde{P}\left[s\right]\cong \tilde{Q}\left[s\right]\hfill \end{array}$$

As usual, any separating conjunction ${\mathcal{P}}_1\ast {\mathcal{P}}_2$ is satisfied by a model $(\mathit{ph},\mathit{pm},s,g)$ if that model can both be split along $\mathit{ph}$ and $\mathit{pm}$ into two disjoint models, such that one satisfies ${\mathcal{P}}_1$ and the other satisfies ${\mathcal{P}}_2$. The semantic meaning of iterated separating conjunctions can be expressed simply in terms of the interpretation of the binary separating conjunction. Magic wands ${\mathcal{P}}_1-\ast {\mathcal{P}}_2$ are satisfied by a model if, for any disjoint extension of that model satisfying ${\mathcal{P}}_1$, the extended model satisfies ${\mathcal{P}}_2$.

Moving to the non-standard connectives; heap ownership assertions $E{\stackrel{\pi }{\hookrightarrow }}_t{E}^{\prime }$ are satisfied if the permission heap holds an entry at location E that matches with the ownership type t, with an associated fractional permission that is at least $\pi$. Process ownership assertions ${\mathtt{Proc}}_{\pi }(E,\tilde{P},\mathsf{\Pi })$ are satisfied if the process map holds a matching entry at the position described by E, with a fractional permission at least $\pi$, and a process that at least includes all the behaviours of the process $\tilde{P}\left[s\right]$. Finally, $\tilde{P}\approx \tilde{Q}$ is satisfied if $\tilde{P}$ and $\tilde{Q}$ are bisimilar with respect to the current state. To give an example of the use of ≈, consider the assertion ${\mathtt{Proc}}_{\pi }(E,0<X:\tilde{P},\mathsf{\Pi })\ast X=2$. One might wish to replace $0<X:\tilde{P}$ with $\tilde{P}$, considering that $X=2$. But since $0<X:\tilde{P}$ is a process that includes program variables (namely X), one can not immediately deduce that it is bisimilar to $\tilde{P}$ according to Definition 7. However, we do have that $0<X:\tilde{P}\approx \tilde{P}\ast X=2$, since for every model $(\mathit{ph},\mathit{pm},s,g)$ satisfying this assertion it holds that $s\left(X\right)=2$. We shall later give entailment rules that allow such context-dependent bisimulation equivalences to be used to simplify processes inside ${\mathtt{Proc}}_{\pi }$ ownership predicates.

Lemma 7.

The ⊨ modelling relation satisfies the following properties:

1. 

$\mathit{ph},\mathit{pm},s,g\models \mathcal{P}$ and $\mathit{pm}{\cong }_{\mathtt{pm}}{\mathit{pm}}^{\prime }$ implies $\mathit{ph},{\mathit{pm}}^{\prime },s,g\models \mathcal{P}$.

2. 

If $\mathit{ph},\mathit{pm},s,g\models \mathcal{P}$, then for any ${\mathit{ph}}^{\prime }$ and ${\mathit{pm}}^{\prime }$ such that $\mathit{ph}{\perp }_{\mathtt{ph}}{\mathit{ph}}^{\prime }$ and $\mathit{pm}{\perp }_{\mathtt{pm}}{\mathit{pm}}^{\prime }$ it holds that $\mathit{ph}{\uplus }_{\mathtt{ph}}{\mathit{ph}}^{\prime },\mathit{pm}{\uplus }_{\mathtt{pm}}{\mathit{pm}}^{\prime },s,g\models \mathcal{P}$.

Lemma 7.1 is essential for allowing replacing process-algebraic abstractions by bisimilar ones inside the program logic. Lemma 7.2 expresses monotonicity, and states that adding resources does not invalidate the satisfiability of any assertion (i.e., adding more resources makes the assertion “more true”). This is a key property of intuitionistic separation logic and is necessary for proving soundness of the weakening rule, which we introduce later in Section 3.4.1.

3.3.8. Semantic Entailment

Let the denotation $\left[\right[\mathcal{P}\left]\right]\triangleq \left\{(\mathit{ph},\mathit{pm},s,g)\left|\right(\mathit{ph},\mathit{pm},s,g)\models \mathcal{P}\right\}$ be the set of all models that are satisfied by the assertion $\mathcal{P}$. Given any two assertions $\mathcal{P}$ and $\mathcal{Q}$, the assertion $\mathcal{P}$ is defined to semantically entail $\mathcal{Q}$, denoted $\mathcal{P}\models \mathcal{Q}$, if every model of $\mathcal{P}$ is also a model of $\mathcal{Q}$, that is, $\mathcal{P}\models \mathcal{Q}\triangleq \left[\right[\mathcal{P}\left]\right]\subseteq \left[\right[\mathcal{Q}\left]\right]$. Semantic entailment is thus a preorder and a congruence for all connectives of the assertion language.

3.4. Proof System

This section introduces the proof system of our model-based verification technique, which consists of structural proof rules (Section 3.4.1) as well as Hoare proof rules (Section 3.4.2). This proof system essentially extends the CSL of [34] by adding permission accounting [36,37] and machinery for handling process-algebraic program abstractions.

3.4.1. Entailment Rules

Figure 3 presents the structural rules of the program logic. The notation $\mathcal{P}⊣⊢\mathcal{Q}$ is a shorthand for both $\mathcal{P}⊢\mathcal{Q}$ and $\mathcal{Q}⊢\mathcal{P}$, and indicates that the rule can be used in both directions.

Figure 3. The entailment rules of the program logic.

The rules for the standard connectives are mostly as expected. PLAIN-DUPL expresses that plain expressions can freely be duplicated, whereas *-PLAIN shows that * has the same meaning as ∧ in the case of plain assertions. The rule *-WEAK shows that our concurrent separation logic is affine (intuitionistic) by allowing to forget about resources. The rules *-ASSOC and *-COMM express that the separating conjunction is associative and commutative, respectively, whereas *-TRUE allows composing any resource with $\mathtt{true}$. The rule TRUE-INTRO is the introduction rule for $\mathtt{true}$, while FALSE-ELIM is the elimination rule for $\mathtt{false}$ stating that anything can be derived from falsehood. The $-\ast$-INTRO and $-\ast$-ELIM rules show that magic wands can be used similarly to the modus ponens inference rule of propositional logic, with respect to *. The rules ∀-INTRO, ∀-ELIM, ∃-INTRO and ∃-ELIM are the standard introduction and elimination rules for universal and existential quantifiers. ITER-SPLIT-MERGE enables splitting and merging iterated separating conjunctions along the associated (finite) index set.

Clarifying the rules for handling heap ownership; $\hookrightarrow$-SPLIT-MERGE expresses that heap ownership predicates ${\stackrel{\pi }{\hookrightarrow }}_t$ of any type t may be split (in the left-to-right direction) as well as be merged (right-to-left) along $\pi$. Note however, that multiple points-to predicates for the same heap location may only co-exist if they have the same ownership type, as indicated by the $\hookrightarrow$-INCOMPATIBLE rule. Any heap ownership assertion with an invalid fractional permission associated to it entails $\mathtt{false}$ by $\hookrightarrow$-INVALID Furthermore, the *-PROCACT-SPLIT-MERGE inference rule states that iterated $\mathtt{procact}$ heap ownership predicates can be split into disjoint iterated $\mathtt{proc}$ and $\mathtt{act}$ predicates, or be merged into one such iteration.

Moving to the entailment rules for handling process-algebraic abstractions; PROC-≅ allows replacing any process by one that is bisimilar in the current context. The rules ≈-REFL, ≈-SYMM and ≈-TRANS show that context-dependent bisimilarity forms an equivalence relation in the logic with respect to separating conjunction, while ≈-CONG-∘, ≈-CONG-SUM, ≈-CONG-COND and ≈-CONG-ITER together show that ≈ is a congruence relation in the logic for all process-algebraic connectives. The rules ≈-COND-TRUE and ≈-COND-FALSE allows eliminating conditionals in any processes (together with the Proc-≅ rule that is). Moreover, ≈-SUM-ALT allows singling out a single choice out of a process-algebraic summation of choices. Notice here that one can pick any arbitrary program expression for singling out such a choice, which makes this rule particularly useful. Similarly to heap ownership, any process ownership with an invalid fractional permission entails $\mathtt{false}$ by Proc-INVALID. The rule ≈-TERM again makes explicit the intuitive meaning of successful termination, matching Proposition 1. Finally, Proc-SPLIT-MERGE allows splitting and merging process ownership predicates in the same style as ${\stackrel{\pi }{\hookrightarrow }}_t$, to distribute parallel processes over parallel threads. Notably, by splitting a predicate ${\mathtt{Proc}}_{{\pi }_1+{\pi }_2}(X,\widetilde{P_1}\Vert \widetilde{P_2},\mathsf{\Pi })$ into two, both parts can be distributed over different concurrent threads in the program logic, so that thread i can establish that it executes as prescribed by its part ${\mathtt{Proc}}_{{\pi }_i}(X,\widetilde{P_i},\mathsf{\Pi })$ of the abstract model. Afterwards, when the threads join again the remaining partial abstractions can be merged back into a single ${\mathtt{Proc}}_{{\pi }_1+{\pi }_2}$ predicate. This system of splitting and merging thus provides a compositional, thread-modular way of verifying that programs meet their abstraction. The logical machinery of this is further discussed in Section 3.4.2.

Any deduction that can be derived using the rules of Figure 3 is sound in the standard sense:

Theorem 2

(Soundness of the entailment rules). $\mathcal{P}⊢\mathcal{Q}$ implies $\mathcal{P}\models \mathcal{Q}$.

3.4.2. Program Judgments

We now define program judgments and give the Hoare rules of the program logic. Judgments of programs are sequents (quintuples) of the form $\mathsf{\Gamma };\mathcal{R}⊢\left\{\mathcal{P}\right\}C\left\{\mathcal{Q}\right\}$. The right-hand side is a traditional Hoare triple, whereas $\mathcal{R}$ is a resource invariant that captures resources available only to atomically executing programs (i.e., in executions that are free of thread interference), and $\mathsf{\Gamma }$ an environment in the style of interface specifications of [38]. These process environments have the following definition.

Definition 29

(Process environments).

$$\begin{array}{c}\mathsf{\Gamma }\in \mathit{ProcEnv}::=\varnothing |\mathsf{\Gamma },\left\{\tilde{B}\right\}P\left(x\right)\end{array}$$

That is, process environments are comma-separated sequences of pairs $\left\{\tilde{B}\right\}P\left(x\right)$ of processes P and their precondition $\tilde{B}$, with x a placeholder variable for an input parameter that may occur freely in both P and $\tilde{B}$. Note that processes do not have postconditions here; if desired one could encode process Hoare triples op top of these pairs as $\left\{\widetilde{B_{\mathit{pre}}}\right\}P\left(x\right)\left\{\widetilde{B_{\mathit{post}}}\right\}\triangleq \left\{\widetilde{B_{\mathit{pre}}}\right\}(P\left(x\right)·?\left(\widetilde{B_{\mathit{post}}}\right))$—by adding a trailing assertion. Moreover, even though process environments are given as sequences, they are used as if they were (finite) sets, as is customary, in the sense that the order of their pairs is unimportant.

Process environments contain the contracts of the process-algebraic models defined for the program under verification. In particular, they allow for assume-guarantee style reasoning: the proof system may assume validity of these contracts when dealing with process-algebraic models, since they must be guaranteed externally, for example via interactive theorem proving or model checking, e.g., using mCRL2  [25]. Validity of process contracts and process environments is defined as follows.

Definition 30

(Validity of process environments). Any pair $\left\{\tilde{B}\right\}P\left(x\right)$ of a process P and its precondition $\tilde{B}$ is defined to be valid, denoted $\models \left\{\tilde{B}\right\}P\left(x\right)$, if $\forall s,\sigma .\left[\left[\tilde{B}\left[s\right]\right]\right]\sigma \Rightarrow \left(P,\sigma \right)$.

Any process environment Γ is defined to be validif ${\models }_{\mathtt{env}}\mathsf{\Gamma }$, which is a judgment inductively defined by the following two rules.

$$\overline{{\models }_{\mathtt{env}}\varnothing }\hspace{1em}\hspace{1em}\frac{{\models }_{\mathtt{env}}\mathsf{\Gamma }\hspace{1em}\models \left\{\tilde{B}\right\}P\left(x\right)}{{\models }_{\mathtt{env}}\mathsf{\Gamma },\left\{\tilde{B}\right\}P\left(x\right)}$$

Figure 4 and Figure 5 give the Hoare rules of the logic. The standard structural rules are essentially the same as the ones of classical CSL [34]. One minor difference is that HT-ATOMIC leaves $\mathtt{true}$ instead of “$\mathtt{emp}$” after obtaining a resource invariant, since our logic is intuitionistic. (The assertion language of classical CSL contains an extra $\mathtt{emp}$ construct, for explicitly denoting that the heap is empty. In our intuitionistic version of the logic, resources are allowed to be thrown away using *-WEAK. As a consequence, assertions cannot express “precise” properties about the content of the heap, including emptiness of heaps.) Moreover, our assertion language does not contain the logical conjunction ∧ connective, but has separating conjunction instead.

Figure 4. Standard proof rules of the program logic.

Figure 5. The extended proof rules related to handling process-algebraic models.

3.4.3. Heap Ownership

The HT-READ rule states that reading from the heap is allowed with any type t of heap ownership ${\stackrel{\pi }{\hookrightarrow }}_t$, whereas heap writing (HT-WRITE) is only allowed with ownership predicates of type $\mathtt{std}$ or $\mathtt{act}$. The HT-WRITE rule thus restricts ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}$ assertions to exclusively grant read-access to the associated location. We will in a moment see that the proof rule for $\mathtt{action}$ programs can upgrade $E{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}{E}^{\prime }$ predicates to $E{\stackrel{\pi }{\hookrightarrow }}_{\mathtt{act}}{E}^{\prime }$ to regain write access to the heap location at E. This system of upgrading enforces that all modifications to E are captured by the program abstraction to which the heap location is subject to, inside an action block. The rule HT-ALLOC for heap allocation generates a new points-to predicate of type $\mathtt{std}$, indicating that the allocated heap location is not (yet) subject to any program abstraction. Heap deallocation (HT-DISPOSE) requires a full standard ownership predicate for the associated heap location, thereby making sure that the deallocation does not break any bindings of active program abstractions, which would be unsound.

3.4.4. Process Ownership

Figure 5 gives the Hoare rules for introducing, eliminating and updating process-algebraic abstractions. The HT-PROC-INIT rule handles initialisation of an abstract model P with input parameter y, over a set of heap locations as specified by $\mathsf{\Pi }$. This rule requires standard heap write ownership for any heap location that is to be bound by P according to $\mathsf{\Pi }$, and these are converted to ${\stackrel{1}{\hookrightarrow }}_{\mathtt{proc}}$. Moreover, HT-PROC-INIT requires that the precondition B of P holds, which is constructed from $\tilde{B}$ by replacing all process variables $x_i$ by the values $E_i$ at the corresponding heap locations as specified by $\mathsf{\Pi }$. (Here we slightly abuse notation for ease of presentation. In the proof rule, we write $\tilde{B}{[x_i/E_i]}_{\forall i\in I}$ for converting a condition $\tilde{B}$ to a condition over only program variables, by substituting all free process variables $x_i$ occurring in $\tilde{B}$ by a program expression $E_i$. However, in our Coq formalisation we of course have a special operation for such conversions.) A ${\mathtt{Proc}}_1$ predicate with full permission is ensured, giving the current thread full ownership of the abstraction.

The HT-PROC-UPDATE rule handles updates to program abstractions, by performing an action $a\left(E^{\prime }\right)$ in the context of an $\mathtt{action}Ea\left(E^{\prime }\right)\mathtt{do}C$ program. This rule imposes four preconditions on handling $\mathtt{action}$ programs. First, a predicate of the form ${\mathtt{Proc}}_{\pi }(E,a\left(E^{\prime }\right)·\tilde{P}+\tilde{Q},\mathsf{\Pi })$ is required for some $\pi$. In particular, the process component must be of the form $a\left(E^{\prime }\right)·\tilde{P}+\tilde{Q}$ and therewith allow performing the a action. After performing a the process will be reduced to $\tilde{P}$, and $\tilde{Q}$ will be discarded as the choice is made not to follow execution as prescribed by $\tilde{Q}$. To get processes in the required format, the entailment rules in Figure 3 can be used together with the bisimulation equivalences given earlier in Figure 2. To give an example, processes of the form $a\left(E^{\prime }\right)·\tilde{P}$ can always be rewritten to $a\left(E^{\prime }\right)·\tilde{P}+\delta$ to obtain the required choice. Second, ${\stackrel{\pi }{\hookrightarrow }}_{\mathtt{proc}}$ predicates are required for any heap location that is bound by $\mathsf{\Pi }$. These points-to predicates are needed to resolve the guard and effect of a. Third, a’s guard must indeed hold. (The notation $\mathtt{guard}a{E}^{\prime }$ is a shorthand for $\left(\mathtt{guard}az\right)[z/E^{\prime }]$ for some fresh $z\in \mathit{ProcVar}$, and likewise for $\mathtt{effect}a{E}^{\prime }$.) And last, the remaining resource $\mathcal{P}$ must hold as well.

Among the premises of HT-PROC-UPDATE is a proof derivation for the sub-program C, in which all required ${\stackrel{{\pi }_i}{\hookrightarrow }}_{\mathtt{proc}}$ predicates are “upgraded” to ${\stackrel{{\pi }_i}{\hookrightarrow }}_{\mathtt{act}}$ and thereby regain write access when ${\pi }_i=1$. However, in case ${\pi }_i<1$ the upgrade does not give any additional privileges, since ${\stackrel{{\pi }_i}{\hookrightarrow }}_{\mathtt{proc}}$ provides read-access just the same. We found that these unnecessary conversions complicate the soundness proof. To avoid unnecessary upgrades, we convert all affected ${\stackrel{{\pi }_i}{\hookrightarrow }}_{\mathtt{proc}}$ predicates to ${\stackrel{{\pi }_i}{\hookrightarrow }}_{\mathtt{procact}}$ instead, which simplifies the correctness proof. The HT-PROC-UPDATE rule ensures a process ownership predicate that holds the resulting process $\tilde{P}$ after execution of a. In addition, updates to the heap are ensured that comply with the postconditions of the proof derivation of C.

HT-PROC-FINISH handles finalisation of process-algebraic models that can successfully terminate. A predicate ${\mathtt{Proc}}_1(E,\epsilon +\tilde{P},\mathsf{\Pi })$ with full permission is required, implying that no other thread can have a fragment of the abstract model. The rule converts all bound ${\stackrel{1}{\hookrightarrow }}_{\mathtt{proc}}$ ownership predicates back to ${\stackrel{1}{\hookrightarrow }}_{\mathtt{std}}$ ownerships to indicate that these are no longer subject to the abstract model.

Lastly, HT-PROC-QUERY allows “querying” for properties $\tilde{B}$ that are verified on the process algebra level. Recall that the main objective of process-algebraic analysis is to verify that all reachable assertions $?\left(\tilde{B}\right)$ hold. Observe that in this rule, the assertions may contain program variables in addition to process-algebraic variables, as these may have been introduced via summations (≈-SUM-ALT) or input parameters (HT-PROC-INIT). The soundness argument of the logic makes sure that the process-algebraic analysis can still be done fully on the process level (i.e., without relying on program state), meaning that this rule really makes a fusion between process-algebraic reasoning and deductive reasoning.

3.5. Soundness

This section defines the semantic meaning of program judgments and discuss the soundness proof of the program logic. This soundness proof has been mechanised using Coq, which was non-trivial and required substantial auxiliary definitions. This section discusses the most important auxiliary definitions and explains their use. For further proof details we refer to the Coq development [19].

The soundness theorem relates program judgments to the operational semantics of programs and boils down to the following: if (1) a proof $\mathsf{\Gamma };\mathcal{R}⊢\left\{\mathcal{P}\right\}C\left\{\mathcal{Q}\right\}$ can be derived for any program C and (2) the contracts in $\mathsf{\Gamma }$ of all abstract models of C are satisfied (proven externally), then C executes safely for any number of computation steps. Execution safety in this sense also includes that C does not fault for any number of reduction steps with respect to the fault semantics of programs; see Definition 13.

Our definition of execution safety extends the well-known inductive definition of configuration safety of Vafeiadis [34] by adding machinery to handle process-algebraic abstractions. The most important extension is a simulation argument between concrete program executions (with respect to $⇝$) and the executions of all active models (with respect to $\stackrel{\alpha }{⟶}$). However, as the reduction steps of these two semantics do not directly correspond one-to-one, this simulation is established via an intermediate instrumented semantics referred to as the ghost operational semantics. This intermediate semantics is defined in Section 3.5.1 in terms of ghost transitions ${⇝}_{\mathtt{ghost}}$ that essentially define the lock-step execution of program transitions $⇝$ and the transitions $\stackrel{\alpha }{⟶}$ of their abstractions. Our definition of “executing safely for n execution steps” includes that all $⇝$ steps can be simulated by ${⇝}_{\mathtt{ghost}}$ steps, and vice versa, for n execution steps. Thus, the end-result is a refinement between programs and their abstractions.

In addition to establishing such refinements, our definition of execution safety must ensure that the HT-PROC-QUERY proof rule is sound. In other words, it must allow relying on any assertions embedded in the process-algebraic models in a sound manner, as these are (assumed to be) verified externally. To account for these assertions, the definition of execution safety needs to maintain the invariant that all active program abstractions preserve their execution safety as defined in Definition 5 for n execution steps, with respect to the current state of the program. (Recall that any process P is said to be safe according to this definition if P’s assertions always hold.) The details of maintaining this invariant are discussed further in Section 3.5.3.

Finally, Section 3.5.4 formally defines process execution safety—the semantic meaning of program judgments—and presents the exact soundness statement.

3.5.1. Ghost Operational Semantics

To establish the refinements between programs and their abstractions, an intermediate semantics is used that administers the states of all active program abstractions. This intermediate semantics is referred to in the sequel as the ghost operational semantics. The ghost semantics is expressed as a transition relation ${⇝}_{\mathtt{ghost}}\subseteq \mathit{GhostConf}$ between ghost configurations $\mathfrak{G}=(C,h,\mathit{pm},s,g)\in \mathit{GhostConf}$, which extend program configurations by two extra components, namely:

• A process map $\mathit{pm}\in \mathit{ProcMap}$ that is used to administer the state of all active (initialised, but not yet finalised) process-algebraic abstractions; and
• An extra store $g\in \mathit{Store}$, referred to as a ghost store, as it is used to map variable names to process identifiers in the context of “ghost” instructions.

The ghost operational semantics uses two stores instead of one, to keep the administration of program data and specification-only (ghost) data strictly separated. Doing so eases establishing that variables referred to in ghost code do not interfere with regular program execution, and vice versa.

Ghost reductions essentially describe the lock-step execution of concrete programs ($⇝$steps) and their abstractions ($\stackrel{\alpha }{⟶}$ steps). Figure 6 presents an excerpt of the transition rules. This excerpt only contains the reduction rules related to program abstraction; all other rules are essentially the same as those of $⇝$, with the two extra configuration components simply carried over and left unchanged. Recall that the blue colourings are merely visual cues and do not have any special semantical meaning.

Figure 6. An excerpt of the transition rules of the ghost operational semantics.

Clarifying the ghost reduction rules, GHOST-PROC-INIT instantiates a new program abstraction and stores it in a free entry in $\mathit{pm}$. GHOST-PROC-FINISH finalises program abstractions that are able to terminate successfully. The rules GHOST-ACT-INIT, GHOST-ACT-STEP and GHOST-ACT-END handle the execution of action blocks. Before discussing these, first observe that the ghost semantics maintains an extra component m in $\mathtt{inact}$   m   Ccommands, containing (ghost) metadata: extra runtime information about the process-algebraic model in whose context the program C is being executed. Concretely, ghost metadata m is defined as a quadruple $m=(a,v,v^{\prime },h)\in \mathit{Act}\times \mathit{Val}\times \mathit{Val}\times \mathit{Heap}$, consisting of:

• The label a of the action that is being executed;
• The input argument v for this action;
• The identifier $v^{\prime }$ of the corresponding process-algebraic model in the process map, in which the action a is to be executed; and
• A copy h of the heap, made when the program started to execute the action block; that is, when the $\mathtt{action}$ program was reduced to $\mathtt{inact}$ by $⇝$.

The ghost-ACT-INIT reduction rule starts executing an $\mathtt{action}$ block by reducing it to an $\mathtt{inact}$ program, thereby assembling and attaching ghost metadata. In particular, a copy of the heap is made at this point, so that the ghost-ACT-END rule for finalising $\mathtt{inact}$ programs is able to access the original contents of the heap. This is needed to allow the abstraction to make a matching $\stackrel{\alpha }{⟶}$ step; in particular to determine the pre-state of such a step. To see how this works, first recall that the process-algebraic state of program abstractions are linked to concrete program state—entries in the heap—via the $\mathsf{\Lambda }$ binders maintained in process maps. Therefore, to be able to make an $\stackrel{\alpha }{⟶}$ step, the ghost-ACT-END rule first needs to construct process-algebraic state out of the current program state. This is done using the auxiliary function $\left|\right|·\left|\right|:\mathit{Binder}\to \mathit{Heap}\to \mathit{ProcStore}$ referred to as the abstract state reification function.

Definition 31

(Abstract state reification).

$$\left|\right|\mathsf{\Lambda }\left|\right|\left(h\right)\triangleq \lambda x\in \mathit{ProcVar}.\left\{\begin{array}{cc}h\left(\mathsf{\Lambda }\right(x\left)\right)\hfill & \mathit{if}x\in \mathtt{dom}\left(\mathsf{\Lambda }\right)\mathit{and}\mathsf{\Lambda }\left(x\right)\in \mathtt{dom}\left(h\right)\hfill \\ {\mathrm{𝟙}}_{\mathit{Val}}\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

The ghost-ACT-STEP rule allows making reductions in the context of $\mathtt{inact}$ programs. Finally ghost-QUERY handles reductions of assertions and synchronises any $\stackrel{\mathit{assn}}{⟶}$ reductions on the process level with reductions of queries on the program level, with respect to the reified program state.

3.5.2. Faulting Ghost Configurations

In addition to faulting program configurations (Definition 13) we also define a fault semantics for ghost configurations. This ghost fault semantics is expressed in terms of a predicate ${↯}_{\mathtt{ghost}}\left(\mathfrak{G}\right)$ over ghost configurations $\mathfrak{G}$. Figure 7 gives an excerpt of the rules. Only the rules related to specification-only constructs are shown. All other rules are essentially the same as those of Definition 13. We shall later show and prove properties that connect the two faulting semantics.

Figure 7. An excerpt of the fault semantics of ghost configurations.

Clarifying the ghost fault semantics; the initialisation of any process-algebraic model faults if there is no free entry available in $\mathit{pm}$ (by ${↯}_{\mathtt{ghost}}$-PROC-FULL). The finalisation of program abstractions can fault if the corresponding entry in the process map is (1) either unoccupied or invalid (${↯}_{\mathtt{ghost}}$-PROC-FINISH-1), or (2) contains a process-algebraic abstraction that is unable to successfully terminate (by the rule ${↯}_{\mathtt{ghost}}$-PROC-FINISH-2). Reductions within action blocks $\mathtt{inact}$   m   C may fault if (1) m does not refer to an abstraction (${↯}_{\mathtt{ghost}}$-ACT-SKIP-1), or (2) the abstraction relies on process variables that have an incorrect binding (by the rule ${↯}_{\mathtt{ghost}}$-ACT-SKIP-2), or (3) the process is not able to make a matching step (${↯}_{\mathtt{ghost}}$-ACT-SKIP-3), or (4) the subprogram C is able to fault (by ${↯}_{\mathtt{ghost}}$-ACT-SKIP). Any $\mathtt{query}$ program can fault under similar conditions as those of action programs.

The ghost semantics enjoys the same progress property as the standard operational semantics.

Theorem 3

(Progress of ${⇝}_{\mathtt{ghost}}$). For any ghost configuration $\mathfrak{G}$ for which $\neg {↯}_{\mathtt{ghost}}\left(\mathfrak{G}\right)$ holds, either $\mathfrak{G}$ is final, or there exists a ${\mathfrak{G}}^{\prime }$ such that $\mathfrak{G}{⇝}_{\mathtt{ghost}}{\mathfrak{G}}^{\prime }$.

Moreover, it is quite straightforward to establish a forward simulation between $⇝$ and ${⇝}_{\mathtt{ghost}}$. A matching backward simulation is ensured by the soundness argument of the program logic, as is customary for establishing refinements [39].

Lemma 8

(Forward simulation). The standard operational semantics and the fault semantics of programs are embeddedin the ghost operational semantics and ghost fault semantics, respectively:

1. 

If $(C,h,\mathit{pm},s,g){⇝}_{\mathtt{ghost}}(C^{\prime },h^{\prime },{\mathit{pm}}^{\prime },s^{\prime },g^{\prime })$, then $(C,h,s)⇝(C^{\prime },h^{\prime },s^{\prime })$.

2. 

If $↯(C,h,s)$, then also ${↯}_{\mathtt{ghost}}\left(C,h,\mathit{pm},s,g\right)$, for any $\mathit{pm}$ and g.

The above theorem also shows that the ghost fault semantics extends ↯. The soundness argument of the program logic establishes that verified programs do not fault with respect to ${⇝}_{\mathtt{ghost}}$, and thus also do not fault with respect to $⇝$ by the above Lemma.

3.5.3. Preservation of Process Execution Safety

As already hinted upon in the preamble of this section, establishing soundness of the program logic requires maintaining an invariant stating that all active program abstractions retain their execution safety throughout program execution, with respect to Definitions 5 and 6. Since process maps are used to administer the status of all active program abstractions, we lift the notion of process configuration safety (Definition 5) to safety of process maps. Process map safety is expressed in terms of judgments of the form $h{\models }_{\mathtt{pm}}\mathit{pm}$ stating that $\mathit{pm}$ is safe if all process-algebraic models stored in $\mathit{pm}$ execute safely with respect to Definition 5 together with a process store that is constructed (reified) from h.

Definition 32

(Process map safety).

$$\begin{array}{cc}h{\models }_{\mathtt{pm}}\mathit{pm}\hfill & \triangleq \forall v\in \mathit{Val}.h{\models }_{\mathtt{mc}}\mathit{pm}\left(v\right)\hfill \end{array}$$

where $h{\models }_{\mathtt{mc}}\mathit{mc}$ is defined by case distinction on $\mathit{mc}$, so that

$$1-1h{\models }_{\mathtt{mc}}\mathit{me}\triangleq \left\{\begin{array}{cc}\mathtt{true}\hfill & \mathit{if}\mathit{me}=\mathtt{free}\hfill \\ ✓\left(P,\left|\right|\mathsf{\Lambda }\left|\right|\left(h\right)\right)\hfill & \mathit{if}\mathit{me}={⟨P,\mathsf{\Lambda }⟩}^{\pi }\mathit{for}\mathit{some}\pi \hfill \\ \mathtt{false}\hfill & \mathit{if}\mathit{me}=\mathtt{inv}\hfill \end{array}\right.$$

Free process cells are always safe whereas corrupted entries $\mathtt{inv}$ are never safe. Moreover, both ${\models }_{\mathtt{pm}}$ and ${\models }_{\mathtt{mc}}$ are closed under bisimilarity of process maps and their entries, respectively.

Lemma 9.

1.

If $h{\models }_{\mathtt{pm}}\mathit{pm}$ and $\mathit{pm}{\cong }_{\mathtt{pm}}{\mathit{pm}}^{\prime }$, then $h{\models }_{\mathtt{pm}}{\mathit{pm}}^{\prime }$.

2.

If $h{\models }_{\mathtt{mc}}\mathit{me}$ and $\mathit{me}{\cong }_{\mathtt{mc}}{\mathit{me}}^{\prime }$, then $h{\models }_{\mathtt{mc}}{\mathit{me}}^{\prime }$.

In a moment we will also define a notion of execution safety for commands. This notion of program execution safety maintains the aforementioned invariant that $h{\models }_{\mathtt{pm}}\mathit{pm}$ always holds throughout program execution, where h and $\mathit{pm}$ are constructed from the current state, at every execution step. This invariant is needed to establish soundness of the HT-PROC-QUERY proof rule.

However, one must be careful on how to exactly state this invariant, to allow re-establishing it after every computation step. In most cases re-establishing the invariant is straightforward. For example, $h{\models }_{\mathtt{pm}}\mathit{pm}$ can be re-established after initialising a new program abstraction using the HT-PROC-INIT proof rule, by Definition 6 and by the structure of that proof rule. The invariant can also trivially be re-established after finalising an abstraction using HT-PROC-FINISH, as the abstraction is then no longer active and thereby removed from $\mathit{pm}$. However, computation steps that involve heap writing (i.e., handling of $\left[E\right]:=E^{\prime }$ programs) may be problematic, as illustrated below.

Technicality 1

(Potential problems due to heap writing). To see the potential problem, consider the following code snippet.

Suppose that $h{\models }_{\mathtt{pm}}\mathit{pm}$ holds on line 5. After computing line 6, the heap h holds the value $-2$ at location $\left[\left[E^{\prime }\right]\right]s$. Moreover, the process map $\mathit{pm}$ has not been changed, since the action program (lines 5–8) has not fully been executed yet. Nevertheless, $h[\left[\left[E^{\prime }\right]\right]s\mapsto -2]{\models }_{\mathtt{pm}}\mathit{pm}$ may now be violated, as the $\mathsf{reset}$ action can no longer be performed, since $x=-2$ after reification, while $\mathsf{reset}$’s guard requires x to be positive.

The root of the problem is that the invariant should not necessarily have to hold during intermediate reduction steps while executing $\mathtt{action}$ programs, but only at the pre- and poststate of such programs. Program execution safety will solve this by making a snapshot of the heap every time an action program is being started on (likewise to ghost-ACT-INIT), and expressing the invariant over these snapshot heaps. Snapshots are recorded at the level of permission heaps, which already have the required structure to do this: action heap cells ${⟨v_1,v_2⟩}_{\mathtt{act}}^{\pi }$ allow storing snapshot values $v_2$ alongside “concrete” values $v_1$. These snapshot values are used to construct snapshot heaps.

Definition 33

(Snapshot heaps). The snapshot of a permission heap is defined in terms of a total function ${\lfloor ·\rfloor }_{\mathsf{snapshot}}:\mathit{PermHeap}\to \mathit{Heap}$, so that ${\lfloor \mathit{ph}\rfloor }_{\mathsf{snapshot}}\triangleq \lambda v\in \mathit{Val}.{\lfloor \mathit{ph}\left(v\right)\rfloor }_{\mathsf{snapshot}}$, with

$${\lfloor \mathit{hc}\rfloor }_{\mathsf{snapshot}}\triangleq \left\{\begin{array}{cc}v\hfill & \mathit{if}\mathit{hc}={⟨v⟩}_{\mathtt{proc}}^{\pi }\mathit{for}\mathit{some}\pi \hfill \\ v_2\hfill & \mathit{if}\mathit{hc}={⟨v_1,v_2⟩}_{\mathtt{act}}^{\pi }\mathit{for}\mathit{some}{v}_1\mathrm{and}\pi \hfill \\ \mathit{undefined}\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

The snapshot heap ${\lfloor \mathit{ph}\rfloor }_{\mathsf{snapshot}}$ of any permission heap $\mathit{ph}$ only contains heap cells bound by process-algebraic models, and is constructed by taking the snapshot values of all $\mathit{ph}$’s action heap cells. As we shall see in a moment, the final invariant maintained by program execution safety will be ${\lfloor \mathit{ph}\rfloor }_{\mathsf{snapshot}}{\models }_{\mathtt{pm}}\mathit{pm}$, where $\mathit{ph}$ and $\mathit{pm}$ are taken from the models of the program logic and represent the current state of the program. This invariant, combined with establishing a refinement between the program and its abstract models, provide sufficient means for proving soundness of the program logic.

3.5.4. Adequacy

This section defines program execution safety and uses it to define the semantic meaning of program judgments, from which the soundness theorem (i.e., adequacy of the logic) can be formulated. Program execution safety extends on the well-known notion of configuration safety of [34], by adding permission accounting, process-algebraic state, and the machinery introduced earlier in this section.

First, in order to help connect the models of the program logic to concrete program state, we define a concretisation function for permission heaps in the same style as snapshot heaps.

Definition 34

(Concretisation). Concretisation of permission heaps is defined as a total function ${\lfloor ·\rfloor }_{\mathtt{concr}}:\mathit{PermHeap}\to \mathit{Heap}$, so that ${\lfloor \mathit{ph}\rfloor }_{\mathtt{concr}}\triangleq \lambda v\in \mathit{Val}.{\lfloor \mathit{ph}\left(v\right)\rfloor }_{\mathtt{concr}}$, with ${\lfloor \mathit{ph}\left(v\right)\rfloor }_{\mathtt{concr}}$ defined as

$${\lfloor \mathit{hc}\rfloor }_{\mathtt{concr}}\triangleq \left\{\begin{array}{cc}v\hfill & \mathit{if}\mathit{hc}={⟨v⟩}_{\mathtt{std}}^{\pi }\mathit{for}\mathit{some}\pi \hfill \\ v\hfill & \mathit{if}\mathit{hc}={⟨v⟩}_{\mathtt{proc}}^{\pi }\mathit{for}\mathit{some}\pi \hfill \\ v_1\hfill & \mathit{if}\mathit{hc}={⟨v_1,v_2⟩}_{\mathtt{act}}^{\pi }\mathit{for}\mathit{some}\pi \mathit{and}{v}_2\hfill \\ \mathit{undefined}\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

The heap concretisation operator constructs (program) heaps out of permission heaps by simply discarding all internal structure regarding process-algebraic models. Only the information relevant for regular program execution is retained. ${\lfloor ·\rfloor }_{\mathsf{snapshot}}$ essentially does the same, but only retains heap cells bound to program abstractions and takes snapshot values whenever possible.

We now have all the ingredients for defining adequacy. Program execution safety is defined in terms of a predicate ${\mathit{safe}}_n(C,\mathit{ph},\mathit{pm},s,g,\mathcal{R},\mathcal{Q})$, stating that C is safe for n reduction steps with respect to a permission heap $\mathit{ph}$, process map $\mathit{pm}$, two stores s and g, a resource invariant $\mathcal{R}$ and postcondition $\mathcal{Q}$.

Definition 35

(Program execution safety). The ${\mathit{safe}}_0(C,\mathit{ph},\mathit{pm},s,g,\mathcal{R},\mathcal{Q})$ predicate always holds, whereas ${\mathit{safe}}_{n+1}(C,\mathit{ph},\mathit{pm},s,g,\mathcal{R},\mathcal{Q})$ holds if and only if the following five conditions hold.

1. 

If $C=\mathtt{skip}$, then $\mathit{ph},\mathit{pm},s,g\models \mathcal{Q}$.

2. 

For every ${\mathit{ph}}_F$ and ${\mathit{pm}}_F$ such that $\mathit{ph}{\perp }_{\mathsf{hc}}{\mathit{ph}}_F$ and $\mathit{pm}{\perp }_{\mathtt{mc}}{\mathit{pm}}_F$, it holds that ${↯}_{\mathtt{ghost}}\left(C,{\lfloor \mathit{ph}{\uplus }_{\mathtt{ph}}{\mathit{ph}}_F\rfloor }_{\mathtt{concr}},\mathit{pm}{\uplus }_{\mathtt{pm}}{\mathit{pm}}_F,s,g\right)$.

3. 

For any $v\in \mathsf{acc}(C,s)$ it holds that $\mathit{ph}\left(v\right)\notin \left\{\mathtt{free},\mathtt{inv}\right\}$.

4. 

For any $v\in \mathsf{writes}(C,s)$ it holds that ${\mathsf{full}}_{\mathsf{hc}}\left(\mathit{ph}\left(v\right)\right)$.

5. 

For any ${\mathit{ph}}_J$, ${\mathit{ph}}_F$, ${\mathit{pm}}_J$, ${\mathit{pm}}_F$, ${\mathit{pm}}_C$, $h^{\prime }$, $s^{\prime }$, and $C^{\prime }$ such that, if:

5a. 

$\mathit{ph}{\perp }_{\mathtt{ph}}{\mathit{ph}}_J$ and $\left(\mathit{ph}{\uplus }_{\mathtt{ph}}{\mathit{ph}}_J\right){\perp }_{\mathtt{ph}}{\mathit{ph}}_F$, and

5b. 

$\mathit{pm}{\perp }_{\mathtt{pm}}{\mathit{pm}}_J$ and $\left(\mathit{pm}{\uplus }_{\mathtt{pm}}{\mathit{pm}}_J\right){\perp }_{\mathtt{pm}}{\mathit{pm}}_F$, and

5c. 

$\neg \mathsf{locked}\left(C\right)$ implies ${\mathit{ph}}_J,{\mathit{pm}}_J,s,g\models \mathcal{R}$, and

5d. 

$\left(\mathit{pm}{\uplus }_{\mathtt{pm}}{\mathit{pm}}_J{\uplus }_{\mathtt{pm}}{\mathit{pm}}_F\right){\cong }_{\mathtt{pm}}{\mathit{pm}}_C$, and

5e. 

${\lfloor \mathit{ph}{\uplus }_{\mathtt{ph}}{\mathit{ph}}_J{\uplus }_{\mathtt{ph}}{\mathit{ph}}_F\rfloor }_{\mathsf{snapshot}}{\models }_{\mathtt{pm}}{\mathit{pm}}_C$, and

5f. 

$(C,{\lfloor \mathit{ph}{\uplus }_{\mathtt{ph}}{\mathit{ph}}_J{\uplus }_{\mathtt{ph}}{\mathit{ph}}_F\rfloor }_{\mathtt{concr}},s)⇝(C^{\prime },h^{\prime },s^{\prime })$;

then there exists ${\mathit{ph}}^{\prime }$, ${\mathit{ph}}_J^{\prime }$, ${\mathit{pm}}^{\prime }$, ${\mathit{pm}}_J^{\prime }$, ${\mathit{pm}}_C^{\prime }$, and $g^{\prime }$, such that

5g. 

${\mathit{ph}}^{\prime }{\perp }_{\mathtt{ph}}{\mathit{ph}}_J^{\prime }$ and $\left({\mathit{ph}}^{\prime }{\uplus }_{\mathtt{ph}}{\mathit{ph}}_J^{\prime }\right){\perp }_{\mathtt{ph}}{\mathit{ph}}_F$, and

5h. 

${\mathit{pm}}^{\prime }{\perp }_{\mathtt{pm}}{\mathit{pm}}_J^{\prime }$ and $\left({\mathit{pm}}^{\prime }{\uplus }_{\mathtt{pm}}{\mathit{pm}}_J^{\prime }\right){\perp }_{\mathtt{pm}}{\mathit{pm}}_F$, and

5i. 

${\lfloor {\mathit{ph}}^{\prime }{\uplus }_{\mathtt{ph}}{\mathit{ph}}_J^{\prime }{\uplus }_{\mathtt{ph}}{\mathit{ph}}_F\rfloor }_{\mathtt{concr}}=h^{\prime }$, and

5j. 

$\left({\mathit{pm}}^{\prime }{\uplus }_{\mathtt{pm}}{\mathit{pm}}_J^{\prime }{\uplus }_{\mathtt{pm}}{\mathit{pm}}_F\right){\cong }_{\mathtt{pm}}{\mathit{pm}}_C^{\prime }$, and

5k. 

${\lfloor {\mathit{ph}}^{\prime }{\uplus }_{\mathtt{ph}}{\mathit{ph}}_J^{\prime }{\uplus }_{\mathtt{ph}}{\mathit{ph}}_F\rfloor }_{\mathsf{snapshot}}{\models }_{\mathtt{pm}}{\mathit{pm}}_C^{\prime }$, and

5l. 

$\neg \mathsf{locked}\left(C^{\prime }\right)$ implies ${\mathit{ph}}_J^{\prime },{\mathit{pm}}_J^{\prime },s^{\prime },g^{\prime }\models \mathcal{R}$, and

5m. 

$(C,{\lfloor \mathit{ph}{\uplus }_{\mathtt{ph}}{\mathit{ph}}_J{\uplus }_{\mathtt{ph}}{\mathit{ph}}_F\rfloor }_{\mathtt{concr}},{\mathit{pm}}_C,s,g){⇝}_{\mathtt{ghost}}(C^{\prime },h^{\prime },{\mathit{pm}}_C^{\prime },s^{\prime },g^{\prime })$, and

5n. 

${\mathit{safe}}_n(C^{\prime },{\mathit{ph}}^{\prime },{\mathit{pm}}^{\prime },s^{\prime },g^{\prime },\mathcal{R},\mathcal{Q})$.

Clarifying the above definition, any configuration is safe for $n+1$ steps intuitively if: the postcondition $\mathcal{Q}$ is satisfied if C has terminated (1); the program C does not fault (2); C only accesses heap entries that are allocated (3); C only writes to heap locations for which full permission is available (4); and finally, after making a computation step the program remains safe for another n steps (5). (The predicate ${\mathsf{full}}_{\mathsf{hc}}\left(\mathit{hc}\right)$ is $\mathtt{true}$ whenever $\mathit{hc}$ is an occupied heap cell with an associated fractional permission $\pi$ equal to 1.) Condition 2 implies race freedom, while conditions 3 and 4 account for memory safety.

Condition 5 is particularly involved. In particular it encodes the backward simulation: if the program can do a $⇝$ step (5f), then it must be able to make a matching ${⇝}_{\mathtt{ghost}}$ step (by 5m). Moreover, the resource invariant $\mathcal{R}$ must remain satisfied (due to 5c and 5l) after making a computation step, whenever the current program is not locked. In addition, the process maps invariably remain safe with respect to the snapshot heap due to 5e and 5k, as discussed in Section 3.5.3.

Lemma 10.

Program execution safety satisfies the following properties.

1. 

If ${\mathit{safe}}_n(C,\mathit{ph},\mathit{pm},s,g,\mathcal{R},\mathcal{Q})$ and $m\le n$, then ${\mathit{safe}}_m(C,\mathit{ph},\mathit{pm},s,g,\mathcal{R},\mathcal{Q})$.

2. 

If ${\mathit{safe}}_n(C,\mathit{ph},{\mathit{pm}}_1,s,g,\mathcal{R},\mathcal{Q})$ and ${\mathit{pm}}_1{\cong }_{\mathtt{pm}}{\mathit{pm}}_2$, then ${\mathit{safe}}_n(C,\mathit{ph},{\mathit{pm}}_2,s,g,\mathcal{R},\mathcal{Q})$.

3. 

If ${\mathit{safe}}_n(C,\mathit{ph},\mathit{pm},s,g,\mathcal{R},\mathcal{Q})$ and $\mathcal{Q}\models {\mathcal{Q}}^{\prime }$, then ${\mathit{safe}}_n(C,\mathit{ph},\mathit{pm},s,g,\mathcal{R},{\mathcal{Q}}^{\prime })$.

1 in Lemma 10 states monotonicity in the sense that being safe for n reduction steps implies safety for less than n steps. 2 in Lemma 10 states that process maps can always be replaced by bisimilar ones in safe configurations. Finally, 3 in Lemma 10 states that postconditions may always be weakened.

3.5.5. Semantics of Program Judgments

The semantics of program judgments is defined in terms of a quintuple $\mathsf{\Gamma };\mathcal{R}\models \left\{\mathcal{P}\right\}C\left\{\mathcal{Q}\right\}$, expressing that C is safe for any number of reduction steps starting from any state satisfying $\mathcal{P}$.

Definition 36

(Semantics of program judgments). $\mathsf{\Gamma };\mathcal{R}\models \left\{\mathcal{P}\right\}C\left\{\mathcal{Q}\right\}$ holds if and only if:

(1) 

$\mathtt{user}\left(C\right)$, and

(2) 

If ${\models }_{\mathtt{env}}\mathsf{\Gamma }$ and $\mathtt{wf}\left(C\right)$, then for any $\mathit{ph},\mathit{pm},s,g$ such that ${\mathtt{valid}}_{\mathtt{ph}}\left(\mathit{ph}\right)$ and ${\mathtt{valid}}_{\mathtt{pm}}\left(\mathit{pm}\right)$ and ${\lfloor \mathit{ph}\rfloor }_{\mathsf{snapshot}}{\models }_{\mathtt{pm}}\mathit{pm}$ and $\mathit{ph},\mathit{pm},s,g\models \mathcal{P}$ hold, it holds that:

$$\forall n.{\mathit{safe}}_n(C,\mathit{ph},\mathit{pm},s,g,\mathcal{R},\mathcal{Q})$$

The underlying idea of the above definition, i.e., having a continuation-passing style definition for program judgments, has first been applied in [40] and has further been generalised in [41,42]. Moreover, the idea of defining execution safety in terms of an inductive predicate originates from [43]. These two concepts have been reconciled in [34] into a formalisation for the classical CSL of Brookes [23], that has been encoded and mechanically been proven in both Isabelle and Coq. Our definition builds on the latter, by having a refinement between programs and abstractions encoded in $\mathit{safe}$.

Observe that only judgments of user programs (i.e., commands free of runtime constructs like $\mathtt{inatom}$ and $\mathtt{inact}$) have a semantic meaning. Also observe that the semantics of program judgments is conditional on the safety of $\mathsf{\Gamma }$. It states that C executes safely for any number n of computation steps with respect to any state satisfying $\mathcal{P}$, only if $\mathsf{\Gamma }$ is safe—that is, only if all process-algebraic models for C are (assumed to be externally) verified. From the above definition it trivially follows that $\mathsf{\Gamma };\mathcal{R}\models \left\{\mathtt{false}\right\}C\left\{\mathcal{P}\right\}$ for any $\mathsf{\Gamma }$, $\mathcal{R}$, $\mathcal{P}$ and user program C. Notice however that $\mathsf{\Gamma };\mathcal{R}\models \left\{\mathcal{P}\right\}C\left\{\mathtt{true}\right\}$ does not hold in general, since C might be able to fault, for example by having data-races.

The following main soundness theorem states that verified programs (i.e., programs for which a proof can be derived according to the proof rules given earlier in Figure 4 and Figure 5) are semantically valid (that is, are fault-free, memory-safe, and refine their process-algebraic models).

Theorem 4

(Soundness). $\mathsf{\Gamma };\mathcal{R}⊢\left\{\mathcal{P}\right\}C\left\{\mathcal{Q}\right\}\Rightarrow \mathsf{\Gamma };\mathcal{R}\models \left\{\mathcal{P}\right\}C\left\{\mathcal{Q}\right\}$.

The soundness proofs of all proof rules have been mechanised using the Coq proof assistant and can be found on the Git repository accompanying this article [19].

The HT-PROC-UPDATE and HT-PROC-QUERY proof rules were the most difficult to prove sound, as their proofs require, among other things, (1) showing that the abstract model can always match the program with a simulating execution step, as well as (2) maintaining the invariant that any process-algebraic abstraction inside the process map is safe with respect to the reified program state. On top of that, the combination of (1) and (2) requires some extra bookkeeping to ensure that the snapshot heaps stored in ghost metadata agree with the snapshot values stored in permission heaps. This additional bookkeeping has been left out of the formalisation presented so far, but the details of this can be studied in the Coq formalisation.

4. Implementation

The presented verification approach has been implemented in the VerCors concurrency verifier, which specialises in automated verification of parallel and concurrent programs written in high-level languages like (subsets of) Java and C [8]. VerCors can reason about programs with heterogeneous concurrency features as in Java, as well as homogeneous concurrency like in OpenCL, and compiler directives as in OpenMP. VerCors allows specifying (concurrent) programs with annotations from a separation logic with permission accounting. VerCors supports reasoning about freedom of data-races, memory safety and functional program behaviour—compliance of the program annotations.

4.1. Tool Support

Tool support for our technique has been implemented in VerCors for languages with fork/join concurrency and statically-scoped parallel constructs [14]. Our technique has been implemented by defining an axiomatic domain for process types in Viper, consisting of constructors for the process-algebraic connectives and standard process-algebraic axioms to support these. The three different ownership types ${\stackrel{\pi }{\hookrightarrow }}_t$ are encoded in Viper by defining extra fields that maintain the ownership status t for each global reference. The ${\mathtt{Proc}}_{\pi }$ assertions are encoded as predicates over process types.

Note however that VerCors does not yet support writing and reasoning about assertional processes $?(·)$. Instead, the properties to verify on a process-algebraic level are specified as postconditions of the models. That is, VerCors currently only allows reasoning about postcondition properties of process-algebraic models, while the formalisation as presented in this article allows reasoning about properties also at intermediate points of process execution. But since the formalisation is more general than the VerCors implementation (as was already indicated in Section 3.4.2), soundness is retained.

Recall that process-algebraic abstractions are to be verified externally with our approach, for example using an interactive theorem prover or a model checker like mCRL2. Nevertheless, VerCors itself also has capabilities to reason about process-algebraic models. This is done by first linearising all specified processes, and then encoding these linearised processes together with their contracts into the Viper language, and delegate further reasoning to Viper. Any process is said to be linear if it does not use the ‖ and connectives. Linearisation is a mechanical (automated) procedure based on a rewrite system that uses a subset of the bisimulation equivalences of Figure 2 as rewrite rules [44] (but in one direction only), to try to eliminate parallel connectives. For example, a process term $(a_1·a_2)\Vert a_3$ can automatically be linearised to the bisimilar process $a_1·a_2·a_3+a_1·a_3·a_2+a_3·a_1·a_2$. Note that linearisation may not always succeed. VerCors outputs a verification error in case linearlisation fails.

Process-algebraic models may also algorithmically be analysed, for example using a model checker. We are currently actively investigating the use of the mCRL2 toolset [21] and the Ivy verifier [45] to reason about (different forms of) processes, and in different use cases; see for example [17], in which we use process-algebraic abstractions to reason about distributed message passing programs.

Finally, we would like to remark that the VerCors implementation of the abstraction technique is much richer than the simple language of Section 3.2 that is used to formalise the approach on. For example, the abstraction language in VerCors supports general recursion instead of Kleene iteration. VerCors also has support for several axiomatic data types that enrich the expressivity of reasoning with program abstractions, like (multi)sets, sequences and option types.

4.2. Coq Formalisation

The formalisation and soundness proof (Section 3.1, Section 3.2, Section 3.3, Section 3.4 and Section 3.5) of the program logic have been fully mechanised using Coq, as a deep embedding inspired by [34]. The overall implementation comprises over $23.000$ lines of code. The Coq development and its documentation are available online [19].

5. Case Study

Finally, we demonstrate our verification approach on a well-known version of the leader election protocol [46] that is based on shared memory. Most importantly, this case study shows how our approach bridges the typical abstraction gap between process algebraic models and program implementations. In particular, it shows how a high-level process algebraic model of a leader election protocol, together with a contract for this model (checked with mCRL2 for various inputs), is formally connected to an actual program implementation of the protocol, using VerCors.

The protocol is performed by N concurrent workers that are organised in a ring, so that worker i only sends to worker $i+1$ and only receives from worker $i-1$, modulo N. The goal is to determine a leader among these workers. To find a leader, the election procedure assumes that each worker i receives a unique integer value to start with, and then operates in N rounds. In every round, (1) each worker sends the highest value it encountered so far to its right neighbour, (2) receives a value from its left neighbour, and (3) remembers the highest of the two. The result after N rounds is that all workers know the highest unique value in the network, allowing its original owner to announce itself as leader.

The case study has been verified with VerCors using the presented approach. All workers communicate via two standard non-blocking operations for message passing: mp_send r,$\mathit{msg}$ for sending a message $\mathit{msg}$ to the worker with rank r, and $\mathit{msg}:=\mathtt{mp}\_\mathtt{recv}r$ for receiving a message from worker r. (The identifiers of workers are typically called ranks in message passing terminology. Ranks are simply natural numbers.) The election protocol is implemented on top of this message passing system.

The main challenge of this case study is to define a message passing system on the process algebra level that matches this implementation. To design such a system we follow the ideas of [46]; by defining two actions, $\mathsf{send}(r,\mathit{msg})$ and $\mathsf{recv}(r,\mathit{msg})$, that abstractly describe the behaviour of the concrete implementations in $\mathtt{mp}\_\mathtt{send}$ and $\mathtt{mp}\_\mathtt{recv}$, respectively. Process algebraic summation ${\Sigma }_x\tilde{P}$ is used to quantify over the possible messages that $\mathtt{mp}\_\mathtt{recv}$ might receive.

The following two rules illustrate how the abstract send and recv actions are connected to the $\mathtt{mp}\_\mathtt{send}$ and $\mathtt{mp}\_\mathtt{recv}$ procedures in the program, respectively. The latter rule uses a summation (shorthand) of the form ${\Sigma }_{x\in \mathit{Msg}}\tilde{P}$ that can be considered equivalent to the process ${\Sigma }_x(x\in \mathit{Msg}:\tilde{P})$.

$$\begin{array}{cc}\{\mathsf{send}(r,\mathit{msg})·\tilde{P}\}\mathtt{mp}\_\mathtt{send}r,\mathit{msg}& \{\tilde{P}\}\\ \{{\Sigma }_{x\in \mathit{Msg}}\mathsf{recv}(r,x)·\tilde{P}\}\mathit{msg}:=\mathtt{mp}\_\mathtt{recv}r& \{\tilde{P}[x/\mathit{msg}]\}\end{array}$$

Finally, we construct a process-algebraic model of the election protocol using send and recv, and verify that the implementation adheres to this model. This model has been analysed with mCRL2 for various inputs (since mCRL2 is essentially finite-state) to establish the global property of announcing the correct leader. The deductive proof of the program can then rely on this property.

5.1. Behavioural Specification

The main goal is proving that the implementation determines the correct leader upon termination. To prove this we first define a behavioural specification of the election protocol that hides all irrelevant implementation details, and prove the correctness property on this specification. Process algebra provides a proper abstraction language that suits our needs well, as the behaviour of leader election can concisely be specified in terms of sequences of sends and receives.

Figure 8 presents the process algebraic specification. In particular, ParElect specifies the global behaviour of the program whereas Elect specifies its thread-local behaviour. The ParElect process encodes the parallel composition of all eligible participants. ParElect takes a sequence $\mathit{vs}$ of initial values as argument, whose length equals the total number of workers by its precondition. ParElect’s postcondition (i.e., trailing assertion) states that $\mathit{lead}$ must be a valid rank after termination and that $\mathit{vs}\left[\mathit{lead}\right]$ be the highest initial worker value. It follows that worker $\mathit{lead}$ is the correctly chosen leader.

Figure 8. The behavioural process-algebraic specification of the leader election protocol. Processes of the form $\mathtt{if}b\mathtt{then}P\mathtt{else}Q$ are a shorthand for $b:P+\neg b:Q$. Moreover, all ensures clauses of ParElect are translated into trailing assertions, as described earlier at the beginning of Section 3.4.2.

The Elect process takes four arguments, which are: the rank of the worker, the initial unique value $v_0$ of that worker, the current highest value v encountered by that worker, and finally the number n of remaining rounds. The rounds are implemented via general recursion. In each round all workers send their current highest value v to their right neighbour (on line 24), receive a value $v^{\prime }$ from their left neighbour (line 25), and continue with the highest of the two. The announce action is declared and used to announce the leader after n rounds. The effect of announce is that $\mathit{lead}$ stores the leader’s rank.

The contracts of send and recv describe the behaviour of standard non-blocking message passing. Communication on the specification level is implemented via message queues. Message queues are defined as sequences of messages taken from a domain $\mathit{Msg}$. Since workers are organised in a ring it suffices to have only a single queue for every worker, meaning that the global communication channel architecture can be defined as a sequence of message queues: $\mathit{chan}$ in the figure. The action contract of $\mathsf{send}(r,\mathit{msg})$ expresses enqueuing $\mathit{msg}$ onto the message queue $\mathit{chan}\left[r\right]$ of the worker with rank r. The effect of send is that $\mathit{msg}$ has been enqueued onto $\mathit{chan}\left[r\right]$ and that the queues $\mathit{chan}\left[r^{\prime }\right]$ for any $r^{\prime }\ne r$ have not been altered. Likewise, $\mathsf{recv}(r,\mathit{msg})$’s contract expresses dequeuing $\mathit{msg}$ from $\mathit{chan}\left[r\right]$. The expression $\backslash \mathtt{old}\left(e\right)$ indicates that e is to be evaluated with respect to the pre-state of computation.

5.2. Protocol Implementation

Figure 9 presents the annotated implementation of the election protocol. (It should be noted here that the presentation is slightly different from the version that is verified with VerCors, to better connect to the theory discussed in the earlier sections to the case study. This is because VerCors uses Implicit Dynamic Frames [47] as its underlying logical framework, which is equivalent to separation logic [48] but handles ownership slightly differently. The details of this are deferred to [8,49].) The elect method contains the code that is executed by every worker. The contract of elect $\mathit{rank},v_0,v$ states that the method body adheres to the behavioural specification $\mathsf{Elect}(\mathit{rank},v_0,v,N)$ of the election protocol. Each worker performing elect enters a for-loop that iterates N times, whose loop invariant states that, at iteration i, the remaining program behaves as prescribed by the process $\mathsf{Elect}(\mathit{rank},v_0,v,i-1)$. The invocations to $\mathtt{mp}\_\mathtt{send}$ and $\mathtt{mp}\_\mathtt{recv}$ on lines 32 and 36 are annotated with $\mathtt{with}$ clauses that resolve the assignments required by the $\mathtt{given}$ clauses in the contracts of $\mathtt{mp}\_\mathtt{send}$ and $\mathtt{mp}\_\mathtt{recv}$. The $\mathtt{given}\overline{\eta }$ annotation expresses that the parameter list $\overline{\eta }$ are extra ghost arguments for the sake of specification. Stated differently, $\overline{\eta }$ is a sequence of logical variables which are universally quantified at the (outer) level of the method contract (the types of these are left implicit for ease of presentation). After N rounds all workers with $v=v_0$ announce themselves as leader. However, since the initial values are chosen to be unique there can only be one such worker. Finally, we can verify that at the post-state of elect the abstract model has been fully executed and thus reduced to $\epsilon$ in the logic.

Figure 9. An excerpt of the annotated implementation of the leader election protocol. Annotations of the form $\mathtt{context}\mathcal{P}$ are shorthand for $\mathtt{requires}\mathcal{P};\mathtt{ensures}\mathcal{P}$.

The $\mathtt{mp}\_\mathtt{send}\mathit{rank},\mathit{msg}$ method implements the operation of enqueuing $\mathit{msg}$ onto the message queue of worker $\mathit{rank}$. Its implementation has been omitted for brevity. The contract of $\mathtt{mp}\_\mathtt{send}$ expresses that the enqueuing operation is abstracted as a $\mathsf{send}(\mathit{rank},\mathit{msg})$ action that is prescribed by an abstract model identified by X. The $\mathtt{mp}\_\mathtt{recv}X,\mathit{rank}$ method implements the operation of dequeuing and returns the first message of the message queue of worker $\mathit{rank}$. The receive is prescribed as an abstract $\mathsf{recv}$ action, where the received message is ranged over by the summation on line 17.

Figure 10 presents bootstrapping code for the implementation of message passing. The main procedure initialises the communication channels whereas parelect spawns all workers. main $\mathit{vs}$ additionally initialises and finalises the abstraction $\mathsf{ParElect}\left(\mathit{vs}\right)$ on the specification level (on lines 76 and 83, resp.) whose analysis allows establishing main’s postconditions. The procedure parelect $\mathit{vs}$ implements the abstract model $\mathsf{ParElect}\left(\mathit{vs}\right)$ by spawning N workers that all execute the elect program. The contract associated to the parallel block (lines 55–59) is called an iteration contract and assigns pre- and postconditions to every parallel instance. For more details on iteration contracts we refer to [50]. Most importantly, the iteration contract of each parallel worker states (on line 58) that it behaves as specified by Elect. Thus, we deductively verify in a thread-modular way that the program implements its behavioural specification. Observe that all the required ownership for the global fields and the ${\mathtt{Proc}}_1$ predicate is split and distributed among the individual workers via the iteration contract and the $\mathtt{with}$ clause on lines 62–64. Finally, the main correctness property is conveyed from the process level to the program level by the $\mathtt{query}X$ annotation on line 82, which “queries” for ParElect’s postconditions.

Figure 10. Bootstrap procedures of the leader election protocol.

5.3. Specification and Verification Details

The VerCors encoding of the presented leader election protocol comprises 433 lines of code, of which 275 are specification annotations ($63.5\%$ of the total) and 27 lines are comments ($6.2\%$ of the total). Out of the 275 lines of specification code, 62 are used for specifying the process-algebraic model ($22.5\%$), and the remaining 213 lines ($77.5\%$) for formally linking this model to the program code.

The average verification time with VerCors is $19.75$ s (average of 30 runs), measured on a Macbook with an Intel Core i5 CPU with 2,9 GHz and 8Gb memory. All verification files are available online [19].

5.4. Industrial Applicability

Apart from the presented leader election case study, our approach has been applied in a larger, industrial case study covering the formal verification of a traffic tunnel emergency control system [15]. In this case study, we successfully verified a safety-critical component of an emergency control system of an actual traffic tunnel that is currently in use in the Netherlands. This particular software component is responsible for handling any emergency situations that occur inside the traffic tunnel. For example, whenever a fire breaks out inside the tunnel or an accident occurs, it must start an emergency procedure to evacuate all people and turn on the emergency lights to help guide them out; control the fans to blow away any smoke; et cetera. Naturally the reliability demands imposed on such a software component are very high. Our research goal was to see if formal verification could help.

Our approach for this case study was to use mCRL2 to construct a formal, process-algebraic model of the software design, which was written informally as a state machine together with pseudo-code descriptions of the different system behaviours. We then analysed the state space of this model and checked whether it satisfies desirable properties, which we composed together with the company that wrote the actual code. Ultimately we found problematic behaviour: the system could, due to an unlucky combination of timing and events, reach a calamity state in which the emergency procedure is not started. However, the software company already knew of this problematic behaviour and deliberately provided us with an older version of their software. Nevertheless, we demonstrated that formal methods can indeed help to improve the quality of real-world industrial software.

In addition to modelling and analysing the software design with mCRL2, we also used VerCors to prove that the actual code implementation is soundly abstracted by the process-algebraic model, using the techniques presented in this article. We did this to increase the value of our formal model, and to ensure that its analysis is meaningful. Moreover, our verification also (indirectly) proved that the code implementation adheres to the pseudo-code specifications in the original software design.

Overall this case study highlights how the presented approach is applicable to real-world projects. We were able to identify potential vulnerabilities in the software design, and could link (a formal model of) the software design to the actual code. We are currently involved in a follow-up project with the same company, and aim to apply our technique during the software development process.

6. Related Work

Significant progress has been made on the theory of concurrent software verification over the last years [1,2,3,4,5,51,52,53]. This line of research proposes advanced program logics that all provide some notion of expressing and restricting thread interference of various complexity, via protocols [54]—formal descriptions of how shared program state is allowed to evolve over time. In our approach protocols have the form of processes.

The original work on CSL [24] allows specifying simple thread interference in shared-memory concurrent programs via resource invariants and critical regions. Later, RGSep [55] merges CSL with rely-guarantee reasoning to enable describing more fine-grained inter-thread interference by identifying atomic concurrent actions. Many modern program logics build on these principles and propose even more advanced ways of verifying shared-memory concurrency. For example, TaDa [5] and CaReSL [3] express thread interference protocols through state-transition systems. iCAP [51] and Iris [56] propose a more unified approach by accepting user-defined monoids to express protocols on shared state, together with invariants restricting these protocols. Iris provides reasoning support for proving language properties in Coq, whereas our focus is on proving (concrete) programs correct.

In the distributed setting, Disel [6] allows specifying protocols for distributed systems. Disel builds on dependent type theory and is implemented as a shallow embedding in Coq. Even though their approach is more expressive than ours, it has to be used in the context of Coq and thus can be applied only semi-automatically at the moment. Villard et al. [57] present a program logic for message passing concurrency, where threads may communicate over channels using native send/receive primitives. This program logic allows specifying protocols via contracts, which are state-machines in the style of Session Types [58] to describe channel behaviour. Our technique is more general however, as the approach of Villard et al. is tailored specifically to reason about basic shared-memory message passing (Section 5 for example demonstrates how a system of message passing can be realised using process-algebraic abstractions). Actor Services [59] is a program logic with assertions to express the consequences of asynchronous message transfers between actors—independent program units that communicate via message passing. The meta-theory of Actor Services has not been proven sound.

Most of the related work given so far is essentially theoretical and tend to focus primarily on expressivity—on contributing approaches that are expressive yet not necessarily easy to implement into SMT-based program verifiers like for example VerCors of Viper. In fact, for most of these approaches it is very challenging to implement such automated tool support. Instead, they have to be applied in pen-and-paper style, or in the context of an interactive theorem prover like Coq or Isabelle. Our abstraction approach is different, in the sense that its aim is not to maximise expressivity (for example by integrating into higher-order separation logics, like for example [60]). Instead, we aim for a verification approach that balances expressivity and usability—an approach that is expressive enough to reason about real-world concurrent programs that follow some protocol, while being implementable into automated code verifiers; in this case, VerCors and Viper.

Related concurrency verifiers are SmallfootRG [61], VeriFast [7], CIVL [62], THREADER [63] and Viper [9,10]; the latter tool is used as the main back-end of VerCors. SmallfootRG is a memory-safety verifier based on RGSep. VeriFast is a rich toolset for verifying (multi-threaded) Java and C programs using separation logic. The CIVL framework can reason about race-freedom and functional correctness of MPI programs written in C [64,65]. The reasoning is done via bounded model checking combined with symbolic execution. THREADER is an automated verifier for multi-threaded C, based on model checking and counterexample-guided abstraction refinement.

One approach that is particularly noteworthy is the one of Penninckx et al. [66], who propose a logic to specify and verify input/output (I/O) behaviour of (sequential) programs. The logic has been implemented in VeriFast. In this approach the I/O behaviour of programs is specified essentially as a Petri Net. Its assertion language has constructs to specify I/O permission tokens, and its proof system has inference rules that allow reducing a Petri Net specification alongside the structure of the program, similar to our approach. However, their specification/verification strategy is to make predictions about the behaviour of the environment (which may or may not turn out true), by specifying assumptions on what the environment will input given a particular I/O operation and output, which is in contrast to our approach. In fact, with our approach one could analyse and use process-algebraic models together with an extra process that models an environment, to achieve stronger reasoning capabilities.

Apart from the proposed technique, VerCors also allows using process algebraic abstractions as histories [67,68]. Also related in this respect are the time-stamped histories of [69], which records atomic state changes in concurrent programs as a history, which are, likewise to our approach, handled as resources in the logic. However, history recording is only suitable for terminating programs.

There is also related earlier work on using process-algebraic abstractions to reason about message passing distributed programs [17]. This work introduces the assertional processes $?(·)$ as well as process-algebraic summation, as they are used in this article. In fact, this article merges the core ideas of [16,17] into a single logical framework, to make the original work of [16] more general.

Finally, there is a lot of general work on proving linearisability [70,71,72], which essentially allows reasoning about fine-grained concurrency by using sequential verification techniques. Our technique, as well as the history-based technique of [67] uses process algebraic linearisation to do so.

7. Conclusions

To reason effectively about realistic concurrent and distributed software, we have presented a verification technique that performs the reasoning at a suitable level of abstraction that hides irrelevant implementation details, is scalable to realistic programs by being modular and compositional, and is practical by being supported by automated tools. The approach is expressive enough to allow reasoning about realistic software as is demonstrated by the case study as well as by [15], and can be implemented as part of an automated deductive SMT-based program verifier, viz. VerCors. The proof system underlying our technique has mechanically been proven sound using Coq. Our technique is therefore supported by a strong combination of theoretical justification and practical usability.

This article extends [16], which we considered to be the beginning of a comprehensive verification framework that aims to capture many different concurrent and distributed programming paradigms. This extended version makes a step forward towards such a framework, by unifying the core ideas of [16,17,18], thereby generalising the original framework, most importantly to include assertional processes.

We are currently further investigating the use of mCRL2 to reason algorithmically about program abstractions, e.g., [73]. We are looking in particular into distributed programs that communicate over channels, since process algebra have been used extensively to model such programs (see for example the work and uses of the $\pi$-calculus). We are also (somewhat more passively) looking into whether Ivy would be a suitable tool to reason about our process specifications, possibly with mild adaptions. Moreover, we are planning to investigate the preservation of liveness properties in addition to safety.