Crystal Plasticity Finite Element Method for Slip Systems Evolution Analysis of α/β Duplex Titanium Alloys during Quasi-Static Tensile Testing
Abstract
1. Introduction
2. Experimental Methods and Simulations
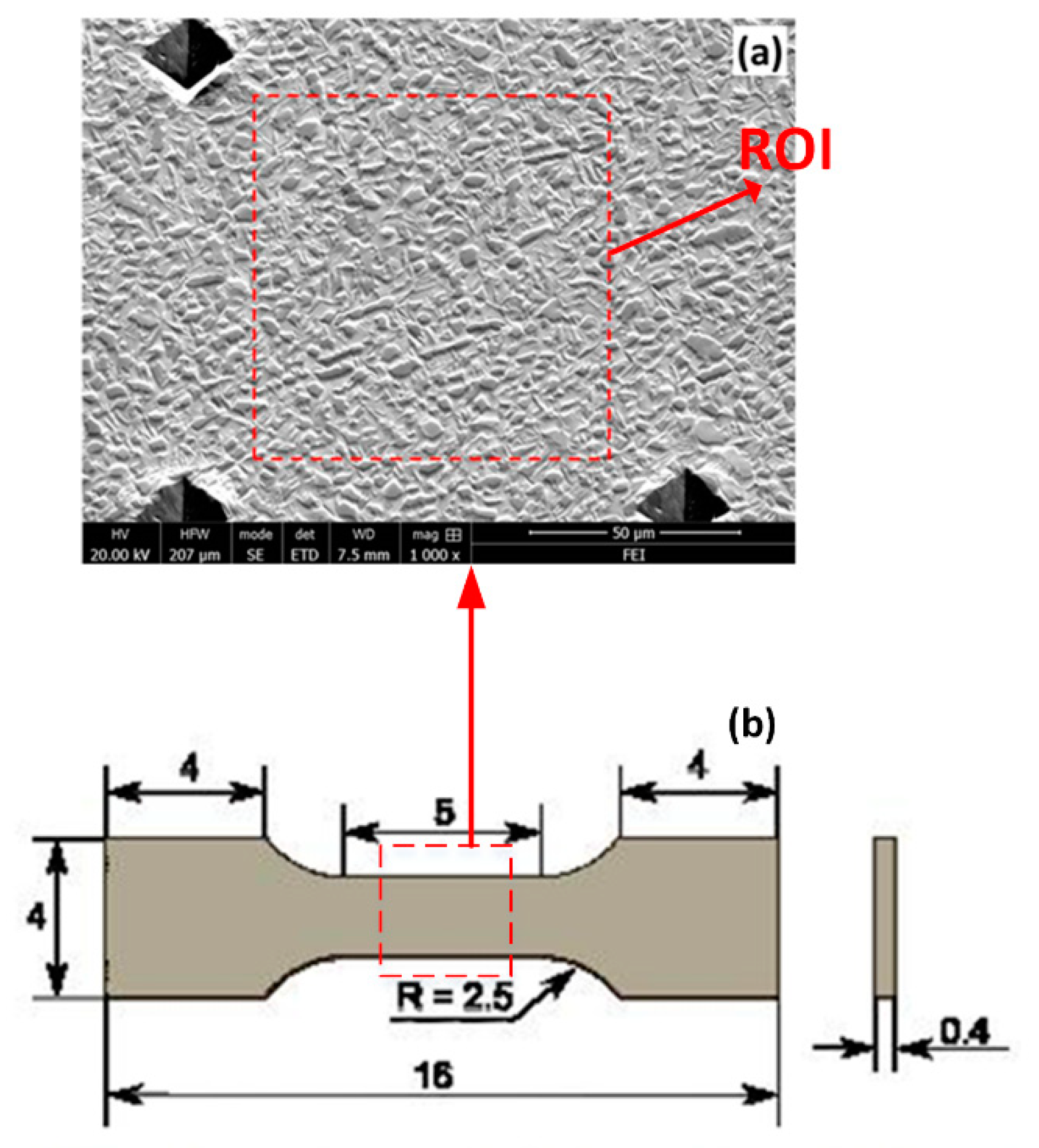
2.1. Material and Characterization Techniques
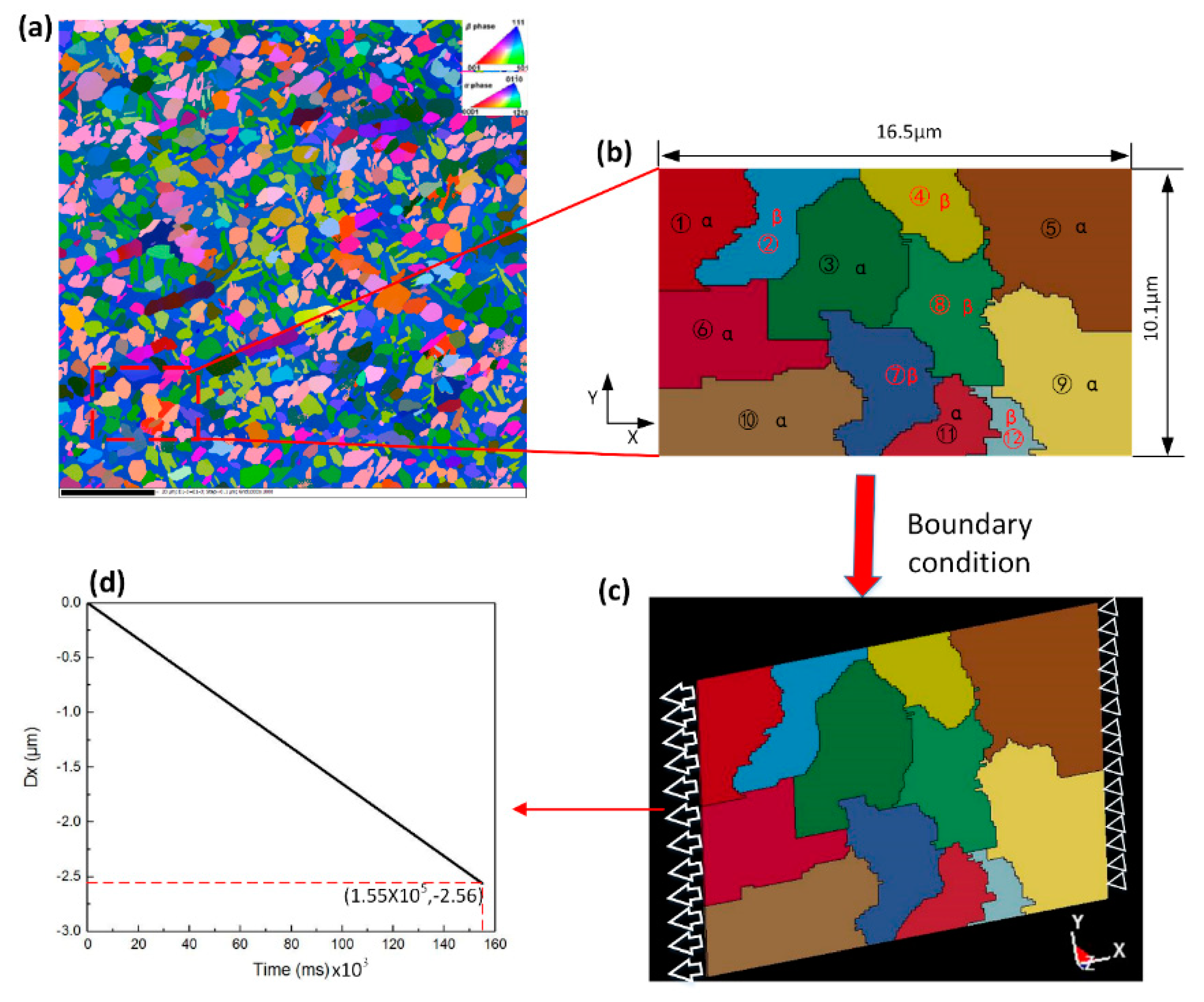
2.2. Simulation Methods
2.2.1. Crystal Plasticity Models
2.2.2. Constitutive Parameters of Single Phase
2.2.3. Misorientation Angle
2.2.4. Resolved Shear Strain
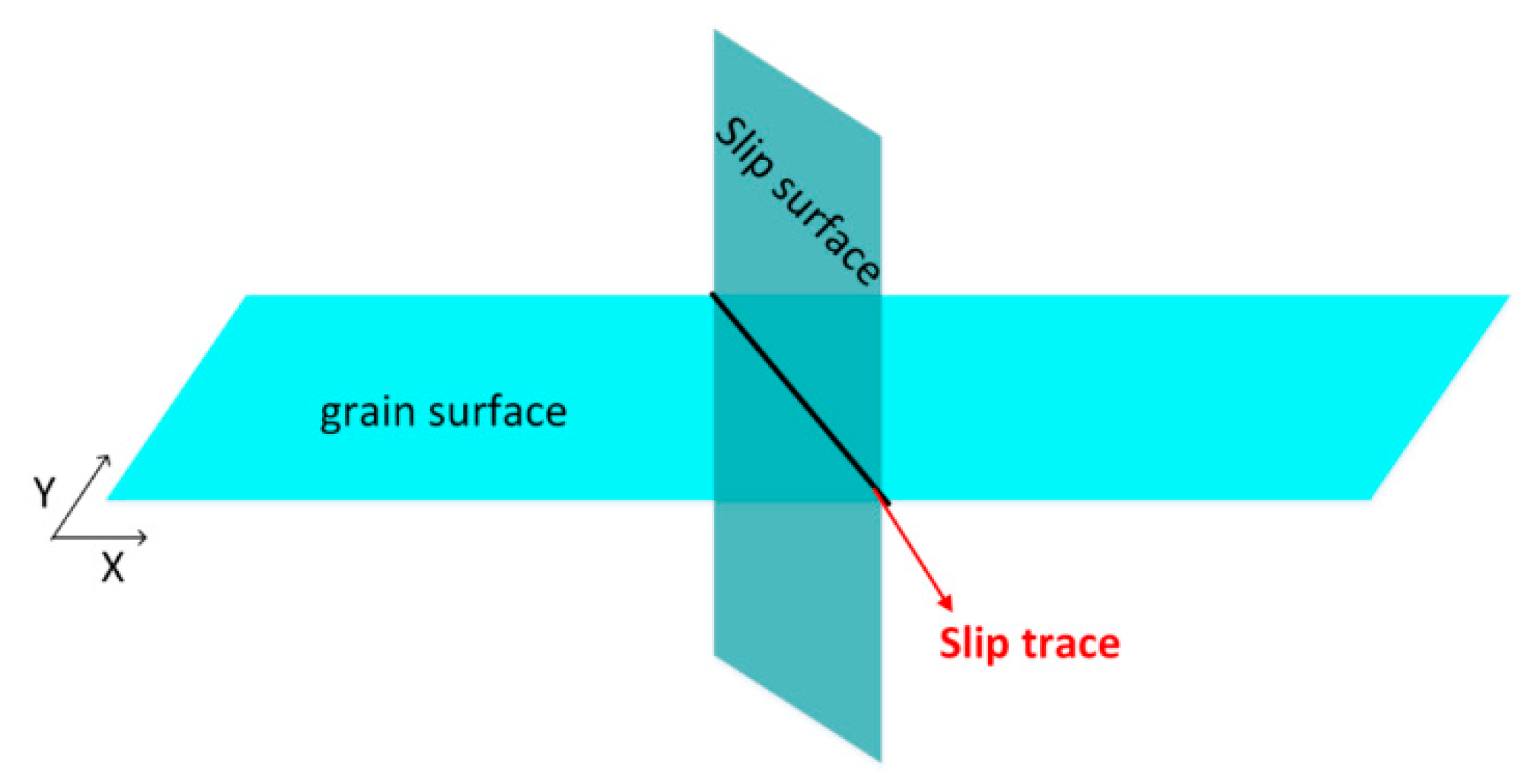
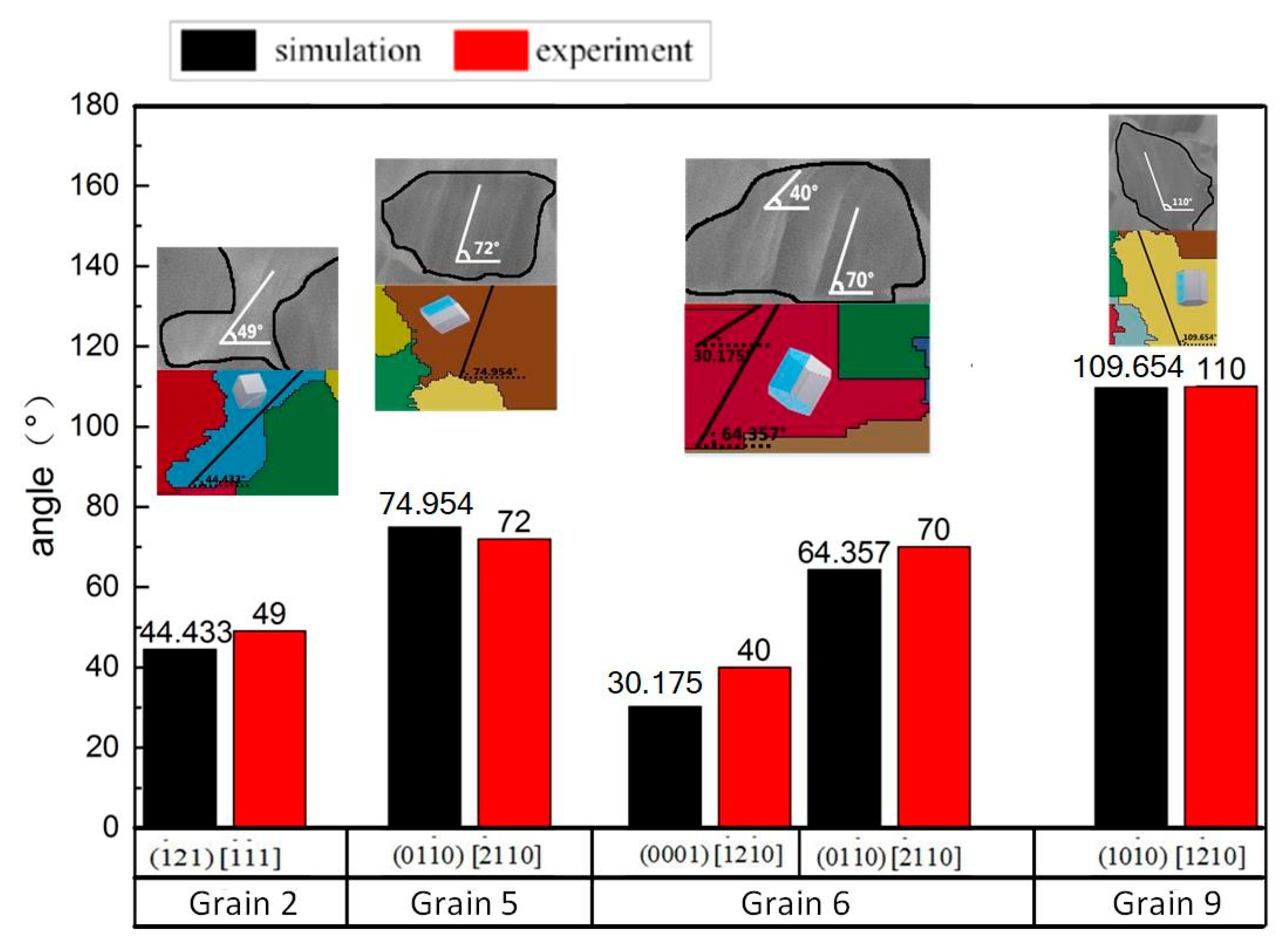
2.2.5. Determination of Slip Trace
3. Discussion
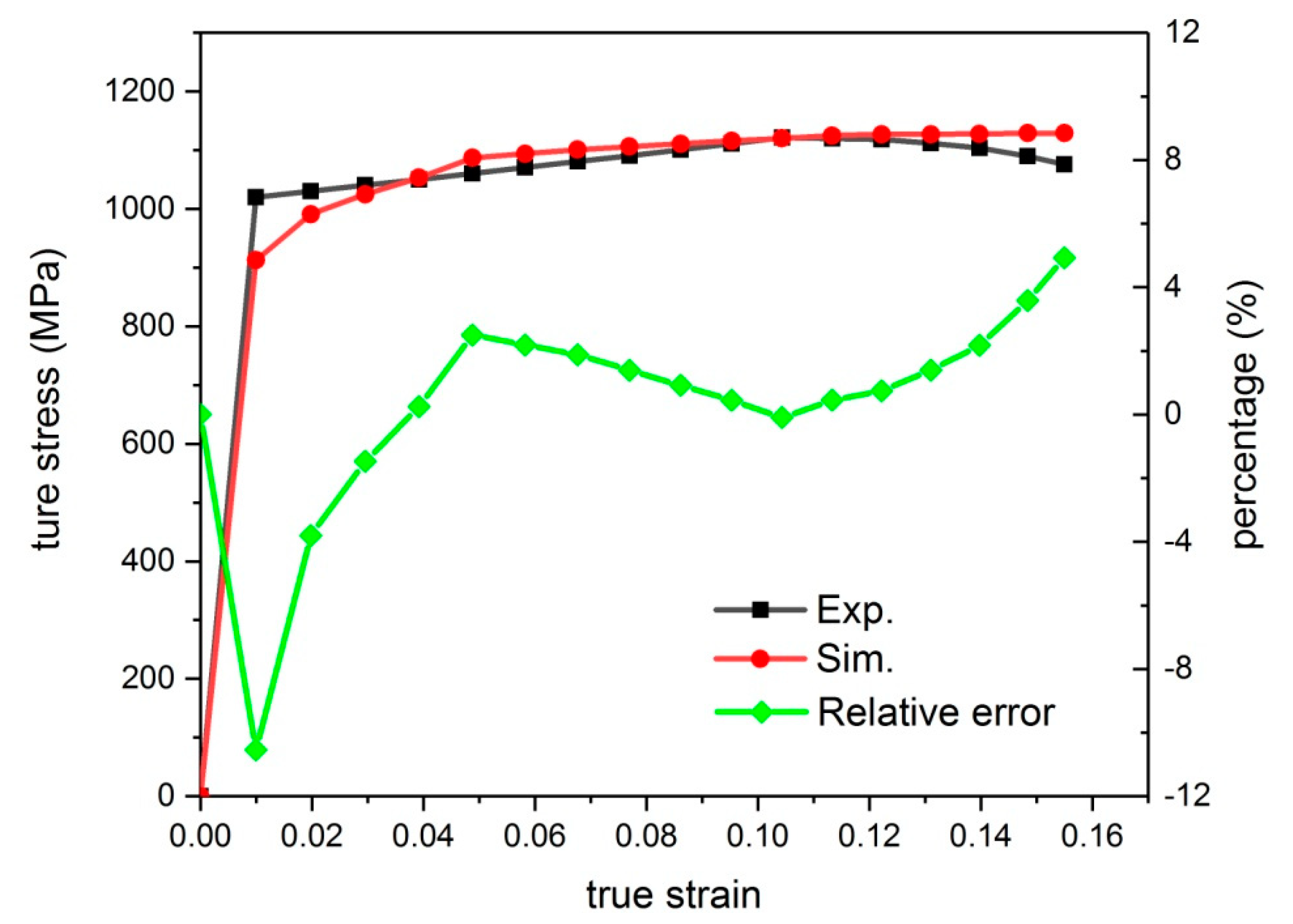
3.1. Reliability Verification
3.2. Evolution of Stress and Strain
3.3. Evolution of Slip Systems
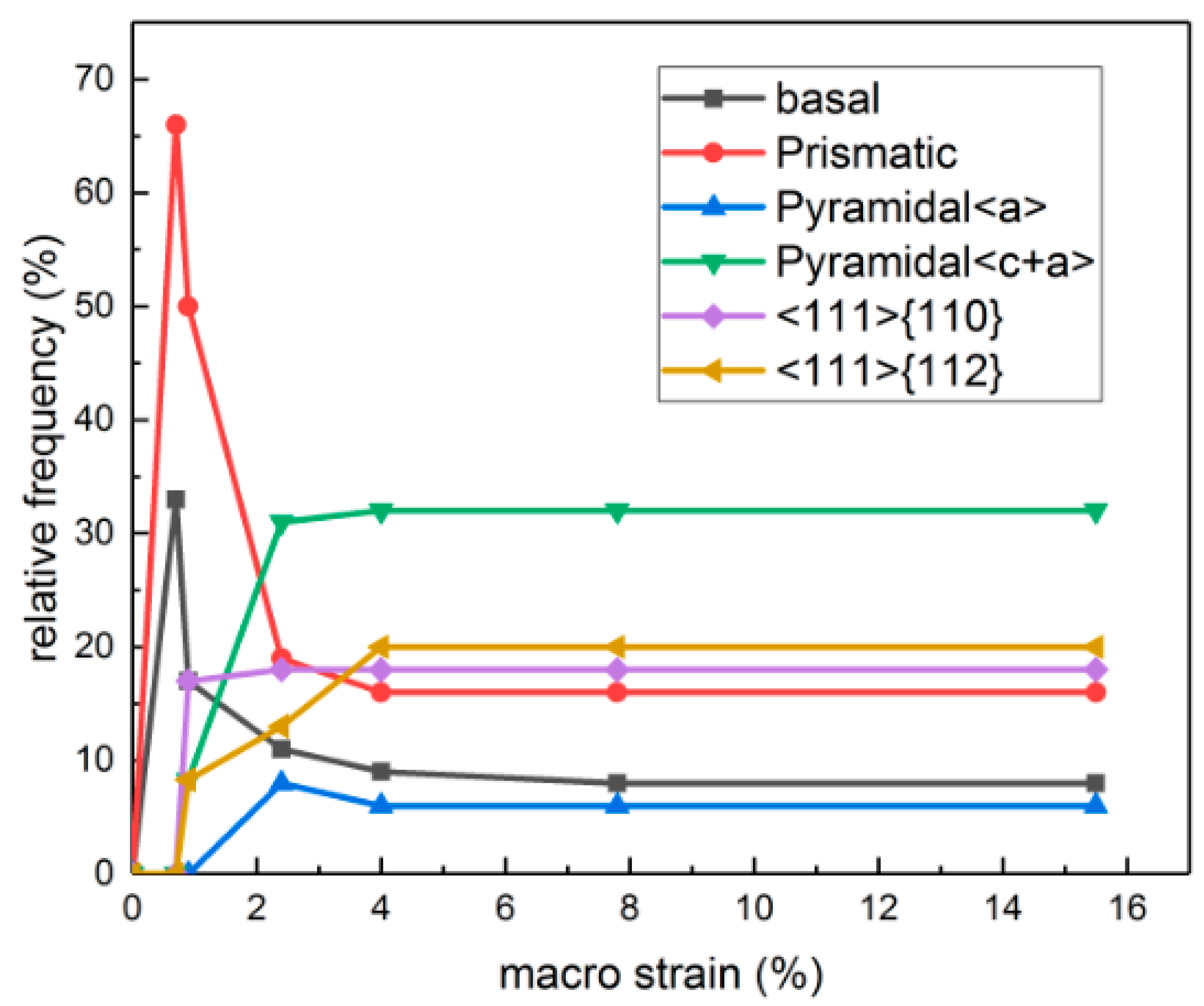
3.3.1. Activation of Slip Systems
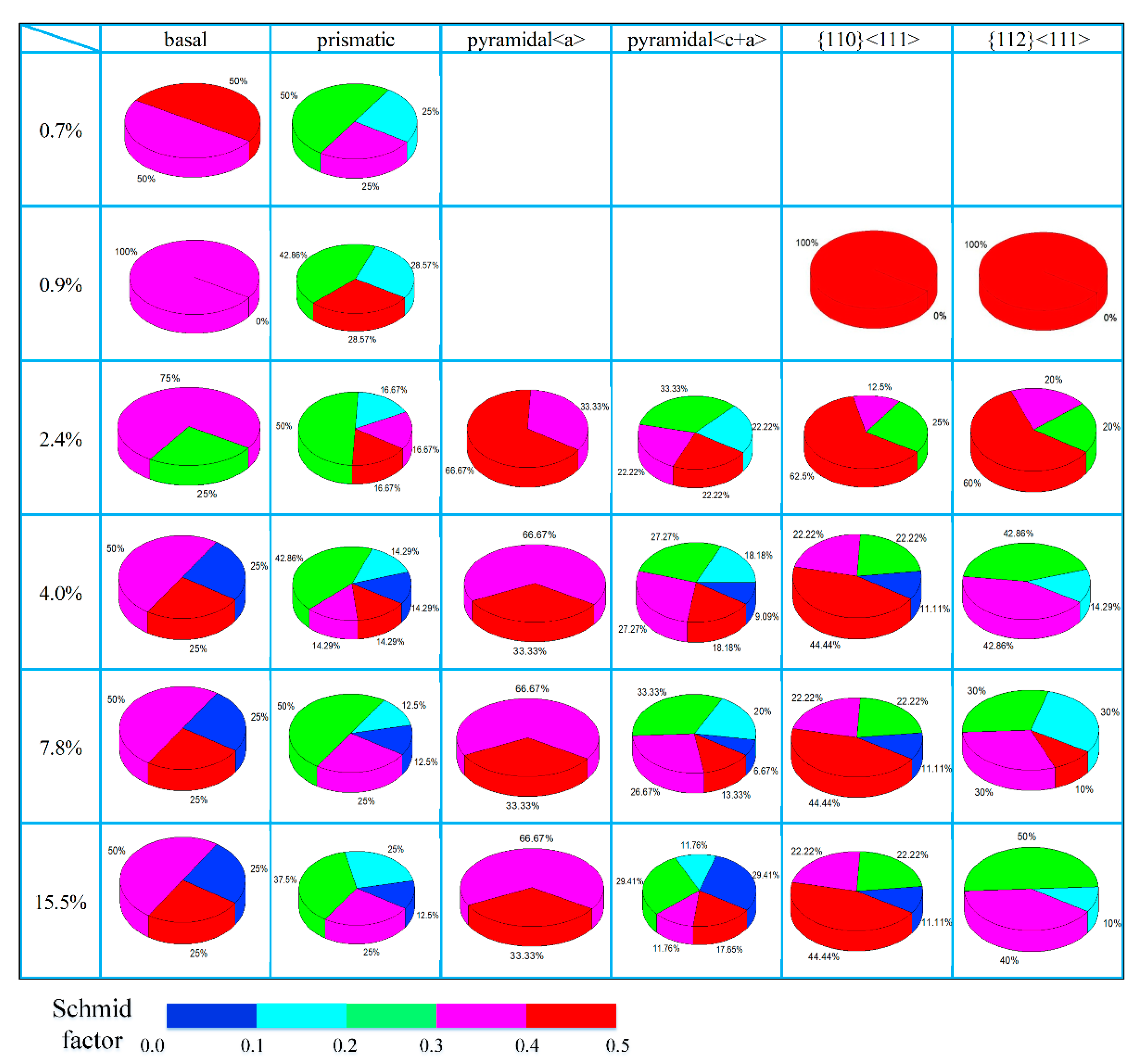
3.3.2. Analysis of Schmid Factors
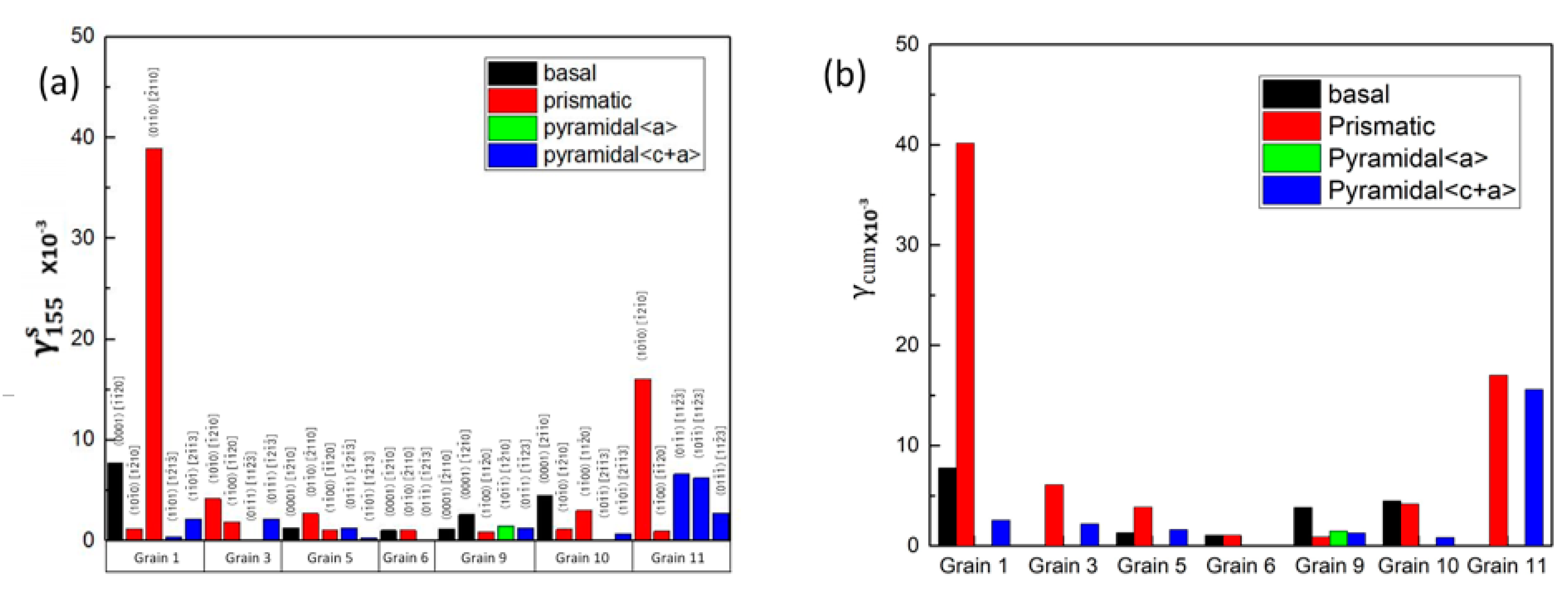
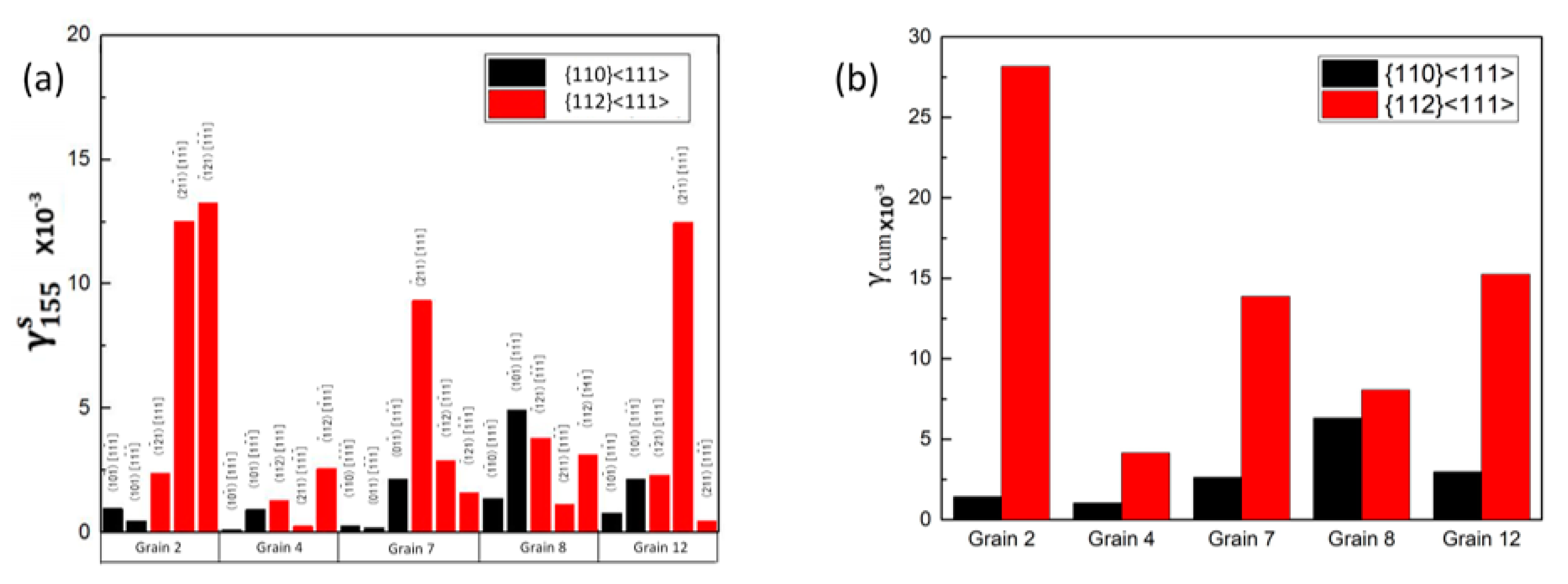
3.3.3. Analysis of Grain Interactions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, H.; Zhao, Z.L.; Ning, Y.Q.; Guo, H.Z.; Yao, Z.K. Characterization of Microstructural Evolution for a Near-α Titanium Alloy with Different Initial Lamellar Microstructures. Metals 2018, 8, 1045. [Google Scholar] [CrossRef]
- Gao, X.X.; Zeng, W.D.; Li, X.; Zhou, D.D.; Xu, J.W.; Wang, Q.J. Effect of boundary on the alpha phase precipitation in a near-alpha titanium alloy. Mater. Lett. 2018, 233, 298–301. [Google Scholar] [CrossRef]
- Vajpai, S.K.; Sharma, B.; Ota, M.; Ameyama, K. Effect of cold rolling and heat-treatment on the microstructure and mechanical properties of β-titanium Ti-25Nb-25Zr alloy. Mater. Sci. Eng. A 2018, 736, 323–328. [Google Scholar] [CrossRef]
- Wronski, M.; Arul Kumar, M.; Capolungo, L.; McCabe, R.J.; Wierzbanowski, K.; Tomé, C.N. Deformation behavior of CP-titanium: Experiment and crystal plasticity modeling. Mater. Sci. Eng. A 2018, 724, 289–297. [Google Scholar] [CrossRef]
- Joseph, S.; Lindley, T.C.; Dye, D. Dislocation interactions and crack nucleation in fatigued near-alpha titanium alloy. Int. J. Plast. 2018, 110, 38–56. [Google Scholar] [CrossRef]
- Hémery, S.; Villechaise, P. Investigation of Size Effects in Slip Strength of Titanium Alloys: α Nodule Size Dependence of the Critical Resolved Shear Stress. Metall. Mater. Trans. A 2018, 49, 4394–4397. [Google Scholar] [CrossRef]
- Shao, H.; Zhao, Y.; Ge, P.; Zeng, W.D. In-situ SEM observations of tensile deformation of the lamellar microstructure in TC21 titanium alloy. Mater. Sci. Eng. A 2013, 559, 515–519. [Google Scholar] [CrossRef]
- Arul Kumar, M.; Wroński, M.; McCabe, R.J.; Capolungo, L.; Wierzbanowski, K.; Tomé, C.N. Role of microstructure on twin nucleation and growth in HCP titanium: A statistical study. Acta Mater. 2018, 148, 123–132. [Google Scholar] [CrossRef]
- Castany, P.; Besse, M.; Gloriant, T. In situ TEM study of dislocation slip in a metastable β titanium alloy. Scr. Mater. 2012, 66, 371–373. [Google Scholar] [CrossRef]
- Zhang, S.; Zen, W.D.; Zhao, Q.Y.; Ge, L.L.; Zhang, M. In situ SEM study of tensile deformation of a near-β titanium alloy. Mater. Sci. Eng. A 2017, 708, 574–581. [Google Scholar] [CrossRef]
- Tan, C.; Sun, C.; Xiao, L.; Zhang, Y.Q.; Sun, J. Characterization of deformation in primary α phase and crack initiation and propagation of TC21 alloy using in-situ SEM experiments. Mater. Sci. Eng. A 2018, 725, 33–42. [Google Scholar] [CrossRef]
- Guo, Y.; Britton, T.B.; Wilkinson, A.J. Slip band–grain boundary interactions in commercial-purity titanium. Acta Mater. 2014, 76, 1–12. [Google Scholar] [CrossRef]
- Girardin, G.; Huvier, C.; Delafosse, D.; Feaugas, X. Correlation between dislocation organization and slip bands: TEM and AFM investigations in hydrogen-containingnickel and nickel-chromium. Acta Mater. 2015, 91, 141–151. [Google Scholar] [CrossRef]
- Franciosi, P.; Le, L.T.; Monnet, G.; Kahloun, C.; Chavanne, M.-H. Investigation of slip system activity in iron at room temperature by SEM and AFM in-situ tensile and compression tests of iron single crystals. Int. J. Plast. 2015, 65, 226–249. [Google Scholar] [CrossRef]
- Asim, U.B.; Siddiq, A.; Demiral, M. Void growth in high strength aluminium alloy single crystals: A CPFEM based study. Model. Simul. Mater. Sci. Eng. 2017, 25, 035010. [Google Scholar] [CrossRef]
- Landon, T.H.; David, T.F.; Eric, R.H.; Robert, H.W.; Lim, H.J.; Jay, D.C.; Zhou, G.W.; Bong, H.J. An investigation of geometrically necessary dislocations and back stress in large grained tantalum via EBSD and CPFEM. Mater. Sci. Eng. A 2020, 772, 138704. [Google Scholar]
- Asim, U.B.; Siddiq, A.; Kartal, M.E. A CPFEM based study to understand the void growth in high strength dual-phase Titanium alloy (Ti-10V-2Fe-3Al). Int. J. Plast. 2019, 122, 188–211. [Google Scholar] [CrossRef]
- Zhang, M.; Bridier, F.; Villechaise, P.; Mendez, J.; McDowell, D.L. Simulation of slip band evolution in duplex Ti–6Al–4V. Acta Mater. 2010, 58, 1087–1096. [Google Scholar] [CrossRef]
- Aubert, I.; Saintier, N.; Olive, J.M.; Plessier, F. A methodology to obtain data at the slip band scale from atomic force microscopy observations and crystal plasticity simulations. Application to hydrogen-induced slip localization on AISI 316L stainless steel. Acta Mater. 2016, 104, 9–17. [Google Scholar] [CrossRef]
- Du, C.; Maresca, F.; Geers, M.G.D.; Hoefnagels, J.P.M. Ferrite slip system activation investigated by uniaxial micro-tensile tests and simulations. Acta Mater. 2018, 146, 314–327. [Google Scholar] [CrossRef]
- Zhang, Z.; Lunt, D.; Abdolvand, H.; Angus, J.W.; Michael, P.; Fionn, P.E.D. Quantitative investigation of micro slip and localization in polycrystalline materials under uniaxial tension. Int. J. Plast. 2018, 108, 88–106. [Google Scholar] [CrossRef]
- Jason, R.M.; Irene, J.B.; Curt, A.B.; Hashem, M. The Influence of Grain Interactions on the Plastic Stability of Heterophase Interfaces. Materials 2014, 7, 302–322. [Google Scholar]
- Woo, W.; Em, V.T.; Kim, E.Y.; Han, S.H.; Han, Y.S.; Choi, S.-H. Stress–strain relationship between ferrite and martensite in a dual-phase steel studied by in situ neutron diffraction and crystal plasticity theories. Acta Mater. 2012, 60, 6972–6981. [Google Scholar] [CrossRef]
- Vajragupta, N.; Uthaisangsuk, V.; Schmaling, B.; Münstermann, S.; Hartmaier, A.; Bleck, W. A micromechanical damage simulation of dual phase steels using XFEM. Comput. Mater. Sci. 2012, 54, 271–279. [Google Scholar] [CrossRef]
- Sommitsch, C.; Krumphals, A.; Candic, M.; Tian, B.H.; Stockinger, M. Modeling of Grain Growth in One and Two Phase Materials by 2D Cellular Automata. In Proceedings of the 6th International Conference on Physical and Numerical Simulation of Materials Processing, Guilin, China, 16–19 November 2010. [Google Scholar]
- Wu, C.; Yang, H.; Li, H.W. Modeling of static coarsening of two-phase titanium alloy in the α+β two-phase region at different temperature by a cellular automata method. Chin. Sci. Bull. 2013, 24, 3023–3032. [Google Scholar] [CrossRef][Green Version]
- Li, G.J.; Shi, R.; Fan, Q.B.; Xia, Y.M.; Zhang, H.M. Three-dimensional microstructure-based micromechanical modeling for TC6 titanium alloy. Mater. Sci. Eng. A 2017, 685, 327–331. [Google Scholar] [CrossRef]
- Prakash, A.; Weygand, S.M.; Riedel, H. Modeling the evolution of texture and grain shape in Mg alloy AZ31 using the crystal plasticity finite element method. Comput. Mater. Sci. 2009, 45, 744–750. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, Q.B.; Liu, X.; Wang, D.D.; Zhu, X.J. Experimental study and crystal plasticity finite element simulations of nano-indentation-induced lattice rotation and the underlying mechanism in TC6 single α-grain. Mater. Des. 2020, 188, 108423. [Google Scholar] [CrossRef]
- Shi, R.; Nie, Z.H.; Fan, Q.B.; Li, G.J. Elastic plastic deformation of TC6 titanium alloy analyzed by in-situ synchrotron based X-ray diffraction and microstructure based finite element modeling. J. Alloys Compd. 2016, 688, 787–795. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Bronkhorst, C.A.; Anand, L. Crystallographic texture evolution in bulk deformation processing of FCC metals. J. Mech. Phys. Solids 1992, 40, 537–569. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Bhattacharyya, A.; Doherty, R.D. Detailed analyses of grain–scale plastic deformation in columnar polycrystalline aluminium using orientation image mapping and crystal plasticity models. Proc. R. Soc. A Math. Phys. Eng. Sci. 2004, 460, 1935–1956. [Google Scholar] [CrossRef]
- Mittemeijer, E.J. Fundamentals of Materials Science; Springer: Berlin/Heidelberg, Germany, 2011; Chapter 11. [Google Scholar]
- Liu, X.; Qian, Y.; Fan, Q.B.; Zhou, Y.; Zhu, X.J.; Wang, D.D. Plastic deformation mode and α/β slip transfer of Ti-5Al-2.5Cr-0.5Fe-4.5Mo-1Sn-2Zr-3Zn titanium alloy at room temperature. J. Alloys Compd. 2020, 826, 154209. [Google Scholar] [CrossRef]
- Basseville, S.; Cailletaud, G.; Ghidossic, T.; Guilhem, Y.; Lacoste, E.; Proudhon, H.; Signor, L.; Villechaise, P. Numerical analysis on the local mechanical fields in polycrystalline 316LN stainless steel under cyclic fatigue loading: Comparison with experimental results. Mater. Sci. Eng. A 2017, 696, 122–136. [Google Scholar] [CrossRef]
- Li, J.G.; Li, Y.L.; Suo, T.; Wei, Q.M. Numerical simulations of adiabatic shear localization in textured FCC metal based on crystal plasticity finite element method. Mater. Sci. Eng. A 2018, 737, 348–363. [Google Scholar] [CrossRef]





| C11(GPA) | C12(GPA) | C13(GPA) | C33(GPA) | C44(GPA) | |
|---|---|---|---|---|---|
| α phase | 160.0 | 86.0 | 55.0 | 183.0 | 54.0 |
| β phase | 130.2 | 70.6 | 70.6 | 70.6 | 45.8 |
| Slip System | CRSS (GPA) | τ1 (GPA) | θ0 (GPA) | θ1 (GPA) |
|---|---|---|---|---|
| 0.36 | 0.13 | 0.115 | 0.0021 | |
| 0.38 | ||||
| 0.5 | ||||
| 0.52 | ||||
| {110} <111> | 0.45 | 0.13 | 0.105 | 0.0016 |
| {112} <111> | 0.46 | |||
| {123} <111> | 0.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, Y.; Fan, Q.; Liu, X.; Wang, D.; Zhou, Y. Crystal Plasticity Finite Element Method for Slip Systems Evolution Analysis of α/β Duplex Titanium Alloys during Quasi-Static Tensile Testing. Appl. Sci. 2020, 10, 7782. https://doi.org/10.3390/app10217782
Qian Y, Fan Q, Liu X, Wang D, Zhou Y. Crystal Plasticity Finite Element Method for Slip Systems Evolution Analysis of α/β Duplex Titanium Alloys during Quasi-Static Tensile Testing. Applied Sciences. 2020; 10(21):7782. https://doi.org/10.3390/app10217782
Chicago/Turabian StyleQian, Yan, Qunbo Fan, Xin Liu, Duoduo Wang, and Yu Zhou. 2020. "Crystal Plasticity Finite Element Method for Slip Systems Evolution Analysis of α/β Duplex Titanium Alloys during Quasi-Static Tensile Testing" Applied Sciences 10, no. 21: 7782. https://doi.org/10.3390/app10217782
APA StyleQian, Y., Fan, Q., Liu, X., Wang, D., & Zhou, Y. (2020). Crystal Plasticity Finite Element Method for Slip Systems Evolution Analysis of α/β Duplex Titanium Alloys during Quasi-Static Tensile Testing. Applied Sciences, 10(21), 7782. https://doi.org/10.3390/app10217782





