Life-Cycle Performance Assessment and Distress Prediction of Subgrade Based on an Analytic Hierarchy Process and the PSO–LSSVM Model
Abstract
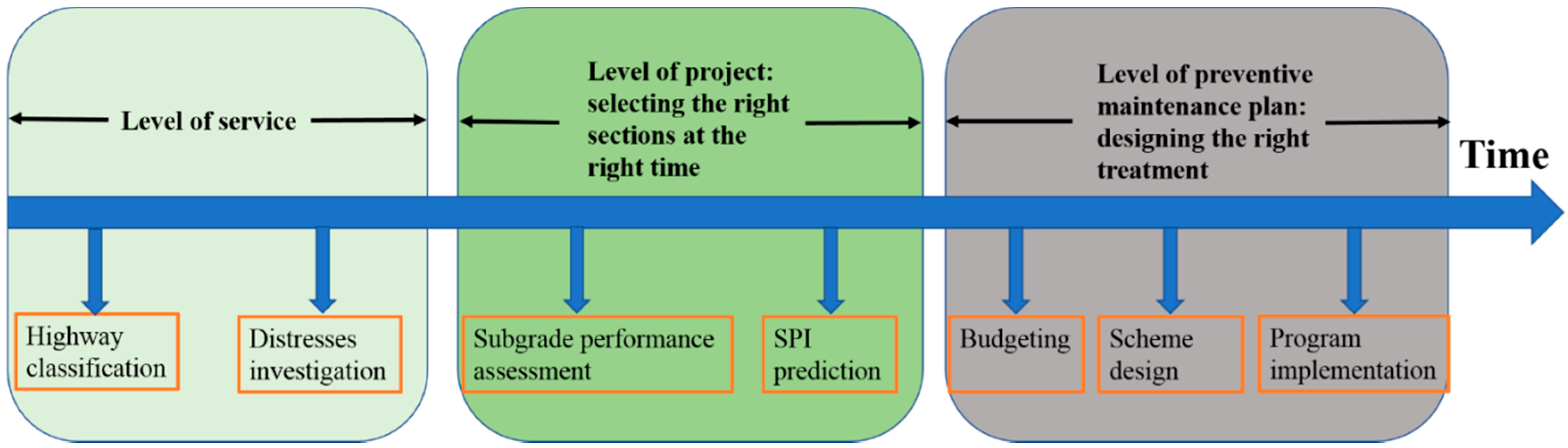
1. Introduction
2. Investigation of Subgrade Distresses in Test Area
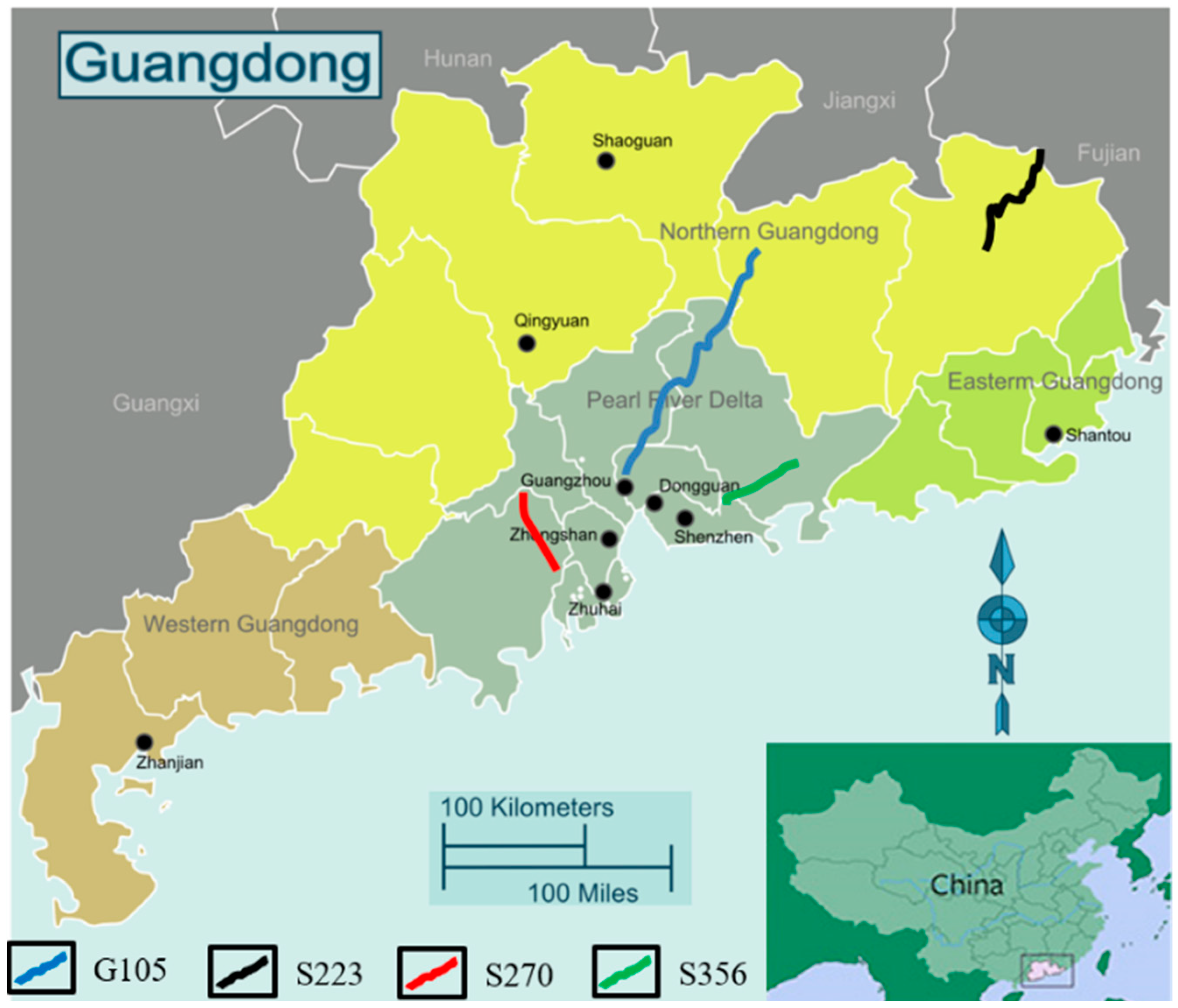
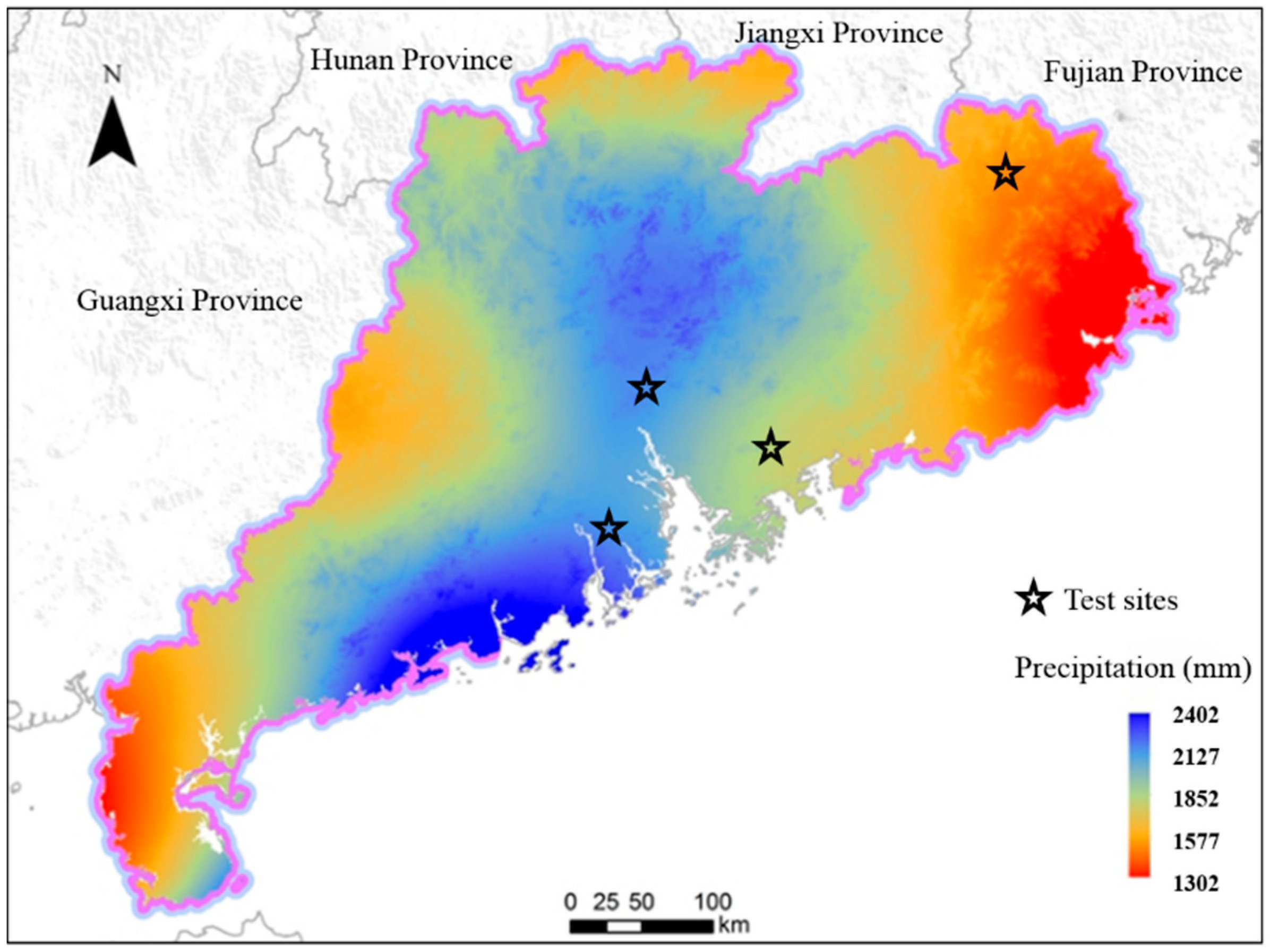
2.1. Description of the Test Area
2.2. Implementation of the Subgrade Distress Investigation and Data Collection
2.2.1. Investigation of the Subgrade Distresses in the Test Section
2.2.2. Subgrade Distress Data Collection
2.3. Evolution Process and Influencing Factors of Subgrade Distress
3. Methodology
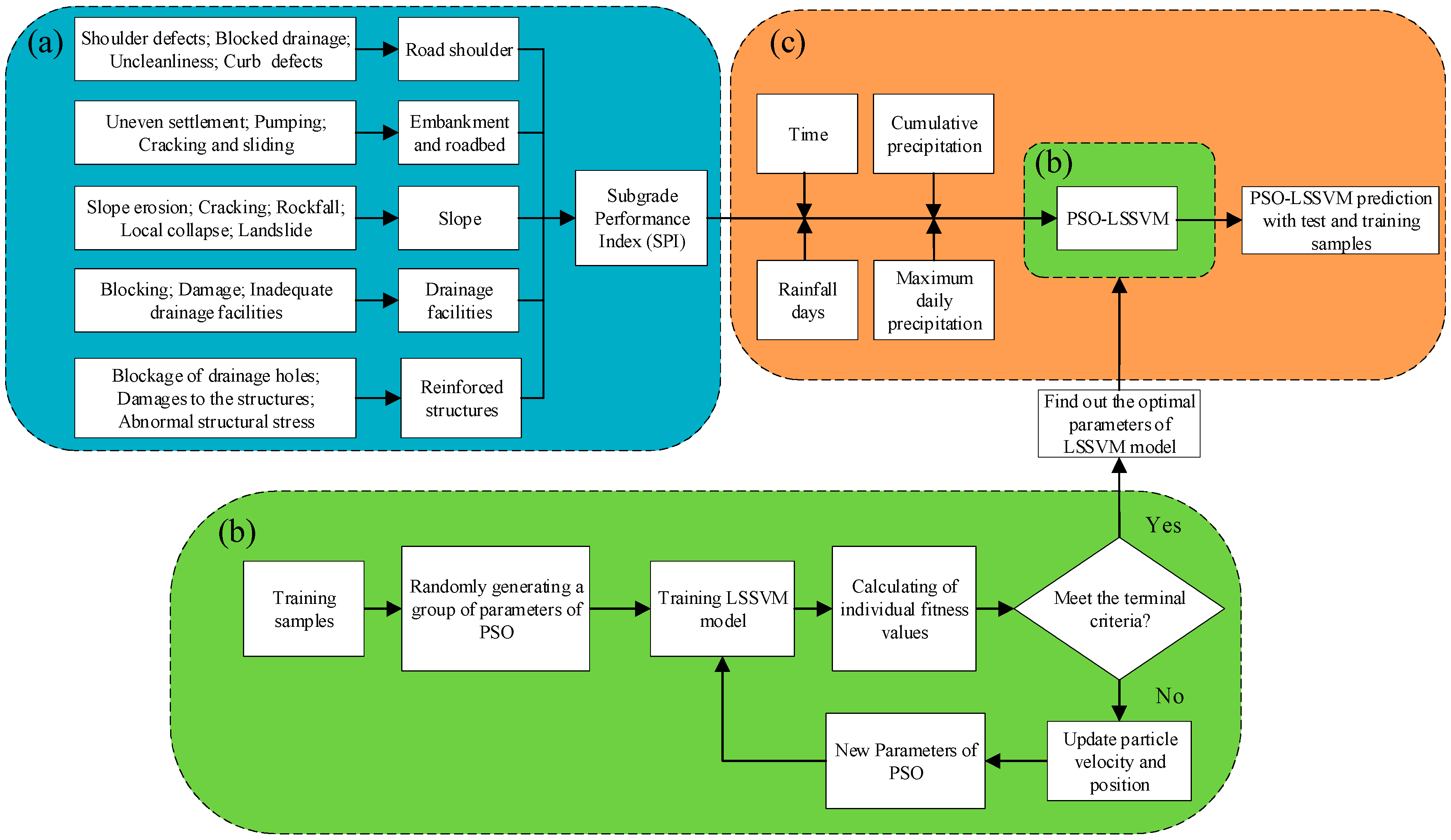
3.1. Systematic Assessment Method of the Subgrade Performance
3.1.1. Hierarchical Structure
3.1.2. Comparison Matrix
3.1.3. Building the Judgment Matrix
3.1.4. Calculation of the Index Weights
3.1.5. Application of the Weight Value
3.2. Principles of the PSO–LSSVM Model
3.2.1. Least Squares Support Vector Machine (LSSVM)
3.2.2. Parameter Selection of the LSSVM Using PSO
4. SPI Prediction and Application
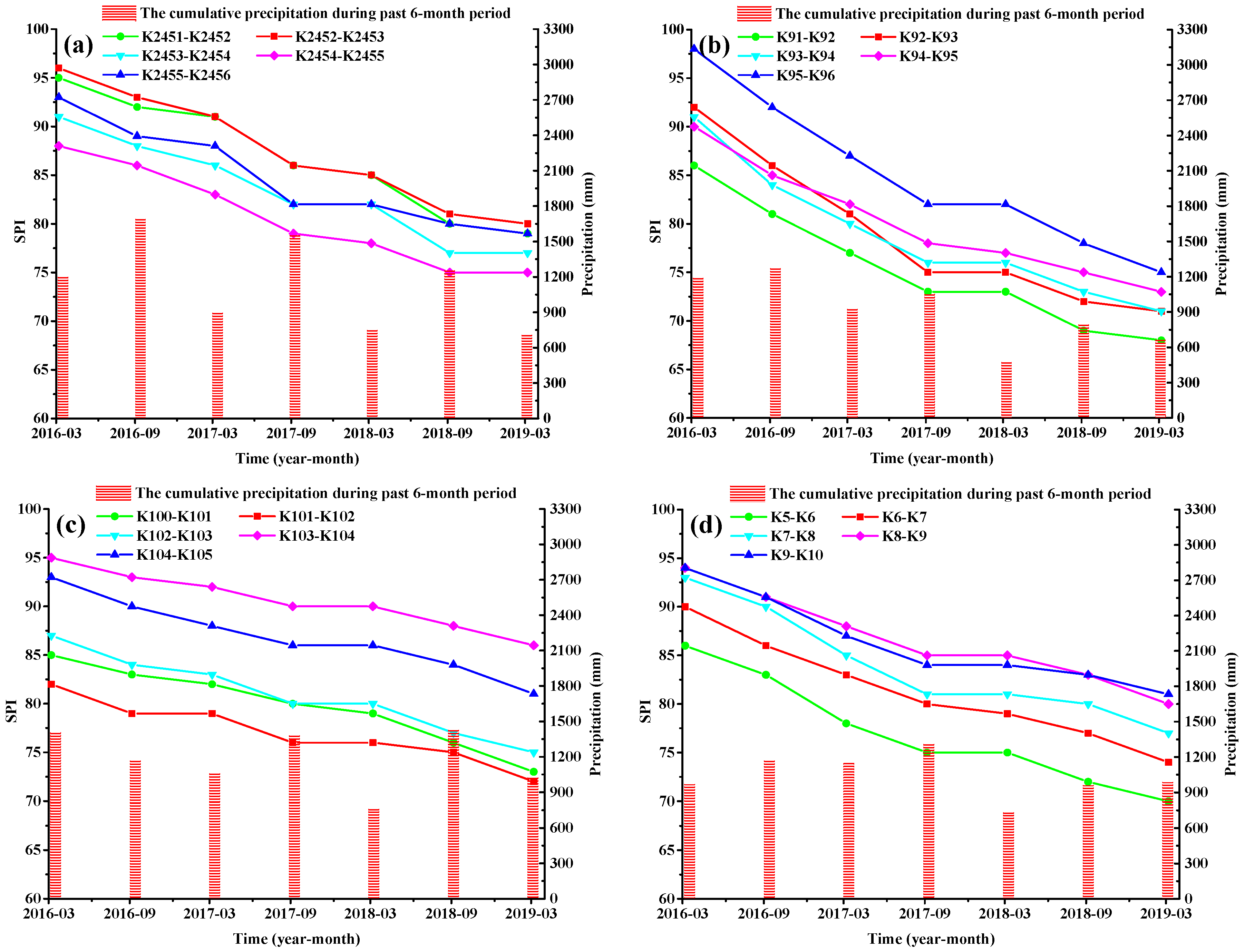
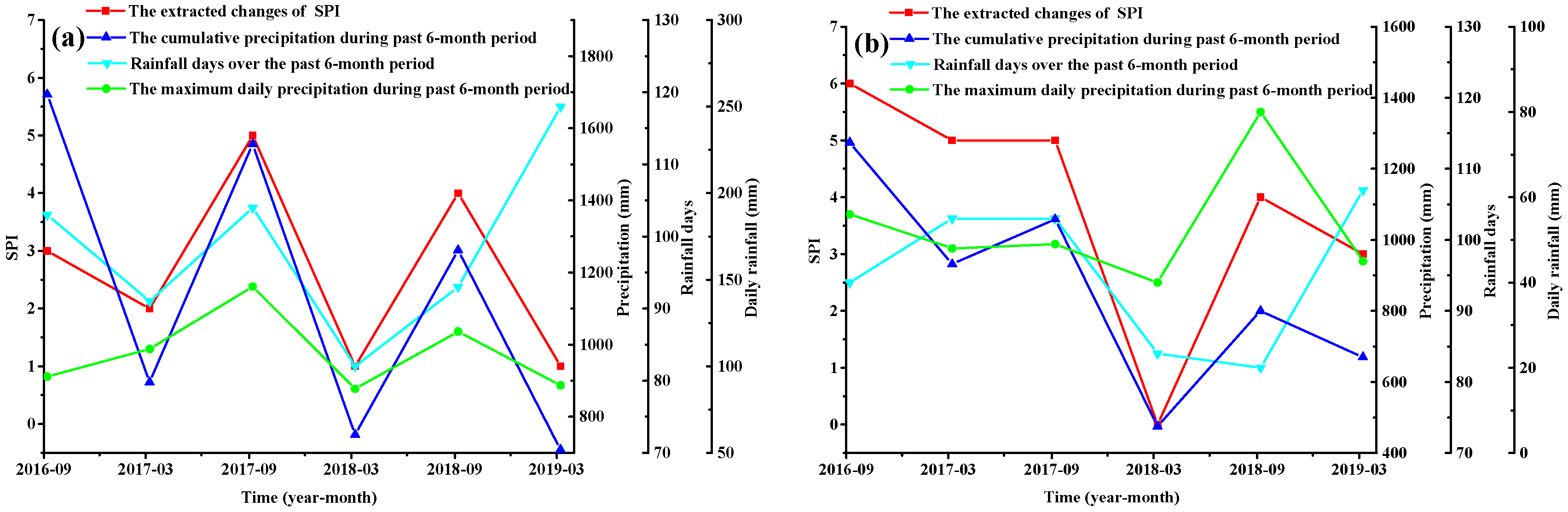
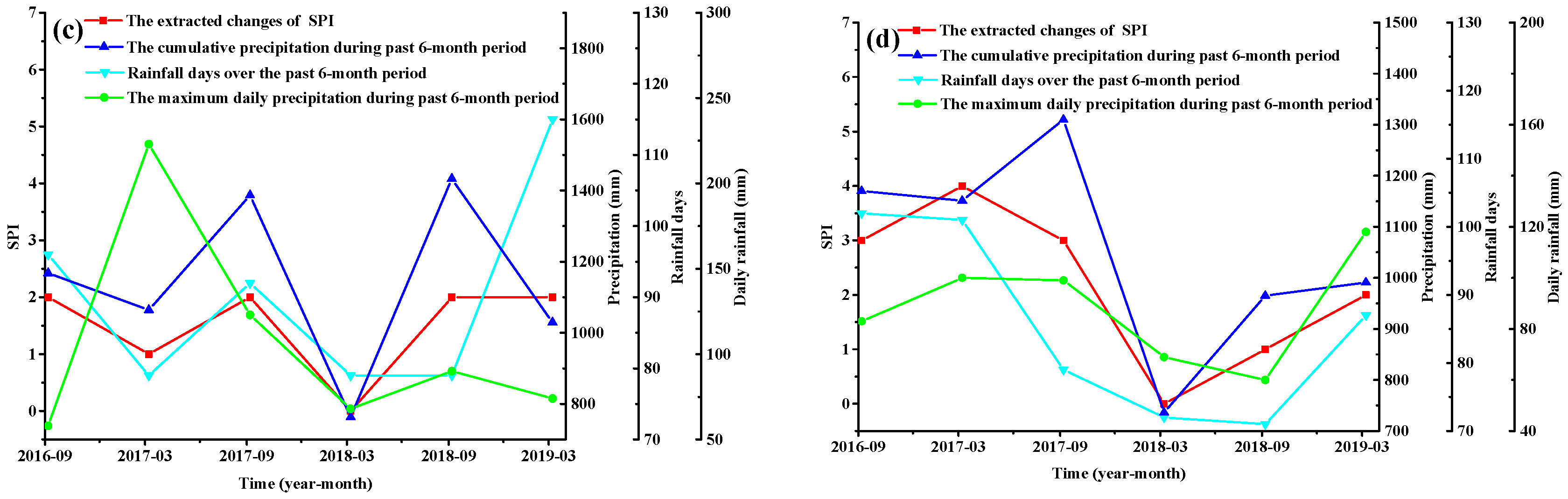
4.1. Analysis of the SPI
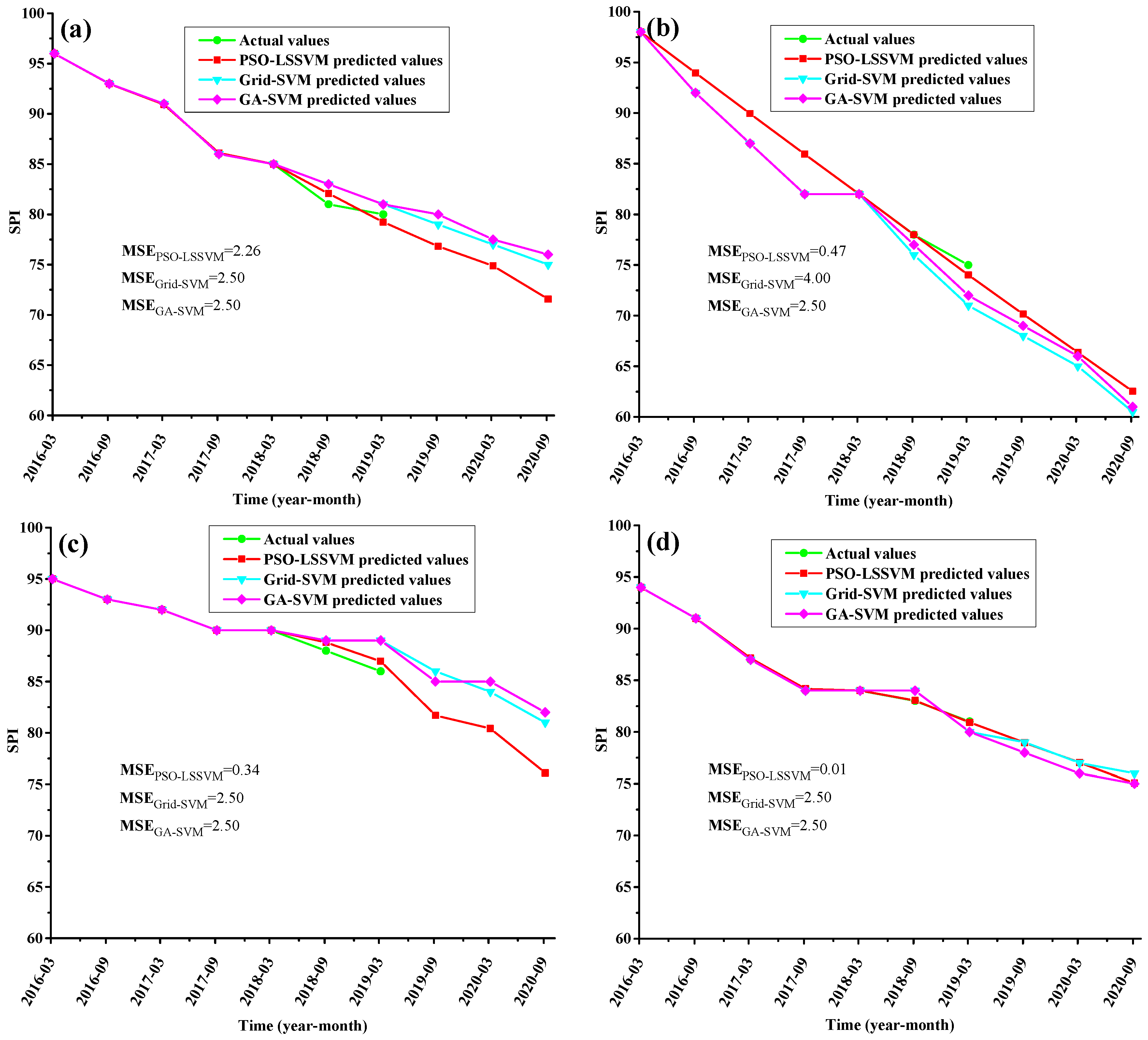
4.2. Building the PSO–LSSVM Model
4.3. Application for the Date of the SPI
5. Conclusions
- (1)
- The development trend of subgrade distress is affected by internal factors. External factors, such as rainfall, directly cause the formation of subgrade distresses. Therefore, the relationships between the internal and external factors are important when analyzing the evolution mechanism of subgrade distress.
- (2)
- The results of the SPI calculations show that the prediction accuracy of the SPI prediction model based on PSO–LSSVM is better than the prediction accuracy of the other two models, which are based on Grid-SVM and GA-SVM. In addition, the PSO–LSSVM model accurately predicts both the gently decreasing type and rapidly decreasing type of SPI.
- (3)
- The prediction accuracy of provincial highways is higher than that of the national highway. This is mainly due to the large traffic volume on the national highway and the frequent occurrence of overloaded trucks, which result in redundant damage to the subgrade, thus increasing the difficulty of SPI prediction.
- (4)
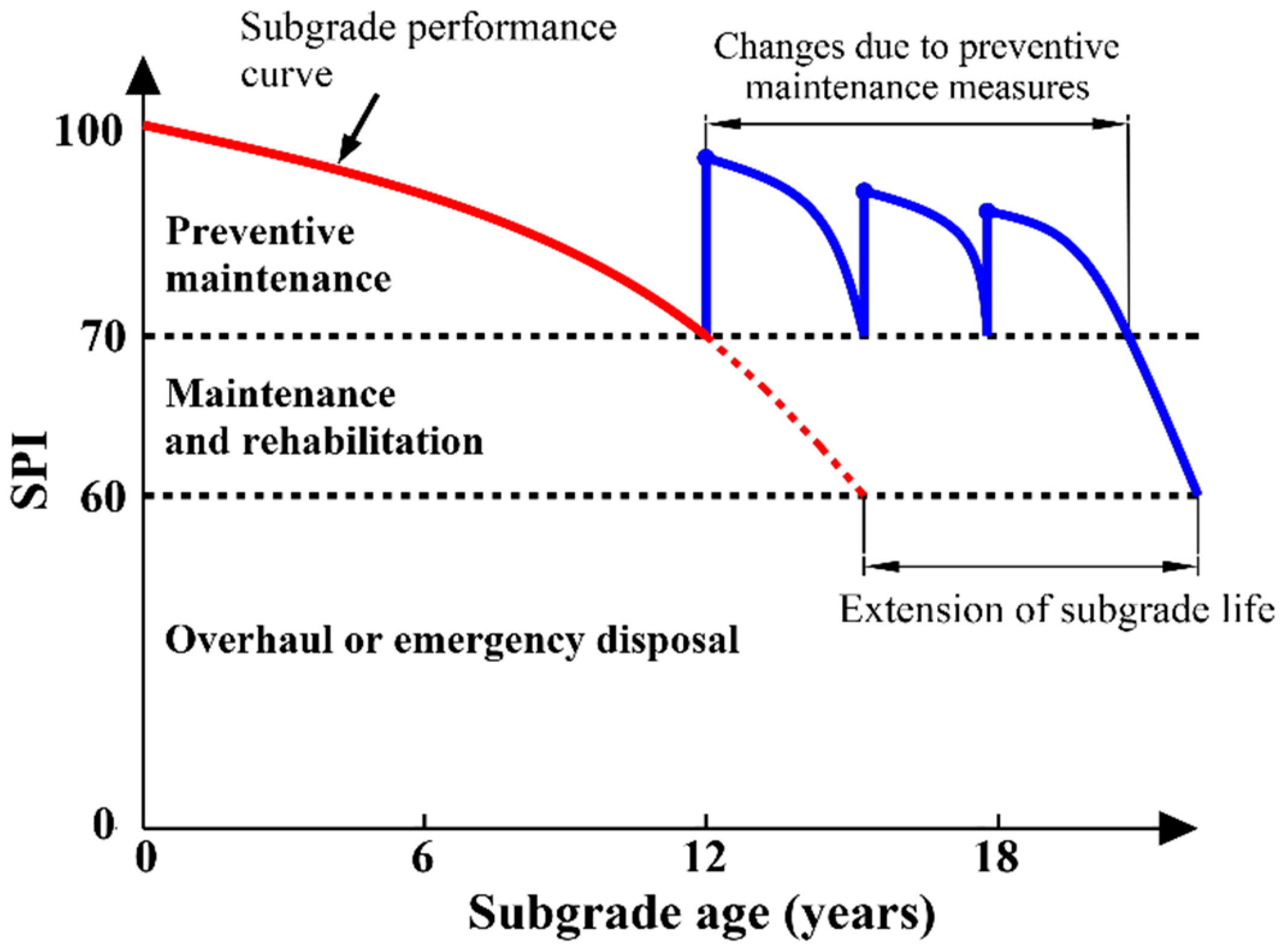
- According to the SPI, the subgrade is divided into four levels. Corresponding maintenance and treatment measures are taken for different levels. Preventive maintenance is applied before the SPI drops below 70.
- (5)
- The establishment of a subgrade performance assessment–prediction–maintenance–management architecture framework provides a clear method for road maintenance managers to reasonably lay out the subgrade life-cycle assessment decision system.
Author Contributions
Funding
Conflicts of Interest
References
- Wang, S.G.; Song, X.G. Maintenance and Reinforcement of Highway Subgrade; China Communications Press Co. Ltd.: Beijing, China, 2010. [Google Scholar]
- Zhang, L.; Wang, Y.M. Analysis on the Technology of Highway Subgrade Disease Prevention and Maintenance in Guangdong Province. Adv. Mater. Res. 2015, 1065–1069, 737–743. [Google Scholar] [CrossRef]
- Zang, Y.Y.G. High Grade Highway Subgrade Disease Analysis and Prevention and Control Technology; China Communications Press: Beijing, China, 2007. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. Technical Specifications for Maintenance of Highway Subgrade; Volume JTG 5150—2020; China Communications Press: Beijing, China, 2020.
- Yang, J.; Lei, L.I.; Ming, W.U.; Jiang, Z.M.; Yan, Z.L. Analysis on Type and Genesis of Subgrade Diseases of Highway in Mountainous Area. Subgrade Eng. 2012, 6. [Google Scholar]
- Liu, F.J.; Jian, L.U.; Zhang, G.Q.; Xiang, Q.J. Evaluation Approach of Expressway Subgrade Maintenance. J. Highw. Transp. Res. Dev. 2006, 5. [Google Scholar]
- Raj, M.; Sengupta, A. Rain-triggered slope failure of the railway embankment at Malda, India. Acta Geotech. 2014, 9, 789–798. [Google Scholar] [CrossRef]
- Sun, H.-Y.; Pan, P.; Lü, Q.; Wei, Z.-L.; Xie, W.; Zhan, W. A case study of a rainfall-induced landslide involving weak interlayer and its treatment using the siphon drainage method. Bull. Eng. Geol. Environ. 2018, 78, 4063–4074. [Google Scholar] [CrossRef]
- Lu, N.; Wayllace, A.; Oh, S. Infiltration-induced seasonally reactivated instability of a highway embankment near the Eisenhower Tunnel, Colorado, USA. Eng. Geol. 2013, 162, 22–32. [Google Scholar] [CrossRef]
- Lou, Z.; Gunaratne, M.; Lu, J.J.; Dietrich, B. Application of Neural Network Model to Forecast Short-Term Pavement Crack Condition: Florida Case Study. J. Infrastruct. Syst. 2001, 7, 166–171. [Google Scholar] [CrossRef]
- Chen, Y.; Davalos, J.F.; Ray, I. Durability Prediction for GFRP Reinforcing Bars Using Short-Term Data of Accelerated Aging Tests. J. Compos. Constr. 2006, 10, 279–286. [Google Scholar] [CrossRef]
- Micelli, F.; Nanni, A. Durability of FRP rods for concrete structures. Constr. Build. Mater. 2004, 18, 491–503. [Google Scholar] [CrossRef]
- Mori, Y.; Ellingwood, B.R. Reliability-Based Service-Life Assessment of Aging Concrete Structures. J. Struct. Eng. 1993, 119, 1600–1621. [Google Scholar] [CrossRef]
- Zhu, X.; Ma, S.-Q.; Xu, Q.; Liu, W.-D. A WD-GA-LSSVM model for rainfall-triggered landslide displacement prediction. J. Mt. Sci. 2018, 15, 156–166. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.-S.; Li, J.-J. System reliability analysis of slopes using least squares support vector machines with particle swarm optimization. Neurocomputing 2016, 209, 46–56. [Google Scholar] [CrossRef]
- Xue, X.; Yang, X.; Chen, X. Application of a support vector machine for prediction of slope stability. Sci. China Technol. Sci. 2014, 57, 2379–2386. [Google Scholar] [CrossRef]
- Li, S.-J.; Zhao, H.-B.; Ru, Z.-L. Deformation prediction of tunnel surrounding rock mass using CPSO-SVM model. J. Cent. South Univ. 2012, 19, 3311–3319. [Google Scholar] [CrossRef]
- Rahbarzare, A.; Azadi, M. Improving prediction of soil liquefaction using hybrid optimization algorithms and a fuzzy support vector machine. Bull. Eng. Geol. Environ. 2019, 78, 4977–4987. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B. Application of time series analysis and PSO–SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China. Eng. Geol. 2016, 204, 108–120. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Su, C.; Wang, L.; Wang, X.; Huang, Z.; Zhang, X. Mapping of rainfall-induced landslide susceptibility in Wencheng, China, using support vector machine. Nat. Hazards 2015, 76, 1759–1779. [Google Scholar] [CrossRef]
- Li, X.Z.; Kong, J.M. Application of GA–SVM method with parameter optimization for landslide development prediction. Nat. Hazards Earth Syst. Sci. 2014, 14, 525–533. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Xie, Y.; Li, Y. Prediction of landslide displacement with step-like behavior based on multialgorithm optimization and a support vector regression model. Landslides 2017, 15, 475–488. [Google Scholar] [CrossRef]
- Tan, X.; Yu, F.; Zhao, X. Support vector machine algorithm for artificial intelligence optimization. Clust. Comput. 2018, 22, 15015–15021. [Google Scholar] [CrossRef]
- Gao, X.; Hou, J. An improved SVM integrated GS-PCA fault diagnosis approach of Tennessee Eastman process. Neurocomputing 2016, 174, 906–911. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Kutlug Sahin, E.; Colkesen, I. Selecting optimal conditioning factors in shallow translational landslide susceptibility mapping using genetic algorithm. Eng. Geol. 2015, 192, 101–112. [Google Scholar] [CrossRef]
- Guo, X.C.; Yang, J.H.; Wu, C.G.; Wang, C.Y.; Liang, Y.C. A novel LS-SVMs hyper-parameter selection based on particle swarm optimization. Neurocomputing 2008, 71, 3211–3215. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Tang, X.; Hong, H.; Shu, Y.; Tang, H.; Li, J.; Liu, W. Urban waterlogging susceptibility assessment based on a PSO-SVM method using a novel repeatedly random sampling idea to select negative samples. J. Hydrol. 2019, 576, 583–595. [Google Scholar] [CrossRef]
- Wei, Z.-L.; Shang, Y.-Q.; Sun, H.-Y.; Xu, H.-D.; Wang, D.-F. The effectiveness of a drainage tunnel in increasing the rainfall threshold of a deep-seated landslide. Landslides 2019, 16, 1731–1744. [Google Scholar] [CrossRef]
- Department of Transportation. Highway Performance Assessment Standards; Volume JTG H20-2007; China Communications Press: Beijing, China, 2007.
- Oh, S.; Lu, N. Slope stability analysis under unsaturated conditions: Case studies of rainfall-induced failure of cut slopes. Eng. Geol. 2015, 184, 96–103. [Google Scholar] [CrossRef]
- Yang, K.-H.; Uzuoka, R.; Thuo, J.N.; Lin, G.-L.; Nakai, Y. Coupled hydro-mechanical analysis of two unstable unsaturated slopes subject to rainfall infiltration. Eng. Geol. 2017, 216, 13–30. [Google Scholar] [CrossRef]
- Senthilkumar, V.; Chandrasekaran, S.S.; Maji, V.B. Rainfall-Induced Landslides: Case Study of the Marappalam Landslide, Nilgiris District, Tamil Nadu, India. Int. J. Geomech. 2018, 18, 05018006. [Google Scholar] [CrossRef]
- Saaty, T.L. What is the Analytic Hierarchy Process? Mitra, G., Greenberg, H.J., Lootsma, F.A., Rijkaert, M.J., Zimmermann, H.J., Eds.; Mathematical Models for Decision Support: Berlin/Heidelberg, Germany, 1988; pp. 109–121. [Google Scholar]
- Yalcin, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Thanh, L.N.; De Smedt, F. Application of an analytical hierarchical process approach for landslide susceptibility mapping in A Luoi district, Thua Thien Hue Province, Vietnam. Environ. Earth Sci. 2011, 66, 1739–1752. [Google Scholar] [CrossRef]
- Ercanoglu, M.; Kasmer, O.; Temiz, N. Adaptation and comparison of expert opinion to analytical hierarchy process for landslide susceptibility mapping. Bull. Eng. Geol. Environ. 2008, 67, 565–578. [Google Scholar] [CrossRef]
- Komac, M. A landslide susceptibility model using the Analytical Hierarchy Process method and multivariate statistics in perialpine Slovenia. Geomorphology 2006, 74, 17–28. [Google Scholar] [CrossRef]
- Myronidis, D.; Papageorgiou, C.; Theophanous, S. Landslide susceptibility mapping based on landslide history and analytic hierarchy process (AHP). Nat. Hazards 2015, 81, 245–263. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Y.; Yan, C.; Zhang, L.; Yin, L.; Zhang, S.; Zhang, G. Lifecycle health monitoring and assessment system of soft soil subgrade for expressways in China. J. Clean. Prod. 2019, 235, 138–145. [Google Scholar] [CrossRef]
- Li, B.; Li, D.; Zhang, Z.; Yang, S.; Wang, F. Slope stability analysis based on quantum-behaved particle swarm optimization and least squares support vector machine. Appl. Math. Model. 2015, 39, 5253–5264. [Google Scholar] [CrossRef]
- Xu, W.Y.; Meng, Q.X.; Wang, R.B.; Zhang, J.C. A study on the fractal characteristics of displacement time-series during the evolution of landslides. Geomat. Nat. Hazards Risk 2016, 7, 1631–1644. [Google Scholar] [CrossRef]
- Wang, X. Two-parameter characterization of elastic–plastic crack front fields: Surface cracked plates under tensile loading. Eng. Fract. Mech. Eng. Fract. Mech 2009, 76, 958–982. [Google Scholar] [CrossRef]
- Momber, A.W.; Buchbach, S.; Plagemann, P.; Marquardt, T. Edge coverage of organic coatings and corrosion protection over edges under simulated ballast water tank conditions. Prog. Org. Coat. 2017, 108, 90–92. [Google Scholar] [CrossRef]
- Taylor, R. Interpretation of the Correlation Coefficient: A Basic Review. J. Diagn. Med. Sonogr. 1990, 6, 35–39. [Google Scholar] [CrossRef]
- Liang, C.; Jaksa, M.B.; Ostendorf, B.; Kuo, Y.L. Influence of river level fluctuations and climate on riverbank stability. Comput. Geotech. 2015, 63, 83–98. [Google Scholar] [CrossRef]
- Duong Thi, T.; Do Minh, D. Riverbank Stability Assessment under River Water Level Changes and Hydraulic Erosion. Water 2019, 11, 2598. [Google Scholar] [CrossRef]
- Briggs, K.M.; Loveridge, F.A.; Glendinning, S. Failures in transport infrastructure embankments. Eng. Geol. 2017, 219, 107–117. [Google Scholar] [CrossRef]
- Shepheard, C.J.; Vardanega, P.J.; Holcombe, E.A.; Michaelides, K. Analysis of design choices for a slope stability scenario in the humid tropics. Proc. Inst. Civil. Eng. Eng. Sustain. 2018, 171, 37–52. [Google Scholar] [CrossRef]
- Cai, Z.; Xu, W.; Meng, Y.; Shi, C.; Wang, R. Prediction of landslide displacement based on GA-LSSVM with multiple factors. Bull. Eng. Geol. Environ. 2015, 75, 637–646. [Google Scholar] [CrossRef]
- Wei, Z.-L.; Lü, Q.; Sun, H.-Y.; Shang, Y.-Q. Estimating the rainfall threshold of a deep-seated landslide by integrating models for predicting the groundwater level and stability analysis of the slope. Eng. Geol. 2019, 253, 14–26. [Google Scholar] [CrossRef]
- Dong, Q.; Huang, B. Failure Probability of Resurfaced Preventive Maintenance Treatments: Investigation into Long-Term Pavement Performance Program. Transp. Res. Rec. 2015, 2481, 65–74. [Google Scholar] [CrossRef]
- Zheng, X.; Easa, S.M.; Yang, Z.; Ji, T.; Jiang, Z. Life-cycle sustainability assessment of pavement maintenance alternatives: Methodology and case study. J. Clean. Prod. 2019, 213, 659–672. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, H.; Dong, Q.; Huang, B. Optimal Thresholds for Pavement Preventive Maintenance Treatments Using LTPP Data. J. Transp. Eng. Part A Syst. 2017, 143, 04017018. [Google Scholar] [CrossRef]
- Chen, D.-H.; Lin, D.-F.; Luo, H.-L. Effectiveness of Preventative Maintenance Treatments Using Fourteen SPS-3 Sites in Texas. J. Perform. Constr. Facil. 2003, 17, 136–143. [Google Scholar] [CrossRef]



| Object | Distress Types | Level | Unit | Deduct Points | Definition |
|---|---|---|---|---|---|
| Road shoulder | Shoulder defects | Minor | Place | 10 | Shallow rutting or potholes less than 25 mm |
| Severe | Place | 20 | Shallow rutting or potholes larger than or equal to 25 mm | ||
| Blocked drainage | Minor | Place | 10 | Along the trend of subgrade, the length of blocking drainage is 5–20 m. | |
| Severe | Place | 20 | Along the trend of subgrade, the length of blocking drainage is more than 20 m | ||
| Uncleanliness | Place | 5 | There are accumulated debris and weeds on the road shoulder | ||
| Curb defects | Place | 5 | Loss, damage, or toppling of curbs | ||
| Drainage facilities | Blocking | Minor | Place | 5 | There are sundries and garbage in the drainage system. Every 10 m is one place, and less than 10 m is maintained |
| Severe | Place | 10 | The full cross-section of the drainage system is blocked, every 10 m is one place, and less than 10 m is maintained | ||
| Damaged | Place | 5 | The lining spalling damage and masonry body cracking occurred | ||
| Inadequate drainage facilities | Km | 100 | One point will be deducted for every 10 m of inadequate drainage facilities, and less than 10 m is maintained | ||
| Reinforced structures | Blockage of drainage holes | Place | 20 | The expansion joint of the structure is used as the dividing section. When 30% or more of the drain holes have poor drainage, it is counted as one place | |
| Damages to the structures | Minor | Place | 10 | Partial foundation washout, wall voids, and slight cracks in supporting structures | |
| Severe | Place | 20 | The overall cracking, inclining, and sliding of the retaining structure appear | ||
| Abnormal structural stress | Place | 50 | Judging by the instability of independent reinforced structures | ||
| Embankment and roadbed | Uneven settlement | Minor | Place | 20 | The height difference of uneven settlement is 30–50 mm |
| Severe | Place | 50 | The height difference of uneven settlement is greater than 50 mm | ||
| Pumping | Place | 5 | The mud gushing out of the roadbed is one place. | ||
| Cracking and sliding | Place | 50 | Arc-shaped cracks along the longitudinal direction of the subgrade pose a greater threat to the safety of the subgrade | ||
| Slope | Slope erosion | Place | 20 | Gullies with a width and depth of 10 cm or more are counted as one place | |
| Cracking | Minor | Place | 20 | There are some vertical cracks in the side boundary of the slope | |
| Severe | Place | 50 | A tensile crack at the top of the slope | ||
| Local collapse | Place | 50 | The rock and soil mass on the slope surface is loose and broken, resulting in local slope collapse | ||
| Rockfall | Place | 20 | The rock mass splits and peels off, causing the gravel to roll off | ||
| Landslide | Place | 100 | The overall slide of the slope causes traffic interruption |
| Second-Level Indexes | Index Weight | First-Level Indexes | Index Weight | Second-Level Indexes | Index Weight | First-Level Indexes | Index Weight |
|---|---|---|---|---|---|---|---|
| Embankment and roadbed | 0.27 | Uneven settlement | 0.376 | Road shoulder | 0.08 | Shoulder defects | 0.255 |
| Pumping | 0.221 | Blocked drainage | 0.413 | ||||
| Cracking and sliding | 0.403 | Uncleanliness | 0.235 | ||||
| Drainage facilities | 0.10 | Blocking | 0.441 | Curb defects | 0.097 | ||
| Damage | 0.347 | Slope | 0.36 | Slope erosion | 0.135 | ||
| Inadequate drainage facilities | 0.212 | Cracking | 0.065 | ||||
| Reinforced structures | 0.19 | Blockage of drainage holes | 0.153 | Local collapse | 0.078 | ||
| Damages to the structures | 0.505 | Rockfall | 0.283 | ||||
| Abnormal structural stress | 0.342 | Landslide | 0.439 |
| Sites | Cumulative Precipitation | Rainfall Days | Maximum Daily Precipitation |
|---|---|---|---|
| K2452–K2453 of G105 | 0.826 | 0.232 | 0.890 |
| K95–K96 of S223 | 0.935 | 0.411 | 0.375 |
| K103–K104 of S270 | 0.802 | 0.550 | 0.159 |
| K9–K10 of S356 | 0.874 | 0.815 | 0.603 |
| Parameters | K2452–K2453 of G105 | K95–K96 of S223 | K103–K104 of S270 | K9–K10 of S356 |
|---|---|---|---|---|
| 14.743 | 0.1 | 1.0 × 106 | 11.455 | |
| 1.922 | 7.672 | 57.009 | 1.313 |
| Sites | Cumulative Precipitation (mm) | Rainfall Days | Maximum Daily Precipitation (mm) | Predictive Values for September 2019 |
|---|---|---|---|---|
| K2452–K2453 of G105 | 1720 | 114 | 108 | 76.82 |
| K95–K96 of S223 | 1333 | 109 | 76 | 70.16 |
| K103–K104 of S270 | 1914 | 116 | 123 | 81.70 |
| K9–K10 of S356 | 1363 | 90 | 63 | 78.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wang, Y.; Zhang, K.; Cheng, Z.; Tao, Z. Life-Cycle Performance Assessment and Distress Prediction of Subgrade Based on an Analytic Hierarchy Process and the PSO–LSSVM Model. Appl. Sci. 2020, 10, 7529. https://doi.org/10.3390/app10217529
Li Q, Wang Y, Zhang K, Cheng Z, Tao Z. Life-Cycle Performance Assessment and Distress Prediction of Subgrade Based on an Analytic Hierarchy Process and the PSO–LSSVM Model. Applied Sciences. 2020; 10(21):7529. https://doi.org/10.3390/app10217529
Chicago/Turabian StyleLi, Qi, Yimin Wang, Kunbiao Zhang, Zhiyuan Cheng, and Ziyu Tao. 2020. "Life-Cycle Performance Assessment and Distress Prediction of Subgrade Based on an Analytic Hierarchy Process and the PSO–LSSVM Model" Applied Sciences 10, no. 21: 7529. https://doi.org/10.3390/app10217529
APA StyleLi, Q., Wang, Y., Zhang, K., Cheng, Z., & Tao, Z. (2020). Life-Cycle Performance Assessment and Distress Prediction of Subgrade Based on an Analytic Hierarchy Process and the PSO–LSSVM Model. Applied Sciences, 10(21), 7529. https://doi.org/10.3390/app10217529






