Appointed-Time Integral Barrier Lyapunov Function-Based Trajectory Tracking Control for a Hovercraft with Performance Constraints
Abstract
1. Introduction
2. Preliminaries and Problem Description
2.1. Appointed-Time Performance Constraint Function
- (1)
- is a positive and decreasing function over the set ;
- (2)
- for all , where is a positive constant.
2.2. A New Integral Barrier Lyapunov Function
2.3. Dynamic Model of a Hovercraft
2.4. Problem Description
3. Control Design and Stability Analysis
3.1. Position Control
3.2. Surge Control
3.3. Sway Control
3.4. Yaw Control
3.5. Stability Analysis
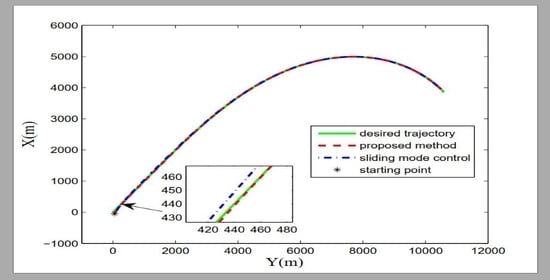
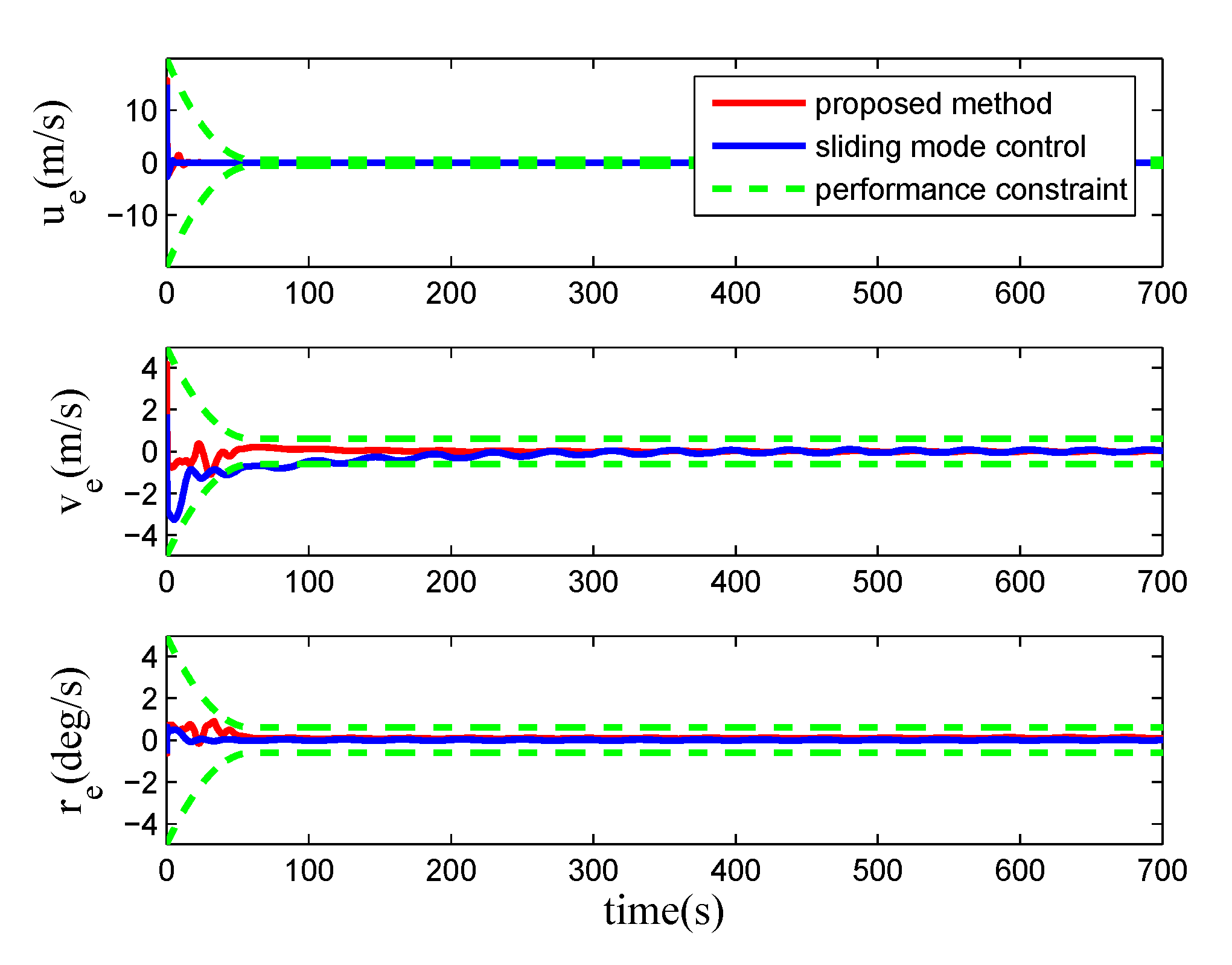
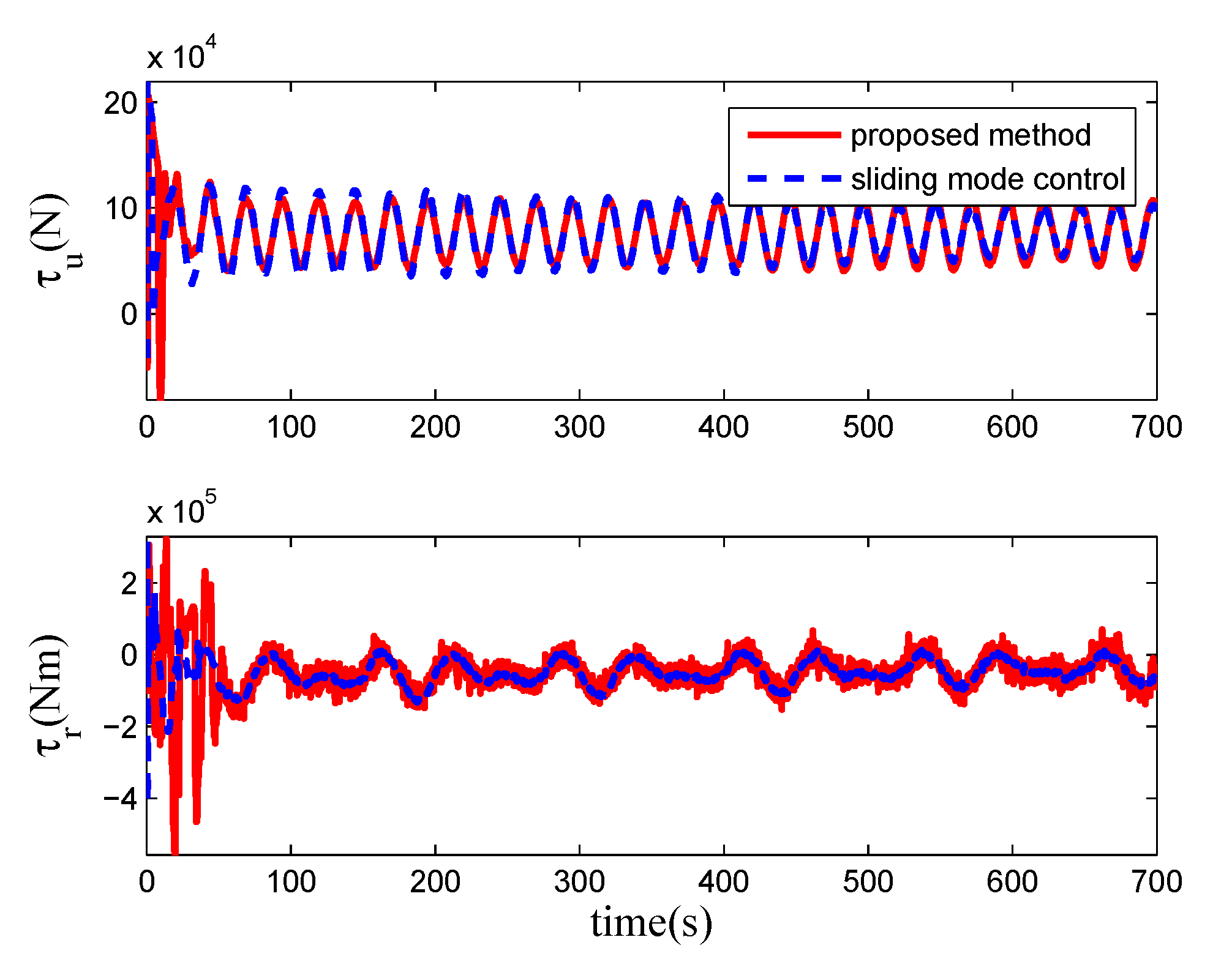
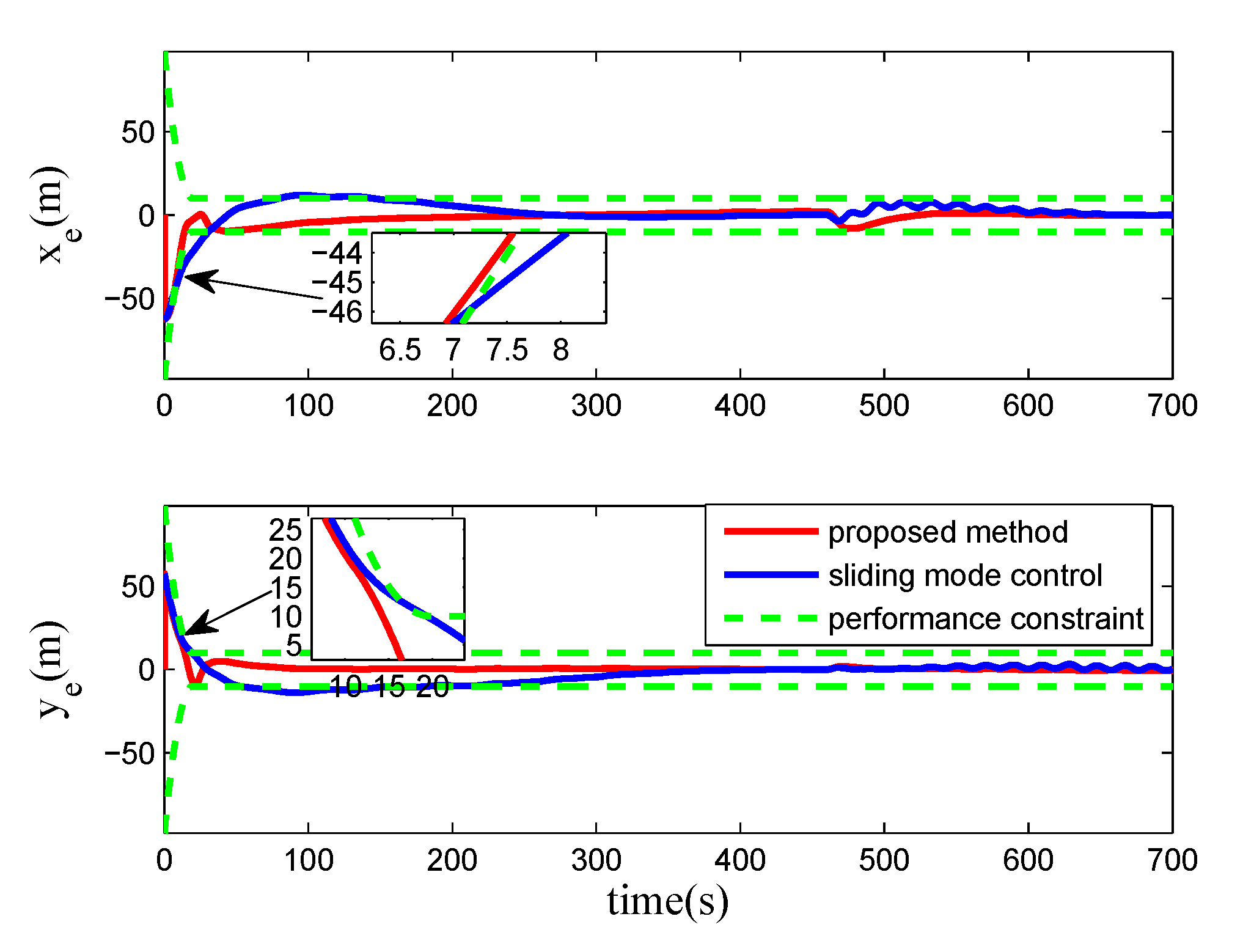
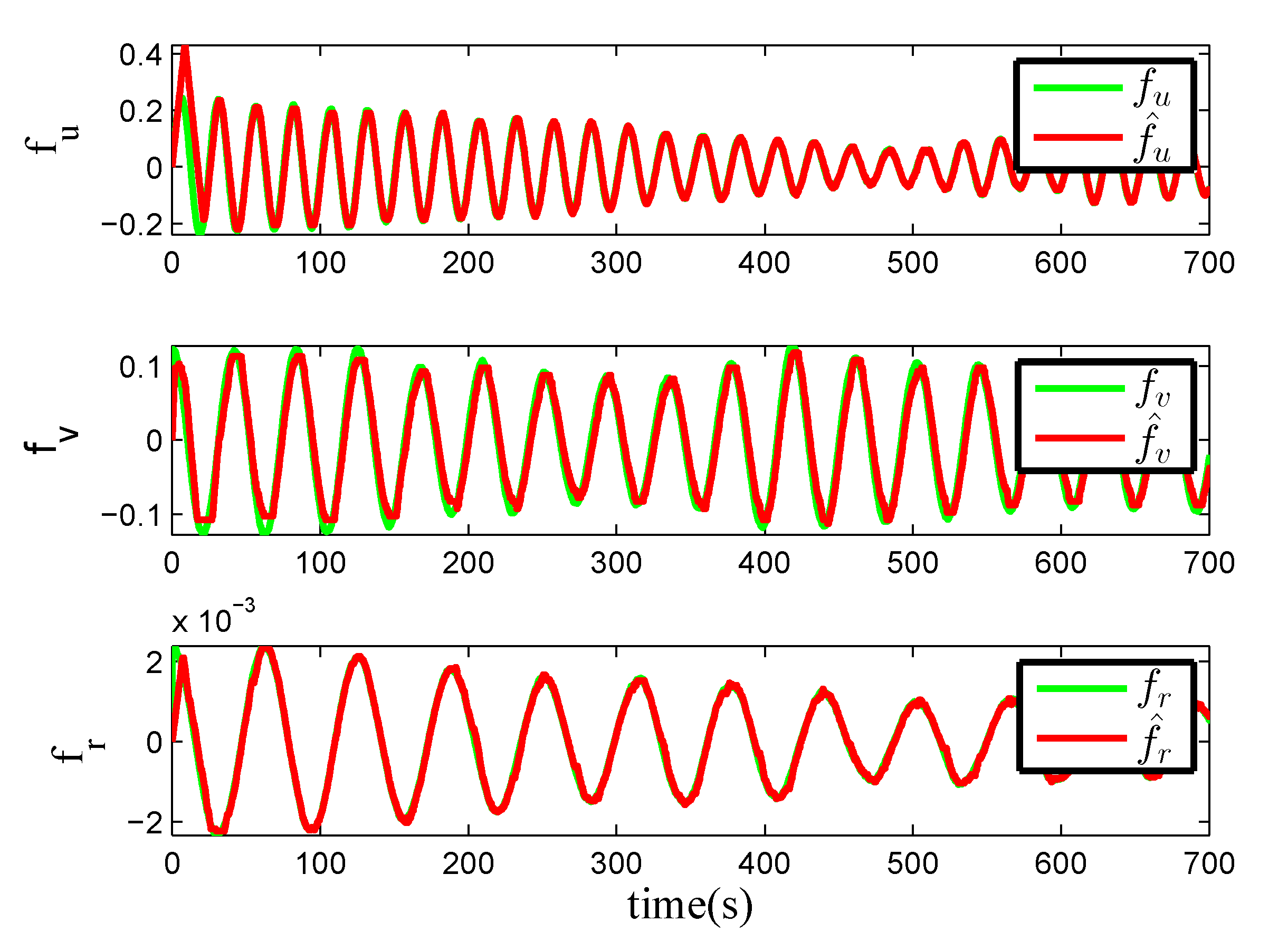
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yun, L.; Bliault, A. Theory and Design of Air Cushion Craft; Elsevier: Amsterdam, The Netherlands, 2000; pp. 458–486. [Google Scholar]
- Sun, Z.; Zhang, G.; Yang, J.; Zhang, W. Research on the sliding mode control for underactuated surface vessels via parameter estimation. Nonlinear Dyn. 2018, 91, 1163–1175. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Muske, K.R.; McNinch, L.C.; Soltan, R.A. Sliding-mode tracking control of surface vessels. IEEE Trans. Ind. Electron. 2008, 55, 4004–4012. [Google Scholar] [CrossRef]
- Li, T.; Zhao, R.; Chen, C.L.P.; Fang, L.; Liu, C. Finite-time formation control of under-actuated ships using nonlinear sliding mode control. IEEE Trans. Cybern. 2018, 48, 3243–3253. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Zhang, X.; Zheng, Y. Adaptive neural path-following control for underactuated ships in fields of marine practice. Ocean Eng. 2015, 104, 558–567. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X. Practical robust neural path following control for underactuated marine vessels with actuators uncertainties. Asian J. Control. 2017, 19, 173–187. [Google Scholar] [CrossRef]
- Ghommam, J.; Chemori, A. Adaptive RBFNN finite-time control of normal forms for underactuated mechanical systems. Nonlinear Dyn. 2017, 90, 301–315. [Google Scholar] [CrossRef]
- Lin, X.; Nie, J.; Jiao, Y.; Liang, K.; Li, H. Adaptive fuzzy output feedback stabilization control for the underactuated surface vessel. Appl. Ocean Res. 2018, 74, 40–48. [Google Scholar] [CrossRef]
- Qiu, D.; Wang, Q.; Yang, J.; She, J. Adaptive fuzzy control for path tracking of underactuated ships based on dynamic equilibrium state theory. Int. J. Comput. Intell. Syst. 2011, 4, 1148–1157. [Google Scholar] [CrossRef]
- Do, K.D. Global robust adaptive path-tracking control of underactuated ships under stochastic disturbances. Ocean Eng. 2016, 111, 267–278. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J.; Jiang, Z.P. Robust adaptive control of underactuated ships on a linear course with comfort. Ocean Eng. 2003, 30, 2201–2225. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Prescribed performance adaptive control for multi-input multi-output affine in the control nonlinear systems. IEEE Trans. Automat. Contr. 2010, 55, 1220–1226. [Google Scholar] [CrossRef]
- Wang, W.; Wen, C. Adaptive actuator failure compensation control of uncertain nonlinear systems with guaranteed transient performance. Automatica. 2010, 46, 2082–2091. [Google Scholar] [CrossRef]
- Wang, C.; Lin, Y. Adaptive dynamic surface control for MIMO nonlinear time-varying systems with prescribed tracking performance. Int. J. Control. 2015, 88, 832–843. [Google Scholar] [CrossRef]
- Bu, X.; Wu, X.; Huang, J.; Wei, D. Robust estimation-free prescribed performance back-stepping control of air-breathing hypersonic vehicles without affine models. Int. J. Control. 2016, 89, 2185–2200. [Google Scholar] [CrossRef]
- Psomopoulou, E.; Theodorakopoulos, A.; Doulgeri, Z.; Rovithakis, G.A. Prescribed performance tracking of a variable stiffness actuated robot. IEEE Trans. Control Syst. Technol. 2015, 23, 1914–1926. [Google Scholar] [CrossRef]
- Zheng, Z.; Feroskhan, M. Path following of a surface vessel with prescribed performance in the presence of input saturation and external disturbances. IEEE/ASME Trans. Mechatron. 2017, 22, 2564–2575. [Google Scholar] [CrossRef]
- Park, B.S.; Yoo, S.J. Robust fault-tolerant tracking with predefined performance for underactuated surface vessels. Ocean Eng. 2016, 115, 159–167. [Google Scholar] [CrossRef]
- Chen, L.; Cui, R.; Yang, C.; Yan, W. Adaptive neural network control of underactuated surface vessels with guaranteed transient performance: Theory and experimental results. IEEE Trans. Ind. Electron. 2020, 67, 4024–4035. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Karras, G.C.; Heshmati-Alamdari, S.; Kyriakopoulos, K.J. Trajectory tracking with prescribed performance for underactuated underwater vehicles under model uncertainties and external disturbances. IEEE Trans. Control Syst. Technol. 2017, 25, 429–440. [Google Scholar] [CrossRef]
- Fu, M.; Gao, S.; Wang, C.; Li, M. Human-centered automatic tracking system for underactuated hovercraft based on adaptive chattering-free full-order terminal sliding mode control. IEEE Access. 2018, 6, 37883–37892. [Google Scholar] [CrossRef]
- Jin, X. Adaptive fixed-time control for MIMO nonlinear systems with asymmetric output constraints ising iniversal barrier functions. IEEE Trans. Automat. Contr. 2019, 64, 3046–3053. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S. Control of state-constrained nonlinear systems using Integral Barrier Lyapunov Functionals. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3239–3244. [Google Scholar]
- Liu, N.; Shao, X.; Yang, W. Integral barrier lyapunov function based saturated dynamic surface control for vision-based quadrotors via back-stepping. IEEE Access. 2018, 6, 63292–63304. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, Y.; Yang, C.; Wang, M.; Annamalai, A. An improved adaptive online neural control for robot manipulator systems using integral Barrier Lyapunov functions. Int. J. Syst. Sci. 2019, 50, 638–651. [Google Scholar] [CrossRef]
- Kong, L.; He, W.; Yang, C.; Li, Z.; Sun, C. Adaptive fuzzy Control for coordinated multiple robots with constraint using impedance learning. IEEE Trans. Cybern. 2019, 49, 3052–3063. [Google Scholar] [CrossRef]
- Zhang, J. Integral barrier Lyapunov functions-based neural control for strict-feedback nonlinear systems with multi-constraint. Int. J. Control. Autom. Syst. 2018, 16, 2002–2010. [Google Scholar] [CrossRef]
- Liu, M.; Shao, X.; Ma, G. Appointed-time fault-tolerant attitude tracking control of spacecraft with double-level guaranteed performance bounds. Aerosp. Sci. Technol. 2019, 92, 337–346. [Google Scholar] [CrossRef]
- Fu, M.; Gao, S.; Wang, C.; Li, M. Design of driver assistance system for air cushion vehicle with uncertainty based on model knowledge neural network. Ocean Eng. 2019, 172, 296–307. [Google Scholar] [CrossRef]
- Chen, M.; Ge, S.S. Direct adaptive neural control for a class of uncertain nonaffine nonlinear systems based on disturbance observer. IEEE Trans. Cybern. 2013, 43, 1213–1225. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S. Control of nonlinear systems with partial state constraints using a barrier Lyapunov function. Int. J. Control. 2011, 84, 2008–2023. [Google Scholar] [CrossRef]
- Zheng, Z.; Sun, L.; Xie, L. Error-constrained LOS path following of a surface vessel with actuator saturation and faults. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 48, 1794–1805. [Google Scholar] [CrossRef]
- Fu, M.; Wang, T.; Wang, C. Barrier lyapunov function-based adaptive control of an uncertain hovercraft with position and velocity constraints. Math. Probl. Eng. 2019, 2019, 1–16. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, M.; Zhang, T.; Ding, F.; Wang, D. Appointed-Time Integral Barrier Lyapunov Function-Based Trajectory Tracking Control for a Hovercraft with Performance Constraints. Appl. Sci. 2020, 10, 7381. https://doi.org/10.3390/app10207381
Fu M, Zhang T, Ding F, Wang D. Appointed-Time Integral Barrier Lyapunov Function-Based Trajectory Tracking Control for a Hovercraft with Performance Constraints. Applied Sciences. 2020; 10(20):7381. https://doi.org/10.3390/app10207381
Chicago/Turabian StyleFu, Mingyu, Tan Zhang, Fuguang Ding, and Duansong Wang. 2020. "Appointed-Time Integral Barrier Lyapunov Function-Based Trajectory Tracking Control for a Hovercraft with Performance Constraints" Applied Sciences 10, no. 20: 7381. https://doi.org/10.3390/app10207381
APA StyleFu, M., Zhang, T., Ding, F., & Wang, D. (2020). Appointed-Time Integral Barrier Lyapunov Function-Based Trajectory Tracking Control for a Hovercraft with Performance Constraints. Applied Sciences, 10(20), 7381. https://doi.org/10.3390/app10207381