Asymmetries in the Technique and Ground Reaction Forces of Elite Alpine Skiers Influence Their Slalom Performance
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
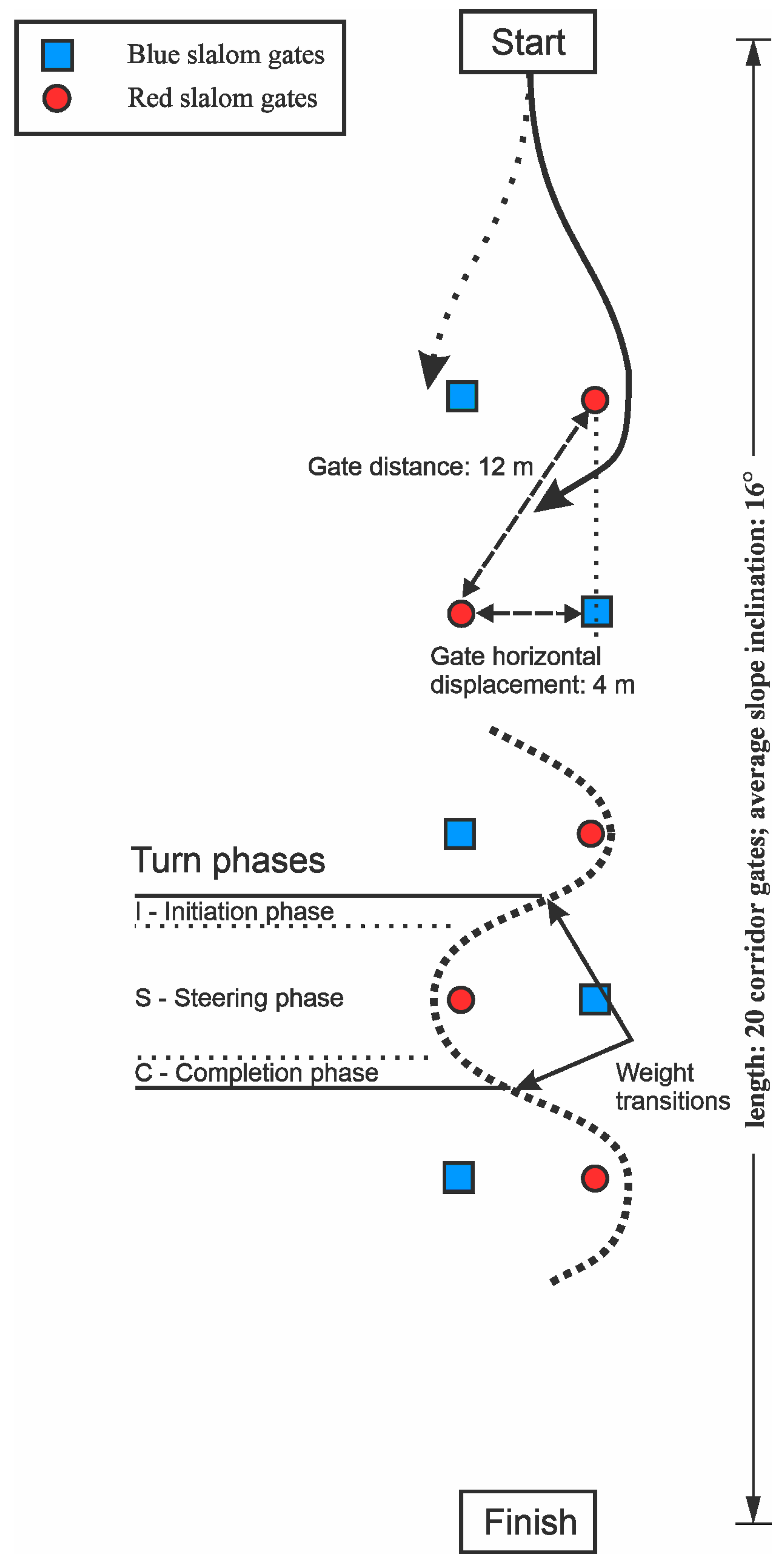
2.2. Experimental Setup
2.3. Computation
2.4. Statistical Analyses
3. Results
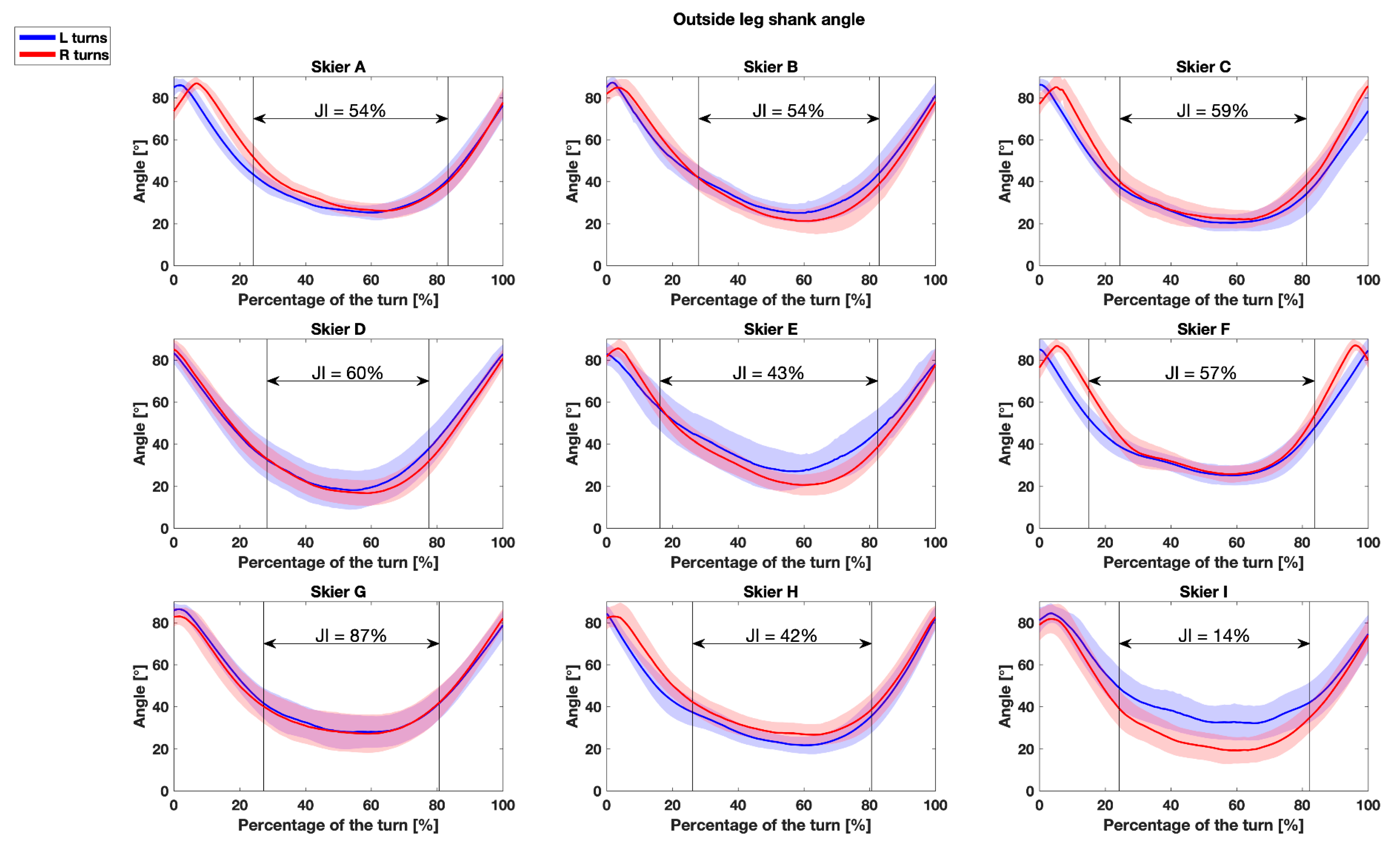
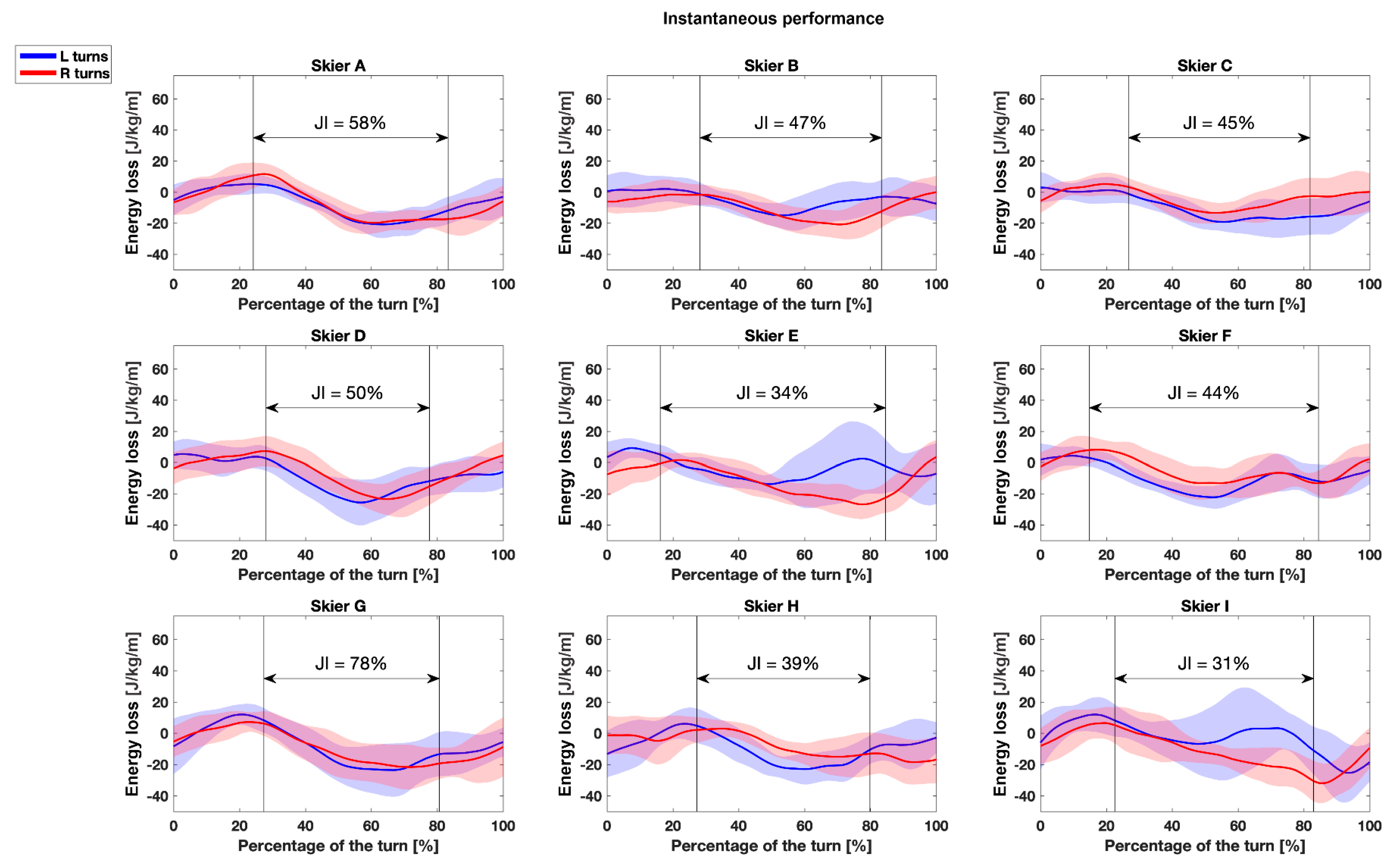
3.1. Descriptive Statistics, Symmetry and Jaccard Indices (SI and JI)
3.2. Multivariable Regression Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Supej, M.; Cernigoj, M. Relations between different technical and tactical approaches and overall time at men’s world cup giant slalom races. Kinesiol. Slov. 2006, 12, 63–69. [Google Scholar]
- Supej, M.; Holmberg, H.C. A new time measurement method using a high-end global navigation satellite system to analyze alpine skiing. Res. Q. Exerc. Sport 2011, 82, 400–411. [Google Scholar] [CrossRef] [PubMed]
- Fasel, B.; Spörri, J.; Kröll, J.; Müller, E.; Aminian, K. A Magnet-Based Timing Tystem to Detect Gate Crossings in Alpine Ski Racing. Sensors 2019, 19, 940. [Google Scholar] [CrossRef]
- Supej, M. Gate-to-Gate Synchronized Comparison of Velocity Retrieved from a High-End Global Navigation Satellite System in Alpine Skiing. In Proceedings of the 28th International Conference on Biomechanics in Sports, Melbourne, Australia, 2–6 July 2012. [Google Scholar]
- Supej, M.; Kipp, R.; Holmberg, H.C. Mechanical parameters as predictors of performance in alpine World Cup slalom racing. Scand. J. Med. Sci. Sports 2011, 21, e72–e81. [Google Scholar] [CrossRef] [PubMed]
- Hébert-Losier, K.; Supej, M.; Holmberg, H.C. Biomechanical factors influencing the performance of elite alpine ski racers. Sports Med. 2014, 44, 519–533. [Google Scholar] [CrossRef] [PubMed]
- Supej, M. Differential specific mechanical energy as a quality parameter in racing alpine skiing. J. Appl. Biomech. 2008, 24, 121–129. [Google Scholar] [CrossRef]
- Federolf, P.A. Quantifying instantaneous performance in alpine ski racing. J. Sports Sci. 2012, 30, 1063–1068. [Google Scholar] [CrossRef] [PubMed]
- Spörri, J.; Kröll, J.; Schwameder, H.; Müller, E. The role of path length- and speed-related factors for the enhancement of section performance in alpine giant slalom. Eur. J. Sport Sci. 2018, 18, 911–919. [Google Scholar] [CrossRef]
- Supej, M.; Nedergaard, N.J.; Nord, J.; Holmberg, H.C. The impact of start strategy on start performance in alpine skiing exists on flat, but not on steep inclines. J. Sports Sci. 2019, 37, 647–655. [Google Scholar] [CrossRef]
- Supej, M.; Holmberg, H.C. How gate setup and turn radii influence energy dissipation in slalom ski racing. J. Appl. Biomech. 2010, 26, 454–464. [Google Scholar] [CrossRef]
- Supej, M.; Kugovnik, O.; Nemec, B. New advances in racing slalom technique. Kinesiol. Slov. 2002, 8, 25–29. [Google Scholar]
- Supej, M.; Kugovnik, O.; Nemec, B. Modelling and simulation of two competition slalom techniques. Kinesiology 2004, 36, 206–212. [Google Scholar]
- Reid, R.C.; Haugen, P.; Gilgien, M.; Kipp, R.W.; Smith, G.A. Alpine Ski Motion Characteristics in Slalom. Front. Sports Act. Living 2020, 2. [Google Scholar] [CrossRef]
- Meyer, F.; Le Pelley, D.; Borrani, F. Aerodynamic drag modeling of alpine skiers performing giant slalom turns. Med. Sci. Sports Exerc. 2012, 44, 1109–1115. [Google Scholar] [CrossRef]
- Supej, M.; Sætran, L.; Oggiano, L.; Ettema, G.; Šarabon, N.; Nemec, B.; Holmberg, H.C. Aerodynamic drag is not the major determinant of performance during giant slalom skiing at the elite level. Scand. J. Med. Sci. Sports 2013, 23, e38–e47. [Google Scholar] [CrossRef]
- Gilgien, M.; Kröll, J.; Spörri, J.; Crivelli, P.; Müller, E. Application of dGNSS in alpine ski racing: Basis for evaluating physical demands and safety. Front. Physiol. 2018, 9, 145. [Google Scholar] [CrossRef]
- Federolf, P.; Scheiber, P.; Rauscher, E.; Schwameder, H.; Lüthi, A.; Rhyner, H.U.; Müller, E. Impact of skier actions on the gliding times in alpine skiing. Scand. J. Med. Sci. Sports 2008, 18, 790–797. [Google Scholar] [CrossRef] [PubMed]
- Maloney, S.J. The Relationship Between Asymmetry and Athletic Performance: A Critical Review. J. Strength Cond. Res. 2019, 33, 2579–2593. [Google Scholar] [CrossRef]
- Bell, D.R.; Sanfilippo, J.L.; Binkley, N.; Heiderscheit, B.C. Lean mass asymmetry influences force and power asymmetry during jumping in collegiate athletes. J. Strength Cond. Res. 2014, 28, 884–891. [Google Scholar] [CrossRef]
- Hoffman, J.R.; Ratamess, N.A.; Klatt, M.; Faigenbaum, A.D.; Kang, J. Do bilateral power deficits influence direction-specific movement patterns? Res. Sports Med. 2007, 15, 125–132. [Google Scholar] [CrossRef]
- Beck, O.N.; Azua, E.N.; Grabowski, A.M. Step time asymmetry increases metabolic energy expenditure during running. Eur. J. Appl. Physiol. 2018, 118, 2147–2154. [Google Scholar] [CrossRef]
- Vaverka, F.; Vodickova, S. Laterality of the lower limbs and carving turn. Biol.Sport 2010, 27, 129–134. [Google Scholar] [CrossRef]
- Supej, M. 3D measurements of alpine skiing with an inertial sensor motion capture suit and GNSS RTK system. J. Sports Sci. 2010, 28, 759–769. [Google Scholar] [CrossRef]
- Krüger, A.; Edelmann-Nusser, J. Application of a full body inertial measurement system in alpine skiing: A comparison with an optical video based system. J. Appl. Biomech. 2010, 26, 516–521. [Google Scholar] [CrossRef]
- Rauch, H.E.; Tung, F.; Striebel, C.T. Maximum likelihood estimates of linear dynamic systems. AIAA J. 1965, 3, 1445–1450. [Google Scholar] [CrossRef]
- Dempster, W.T. Space Requirements of the Seated Operator: Geometrical, Kinematic, and Mechanical Aspects of the Body with Special Reference to the Limbs; Wright Air Development Center: Wright-Patterson Air Force Base, OH, USA, 1955. [Google Scholar]
- Jaccard, P. Distribution florale dans une portio des Alpes du Jura. Bull. Soc. Vaud. Sc. Nat. 1901, 37, 547–579. [Google Scholar] [CrossRef]
- Gilgien, M.; Reid, R.; Raschner, C.; Supej, M.; Holmberg, H.C. The Training of Olympic Alpine Ski Racers. Front. Physiol. 2018, 9, 1772. [Google Scholar] [CrossRef]
- Supej, M.; Holmberg, H.C. Recent Kinematic and Kinetic Advances in Olympic Alpine Skiing: Pyeongchang and Beyond. Front. Physiol. 2019, 10, 111. [Google Scholar] [CrossRef]
- Steidl-Muller, L.; Hildebrandt, C.; Muller, E.; Fink, C.; Raschner, C. Limb symmetry index in competitive alpine ski racers: Reference values and injury risk identification according to age-related performance levels. J. Sport Health Sci. 2018, 7, 405–415. [Google Scholar] [CrossRef] [PubMed]
- Howe, J. The New Skiing Mechanics: Including the Technology of Short Radius Carved Turn Skiing and the Claw Ski; McIntire: Waterford, Ireland, 2001. [Google Scholar]
- Lind, D.A.; Sanders, S.P. The Physics of Skiing: Skiing at the Triple Point; Springer: New York, NY, USA, 2013. [Google Scholar]
- Federolf, P.; Roos, M.; Lüthi, A.; Dual, J. Finite element simulation of the ski–snow interaction of an alpine ski in a carved turn. Sports Eng. 2010, 12, 123–133. [Google Scholar] [CrossRef]
- Falda-Buscaiot, T.; Hintzy, F.; Rougier, P.; Lacouture, P.; Coulmy, N. Influence of slope steepness, foot position and turn phase on plantar pressure distribution during giant slalom alpine ski racing. PLoS ONE 2017, 12, e0176975. [Google Scholar] [CrossRef]
- Zorko, M.; Nemec, B.; Babic, J.; Lesnik, B.; Supej, M. The waist width of skis influences the kinematics of the knee joint in alpine skiing. J. Sports Sci. Med. 2015, 14, 606–619. [Google Scholar] [PubMed]
- Spörri, J.; Kröll, J.; Fasel, B.; Aminian, K.; Müller, E. Course setting as a prevention measure for overuse injuries of the back in alpine ski racing: A kinematic and kinetic study of giant slalom and slalom. Orthop. J. Sports Med. 2016, 4, 2325967116630719. [Google Scholar] [CrossRef] [PubMed]
- Spörri, J.; Kröll, J.; Fasel, B.; Aminian, K.; Müller, E. Standing Height as a Prevention Measure for Overuse Injuries of the Back in Alpine Ski Racing: A Kinematic and Kinetic Study of Giant Slalom. Orthop. J. Sports Med. 2018, 6, 2325967117747843. [Google Scholar] [CrossRef]
- Spörri, J.; Kröll, J.; Haid, C.; Fasel, B.; Müller, E. Potential mechanisms leading to overuse injuries of the back in alpine ski racing: A descriptive biomechanical study. Am. J. Sports Med. 2015, 43, 2042–2048. [Google Scholar] [CrossRef]
- Lüthi, A.; Federolf, M.; Fauve, M.; Oberhofer, K.; Rhyner, H.; Ammann, W.; Stricker, G.; Shiefermüller, C.; Eitzlmair, E.; Schwameder, H.; et al. Determination of forces in carving using three independent methods. In Science and Skiing III; Müller, E., Bacharach, D., Klika, R., Lindinger, S., Schwameder, H., Eds.; Meyer & Meyer Sport: Oxford, UK, 2005; pp. 96–106. [Google Scholar]
- Stricker, G.; Scheiber, P.; Lindenhofer, E.; Müller, E. Determination of forces in alpine skiing and snowboarding: Validation of a mobile data acquisition system. Eur. J. Sport Sci. 2010, 10, 31–41. [Google Scholar] [CrossRef]
- Supej, M.; Hébert-Losier, K.; Holmberg, H.C. Impact of the steepness of the slope on the biomechanics of World Cup slalom skiers. Int. J. Sports Physiol. Perform. 2015, 10, 361–368. [Google Scholar] [CrossRef]



| Variable | Left Turn | Right Turn | p-Value | SI [%] | JI [%] |
|---|---|---|---|---|---|
| Shank angle [ °] | |||||
| Outside leg | 30.8 ± 4.5 | 29.4 ± 4.6 | 0.49 | 93.8 ± 5.4 | 52.2 ± 19.5 |
| Inside leg | 33.2 ± 3.8 | 34.2 ± 2.4 | 0.84 | 92.8 ± 4.0 | 41.5 ± 16.2 |
| Knee flexion [ °] | |||||
| Outside leg | 46.99 ± 8.9 | 52.20 ± 7.2 | 0.11 | 92.5 ± 4.4 | 28.7 ± 24.3 |
| Inside leg | 85.73 ± 9.3 | 81.25 ± 9.9 | 0.34 | 96.1 ± 2.2 | 39.1 ± 21.7 |
| Hip flexion [ °] | |||||
| Outside leg | 37.4 ± 3.3 | 28.02 ± 3.0 | 0.70 | 95.71 ± 2.2 | 53.35 ± 14.9 |
| Inside leg | 71.8 ± 4.4 | 68.79 ± 5.5 | 0.22 | 97.52 ± 1.7 | 50.64 ± 15.5 |
| GRF (pressure insoles) [% BW] On the entire foot | |||||
| Outside leg | 126.2 ± 19.2 | 113.6 ± 21.6 | 0.21 | 92.9 ± 4.7 | 56.1 ± 18.9 |
| Inside leg | 66.8 ± 7.4 | 76.0 ± 10.0 | 0.04 | 91.4 ± 5.7 | 56.0 ± 19.6 |
| On the fore foot [% BW] | |||||
| Outside leg | 62.5 ± 20.6 | 58.7 ± 26.85 | 0.75 | 88.4 ± 8.4 | 47.2 ± 21.6 |
| Inside leg | 27.4 ± 9.2 | 37.8 ± 17.6 | 0.14 | 85.1 ± 10.1 | 42.7 ± 23.2 |
| On the rear foot [% BW] | |||||
| Outside leg | 63.8 ± 7.7 | 54.9 ± 16.6 | 0.17 | 87.8 ± 7.3 | 51.6 ± 14.4 |
| Inside leg | 39.4 ± 9.13 | 38.6 ± 15.8 | 0.85 | 85.8 ± 15.2 | 52.9 ± 23.2 |
| GRF * | |||||
| Overall [% BW] | 287.5 ± 26.3 | 283.7 ± 17.5 | 0.72 | 98.2 ± 1.1 | 71.3 ± 2.7 |
| Dependent Variable | Left Turn | Right Turn | p-Value | SI [%] | JI [%] |
|---|---|---|---|---|---|
| Time | |||||
| Turning time [s] | 0.87 ± 0.03 | 0.87 ± 0.03 | 0.68 | 97.5 ± 1.7 | n/a |
| Trajectory | |||||
| Turning length [m] | 12.61 ± 0.30 | 12.51 ± 0.39 | 0.59 | 97.9 ± 1.5 | n/a |
| Turningradius[m] | 9.34 ± 0.44 | 9.32 ± 0.52 | 0.95 | 97.6 ± 1.5 | 56.1 ± 18.9 |
| Velocity | |||||
| Average velocity [m/s] | 14.5 ± 0.42 | 14.5 ± 0.37 | 0.97 | 99.6 ± 0.00 | n/a |
| Energy associated with | |||||
| Instantaneous performance [J/kg/m] | −10.69 ± 4.67 | −10.51 ± 2.98 | 0.92 | 70.6 ± 23.0 | 47.3 ± 14.1 |
| Sectional performance [Js/kg/m] | −1.90 ± 0.39 | −1.87 ± 0.50 | 0.91 | 84.2 ± 13.7 | n/a |
| Dependent Variables → Independent Variables ↓ | SI for Turning Time | SI for Turning Length | JI for Turning n Radius | SI for Turning Radius | SI for Average Velocity | SI for Instantaneous Performance | SI for Sectional Performance |
|---|---|---|---|---|---|---|---|
| Shank angle | |||||||
| JI for outside leg | - | - | 0.33 **,#4 | - | - | - | - |
| SI for outside leg | - | - | - | - | - | 3.97 ***,#10 | 3.01 **,#13 |
| JI for inside leg | 0.08 *,#1 | 0.07 **,#2 | - | - | - | - | - |
| SI for inside leg | - | - | - | - | - | 5.77 **,#11, 7.16 **,#12 | - |
| Hip flexion | |||||||
| JI for outside leg | - | - | - | −0.10 *,#5 | 0.01 *,#6 | - | - |
| SI for outside leg | - | - | - | - | 0.09 *,#7 | 8.33 *,#12 | - |
| GRF on entire foot a | |||||||
| JI for GRF outside leg | - | - | 0.25 *,#4 | - | - | - | - |
| SI for GRF outside leg | - | - | - | 0.46 **,#5 | - | - | - |
| SI for GRF inside leg | 0.14 *,#1 | 0.13 **,#2, 0.11 *,#3 | - | - | - | - | - |
| JI for GRF inside leg | - | - | - | - | - | - | 0.56 *,#13 |
| GRF on rear foot a | |||||||
| JI for outside leg | - | - | - | - | −0.02 **,#8 | −1.03 **,#11 | - |
| SI for GRF outside leg | - | - | - | - | −0.03 **,#9 | - | - |
| Overall GRF b | |||||||
| JI | - | 0.16 *,#3 | - | - | - | - | - |
| SI | - | - | - | - | 0.10 *,#6, 0.12 **,#7, 0.15 **,#8, 0.16 **,#9 | - | - |
| R2 | 0.72 *,#1 | 0.80 **,#2, 0.75 *,#3 | 0.80 **,#4 | 0.74 *,#5 | 0.73 *,#6, 0.81 **,#7, 0.84 **,#8, 0.83 **,#9 | 0.86 ***,#10, 0.82 **,#11, 0.84 **,#12 | 0.76 **,#13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Supej, M.; Ogrin, J.; Šarabon, N.; Holmberg, H.-C. Asymmetries in the Technique and Ground Reaction Forces of Elite Alpine Skiers Influence Their Slalom Performance. Appl. Sci. 2020, 10, 7288. https://doi.org/10.3390/app10207288
Supej M, Ogrin J, Šarabon N, Holmberg H-C. Asymmetries in the Technique and Ground Reaction Forces of Elite Alpine Skiers Influence Their Slalom Performance. Applied Sciences. 2020; 10(20):7288. https://doi.org/10.3390/app10207288
Chicago/Turabian StyleSupej, Matej, Jan Ogrin, Nejc Šarabon, and Hans-Christer Holmberg. 2020. "Asymmetries in the Technique and Ground Reaction Forces of Elite Alpine Skiers Influence Their Slalom Performance" Applied Sciences 10, no. 20: 7288. https://doi.org/10.3390/app10207288
APA StyleSupej, M., Ogrin, J., Šarabon, N., & Holmberg, H.-C. (2020). Asymmetries in the Technique and Ground Reaction Forces of Elite Alpine Skiers Influence Their Slalom Performance. Applied Sciences, 10(20), 7288. https://doi.org/10.3390/app10207288







