1. Introduction
Network representation learning (NRL) is a crucial task in social and information network analysis. The idea of NRL is to learn a mapping function that converts each node into a low-dimensional embedding space while preserving the structural proximity between nodes in the given network. The derived node embedding vectors can be utilized for downstream tasks, including node classification, link prediction, and community detection. Typical NRL methods include DeepWalk [
1], LINE [
2], and node2vec [
3], which consider structural neighborhood to depict every node. Metapath2vec [
4] extends the skip-gram based NRL to heterogeneous information networks that contain multiple types of nodes and links. DANE [
5] incorporates the similarity between node attributes into NRL. GCN [
6] further learns node embeddings for semi-supervised node classification through a layer-wise propagation with graph convolution.
Regarding the typical NRL approaches [
1,
2,
3] that preserve structural proximity in node embeddings, we think there are two major insufficiencies. First, every node is only aware of its few-hop neighbors by random walk sampling, which push them to be close in the embedding space. Nevertheless, as illustrated in the general node embedding space in
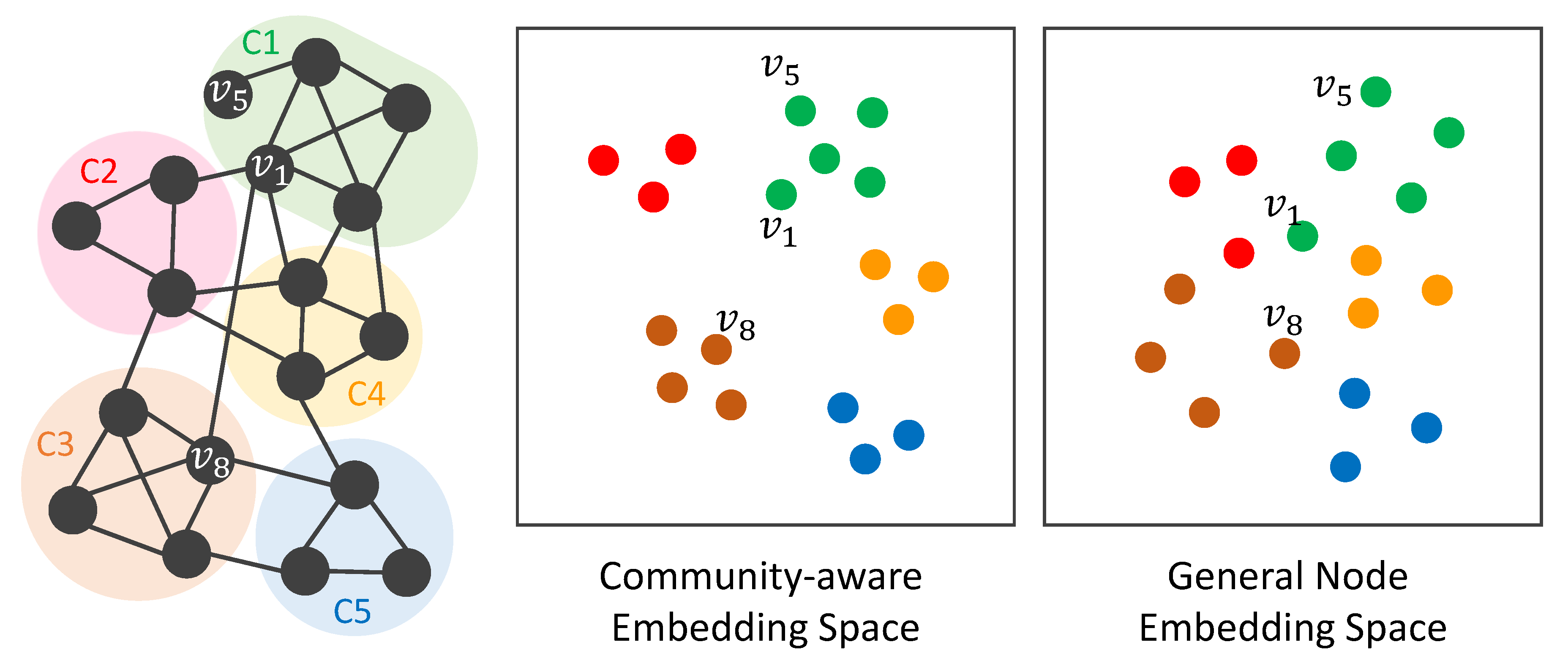
Figure 1, non-neighbor nodes (
) being pushed away by negative sampling could still have some connections with the target node (
), e.g., belonging to the same network community (C1). In addition, neighbor nodes (
) sampled by random walks being pushed together could have weak connections to the target node (
), e.g., belonging to different communities (C1 and C3). In other words, community-level information cannot be incorporated into the learning of node embeddings. We think network communities can inform nodes to better recognize which nodes should better push together and away, as shown in the community-aware embedding space in
Figure 1. Second, the given graph depicts only the fine-grained interactions between nodes. As shown in
Figure 1, the given graph is a collaboration network, and thus the links depict co-authorships. The coarse-grained semantics, including how authors involve in different research areas and belong to different institutes, together with their interactions, is not aware by typical NRL approaches. We think encoding coarse-grained semantics can improve the effectiveness of node embeddings.
In this paper, we propose a novel framework, Structural Hierarchy Enhancement (SHE), to enhance the effectiveness of network representation learning. The main idea is two-fold. First, we construct a structural hierarchy that depicts both fine-grained and coarse-grained semantics of nodes and their interactions. We consider that node semantics is depicted by communities (i.e., clusters of nodes), and thus utilize community detection techniques to produce the structural hierarchy. By learning the embeddings of nodes in different levels of the hierarchy, our model will be capable of encoding multiple different views of each node. Hence, the semantics of nodes can be enriched, and nodes can be better distinguished from one another in the embedding space. Second, we utilize such a hierarchy to enhance NRL. Our SHE can be seamlessly applied to enhance any of existing typical NRL models mentioned above. Besides, any existing and state-of-the-art hierarchical community detection algorithm can be applied to generate the hierarchy. In other words, our SHE model provides great flexibility to be compatible with different combinations of NRL methods and community detection techniques.
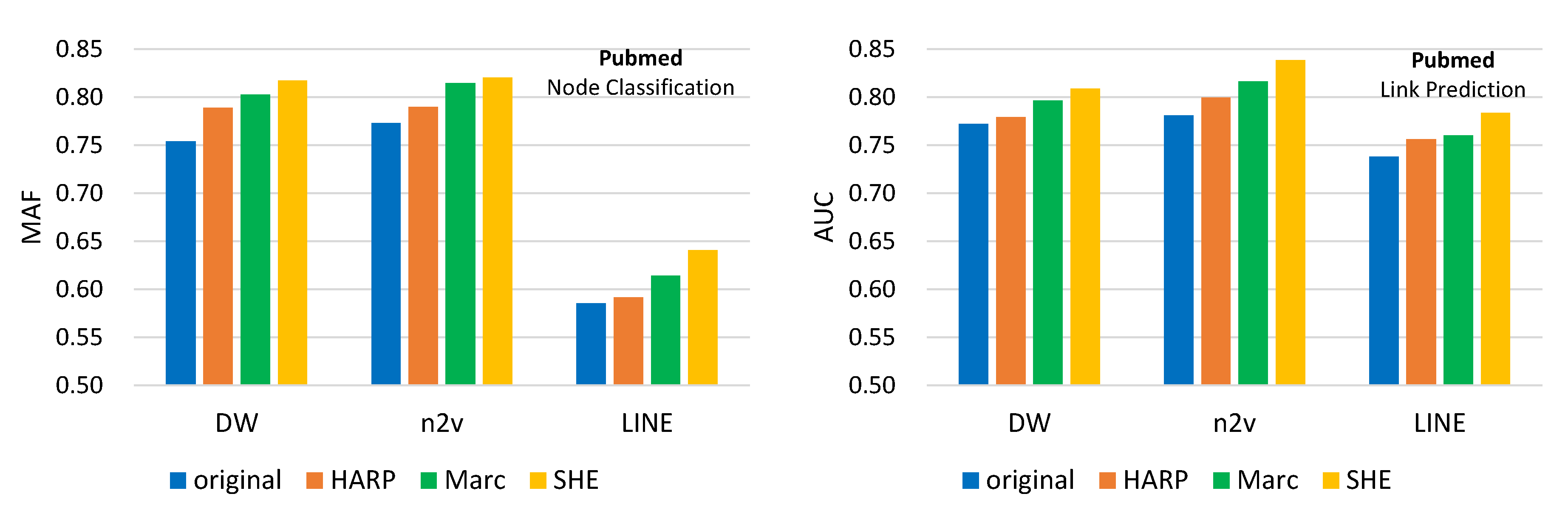
Related Work. The most relevant studies are HARP [
7] and Marc [
8], which are hierarchical NRL methods. HARP collapses nodes according to edge and star connections so that the hierarchy can be constructed for NRL. Marc iteratively consider 3-cliques as super nodes to construct the hierarchy. However, community knowledge in networks is not considered in both HARP and Marc. Besides, different-level’s node embeddings are learned independently in HARP and Marc. That said, higher-level NRL cannot utilize node embeddings derived from lower-level NRL. We will compare the proposed SHE with HARP and Marc in the experiments. As for NRLs using various hierarchical information, NetHiex [
9] assumes each node is associated with a category, and categories form a hierarchical taxonomy, which is used for NRL. HRE [
10] uses the relational hierarchy that comes from edge attributes for heterogeneous NRL. MINES [
11] models multi-dimensional relations between different node types, along with their hierarchical connections, into the embeddings of users and items for recommender systems. Poincare [
12] specializes NRL for graphs whose nodes naturally form a hierarchical structure. DiffPool [
13] classifies graphs by learning their embeddings based on differentiable pooling applied to hierarchical groups of nodes. While these studies presume a variety of additional hierarchical information, i.e., category taxonomy, edge attributes, edge relations, hierarchical graph, and node groups, is accessible, our work does not rely on any of them.
3. The Proposed SHE-NRL Model
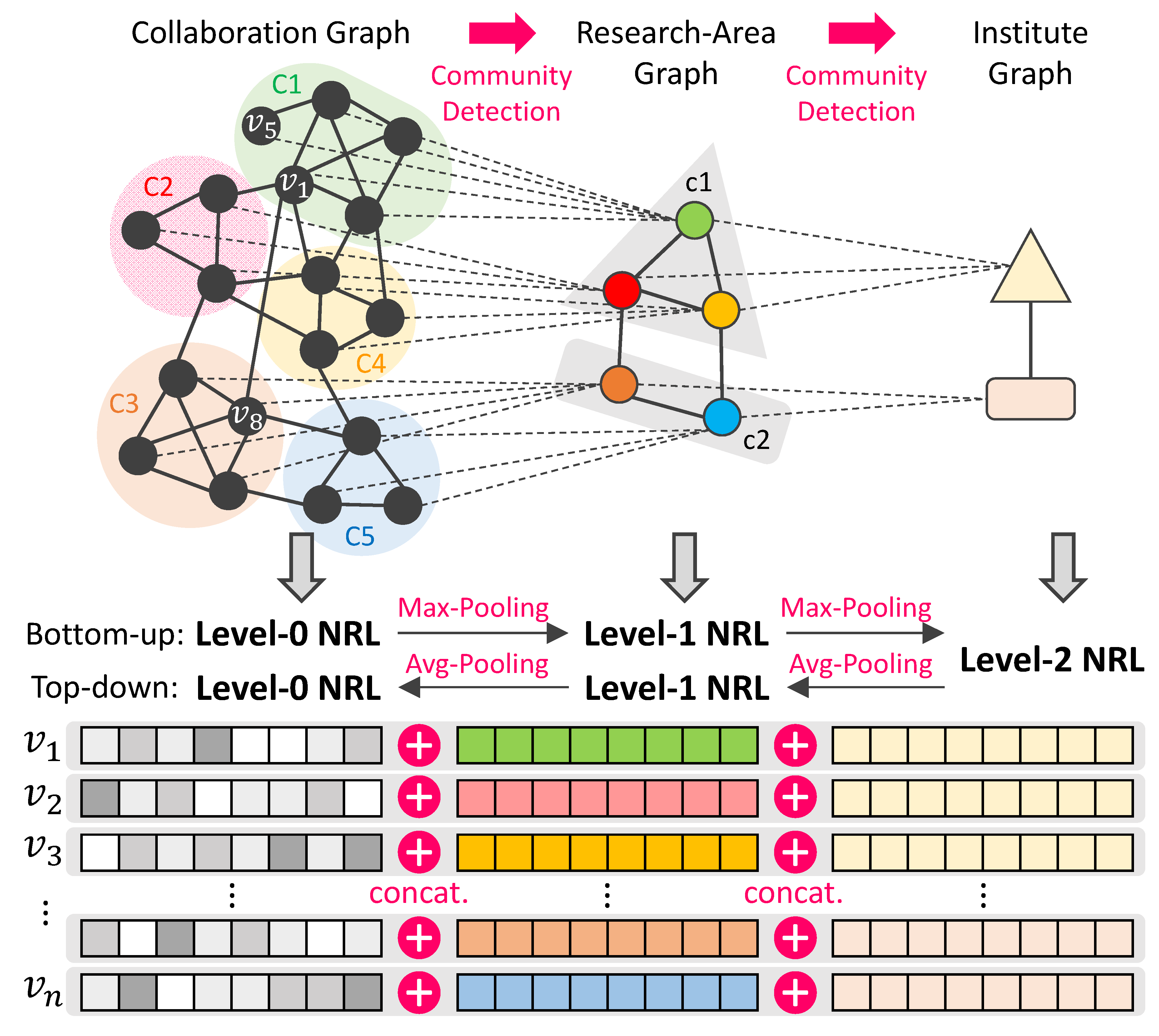
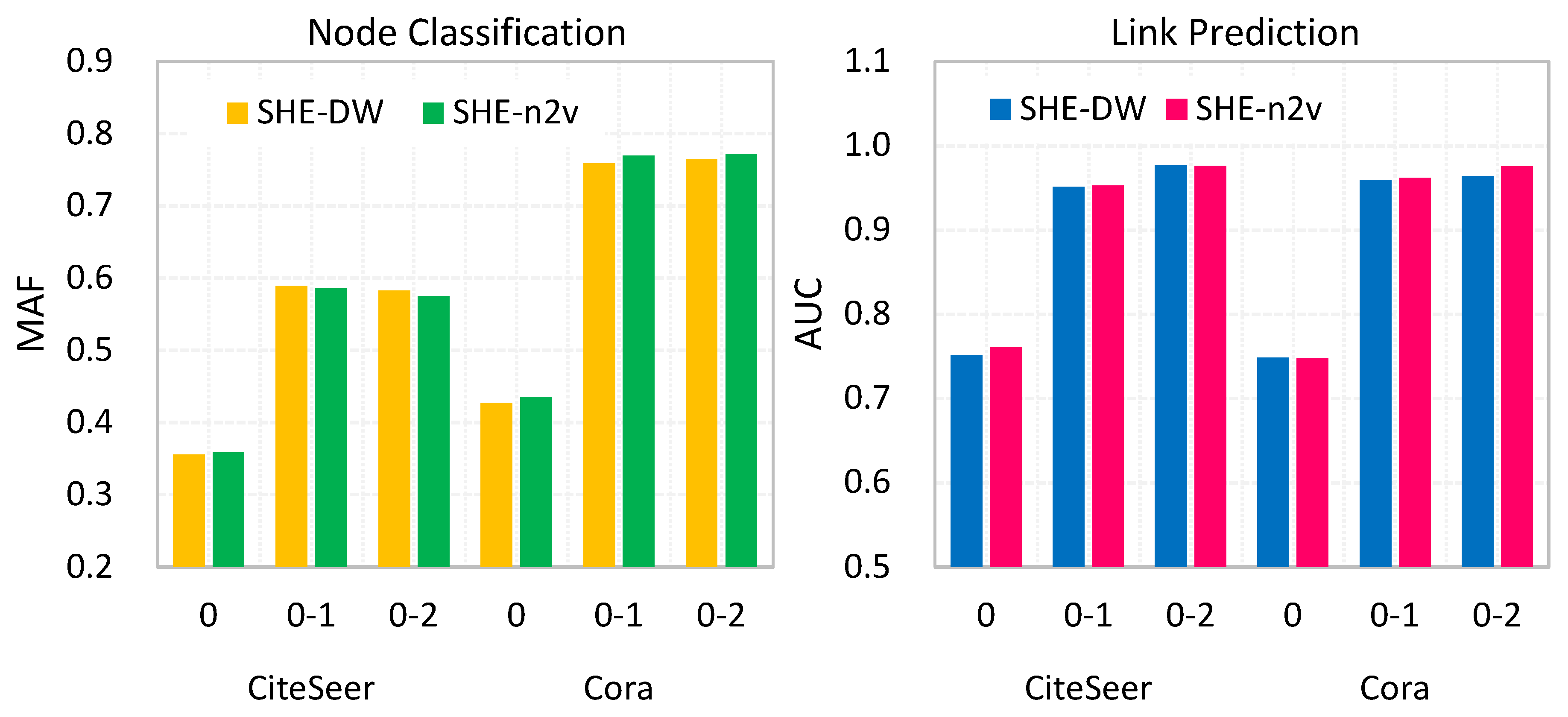
The proposed SHE-NRL consists of four phases: (1) construction of structural hierarchy, (2) intra-level NRL, (3) level-wise pooling mechanism, and (4) generating final node embeddings. We first elaborate these four phases based on
Figure 2. First, we construct the structural hierarchy by performing network community detection algorithm from lower- to higher-level graphs. Second, an existing or state-of-the-art NRL method is performed at the level-
h graph (the original graph is level-0 graph) to generate level-
h node embeddings. Third, a level-wise pooling mechanism is utilized to aggregate level-
h node embeddings to not only initialize the level-
node embeddings for its NRL in a bottom-up manner, but also to initialize the level-
node embeddings for level-
NRL in a top-down manner. The second and third phases are performed iteratively until the highest level of the hierarchy is reached. Lastly, the final node embeddings can be produced by concatenating node embeddings at different levels based on their community memberships.
Phase 1: Construction of Structural Hierarchy. The structural hierarchy
is constructed from a network
G. By applying a certain community detection algorithm to level-
h graph
, we can obtain a set of communities (i.e., node sets)
, where
is the number of communities in
, and
is the
i-th community. These communities are treated as nodes at level-
graph
, given by:
where
is the set of edges that connect communities. For every pair of communities
and
, we create an edge
to connect them in
if there exists at least one edge between nodes in
and nodes in
in
. To adaptively determine the number of communities
for every graph
, we utilize Louvain [
14] algorithm for community detection. We do not pre-define the number of levels
in the hierarchy, but continue to produce
from
until
, where
is a hyperparameter controlling the height of the hierarchy. We set
by default. In other words, we will not generate level-
graph
if the number of nodes
in
is lower than
. In other words, the hyperparameter
is the minimum number of communities at the last (highest) level of the hierarchy, rather than the hierarchy height. Another hyperparameter
, described in Phase 2, is the hierarchy height. The
is automatically determined by repeatedly generating new communities from the previous level’s graph until
, where
is the number of communities in level-
h’s graph
.
Phase 2: Intra-level NRL. Given level-
h graph
, we perform intra-level NRL. We allow any of NRL methods that preserves structural proximity between nodes in our SHE-NRL framework. That said, typical NRL methods, such as DeepWalk [
1], LINE [
2], and node2vec [
3], can be used for intra-level NRL. Let
be the generated embedding matrix for all nodes in
. The intra-level NRL is iteratively performed in a one-round circular manner. The bottom-up way is first executed, followed by the top-down way. Specifically, the intra-level NRL is performed one after another from
,
to
, i.e., the bottom-up way. Then we again iteratively perform the intra-level NRL from
,
to
, i.e., the top-down way. The bottom-up way brings fine-grained level’s interactions between nodes into the intra-level NRLs at higher levels in the hierarchy. The top-down way of message passing makes the intra-level NRLs at lower levels be aware of coarse-grained community knowledge. All intra-level NRLs at level-
h graphs
(
) are executed twice while the level-
NRL is executed only one time. In the next phase, we will discuss how
can be used to initialize the node embeddings of graphs
and
. We randomly initialize the embeddings of nodes for NRL in the original graph
.
Phase 3: Level-wise Pooling Mechanism. In order to bring fine-grained information of node interactions into higher-level NRLs, and make lower-level NRLs be aware of coarse-grained community knowledge at higher levels of the hierarchy, we propose the level-wise pooling mechanism. The pooling mechanism consists of bottom-up pooling and top-down pooling. The bottom-up pooling utilizes the node embeddings
of
to initialize the node embeddings of
’s NRL. The max pooling is adopted as the bottom-up pooling. The max pooling is performed to initialize the embedding of node
at
from the corresponding
i-th community
at
. We exploit the most significant learned node embedding in community
at
to be the initial node embedding of node
at
. On the other hand, the average pooling is adopted as the top-down pooling. The average pooling is performed to initialize the embeddings of all nodes in the
i-th community
at
from the learned node embedding of node
at
. That said, given the new-learned node embedding of node
at
, denoted by
, and the previously-generated embedding of corresponding lower-level node
at
, denoted by
, we have the new initial embedding of node
, denoted by
, based on the equation:
Utilizing the average pooling for the top-down way of NRLs is able to distribute coarse-grained community knowledge back to the NRLs at lower-level graphs. Note that we utilize two different letters v and u here is to better distinguish nodes at different levels, i.e., v refers to a node at level h and u refers to a node at level .
Phase 2 and Phase 3 are iteratively adopted one after the other in first the bottom-up way, then the top-down way. In other words, in the bottom-up way, when node embeddings are generated by NRL in (Phase 2), they are immediately brought to initialize the embeddings of nodes in via max pooling (Phase 3). In the top-down way, when node embeddings are produced by NRL in (Phase 2), they are instantaneously employed to initialize the embeddings of nodes in via average pooling (Phase 3).
We utilize
Figure 2 to better elaborate the interweaved process between Phase 2 and Phase 3 in an alternative view. In this paragraph, that said, we will describe the bottom-up process, followed by the top-down process. Given the structural hierarchy, consisting of three graphs at different levels, i.e.,
,
, and
, in the bottom-up process, we first perform a typical NRL method on
and obtain node embedding
for every
. Then we apply max pooling on nodes, which belong to the same level-1 community, to initialize the embedding of each level-1 community node in
. We again apply the same NRL method to
to obtain node embedding for every level-1 community node, and use max pooling to initialize each level-2 community node in
. Then NRL method is applied again on
. Next, we are doing the top-down process. We utilize average pooling in Equation (
2) to initialize level-1 community node embedding from level-2 community node embedding. Then the NRL method is applied to
, followed by performing average pooling to initialize node embeddings in
. The last NRL is executed on
to generate the embeddings of nodes in the original graph.
Phase 4: Generating Final Node Embeddings. Equipped with the derived node embedding matrix at every level-h graph, we can generate the final embeddings for all nodes in the original network G (i.e., ). To let final node embeddings contain both fine-grained and coarse-grained information, the concatenation operation is adopted. We concatenate the embedding vector of node v in with all of its corresponding higher-level embedding vectors in , where . Suppose the dimension of each level’s node embedding is equal and denoted as b. The dimension of final node embeddings will be .
Note that it is apparent that there can be alternative approaches, such as the operators of average, Hadamard, and weighted-L2 [
3], to fuse node embeddings at different levels of the hierarchy. We leave the design of better embedding aggregation for future investigation.
Remark. Two of the important ideas in the proposed SHE-NRL model are the bottom-up and top-down correlations on embedding vectors. If we first generate node embeddings for every level from to , then apply the top-down corrections, our model can encounter a critical issue—missing the interactions and connections between levels. Bottom-up and top-down correlations are to bring the fine-grained semantics encoded by lower-level node embeddings to higher-levels ones, and to deliver the coarse-grained semantics to lower-level nodes, respectively. Such a design follows the realistic intuition that, for an example in the university, a graduate student is depicted by her advisor, her college, and her school in order. We need to make the advisor recognize that student, and make the college see the advisor, and so on. By doing so, through the immediate correction of vectors in level based on the vectors, the node embeddings can better encode the semantics, and become more robust.