Relationship between Aspect Ratio and Crack Density in Porous-Cracked Rocks Using Experimental and Optimization Methods
Abstract
1. Introduction
2. Background Theory
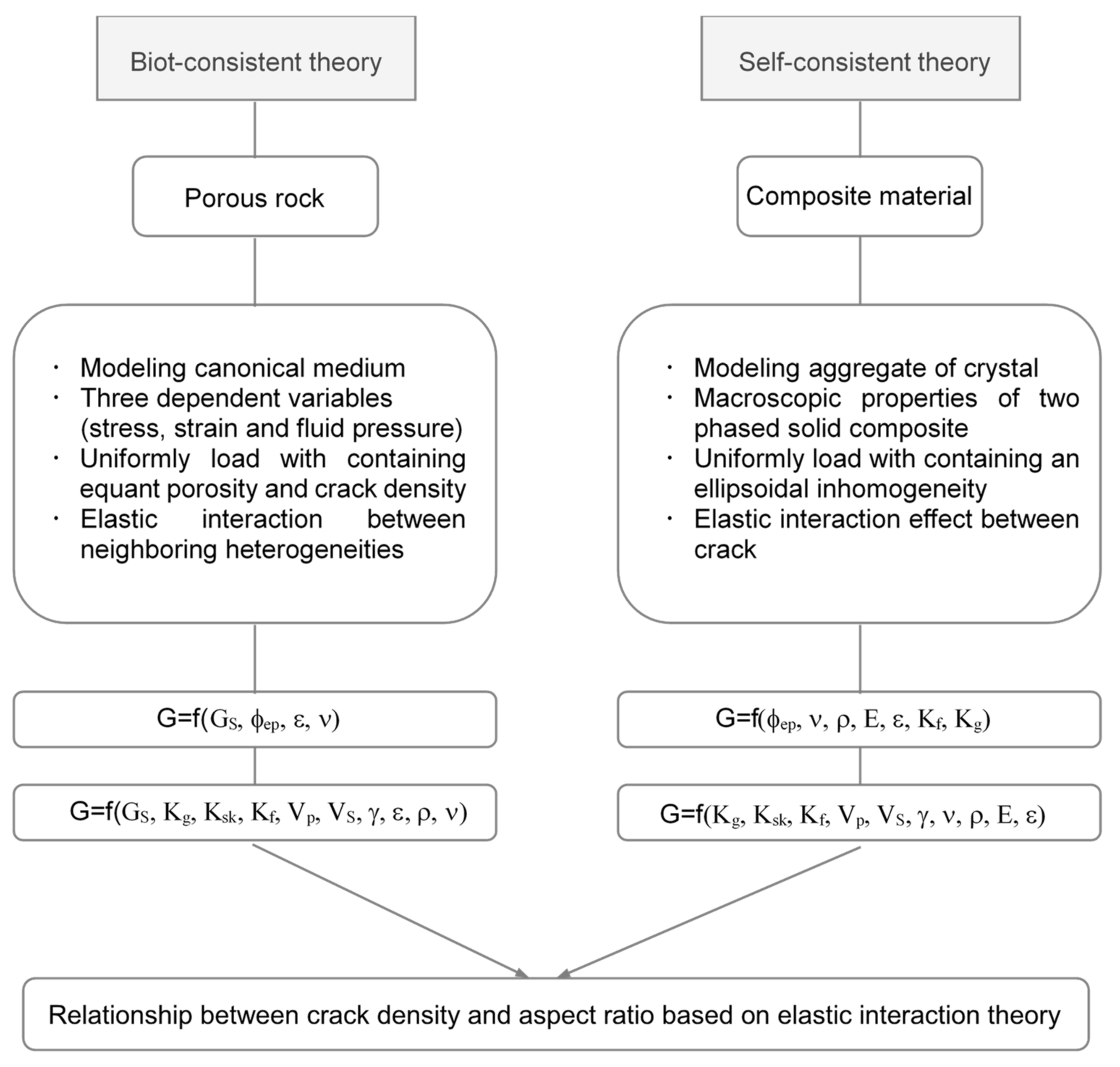
2.1. Aspect Ratio and Crack Density
2.2. Random Forest Algorithm
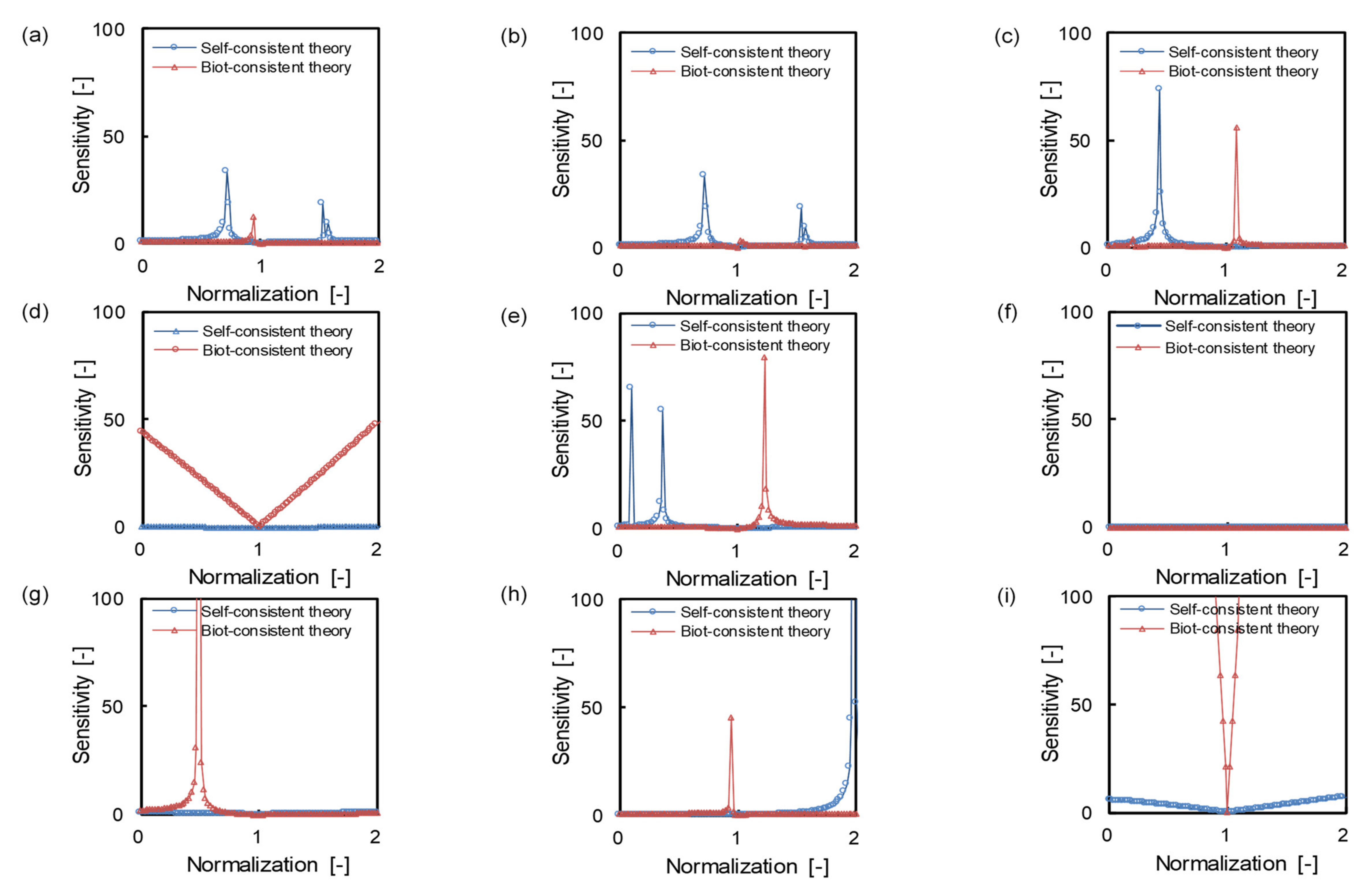
2.3. Sensitivity Analysis of Each Theory
3. Methodology
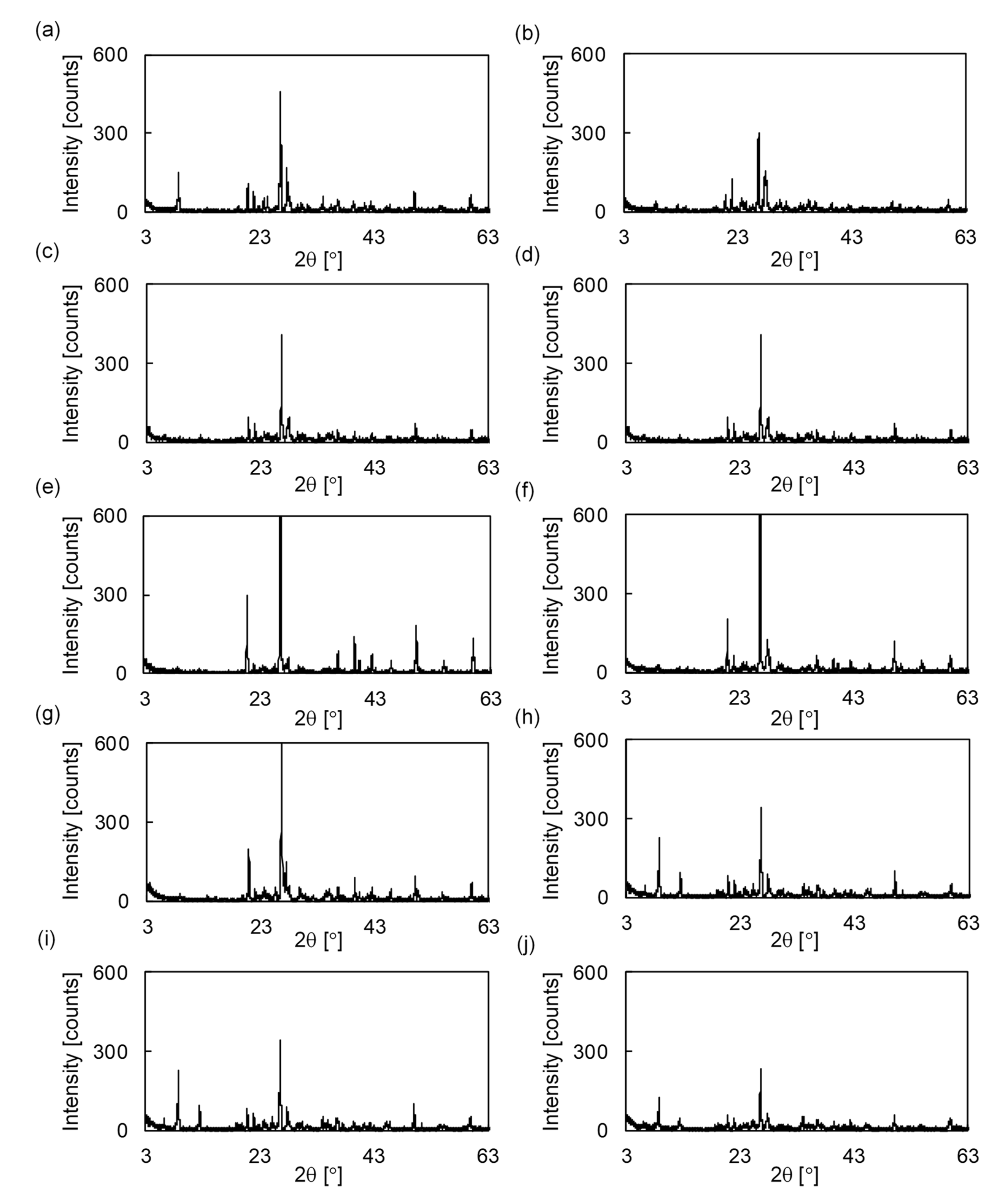
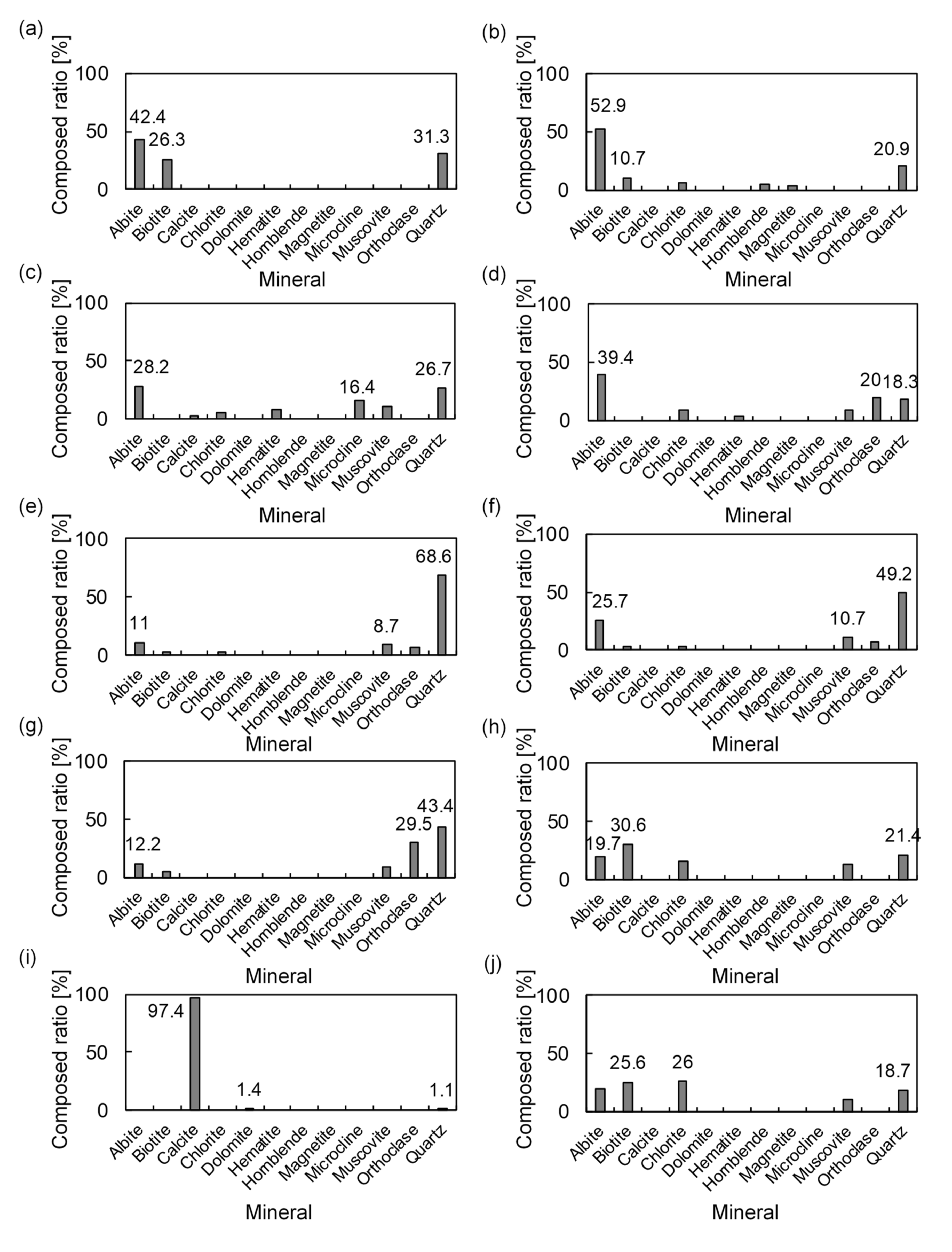
3.1. Rock Sample Characterization
3.2. Weathering Experiments
3.3. Measurement Techniques
4. Results and Discussion
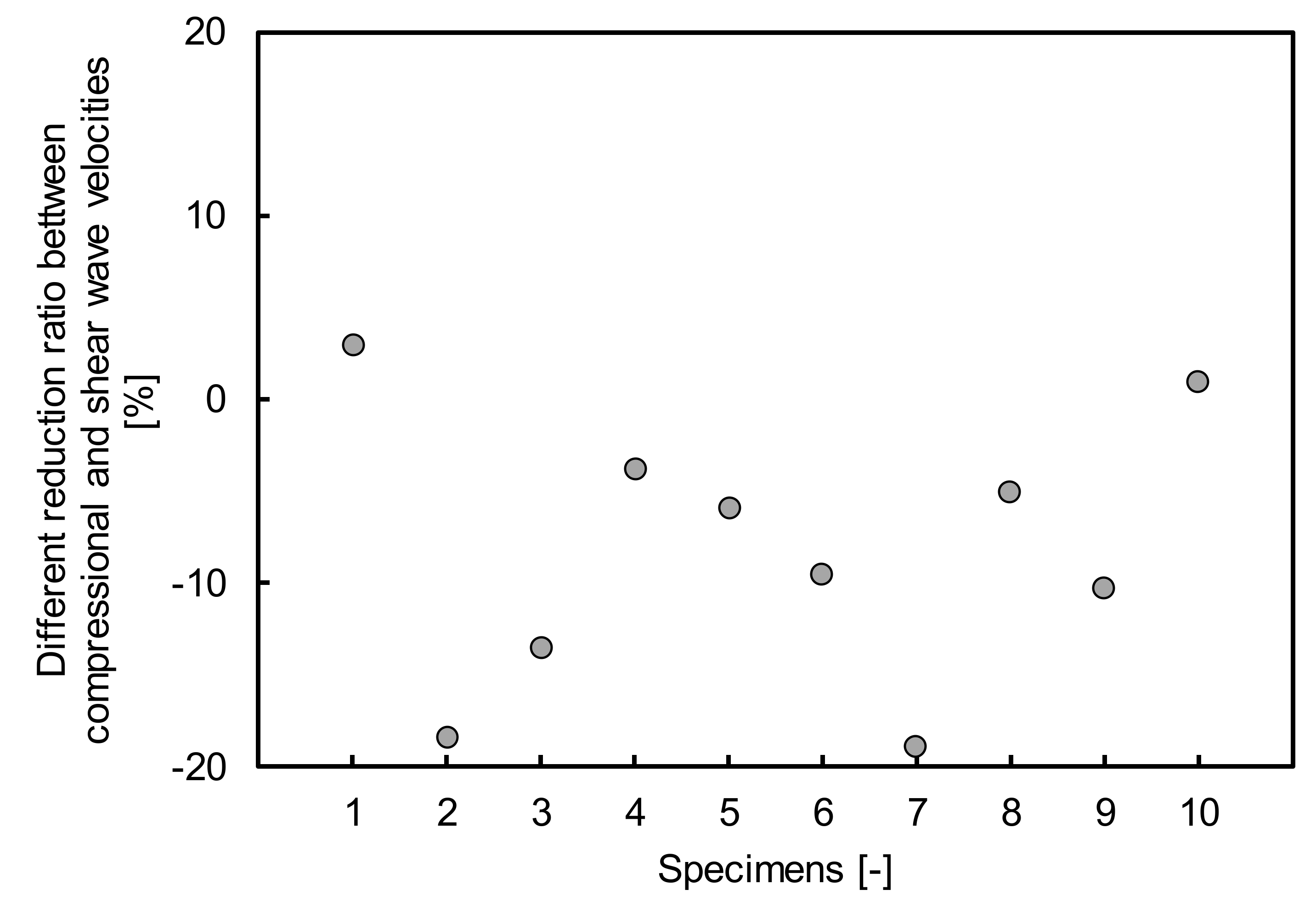
4.1. Elastic Wave Velocity
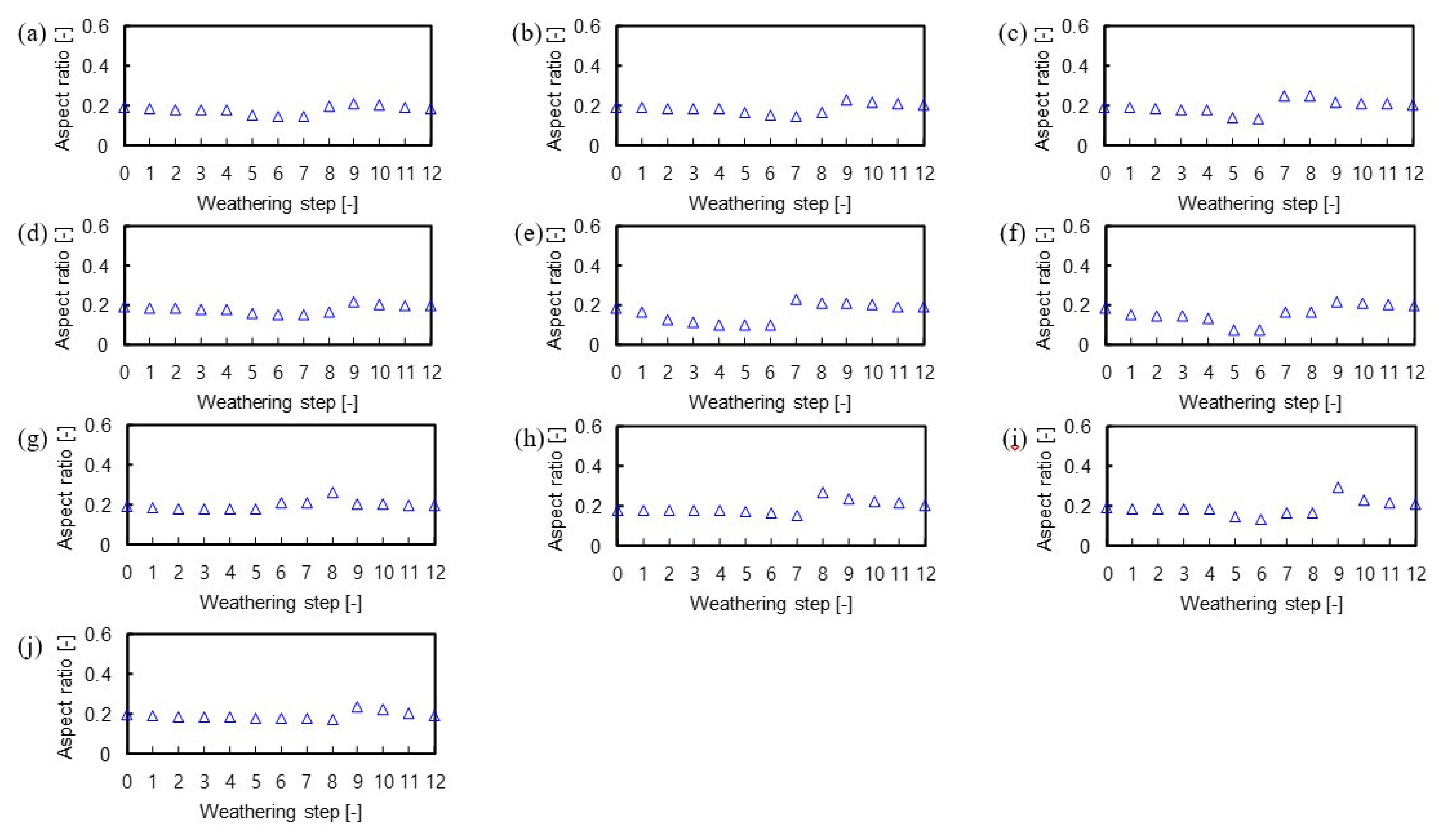
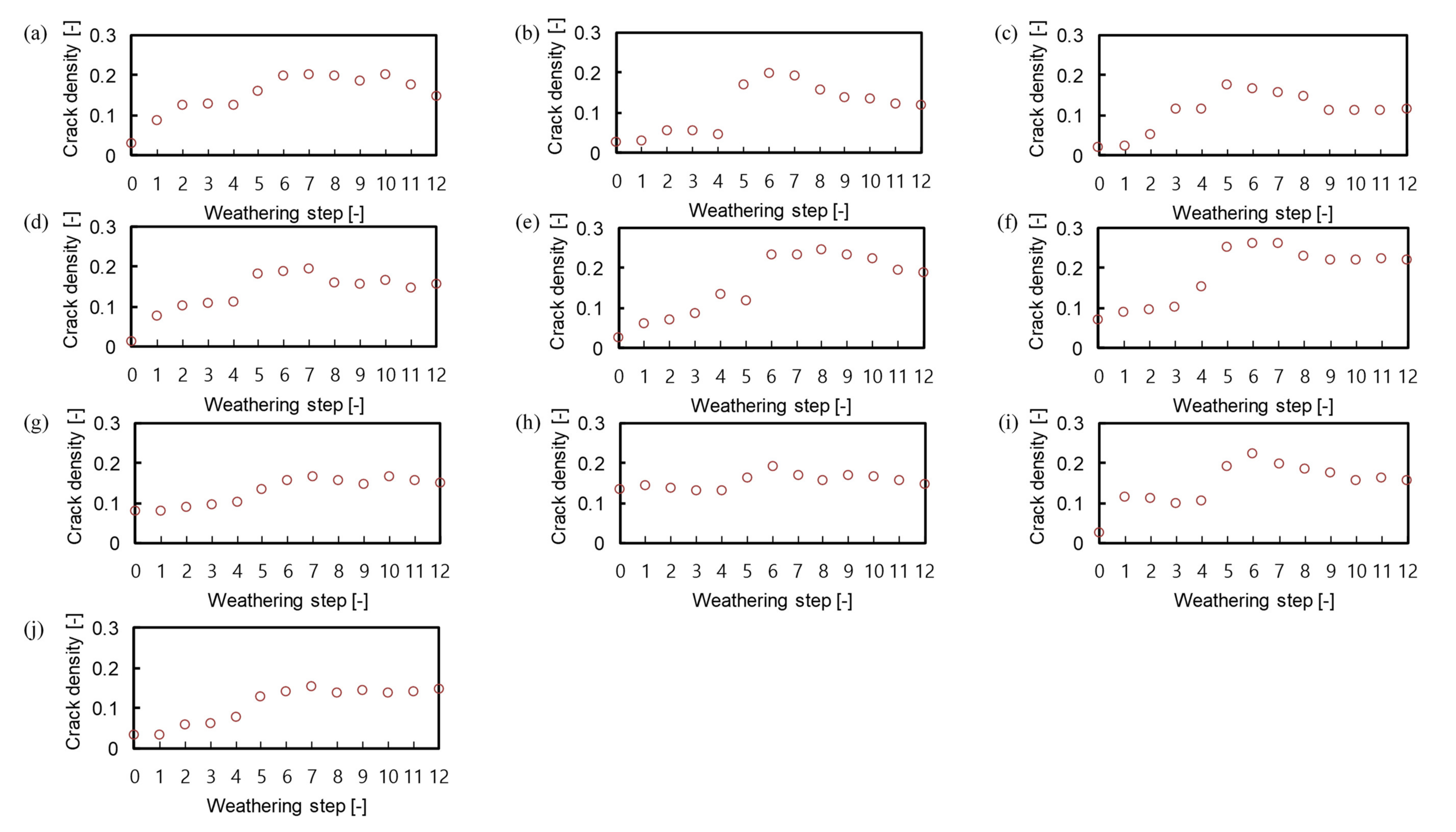
4.2. Quantifying Aspect Ratio and Crack Density
4.3. Importance of Each Variable Based on Random Forest
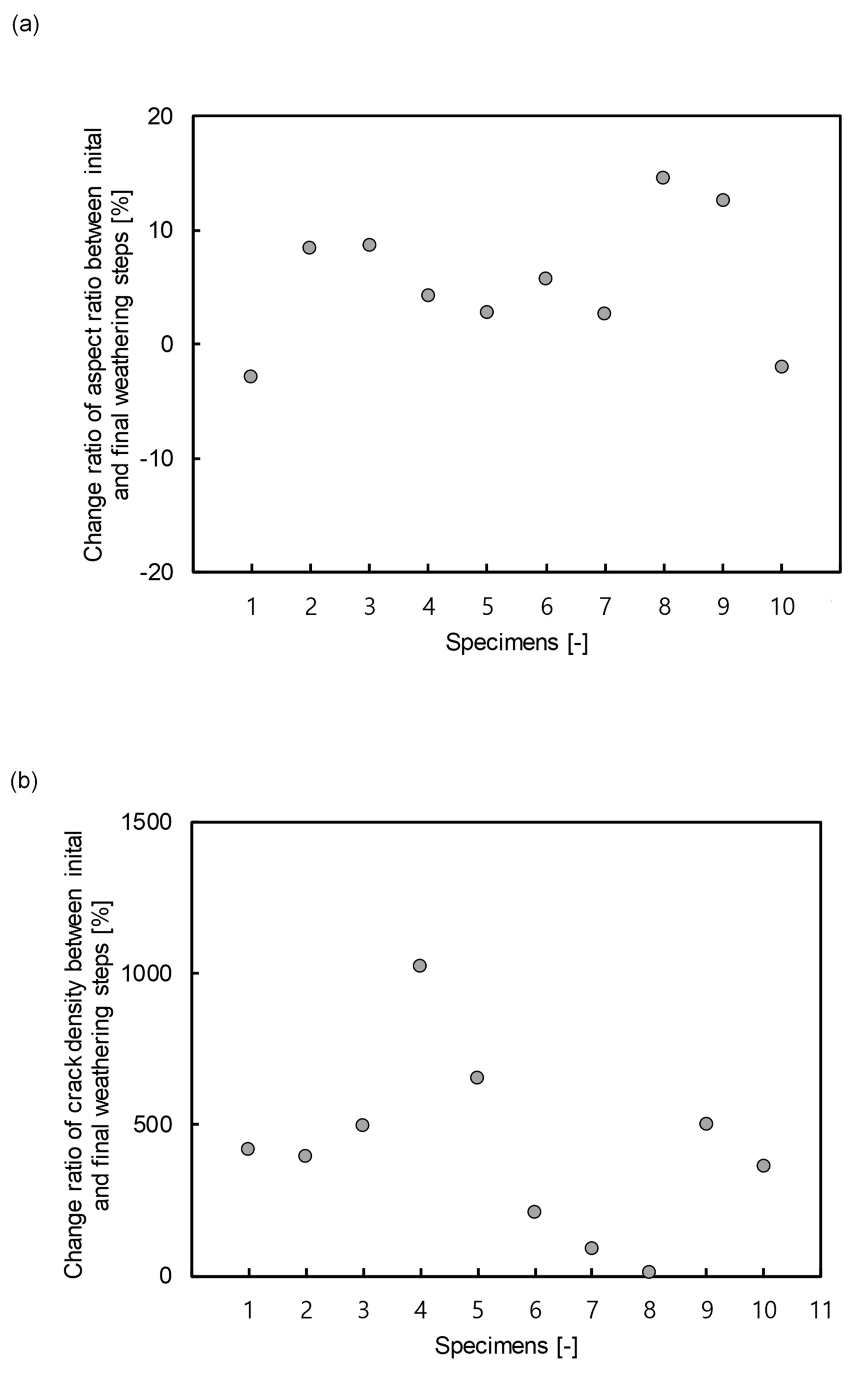
4.4. Relationship between Aspect Ratio and Crack Density
4.5. Verification
5. Conclusions
- Various parameters included in two constitutive equations were rearranged and simplified to define elastic wave velocity, with aspect ratio and crack density as the main variables to be solved.
- Ten rock columns were each subjected to three chemical and nine physical experimental weathering cycles. The elastic wave velocity was continually measured in each column, allowing predictions of their evolving aspect ratio and crack density.
- The reliability of the calculated aspect ratio and crack density data was verified by measuring the ratio of crack porosity to total porosity. These data allowed for the formulation of a relationship between aspect ratio and crack density that may be applied to a broad spectrum of samples.
Funding
Conflicts of Interest
References
- Tuǧrul, A. The effect of weathering on pore geometry and compressive strength of selected rock types from Turkey. Eng. Geol. 2004, 75, 215–227. [Google Scholar] [CrossRef]
- Wang, P.; Xu, J.; Liu, S.; Wang, H.; Liu, S. Static and dynamic mechanical properties of sedimentary rock after freeze-thaw or thermal shock weathering. Eng. Geol. 2016, 210, 148–157. [Google Scholar] [CrossRef]
- Palmstrom, A. RMi-a Rock Mass Characterization System for Rock Engineering Purposes. Ph.D. Thesis, University of Oslo, Oslo, Norway, 1995. [Google Scholar]
- Byun, J.H.; Lee, J.S.; Park, K.; Yoon, H.K. Prediction of crack density in porous-cracked rocks from elastic wave velocities. J. Appl. Geophys. 2015, 115, 110–119. [Google Scholar] [CrossRef]
- Nasseri, M.H.B.; Schubnel, A.; Young, R.P. Coupled evolutions of fracture toughness and elastic wave velocities at high crack density in thermally treated Westerly granite. Int. J. Rock Mech. Min. Sci. 2007, 44, 601–616. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Bristow, J.R. Microcracks, and the static and dynamic elastic constants of annealed and heavily cold-worked metals. Br. J. Appl. Phys. 1960, 11, 81. [Google Scholar] [CrossRef]
- Walsh, J.B. New analysis of attenuation in partially melted rock. J. Geophys. Res. 1969, 74, 4333–4337. [Google Scholar] [CrossRef]
- Garbin, H.D.; Knopoff, L. The compressional modulus of a material permeated by a random distribution of circular cracks. Q. Appl. Math. 1973, 30, 453–464. [Google Scholar] [CrossRef]
- Budiansky, B.; O’Connell, R.J. Elastic moduli of a cracked solid. Int. J. Solids Struct. 1976, 12, 81–97. [Google Scholar] [CrossRef]
- Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Berryman, J.G. Long-wavelength propagation in composite elastic media II. Ellipsoidal inclusions. J. Acoust. Soc. Am. 1980, 68, 1820–1831. [Google Scholar] [CrossRef]
- Adelinet, M.; Fortin, J.; Guéguen, Y. Dispersion of elastic moduli in a porous-cracked rock: Theoretical predictions for squirt-flow. Tectonophysics 2011, 503, 173–181. [Google Scholar] [CrossRef]
- Tang, X. A unified theory for elastic wave propagation through porous media containing cracks—An extension of Biot’s poroelastic wave theory. Sci. China Earth Sci. 2011, 54, 1441. [Google Scholar] [CrossRef]
- Comert, R.; Avdan, U.; Gorum, T.; Nefeslioglu, H.A. Mapping of shallow landslides with object-based image analysis from unmanned aerial vehicle data. Eng. Geol. 2019, 260, 105264. [Google Scholar] [CrossRef]
- Đurić, U.; Marjanović, M.; Radić, Z.; Abolmasov, B. Machine learning based landslide assessment of the Belgrade metropolitan area: Pixel resolution effects and a cross-scaling concept. Eng. Geol. 2019, 256, 23–38. [Google Scholar] [CrossRef]
- Lü, Q.; Chan, C.L.; Low, B.K. Probabilistic evaluation of ground-support interaction for deep rock excavation using artificial neural network and uniform design. Tunn. Undergr. Space Technol. 2012, 32, 1–18. [Google Scholar] [CrossRef]
- Sudakov, O.; Burnaev, E.; Koroteev, D. Driving digital rock towards machine learning: Predicting permeability with gradient boosting and deep neural networks. Comput. Geosci. 2019, 127, 91–98. [Google Scholar] [CrossRef]
- Karimpouli, S.; Tahmasebi, P. Segmentation of digital rock images using deep convolutional autoencoder networks. Comput. Geosci. 2019, 126, 142–150. [Google Scholar] [CrossRef]
- Mills, G.; Fotopoulos, G. Rock surface classification in a mine drift using multiscale geometric features. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1322–1326. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Du, X.; Tang, X. Prediction of open stope hangingwall stability using random forests. Nat. Hazards 2018, 92, 1179–1197. [Google Scholar] [CrossRef]
- Biot, M.A. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. 1962, 33, 1482–1498. [Google Scholar] [CrossRef]
- Biot, M.A.; Willis, D.G. The elastic coeff cients of the theory of consolidation. J. Appl. Mech. 1957, 24, 594–601. [Google Scholar]
- Hershey, A.V. The elasticity of an isotropic aggregate of anisotropic cubic crystals. J. Appl. Mech. Trans. ASME 1954, 21, 236–240. [Google Scholar]
- Kröner, E. Berechnung der elastischen Konstanten des Vielkristalls aus den Konstanten des Einkristalls. Z. für Phys. 1958, 151, 504–518. [Google Scholar] [CrossRef]
- Kachanov, M. Elastic solids with many cracks and related problems. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1993; Volume 30, pp. 259–445. [Google Scholar]
- Zhang, J.J.; Bentley, L.R. Pore geometry and elastic moduli in sandstones. CREWES Res. Rep. 2003, 115, 1–20. [Google Scholar]
- Lee, J.S.; Yoon, H.K. Theoretical relationship between elastic wave velocity and electrical resistivity. J. Appl. Geophys. 2015, 116, 51–61. [Google Scholar] [CrossRef]
- Breiman, L. Random forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.Y.; Jin, Y.F.; Chan, T.H. A novel hybrid surrogate intelligent model for creep index prediction based on particle swarm optimization and random forest. Eng. Geol. 2020, 265, 105328. [Google Scholar] [CrossRef]
- Liu, Z.; De Schutter, G.; Deng, D.; Yu, Z. Micro-analysis of the role of interfacial transition zone in “salt weathering” on concrete. Constr. Build. Mater. 2010, 24, 2052–2059. [Google Scholar] [CrossRef]
- Sengun, N.; Demirdag, S.; Ugur, I.; Akbay, D.; Altindag, R. Assessment of the physical and mechanical variations of some travertines depend on the bedding plane orientation under physical weathering conditions. Constr. Build. Mater. 2015, 98, 641–648. [Google Scholar] [CrossRef]
- Deo, P. Shales as embankment materials. Jt. Highw. Res. Proj. 1972, 45, 100–150. [Google Scholar]
- Lee, J.S.; Byun, Y.H.; Yoon, H.K. Study of Activation Energy in Soil through Elastic Wave Velocity and Electrical Resistivity. Vadose Zone J. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Lee, J.S.; Yoon, H.K. Application example: Field Velocity Resistivity Probe (FVRP) for predicting pore pressure parameter B. Soil Dyn. Earthq. Eng. 2018, 107, 214–217. [Google Scholar] [CrossRef]
- Fortin, J.; Stanchits, S.; Vinciguerra, S.; Guéguen, Y. Influence of thermal and mechanical cracks on permeability and elastic wave velocities in a basalt from Mt. Etna volcano subjected to elevated pressure. Tectonophysics 2011, 503, 60–74. [Google Scholar] [CrossRef]
- Sun, Y.F.; Goldberg, D. Estimation of aspect-ratio changes with pressure from seismic velocities. Geol. Soc. Lond. Spec. Publ. 1997, 122, 131–139. [Google Scholar] [CrossRef]
- Sausse, J.; Jacquot, E.; Fritz, B.; Leroy, J.; Lespinasse, M. Evolution of crack permeability during fluid–rock interaction. Example of the Brezouard granite (Vosges, France). Tectonophysics 2001, 336, 199–214. [Google Scholar] [CrossRef]
- Endres, A.L.; Knight, R.J. Incorporating pore geometry and fluid pressure communication into modeling the elastic behavior of porous rocks. Geophysics 1997, 62, 106–117. [Google Scholar] [CrossRef]


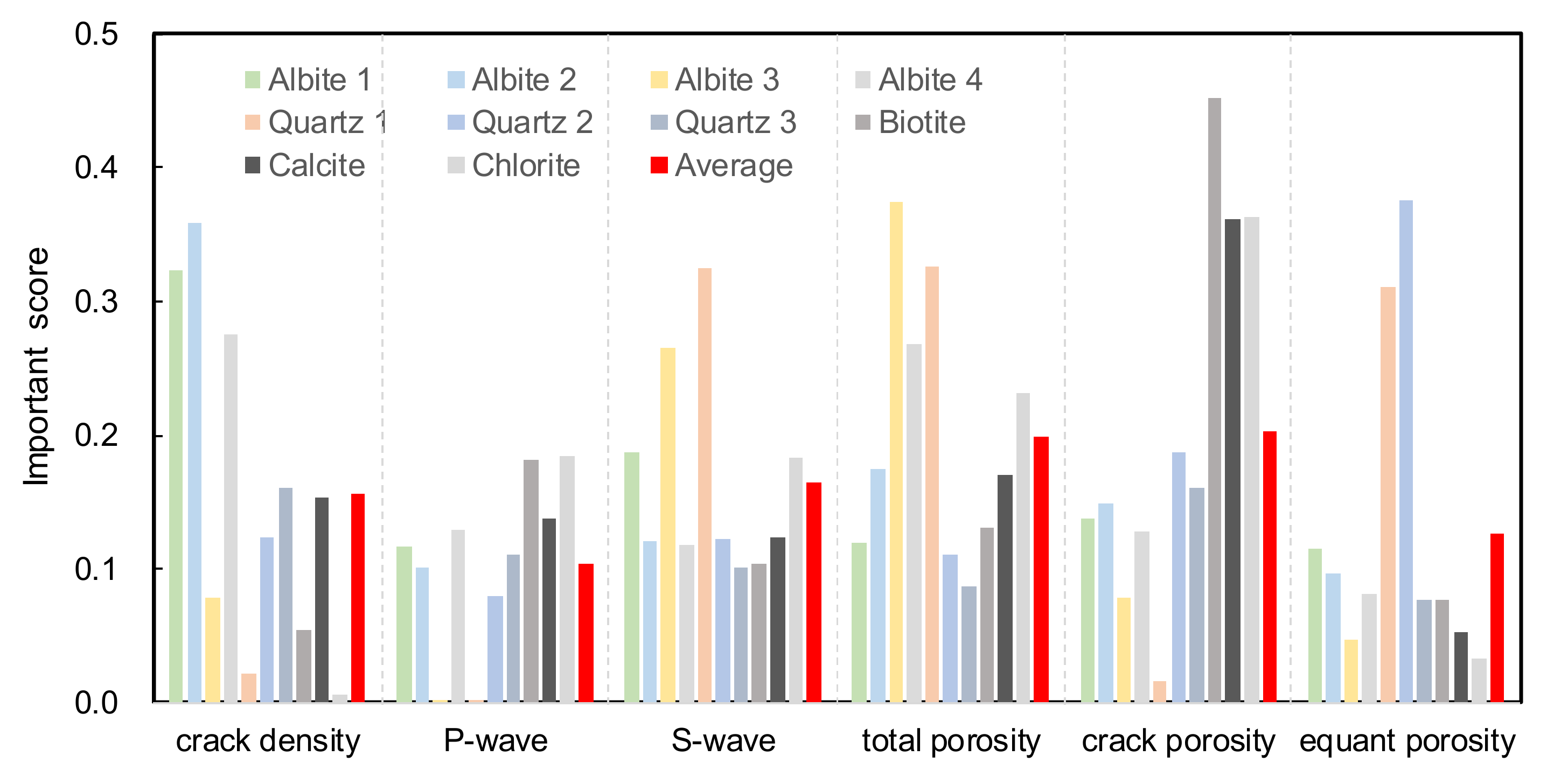
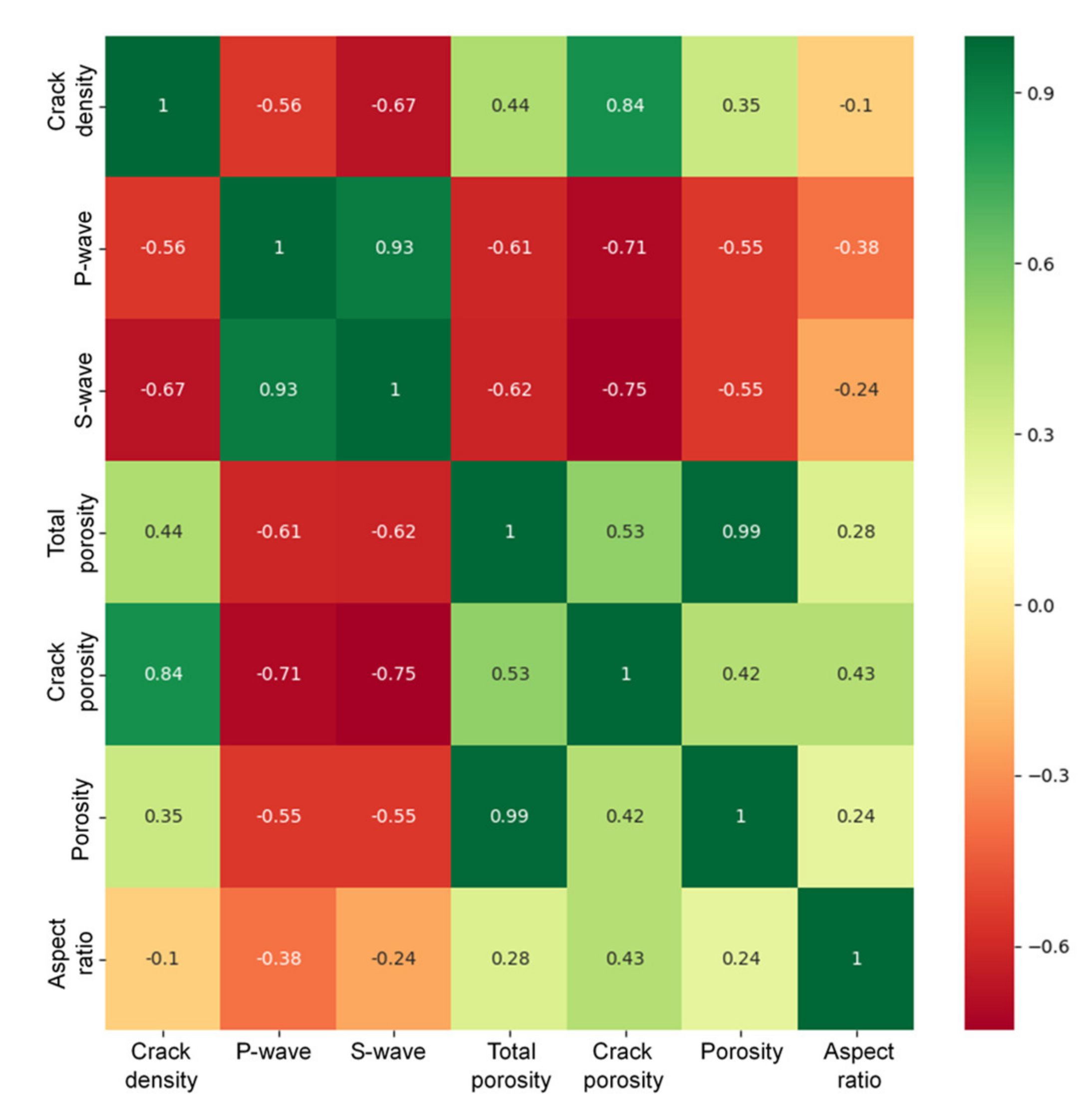
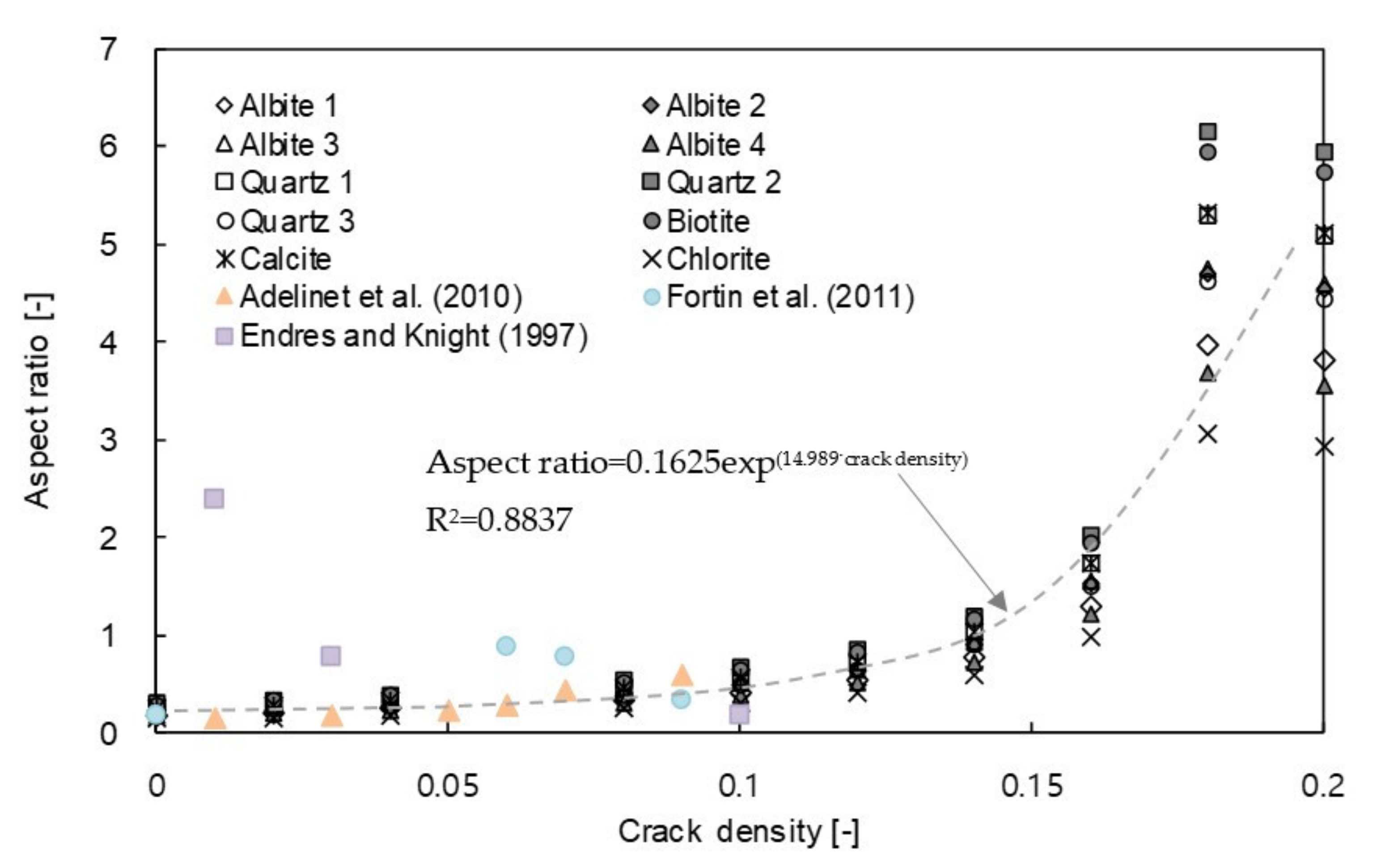
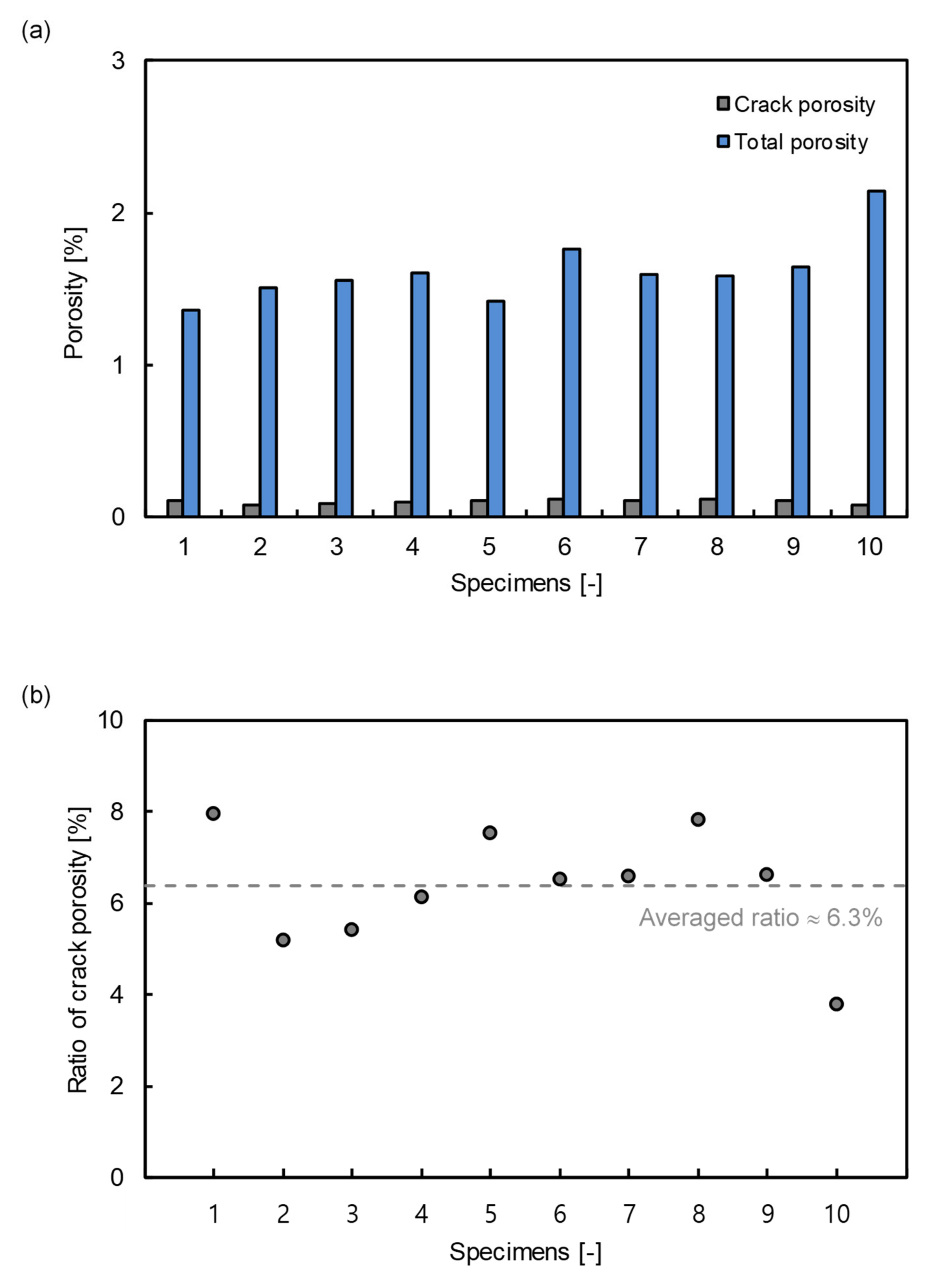
| Input Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Compressional wave velocity | VP | 3837 | m/s |
| Shear wave velocity | VS | 2213 | m/s |
| Mass density | γ | 2800 | kg/m3 |
| Poisson’s ratio | ν | 0.1 | - |
| Bulk modulus of grain | Kg | 15,000,000,000 | Pa |
| Bulk modulus of skeleton | Ksk | 7,780,000 | Pa |
| Bulk modulus of fluid | Kf | 2,180,000,000 | Pa |
| Shear modulus of grain | GS | 13,000,000,000 | Pa |
| Aspect ratio | ρ | 0.19 | - |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, H.-K. Relationship between Aspect Ratio and Crack Density in Porous-Cracked Rocks Using Experimental and Optimization Methods. Appl. Sci. 2020, 10, 7147. https://doi.org/10.3390/app10207147
Yoon H-K. Relationship between Aspect Ratio and Crack Density in Porous-Cracked Rocks Using Experimental and Optimization Methods. Applied Sciences. 2020; 10(20):7147. https://doi.org/10.3390/app10207147
Chicago/Turabian StyleYoon, Hyung-Koo. 2020. "Relationship between Aspect Ratio and Crack Density in Porous-Cracked Rocks Using Experimental and Optimization Methods" Applied Sciences 10, no. 20: 7147. https://doi.org/10.3390/app10207147
APA StyleYoon, H.-K. (2020). Relationship between Aspect Ratio and Crack Density in Porous-Cracked Rocks Using Experimental and Optimization Methods. Applied Sciences, 10(20), 7147. https://doi.org/10.3390/app10207147




