Abstract
One of the strategies to control the spread of infectious diseases is based on the use of specialized applications for smartphones. These apps offer the possibility, once individuals are detected to be infected, to trace their previous contacts in order to test and detect new possibly-infected individuals. This paper evaluates the effectiveness of recently developed contact tracing smartphone applications for COVID-19 that rely on Bluetooth to detect contacts. We study how these applications work in order to model the main aspects that can affect their performance: precision, utilization, tracing speed and implementation model (centralized vs. decentralized). Then, we propose an epidemic model to evaluate their efficiency in terms of controlling future outbreaks and the effort required (e.g., individuals quarantined). Our results show that smartphone contact tracing can only be effective when combined with other mild measures that can slightly reduce the reproductive number (for example, social distancing). Furthermore, we have found that a centralized model is much more effective, requiring an application utilization percentage of about 50% to control an outbreak. On the contrary, a decentralized model would require a higher utilization to be effective.
1. Introduction
The eruption of COVID-19 has become a severe threat to our society. At present over a million people have died, and more than 20 million have been infected. The social and economic effects of this pandemic are incalculable. International organizations such as the United Nations (UN) and UNICEF have warned about the risks to peace and social cohesion. Furthermore, it has been shown that COVID-19 can exceed the capacities of current health systems, including those with the most resources [1].
Countries dealt with the initial outbreak of COVID-19 in different ways and with very different results. Some countries exhaustively tested all the individuals with symptoms, and when an infected case was detected, their previous contacts were traced. The use of mobility traces has been fundamental to accomplishing this result (see [2]), and COVID-19 could be controlled without taking drastic measures. On the other hand, countries not performing this contact tracing could not control the outbreak, having eventually, no other option than to take extreme measures, such as lockdowns and stringent social distancing.
Contact tracing can be considered a more selective isolation measure targeted to the population most likely to have the infection [3]. Nevertheless, as shown with the COVID-19 pandemic, if the basic reproductive number is large and most infected individuals are asymptomatic, contact tracing has to be really efficient and rapid in order to be effective.
The so-called digital epidemiology [4] takes advantage of the global penetration of mobile phones to provide a way to track infectious diseases such as COVID-19, and to allow new approaches to deal with epidemics [3]. The FluPhone mobile application, which was developed at Cambridge University, is considered one of the first attempts to estimate infectious contacts by using mobile phones [5]. The idea was to use Bluetooth and other wireless signals to detect physical contacts, and then ask users to report flu-like symptoms for evaluating their risk of infection. For example, the Singaporean government developed and released the TraceTogether mobile application for tracing that also relied on Bluetooth contacts [6]. Other similar proposals are SafePaths [7,8] and PEPP-PT (Pan-European Privacy-Preserving Proximity Tracing) [9]. Finally, Apple and Google have recently teamed up to develop similar solutions in their smartphone operating systems. Furthermore, by being integrated into the mobile operating systems, it becomes more efficient, and what is more important is that it will reach nearly all smartphone users.
Most of the technology of these mobile applications is based on the results of years of research on mobile computing, and singularly on opportunistic networking (usually known as OppNet or opportunist networks) and mobile crowdsensing (MCS). The main idea behind OppNet [10] is to opportunistically exchange messages between nearby devices when establishing some communication link (for example, Bluetooth). As their behavior and dynamics can be comparable to the epidemic spread of messages, the models developed to evaluate opportunistic networks are usually adaptations of known epidemic models [11]. The study of human mobility and their social behavior is also essential for evaluating information dissemination in communication networks [12]. We consider that all this knowledge can help to tackle the spread of infectious diseases too. While the main goal of these previous research works was to increase information dissemination, we now set our primary objective to reducing or avoiding the diffusion of infectious diseases by reusing the various mathematical models and simulation tools previously developed [13,14,15,16].
In a previous work [17], we focused on evaluating how different technologies can be used for contact-tracing, and their impacts on the spread of infectious disease, confirming that Bluetooth is the most efficient technology for these cases. In fact, Bluetooth is being widely adopted in most tracing applications for COVID-19. We now focus our study on how recently developed smartphone contact tracing solutions can impact the spread of infectious diseases, particularly for COVID-19. Firstly, we describe how these applications work by characterizing their effectiveness in detecting contacts based on their utilization (i.e., the percentage of users using the application) and the users’ willingness to check their exposure. We then compare the application model (centralized vs. decentralized), and how this model impacts the tracing process (mainly on the tracing speed). Then, using an epidemic deterministic model, we evaluate how these issues impact the spread and management of the COVID-19 epidemics.
The main conclusions of this paper are the following: smartphone contact tracing, when no other measures are taken, can only be effective using a centralized model and when a very significant proportion (more than 80%) of the population uses the smartphone application. Under these conditions, smartphone-based contact tracing is an unfeasible solution. Nevertheless, when combined with other mild measures that can slightly reduce the reproductive number (for example, social distancing), smartphone contact tracing can be feasible and very effective. This efficiency clearly depends on the implementation model. A centralized model is much more effective, requiring a percentage of utilization of about 50% to control an outbreak, which can be considered a realistic objective. On the contrary, a decentralized model would require a higher utilization, in the range of 60% to 80% depending on the tracing speed.
This paper is organized as follows: the related research works are discussed in the following section. Section 3 describes how mobile tracing works and details how its precision and utilization can be parametrized, which are then used in the deterministic model detailed in Section 4. In particular, Section 4 describes the models and their precision, while Section 5 evaluates how the infection is controlled (or not), and the required effort to control it, that is, the number of people quarantined. Finally, in Section 6 we present the conclusions.
2. Related Works
Surveillance and control of emerging infectious diseases are essential for public health. The utilization of new technologies, such as Internet-based monitoring, remote sensing, infectious disease modeling, mobile phones and telecommunication, can predict, prevent and control these infectious diseases [18]. It is a new approach to deal with epidemics, usually named digital epidemiology [4]. Particularly, mobile devices can help with the detection of infectious contacts, as detailed in this paper.
Mobile crowdsensing (MCS) can be used to address COVID-19 [19]. The combination of mobile crowdsensing (MCS) with opportunistic networking (OppNet) allows mobile users to share sensed data easily and conveniently without the use of fixed infrastructure [20]. The combination of these two technologies is referred to as opportunistic mobile crowdsensing (OMC). Particularly, OMC is inexpensive, since there is no need for network deployment, offering also good spatiotemporal coverage. Opportunistic mobile crowdsensing can use two sensing approaches: (i) mobile sensing, based on obtaining data from the mobile’s hardware sensors, such as accelerometers, gyroscopes, GPS, network connectivity, camera, microphone, etc.; and (ii) social sensing, which leverages user-contributed data from social networks, considering participants as social sensors. Nevertheless, this social sensing might serve as a complementary source to physical mobile sensing [21].
A way to detect and trace contacts is by using wireless sensor network technologies, such as ZigBee or Bluetooth. Salathe et al. [22] performed one of the first experiments using MOTES. They obtained high-resolution data of interpersonal contacts during a typical day at high school, allowing the reconstruction of the social network that was relevant from an infectious disease transmission perspective. The paper includes an extension of the basic SIR epidemic model which includes the exposed individuals with the aim of evaluating the disease spread and the impact of vaccination measures.
In recent years there has been a growing concern in evaluating the effectiveness of contact tracing in epidemics. Contact tracing can be a useful tool, where the latent next-generation cases are the primary focus. It has been proven to be a very successful strategy when the quantity of infectious cases is low, or at the early stages of an outbreak, or particularly when the disease may be asymptomatic (but still contagious) [3]. Other papers estimate the factors that makes an infection controllable [23,24]. For example, in [23], the authors showed that the success of control measures such as isolation and quarantine is determined by the proportion of transmission occurring prior to the onset of overt clinical symptoms (or via asymptomatic infection) as measured by the reproductive number R0. Klinkenberg et al. [24] concluded that the variability in time to detection is favorable for effective tracing and that tracing effectiveness need not be sensitive to the duration of the latent period and tracing delays.
The two main approaches for modeling contact tracing are the following [25]: population-based modeling and agent-based modeling. The former is a top-down approach representing disease dynamics on a system level which is typically used to analyze research questions from a macroscopic perspective; the latter is a bottom-up approach dealing with each person as an agent with their own movements and infection states and is usually used to evaluate heterogeneous and adaptive behaviors. In general, agent-based modeling is more realistic, although it can be computationally demanding. Some works [26,27] have introduced detailed stochastic models which are simplified to a deterministic model to get the most significant dynamics of the epidemics.
Most of the epidemic models (population-based modeling) are based on the basic SIR (susceptible infected recovered) model, considering also quarantine and isolation measures. That is the basic model used in this paper. Other models also consider exposed individuals with incubation periods (asymptomatic individuals with no capacity of infection), such as the model developed by Lipsitch et al. [28] for the SARS disease, based on the SEIR model (susceptible–exposed (noninfectious)–infectious–recovered), or the incubation time used in the simulation process, such as the one presented by Hellewell et al. [29].
Farrahi et al. [30] utilized population-based modeling using a stochastic model. The authors estimated physical contacts from communication traces obtained using mobile phones, and thus helped to quarantine people selectively. They showed that contact tracing is only effective at the beginning of the outbreak due to the quickly increasing costs as the epidemic grows. Yang et al. [31] introduced a different method to model the spread of infectious diseases by analyzing the dynamics of the nodes using temporal graphs.
Other papers have studied the technology behind contact tracing. For example, Leith et al. [32] have evaluated the potential of using Bluetooth. Their results show that Bluetooth received signal strength can vary substantially depending on the relative orientations of handsets, on absorption by the human body and reflection/absorption of radio signals in buildings and trains. A more detailed study on the technological aspects that can affect the precision of smartphone-based contact tracing has been recently introduced by Kindt et al. [33]. Finally, for further information about automated contact tracing technologies, please refer to the following recent surveys [34,35].
Regarding the COVID-19 pandemic, the following authors have evaluated its impact: Ferretti et al. [36] state that contact tracing and isolation as currently practiced is not helping to prevent the COVID-19 pandemic. This is essentially due to the large number of undetected asymptomatic infected individuals helping to spread the infection. Therefore, the authors propose the use of smartphones to trace the prior contacts, proving that even when not all the population is willing to use the application, it can be feasible to contain epidemics (although the required portion should be significantly high). Another study by Cencetti et al. [37] showed that isolation and tracing alone were unlikely to be sufficient to keep an outbreak under control, and additional measures would need to be implemented simultaneously. Moreover, we confirm that a high level of application adoption is crucial to make digital contact tracing an effective measure. Finally, Kretzschmar et al. [38] drew similar conclusions: reducing the testing delay, that is, shortening the time between symptom onset and test positivity, is the most crucial aspect to enhance the effectiveness of contact tracing.
Hellewell et al. [29] obtained a similar outcome using a simulated model. That is, in most scenarios, very efficient contact tracing and people isolation is enough to control a new COVID-19 outbreak when at least 79% of the contacts are traced. These strong requirements make smartphone-based contact tracing an infeasible solution. Finally, Lambert [39] has also proven, using an analytical model, that moderate rates of adoption of a contact tracing application can reduce the reproductive number , but are by no means sufficient to reduce it below 1 (that is, a control of the outbreak) unless other measures are taken.
Wrapping up, most of the previous papers are focused on the epidemiological aspects of the disease from a medical point of view. Our paper is more oriented toward evaluating the impacts that the design and architecture of the contact tracing application have.
3. Smartphone-Based Contact Tracing
In this section, we describe how smartphone-based contact tracing works, detailing how its precision and utilization can be parametrized. The idea is to evaluate how the different implementation alternatives impact the detection and precision of previous possible contacts, in order to be used in the epidemic model described in Section 4.
3.1. Contact Tracing Applications
Traditionally, contact tracing is carried out manually by trained people who investigate a recent positive patient in order to obtain their previous contacts or locations visited. This method is widely used for some kinds of diseases (especially sexually transmitted ones) where the contacts are easy to identify. Nevertheless, contact tracing is a costly and lengthy procedure, involving personal interviews of the patient, family and acquaintances. Nevertheless, in most of the infectious diseases, personal interviews only provide very poor tracing of previous contacts and locations.
The goal of contact tracing applications is to predict exposure to a given infection based on detecting contacts using some of the current localization or communication technologies, such as GPS, Wi-Fi, mobile phones and Bluetooth. In this paper we focus on Bluetooth-based applications since most of the current solutions for the COVID-19 disease are based on this technology.
The idea is that, by using Bluetooth, one can identify the surrounding devices and also infer the distance to them. To this end, mobile nodes have to scan and periodically store the information of all these surrounding devices, using the received signal strength indicator (RSSI), for calculating the distance between the devices. For example, if Bluetooth is used, a contact trace of the nearby devices can be obtained with a resolution of 1–2 m, so it can be used to detect close personal contacts that are more likely to produce infections. Exposure to COVID-19 is calculated as a function of time and distance to an infected person. Experiments have shown that the exposure risk decreases for distances beyond 2 m, and for periods shorter than 15 min [40]. Additionally, it is considered that it is required to trace back for a period of only two weeks.
In order to preserve privacy, mobile phones exchange anonymous key codes when a potential nearby contact is identified. No information is sent about the people using the smartphone or their location. Therefore, this process generates data with the possible users’ contacts that complies with the countries’ regulations on data protection and privacy. This has lead to two different models for handling and storing these data: centralized and decentralized. Please, see Figure 1 for a visual illustration of the differences between the two different approaches. In the centralized model, the anonymized data are uploaded from people’s mobile phones to centralized servers. Then, health authorities can check, notify and manage previous contacts. On the contrary, the decentralized model locally stores these key codes and allows the users, firstly, to notify (or not) a positive, so the mobile application will upload the last 14 days of locally stored keys to the server; and secondly, to voluntary check (or not) their risk exposure, that is, whether they have been in contact with someone who may have been infected by downloading the uploaded keys from the server, and matching locally against the stored keys for evaluating the risk of exposure. For example, the decentralized option is the approach followed by Apple and Google. The API provided by these companies allows health authorities to develop their contact tracing solution.
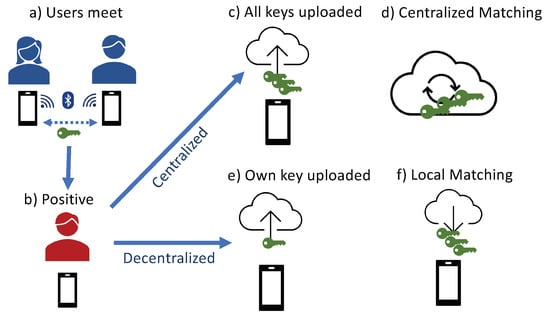
Figure 1.
Centralized vs. decentralized contact tracing approaches: (a) when two users’ smartphones are in range, they exchange their anonymous key codes; (b) when an individual is detected as positive, he/she notifies the application of his/her this new status; in the centralized approach (c), the smartphone uploads its key and also the other keys gathered from its previous contacts; (d) the possible risk contacts are detected using the centralized servers; in the decentralized approach (e), the smartphone only uploads its key; and (f) all keys of detected positives are downloaded by the application and the matching is performed locally.
Regarding privacy considerations, both approaches (centralized and decentralized) can comply with privacy and data protection regulations, although the decentralized one may offer a higher degree of privacy. Both approaches use the same method of exchanging anonymized key codes for identifying nearby contacts. The differences are where and when the checking for possible positive contacts is performed. Since, in the centralized model, the matching of possible positive contact is performed in centralized servers, it provides health authorities more control and information about the disease spreading and the social relationships between infected individuals. On the contrary, in the decentralized model, the matching between infected and users is carried out on the mobile, in the most anonymous way possible and without revealing information. The health authorities do not have access to these data, so they do not know exactly which contact has raised this risk notification; hence, no information is revealed, so privacy is preserved, although at the cost of not providing health measures to all these possible affected individuals.
3.2. Characterizing Contact Tracing Effectiveness
There are three main aspects of current contact tracing application that can impact their effectiveness: precision, utilization and speed. In this section, we parametrize the impact of these aspects on the fraction of possible traced contacts and the tracing time, which will be used in the epidemic model.
Precision is fundamental in detecting real contacts. We are not talking about detecting the contacts that have effectively produced an infection, which would depend on many other factors. Instead, precision is measured as the capacity of detecting the physical contacts that the health authorities determine that supposes an exposure to a significant risk of infection. For example, if health authorities determine that contacts that last at least 15 min in a range of 2 m are an exposure to risk (as detailed in [40]), the mobile application should detect only these contacts. Nevertheless, Bluetooth technology is far from being perfect, and it has been shown that many factors can affect the correct computation of distances [32].
The goal of contact tracing is to precisely detect the defined risky physical contacts, that is, a positive contact. As was previously said, Bluetooth technology for detecting exposure contacts is not precise enough (for example, when the distance is wrongly measured), and there might be some contacts missing (false negatives), and some other contacts added that should not have been (false positives). We measure this precision using the following ratios: the false negative ratio, , which corresponds to the probability of failing to detect a positive contact; and the false positive ratio , as the ratio over the number of positives. Note that the false positive ratio is usually defined based on the proportion of all negatives that yields a (false) positive. Nevertheless, in this case, there is no clear way to define all real negative contacts.
Considering that, in a day, the number of true positive contacts are , we can obtain the whole number of contacts generated by the tracing application as . That is, we add the false positives and the true positives . We define the relative error as:
which ranges from 0 (no error) to 1 (no real contact is detected).
The second aspect that impacts on the effectiveness is the utilization (adoption) of the application. In other words, how many people would use a contact tracing application? This question has not a simple answer and depends on many factors. As an example, Singapore’s official contact tracing app, TraceTogether, was only used by 20% of the population [6].
Based on the ratio of utilization U of the contact tracing application we can estimate the number of contacts traced. Assume that, throughout a day, the average number of physical contacts of an individual is k. Detecting a contact requires that two individuals use the application. Thus, the probability of detecting a contact will be simply (both individuals used the application), and the average number of contacts traced by individuals will be . For example, considering the contact tracing ratio of utilization of , we have that only 4% of the contacts are detected.
Therefore, in order to be effective, the utilization of the applications must be increased. A straightforward solution could be that governments compel their citizens to use the application. Nevertheless, this approach can be seen in most countries as a restriction of personal freedom and privacy, and is, therefore, not applicable. An alternative is to encourage the population to download (or activate) the application, although, as we have already seen in Singapore, with poor results. Recently, the Apple and Google COVID-19 solution has already been implemented in their latest operating systems versions, so, with a simple firmware update, users can have the contact tracing application; this approach could increase the number of users using the application. Nevertheless, this new facility is disabled by default, meaning that users should proactively opt-in for using the application, penalizing its utilization. The other option could be to have the application activated by default, with the option of opting-out whenever the user wants to. In this case, the user who has concerns about her/his privacy can disable it. Nevertheless, this makes a huge difference, since most people would not opt-out [41]. Therefore, in order to achieve a useful utilization, the only option is to allow users to opt-out. As it will be shown in the experiments, if no other measures are taken, the goal should be a utilization between 75% to 90%, a value that would allow tracing about 56% to 80% of the contacts.
An alternative to improve the utilization is to consider a reduced set of the population. Individuals can be forced to use the contact tracing application in some locations (companies, festivals, universities, conferences, etc.) in order to detect the possible contacts only in those defined areas. This way, the utilization of the application for this population subset would be nearly 100%, and so practically all contacts produced in the defined location can be traced.
Finally, the last aspect to analyze is the contact tracing speed. It has been shown that, for COVID-19, fast detection and isolation of infected individuals is essential to control new outbreaks. The tracing speed will depend mainly on whether the solution is centralized or decentralized. A centralized solution will be very fast since, when a newly infected individual is detected, health authorities can immediately trace their previous contacts. On the contrary, a decentralized solution will depend on the user’s willingness. Firstly, the newly infected citizen should self-report her/his positive using the application. Nevertheless, since self-reporting is prone to false alarms, we assume that health authorities, when individuals are tested as positive, should assure and control that users correctly notify about their positive. Secondly, the previous contacts of this individual should proactively check the application, and then communicate their situation. Therefore, it would take several days to trace all possible contacts, and, furthermore, some of the contacts will be lost.
It is clear that a centralized approach is a more effective approach, with tracing times of less than one day. A decentralized approach will suppose a double penalty: it will increase the tracing time, and it will also reduce the number of possible traced contacts. We can measure these penalties: (i) for the increase of tracing time, we consider the average tracing time will be , measured in days. In the centralized approach, this value will always be one, which is the unit time used in our model; (ii) for the reduction on the number of traced contacts, we consider the ratio of users checking for their exposure in the application, , which depends on the willingness of the users. Note that this value will be one for the centralized approach since the checking is always performed in the centralized servers.
Now, based on all the previous parameters, we define two different fractions of the real contacts that can be traced using the application. The idea here is to obtain an expression considering all the different aspects that can reduce the number of real contacts detected by the application, that is, the precision, the utilization and the ratio of user checking for exposure. These expressions will be used in the epidemic model to determine the people to be quarantined. The first one is for the quarantine of the infected nodes , that is an estimation of the final ratio of physical contacts traced:
This ratio depends only on the false negative ratio, as we are considering the real contacts with infected individuals. On the other hand, an increased number of false positives will increase the whole number of contacts detected by the application, but only for non-infected individuals, so will be the fraction of susceptible individuals traced (and quarantined):
That is, value determines the fraction of real contacts with infected individuals that are being traced and that can be potentially infected, and is the equivalent for the non-infected individuals. For example, a value of means that only 10% of all the real contacts have been traced, while a value of means that the number of contacts traced (including the false positives) is a 30% of the real contacts. Note that could be much greater than , since the contact-tracing mobile application can detect more false contacts than the real ones.
4. Epidemic Model
In this section, we introduce our model to evaluate the effect of contact tracing on the diffusion and control of an epidemic outbreak. We use a susceptible, infected, recovered (SIR) epidemic model with quarantine considering a population of N individuals We consider a closed system with no natural births and deaths, as the time scale is small enough to allow skipping this variation on the population.
We assume, as all deterministic models do, a homogeneity on the contacts. If we want to consider the heterogeneity of the contacts, we should use a stochastic one, like the one presented by the authors in [17]. As shown in this paper, when considering an average number of contacts and tracing intensity (i.e., a mean-field approximation), a stochastic model can be transformed into a deterministic model. This continuous model is useful in assessing the dynamics of the epidemic and the impact of the various quarantine methods, taking into account greater populations. The accuracy of this continuous model depends not only on the homogeneity and distribution of the contacts patterns but also on the number of individuals considered (population), becoming more accurate when there is a high number of nodes.
We consider in our model a population of N individuals that can be in the following classes, representing the number of individuals on each class: S, susceptible individuals (not infected); I, infected individuals; R, individuals recovered from the infection; infected individuals that have been detected (or traced) and as a result quarantined; , susceptible individuals that are quarantined after being traced; and , infected individuals that have been detected and are being traced. Finally, as for most of the epidemic models, the time unit is one day. For reference to the notation used in the model see Table 1.

Table 1.
Notation table.
We can obtain the transmission rate as the product of the average number of contacts with infected individuals at the time unit t (i.e., during a day), k; and the transmission probability of the disease, b. This value b depends on the type of disease. The infected individuals recover after days, being the recovery rate. All these values are related to the basic reproductive number as . Therefore, b can be obtained using some simple parameters of the disease, such as the reproductive number , the transmission rate and the contact rate k. is one of the most significant figures in epidemiology, representing the number of people that one infected person will pass the virus on to, on average. If , the infection will start spreading, but not if . In general terms, the greater the value, the harder it is to contain the outbreak.
In order to determine the transition rates between classes we need to consider the detection and quarantine measures to be taken. Firstly, we assume that when an infected individual is detected, she/he is immediately quarantined. Then, using contact tracing, her/his previous contacts are analyzed to detect individuals having a high probability of being infected, which also are quarantined.
As detailed in the previous section, in our model we also consider that not all real contacts will be traced positively. This efficiency depends on several factors: the percentage of people using the mobile application and their willingness to check their risk, and the precision on detecting a physical contact (false positives and negatives). As detailed in the previous section, we consider two different fractions of traced contacts to be quarantined: for infected individuals and for susceptible individuals, as expressed in Equations (2) and (3).
Thus, we consider the following transitions between classes:
- : Infected individuals who are not traced and consequently, not quarantined. In general, the transmission rate, that is the rate in which the infection is transmitted from one infected individual to one susceptible individual, is formed from the product of the number of contacts per time unit k, and the probability to transmit the disease b; hence, newly infected individuals are generated with a whole rate . Note that this rate is for all infected individuals. Since in this transition we are only considering the infected ones that are not traced, the previous rate is multiplied by , that is the fraction of non-traced contacts, so that the transition rate is . The other fraction of infected individuals is considered in transition .
- : Infected individuals who are being traced and go directly to the tracing state. When infected individuals are detected (that is, when they are in class ) their previous contacts that are in the susceptible class are traced, and some of them are quarantined. Therefore, this transition considers only the traced contacts, that is the fraction , so the rate is . It refers to the individuals that may have been infected during the day.
- : Non-infected individuals traced and quarantined. The transition rate is , considering that is the probability of not transmitting the disease. In this transition rate, the fraction considers the effect of false positives, which can increase the number of people unnecessarily quarantined.
- : Detection of infected individuals, triggering the tracing of their previous contacts using the application while being quarantined. In our model, infected individuals are detected, traced and quarantined with rate, staying in quarantine for an average time of days. Prior to going to the final quarantine class , these individuals stay during a short time in class , for tracing their previous contacts. This time is the tracing time () that models the necessary time to trace the contacts, allowing to compare the fast-tracing centralized approach versus the slower-tracing decentralized approach.
- : This transition supposes the end of the tracing. After the tracing time they move to the class, to finish their quarantine.
- : End of quarantine and infection. In this class, individuals continue their quarantine for the remaining quarantine time, which is obtained as = , and, finally, they are considered recovered and move to the R class afterward.
- : Non detected infected individuals recovered from the disease. This transition considers those infected individuals not detected, that is, asymptomatic ones which have not been tested. The rate is simply the recovery rate .
- : End of quarantine for susceptible individuals. After being quarantined, individuals in the class return to the susceptible class, after staying in quarantine for days.
Based on these transitions, the model is defined by the following equations:
The time has been omitted in all the classes. For example, for class I, and ). Note also that we have chosen not to simplify some mathematical expressions to clearly differentiate the transitions between classes.
Note that, in the case that the tracing time would be greater than one, and values must be normalised considering the whole average tracing time. The idea is to distribute these fractions of traced contacts among the tracing time, using the following expressions: and . That is, if the tracing time is longer (as in the decentralized model), it is because it will take more time to trace back the prior contacts.
In epidemic management and control, it is crucial to reduce the number of undetected infected individuals who may contribute to the rapid spread of the infection (this is known as one of the leading causes of COVID-19’s rapid spread). This goal can be obtained by increasing the detection ratio (for example, by incrementing the number of tests even for asymptomatic individuals), and also by increasing the number of traced individuals. It is easy to see from the equations of the previous model, that the condition to control an outbreak is when the number of infected individuals I decreases, that is, when is negative. Therefore, the condition for to be negative in expression (4) is:
considering that . Using this expression the threshold for an epidemic outbreak can be easily obtained. This threshold depends on (the basic reproductive number) and the ratio of susceptible individuals (). Note that this threshold depends on and not on . The reason is that the spread of the infection can only be stopped by the detection and quarantine of infected individuals. This also means that less precise contact tracing will increase the number of susceptible quarantined individuals. That is, considering the same number of traced quarantined people, a less precise tracing will be less effective. If we also want to evaluate the impact of the application utilization (U and ), combining this Equation (5) with the value of defined in Equation (2) we can obtain the threshold values of depending on U as:
Finally, as Equation (4) do not have an algebraic solution, a numerical solution is needed (for example, using the Euler’s method or more efficient and precise numerical methods such as Matlab’s function ode45, which is the one used in this paper). For solving this model, we consider an initial value of and (that is, the number of recovered and infected individuals at the beginning of an outbreak). Note, that in most of our experiments these values , are 0, as we consider an initial outbreak with no people infected or immunized. Then, the initial number of susceptible individuals is obtained as , and the other classes are zero. Next, the model is numerically solved for a given time (for example, one year), or until there are no infected individuals. That is when the sum of classes is smaller than one, which means that the infection is over. In this case, the duration of the epidemic is obtained as the time t when .
For evaluating the effectiveness of the different isolation methods, we can obtain the number of individuals that have been quarantined using contact tracing. A highly effective quarantine strategy will be the one that minimizes the people quarantined while controlling the spread of the disease. This value, , that depends on time t can be obtained as:
Notice that often, if the length of the infection is long, individuals can be quarantined many times, that is, they return to the susceptible class when they end the quarantine so they can be quarantined again.
5. Evaluation
In this section, we evaluate the impact of the user’s utilization of the contact tracing mobile application, and the speed of contact tracing, which mainly depends on the centralized/decentralized type of implementation. In general, the idea is to evaluate how the infection is controlled (or not), and the required effort to control it, that is, the number of people quarantined.
For the following experiments, we consider that the precision of using the Bluetooth technology is: and , meaning that 50% of the real contacts are detected, and 70% additional false contacts are generated. According to Equation (1), the error is . The COVID’19 estimated parameters used in the experiments are shown in Table 2. In general, we consider a population of 1 million () and an outbreak with 10 infected individuals nd no immunized individuals (that is, ). Finally, the average contacts per day is considered to be 8 (). Note that, although the experiments are done with a given population and contact rate, based on the obtained results using data from students from a university campus, the results are scalable to any population, and most of the times we are plotting the results as a percentage of the population. Refer to [17] for the detailed study of the precision depending on the technology and details about the mobility trace.

Table 2.
Some estimated parameters for COVID-19 (the time unit is days) [29,36,42].
5.1. Impact of Utilization
We first evaluate the dynamics of an infection using the epidemic model introduced in the previous section under different utilization percentages of the contact tracing mobile application. The idea is to provide a better understanding of the dynamics of the spread disease, and the people quarantined using contact tracing.
We start analyzing the situation when no measures are taken: that is, individuals are neither detected nor quarantined (). Figure 2a show these results. It clearly depicts the evolution of the deterministic SIR epidemic model where most individuals gets infected due to the COVID-19’s high reproductive number (). Figure 2b represents the case where a proportion of the infected individuals are being detected and isolated (i.e., with a detection rate of ). This simple measure reduces the percentage of individuals infected (about 60%), flattening the curve of infected individuals. Such an effect of flattening the curve means that the infection is lengthier.
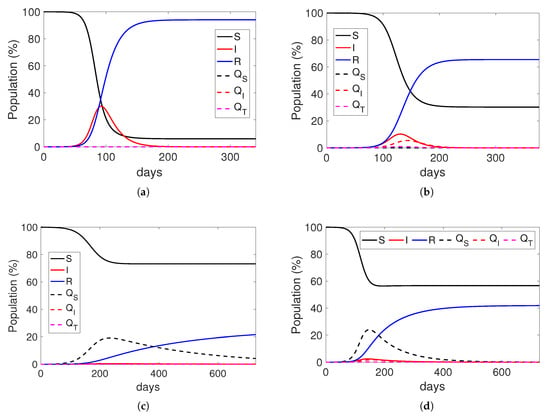
Figure 2.
Epidemic dynamics with different mobile contact tracing utilization for COVID-19 infection. (a) No measures (); (b) detection and isolation of individuals, no contact tracing (, ); (c) with mobile contact tracing (optimistic utilization) (, ); (d) with mobile contact tracing (pessimistic utilization) (, ).
Now, we assess the effect that smartphone-based contact tracing has in the spread of the infection. We consider an optimistic utilization of the application of 75% (), and that the ratio of users checking the application is also high (). Using Equations (2) and (3) with these values, we obtain and . We consider also a short average tracing time of one day (). The results are presented in Figure 2c, showing that the infected curve has been mostly flattened, and the percentage of infected individuals is also reduced to about 20% of the population. Nevertheless, if we consider a non-optimistic utilization of the contact tracing application ( and ), we can see in Figure 2d that the reduction is relatively small (about 40%) when compared to the results shown in Figure 2b.
In order to control the outbreak of the disease, a non-realistic utilization close to 100% is required (not displayed for being completely flat curves). The threshold utilization values for controlling a COVID-19 outbreak can be obtained using Equation (6). The results are those in Figure 3, showing the threshold values for the application utilization (U) and user checking (). The presented results are very significant. For an initial outbreak, that is when all nodes are susceptible (), we can see that the required utilization is unrealistically high (greater than 90%). Fortunately, using some mild measure of social distancing, the effective reproductive number can be reduced significantly. In the paper, we use the notation for both the basic reproductive number and effective reproductive number, although the basic reproductive ratio is when no measures are taken. Additionally, note that by taking measures such as social distancing, the number of contacts (k) and the probability to transmit the disease (b) are reduced, and these are the main components of the reproductive number.
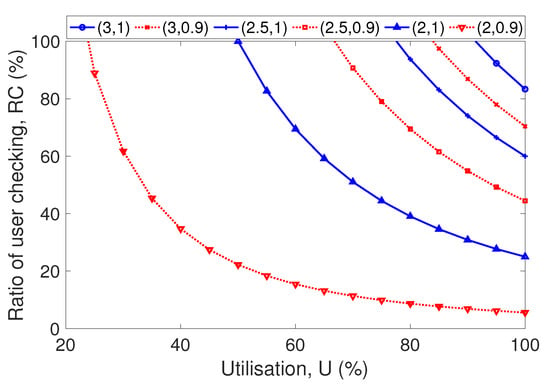
Figure 3.
Contact tracing application utilization thresholds for controlling an infection, considering different values of reproduction ratio () and percentage of susceptible people (). The pair of values above the lines results in a disease-free equilibrium.
It is also foreseeable, that for future outbreaks, some proportion of the population has gained immunity after being recovered, and so the ratio could be smaller. We can see in Figure 3 that, for , the required utilization can be 60% considering also an RC of 60%. Additionally, if we consider that 10% of the population has gained immunization, the required utilization can be above 40%. These scenarios are highly probable, making mobile contact tracing a feasible solution for new outbreaks. Now, we evaluate the scenario when the infection could not be controlled and most people are getting infected. The idea is to study the impact of contact tracing in two main aspects: infection rate, and people quarantined. For this evaluation, we only show the final results, that is when the infection is over. Figure 4a displays the proportion of infected individuals depending on the application utilization U for several values of . Note that the infected and quarantine figures are represented as a percentage of the population. We can see that, even with low percentages of utilization, there is a significant reduction on the people infected. Nevertheless, the cost can be very high, requiring a lot of people to be quarantine as shown in Figure 4b. We again recall that percentages greater than 100 mean that some people have been quarantined more than once, or for periods longer than 14 days, which was the quarantine time used in the experiments.

Figure 4.
Efficiency of the contact tracing application depending on utilization: (a,b) percentage of population infected and quarantined for ; (c,d) percentage of population infected and quarantined considering other measures (for ); (d) proportion of population quarantined considering also other measures ().
Finally, if we consider that some additional measures are taken so that the effective reproduction ratio is reduced to , we can see in Figure 4c that we can obtain a significant reduction of the infected population even for utilization percentages, and that is more important with a relative cost, since the percentage of quarantined people is hugely reduced (see Figure 4d). The results considering a ratio of already immunized people also evidenced a significant reduction of the quarantines required. These results confirm the utility of contact tracing applications for future outbreaks, even for utilization levels between 40% and 60%.
5.2. Impact of Accuracy
In this subsection, we evaluate the impact of the detection accuracy on the number of infected and quarantined individuals. Particularly, we have evaluated how false positive (FP) and false negative (FN) ratios impact these aspects.
We repeated the experiments of Figure 4 with and , considering six different combinations of FP and FN ratios. Specifically, we evaluated the proportions of infected individuals and people quarantined depending on the utilization of the smartphone application for the following pairs of FP and FN ratios: . From these pairs of values we can obtain the relative error using expression (1): (that is, the FP and FN pairs are in decreasing relative error). Figure 5 shows the results. Regarding the proportion of infected individuals (Figure 5b), we can see, as expected, that for lower ratios of FP and FN, the infected individuals are reduced, especially when the utilization is high. It is also important to point out that there is no significant difference between the red and blue curves—that is, when the FP ratio varies. For example, we can see that for the (FP, FN) pairs , the curves are mostly the same. This means that the impact of the FP ratio on the infected individuals is very reduced. On the other hand, the FP ratio has a very significant impact on the people quarantined, as shown in Figure 5b. Actually, both ratios have a significant impact on the number of people in quarantine, since reducing the detection accuracy increases the people quarantined.
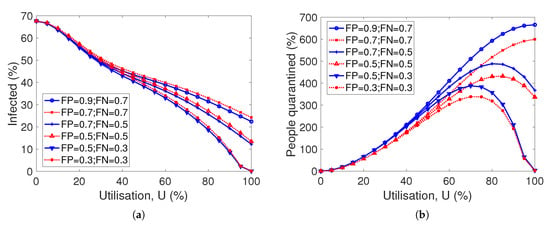
Figure 5.
Impact of accuracy. That is, the impacts of false positive and false negative ratios on the efficiency of contact tracing. All plots are for , day and : (a) percentage of population infected; (b) percentage of population quarantined.
Repeating the previous experiments with other values of and led us to similar results and conclusions. Summing up, the results show that the false positive ratio has little effect on the final number of infected individuals, but it has a huge effect on the number of individuals quarantined. This is a logical outcome, since the consequence of a higher ratio of false positives is that more people are unnecessarily quarantined.
5.3. Centralized vs. Decentralized Solutions
We now evaluate the efficiency of the centralized and decentralized approaches, which rely mainly on the tracing time ( and the ratio of users checking for exposure (). The latter parameter has already been evaluated in the previous subsection. In a centralized approach, will be 1, and so the results in Figure 4 clearly show a greater efficiency when compared with lower values of associated with the decentralized approach.
Therefore, in this subsection, we focus on the tracing time. We increase this value () from 1 day to 2 and 4 days in order to evaluate its impact. We repeated the experiments in Figure 4c,d, which had a tracing time of one day. The results are shown in Figure 6. Increasing the tracing time to 2 days (Figure 6a,b) evidences a substantial increase in the percentage of individuals infected for similar utilization levels, requiring also more people to be quarantined. The results for a tracing time of 4 days confirm the significant impacts on the control and spread of the epidemics. Figure 6c not only shows an increased proportion of people infected, but also that only with an application utilization near to 100% can the outbreak be controlled (compare these results with the one of Figure 4c where for an utilization of about 50% the outbreak can be controlled with practically no quarantine). These results confirm the necessity of a fast tracing of the previous contacts in order to get an effective quarantine.
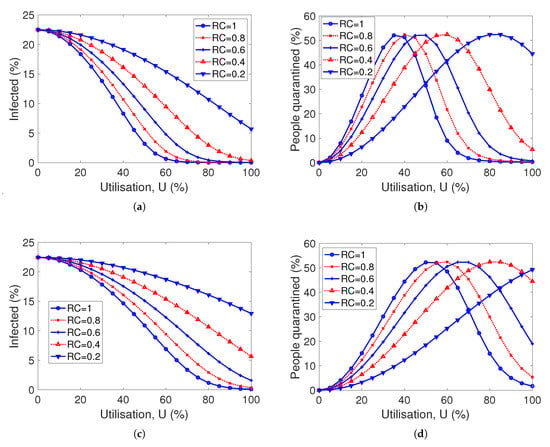
Figure 6.
Efficiency of the contact tracing application considering the tracing time (all plots are for ): (a,b) percentage of population infected and quarantined when tracing time is 2 days (); (c,d) percentage of population infected and quarantined considering when tracing time is 4 days ().
6. Conclusions
In this paper, we have evaluated how smartphone-based contact tracing can control the spreading of infectious diseases, particularly focusing on COVID-19. We have studied what the main implementation aspects are, which, combined with an epidemic deterministic model, allowed us to evaluate their efficiency.
The results show that when no other measures are taken, smartphone contact tracing is not a feasible solution: it is only effective using a centralized model and considering that a very significant proportion of the population (more than 80%) is willing to use the smartphone application. Moreover, in order to be effective, its use must be combined with other mild measures (for example, social distancing). Finally, the efficiency of this solution depends on the implementation model: a centralized model is much more effective, requiring a utilization percentage of about 50% to control an outbreak (a very realistic objective). On the contrary, a decentralized model would require a higher utilization, in the range of 60% to 80% depending on the tracing speed.
To conclude, we are experiencing one of the major crises of our recent history. The COVID-19 pandemic is causing a great number of deaths. Social lockdown and distancing measures are slowly mitigating the spread of the virus. These measures are the only tool available until the long-awaited vaccine can be distributed to the entire population. We think that the use of smartphone-based contact tracing can help to tackle this pandemic.
Author Contributions
Conceptualization, E.H.O.; formal analysis, E.H.O. and P.M.; funding acquisition, C.T.C. and J.-C.C.; investigation, E.H.O.; methodology, E.H.O. and P.M.; data curation, E.H.O.; visualization, E.H.O.; project administration, C.T.C.; resources, J.-C.C.; supervision, C.T.C., J.-C.C., E.H.-O. and P.M.; validation, C.T.C., J.-C.C., E.H.-O. and P.M.; writing C.T.C., J.-C.C., E.H.-O. and P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the “Ministerio de Ciencia, Innovación y Universidades, Programa Estatal de Investigación, Desarrollo e Innovación Orientada a los Retos de la Sociedad, Proyectos I+D+I 2018”, Spain, under Grant RTI2018-096384-B-I00.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, R.; Rivers, C.; Tan, Q.; Murray, M.B.; Toner, E.; Lipsitch, M. The demand for inpatient and ICU beds for COVID-19 in the US: Lessons from Chinese cities. medRxiv 2020. [Google Scholar] [CrossRef]
- COVID-19 National Emergency Response Center, Epidemiology and Case Management Team, Korea Centers for Disease Control and Prevention. Contact Transmission of COVID-19 in South Korea: Novel Investigation Techniques for Tracing Contacts. Osong Public Health Res Perspect 2020, 11, 60–63. [Google Scholar] [CrossRef]
- Eames, K.; Keeling, M. Contact Tracing and Disease Control. Proc. Biol. Sci. R. Soc. 2004, 270, 2565–2571. [Google Scholar] [CrossRef]
- Salathé, M. Digital epidemiology: What is it, and where is it going? Life Sci. Soc. Policy 2018, 14, 1. [Google Scholar] [CrossRef]
- Computer Laboratory-University of Cambridge. The FluPhone Study. 2010. Available online: https://www.fluphone.org (accessed on 24 May 2020).
- Singapore Government. Tracetogether. 2020. Available online: https://www.tracetogether.gov.sg (accessed on 15 April 2020).
- MIT. Safe Paths. 2020. Available online: http://safepaths.mit.edu (accessed on 22 April 2020).
- Raskar, R.; Schunemann, I.; Barbar, R.; Vilcans, K.; Gray, J.; Vepakomma, P.; Kapa, S.; Nuzzo, A.; Gupta, R.; Berke, A.; et al. Apps Gone Rogue: Maintaining Personal Privacy in an Epidemic. arXiv 2020, arXiv:2003.08567. [Google Scholar]
- PePP-PT e.V. i.Gr. Pan-European Privacy-Preserving Proximity Tracing (PEPP-PT). 2020. Available online: https://www.pepp-pt.org (accessed on 15 September 2020).
- Pelusi, L.; Passarella, A.; Conti, M. Opportunistic networking: Data forwarding in disconnected mobile ad hoc networks. Commun. Mag. IEEE 2006, 44, 134–141. [Google Scholar] [CrossRef]
- Zhang, X.; Neglia, G.; Kurose, J.; Towsley, D. Performance modeling of epidemic routing. Comput. Netw. 2007, 51, 2867–2891. [Google Scholar] [CrossRef]
- Helgason, Ó.; Kouyoumdjieva, S.T.; Karlsson, G. Opportunistic Communication and Human Mobility. IEEE Trans. Mob. Comput. 2014, 13, 1597–1610. [Google Scholar] [CrossRef]
- Chancay-García, L.; Hernández-Orallo, E.; Manzoni, P.; Calafate, C.T.; Cano, J. Evaluating and Enhancing Information Dissemination in Urban Areas of Interest Using Opportunistic Networks. IEEE Access 2018, 6, 32514–32531. [Google Scholar] [CrossRef]
- Dede, J.; Förster, A.; Hernández-Orallo, E.; Herrera-Tapia, J.; Kuladinithi, K.; Kuppusamy, V.; Manzoni, P.; bin Muslim, A.; Udugama, A.; Vatandas, Z. Simulating Opportunistic Networks: Survey and Future Directions. IEEE Commun. Surv. Tutor. 2018, 20, 1547–1573. [Google Scholar] [CrossRef]
- Hernández-Orallo, E.; Murillo-Arcila, M.; Calafate, C.T.; Cano, J.C.; Conejero, J.A.; Manzoni, P. Analytical evaluation of the performance of contact-Based messaging applications. Comput. Netw. 2016, 111, 45–54. [Google Scholar] [CrossRef][Green Version]
- Hernandez-Orallo, E.; Serrat Olmos, M.; Cano, J.C.; Calafate, C.; Manzoni, P. CoCoWa: A Collaborative Contact-Based Watchdog for Detecting Selfish Nodes. IEEE Trans. Mob. Comput. 2015, 14, 1162–1175. [Google Scholar] [CrossRef]
- Hernández-Orallo, E.; Manzoni, P.; Calafate, C.T.; Cano, J. Evaluating How Smartphone Contact Tracing Technology Can Reduce the Spread of Infectious Diseases: The Case of COVID-19. IEEE Access 2020, 8, 99083–99097. [Google Scholar] [CrossRef]
- Christaki, E. New technologies in predicting, preventing and controlling emerging infectious diseases. Virulence 2015, 6, 558–565. [Google Scholar] [CrossRef] [PubMed]
- Cecilia, J.M.; Cano, J.C.; Hernández-Orallo, E.; Calafate, C.T. Mobile crowdsensing approaches to address the COVID-19 pandemic in Spain. IET Smart Cities 2020, 2, 58–63. [Google Scholar] [CrossRef]
- Hernández-Orallo, E.; Borrego, C.; Manzoni, P.; Marquez-Barja, J.M.; Cano, J.C.; Calafate, C.T. Optimising data diffusion while reducing local resources consumption in Opportunistic Mobile Crowdsensing. Pervasive Mob. Comput. 2020, 67, 101201. [Google Scholar] [CrossRef]
- Doran, D.; Severin, K.; Gokhale, S.; Dagnino, A. Social media enabled human sensing for smart cities. AI Commun. 2016, 29, 57–75. [Google Scholar] [CrossRef]
- Salathé, M.; Kazandjieva, M.; Lee, J.W.; Levis, P.; Feldman, M.W.; Jones, J.H. A high-resolution human contact network for infectious disease transmission. Proc. Natl. Acad. Sci. USA 2010, 107, 22020–22025. [Google Scholar] [CrossRef]
- Fraser, C.; Riley, S.; Anderson, R.; Ferguson, N. Factors that make an infectious disease outbreak controllable. Proc. Natl. Acad. Sci. USA 2004, 101, 6146–6151. [Google Scholar] [CrossRef]
- Klinkenberg, D.; Fraser, C.; Heesterbeek, H. The Effectiveness of Contact Tracing in Emerging Epidemics. PLoS ONE 2006, 1, e12. [Google Scholar] [CrossRef]
- Kwok, K.O.; Tang, A.; Wei, V.W.; Park, W.H.; Yeoh, E.K.; Riley, S. Epidemic Models of Contact Tracing: Systematic Review of Transmission Studies of Severe Acute Respiratory Syndrome and Middle East Respiratory Syndrome. Comput. Struct. Biotechnol. J. 2019, 17, 186–194. [Google Scholar] [CrossRef] [PubMed]
- Müller, J.; Kretzschmar, M.; Dietz, K. Contact tracing in stochastic and deterministic epidemic models. Math. Biosci. 2000, 164, 39–64. [Google Scholar] [CrossRef]
- Huerta, R.; Tsimring, L.S. Contact tracing and epidemics control in social networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002, 66, 056115. [Google Scholar] [CrossRef] [PubMed]
- Lipsitch, M.; Cohen, T.; Cooper, B.; Robins, J.M.; Ma, S.; James, L.; Gopalakrishna, G.; Chew, S.K.; Tan, C.C.; Samore, M.H.; et al. Transmission dynamics and control of severe acute respiratory syndrome. Science 2003, 300, 1966–1970. [Google Scholar] [CrossRef] [PubMed]
- Hellewell, J.; Abbott, S.; Gimma, A.; Bosse, N.I.; Jarvis, C.I.; Russell, T.W.; Munday, J.D.; Kucharski, A.J.; Edmunds, W.J.; Sun, F.; et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 2020, 8, e488–e496. [Google Scholar] [CrossRef]
- Farrahi, K.; Emonet, R.; Cebrian, M. Epidemic contact tracing via communication traces. PLoS ONE 2014, 9, e95133. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.X.; Wang, W.X.; Lai, Y.C.; Wang, B.H. Traffic-driven epidemic spreading on networks of mobile agents. EPL (Europhys. Lett.) 2012, 98, 68003. [Google Scholar] [CrossRef]
- Leith, D.J.; Farrell, S. Coronavirus Contact Tracing: Evaluating the Potential of Using Bluetooth Received Signal Strength For Proximity Detection; Technical Report; School of Computer Science and Statistics, Trinity College: Dublin, Ireland, 2020. [Google Scholar]
- Kindt, P.H.; Chakraborty, T.; Chakraborty, S. How Reliable is Smartphone-based Electronic Contact Tracing for COVID-19? arXiv 2020, arXiv:2005.05625. [Google Scholar]
- Anglemyer, A.; Moore, T.; Parker, L.; Chambers, T.; Grady, A.; Chiu, K.; Parry, M.; Wilczynska, M.; Flemyng, E.; Bero, L. Digital contact tracing technologies in epidemics: A rapid review. Cochrane Database Syst. Rev. 2020. [Google Scholar] [CrossRef]
- Braithwaite, I.; Callender, T.; Bullock, M.; Aldridge, R.W. Automated and partly automated contact tracing: A systematic review to inform the control of COVID-19. Lancet Digit. Health 2020, 9, 5. [Google Scholar] [CrossRef]
- Ferretti, L.; Wymant, C.; Kendall, M.; Zhao, L.; Nurtay, A.; Abeler-Dorner, L.; Parker, M.; Bonsall, D.; Fraser, C. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 2020, 368, 6491. [Google Scholar] [CrossRef] [PubMed]
- Cencetti, G.; Santin, G.; Longa, A.; Pigani, E.; Barrat, A.; Cattuto, C.; Lehmann, S.; Lepri, B. Using real-world contact networks to quantify the effectiveness of digital contact tracing and isolation strategies for Covid-19 pandemic. medRxiv 2020. [Google Scholar] [CrossRef]
- Kretzschmar, M.E.; Rozhnova, G.; Bootsma, M.; van Boven, M.E.; van de Wijgert, J.; Bonten, M. Time is of the essence: Impact of delays on effectiveness of contact tracing for COVID-19. medRxiv 2020. [Google Scholar] [CrossRef]
- Lambert, A. A mathematical assessment of the efficiency of quarantining and contact tracing in curbing the COVID-19 epidemic. medRxiv 2020. [Google Scholar] [CrossRef]
- Sattler, F.; Ma, J.; Wagner, P.; Neumann, D.; Wenzel, M.; Schäfer, R.; Wiegand, T. Risk estimation of SARS-CoV-2 transmission from bluetooth low energy measurements. NPJ Digit. Med. 2020, 3, 1. [Google Scholar] [CrossRef]
- Pueyo, T. Coronavirus: How to Do Testing and Contact Tracing. Medium. 2020. Available online: https://medium.com/@tomaspueyo (accessed on 11 June 2020).
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2). Science 2020, 368, 489–493. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).