2.2. Lifetime Calculation
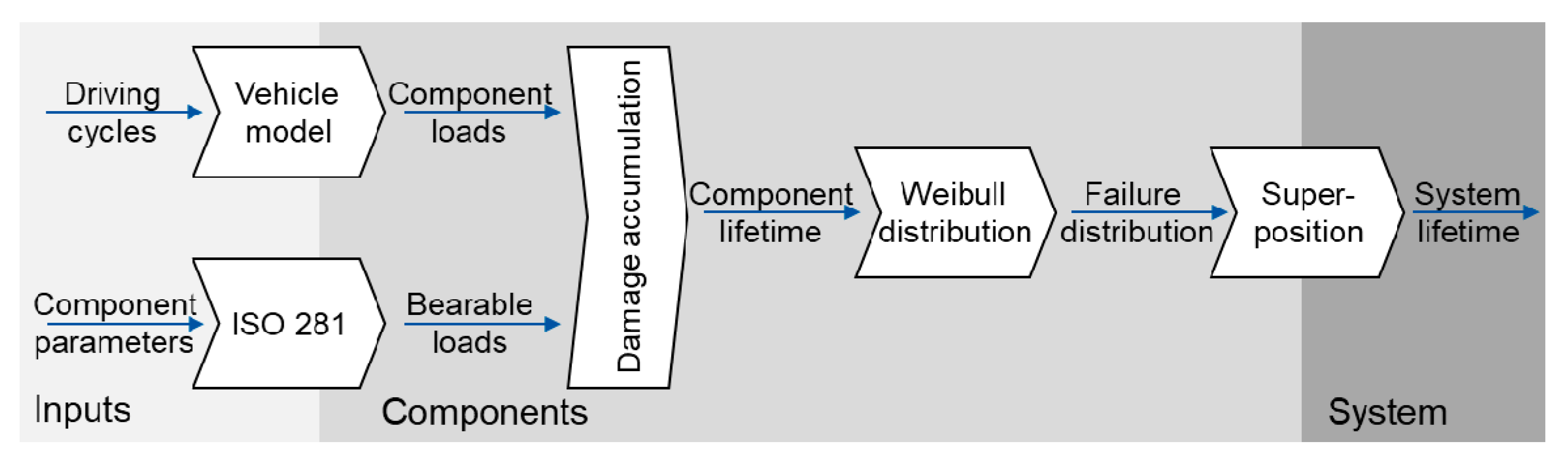
In this paper, the bearing lifetime of the transmission is calculated on the basis of damage due to material fatigue. For this, the approach according to
Figure 3 is applied. As shown in [
28], the approach can also be adapted to other machine elements that fail due to fatigue, such as gears or shafts. By making suitable assumptions, wear-related failures such as those of friction clutches or seals can also be calculated [
29], but these are omitted in this paper for brevity. The approach for considering component lifetime is based on existing standards and established procedures in the automotive industry. The core aspect of the approach is the comparison of occurring and bearable loads, which is necessary for the quantitative assessment of component lifetime [
26].
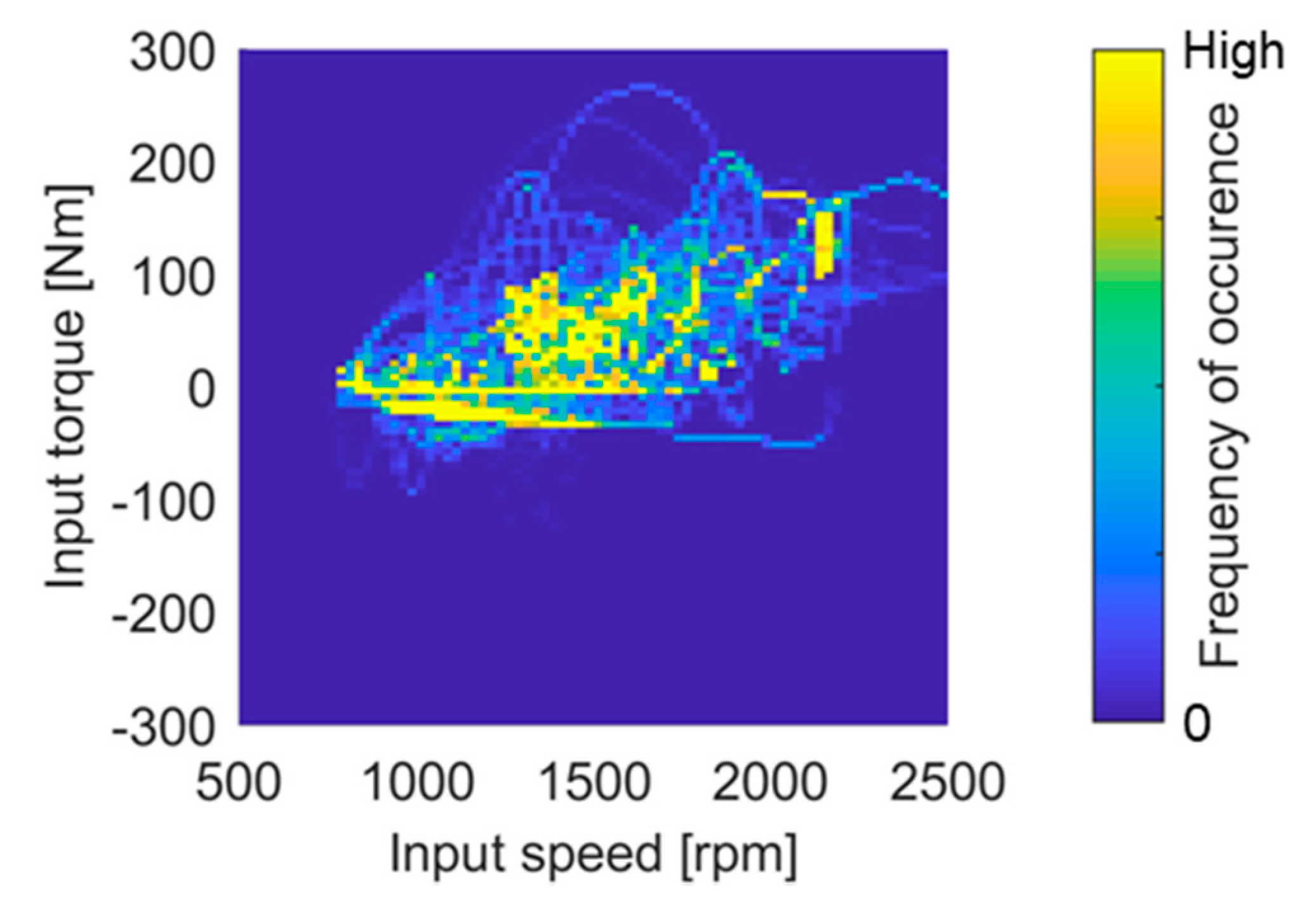
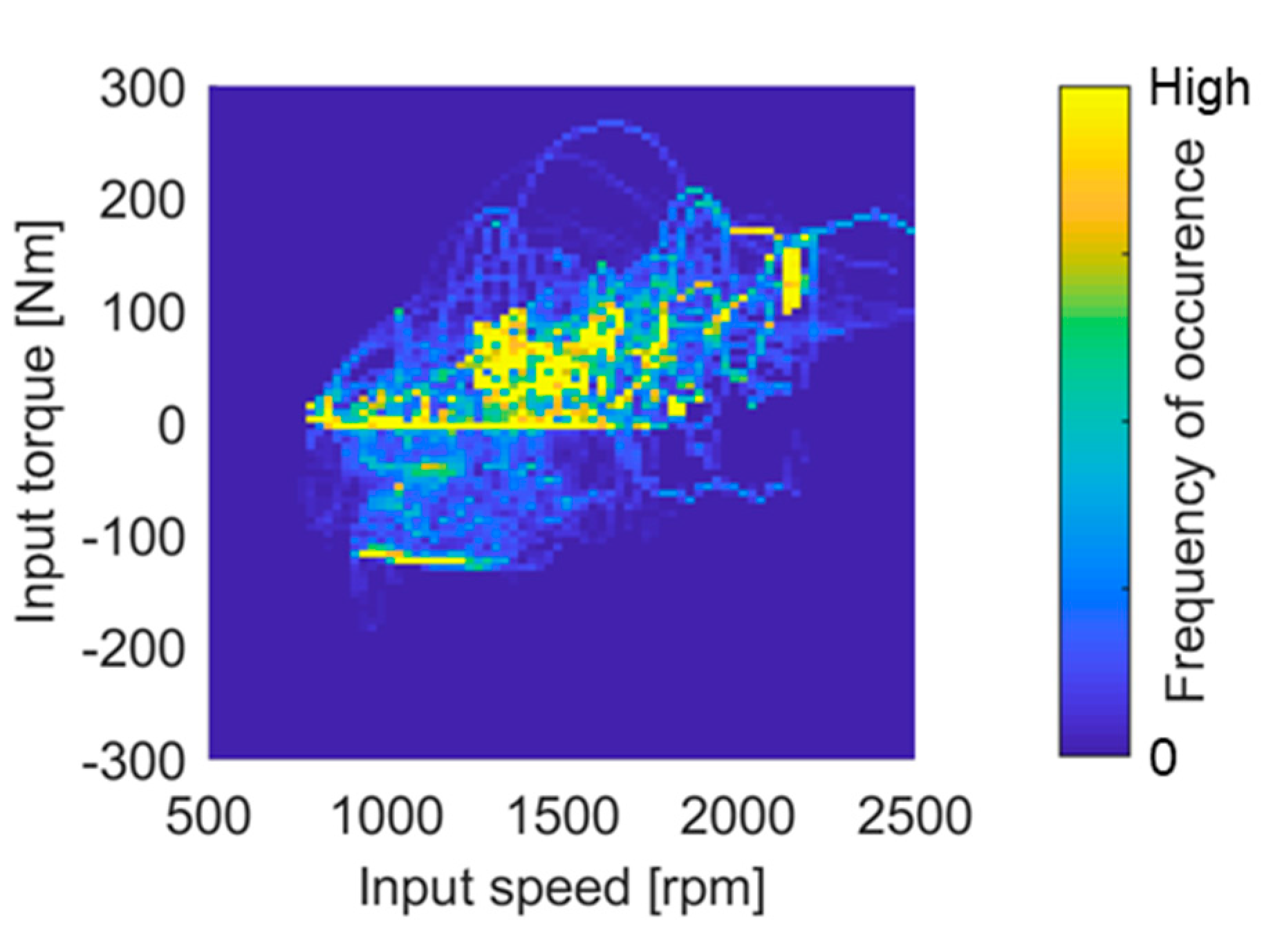
Here, a comparison is made computationally using a damage accumulation hypothesis. An alternative to simulation is testing, but this is usually associated with a high expenditure of time and money. Initially, driving cycles are defined to determine the bearing loads for the computational analysis. The cycles represent the assumed use of the transmission consisting of various boundary conditions such as driver, driving distance, special events and others. The influence of the vehicle is represented by a simulation model. The simulation model considers the interaction of the subsystems in a selected level of detail and outputs time-based records of the bearing loads (axial and radial forces) and their frequency of occurrence in the form of the rotational speed. The speed and load of the bearings depend on which gear is engaged, whether the vehicle accelerates or decelerates and whether gearshifts occur. In the case of measurement of the occurring loads, the bearing loads are typically calculated back from an easily measurable variable, such as the input torque of the transmission [
26]. Bearings can be subjected to a combined load from radial
and axial forces
. However, for the comparison of the occurring and bearable loads, a reduced quantity is required, i.e., the dynamically equivalent force
. The calculation is carried out according to Equation (1).
and
are the dynamic radial and axial load factor, respectively. They can either be obtained directly from the bearing manufacturer or calculated using analytical equations of ISO 281 [
30].
The resulting time records
per bearing are then simplified to load spectra with the aid of the two-parametric time-at-level counting [
31]. The occurring loads and speeds are divided into 64 classes according to the recommendation of [
32].
The bearable loads of the bearings required for the accumulation of damage are determined using ISO 281 [
30]. The possible number of rotations
of a load class
with a failure probability of 10% is obtained in 10
6 bearing revolutions, according to Equation (2).
The life modification factor
takes into account the type, quality and geometry of the bearing, as well as the fatigue limit of the raceway material [
30].
is the dynamic load rating of the bearing, and can be obtained from the bearing manufacturer. The exponent
is 3 for ball bearings and
for roller bearings.
is the dynamically equivalent bearing load of a load class. Information on the bearing data, taken from bearing manufacturer catalogues, can be found in
Table A1.
In the damage accumulation, occurring and bearable loads are compared and summed to yield damage
over all
load classes (Equation (3)).
denotes the number of bearing revolutions occurring for an individual load class in the cycle.
Based on the cumulative damage
and the cycle duration
, the component lifetime
of a bearing is calculated (Equation (4)).
The failure distribution of a single bearing
over time is described using the Weibull distribution (Equation (5)).
is the failure-free time and can take values between
and
for bearings [
32]. In this paper
is used.
is a shape parameter and equals 1.1 for ball bearings and 1.35 for roller bearings [
32]. The characteristic lifetime
of a single
is calculated using Equation (6).
The system failure distribution or the failure distribution of all bearings as a group
over time is calculated by a superposition of the failure probabilities of the individual bearings. Here, it is assumed that the group of bearings fails as soon as one bearing fails. The underlying Boolean relationship is given in Equation (7).
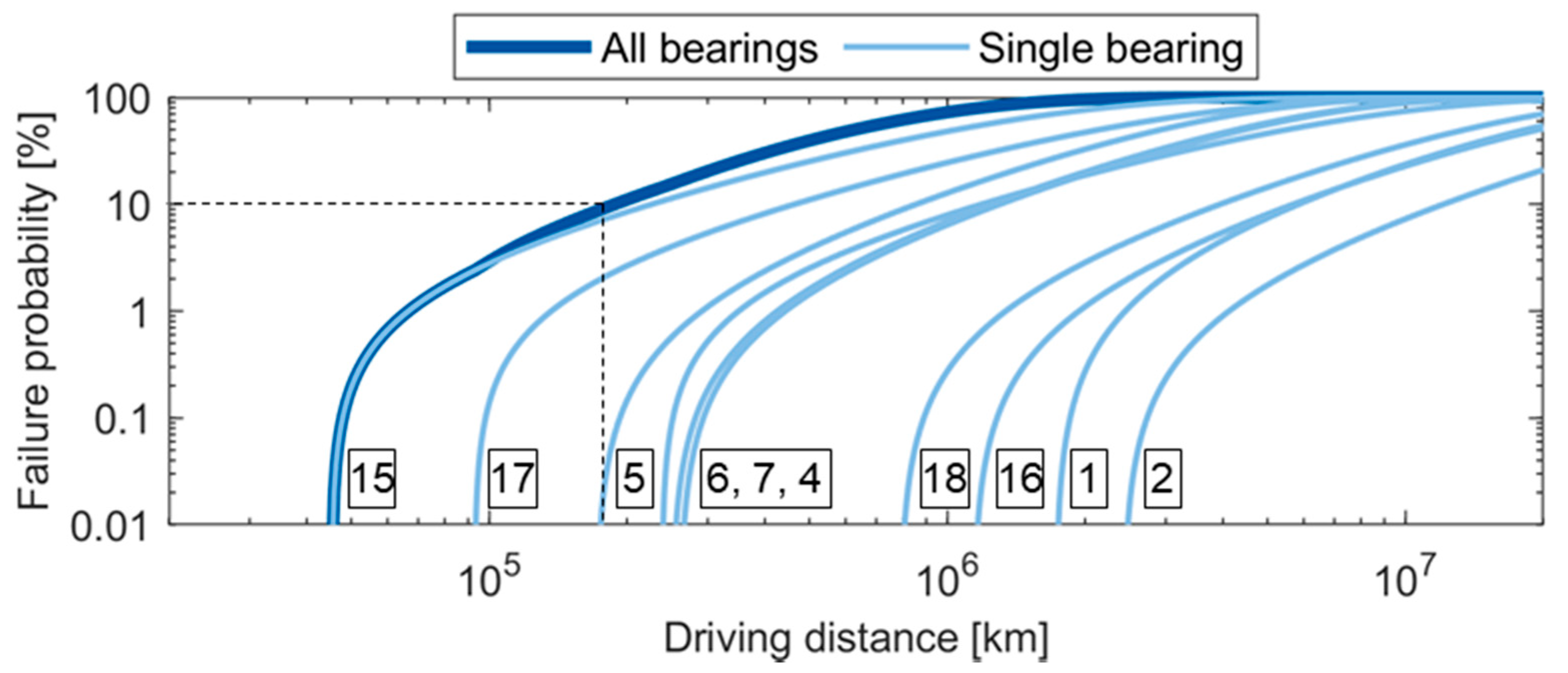
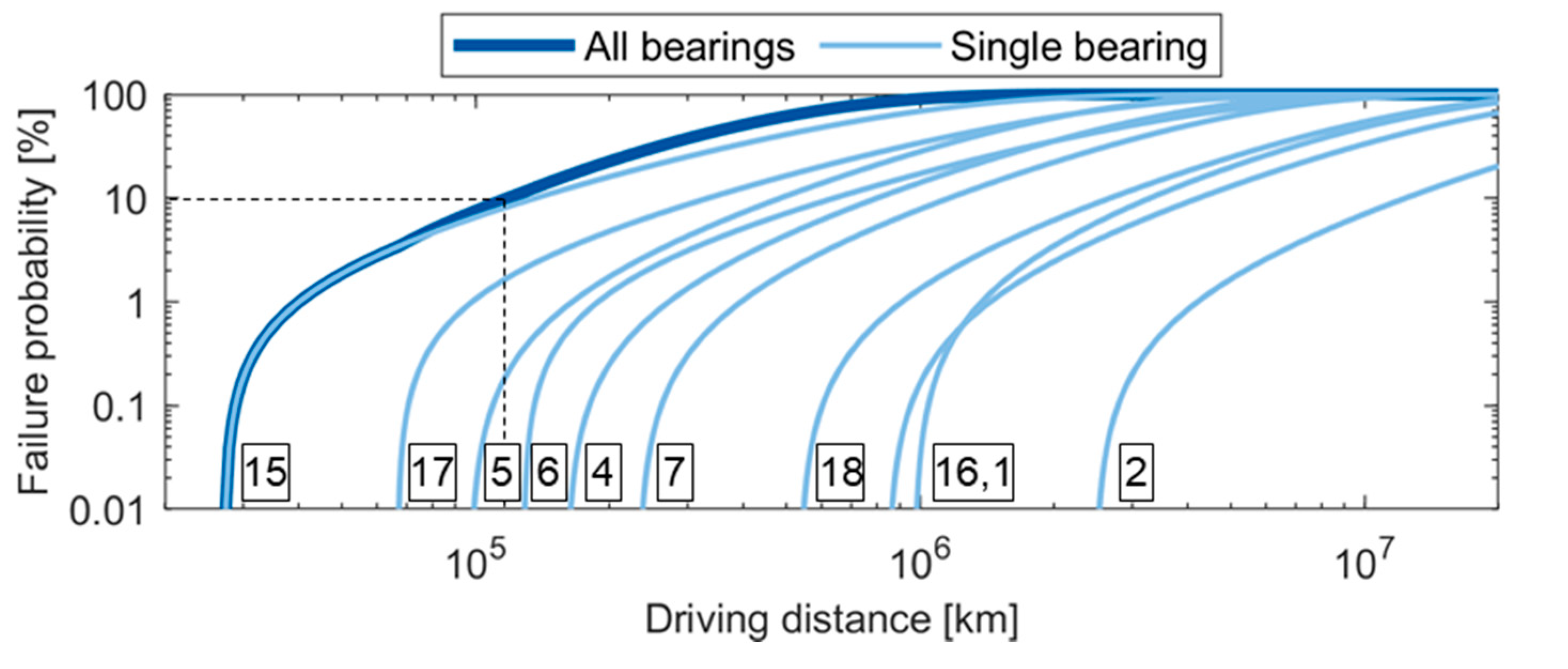
The system lifetime or the lifetime of all bearings as a group with a failure probability of 10% is the time at which reaches the value 0.1.
For further information on the approach described, we refer the reader to references [
28,
29].
2.3. System Model
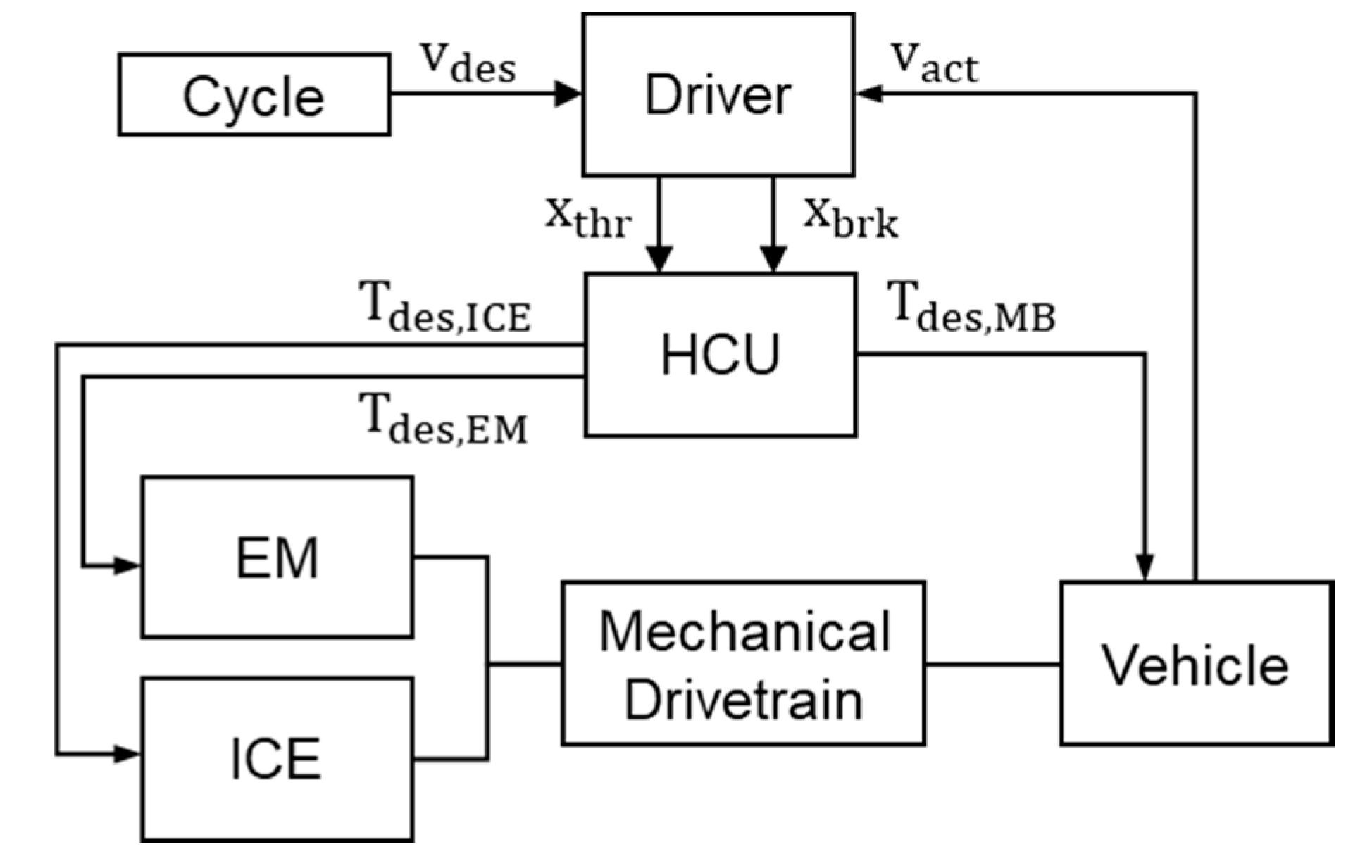
To determine the operating conditions of the bearings in terms of force and rotational speed, a detailed forward oriented overall vehicle model is built in Matlab/Simulink using the Simscape library. The high-level structure of the model is shown in
Figure 4. The submodels are divided into ICE, EM, mechanical drivetrain, vehicle, driver and hybrid control unit (HCU). On the input side, the model receives a driving cycle-dependent time-based desired velocity
. In the driver model, the desired velocity is compared to the actual velocity
and the deviation is converted into an accelerator
or brake pedal position
by a PI-controller.
The pedal positions are converted into desired torques of the ICE
, the EM
and the mechanical brake (MB)
by the HCU. In this paper, a simplified operating strategy is considered, since the influence of regenerative braking on the bearing lifetime of the transmission is investigated. The vehicle is driven purely by the ICE. The deceleration of the vehicle is implemented by splitting the braking torque between ICE, EM and the MB. For this, a required deceleration torque
is calculated from the brake pedal position. This deceleration torque is applied with priority by the drag torque of the ICE. The desired ICE torque is calculated according to Equation (8) with the current transmission gear ratio
(see
Table A2).
If the maximum drag torque
of the ICE is not sufficient for the deceleration of the vehicle, the EM is used as a generator (Equation (9)).
For stronger braking which cannot be achieved by the drag torque of the ICE and the generator operation of the EM
, the mechanical brake is applied (Equation (10)).
In the ICE model, the desired torque
is converted into an acting torque
by a first-order delay with a time constant of
[
33]. The maximum drive torque is limited in the model by a full load characteristic curve. For coast operation, an analytically derived thrust characteristic curve is used [
26], which decreases in proportion to engine speed to −10% of the nominal torque (
Figure 5a).
In the EM model, the desired torque
is converted into an acting torque
by a first-order delay with a time constant of
[
33]. The maximum deliverable motor and generator torques are limited by power hyperbolas and constant torque curves (
Figure 5b).
In the vehicle model, the effective driving resistance force
is calculated as a function of the vehicle velocity
according to Equation (11).
and
are driving resistance coefficients which cause constant and velocity proportional driving resistances.
causes a resistance force which is proportional to the square of the vehicle velocity. The values of the coefficients are listed in
Table A3.
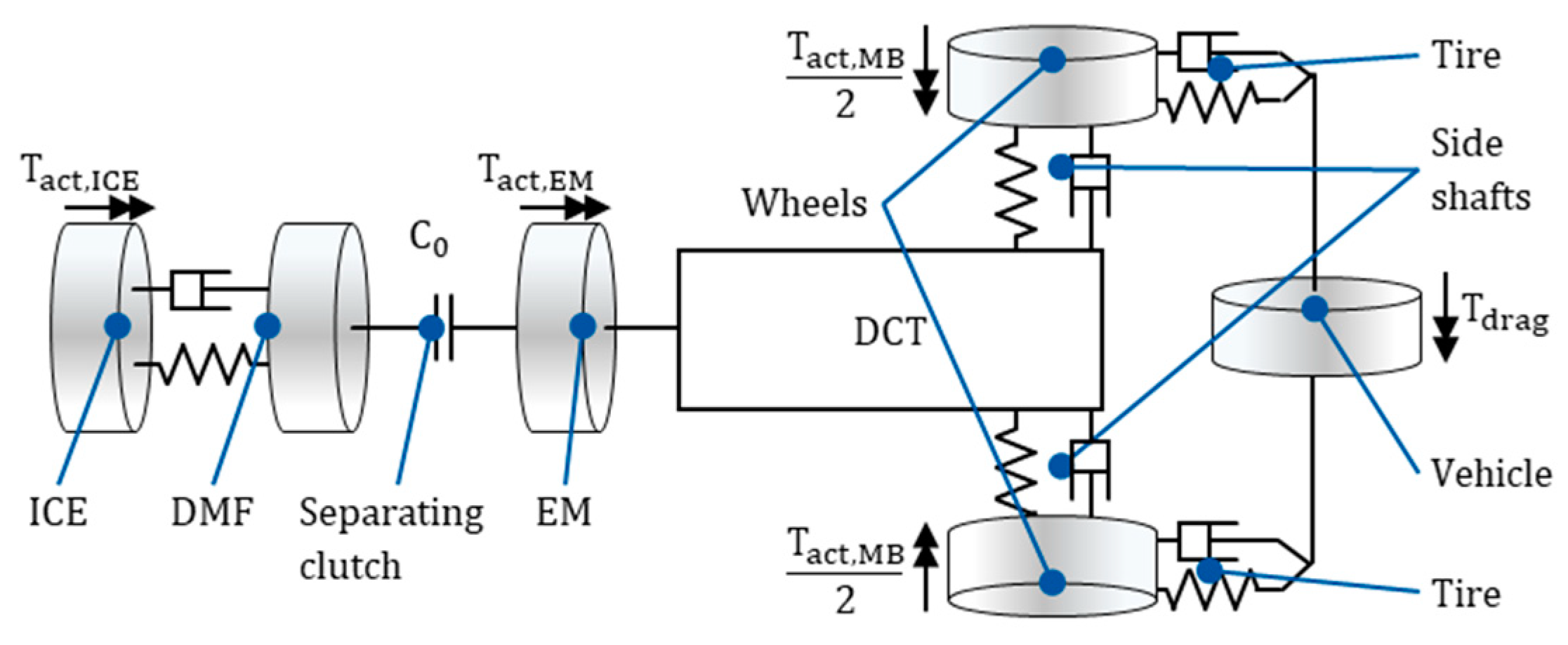
The forces and torques described above act on a torsional vibration model of the mechanical drivetrain (
Figure 6). Individual inertias are represented as cylinders connected by spring-damper combinations or clutches. External torques act through the ICE, EM, MB and driving resistance. For the recommended [
19] consideration of the lower natural frequencies of the drivetrain, the dual mass flywheel (DMF), the side shafts and the tires were modeled elastically [
34]. The wheel-to-ground contact is modelled ideally (i.e., ideal rolling), since special events such as loss of tire grip will not be investigated in this paper.
Since the vehicle motion is calculated in the torsional vibration model and the driving resistances are calculated in the translational degree of freedom, a transfer of the corresponding quantities is carried out with Equations (12) and (13).
is the equivalent driving resistance torque for a driving resistance force acting on the tire radius
. The vehicle velocity is calculated from the angular velocity of the equivalent inertia of the vehicle
in the torsional vibration model.
The motion of the individual drivetrain inertias is described in the torsional degree of freedom and is shown as an example for the vehicle inertia in Equation (14).
,
and
thus describe angular acceleration, angular velocity and angle of the corresponding inertia, respectively.
and
are stiffness and damping of the tires, respectively. The equivalent inertia of the vehicle
is calculated using Equation (15). The parameters of the torsional vibration model are summarized in
Table A4.
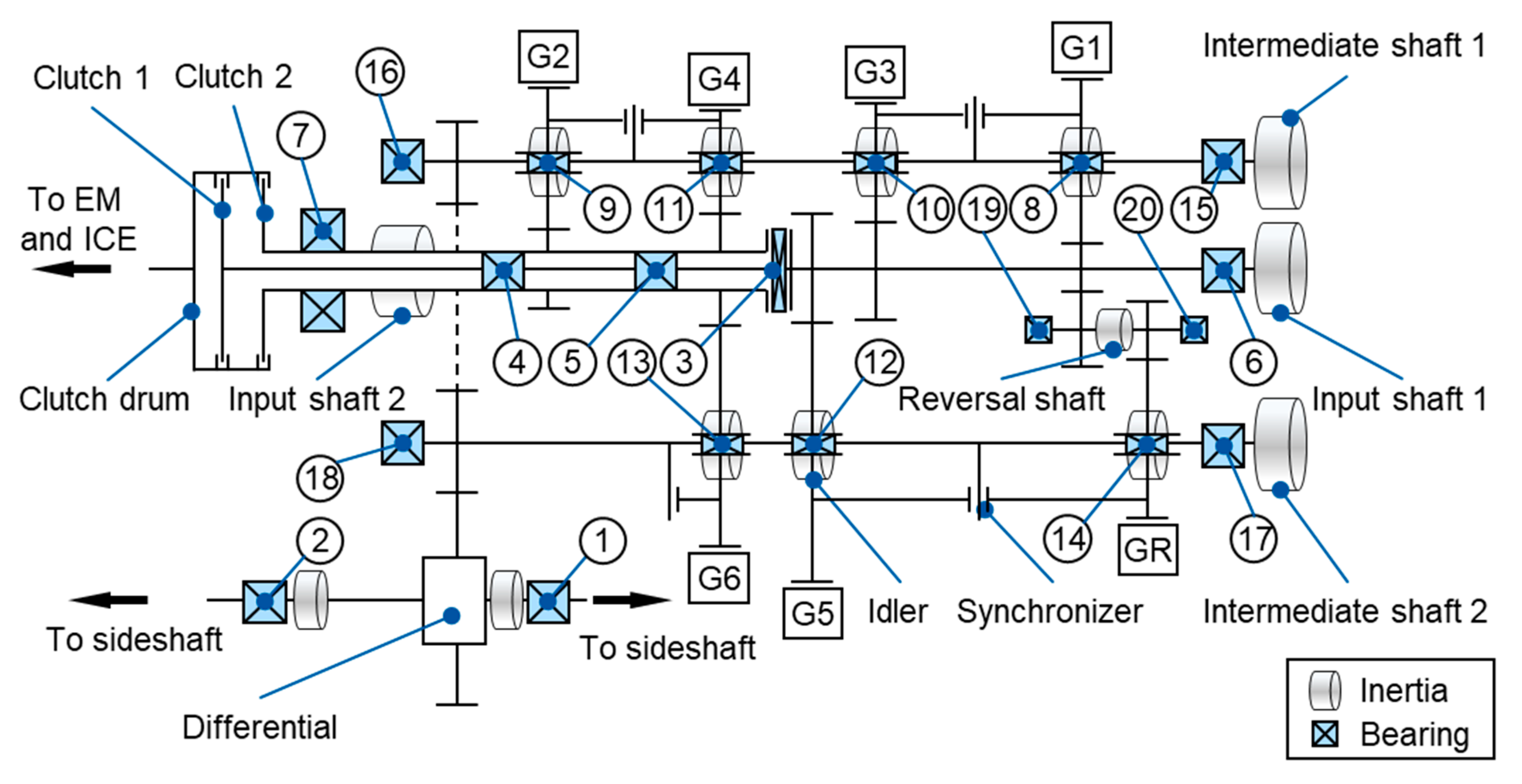
A rigid body model of the transmission (
Figure 2), including a transmission control unit (TCU), is embedded in the drivetrain model. The overall purpose of the transmission model is to calculate the motion and load condition of each bearing. The rotational speeds of the bearings directly result from the torsional motion of the model, which is calculated for each individual shaft using Equation (16).
is an individual shaft inertia in and
its corresponding angular acceleration.
are the torques acting on the shaft and consider driving torques and torque losses [
35].
The bearing loads result from the support of the tangential (
), radial (
) and axial (
) gear forces. To determine the bearing forces, static equilibria are evaluated for the individual transmission shafts (Equations (17) and (18)) at each time step. However, in Equation (18) only the bending moments are considered, since the torsional behavior is calculated in the rigid body model.
The forces are strongly dependent on the geometry of the shaft and gears, as well as the arrangement of the gears on the shaft.
Figure 7 shows an exemplary force diagram of intermediate shaft 1 for the calculation of bearing forces
and
. For illustration purposes, all forces are rotated into the section plane, since the tooth meshes are not arranged identically around the circumference for all gears. The locations (gear diameters
and shaft section lengths
) of the gear forces are considered in the model. FD is a gear of the final drive.
An acting tangential force
is calculated using Equation (19).
is the acting torque on a gear wheel. It is read from the transmission model at each time step, taking into account the meshing losses. The direction of the tangential force depends on the torque direction.
The acting radial force
is calculated using Equation (20).
is the normal pressure angle and
the helix angle of the corresponding gear. The amplitude of the radial force is dependent on the amplitude of the tangential force. Since the radial force is always oriented to the center of the gear, the radial force of an idler corresponds to its needle bearing load.
The axial force
is given by Equation (21). Its direction depends on the direction of the tangential force, as well as on the helix direction of the gear.
In addition to the calculation of the motion and load of the individual bearings, the influences of gear shifts, synchronizations and losses are taken into account. In gear shifts and synchronizations of gears, additional synchronization torques act in addition to the driving resistances, which cause higher gear forces and must ultimately be supported by the bearings. For this purpose, both input clutches and the seven synchronizers were modeled, which are operated by an implemented TCU on the basis of a shift map. This enables launching with the ICE and gear shifts without interrupting the tractive force. These friction elements have identical models that distinguish between a slip and a stick state. In the slip state, the torque capacity set by the TCU acts on the two neighboring inertias of the friction element as a synchronizing torque. If both speeds are synchronized, the friction element changes to the stick state and the torque transmitted by the friction element is limited by the set torque capacity. For reasons of simplification, the set torque of the TCU is applied without delay to the friction elements. To evaluate transmission losses, modules are implemented which take into account load-dependent and -independent bearing and gear losses, drag losses of the wet input clutches and seal losses. The loss calculation was validated in an earlier publication in large parts of the operating range of the transmission so that the calculated power flows were plausibly represented. For further information on the validation, transmission controls and loss calculation, we refer the reader to [
35].