Optimal Neural Tracking Control with Metaheuristic Parameter Identification for Uncertain Nonlinear Systems with Disturbances
Abstract
1. Introduction
2. Neural Observer Based on RHONN
3. Discrete-Time Inverse Optimal Control
Definition: Tracking Inverse Optimal Control
- (i)
- (global) asymptotic stability of along reference is achieved
- (ii)
- is a (radially unbounded) positive definite function and satisfies the inequality
4. Metaheuristic Optimization Algorithms
4.1. Ant Lion Optimizer
4.2. Grey Wolf Optimizer
4.3. Harris Hawks Optimization
4.4. Whale Optimization Algorithm
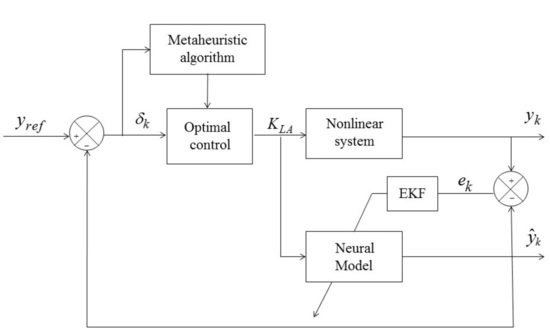
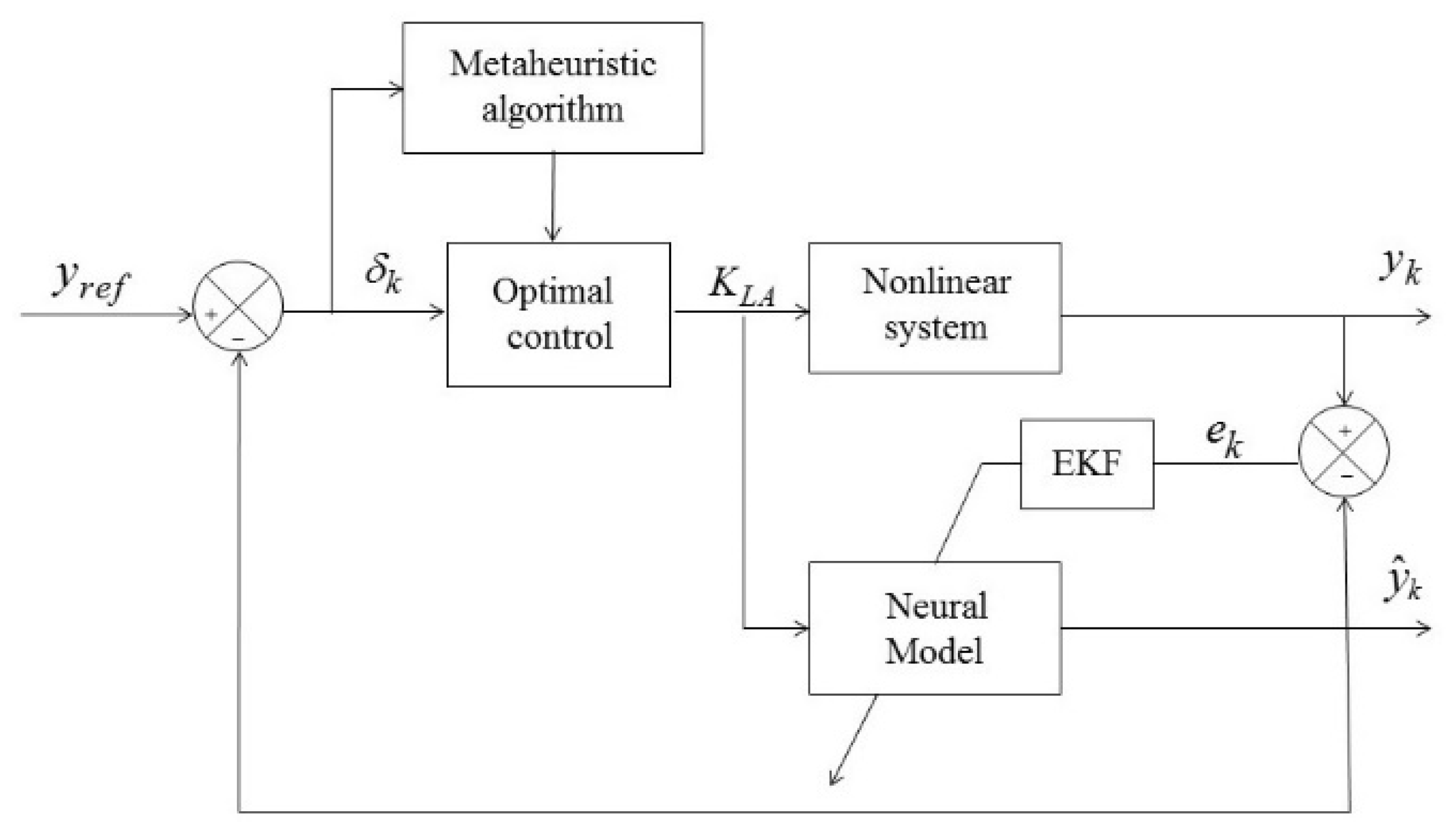
5. Optimal Control Strategy Architecture
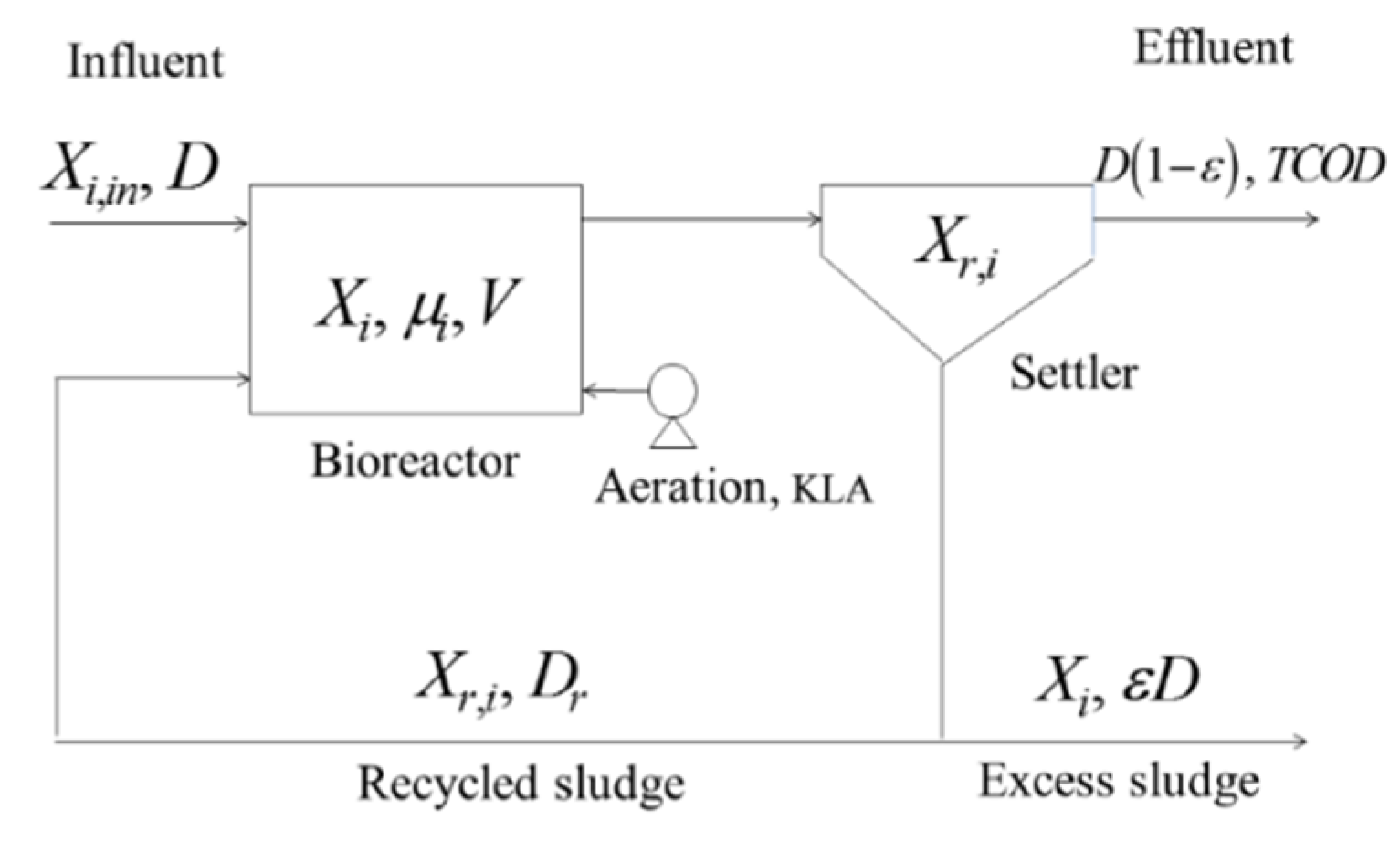
6. Case Study
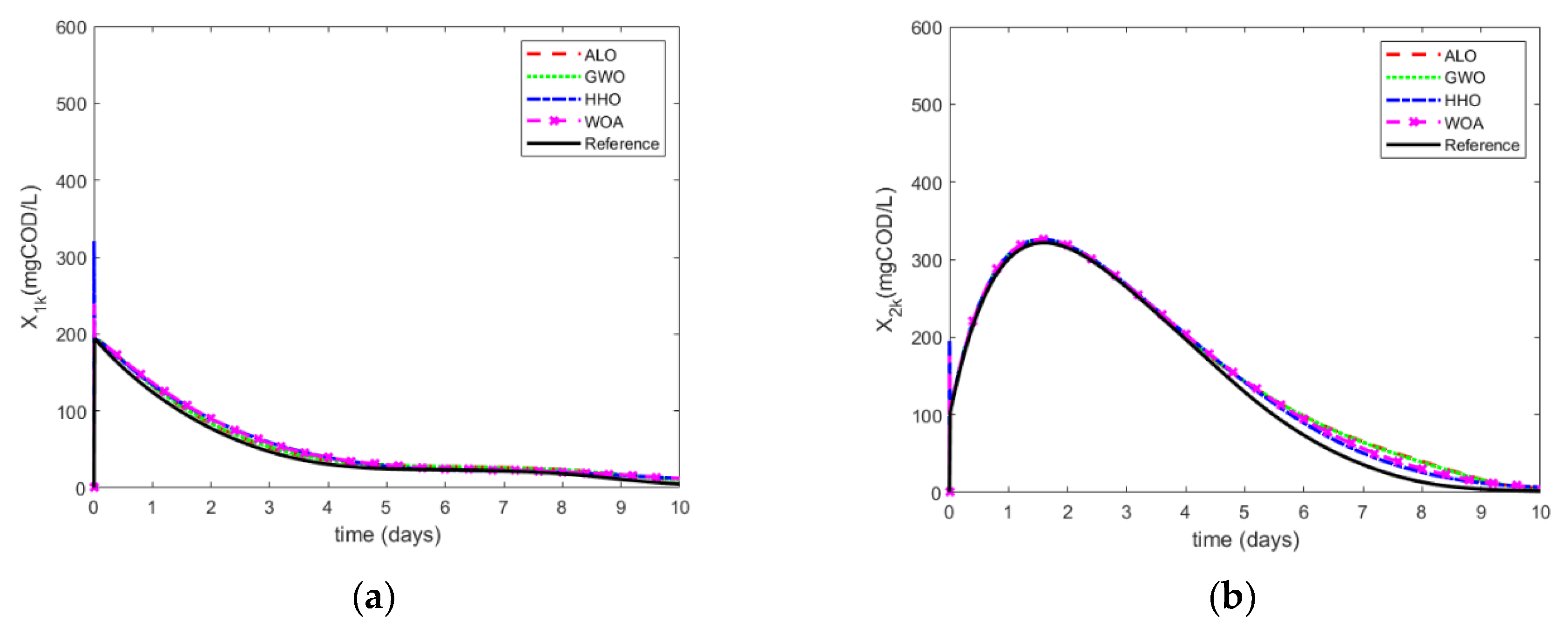
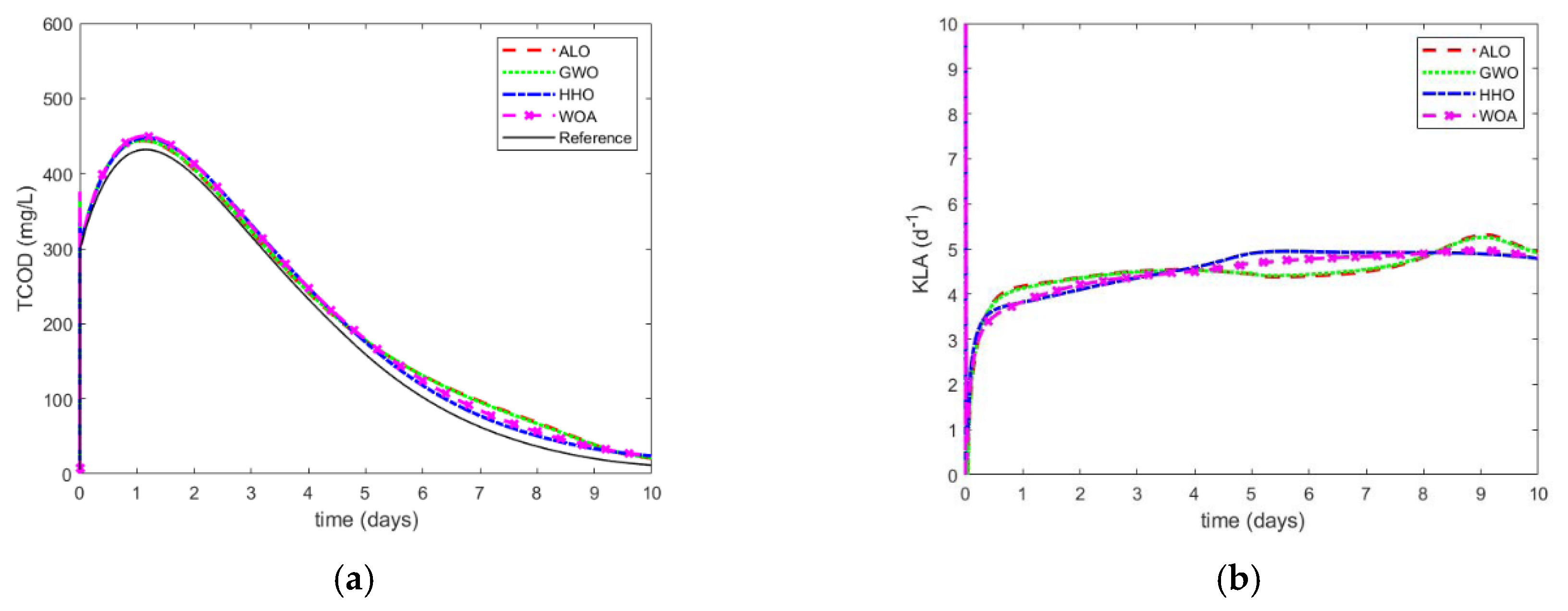
7. Results
7.1. External Disturbance
7.2. Parameter Uncertainty
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Stoichiometric Coefficient | |||
|---|---|---|---|
| Parameter | Values | Units | Description |
| YA | 0.24 | g COD/g N | Autotrophic yield coefficient |
| YH | 0.67 | g CDO/g COD | Heterotrophic yield coefficient |
| μmax,A | 0.8 | d−1 | Maximum specific growth rate for autotrophs |
| μmax,H | 6 | d−1 | Maximum specific growth rate for heterotrophs |
| μ1 | - | - | Monod kinetics for readily biodegradable soluble substrate |
| μ2 | - | - | Monod kinetics for the component X5,k as function of X4,k |
| μ3 | - | - | Monod kinetics for the component X5,k as function of X3,k |
| μ4 | - | - | Monod kinetics for soluble nitrate and nitrite nitrogen |
| μ5 | - | - | Monod kinetics for soluble ammonium nitrogen |
| μ6 | - | - | Inhibition kinetics for X5,k |
| μ7 | - | - | Saturation kinetics |
| b | 0.9 | - | Fraction coefficient for Dr |
| bA | 0.05 | d−1 | Autotrophic decay coefficient |
| bH | 0.22 | d−1 | Heterotrophic decay coefficient |
| fP | 0.08 | (-) | Fraction of biomass yielding particulate products |
| iXB | 0.086 | mg N/mg SS | Nitrogen content in biomass |
| iXP | 0.06 | mg N/mg SS | Nitrogen content in inert particulate |
| kA | 0.081 | L/g COD. d | Ammonification coefficient |
| kh | 3 | d−1 | Hydrolysis coefficient |
| 0.8 | (-) | Correction factor for anoxic growth of heterotrophs | |
| 0.4 | (-) | Correction factor for anoxic hydrolysis | |
| IS | 5 | mg COD/L | Concentration of soluble and particulate inert organic matter |
| CSTR Parameters | |||
| Parameter | Values | Units | Description |
| D | 2 | (d−1) | Dilution rate |
| Dr | 1 | (d−1) | Dilution recycle rate |
| KLA | - | d−1 | Oxygen transfer coefficient |
| Xi,in | 200 | mg COD/L | Initial condition of X1,k |
| X2,in | 100 | mg COD/L | Initial condition of X2,k |
| X3,in | 0 | mg COD/L | Initial condition of X3,k |
| X4,in | 0 | mg COD/L | Initial condition of X4,k |
| X5,in | 2 | mg/L | Initial condition of X5,k |
| X6,in | 1 | mg N/L | Initial condition of X6,k |
| X7,in | 15 | mg N/L | Initial condition of X7,k |
| X8,in | 9 | mg N/L | Initial condition of X8,k |
| X9,in | 0 | mg COD/L | Initial condition of X9,k |
| X5,max | 10 | mg/L | Maximum concentration of soluble oxygen |
| V | 15 | L | Tank volume |
| Parameter | Values | Units | Description |
|---|---|---|---|
| RZ | 0.2 | - | Weighting on control efforts |
| PL | a11 = 0.007444 a12 = a21 = 0.001412 a22 = 0.000546 | - | Symmetric matrix of CLF (found by metaheuristic algorithm) |
| Parameter | Values | Units | Description |
|---|---|---|---|
| P1,(0) | 1400 | - | prediction error associated covariance matrix for X1,k estimation |
| Q1,(0) | 1 | - | state noise associated covariance matrix for X1,k estimation |
| R1,(0) | 61 | - | measurement noise associated covariance matrix for X1,k estimation |
| P2,(0) | 1500 | - | prediction error associated covariance matrix for X2,k estimation |
| Q2,(0) | 1.3 | - | state noise associated covariance matrix for X2,k estimation |
| R2,(0) | 63 | - | measurement noise associated covariance matrix for X2,k estimation |
| η1 | 2 | - | EKF learning rate for X1,k estimation |
| η2 | 1.07 | - | EKF learning rate for X2,k estimation |
| W1 | [6 × 1] = 0.1 | - | Weight vector for X1,k estimation (online learned) |
| W2 | [6 × 1] = 0.5 | - | Weight vector for X2,k estimation (online learned) |
| g1, g2 | [1 × 2] = 0.12 | - | Luenberger gains |
| Ki,k | - | - | Kalman gain matrix |
| Mi,k | - | - | Global scaling matrix |
References
- Kumar, A.; Jain, T. Sub-optimal Control Design for Second Order Non-linear Systems using Krotov Sufficient Conditions. IFAC Pap. 2020, 53, 272–276. [Google Scholar] [CrossRef]
- Yu, Q.; Hou, Z.; Bu, X.; Yang, J. Observer-based data-driven constrained norm optimal iterative learning control for unknown non-affine non-linear systems with both available and unavailable system states. J. Frankl. Inst. 2020, 357, 5852–5877. [Google Scholar] [CrossRef]
- Ballesteros, M.; Chairez, I.; Poznyak, A. Robust optimal feedback control design for uncertain systems based on artificial neural network approximation of the Bellman’s value function. Neurocomputing 2020, 413, 134–144. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Wang, M.; Lee, K.Y. Intelligent predictive control of large-scale solvent-based CO2 capture plant using artificial neural network and particle swarm optimization. Energy 2020, 196, 117070. [Google Scholar] [CrossRef]
- Gurubel, K.J.; Sanchez, E.N.; Coronado-Mendoza, A.; Zuniga-Grajeda, V.; Sulbaran-Rangel, B.; Breton-Deval, L. Inverse optimal neural control via passivity approach for nonlinear anaerobic bioprocesses with biofuels production. Optim. Contr. Appl. Methods 2019, 40, 848–858. [Google Scholar] [CrossRef]
- Mcclamroch, N.H.; Kolmanovsky, I. Performance benefits of hybrid control design for linear and nonlinear systems. Proc. IEEE 2000, 88, 1083–1096. [Google Scholar] [CrossRef]
- Gurubel, K.J.; Sanchez, E.N.; González, R.; Coss y León, H.; Recio, R. Artificial Neural Networks Based on Nonlinear Bioprocess Models for Predicting Wastewater Organic Compounds and Biofuel Production. In Artificial Neural Networks for Engineering Applications; Academic Press: St. Louis, MI, USA, 2019; pp. 79–96. [Google Scholar] [CrossRef]
- Alanis, A.Y.; Sanchez, E.N. Discrete-Time Neural Observers: Analysis and Applications; Academic Press: London, UK, 2017. [Google Scholar]
- Alanis, A.Y.; Sanchez, E.N.; Loukianov, A.G.; Hernandez, E.A. Discrete-time recurrent high order neural networks for nonlinear identification. J. Frankl. Inst. 2010, 347, 1253–1265. [Google Scholar] [CrossRef]
- Siregar, S.P.; Wanto, A. Analysis of Artificial Neural Network Accuracy Using Backpropagation Algorithm In Predicting Process (Forecasting). Int. J. Inf. Syst. Technol. 2017, 1, 34–42. [Google Scholar] [CrossRef]
- Pisa, I.; Morell, A.; Vicario, J.L.; Vilanova, R. Denoising Autoencoders and LSTM-Based Artificial Neural Networks Data Processing for Its Application to Internal Model Control in Industrial Environments-the Wastewater Treatment Plant Control Case. Sensors 2020, 20, 3743. [Google Scholar] [CrossRef]
- Schmitt, F.; Banu, R.; Yeom, L.-T.; Do, K.-U. Development of artificial neural networks to predict membrane fouling in an anoxic-aerobic membrane bioreactor treating domestic wastewater. Biochem. Eng. J. 2018, 133, 47–58. [Google Scholar] [CrossRef]
- Sadeghassadi, M.; Macnab, C.J.B.; Gopaluni, B.; Westwick, D. Application of neural networks for optimal-setpoint design and MPC control in biological wastewater treatment. Comput. Chem. Eng. 2018, 115, 150–160. [Google Scholar] [CrossRef]
- Leon, B.S.; Alanis, A.Y.; Sanchez, E.N.; Ornelas-Tellez, F.; Ruiz-Velazquez, E. Neural Inverse Optimal Control via Passivity for Subcutaneous Blood Glucose Regulation in Type 1 Diabetes Mellitus Patients. Intell. Autom. Soft. Comput. 2014, 20, 279–295. [Google Scholar] [CrossRef]
- Mirjalili, S.; Dong, J.S.; Lewis, A. Nature-Inspired Optimizers: Theories, Literature Reviews and Applications; Springer: Cham, Switzerland, 2019; Volume 811. [Google Scholar] [CrossRef]
- Heidari, A.A.; Faris, H.; Mirjalili, S.; Aljarah, I.; Mafarja, M. Ant lion optimizer: Theory, literature review, and application in multi-layer perceptron neural networks. In Nature-Inspired Optimizers; Springer: Cham, Switzerland, 2020; pp. 23–46. [Google Scholar] [CrossRef]
- Fathy, A.; Kassem, A.M. Antlion optimizer-ANFIS load frequency control for multi-interconnected plants comprising photovoltaic and wind turbine. ISA Trans. 2019, 87, 282–296. [Google Scholar] [CrossRef]
- Pradhan, R.; Majhi, S.K.; Pradhan, J.K.; Pati, B.B. Antlion optimizer tuned PID controller based on Bode ideal transfer function for automobile cruise control system. J. Ind. Inf. Integr. 2018, 9, 45–52. [Google Scholar] [CrossRef]
- Verma, S.; Mukherjee, V. Optimal real power rescheduling of generators for congestion management using a novel ant lion optimiser. IET Gener. Transm. Dis. 2016, 10, 2548–2561. [Google Scholar] [CrossRef]
- Gupta, E.; Saxena, A. Performance evaluation of antlion optimizer based regulator in automatic generation control of interconnected power system. J. Eng. 2016. [Google Scholar] [CrossRef]
- Saikia, L.C.; Sinha, N. Automatic generation control of a multi-area system using ant lion optimizer algorithm based PID plus second order derivative controller. Int. J. Electr. Power. 2016, 80, 52–63. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Oliveira, J.; Oliveira, P.M.; Boaventura-Cunha, J.; Pinho, T. Evaluation of Hunting-Based Optimizers for a Quadrotor Sliding Mode Flight Controller. Robotics 2020, 9, 22. [Google Scholar] [CrossRef]
- Arefi, M.; Chowdhury, B. Post-fault transient stability status prediction using Grey Wolf and Particle Swarm Optimization. In Proceedings of the SoutheastCon 2017, Charlotte, NC, USA, 30 March–2 April 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Tien Bui, D.; Abdullahi, M.M.; Ghareh, S. Fine-tuning of neural computing using whale optimization algorithm for predicting compressive strength of concrete. Eng. Comput. 2019. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Generat. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Devarapalli, R.; Bhattacharyya, B. Application of Modified Harris Hawks Optimization in Power System Oscillations Damping Controller Design. In Proceedings of the 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Alanis, A.Y.; Sanchez, E.N.; Ricalde, L.J. Discrete-time reduced order neural observers for uncertain nonlinear systems. Int. J. Neural Syst. 2010, 20, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Haykin, S. Kalman Filtering and Neural Networks; John Wiley & Sons: New York, NY, USA, 2004; Volume 47. [Google Scholar]
- Sanchez, E.N.; Alanís, A.Y.; Loukianov, A.G. Discrete-Time High Order Neural Control Trained with Kalman Filtering; Springer: Berlin, Germany, 2008. [Google Scholar]
- Sanchez, E.N.; Ornelas-Tellez, F. Discrete-Time Inverse Optimal Control for Nonlinear Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wang, D.; Liu, D.; Wei, Q.; Zhao, D.; Jin, N. Optimal control of unknown nonaffine nonlinear discrete-time systems based on adaptive dynamic programming. Automatica 2012, 48, 1825–1832. [Google Scholar] [CrossRef]
- Henze, M.; Gujer, W.; Mino, T.; van Loosdrecht, M.C. Activated Sludge Models ASM1, ASM2, ASM2d and ASM3; IWA Publishing: London, UK, 2000. [Google Scholar]
- Nelson, M.I.; Sidhu, H.S. Analysis of the activated sludge model (number 1). Appl. Math. Lett. 2009, 22, 629–635. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Recio-Colmenares, R.; Gurubel-Tun, K.J.; Zúñiga-Grajeda, V. Optimal Neural Tracking Control with Metaheuristic Parameter Identification for Uncertain Nonlinear Systems with Disturbances. Appl. Sci. 2020, 10, 7073. https://doi.org/10.3390/app10207073
Recio-Colmenares R, Gurubel-Tun KJ, Zúñiga-Grajeda V. Optimal Neural Tracking Control with Metaheuristic Parameter Identification for Uncertain Nonlinear Systems with Disturbances. Applied Sciences. 2020; 10(20):7073. https://doi.org/10.3390/app10207073
Chicago/Turabian StyleRecio-Colmenares, Roxana, Kelly Joel Gurubel-Tun, and Virgilio Zúñiga-Grajeda. 2020. "Optimal Neural Tracking Control with Metaheuristic Parameter Identification for Uncertain Nonlinear Systems with Disturbances" Applied Sciences 10, no. 20: 7073. https://doi.org/10.3390/app10207073
APA StyleRecio-Colmenares, R., Gurubel-Tun, K. J., & Zúñiga-Grajeda, V. (2020). Optimal Neural Tracking Control with Metaheuristic Parameter Identification for Uncertain Nonlinear Systems with Disturbances. Applied Sciences, 10(20), 7073. https://doi.org/10.3390/app10207073