Resonant Transmission Through a Single Subwavelength Slit for Varied Metallic Permittivities and Its Modal Orthogonality

Featured Application

The results obtained in this work provide a useful set of benchmark data to interpret experimental results and to inform design efforts of slit-based structures in the terahertz range. The present method of analysis can also be applicable to problems involving multiple slits with different widths.

Abstract

This article investigates resonant transmission phenomena through a single metallic subwavelength slit when the permittivity of a real metal varies. The single metallic slit is utilized as a metal–insulator–metal waveguide, and a mode-matching technique is employed to obtain the transmitted power. The periodic resonant transmission phenomena (in terms of the metallic plate thickness) are solved, and the resonances can be understood by their guide wavelengths. Even when the permittivity of the real metal includes imaginary parts (i.e., metal with loss), the resonant transmittances are obtained. However, the peaks of the transmittances decrease, as the plate thickness increases. The orthogonal relationship of an incomplete orthogonal set is maintained despite metallic loss (given a relatively small amount of loss), due to the complex permittivity of the real metal.

1. Introduction

Electromagnetic resonant transmission through one- or two-dimensional slits has been discussed for several decades, and research on extraordinary optical transmission [1,2,3,4] has led to significant physical and practical achievements. In earlier research [5,6], perforated metallic plates are generally assumed to be perfect electric conductors (PECs), and corresponding resonant transmission characteristics through PEC slits were investigated. However, studies were limited to the microwave or millimeter-wave regimes and did not extend to the terahertz (THz) range. Therefore, it remains important to investigate resonant transmission phenomena through real metallic slits by considering actual permittivities of metals, when the frequency goes beyond the microwave range. To extend transmittance study to the THz range, the geometry of a metal–insulator–metal (MIM) waveguide was adopted, and the resulting modes formed in the MIM waveguide were examined. The resonant transmission phenomena were then systematically analyzed through a real metallic slit in the THz range [7,8,9]. Thanks to this fundamental research, resonant transmission phenomena have been investigated at wide THz frequencies by taking into account actual permittivities for various real metals [10,11] and discussing transmittances through periodic metallic slits [12]. These studies found that transmittance phenomena through metallic slits are similar to those in PEC cases at lower frequencies. However, large discrepancies are apparent at higher THz frequencies [10].

Slit transmittances in wide THz ranges can usually be solved easily via the finite-difference time-domain (FDTD) or finite element method [13,14] and etc. [15,16]. While transmittance results can be obtained directly under those methods, their physical meanings are not easily understood using such “brute-force” numerical techniques. Brute-force numerical techniques require substantial numbers of mesh grids, causing corresponding numerical dispersion errors to increase gradually at higher frequencies [14]. By contrast, the mode-matching technique (MMT) does not require grids and, consequently, has no dispersion errors. The MMT also provides physical meanings by obtaining the guide wavelengths of an MIM waveguide, making it easy to understand the resonant transmittance as a function of the metallic plate thickness. Once the eigenvalues for the geometry are obtained herein, then the transmittances as a function of the plate thickness can be resolved easily.

Since electromagnetic waves do not penetrate into a PEC, no mode in the PEC region needs to be accounted for. For actual metallic plates, however, modes in the metallic region should be considered, because a tiny amount of each mode permeates into the metallic region due to their finite conductivities. To be precise, modal components in the metallic region (as well as the slit region) should be fully considered when solving transmittances. In addition, for the finite conductivity of a metal, orthogonal properties are not completely satisfied, while the orthogonality for the PEC MIM waveguide is completely fulfilled. Therefore, a validation issue of slit transmittances could be raised for real metallic slits in accordance with orthogonality.

In this research, the procedure obtaining the transmittances by the MMT is as follows. First, the modes constituting each region in the free space and an MIM waveguide need to be obtained in advance. To calculate modal eigenvalues in the MIM waveguide, a dispersion equation should be applied [9]. Then, tangential incident, reflected, and transmitted electromagnetic fields are set to be continuous at each junction. The unknowns in the electromagnetic field equations can be solved though the system of equations, and the reflection and transmission coefficients can be determined. The overall reflected and transmitted electromagnetic fields of a single-slit geometry can be obtained by using multiregion problems. The entire computing procedure is listed and explained in detail in [10].

The results using the MMT in this paper have several unique features compared to previous studies in the following aspects. First, resonant transmittance patterns are studied in detail as a function of the permittivity of a real metal, when the metal is lossy. Then, periodic transmission peaks and attenuations are examined, as the thickness of the plate increases. We also observe changes in guide wavelengths and resonant transmittances, as the imaginary part of the permittivity of the metal decreases, which cannot be obtained by other numerical techniques, such as the FDTD method or finite element method. Finally, orthogonal relations are thoroughly studied for lossless and lossy metallic plates.

These resonant transmissions or extraordinary transmissions can be applied to practical devices like band-selective spatial filters [17,18] and chemical sensors [19,20]. In addition, controllable dual transmissions have attracted significant attention to research societies, because these phenomena can be practically applicable to research areas such as switching, sensing, polarimetry microscopy, hyperspectral imaging, and security encryption [21,22,23,24,25,26].

In this paper, a dispersion equation applied into the MMT formulation is explained first. Two transmission quantities are subsequently introduced, before the transmittances for lossless metals are obtained. Transmission characteristics for the lossy metal case are then computed, and the results are compared with the lossless case. The modal orthogonal relation, which is an important prerequisite of the MMT, is finally discussed when considering both lossy and lossless metals.

2. Transmission Cross-Sections (TCSs) through a Subwavelength Slit for a Lossless Conducting Plate

Figure 1 shows the geometry of an MIM waveguide, including a gap width of 2g and a metal plate thickness of d. In this section, 2g is fixed as 0.03λ₀, while d is a variable and the structure is constant along the y-axis. An electromagnetic plane wave with parallel polarization propagates along the z-axis. In the metallic region, the permittivity of the metal ε_r is generally negative and will be varied in this work to investigate resonant transmittances. We consider only even modes, because even modes are sufficient for describing normal incidence in the MIM waveguide.

The dispersion equation is the most fundamental equation in the MIM waveguide and obtained as follows [10]:

tanh(κ_i,ng) = −(κ_m,n × ε_r,i)/(κ_i,n × ε_r,m),

(1)

where (k_z,n)² = (κ_m,n)² + ω²με_r,m = (κ_i,n)² + ω²με_r,i,

(2)

where ε_r,m and ε_r,i are permittivities in the metal and the insulator, respectively, κ_m,n and κ_i,n are nth transverse propagation constants in the metal and the insulator, respectively, and k_z,n is the nth propagation constant along the z-axis. The subscripts n in κ_m,n, κ_i,n, and k_z,n commonly indicate the nth modes, which are coupled to one another in Equation (2). The roots {κ_m,n}s of the dispersion equation are found using Muller’s method [10] while varying the geometrical parameter of 2g and the relative permittivity of ε_r,m for the metal.

The TCS transmitted into the right free space is defined as:

$$\mathrm{TCS}\left[m\right]=\frac{P_t}{W_i}=\frac{1}{2W_i}{\int }_S\mathit{Re}[\overrightarrow{E}\times \overrightarrow{H}{}^{*}]\cdot \left({\overrightarrow{a}}_{z}ds\right),$$

(3)

where P_t and W_i are transmitted power (W) and incident power density (W/m), respectively. As another quantity, the transmittance into the right free space is also widely used [6,10] and defined as:

$$\tau \left[\mathrm{dimensionless}\right]=\frac{1}{2g}\frac{P_t}{W_i}=\frac{1}{2g}\cdot \frac{1}{2W_i}{\int }_S\mathit{Re}[\overrightarrow{E}\times \overrightarrow{H}{}^{*}]\cdot \left({\overrightarrow{a}}_{z}ds\right).$$

(4)

From Equation (3), the TCSs were obtained by the MMT and plotted in Figure 2a–d as a function of the permittivities of real metals. Figure 2a shows the TCS through a PEC slit versus the thickness of a metallic plate of d. The maximum periodic TCSs are observed at a plate thickness of (0.486 + 0.5n)λ₀, where n is an integer. Figure 2b–d shows the TCSs in terms of thickness of the metallic plate when the permittivities of a metal ε_r,m are −2000, −100, and −5, respectively. The maximum periodic TCSs in Figure 2b–d are also observed at specific thicknesses of the metallic plate. The value of the maximum TCS for the PEC case in Figure 2a is found to be about 0.3183, which is the same as a known theoretical value [27]. By contrast, the maximum TCSs in Figure 2b–d do not reach the theoretical TCS value, because the incident wave from Figure 1 is slightly absorbed into the metallic plate. This could be understood by the fact that a lower metallic permittivity causes greater incident wave absorption into the metallic region [9]. From Equation (4), the transmittance τ is obtained as described in the inset of Figure 2a. While the pattern is the same as the TCS, numerical values and transmitting units are different, as represented in Equation (4).

Guide wavelengths are helpful to understand resonant transmission characteristics and can be solved from Equations (1) and (2). The guide wavelength λ_g for each MIM waveguide in Figure 1 is listed in

Table 1. Guide wavelengths with respect to metallic permittivities and computed maximum TCS intervals.

Permittivities in Metal	Guide Wavelength (ΛG)	Maximum TCS Interval
PEC	1.0λ0	0.5λ0
εr = −2000	1.1124λ0	0.4495λ0
εr = −100	1.4406λ0	0.3471λ0
εr = −5	3.0307λ0	0.1650λ0

. The values of λ_g for cases of low permittivity are relatively great, while the λ_g values for high permittivity cases are smaller. Meanwhile, the intervals of TCSs peaks were obtained as 0.5λ₀ and 0.1650λ₀ for the PEC and the metallic permittivity of −5, respectively, as found in Figure 2. These intervals, computed by the MMT, are exactly the same as 1/(2λ_g), as listed in the last column of Table 1. Therefore, resonant transmission phenomena were systematically solved as a function of metallic permittivity, and their periodicity can be easily understood.

3. Transmittance through a Subwavelength Slit on a Real Metallic Plate

In Section 2, transmittance results were obtained, when a metal was a PEC or lossless conductor having a finite conductivity, and transmittances for lossy metals are discussed in this section. Figure 1 is again adopted for the geometry, but the conductor is changed into a realistic metal characterized by a finite conductivity with loss, which depends on the function of THz frequencies. The relative permittivity of a real metal has not only a real part, but also an imaginary part considering metallic loss. The metal we deal with is silver (Ag), and its relative permittivity is −14.88 − j0.39 when λ₀ = 582.08 nm [28]. The complex numbered ε_r,m can be inserted into the dispersion equation known as Equation (1). The corresponding transverse propagation constants (κ_m,n and κ_i,n) and propagation constant (k_z,n), which are all complex numbers, can then be easily solved. The reflection and transmission coefficients at each boundary can be subsequently calculated by the MMT, obtaining the overall transmission results [9,10,11,12].

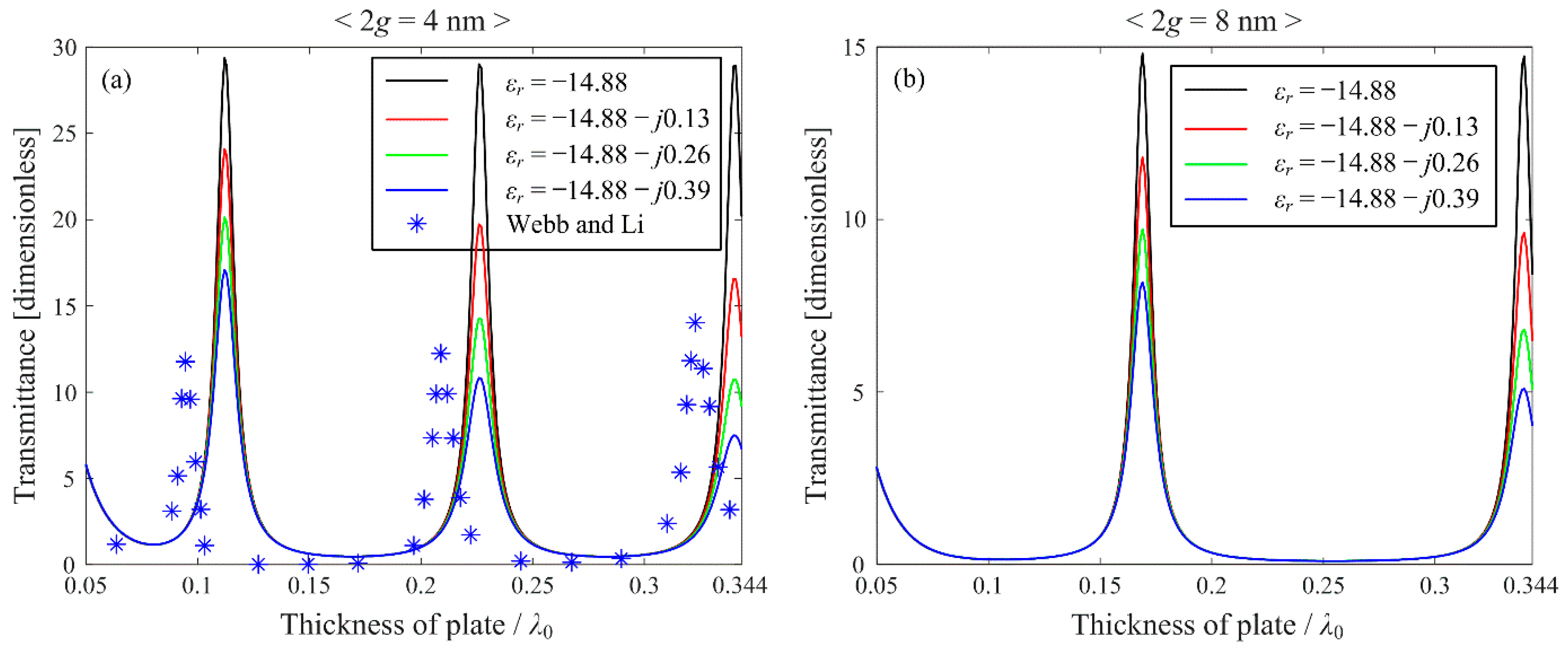
The transmittances are represented by Figure 3a,b, when the gap widths 2g become 4 and 8 nm, respectively. The transmittances are investigated by gradually reducing, and finally eliminating, the imaginary part of ε_r,m, even if the actual relative permittivity at λ₀ = 582.08 nm is 14.88 − j0.39 [28]. Figure 3a shows the transmittances through a subwavelength slit versus the thickness of a metallic plate when the gap width 2g is 4 nm (~0.0069λ₀). With no imaginary part in ε_r,m, periodically obtained peak transmittances are maintained although the thickness of the plate increases, because there is no metallic loss, producing the same result trend shown in Figure 2. By contrast, resonant peak transmittances are gradually reduced as the imaginary part of ε_r,m increases. This can be understood that increasing the plate thickness makes electromagnetic waves to pass through the metal over a longer distance, causing more power to be lost due to metallic loss. As the imaginary part of the relative permittivity increases up to −j0.39, attenuation phenomena can be observed clearly.

Figure 3b shows the transmittances by varying the relative permittivities, when the gap width 2g becomes 8 nm (0.0137λ₀). The resonant plate thicknesses are maintained despite increased imaginary parts of the permittivities, and the peak transmittances are gradually reduced as the imaginary part of ε_r,m increases. However, the interval, at which resonant peaks occur, is increased compared to the interval in Figure 3a. This can be understood using

Table 2. Guide wavelengths (λ_g) with respect to the Ag permittivity and modified permittivities, when the gap width 2g of 4 and 8 nm are used. (ε_r = −14.88 − j0.39 at λ₀ = 582.08 nm [28]).

Permittivities of Metal	2g = 4 nm	2g = 8 nm
εr = −14.88	4.3822	2.9284
εr = −14.88 − j0.13	4.3820 − j0.0194	2.9283 − j0.0093
εr = −14.88 − j0.26	4.3815 − j0.0388	2.9281 − j0.0185
εr = −14.88 − j0.39	4.3805 − j0.0582	2.9277 − j0.0277

, which shows the guide wavelengths as functions of the gap width 2g and the relative permittivity of Ag. From each value, the real part of the guide wavelength represents the interval of the periodic transmission peaks, and the imaginary part stands for the attenuation of their peaks. As the real part of the guide wavelength increases, the interval of the transmission peaks decreases, as shown in Figure 3, illustrating the same principle as Table 1. Consequently, as the imaginary part of the guide wavelength increases, the attenuation of the transmission peaks also increases. When the relative permittivity has only a real part, constant maximum transmission peaks in Figure 3a,b are found. The maximum transmission peaks are obtained as 29.23 and 14.55, when the gap widths are 4 and 8 nm, respectively. It is important to understand the meaning of these values. First, 29.23 times the incident power density for the gap width of 4 nm [Figure S1] is transmitted into the opposite (right-hand) region in Figure 1. The same applies to 14.55 times the incident power density for the gap width of 8 nm [Figure S2] in Figure 3b. Whenever the resonant conditions for both cases are satisfied, the constant width (m) times the incident power density (W/m) is transmitted into the opposite region, regardless of the width of the subwavelength slit. In other words, the incident power density having a constant width, which is much wider than that of the subwavelength slit, is transmitted into the right side of Figure 1 regardless of the gap width 2g, when the resonant condition (thickness of the plate) is satisfied.

It is necessary to mention the blue asterisks in Figure 3a, which are remarked from [29]. The transmittances versus the thickness of the Ag plate are obtained when Ag is −14.88 − j0.39 (at λ₀ = 582.08 nm), which is the same relationship as indicated by the blue solid line using the MMT. The overall transmittance levels are similar to each other, and the intervals of the maximum transmittances are also analogous. The maximum transmittances are observed at different resonant thicknesses of the plate, and the difference between [29] and our result is roughly 0.02λ₀. Furthermore, the maximum transmittance markers increase, even though the thickness of the plate increases. This is unnatural, because the electromagnetic wave passing through the slit should be dissipated more as the plate thickness increases. On the contrary, the maximum transmittances by the solid lines of our work gradually decrease and are physically agreeable. Therefore, the transmittances of our work are more convincing than those of [29].

4. Orthogonality and Discussions

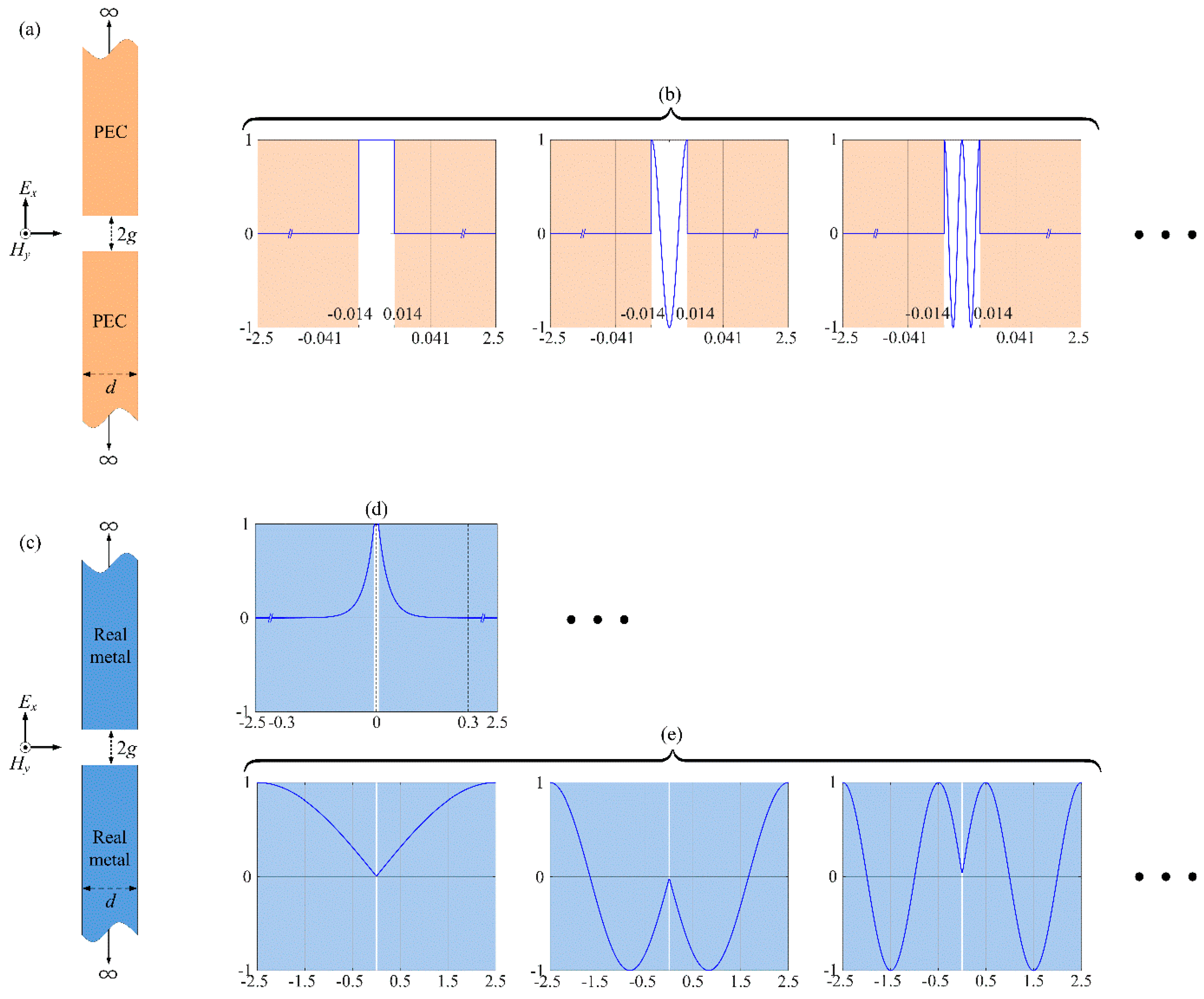
When the metal of an MIM waveguide is a PEC, field profiles of entire modes (including a transverse electromagnetic mode) can be expressed easily, and the sinusoidal modal variations are found in the slit of the waveguide, while field profiles cannot be expressed in the PEC region. The orthogonal property is completely satisfied, because inner products among the sinusoidal harmonics in the silt are perfectly orthogonal. (In this work, only cosine functions are considered, because only a normally incident wave is dealt with.) The n-th modal electromagnetic fields of the parallel plate waveguide in Figure 4a can be expressed as follows:

$$H_y^n=cos({\gamma }_{n}x)e^{-k_{n}z},$$

(5)

$$E_x^n=-\frac{1}{j\omega \epsilon }\frac{\partial H_y^n}{\partial z} ,$$

(6)

$${\gamma }_n=\frac{2n\pi }{2g}\mathrm{and}{k}_n=\sqrt{{\gamma }_n^2-{\omega }^2\mu \epsilon },n=0,1,2,\cdots .$$

(7)

From the geometry in Figure 4a, the field profiles of the first three even modes are described in Figure 4b. Note that the scales are different for the slit (white) and metal (light orange) regions. By applying higher-order modes and the first three modes into the MMT, the transmittances are solved. The orthogonal properties among the modes are calculated and confirmed from the following equations [30]:

$$\frac{1}{{\eta }_0}\frac{k_0}{k_n}\frac{1}{2g}{\int }_{-g}^g\left[E_x^n{(H_y^m)}^{*}\right]dx={\delta }_{nm},$$

(8)

$${\delta }_{nm}=\{\begin{array}{c}1,n=m\\ 0,n\ne m\end{array} .$$

(9)

From Equations (8) and (9), the calculated result is 1 when the modes are the same, and 0 when the two modes are different. Therefore, the orthogonal property is completely satisfied, when the metal of the MIM waveguide is a PEC. When the metal has a finite conductivity, the geometry of the single slit can be depicted by Figure 4c with the blue-colored metallic region and the corresponding field profiles shown in Figure 4d,e. The equations for the field profiles are represented as [9]:

$$H_y^n=\{\begin{array}{c}\frac{cosh({\kappa }_{i,n}x)}{cosh({\kappa }_{i,n}g)}{e}^{-k_{z,n}z},0<x<g\\ e^{-{\kappa }_{m,n}\left(x-g\right)}{e}^{-k_{z,n}z},g<x<\infty \end{array}.$$

(10)

By inserting ε_r,m into Equations (1) and (2), the n-th transverse propagation constants (κ_i,n and κ_m,n) and the n-th propagation constant (k_z,n) are easily obtained. The field profiles can then be obtained from Equation (10) and are described in Figure 4d,e, which stand for the field profiles of a point spectrum (PS) and a discretized continuous spectrum (DCS) [9], respectively. The PS and DCS correspond to the guided and radiation modes in the dielectric slab waveguide, respectively. The PS can describe the sinusoidal electromagnetic field patterns mainly in the “insulator”, while the DCS depicts the sinusoidal field patterns mainly in the “metal” region [9,10]. The right-hand side of Equation (8), for a metal having a finite conductivity, is not solved exactly as 1 or 0, which indicates the orthogonality is not perfectly satisfied, but the modes are applied into the MMT and the corresponding transmittances are solved.

The field profiles of the PS and the DCS are described in Figure 4d,e, respectively, where the gap width 2g is 4 nm and ε_r,m is −14.88. Figure 4d shows the field profiles for the first mode of the PS and may correspond to the first field profile of Figure 4b. The field shape in the white insulator region is almost maintained; however, the field shape in the sky-blue metal region is different. The field at the boundary between the insulator and the metal penetrates into the metal region, because the metal is no longer a PEC. Figure 4e describes the field profiles of the first, second, and third modes of the DCS. The field profiles represent sinusoidal harmonics in the metal region, and various field patterns in the metal region can be described by superposition of the modes in the DCS.

The numbers of the PS and the DCS used in the MMT formulation are 1 and 50, respectively. Only one mode of the PS is applied to solve the transmittance, because the slit is too narrow compared to the wavelength. That being said, a sufficient number of modes of the DCS should be applied, given the wideness of the metal region compared to that of the slit region [12]. The sufficient number of DCS modes is obtained as follows: We start to apply 5 trial DCS modes and investigate the reflection and transmission coefficients. Computing the coefficients by increasing the number of the DCS modes to 5 are repeated, and then the coefficients are arranged with respect to the number of DCS modes. Once the convergence is found, the updated number of the DCS modes are obtained.

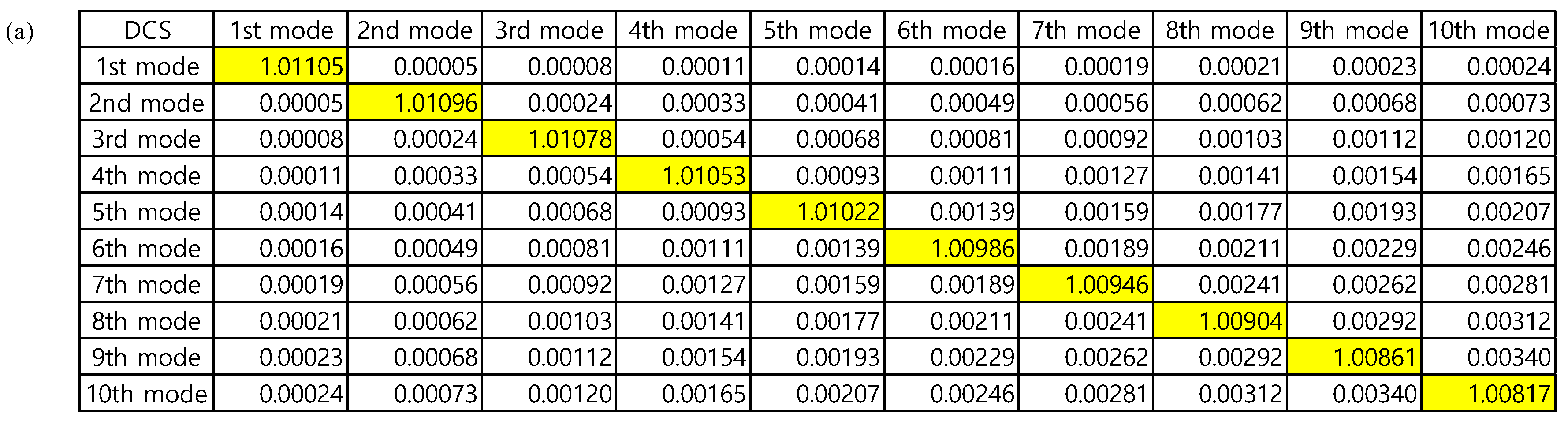
From the viewpoint of orthogonality, the PS and the DCS are clearly independent, because the field patterns of both are formed in different regions; therefore, the result of Equations (8) and (9) between the two approaches 0. However, the orthogonal properties among 50 DCS modes require investigation, since the metal is not a PEC. Figure 5 indicates in Figure 5a the results of Equations (8) and (9) of the first 10 DCS modes when ε_r,m of the MIM waveguide is −14.88. Each cell represents the result of Equations (8) and (9) between two modes. What we need to pay attention to Equations (8) and (9) for the MIM waveguide is the interval of integration. The interval should cover the entire waveguide junction including the metal region as well as the gap region of 2g, while the interval of integration 2g in Equations (8) and (9) is still valid in the case of the PEC waveguide. The diagonal components approach approximately 1 when the DCS modes used in Equations (8) and (9) are identical, while the off-diagonal results go to approximately 0 when the modes differ. For the first 10 modes of the DCS, the values from Equations (8) and (9) are within [1.0082, 1.0111] for the same modes, whereas the values are within [4.878 × 10⁻⁵, 0.00340] for different modes. These computed results are still effective up to the next 40 DCS modes.

The orthogonality changes slightly but remains almost constant despite the inclusion of an imaginary part in the permittivity of the metal. The field profiles of the PS and the DCS in Figure 4d,e change slightly, although ε_r,m becomes −14.88 − j0.39. Figure 5b shows the orthogonal results of Equations (8) and (9) among the first 10 DCS modes, when ε_r,m is −14.88 − j0.39. The solved results are very similar to Figure 5a, even though the imaginary part of the permittivity is included. For the first 10 modes of the DCS, the values from Equations (8) and (9) are within [1.0064, 1.0085] for the identical modes, while the values are within [4.945 × 10⁻⁵, 0.00343] for different modes. Therefore, the orthogonal relationships are almost the same when ε_r,m is −14.88, where an orthogonal set is almost remains. As the relationships of the next 40 DCS modes are considered, the orthogonal properties are maintained. Although the orthogonality for the real metal case is not completely satisfied, it is not enough to affect the accuracy of transmittance. Despite this incomplete orthogonality, the transmission characteristics are mainly determined by the fundamental mode, so that the accurate results can still be maintained. The field profiles by higher-order modes change more, but the higher-order modes do not significantly affect the slit transmission.

The guide wavelengths λ_g of the DCS, as well as that of the PS modes, are also investigated to allow the transmission fundamentals to be understood. The λ_g value of the first PS mode is 4.382, when the gap width 2g is 4 nm and the permittivity of Ag ε_r,m is −14.88. By contrast, the λ_g value of the first DCS mode is purely imaginary and roughly −j3.859 under the same conditions. This is significantly greater than the imaginary parts of the PS listed in Table 2, demonstrating the λ_g value of the DCS attenuates significantly and cannot contribute to the transmission. Therefore, the DCS modes do not contribute to the transmission but perform a complete orthogonal set for the MMT [10].

5. Conclusions

In this paper, resonant transmission phenomena through a single metallic subwavelength slit were investigated, when the permittivity of Ag was changed with varying frequencies. The concept of the MIM waveguide was adopted for the single metallic slit, and the complex permittivity of real metal was considered regarding the MIM waveguide. The eigenvalues of the MIM waveguide were then applied to the MMT, and the transmittances were solved. The periodic transmission characteristics versus the thicknesses of the plate were obtained as a function of metallic permittivity, and their periodicities were easily understood using each guide wavelength. The imaginary parts of the permittivities for real metals were subsequently included to obtain corresponding transmittance characteristics. Similarly, the periodicities and attenuations were understood, thanks to the guide wavelengths of the MIM geometry. Finally, the orthogonal properties among the eigenvalues of the DCS were investigated for given lossy and lossless real metals in order to investigate the validity of their MMT formulations. For all cases, the orthogonal relationships among the same modes were obtained at approximately one, while the orthogonal relationships among different modes were obtained at no more than 0.0034. Therefore, the MMT formulations, even for the lossy cases, were deemed reasonable to solve transmittances.