Fractional View Analysis of Acoustic Wave Equations, Using Fractional-Order Differential Equations
Abstract
1. Introduction
2. Preliminaries Concepts
3. The Procedure of VHPTM
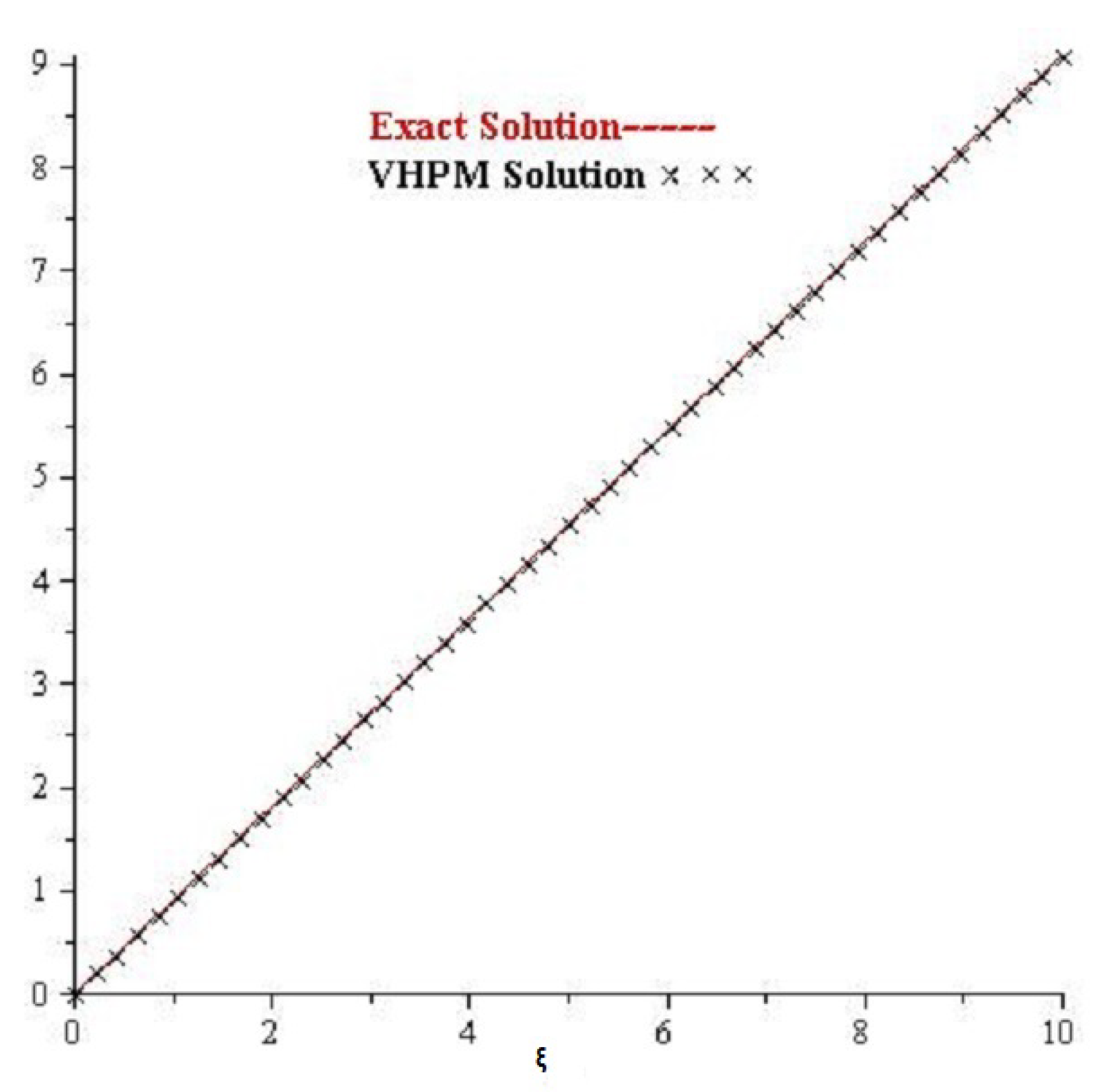
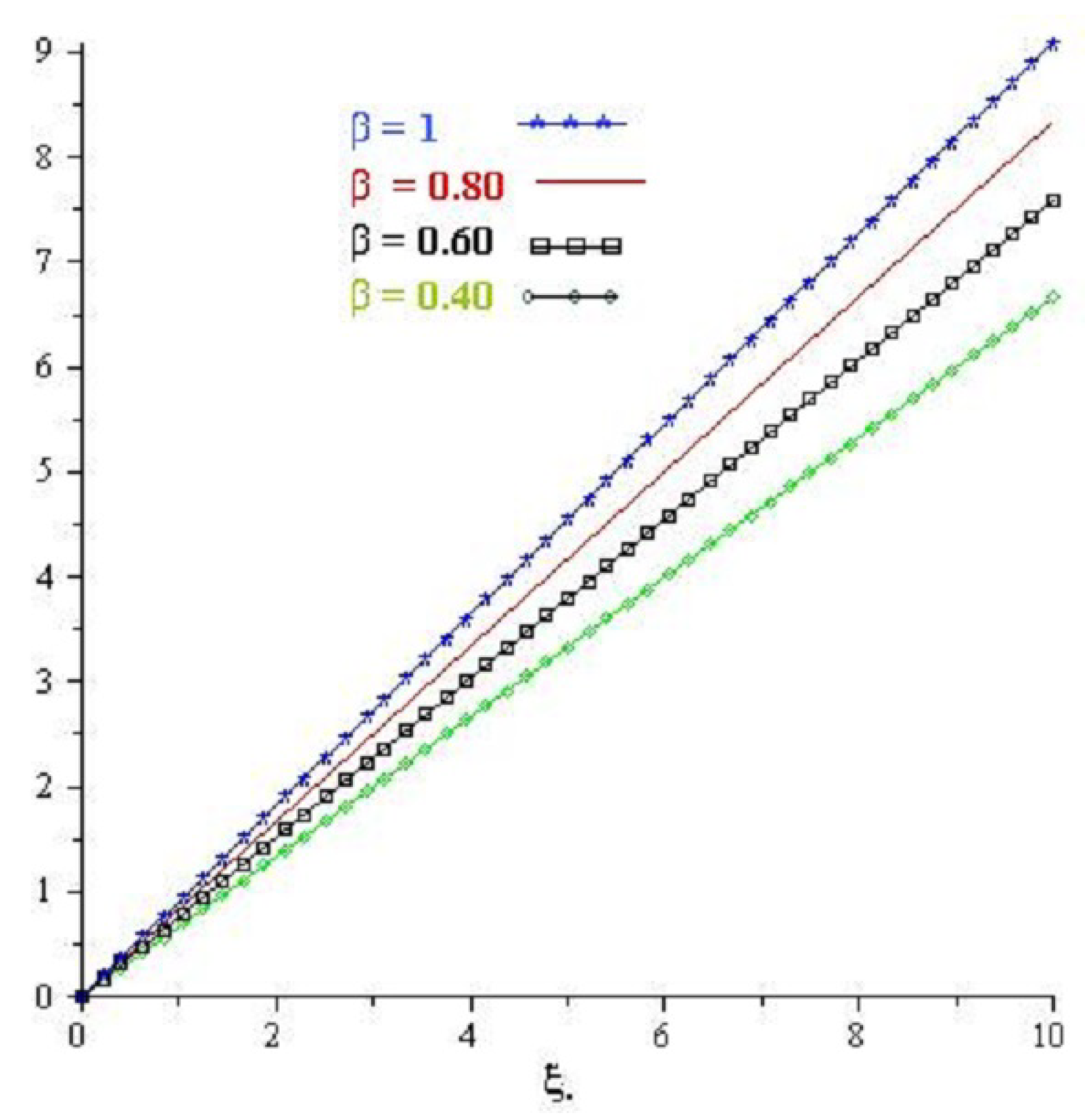
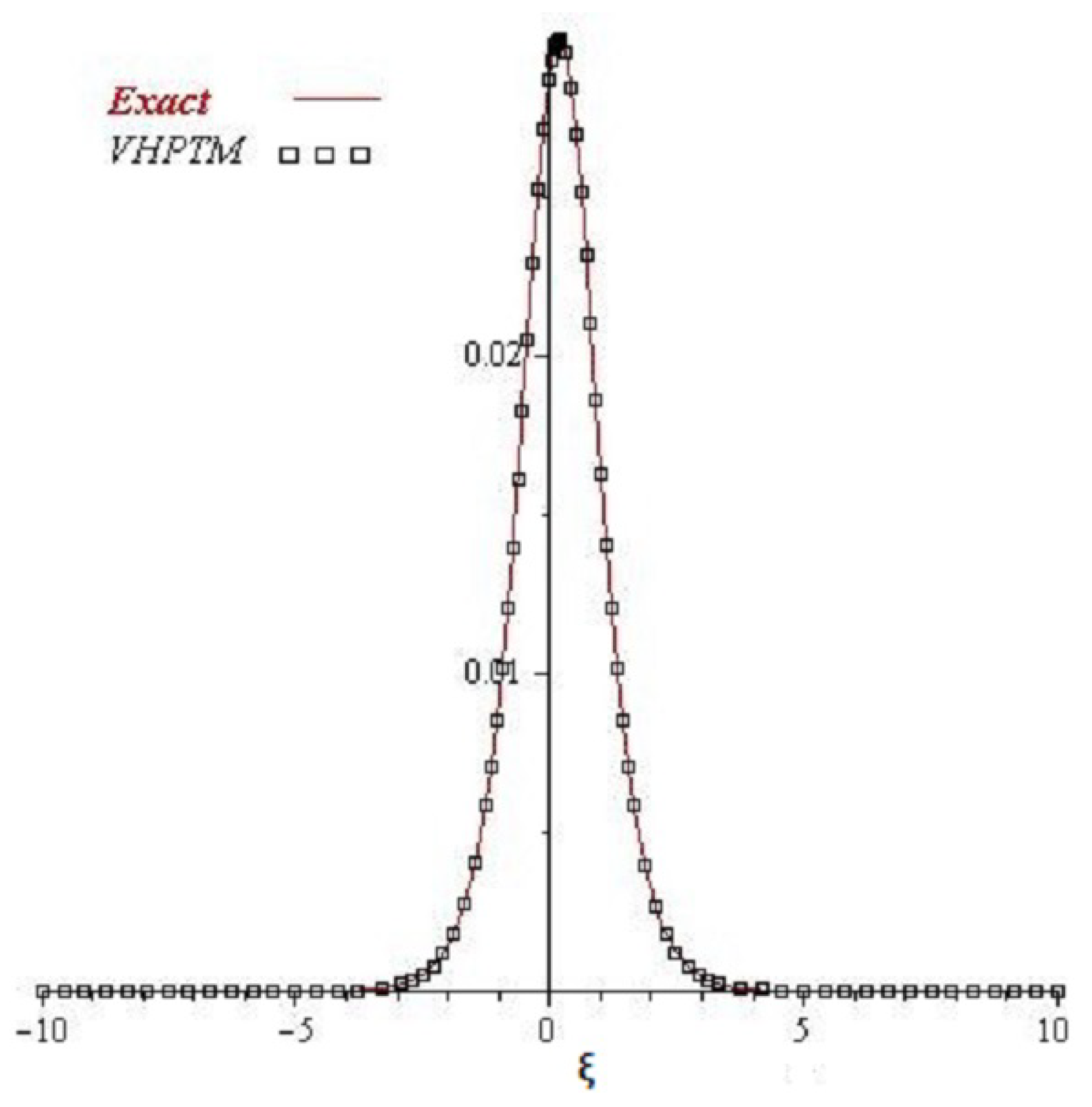
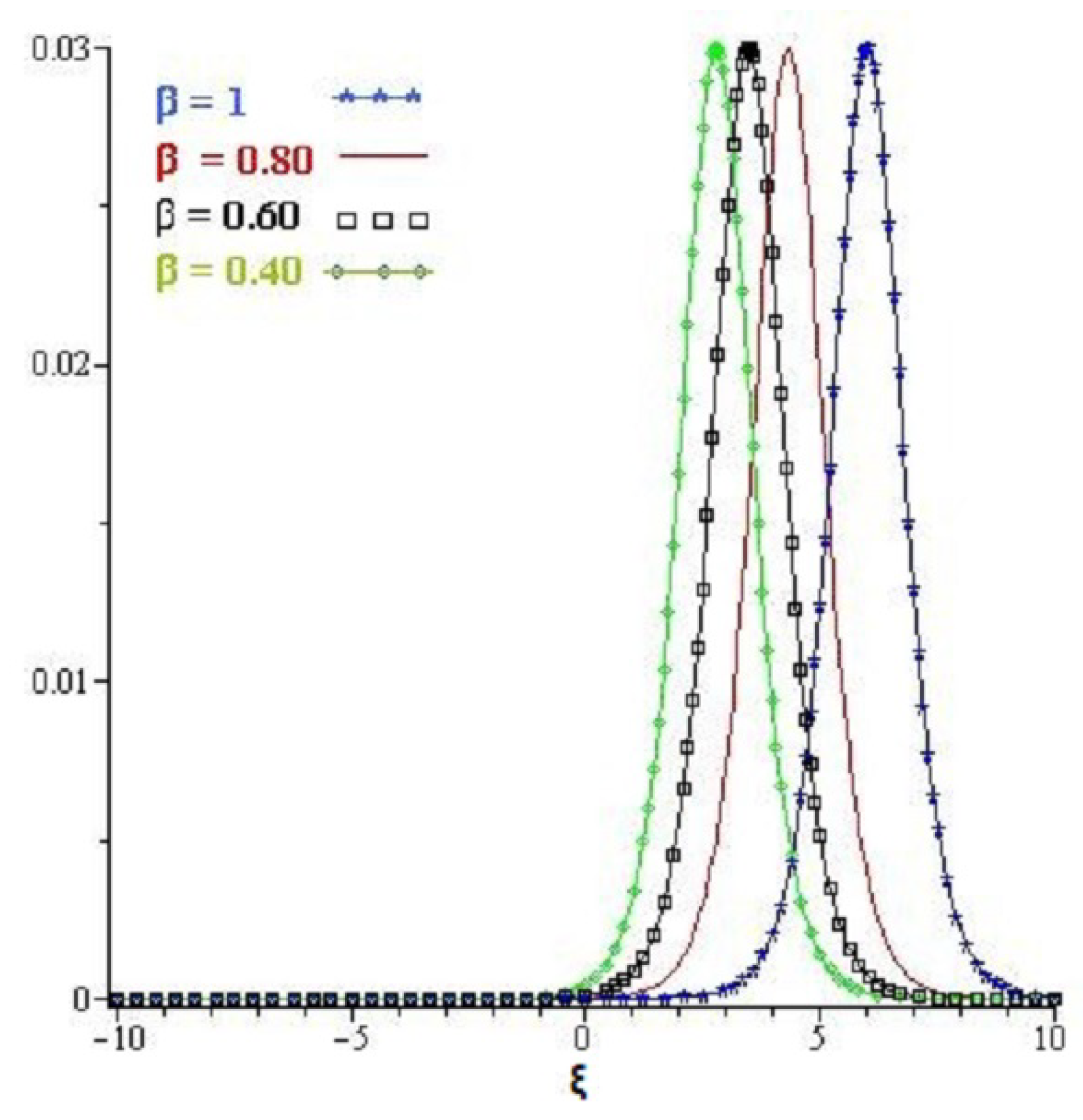
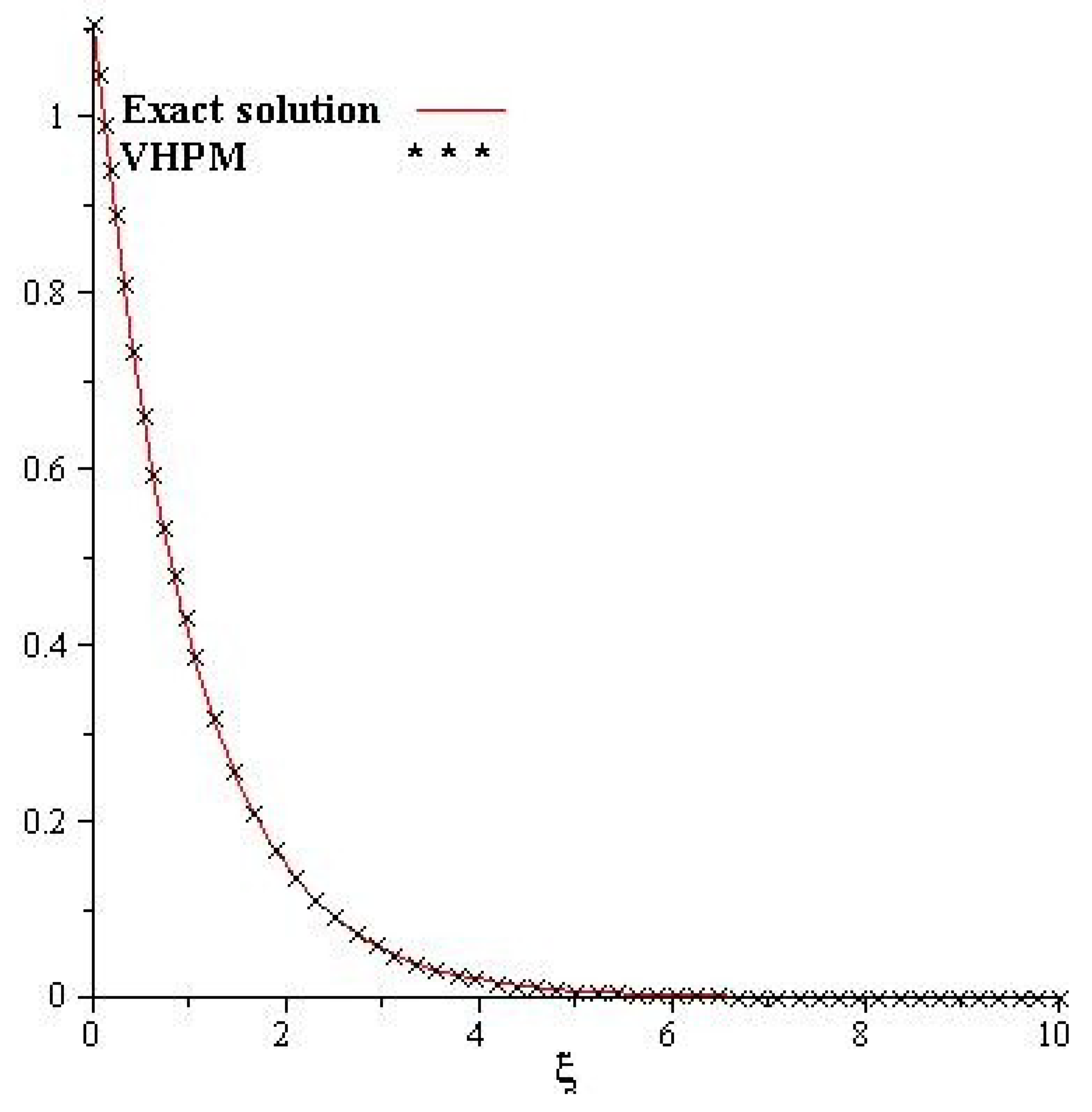
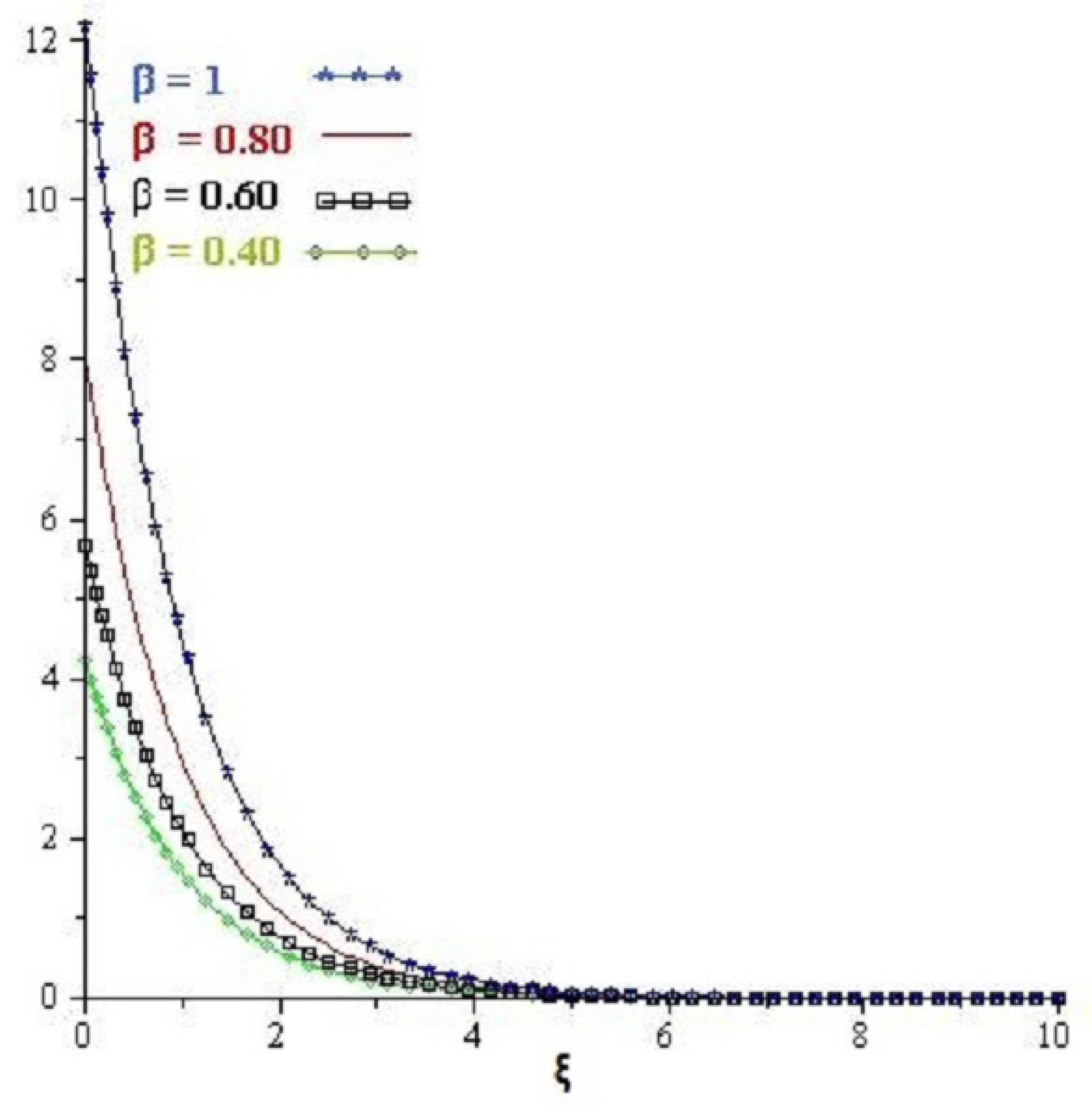
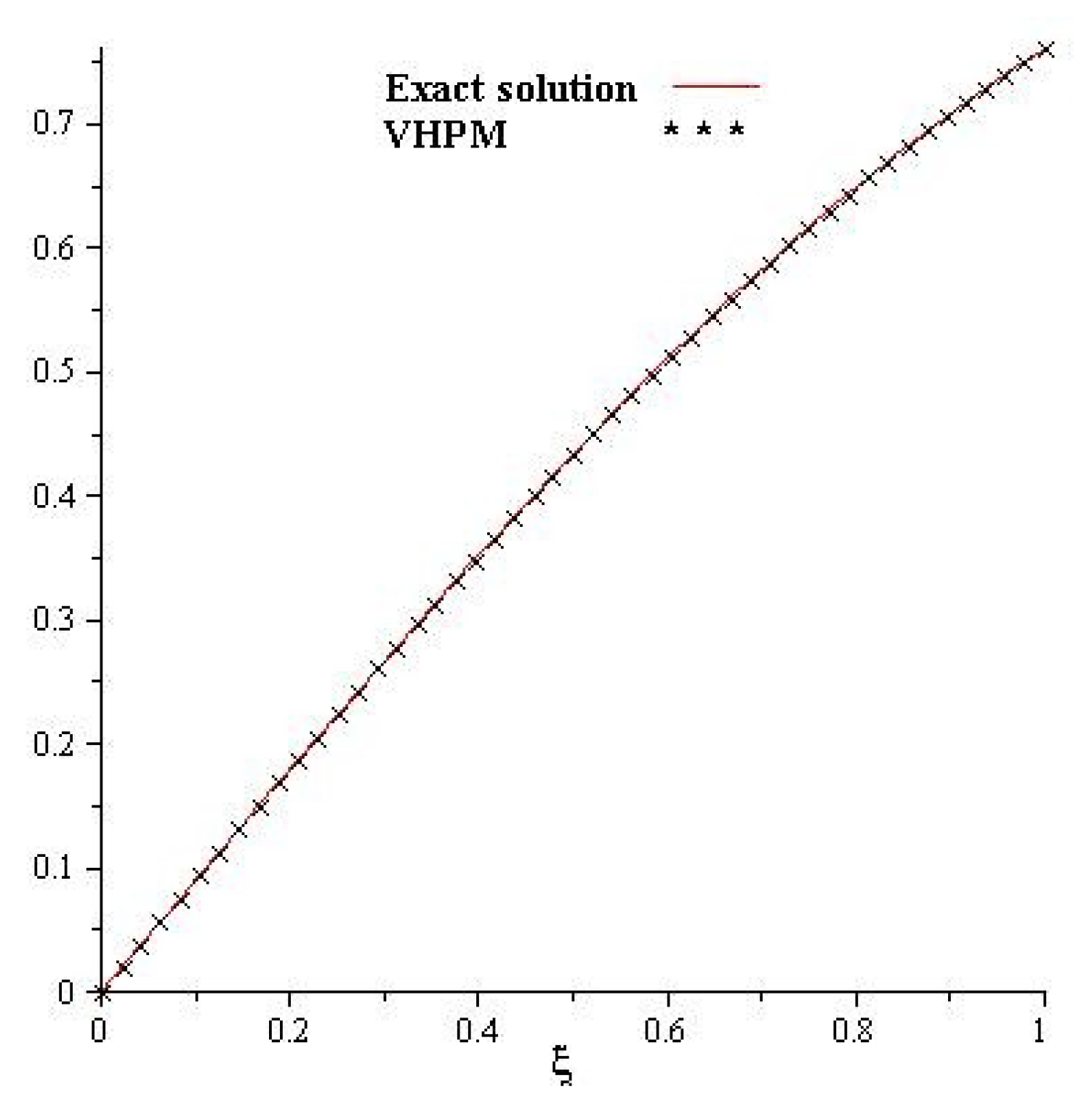
4. Numerical Examples
4.1. Example
4.2. Example
4.3. Example
4.4. Example
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Debnath, L. Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2003, 54, 3413–3442. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Parvizi, M.; Eslahchi, M.R.; Dehghan, M. Numerical solution of fractional advection-diffusion equation with a nonlinear source term. Numer. Algorithms 2015, 68, 601–629. [Google Scholar] [CrossRef]
- Bu, W.; Liu, X.; Tang, Y.; Yang, J. Finite element multigrid method for multi-term time fractional advection diffusion equations. Int. J. Model. Simul. Sci. Comput. 2015, 6, 1540001. [Google Scholar] [CrossRef]
- Donatelli, M.; Mazza, M.; Serra-Capizzano, S. Spectral analysis and structure preserving preconditioners for fractional diffusion equations. J. Comput. Phys. 2016, 307, 262–279. [Google Scholar] [CrossRef]
- Donatelli, M.; Mazza, M.; Serra-Capizzano, S. Spectral analysis and multigrid methods for finite volume approximations of space-fractional diffusion equations. SIAM J. Sci. Comput. 2018, 40, A4007–A4039. [Google Scholar] [CrossRef]
- Lin, X.L.; Ng, M.K.; Sun, H.W. A multigrid method for linear systems arising from time-dependent two-dimensional space-fractional diffusion equations. J. Comput. Phys. 2017, 336, 69–86. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Kumam, P.; Arif, M. An Analytical Technique to Solve the System of Nonlinear Fractional Partial Differential Equations. Mathematics 2019, 7, 505. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. Analytical Solution of Fractional-Order Hyperbolic Telegraph Equation, Using Natural Transform Decomposition Method. Electronics 2019, 8, 1015. [Google Scholar] [CrossRef]
- Goswami, A.; Singh, J.; Kumar, D.; Gupta, S. An efficient analytical technique for fractional partial differential equations occurring in ion acoustic waves in plasma. J. Ocean Eng. Sci. 2019, 4, 85–99. [Google Scholar] [CrossRef]
- Khan, Y.; Taghipour, R.; Falahian, M.; Nikkar, A. A new approach to modified regularized long wave equation. Neural Comput. Appl. 2013, 23, 1335–1341. [Google Scholar] [CrossRef]
- Peregrine, D.H. Calculations of the development of an undular bore. J. Fluid Mech. 1966, 25, 321–330. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Bona, J.L.; Mahony, J.J. Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1972, 272, 47–78. [Google Scholar] [CrossRef]
- Khalifa, A.K.; Raslan, K.R.; Alzubaidi, H.M. Numerical study using ADM for the modified regularized long wave equation. Appl. Math. Model. 2008, 32, 2962–2972. [Google Scholar] [CrossRef]
- Achouri, T.; Omrani, K. Numerical solutions for the damped generalized regularized long-wave equation with a variable coefficient by Adomian decomposition method. Commun. Nonlinear Sci. Numer Simul. 2009, 14, 2025–2033. [Google Scholar] [CrossRef]
- İdris, D. Least-squares quadratic B-spline finite element method for the regularised long wave equation. Comput. Methods Appl. Mech. Eng. 2000, 182, 205–215. [Google Scholar]
- Bota, C.; Căruntu, B. Approximate analytical solutions of the regularized long wave equation using the optimal homotopy perturbation method. Sci. World J. 2014, 2014, 721865. [Google Scholar] [CrossRef]
- Ganji, D.D.; Tari, H.; Jooybari, M.B. Variational iteration method and homotopy perturbation method for nonlinear evolution equations. Comput. Math. Appl. 2007, 54, 1018–1027. [Google Scholar] [CrossRef]
- Inc, M.; Uğurlu, Y. Numerical simulation of the regularized long wave equation by He’s homotopy perturbation method. Phys. Lett. A 2007, 369, 173–179. [Google Scholar] [CrossRef]
- Noor, M.A.; Mohyud-Din, S.T. Modified variational iteration method for heat and wave-like equations. Acta Appl. Math. 2008, 104, 257–269. [Google Scholar] [CrossRef]
- Noor, M.A.; Mohyud-Din, S.T. Variational homotopy perturbation method for solving higher dimensional initial boundary value problems. Math. Probl. Eng. 2008, 2008, 696734. [Google Scholar] [CrossRef]
- Mohammad Mehdi Hosseini, S.; Tauseef Mohyud-Din, S.; Ghaneai, H. Variational iteration method for Hirota-Satsuma coupled KdV equation using auxiliary parameter. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 277–286. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Yildirim, A.; Hosseini, M.M. Variational iteration method for initial and boundary value problems using He’s polynomials. Int. J. Differ. Equ. 2010, 2010, 426213. [Google Scholar] [CrossRef]
- Liu, Y. Variational homotopy perturbation method for solving fractional initial boundary value problems. In Abstract and Applied Analysis; Hindawi: London, UK, 2012; Volume 2012. [Google Scholar]
- Shah, R.; Khan, H.; Baleanu, D. Fractional Whitham–Broer–Kaup Equations within Modified Analytical Approaches. Axioms 2019, 4, 125. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Farooq, U.; Baleanu, D.; Kumam, P.; Arif, M. A New Analytical Technique to Solve System of Fractional-Order Partial Differential Equations. IEEE Access 2019, 7, 150037–150050. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Arif, M.; Kumam, P. Application of Laplace-Adomian Decomposition Method for the Analytical Solution of Third-Order Dispersive Fractional Partial Differential Equations. Entropy 2019, 21, 335. [Google Scholar] [CrossRef]
- Mahmood, S.; Shah, R.; Arif, M. Laplace Adomian Decomposition Method for Multi Dimensional Time Fractional Model of Navier-Stokes Equation. Symmetry 2019, 11, 149. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Baleanu, D.; Arif, M. An Efficient Analytical Technique, for The Solution of Fractional-Order Telegraph Equations. Mathematics 2019, 7, 426. [Google Scholar] [CrossRef]
- Shah, K.; Khalil, H.; Khan, R.A. Analytical solutions of fractional order diffusion equations by natural transform method. Iran. J. Sci. Technol. Trans. A Sci. 2018, 42, 1479–1490. [Google Scholar] [CrossRef]

| VHPTM | VHPTM | VHPTM | Exact | Absolute Error | Absolute Error | |
|---|---|---|---|---|---|---|
| 0.1 | 0.0966295721 | 0.0993928867 | 0.0999000999 | 0.0999001000 | ||
| 0.2 | 0.1932591443 | 0.1987857735 | 0.1998001998 | 0.1998002000 | ||
| 0.3 | 0.2898887165 | 0.2981786602 | 0.2997002997 | 0.2997003000 | ||
| 0.4 | 0.3865182887 | 0.3975715470 | 0.3996003996 | 0.3996004000 | ||
| 0.5 | 0.4831478608 | 0.4969644337 | 0.4995004995 | 0.4995005000 | ||
| 0.6 | 0.5797774330 | 0.5963573204 | 0.5994005994 | 0.5994006000 | ||
| 0.7 | 0.6764070052 | 0.6957502072 | 0.6993006993 | 0.6993007000 | ||
| 0.8 | 0.7730365774 | 0.7951430939 | 0.7992007992 | 0.7992008000 | ||
| 0.9 | 0.8696661495 | 0.8945359807 | 0.8991008991 | 0.8991009000 | ||
| 1 | 0.9662957217 | 0.9939288674 | 0.9990009990 | 0.9990010000 |
| VHPTM | Exact | Absolute Error | Absolute Error | |
|---|---|---|---|---|
| 0.1 | 0.9048374271 | 0.9048374180 | 8.396197700 | 9.1000000 |
| 0.2 | 0.8187307613 | 0.8187307531 | 2.343247660 | 8.2000000 |
| 0.3 | 0.7408182281 | 0.7408182207 | 1.098518064 | 7.4000000 |
| 0.4 | 0.6703200527 | 0.6703200460 | 2.435301980 | 6.7000000 |
| 0.5 | 0.6065306658 | 0.6065306597 | 3.925301546 | 6.1000000 |
| 0.6 | 0.5488116416 | 0.5488116361 | 5.222691016 | 5.5000000 |
| 0.7 | 0.4965853088 | 0.4965853038 | 6.061930396 | 5.0000000 |
| 0.8 | 0.4493289686 | 0.4493289641 | 6.351737693 | 4.5000000 |
| 0.9 | 0.4065696638 | 0.4065696597 | 6.159048138 | 4.1000000 |
| 1 | 0.3678794449 | 0.3678794412 | 5.612475460 | 3.7000000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, I.; Khan, H.; Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. Fractional View Analysis of Acoustic Wave Equations, Using Fractional-Order Differential Equations. Appl. Sci. 2020, 10, 610. https://doi.org/10.3390/app10020610
Ali I, Khan H, Shah R, Baleanu D, Kumam P, Arif M. Fractional View Analysis of Acoustic Wave Equations, Using Fractional-Order Differential Equations. Applied Sciences. 2020; 10(2):610. https://doi.org/10.3390/app10020610
Chicago/Turabian StyleAli, Izaz, Hassan Khan, Rasool Shah, Dumitru Baleanu, Poom Kumam, and Muhammad Arif. 2020. "Fractional View Analysis of Acoustic Wave Equations, Using Fractional-Order Differential Equations" Applied Sciences 10, no. 2: 610. https://doi.org/10.3390/app10020610
APA StyleAli, I., Khan, H., Shah, R., Baleanu, D., Kumam, P., & Arif, M. (2020). Fractional View Analysis of Acoustic Wave Equations, Using Fractional-Order Differential Equations. Applied Sciences, 10(2), 610. https://doi.org/10.3390/app10020610








