The Seepage and Soil Plug Formation in Suction Caissons in Sand Using Visual Tests
Abstract
1. Introduction
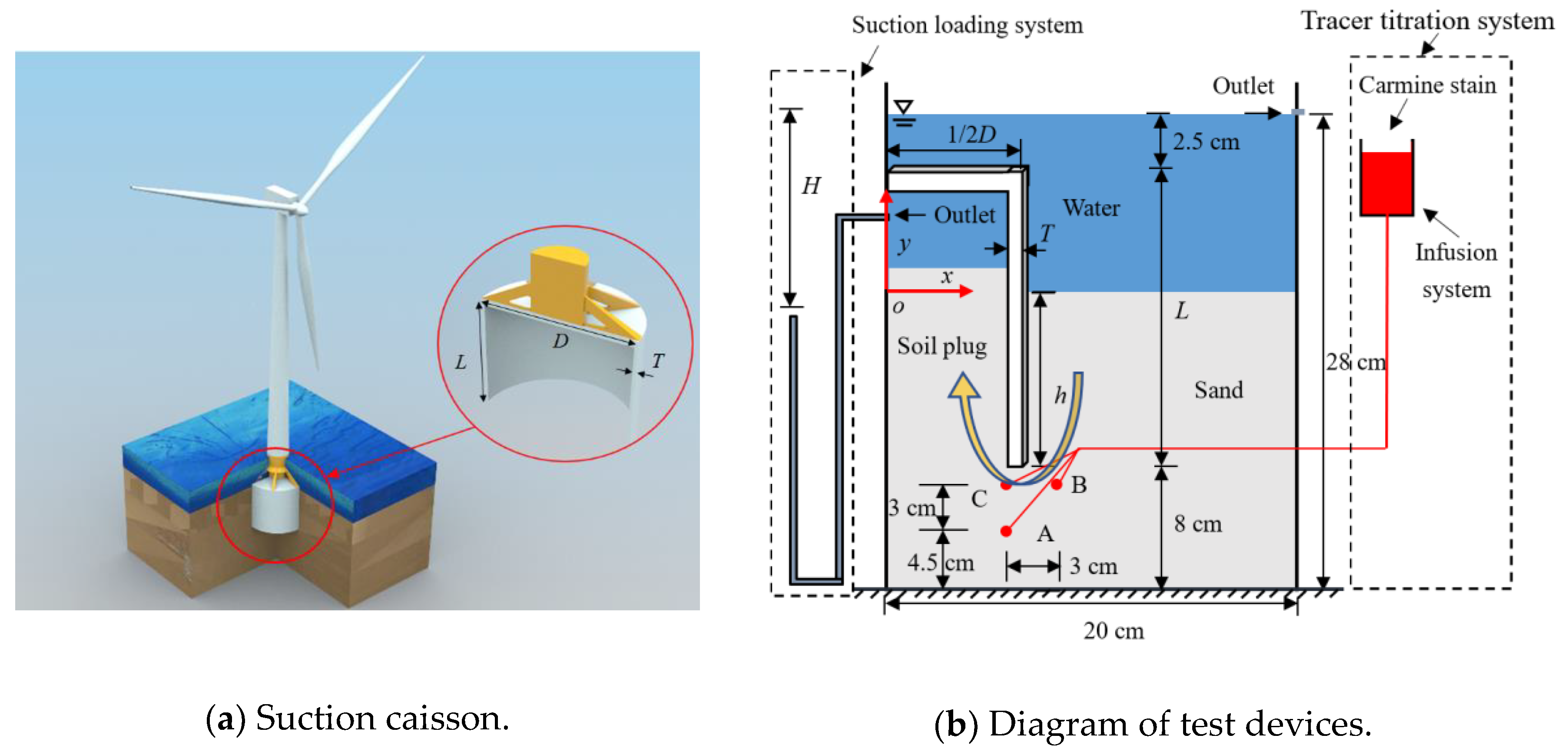
2. Experimental Program
3. Test Results and Discussion
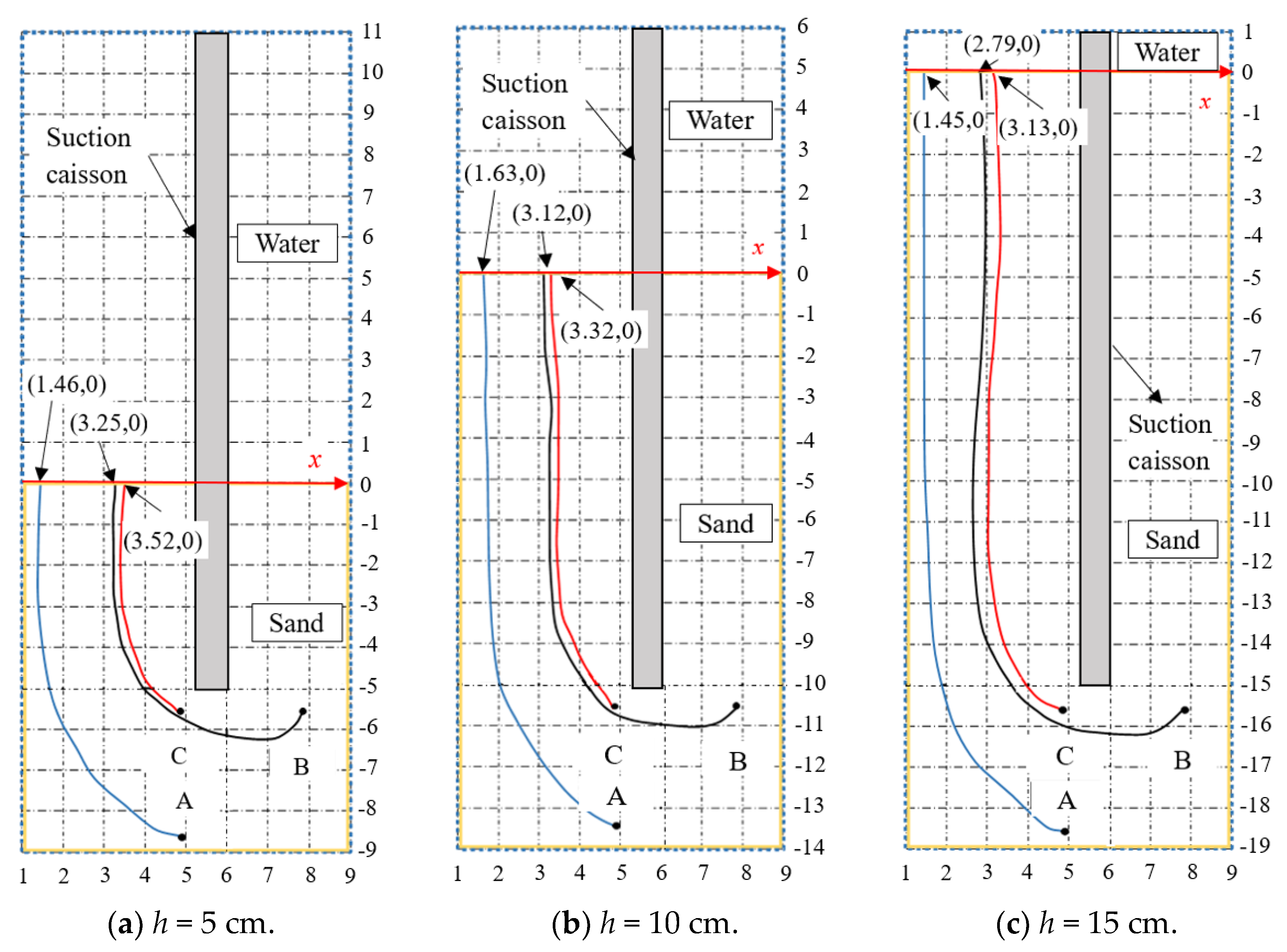
3.1. Visual Seepage Paths
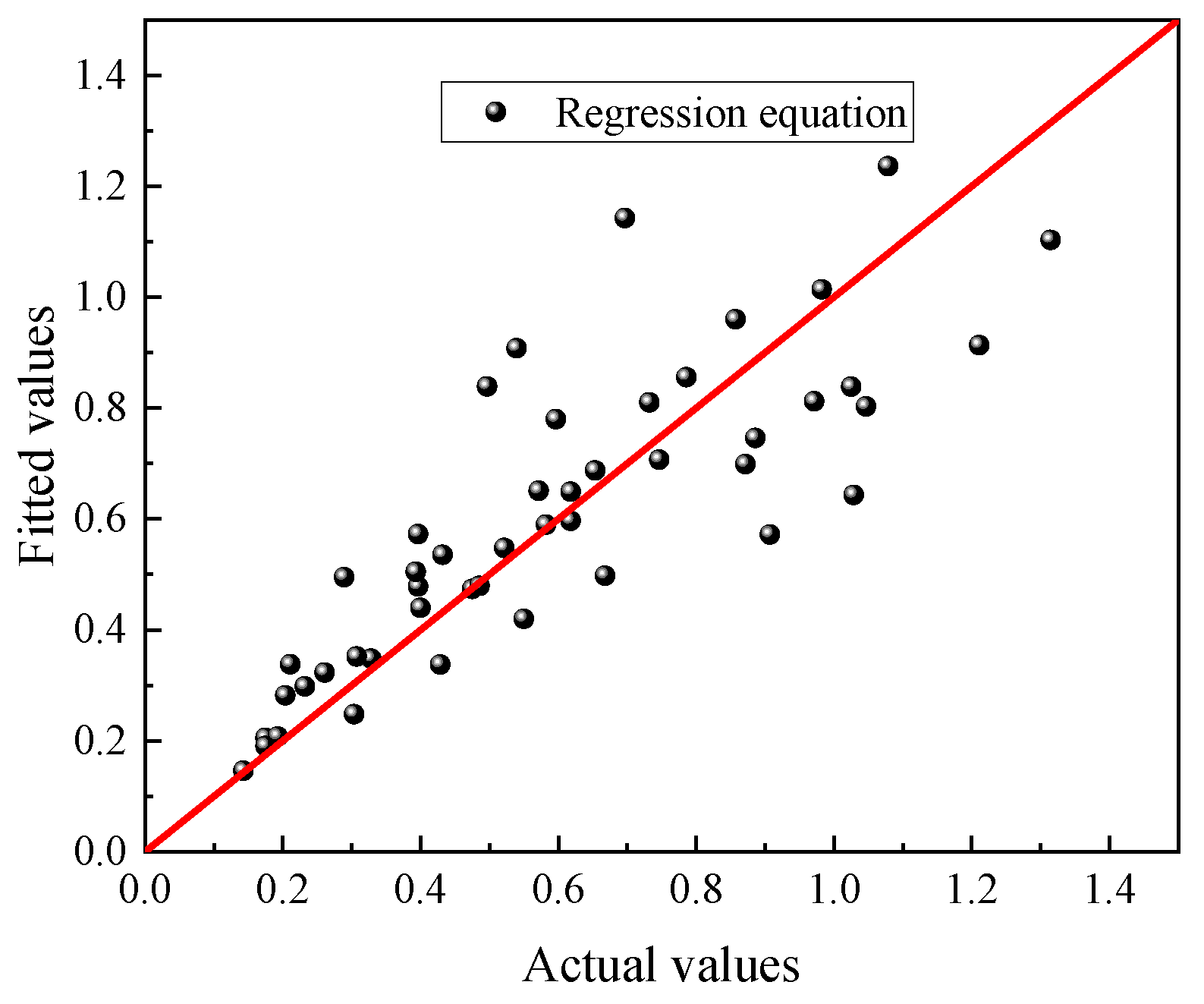
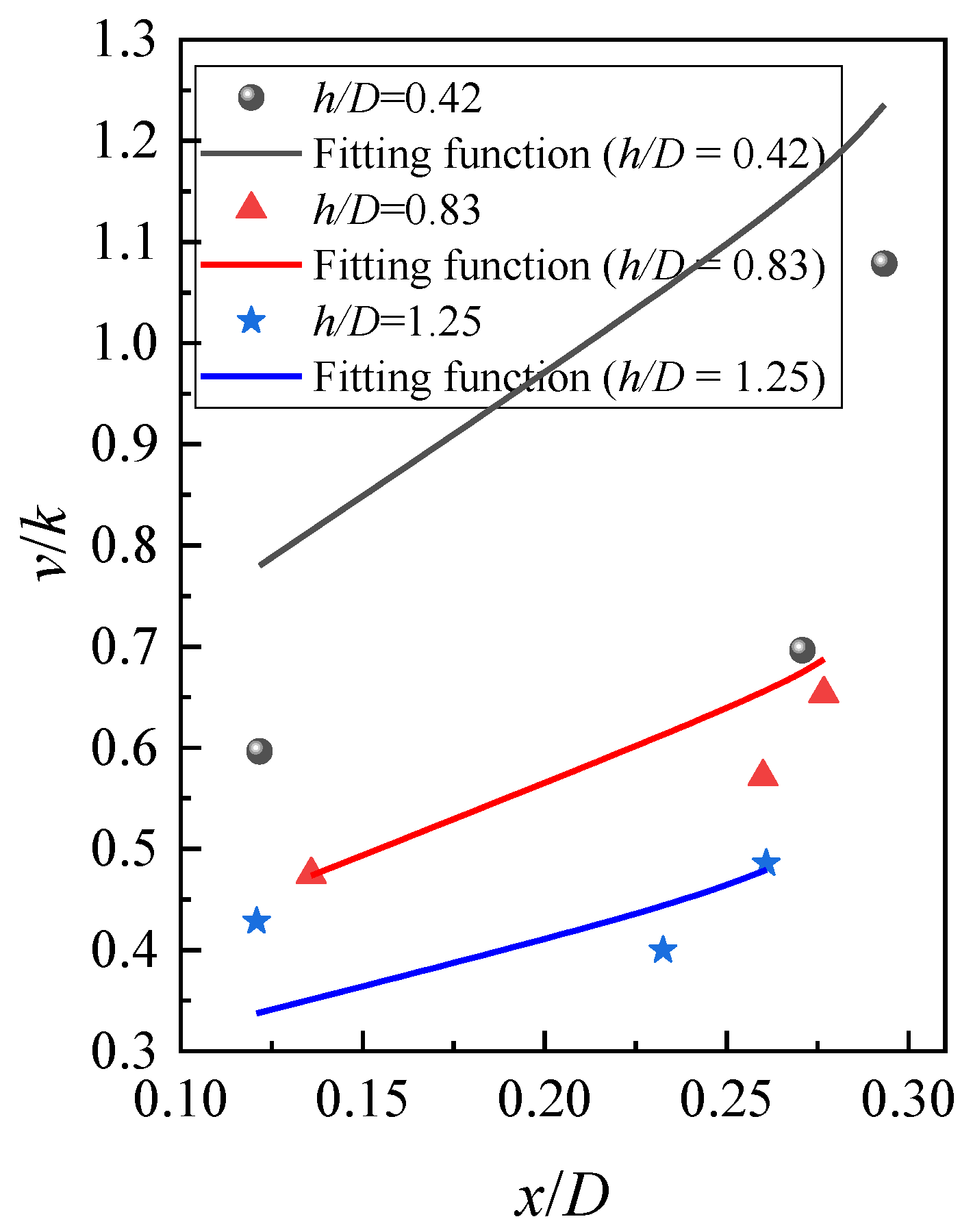
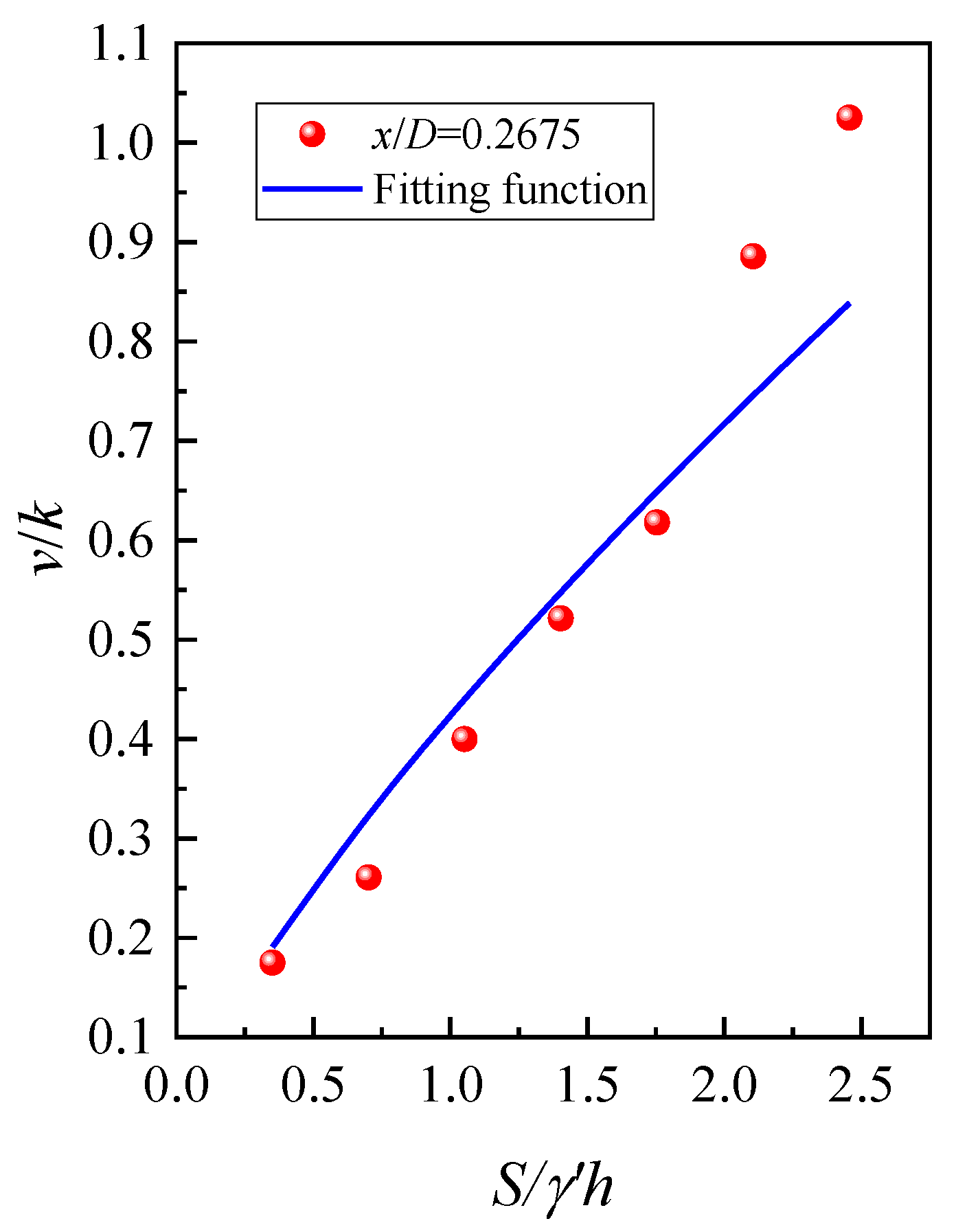
3.2. Hydraulic Gradient Analysis
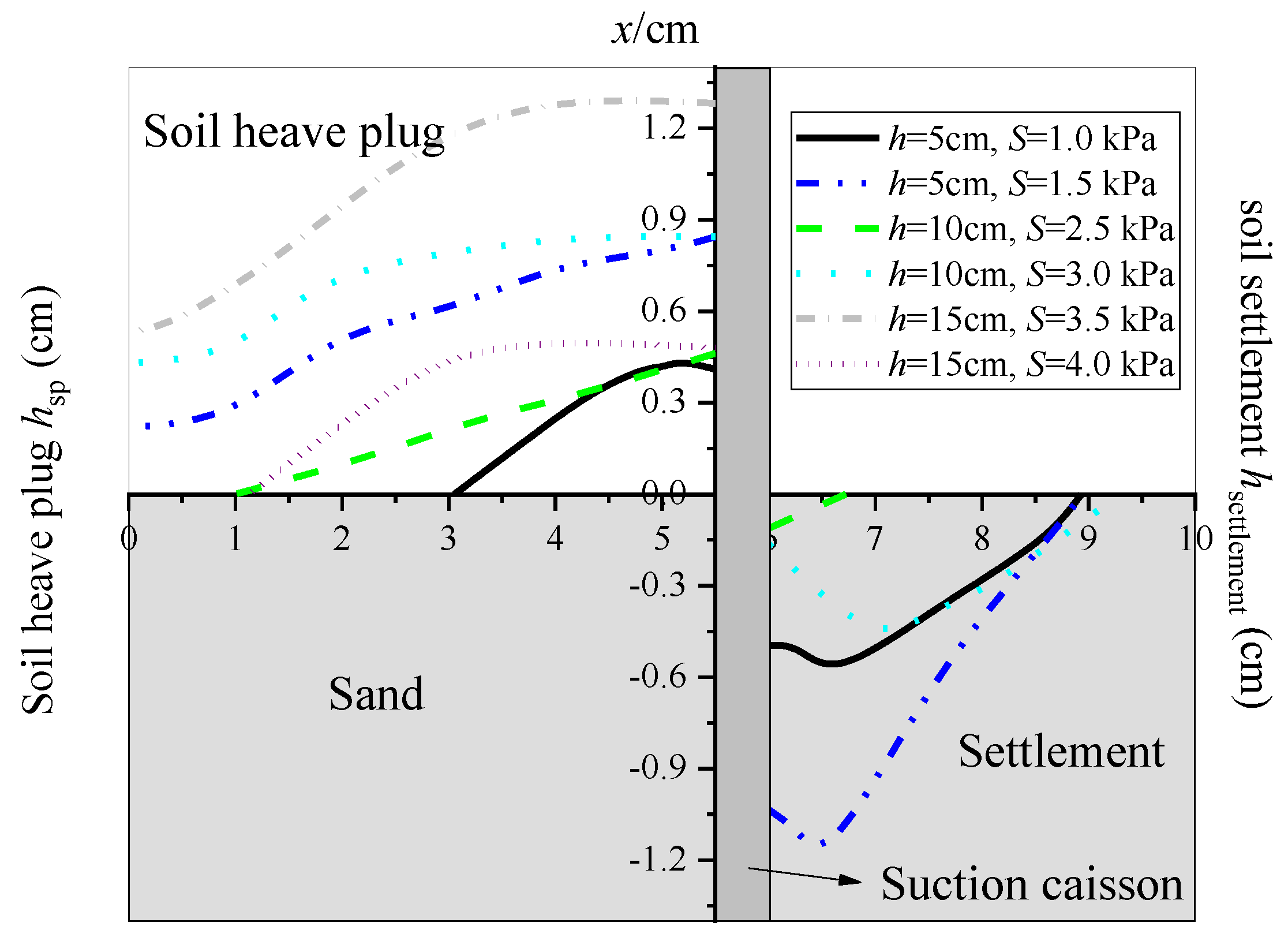
3.3. Soil Plug and Settlement Formation
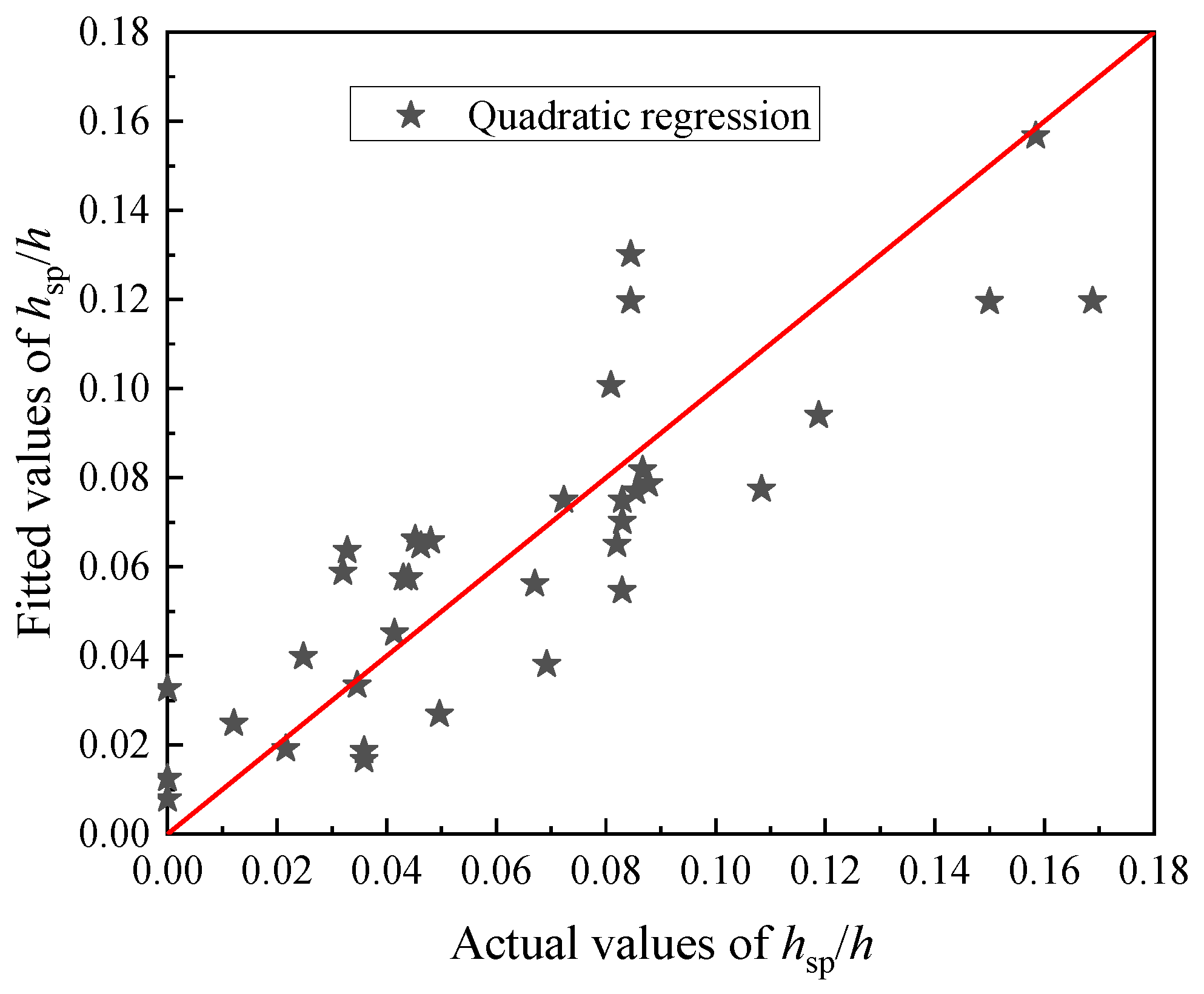
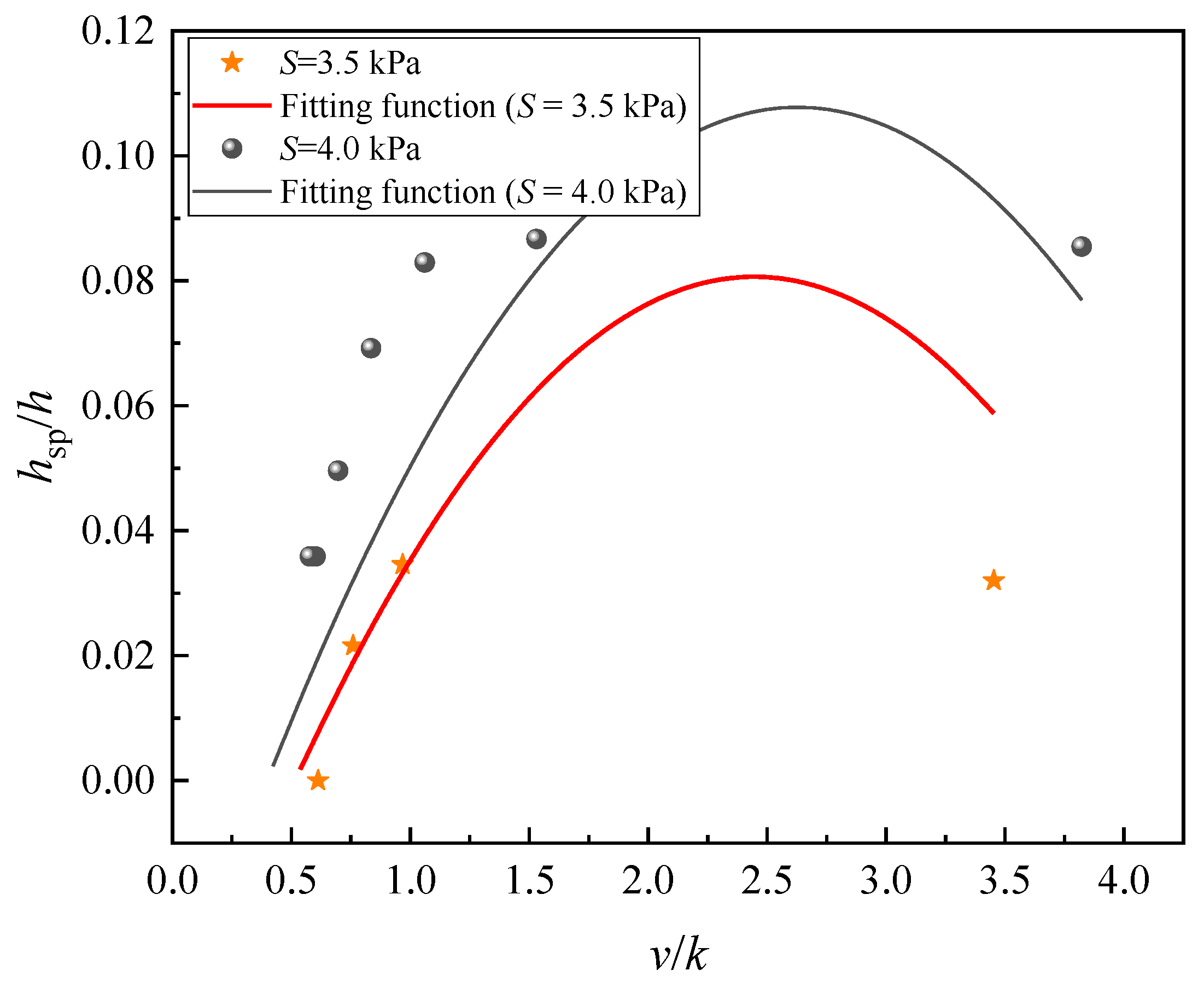
3.4. Prediction of Soil Plug Height
4. Conclusions
- (1)
- The seepage field can be visualized while the carmine stain flows along a streamline in the soil around the suction caisson. The seepage velocity is larger as the streamline moves toward the wall of the suction caissons. The pre-test results show that the seepage failure took place in the sand when the suction in the caisson with buried depths of 5, 10, and 15 cm was greater than 2.0, 3.5, and 4.0 kPa, respectively. The results indicated that the seepage path of the soil is unrelated to S applied in the caisson and is affected by the penetration depth during the installation of the foundation.
- (2)
- The hydraulic gradient v/k of the sand in tests at the mudline was proposed by using the regression function. It can be seen that the fitted values agree well with the actual values. Darcy’s law is not applicable, and the hydraulic gradient v/k increases with the increase of x/D. The results indicated that the seepage velocity is larger as the streamline moves toward the wall of the suction caissons. The v/k when S/γ’h = 2.451 is 5.85 times greater than when S/γ’h = 0.351 in tests. The minimum relative error is 5.05% for Equation (1) when S/γ’h = 5.478.
- (3)
- There is no soil plug in the caissons with small suction applied during suction penetration. The maximum heights of the soil plugs in the suction caisson models with buried depths of 5, 10, and 15 cm are 0.169, 0.085, and 0.087 times the buried depths, respectively. The height of soil plug hsp increases with the increase of x as a result of the distribution of seepage velocity, which is greater as it moves toward the wall of suction caissons. The influence of the soil heaved by the soil plug increases with the increase of h. The volume of the soil heaved begins to rise as the velocity of the seepage reaches a certain value. The dimensionless soil plug hsp/h first increases and then decreases with the increase of v/k.
Author Contributions
Funding
Conflicts of Interest
Notation
| S | Applied suction in the caisson |
| H | Water head |
| γw | Unit weight of water (10 kN/m3) |
| D | External diameter of the suction caisson |
| L | Height of the suction caisson |
| T | Thickness of the wall of the suction caisson |
| ρd | Dry density of the sand |
| Gs | Specific gravity of the sand |
| d10 | Effective size of the sand |
| e | Void ratio of the sand |
| γsat | Saturated weight of the sand |
| k | Permeability coefficient |
| h | Buried depth of the suction caisson |
| x | Abscissa value in Figure 1 |
| γ’ | Effective unit weight of soil |
| c | Cohesion of soil |
| φ | Angle of internal friction |
| hsp | Height of soil plug |
| hsettlement | Soil settlement outside the caisson |
References
- Jalbi, S.; Arany, L.; Salem, A.; Cui, L.; Bhattacharya, S. A method to predict the cyclic loading profiles (one-way or two-way) for monopile supported offshore wind turbines. Mar. Struct. 2019, 63, 65–83. [Google Scholar] [CrossRef]
- Chen, J.; Hu, Z.; Liu, G.; Wan, D. Coupled aero-hydro-servo-elastic methods for floating wind turbines. Renew. Energy 2019, 130, 139–153. [Google Scholar] [CrossRef]
- Li, D.; Ma, S.; Zhang, Y. Undrained pullout capacity of modified suction caisson in clay by finite element limit analysis. Mar. Georesour. Geotechnol. 2019, 37, 291–300. [Google Scholar] [CrossRef]
- Guo, Z.; Jeng, D.; Guo, W.; Wang, L. Failure mode and capacity of suction caisson under inclined short-term static and one-way cyclic loadings. Mar. Georesour. Geotechnol. 2018, 36, 52–63. [Google Scholar] [CrossRef]
- Lee, J.; Tran, N.X.; Kim, S. Development and field application of GFRP suction pile. Ocean Eng. 2019, 173, 308–318. [Google Scholar] [CrossRef]
- Li, D.; Ma, S.; Zhang, Y.; Chen, F. Lateral Bearing Capacity of Modified Suction Caissons Determined by Using the Limit Equilibrium Method. China Ocean Eng. 2018, 32, 461–466. [Google Scholar] [CrossRef]
- Byrne, B.W.; Houlsby, G.T. Experimental Investigations of the Response of Suction Caissons to Transient Combined Loading. J. Geotech. Geoenviron. 2004, 130, 240–253. [Google Scholar] [CrossRef]
- Kourkoulis, R.S.; Lekkakis, P.C.; Gelagoti, F.M.; Kaynia, A.M. Suction caisson foundations for offshore wind turbines subjected to wave and earthquake loading: Effect of soil-foundation interface. Géotechnique 2014, 64, 171. [Google Scholar] [CrossRef]
- Ukritchon, B.; Wongtoythong, P.; Keawsawasvong, S. New design equation for undrained pullout capacity of suction caissons considering combined effects of caisson aspect ratio, adhesion factor at interface, and linearly increasing strength. Appl. Ocean Res. 2018, 75, 1–14. [Google Scholar] [CrossRef]
- Chen, F.; Lian, J.; Wang, H.; Liu, F.; Wang, H.; Zhao, Y. Large-scale experimental investigation of the installation of suction caissons in silt sand. Appl. Ocean Res. 2016, 60, 109–120. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Byrne, B.W. Design procedures for installation of suction caissons in sand. Proc. Inst. Civil Eng. Geotechnol. 2005, 158, 135–144. [Google Scholar] [CrossRef]
- Senders, M.; Randolph, M.F. CPT-Based Method for the Installation of Suction Caissons in Sand. J. Geotech. Geoenviron. 2009, 135, 14–25. [Google Scholar] [CrossRef]
- Andersen, K.H.; Jostad, H.P.; Dyvik, R. Penetration Resistance of Offshore Skirted Foundations and Anchors in Dense Sand. J. Geotech. Geoenviron. 2008, 134, 106–116. [Google Scholar] [CrossRef]
- Erbrich, C.T.; Tjelta, T.I. Installation of bucket foundations and suction caissons in sand-geotechnical performance. In Proceedings of the Offshore Technology Conference 1999, Houston, TX, USA, 3–6 May 1999. [Google Scholar]
- Harireche, O.; Mehravar, M.; Alani, A.M. Suction caisson installation in sand with isotropic permeability varying with depth. Appl. Ocean Res. 2013, 43, 256–263. [Google Scholar] [CrossRef]
- Tran, M.N.; Randolph, M.F.; Airey, D.W. Study of Sand Heave Formation in Suction Caissons Using Particle Image Velocimetry (PIV). In Frontiers in Offshore Geotechnics, Proceedings of the 1st International Symposium on Frontiers in Offshore Geotechnics, Perth, Australia, 19–21 September 2005; Francis: London, UK, 2005; pp. 259–265. [Google Scholar]
- Harireche, O.; Mehravar, M.; Alani, A.M. Soil conditions and bounds to suction during the installation of caisson foundations in sand. Ocean Eng. 2014, 88, 164–173. [Google Scholar] [CrossRef]
- Allersma, H. Centrifuge Research on Suction Piles: Installation and Bearing Capacity. In BGA International Conference on Foundations: Innovations, Observations, Design and Practice, Proceedings of the International Conference Organised by British Geotechnical Association and Held in Dundee, Dundee, UK, 2–5 September 2003; Thomas Telford Publishing: London, UK, 2003; pp. 91–98. [Google Scholar]
- Tran, M.N.; Randolph, M.F.; Airey, D.W. Installation of Suction Caissons in Sand with Silt Layers. J. Geotech. Geoenviron. 2007, 133, 1183–1191. [Google Scholar] [CrossRef]
- Tran, M.N.; Airey, D.W.; Randolph, M.F. Study of Seepage Flow and Sand Plug Loosening in Installation of Suction Caissons in Sand. In Proceedings of the Fifteenth International Offshore and Polar Engineering Conference, Seoul, Korea, 19–24 June 2005; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2005. [Google Scholar]
- Lu, T.; Liu, Z. Advanced Soil Mechanics; China Machine Press: Beijing, China, 2006. [Google Scholar]
- Wang, L.; Li, Y.; Zhao, G.; Chen, N.; Xu, Y. Experimental Investigation of Flow Characteristics in Porous Media at Low Reynolds Numbers (Re→0) under Different Constant Hydraulic Heads. Water 2019, 11, 2317. [Google Scholar] [CrossRef]
- Guo, W.; Chu, J.; Kou, H. Model tests of soil heave plug formation in suction caisson. Proc. Inst. Civil Eng. Geotechnol. 2016, 169, 214–223. [Google Scholar] [CrossRef]



| Property | Specific Gravity Gs | Void Ratio e | Saturated Weight γsat (kN/m3) | Permeability Coefficient k (cm/s) | Cohesion c (kPa) | Angle of Internal Friction φ (°) |
|---|---|---|---|---|---|---|
| Value | 2.66 | 0.75 | 19.5 | 0.28 | 0 | 31 |
| Buried Depth h (cm) | Suction S (kPa) | ||||||
|---|---|---|---|---|---|---|---|
| 5 | 0.5 | 1.0 | 1.5 | - | - | - | - |
| 10 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | - |
| 15 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
| h = 5 cm | h = 10 cm | h = 15 cm | ||||
|---|---|---|---|---|---|---|
| S = 0.1 kPa | S = 1.5 kPa | S = 2.5 kPa | S = 3.0 kPa | S = 3.5 kPa | S = 4.0 kPa | |
| Vsettlement (cm3) | 0.544 | 0.970 | 0.020 | 0.473 | 0.000 | 0.000 |
| Vsp (cm3) | 0.344 | 1.520 | 0.519 | 1.954 | 0.849 | 2.827 |
| Vsettlement/Vsp | 1.581 | 0.638 | 0.039 | 0.242 | 0.000 | 0.000 |
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0.57495 | −0.49370 | 0.09759 | 0.05075 | −0.02168 | 0.02252 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Ma, S.; Lin, T. The Seepage and Soil Plug Formation in Suction Caissons in Sand Using Visual Tests. Appl. Sci. 2020, 10, 566. https://doi.org/10.3390/app10020566
Xie L, Ma S, Lin T. The Seepage and Soil Plug Formation in Suction Caissons in Sand Using Visual Tests. Applied Sciences. 2020; 10(2):566. https://doi.org/10.3390/app10020566
Chicago/Turabian StyleXie, Liquan, Shili Ma, and Tiantian Lin. 2020. "The Seepage and Soil Plug Formation in Suction Caissons in Sand Using Visual Tests" Applied Sciences 10, no. 2: 566. https://doi.org/10.3390/app10020566
APA StyleXie, L., Ma, S., & Lin, T. (2020). The Seepage and Soil Plug Formation in Suction Caissons in Sand Using Visual Tests. Applied Sciences, 10(2), 566. https://doi.org/10.3390/app10020566





