Abstract
When pedestrians walk along a corridor in both directions, a frequently observed phenomenon is the segregation of the whole group into lanes of individuals moving in the same direction. While this formation of lanes facilitates the flow and benefits the whole group, it is believed that results from the actions of the individuals acting on their behalf, without considering others. This phenomenon is an example of self-organization and has attracted the attention of a number of researchers in diverse fields. We introduce and analyze a simple model. We assume that individuals move around a multi-lane circular track. All of them move at the same speed. Half of them in one direction and the rest in the opposite direction. Each time two individuals collide, one of them moves to a neighboring lane. The individual changing lanes is selected randomly. We prove that the system self-organizes. Eventually, each lane is occupied with individuals moving in only one direction. Our analysis supports the belief that global self-organization is possible even if each member of the group acts without considering the rest.
1. Introduction
Spontaneous organization in systems composed of several units is known as self-organization. Self-organization is pervasive and is observed even when the units act responding to local stimuli, without considering the rest of the group. Researchers are interested in understanding how local interactions among units and with the environment leads to self-organization. Some books and review articles on self-organization in biological systems include [1,2,3,4].
Self-organization is observed when humans are walking in crowded environments. As a first example, consider two adjacent rooms connected by a door that is initially closed. Assume a large number of individuals is in each room and they all want to go to the other room. Suddenly, the door is opened. Under these circumstances, the spontaneous formation of an alternating flow is frequently observed. By alternating flow, we mean that the individuals take turns. Individuals from only one of the rooms cross the door for a period of time and then there is a sudden switch, individuals from the other room are the only ones crossing the door after the switch. This switching, or turn taking, persists while the environment remains crowded [5].
A second example of self-organization due to walking individuals interacting among themselves and with the environment is the formation of trails. More precisely, assume individuals need to cross, possibly in different directions, the same mildly dense grass field on a regular basis. Individuals will try to walk along the areas where the grass is shorter and less dense, even if the path they take as a result is not the shortest. Stepping on the grass is how the individuals affect the environment. Grass has a harder time growing in the areas heavily transited. As a result, dirt path trails form [6].
A third example of self-organization is the different pattern formations observed when the crowd is a collection of several smaller groups. For example, groups of friends or families. We refer the reader to [7] for more details. In this and the previous two examples, the coordinated behaviors observed are not planned by the crowd as a whole or by any member or group of members within the crowd. Instead, they emerge spontaneously, as a consequence of the individuals acting in response to local stimuli and motivated by their own goals.
The study of the dynamics of crowds is of interest for several reasons. It is a source of examples of self-organization. It may lead to strategies to increase the safety in crowded areas such as bridges [8] or stadiums. It can provide guidelines in the design of movie theaters, shopping malls, or other similar types of heavily transited buildings, where optimal crowd flow is desired because of economical and safety reasons. Accordingly, the study of dynamics of crowds, both theoretically (early works include [9,10], more recent work includes [11,12,13,14,15,16], see also [1,17] for reviews) and experimentally [18,19,20], is a very active area of research.
Microscopic mathematical models to study dynamics of crowds are those that keep track of each individual. Cellular automata models [18,21,22,23], lattice gas automata models [24,25], algorithms [26], and large systems of odes, are all examples of microscopic models. When large systems of odes are used, the mass times acceleration of each individual is set equal to the sum of generalized or social forces the individual feels [27,28,29,30,31]. These social forces are not real forces. They model the responses of the individuals to the environment and the presence and actions of the other individuals [32]. Some of these models are known as self-propelled particles models [33] and others, as individual based models [32,34].
Mesoscopic, kinetic or Boltzman-type models to study the dynamics of crowds, are integro-partial differential equations that describe the evolution of probability densities of the position and velocities of the individuals [35,36]. Macroscopic or continuum models are partial differential equations (conservation equations), where the dependent variables are the density and local average velocity of individuals [1,37,38,39,40]. Some works connect microscopic to macroscopic models [41,42,43]. Also, network models have been introduced [44] and optimal control theory has been used [45] to study the dynamics of crowds.
Assume a corridor or street is crowded with persons walking. Some of the pedestrians are walking in one direction, while the others, in the opposite direction. A self-organizing phenomenon frequently observed is that the individuals segregate into lanes of individuals moving only in one direction [46,47,48]. Needless to say, this formation of lanes benefits the whole group, as it results in an easier flow in both directions [49]. Motivated by this phenomenon, we introduce and analyze a new mathematical model. Our work supports the claim that the simple behavior by the individuals of moving out of the way to avoid imminent collisions leads to the self-organization of the system.
We describe the model in Section 2. Briefly, individuals move around a multi-lane circular track with the same angular speed. Half of them walk clockwise and the rest, counterclockwise. Each individual remains in its lane unless it collides with an other individual walking in the same lane but in the opposite direction. When such a collision occurs, one of the colliding individuals moves to a neighboring lane. The individual changing lanes is selected randomly. In Section 3, we present numerical simulations.
This is not the first article of the author studying this problem. The two-lane version of this model was introduced and studied in [50,51]. However, in the model introduced and studied here, the number of lanes is not restricted to two, it can have any number of lanes. Going from two to any number of lanes is not a simple extension. As a result, the analysis and methods used here are completely different. In short, this is a novel article and not a mere extension of previous work of the author.
Section 4, Section 5, Section 6, Section 7 and Section 8 consist of analysis of the system. In Section 8, we prove that, with probability 1, the system will self-organize, i.e., eventually, all the individuals within each lane move in the same direction. We finish the article with a short discussion in Section 9.
2. The Model
We consider the following scenario: individuals or pedestrians walk around a multi-lane circular track. Half of the individuals move in a clockwise direction and the other half, in a counterclockwise direction. Each time two individuals moving in opposite directions and in the same lane meet, we say they collide. When two individuals collide, exactly one of them, randomly chosen, with each having the same probability of of being chosen, moves to a neighboring lane. If the collision occurs in the most inner or most outer lane, there is only one neighboring lane. If the collision takes place in another lane, the neighboring lane to which the individual changing lanes moves is also chosen randomly.
Next, we enumerate a list of statements. The ith statement will be referred as statement i from Section 2. These statements are either rules that help precisely define the dynamics of our system, or observations that are consequences of those rules and will be needed in the analysis in subsequent sections.
- individuals move around a circular track with L lanes. Each lane is labeled with a number. The inner lane is lane 1, the lane next to lane 1 is lane 2, and so on. Note that the outer lane is lane L.
- N individuals move in the counterclockwise direction and the other N in the clockwise direction.
- All individuals move with the same constant angular speed and thus, it takes each individual a time of to complete a loop.
- Each individual moving counterclockwise is labeled with an integer i, where . The position of the individual i moving counterclockwise at time t is described by an angle and by , the number of the lane the individual is at time t. For simplicity, we require to be a continuous function and thus, since the angular speed is constant, we have . For convenience, we assume the initial angles to satisfy . Note that the function will be discontinuous at the times t when the counterclockwise moving individual i changes lanes. Strictly speaking, is not defined at the times it is discontinuous. This will not cause any problems.
- Each individual moving clockwise is also labeled with an integer j, with . The position of the individual j moving clockwise at time t is described by the angle , where , and by , the number of the lane the individual is at time t.
- We assume that initially, i.e., at time , all the angles defined above are different. This means not only that individuals start at different positions, but also that, at , any two individuals do not have positions that correspond to the same angle. If an individual at looks to its sides, it will not see any other individual in the other lanes with the same initial angle.
- Given the last statement, two individuals moving in the same direction will never have the same angle.
- Two individuals collide at time t if they reach the same location at that time. Given the last statement, if two individuals collide, they move in opposite directions. In mathematical terms, the individual i moving counterclockwise and the individual j moving clockwise collide at time t if for some integer k and . In the last equation, denotes the right limit as s tends to t, that is, s approaches t but under the restriction . This limit is taken because one of the individuals will change lanes at time t and thus, either or will not be defined at exactly that time. Note also that the angles of the colliding individuals do not have to be equal. It is enough that they differ by an integer multiple of , which includes the case of them being equal. Adding or subtracting to an angle does not change the position.
- For all pairs i, j such that , we defineWe assume that if or . Equation (1) will be further discussed in the next section. The discussion in that section should make the reader clear that the assumption if or implies that two different collisions never occur at the same time.
- If two individuals, the individual i moving counterclockwise and the individual j moving clockwise, collide at time t, exactly one of them changes lanes at that time. The probability that the individual i changes lanes is and thus, is also the probability that j changes lanes. Assume the collision occurs in lane ℓ. If , the individual changing lanes moves to lane with probability or to lane , also with probability . If , the individual changing lanes moves to lane 2, and if , it moves to lane .
- An individual can only change lanes when it collides with an other individual.
We note that the assumptions in points 6 and 9 above are not restrictive at all. For example, if the initial angles were to be selected randomly with a uniform probability distribution around the track, assumptions in points 6 and 9 would be satisfied with probability 1. Those assumptions are made to simplify the analysis but are not fundamental.
Our model is very simple and is based on local responses only. The selection of the individual that changes lanes, and the lane it moves to, are independent of the location of all the other individuals. The individuals do not make smart decisions attempting to prevent future collisions.
3. Numerical Simulations
Figure 1 shows the results of a numerical simulation with 120 individuals in a circular track with 4 lanes. The individuals move at one revolution per unit time. Figure 1 shows the positions of the individuals at three different times: , and . The number of collisions that occurred by those times are also indicated in Figure 1. The initial angles of the individuals were randomly chosen with uniform probability distribution around the track. The lane where each individual started was also randomly selected, with each lane having 1/4 as the probability of being chosen.
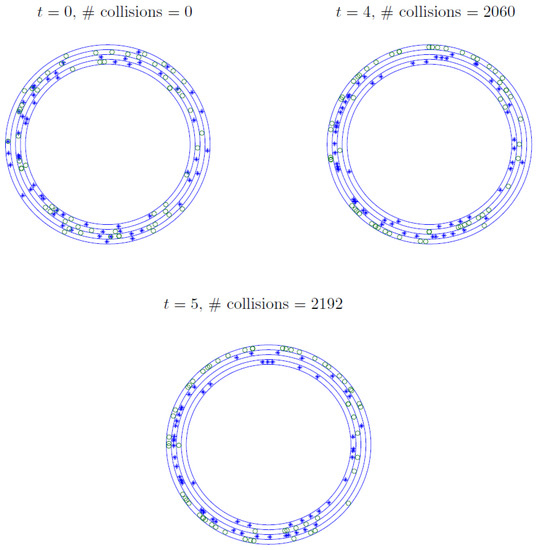
Figure 1.
Positions of the pedestrians at different times. The circles are the pedestrians moving clockwise. The exes are the pedestrians moving counterclockwise.
Note that, in the realization of Figure 1, at (in fact slightly before that), after 2192 collisions, all the pedestrians moving in the counterclockwise direction are in the inner lane, which is lane 1, and in lane 3. All those moving in the clockwise direction are in lanes 2 and 4, the outer lane. No more collisions occur after this time. We say that the system has self-organized.
We have run several simulations with different randomly generated initial conditions (not shown here) and in all those simulations, the system self-organized. Our numerical simulations suggest that the system always self-organizes. We will prove that this is the case with probability 1.
4. Possible Collision Times
We recall the reader that two individuals collide at time t if they are in the same lane at that time and their angles differ by an integer multiple of . When we say they are in the same lane at time t, we mean they are in the same lane just before one of them changes lanes. Note that, since 0 is an integer, the angles differing by an integer multiple of includes the case when the angles are equal.
We define to be the first time that the angle of the individual i moving counterclockwise and the angle of the individual j moving clockwise differ by an integer multiple of . These two individuals do not collide for any t satisfying and they collide at if and only if they are in the same lane at that time. Thus, we refer to as the first or smallest possible collision time between the individual i moving counterclockwise and the individual j moving clockwise.
Recall that the angle of the individual i moving counterclockwise and the angle of the individual j moving clockwise are given by and , respectively. Recall also that all the initial angles are greater than or equal to 0 and less than . Given these two facts, little thought is necessary to convince the reader about the validity of the Equation (1). Note that the time always satisfies .
We define to be the set of all positive times when the difference between the angles of the individual i moving counterclockwise and the individual j moving clockwise differ by an integer multiple of . Straight forward algebra shows that is the set of all times of the form , where n is any non-negative integer,
If the individual i moving counterclockwise and the individual j moving clockwise collide, they so do at some time t in . In fact, these two individuals collide at time t if and only if and they are both in the same lane at time t. Given these facts, we refer to the set as the set of possible collision times between the individual i moving counterclockwise and the individual j moving clockwise.
We define to be the union of the sets , where the union is taken over all individuals i moving counterclockwise and individuals j moving clockwise
If there is a collision at time t, then t is in the set . Thus, we refer to as the set of possible collision times.
We sort the elements in and label them as with . In other words, the sequence , with , is defined by the facts that for all positive integers n, and
For convenience, we define , but we do keep out of the set .
Note that the assumption in Point 9 in Section 2 implies that the sets are pairwise disjoint. Thus, is a first possible collision time between two individuals, i.e., for some i and j, if and only if . Thus, we have that . Note also that for all . Also note that, for every pair i, j, with , there exists n such that and .
5. Evolution Equations
Given any positive integer n, the time is a possible collision time between two individuals. We denote by , the integer corresponding to the individual moving counterclockwise and by , the integer corresponding to the individual moving clockwise involved in the possible collision at time . In other words, the functions and are defined by the following statement: is a possible collision time between the individual moving counterclockwise and the individual moving clockwise. Following the discussion of Section 4, it can be easily shown that and for all n.
A simple but important observation is that each individual remains in the same lane in between consecutive possible collisions times. i.e., and remain constant in time intervals of the form for all n, i and j. Thus, for any and , we define
For each integer n, we regard as the component of a -vector that we call and we regard as the component of the same vector,
We also denote the component of by . Thus, we have if , and if .
We define to be the set of -vectors, whose components are positive integers no greater than L
Note that is in for all n.
Let and be two elements in . Next, we describe the probability that given that . The standard notation for this probability, known as conditional probability, is . Before we proceed, note that implies that and .
- If , there is no collision at time . Thus,
- If , at time , the individual moving counterclockwise and the individual moving clockwise collide in lane 1. Thus,The first condition in the above equation corresponds to the individual moving counterclockwise, changing from lane 1 to lane 2. The second condition corresponds to the individual moving clockwise, changing from lane 1 to lane 2.
- If , at time , the individual moving counterclockwise and the individual moving clockwise collide in lane L. Thus,The first condition in the above equation corresponds to the individual moving counterclockwise, changing from lane L to lane . The second condition corresponds to the individual moving clockwise, changing from lane L to lane .
- If , with , at time , the individual moving counterclockwise and the individual moving clockwise collide in a lane other than lanes 1 and L. Thus,The first condition in the above equation corresponds to the individual moving counterclockwise, changing from lane ℓ to lane . The second condition corresponds to the individual moving counterclockwise, changing from lane ℓ to lane . The third condition corresponds to the individual moving clockwise, changing from lane ℓ to lane . The fourth condition corresponds to the individual moving clockwise, changing from lane ℓ to lane .
6. Self-Organized Configurations
We say that the system is self-organized if there are no more collisions. This can only occur if each lane contains only individuals moving in the same direction. Note that once the system is self-organized, it remains self-organized for all later times since there are no more collisions and thus, no more lane changes by any individual.
Assume the system is self-organized after the possible collision time, i.e., for . Thus, for any pair i, j, where , the individual i moving counterclockwise is in a different lane than the individual j moving clockwise, i.e., . Equivalently, . A more mathematical description is possible. We define the set
The system is self-organized for if and only if is in A.
7. Probabilities to Reach Self-Organization
For each non-negative integer n and each in , we define to be the probability that the system eventually self-organizes given that . According to the discussion of the last section,
Given the periodicity of the pairs of individuals involved in the possible collisions, i.e., and , we have that for all non-negative integers n and all in . Note also that for all in A.
Following standard arguments in the analysis of Markov Chains, we can obtain the following equation
8. Self-Organization Occurs with Probability 1
Since has only a finite number of elements, to be precise, and for all non-negative integers n and all in , the set such that n is a non-negative integer and is in contains, at most, different numbers. Thus, since it is finite, this set has a minimum. For future reference, we summarize this statement in the next observation.
Observation 1.
There exists a non-negative integer n, that can be taken to be no greater than , and in Ω such that for any non-negative integer k and in Ω. For future reference, we call this minimum value λ, i.e.,
where the minimum is taken over all non-negative integers k and all in Ω.
Let be all real numbers. We say that x is a convex combination of if there exits non-negative numbers such that and . There is a very simple and well known fact that will be useful to us. Namely, if x is a convex combination of with positive coefficients (i.e., for all i) and for all i, then for all .
Note that Equation (14) implies that is a convex combination of with in . By restricting the sum on the right hand side of Equation (14) to only those such that , we can apply the fact stated in the previous paragraph to prove the validity of the following observation.
Observation 2.
Let n be a non-negative integer and in Ω. Assume (as defined in Equation (15)). Let be also in Ω. If , then .
Repeated applications of Observation 2 leads to the next Observation.
Observation 3.
Let m be a non-negative integer and in Ω. Assume . Let be elements in Ω. Assume that for all , then .
For each positive integer n, we define a set of functions defined on that also take values on . Setting , these functions are determined by the following rules:
- If then .
- If then and for all .
- If then and for all .
Note that, if and , each individual stayed in its lane if there was no collision at time ; the individual moving clockwise moved to lane 2 if there was a collision at time and that collision occurred in lane 1; the individual moving counterclockwise moved to lane if there was a collision at time and that collision occurred in lane ℓ with .
Note that, when we think of the individuals moving around the track, the effect of applying the functions successively, i.e., for is to get any clockwise moving individual out of lane 1 and into lane 2, and to move any counterclockwise moving individual toward lane 1. All these changes of lanes are possible within our model with positive probability.
Observation 4.
for all positive integers n and all in Ω.
The validity of this last Observation can be easily verified using the discussion of Section 5 and the definition of the functions . In fact, we have
Observation 5.
Let . Then, and for all , with exactly one of these inequalities being a strict inequality unless .
The validity of this last Observation is immediate from the definition of the functions .
Observation 6.
Let r be a non-negative integer. Let be in Ω and let be defined recursively by , where . Assume there exist such that . Then, for all .
This Observation results from Observation 5. For any , the component of with forms a monotone sequence. Thus, unless it remains constant, it can not return to its initial value (with ). Since , there exists such that the component of is different than the component of . Thus, the component of is different to the component of for all .
We recall that the set A was defined in Equation (12). The system is self-organized for if and only if is in A.
Observation 7.
Let r be a non-negative integer. Let be in Ω and let be defined recursively by , where . Assume there exist and such that . Then, belongs to A.
From Observation 6, implies that for all n satisfying . This can only happen if for all . Thus, since and for all s, and , we have that in fact for all . However, this implies that there will no be any more collisions for if and thus, belongs to A.
Observation 8.
Let r be a non-negative integer. Let be in Ω and let be defined recursively by for . Then, there exists such that belongs to A.
The proof of this Observation is as follows. is a finite set. Thus, there exists integer and such that . Then, from Observation 7, belongs to A.
Observation 9.
Let λ be as defined in Equation (15). Then .
Let be in and r an integer satisfying such that . Let and let be defined recursively by for all .
Apply Observation 4 with to get for all .
Now apply Observation 3, with the role of in that observation being played by for all and the role of m being played by r to get that for all . Note that we are under the hypothesis of that Observation since .
From Observation 8 there exists such that belongs to A. Thus, for all integers m. However, we have obtained that for all . Setting , we get and thus, the statements of this paragraph imply that .
Theorem 1.
The system self-organizes with probability 1 no matter the initial conditions. In other words, let in Ω. Assume . Then, .
The proof is immediate. By definition, . However, . Since we proved that and probabilities can not exceed 1, the theorem is proved.
9. Discussion
We have introduced a simple model to study the formation of lanes in crowds of individuals moving in opposite directions. Our model has proved simple enough to be amenable to analytical analysis.
The model studied in this article is different in nature from the existing models that can be found in the literature. This model is the simplest model we could think of that isolates the effect of pedestrians avoiding collisions in a very simple way. This model, that could be considered a toy model, has the usual advantage of simple models: (1) The results obtained are clear, concrete and easy to interpret, (2) Its simplicity makes it amenable to analytical analysis.
Our model belongs to the class of microscopic models, i.e., the model follows the trajectory of each individual. Many microscopic models that can be found in the literature consist of a set of coupled odes. Our model is different. Our model is a Markov Chain. Cellular automata models are somewhat closer in flavor to our model, but our set up and the rules governing the dynamics of our system are different to what can be found in the literature.
Our model, as presented and analyzed here, cannot be used to make any deep comparison with experimental data. The only comparison that can be made is that our model predicts that self-organization occurs.
There is a trade off, and with simplicity we sometimes lose generality. Most models in the literature do not lend themselves to the simple analytical analysis presented in this article. Instead, they have to be solved numerically. However, they are more general in the sense that different phenomena can be studied by simply changing boundary or initial conditions or parameters. We believe that both strategies, the study of simple toy models, as in this article, and the study of comprehensive more complex models, as most of the studies found in the literature, are very valuable and complement each other.
While several extensions of the work presented here are possible, understanding the expected time that it takes the system to self-organize is, in the view of the author, both challenging and interesting. The author plans to pursue this research direction.
We believe this article is a step towards the understanding of self-organization in biological systems, and we hope the modeling style of this article will be adopted by other researchers to study this and other self-organization phenomena in biological systems.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Bellomo, N.; Dogbe, C. On the modeling of traffic and crowds: A survey of models, speculations, and perspectives. SIAM Rev. 2011, 53, 409–463. [Google Scholar] [CrossRef]
- Camazine, S. Self-Organization in Biological Systems; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Sumpter, D.J. Collective Animal Behavior; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Vicsek, T.; Zafeiris, A. Collective motion. Phys. Rep. 2012, 517, 71–140. [Google Scholar] [CrossRef]
- Kretz, T.; Wölki, M.; Schreckenberg, M. Characterizing correlations of flow oscillations at bottlenecks. J. Stat. Mech. Theory Exp. 2006, 2006, P02005. [Google Scholar] [CrossRef][Green Version]
- Helbing, D.; Keltsch, J.; Molnar, P. Modelling the evolution of human trail systems. Nature 1997, 388, 47–50. [Google Scholar] [CrossRef]
- Moussaïd, M.; Perozo, N.; Garnier, S.; Helbing, D.; Theraulaz, G. The walking behaviour of pedestrian social groups and its impact on crowd dynamics. PLoS ONE 2010, 5, e10047. [Google Scholar] [CrossRef] [PubMed]
- Bruno, L.; Venuti, F. Crowd–structure interaction in footbridges: modelling, application to a real case-study and sensitivity analyses. J. Sound Vib. 2009, 323, 475–493. [Google Scholar] [CrossRef]
- Henderson, L. The statistics of crowd fluids. Nature 1971, 229, 381–383. [Google Scholar] [CrossRef] [PubMed]
- Henderson, L. On the fluid mechanics of human crowd motion. Transp. Res. 1974, 8, 509–515. [Google Scholar] [CrossRef]
- Barbosa, H.; Barthelemy, M.; Ghoshal, G.; James, C.R.; Lenormand, M.; Louail, T.; Menezes, R.; Ramasco, J.J.; Simini, F.; Tomasini, M. Human mobility: Models and applications. Phys. Rep. 2018, 734, 1–74. [Google Scholar] [CrossRef]
- Cristín, J.; Méndez, V.; Campos, D. General scaling in bidirectional flows of self-avoiding agents. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef]
- Festa, A.; Tosin, A.; Wolfram, M.T. Kinetic description of collision avoidance in pedestrian crowds by sidestepping. arXiv 2016, arXiv:1610.05056. [Google Scholar] [CrossRef]
- Qin, X.; Liu, H.; Zhang, H.; Liu, B. A collective motion model based on two-layer relationship mechanism for bi-direction pedestrian flow simulation. Simul. Model. Pract. Theory 2018, 84, 268–285. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M. Crowd behaviour and motion: Empirical methods. Transp. Res. Part B Methodol. 2018, 107, 253–294. [Google Scholar] [CrossRef]
- Rahmati, Y.; Talebpour, A. Learning-based game theoretical framework for modeling pedestrian motion. Phys. Rev. E 2018, 98, 032312. [Google Scholar] [CrossRef]
- Helbing, D. Traffic and related self-driven many-particle systems. Rev. Mod. Phys. 2001, 73, 1067. [Google Scholar] [CrossRef]
- Blue, V.J.; Adler, J.L. Cellular automata microsimulation for modeling bi-directional pedestrian walkways. Transp. Res. Part B Methodol. 2001, 35, 293–312. [Google Scholar] [CrossRef]
- Moussaïd, M.; Helbing, D.; Garnier, S.; Johansson, A.; Combe, M.; Theraulaz, G. Experimental study of the behavioural mechanisms underlying self-organization in human crowds. Proc. R. Soc. B Biol. Sci. 2009, 276. [Google Scholar] [CrossRef]
- Moussaid, M.; Guillot, E.G.; Moreau, M.; Fehrenbach, J.; Chabiron, O.; Lemercier, S.; Pettré, J.; Appert-Rolland, C.; Degond, P.; Theraulaz, G. Traffic instabilities in self-organized pedestrian crowds. PLoS Comput. Biol. 2012, 8, e1002442. [Google Scholar] [CrossRef]
- Chen, L.; Tang, T.Q.; Huang, H.J.; Wu, J.J.; Song, Z. Modeling pedestrian flow accounting for collision avoidance during evacuation. Simul. Model. Pract. Theory 2018, 82, 1–11. [Google Scholar] [CrossRef]
- Ma, J.; Song, W.G.; Zhang, J.; Lo, S.M.; Liao, G.X. k-Nearest-Neighbor interaction induced self-organized pedestrian counter flow. Phys. A Stat. Mech. Its Appl. 2010, 389, 2101–2117. [Google Scholar] [CrossRef]
- Weifeng, F.; Lizhong, Y.; Weicheng, F. Simulation of bi-direction pedestrian movement using a cellular automata model. Phys. A Stat. Mech. Its Appl. 2003, 321, 633–640. [Google Scholar] [CrossRef]
- Hua, K.; Xing-Li, L.; Yan-Fang, W.; Tao, S.; Shi-Qiang, D. Effect of following strength on pedestrian counter flow. Chin. Phys. B 2010, 19, 070517. [Google Scholar] [CrossRef]
- Muramatsu, M.; Irie, T.; Nagatani, T. Jamming transition in pedestrian counter flow. Phys. A Stat. Mech. Its Appl. 1999, 267, 487–498. [Google Scholar] [CrossRef]
- Gipps, P.G.; Marksjö, B. A micro-simulation model for pedestrian flows. Math. Comput. Simul. 1985, 27, 95–105. [Google Scholar] [CrossRef]
- Helbing, D. A mathematical model for the behavior of pedestrians. Behav. Sci. 1991, 36, 298–310. [Google Scholar] [CrossRef]
- Helbing, D.; Molnar, P.; Farkas, I.J.; Bolay, K. Self-organizing pedestrian movement. Environ. Plan. B 2001, 28, 361–384. [Google Scholar] [CrossRef]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef]
- Jian, L.; Lizhong, Y.; Daoliang, Z. Simulation of bi-direction pedestrian movement in corridor. Phys. A Stat. Mech. Its Appl. 2005, 354, 619–628. [Google Scholar] [CrossRef]
- Treuille, A.; Cooper, S.; Popović, Z. Continuum crowds. ACM Trans. Graph. (TOG) 2006, 25, 1160–1168. [Google Scholar] [CrossRef]
- Degond, P.; Hua, J. Self-Organized Hydrodynamics with congestion and path formation in crowds. J. Comput. Phys. 2013, 237, 299–319. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Farkas, I.J.; Helbing, D. Application of statistical mechanics to collective motion in biology. Phys. A Stat. Mech. Its Appl. 1999, 274, 182–189. [Google Scholar] [CrossRef]
- Degond, P.; Appert-Rolland, C.; Moussaid, M.; Pettré, J.; Theraulaz, G. A hierarchy of heuristic-based models of crowd dynamics. J. Stat. Phys. 2013, 152, 1033–1068. [Google Scholar] [CrossRef]
- Bellomo, N.; Bianca, C.; Delitala, M. Complexity analysis and mathematical tools towards the modelling of living systems. Phys. Life Rev. 2009, 6, 144–175. [Google Scholar] [CrossRef]
- Helbing, D. A fluid dynamic model for the movement of pedestrians. arXiv 1998, arXiv:cond-mat/9805213. [Google Scholar]
- Appert-Rolland, C.; Degond, P.; Motsch, S. Two-way multi-lane traffic model for pedestrians in corridors. arXiv 2011, arXiv:1105.0203. [Google Scholar]
- Hughes, R.L. The flow of human crowds. Annu. Rev. Fluid Mech. 2003, 35, 169–182. [Google Scholar] [CrossRef]
- Jiang, Y.Q.; Zhang, P.; Wong, S.; Liu, R.X. A higher-order macroscopic model for pedestrian flows. Phys. A Stat. Mech. Its Appl. 2010, 389, 4623–4635. [Google Scholar] [CrossRef]
- Piccoli, B.; Tosin, A. Time-evolving measures and macroscopic modeling of pedestrian flow. Arch. Ration. Mech. Anal. 2011, 199, 707–738. [Google Scholar] [CrossRef]
- Chertock, A.; Kurganov, A.; Polizzi, A.; Timofeyev, I. Pedestrian flow models with slowdown interactions. Math. Model. Methods Appl. Sci. 2014, 24, 249–275. [Google Scholar] [CrossRef]
- Cristiani, E.; Piccoli, B.; Tosin, A. Multiscale modeling of granular flows with application to crowd dynamics. Multiscale Model. Simul. 2011, 9, 155–182. [Google Scholar] [CrossRef]
- Di Francesco, M.; Rosini, M.D. Rigorous derivation of nonlinear scalar conservation laws from follow-the-leader type models via many particle limit. Arch. Ration. Mech. Anal. 2015, 217, 831–871. [Google Scholar] [CrossRef]
- Løvås, G.G. Modeling and simulation of pedestrian traffic flow. Transp. Res. Part B Methodol. 1994, 28, 429–443. [Google Scholar] [CrossRef]
- Hoogendoorn, S.; Bovy, P.H.L. Simulation of pedestrian flows by optimal control and differential games. Optim. Control. Appl. Methods 2003, 24, 153–172. [Google Scholar] [CrossRef]
- Kretz, T.; Grünebohm, A.; Kaufman, M.; Mazur, F.; Schreckenberg, M. Experimental study of pedestrian counterflow in a corridor. J. Stat. Mech. Theory Exp. 2006, 2006, P10001. [Google Scholar] [CrossRef]
- Milgram, S.; Toch, H. Collective behavior: Crowds and social movements. In The Handbook of Social Psychology; ResearchGate: Berlin, Germany, 1969; Volume 4. [Google Scholar]
- Older, S. Movement of pedestrians on footways in shopping streets. Traffic Eng. Control 1968, 10, 160–163. [Google Scholar]
- Helbing, D.; Vicsek, T. Optimal self-organization. New J. Phys. 1999, 1, 13. [Google Scholar] [CrossRef]
- Goldsztein, G.H. A Mathematical Model of the Formation of Lanes in Crowds of Pedestrians Moving in Opposite Directions. Discret. Dyn. Nat. Soc. 2015, 2015. [Google Scholar] [CrossRef]
- Goldsztein, G.H. Particles Moving Around a Two-Lane Circular Track in Both Directions. Avoiding Collisions Leads to Self-Organization. SIAM J. Appl. Math. 2016, 76, 1433–1445. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).