Abstract
Partial orders are the natural mathematical structure for comparing multivariate data that, like colours, lack a natural order. We introduce a novel, general approach to defining rank features in colour spaces based on partial orders, and show that it is possible to generalise existing rank based descriptors by replacing the order relation over intensity values by suitable partial orders in colour space. In particular, we extend a classical descriptor (the Texture Spectrum) to work with partial orders. The effectiveness of the generalised descriptor is demonstrated through a set of image classification experiments on 10 datasets of colour texture images. The results show that the partial-order version in colour space outperforms the grey-scale classic descriptor while maintaining the same number of features.
1. Introduction
It is, at first sight, peculiar that one of the most robust tools for image description, namely rank features, have only seen limited application to colour images. The problem is, of course, that while they are very effective at dealing with noise, rank features run afoul of the main theoretical difficulty associated with colour spaces—that is the absence of a natural order.
In recent years there has been a revival of interest in ranking of colour pixels. Notably, Ledoux et al. [1] published an extensive comparative study in the use of total orders as rank features for texture recognition. However, interest has been keenest in the field of colour morphology, where several solutions have been proposed—from adaptive orders that work around the ‘false colour problem’ to the natural mathematical structure for ordering higher-dimensional sets—that is partial orders [2,3,4,5,6].
In partially-ordered sets we simply admit that there will be couples of elements incomparable to each other. Partial orders are therefore particularly suitable for dealing with colour spaces, where statements like “yellow is greater than green” make little or no sense at all.
The objective of this work is to introduce a novel category of rank features based on partial orders. In the remainder, after providing some background on partial orders (Section 2), we detail the ways in which rank features can be defined (Section 2.5) and extend a classical descriptor (the Texture Spectrum) to work with partial orders (Section 3.1). We demonstrate the feasibility of the method through a set of experiment on 10 datasets of colour texture images (Section 3.2) and show that partial orders in colour space can outperform grey-scale total ordering (Section 4).
2. Background
2.1. Rank Features
Rank features are a well established technique for dealing with noise in images, enforcing invariance to all sorts of contrast or illumination variations and sensor nonlinearities [7]. Because of their robustness, they were first developed in the context of wide-baseline stereo matching—see for instance the census and rank transforms [8]. More recently, descriptors in the popular Local Binary Pattern (LBP) family, including Texture Spectrum, Binary Gradient Contours, etc. [9,10] have turned rank features into a general purpose tool, with applications—among others—in texture classification, face recognition, surface inspection and content-based image retrieval [11]. The descriptive power of rank features has been expanded to explicitly capture orientation (Ranklets [12]) and second-order stimuli (Variance Ranklets [13]), all types of information that were seen as the preserve of linear filters or ad-hoc algorithms.
Common to all rank features is the fact that they are defined in terms of ordinal information between pixels only, with the actual pixel values being discarded. This can be done in terms of pairwise pixel comparisons (rank and census transform, LBP), pixel ranks (Ranklets) or a permutation of ranks (Variance Ranklets), but it is easy to see that the two approaches are equivalent [12] and that all descriptors rely on the natural order relation (≤) between pixel values.
Before proceeding to definitions it is worth noting that, notwithstanding the trend towards the use of convolutional neural networks as feature extractors [14], rank features are still competitive in texture applications [15]. In the following section we recall the axioms for an order relation.
2.2. Order Relations
An order relation is an abstraction of the common notion of “greater than” used to compare numerical values, in our case pixel values in (typically the set of 8-bit intensity values). In order to be called a (total) order, a binary relation ≤ needs to satisfy the following four conditions:
Definition 1
(Order axioms). For all ,
- 1.
- (reflexivity).
- 2.
- if and then (antisymmetry).
- 3.
- if and then (transitivity).
- 4.
- either or (totality).
The last condition guarantees that we know how to compare any pair of pixel values.
2.3. Ordering High-Dimensional Data
The application of rank features to multi-channel images or higher dimensional data is hindered by the fact that there is no natural way of ordering multivariate data. It is certainly possible to provide a total order for a colour space; for instance, one could order RGB data lexicographically using the R channel as the primary sorting key, followed by G and finally by B. However, like other similar options, this has a disadvantage, namely, there are colours that are very close to each other in colour space, but very far in the order—and is therefore of limited practical interest (a sub-relation of the lexicographical order, the product order, is indeed of practical interest and will be discussed in detail in this paper, see Section 2.5.1). In general, it is best to resort to some sort of sub-ordering principle. These can be broadly divided in four categories [16]:
- Marginal ordering (M-ordering).
- Reduced (aggregate) ordering (R-ordering).
- Conditional (sequential) ordering (C-ordering).
- Partial ordering (R-ordering).
In marginal ordering, ranking is carried out on one or more components (marginals) of the multivariate data. Ranking colour data in the RGB space by the value of red is an example of M-ordering; lexicographical ordering is another one. Reduced (aggregate) ordering relies on converting multivariate data to univariate through suitable transformations. A common way to do this consists of establishing a reference point in the data space and using the distance from that point to rank the data. Conditional ordering occurs when we sort a random multivariate sample based on the corresponding (usually marginally-sorted) values of another sample. C-ordering is closely related to the concept of concomitants in Statistics [17]. Partial ordering will be discussed in detail in Section 2.5.
Interestingly, many of the common ways of dealing with order in colour space fall under the first two categories, i.e., marginal and reduced (aggregate) ordering. For instance, ranking based on intensity can be seen as a marginal ordering of the HSV space along the V axis; or as a reduced or aggregate ordering over the RGB space, where the aggregating function is the grey-level intensity. Other examples of aggregating orders will be given in Section 3.1.
In this paper, we will focus on rank features based on partial orders. Before introducing these, we review recent approaches to using multivariate orders on colour images.
2.4. Rank-Based Approaches to Colour Processing
Previous approaches to rank-based colour features typically extend grey-scale rank-based methods to the colour domain by considering either the colour channels separately (intra-channel features) and/or in pairwise combination (inter-channel features). Mäenpää and Pietikäinen [18] for instance extended classic LBP by applying it both to each R, G and B colour channel separately and pairwise between each of the R–G, R–B and G–B pairs. Bianconi et al. [19] adopted the same approach for extending grey-scale ranklets [12] to the colour domain. Lee et al. [20] defined Local Colour Vector Binary Patterns (LCVBP) by decomposing the colour triplets into a norm and angular component and by computing LBP on each of them. More recently, Cusano et al. [21] introduced Local Angular Patterns (LAP) which consider the angular component only and discard the norm part altogether.
Another possible strategy consists of establishing some sort of a priori total ordering on the colour data. This approach is not uncommon in colour morphology—see for instance Angulo [4], van De Gronde and Roerdink [6]—and has been advocated for extending LBP to colour images by Barra [22]. Of late, this family of methods has been extensively investigated by Ledoux et al. [1] and Bello-Cerezo et al. [23]. The problem is that imposing a total ordering on the colour data inevitably entails a certain degree of arbitrariness, with the consequence that the results tend to be dataset-dependent. On the other hand, morphology for tensor-valued images (that arise from certain magnetic resonance techniques) has relied on the Loewner order, that is in fact a partial order (see for instance Burgeth et al. [24]; more on this in Section 2.5.2). More recently, this approach has been extended to morphology for colour images Burgeth and Kleefeld [5]. Partial ordering circumvents the problem of ordering multivariate data totally, at the expense of not allowing comparisons between some colour values.
2.5. Partial Orders
A partial order differs from a total order in that the fourth axiom in Definition 1 is waived, i.e., there are pairs of elements in the set that are incomparable. In order to distinguish this from a total order we use the notation . If the elements x and y are incomparable, we shall write .
In the following, we describe two types of partial orders that are applicable to colour spaces with Cartesian and polar coordinates respectively.
2.5.1. Product Order
By product order we mean the relation obtained from the component-wise comparison of colour values. Given and two triplets representing colours in a generic space we write:
Note that this is a subset of the lexicographical order introduced in Section 2.3; it is however of higher practical interest as it treats all three channels symmetrically. In the RGB space, for instance, a given colour weakly dominates the rectangular parallelepiped with three edges along the axes and a vertex in the colour itself (see Figure 1). For any colour that does not dominate all of , .
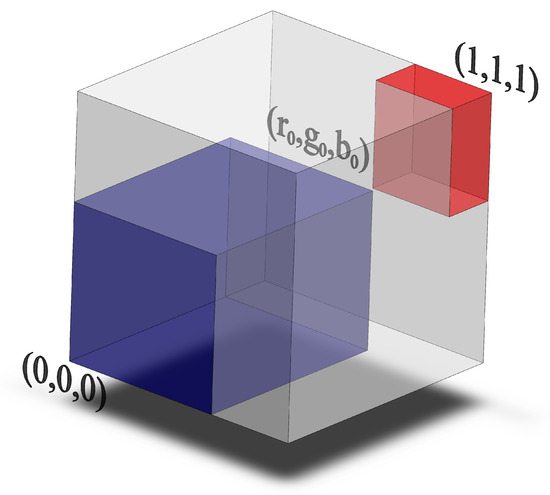
Figure 1.
Product order in the RGB space: A generic colour dominates all the colours in the blue volume and is dominated by all the colours in the red volume.
The product order can of course be applied to any colour space, giving relations of various degree of interpretability and effectiveness for pattern recognition (see Section 3.1 and Section 4).
2.5.2. Loewner Order
The Loewner (partial) order is defined on symmetric matrices. Given two symmetric matrices , we write:
where indicates the set of positive semi-definite matrices. Applying this to a colour space requires mapping colour values to symmetric matrices. Following [5], we start from a modified colour space obtained from HSL ([25], Section 4.6) by setting for the (modified) luminance and replacing saturation with chroma . The resulting colour gamut fills a bicone with axis and opening angle 90. We isometrically map colours to the space Sym of symmetric matrices by setting [5]:
For two colours and in the space we therefore write:
where is defined in Equation (2). Geometrically (Figure 2), a given colour weakly dominates all colours of lower luminance that fall in a cone with its vertex in and its axis parallel to the axis.
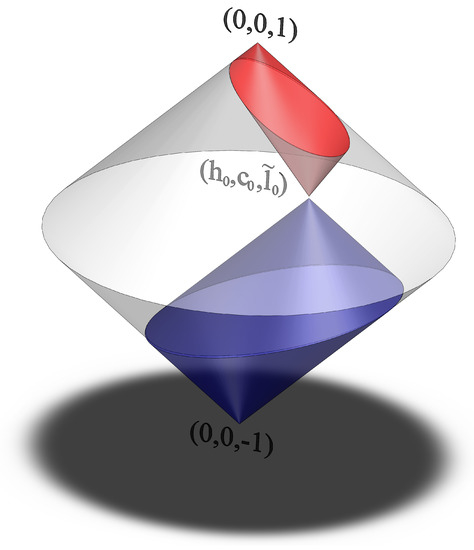
Figure 2.
Loewner order in the space: A generic colour dominates all the colours in the blue volume and is dominated by all the colours in the red volume.
3. Materials and Methods
3.1. Rank Features on Partial Orders
In this section we show how to generalise existing rank-based descriptors by replacing total order in grey-scale with suitable partial orders in colour space. In the remainder we shall use the Texture Spectrum [26] as our reference model—though other descriptors such as Local Binary Patterns and Local Ternary Patterns are amenable to the same procedure with virtually no effort.
In Texture Spectrum, a local image pattern is assigned a unique decimal code as follows:
where represents the central pixel and , the peripheral pixels, which we assume to be arranged on a circle around the central pixel. We also assume that represents a point in a 3D colour space, though again extension to multi-spectral data is straightforward. In Equation (5) the function stands for a generic conversion from colour into grey-scale, whereas indicates the ternary thresholding function:
An image is represented by the dense, orderless statistical distribution over the set of possible codes. For Texture Spectrum, the number of (directional) features generated by the method is clearly . Invariance under rotations and/or reflections can be obtained by grouping together all those codes that represent patterns which can be transformed into one another by such transforms. The corresponding mathematical structures are necklaces and bracelets, respectively for invariance under rotations (i.e., cyclic group of order n; ) and under rotations + reflections (i.e., dihedral group of order n; ). For general formulas about the number of resulting - and -invariant features and for other mathematical details please refer to González et al. [27], Zelenyuk and Zelenyuk [28]. Specifically, for (which is the case considered herein—see below) the number of features is respectively 834 and 498.
A ternary rank feature for partially ordered data analogous to Texture Spectrum—the Partial Order Texture Spectrum (POTS)—can easily be defined in the following way:
where ⪯ indicates a generic partial order relation in the colour space (see Section 2.5). Notably, the number of features generated by this formulation is the same as generated by the Texture Spectrum.
In the experiments we considered the following partial order/colour space combinations: product order (Section 2.5.1) in the RGB, Ohta’s and opponent spaces [25]; Loewner order (Section 2.5.2) in the space. When reporting experimental results we use subscripts ‘RGB’, ‘ohta’ and ‘opp’ to indicate the colour spaces, and superscripts and respectively for the product and Loewner orders (see Equations (1) and (4)). No superscript was used to indicate the natural total order on greyscale values.
Conversion from RGB to grey-scale was also performed in three different ways: (1) through the standard PAL/NTSC formula ([25], Section 4.3.1); (2) by computing the average of the three channels; and (3) by determining, for each image, the principal axes of the colour distribution in the RGB space and projecting each triplet onto the first axis. In the remainder we denote the corresponding variations of Texture Spectrum respectively as TS, TS and TS.
Finally, we computed - and -invariant features over , non-interpolated, square neighbourhoods of radius 1px and 2px. The overall feature vector was obtained by concatenating the feature vectors obtained at each resolution—see also González et al. [27] for details. These settings respectively generates and features.
3.2. Experiments
To test the effectiveness of the partial-order rank features described in Section 3.1 we ran a set of supervised image classification experiments. Datasets, classification strategy and accuracy estimation are described in the following subsections.
3.3. Datasets
We used ten datasets of colour texture images from different sources as described below. The main properties of each dataset are summarised in Table 1.

Table 1.
Datasets used in the experiments: round-up table.
3.3.1. Epistroma
Contains 1376 histopathological images from colorectal cancer representing either epithelium (825 images) or stroma (551 images). The image size ranges from 93 px to 2372 px in width and from 94 px to 2373 px in height. Further details about tissue preparation and digitisation procedure are available in Linder et al. [29].
3.3.2. KTH-TIPS
Includes 10 classes of common materials (e.g., aluminum foil, bread, corduroy, etc.) with 81 image samples for each class [30,31]. Each material was acquired under nine scales, three rotation angles and three lighting directions.
3.3.3. KTH-TIPS2b
Features 11 classes of materials (432 sample images per class) and is actually an extension of KTH-TIPS. The image acquisition settings were the same as in KTH-TIPS, but four rather than three illumination conditions were used in this case [32].
3.3.4. Kylberg–Sintorn
Is composed of 25 classes of heterogeneous materials, such as food (e.g., lentils, oatmeal and sugar), fabric (e.g., knitwear and towels) and tiles [33,34]. For each class one sample image was acquired using invariable illumination conditions and under nine different rotation angles—of which only the images at 0 were included in our experiments. Each image was further subdivided into six non-overlapping sub-images of dimension 1728 × 1728 px.
3.3.5. MondialMarmi
Comprises 25 classes of marble and granite products identified by their commercial denominations, e.g., Azul Platino, Bianco Sardo, Rosa Porriño and Verde Bahía [35]. Each class is represented by four tiles; ten images for each tile were acquired under steady illumination conditions and at rotation angles from 0 deg to 90 in steps of 10. In the experiments we only used the images at 0; moreover, we subdivided each image into four non-overlapping sub-images therefore obtaining 16 image samples for each class.
3.3.6. OUTEX-13 and OUTEX-14
Are based on the same sets of images that respectively make up the OUTEX_ TC_00013 and OUTEX_TC_00014 test suites—see Ojala et al. [36] for details. Specifically, OUTEX-13 features 68 classes of materials with 20 images per class acquired under invariable illumination conditions; OUTEX-14 contains the same classes—but in this case the image samples were acquired under three different illumination conditions—therefore there are 60 samples per class. Please notice, however, that in order to maintain the same evaluation protocol for all the datasets considered here (see Section 3.4), the subdivisions into train and test sets used in our experiments were not the same as in the OUTEX_TC_00013 and OUTEX_TC_00014 test suites.
3.3.7. Pap Smear
Consists of 917 PAP-stained images of variable dimension representing cells from the cervix [37]. The images represent either abnormal cases—675 samples or normal cases—242 samples. The dataset also comes with a further subdivision into seven sub-classes which was not considered in our experiments. The image size ranges from 84 × 88 px to 392 × 262 px. In our experiments we considered a balanced sub-set containing 204 samples for each of the two classes.
3.3.8. Plant Leaves
Includes a total of 1200 samples of plant leaves from 20 different classes with 60 samples per class [38]. The images were acquired using a planar scanner and have a dimension of 128 × 128 px.
3.3.9. RawFooT
Comprehends 68 classes of raw food and grains such as corn, chicken breast, pomegranate, salmon and tuna [39,40]. The materials were acquired under 46 different illumination conditions resulting in as many image samples for each class. We further subdivided the images into four non-overlapping sub-images, thus obtaining 184 samples for each class. The dimension of the resulting image tiles was 400 × 400 px.
3.4. Classification and Accuracy Estimation
For each dataset described in Section 3.3 we performed supervised classification using a nearest neighbour classifier (1-NN) with the (‘Manhattan’) distance. In detail, after extracting a feature vector from all images according to one of the descriptors tested, we computed the distance between such vectors as the sum of the absolute differences between components. We then assigned each test vector to the class of the closest training vector. The absence of tuning parameters, the ease of implementation and other desirable asymptotic properties make the 1-NN particularly appealing for comparison purposes. Its use in related works is indeed customary: see for instance Cusano et al. [39], Kandaswamy et al. [41], Liu et al. [42].
Accuracy estimation was based on split-half validation with stratified sampling—for each dataset we used half of the samples of each class to train the classifier (train set) and the other half (test set) to compute the accuracy. This was defined as the ratio between of number of samples of the test set correctly classified () and the total number of samples of the test set (N):
For a stable estimation we averaged the above value over a hundred different subdivisions into train and test set:
where indicates the accuracy achieved in the i-th subdivision into train and test set. In Table 2 we report the 95% confidence intervals for (computed under the simplifying assumption of normal distribution).

Table 2.
Overall classification accuracy: confidence intervals for the cross-validated accuracy . Best results highlighted for grey-level (orange) and colour space features (blue). Boldface figures indicate statistically significant differences.
4. Results and Discussion
Table 2 reports the confidence intervals for the means of the overall classification accuracy (see Section 3.4). For each dataset we highlighted in orange the best result obtained by total-order grey-scale rank features; in blue the best result obtained by partial order rank features (POTS) in colour space. When there was a statistically significant difference between the two, the best figure was indicated in boldface. As can be seen, partial order rank features in colour space performed significantly better in five datasets out 10, whereas the reverse occurred in one dataset only (dataset six). In the remaining four datasets there was no significant difference between the two methods.
As for grey-scale rank features, the results show that in most cases (i.e., 8 datasets out of 10) the best performance was obtained using standard PAL/NTSC grey-scale conversion. By contrast, partial-order rank features denoted a higher dependence on the colour space used.
The computational cost of all the descriptors considered is roughly equivalent, as the number of features is the same and the complexity of computing a partial or total order comparison in colour space is comparable to the cost of a colour space transformation. Indeed, as we have just described, even the traditional TS requires a grey-scale conversion, the choice of which can be seen as an integral part of the descriptor.
In Table 3 we compare our results to published results obtained using rank-based descriptors in conjunction with other ordering methods in colour spaces. As can be seen, in most cases our partial-order based approach improves significantly over previous results. We should here emphasise that the computational requirements of our partial-order descriptors are not higher than those of the other ordering methods cited.

Table 3.
Comparison with the results obtained by other ordering methods as reported in the references indicated. Key to symbols: ‘cvn’ = colour vector norm, ‘lex’ = lexicographic ordering, ‘rcl’ = preorder based on white as reference colour. Please refer to the cited works for further details.
5. Conclusions and Future Work
The lack of a natural order among colours represents an intrinsic impediment to the definition of rank features in colour space. In this paper we have introduced a novel and general approach based on partial orders. Partial orders overcome the problems inherent to ordering multivariate data at the expense of admitting that not all pairs of colours can be compared to each other. We showed that this scheme fits in well with existing grey-scale local image descriptors, that are amenable to extension to the colour domain with little effort. Taking the Texture Spectrum as a model, we showed that its partial-order version in colour space (POTS) can outperform the grey-scale classic descriptor while maintaining the same number of features and with comparable computational complexity. Previous studies have also demonstrated that the use of colour can improve texture discrimination, but at the expense of employing a higher number of features [44,45,46]. Notably, our approach improves on published results that use descriptors based specifically on (total) colour space ordering (see Table 3).
To the best of our knowledge this is the first time that partial orders have been used to define rank features for pattern recognition. The method is conceptually simple, fairly general and shows potential for application in a wide number of computer vision tasks. Future studies will be focussed on extending the approach to the broader class of descriptors known as Histograms of Equivalent Patterns [9]. The effect of the colour space on the performance of rank features based on partial orders is also an important topic for further investigation. Finally, the insertion of partial order based algorithms in more involved image processing pipelines (e.g., convolutional neural networks) also represents an interesting opportunity for future research; integration at the level of matching [47] has so far been successful.
Author Contributions
Conceptualization, F.S. and F.B.; Formal analysis, F.S., F.B. and A.F.; Methodology, F.S., F.B., A.F. and E.G.; Software, F.S. and F.B.; Validation, F.S., F.B., A.F. and E.G.; Visualization, F.B. and A.F.; Writing—original draft, F.S. and F.B.; Writing—review & editing, A.F. and E.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Spanish Government under projects AGL2014-56017-R and TIN2014-56919-C3-2-R, and by the Department of Engineering at the Università degli Studi di Perugia (UniPG Eng), Italy, under project Machine learning algorithms for the control of autonomous mobile systems and the automatic classification of industrial products and biomedical images (Fundamental resarch grants 2017). F.S. performed part of this work as a Visiting Researcher at UniPG Eng. He gratefully acknowledges the support of UniPG under international mobility grant ‘D.R. n.2270/2015’.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ledoux, A.; Losson, O.; Macaire, L. Color local binary patterns: Compact descriptors for texture classification. J. Electron. Imaging 2016, 25, 061404. [Google Scholar] [CrossRef]
- Hanbury, A.; Serra, J. Mathematical morphology in the CIELAB space. Image Anal. Stereol. 2002, 21, 201–206. [Google Scholar] [CrossRef]
- Aptoula, E.; Lefèvre, S. A comparative study on multivariate mathematical morphology. Pattern Recognit. 2007, 40, 2914–2929. [Google Scholar] [CrossRef]
- Angulo, J. Morphological colour operators in totally ordered lattices based on distances: Application to image filtering, enhancement and analysis. Comput. Vis. Image Underst. 2007, 107, 56–73. [Google Scholar] [CrossRef]
- Burgeth, B.; Kleefeld, A. Morphology for color images via Loewner order for matrix fields. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2013; Volume 7883 LNCS, pp. 243–254. [Google Scholar]
- van De Gronde, J.; Roerdink, J. Group-invariant colour morphology based on frames. IEEE Trans. Image Process. 2014, 23, 1276–1288. [Google Scholar] [CrossRef] [PubMed]
- Hodgson, R.; Bailey, D.; Naylor, M.; Ng, A.; McNeill, S. Properties, implementations and applications of rank filters. Image Vis. Comput. 1985, 3, 3–14. [Google Scholar] [CrossRef]
- Zabih, R.; Woodfill, J. Non-parametric Local Transforms for Computing Visual Correspondence. In European Conference on Computer Vision; Springer: Stockholm, Sweden, 1994; pp. 151–158. [Google Scholar]
- Fernández, A.; Álvarez, M.X.; Bianconi, F. Texture description through histograms of equivalent patterns. J. Math. Imaging Vis. 2013, 45, 76–102. [Google Scholar] [CrossRef]
- Liu, L.; Fieguth, P.; Wang, X.; Pietikäinen, M.; Hu, D. Evaluation of LBP and deep texture descriptors with a new robustness benchmark. In Proceedings of the 14th European Conference on Computer Vision (ECCV 2016), Amsterdam, The Netherlands, 11–14 October 2016; Springer: Amsterdam, The Netherlands, 2016; Volume 9907, pp. 69–86. [Google Scholar]
- Brahnam, S.; Jain, L.; Nanni, L.; Lumini, A. (Eds.) Local Binary Patterns: New Variants and Applications; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2014; Volume 506. [Google Scholar]
- Smeraldi, F. Ranklets: Orientation selective non-parametric features applied to face detection. In Proceedings of the 16th International Conference on Pattern Recognition (ICPR’02), Quebec City, QC, Canada, 11–15 August 2002; Volume 3, pp. 379–382. [Google Scholar]
- Azzopardi, G.; Smeraldi, F. Variance Ranklets: Orientation-selective rank features for contrast modulations. In Proceedings of the British Machine Vision Conference, BMVC 2009, London, UK, 7–10 September 2009. [Google Scholar]
- Liu, L.; Chen, J.; Fieguth, P.; Zhao, G.; Chellappa, R.; Pietikäinen, M. From BoW to CNN: Two decades of texture representation for texture classification. Int. J. Comput. Vis. 2019, 127, 74–109. [Google Scholar] [CrossRef]
- Bello-Cerezo, R.; Bianconi, F.; Di Maria, F.; Napoletano, P.; Smeraldi, F. Comparative Evaluation of Hand-Crafted Image Descriptors vs. Off-the-Shelf CNN-Based Features for Colour Texture Classification under Ideal and Realistic Conditions. Appl. Sci. 2019, 9, 738. [Google Scholar] [CrossRef]
- Barnett, V. The ordering of multivariate data. J. R. Stat. Soc. Ser. A (Gen.) 1976, 139, 318–355. [Google Scholar] [CrossRef]
- Yang, S. Distribution Theory of the Concomitants of Order Statistics. Ann. Stat. 1977, 5, 996–1002. [Google Scholar] [CrossRef]
- Mäenpää, T.; Pietikäinen, M. Texture analysis with local binary patterns. In Handbook of Pattern Recognition and Computer Vision, 3rd ed.; Chen, C., Wang, P., Eds.; World Scientific: Singapore, 2005; pp. 197–216. [Google Scholar]
- Bianconi, F.; Fernández, A.; González, E.; Armesto, J. Robust color texture features based on ranklets and discrete Fourier transform. J. Electron. Imaging 2009, 18, 043012. [Google Scholar]
- Lee, S.; Choi, J.; Ro, Y.; Plataniotis, K. Local color vector binary patterns from multichannel face images for face recognition. IEEE Trans. Image Process. 2012, 21, 2347–2353. [Google Scholar] [CrossRef] [PubMed]
- Cusano, C.; Napoletano, P.; Schettini, R. Local angular patterns for color texture classification. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2015; Volume 9281, pp. 111–118. [Google Scholar]
- Barra, V. Expanding the local binary pattern to multispectral images using total orderings. Commun. Comput. Inf. Sci. 2011, 229 CCIS, 67–80. [Google Scholar]
- Bello-Cerezo, R.; Fieguth, P.; Bianconi, F. LBP-Motivated Colour Texture Classification. In Proceedings of the 2nd International Workshop on Compact and Efficient Feature Representation and Learning in Computer Vision (in Conjunction with ECCV 2018), Munich, Germany, 9 September 2018; Volume 11132, pp. 517–533. [Google Scholar]
- Burgeth, B.; Welk, M.; Feddern, C.; Weickert, J. Mathematical morphology on tensor data using the Loewner ordering. In Visualization and Processing of Tensor Fields; Mathematics and Visualization; Springer: Berlin/Heidelberg, Germany, 2006; pp. 357–368. [Google Scholar]
- Palus, H. Representations of colour images in different colour spaces. In The Colour Image Processing Handbook; Sangwine, S.J., Horne, R.E.N., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 67–90. [Google Scholar]
- He, D.C.; Wang, L. Texture Unit, Texture Spectrum, And Texture Analysis. IEEE Trans. Geosci. Remote. Sens. 1990, 28, 509–512. [Google Scholar]
- González, E.; Bianconi, F.; Fernández, A. An investigation on the use of local multi-resolution patterns for image classification. Inf. Sci. 2016, 361–362, 1–13. [Google Scholar] [CrossRef]
- Zelenyuk, Y.; Zelenyuk, Y. Counting symmetric bracelets. Bull. Aust. Math. Soc. 2014, 89, 431–436. [Google Scholar] [CrossRef]
- Linder, N.; Konsti, J.; Turkki, R.; Rahtu, E.; Lundin, M.; Nordling, S.; Haglund, C.; Ahonen, T.; Pietikäinen, M.; Lundin, J. Identification of tumor epithelium and stroma in tissue microarrays using texture analysis. Diagn. Pathol. 2012, 7, 22. [Google Scholar] [CrossRef]
- Hayman, E.; Caputo, B.; Fritz, M.; Eklundh, J.O. On the Significance of Real-World Conditions for Material Classification. In Proceedings of the 8th European Conference on Computer Vision (ECCV 2004), Prague, Czech Republic, 11–14 May 2004; Springer: Prague, Czech Republic, 2004; Volume 3024, pp. 253–266. [Google Scholar]
- The KTH-TIPS and KTH-TIPS2 Image Databases. 2004. Available online: http://www.nada.kth.se/cvap/databases/kth-tips/ (accessed on 21 September 2016).
- Caputo, B.; Hayman, E.; Mallikarjuna, P. Class-specific material categorisation. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–20 October 2005; Volume II, pp. 1597–1604. [Google Scholar]
- Kylberg, G. Automatic Virus Identification Using TEM. Image Segmentation and Texture Analysis. Ph.D. Thesis, Faculty of Science and Technology, University of Uppsala, Uppsala, Sweden, 2014. [Google Scholar]
- Kylberg Sintorn Rotation Dataset. 2013. Available online: http://www.cb.uu.se/gustaf/KylbergSintornRotation/ (accessed on 6 January 2016).
- Bello-Cerezo, R.; Bianconi, F.; Fernández, A.; González, E.; Di Maria, F. Experimental comparison of color spaces for material classification. J. Electron. Imaging 2016, 25, 061406. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikäinen, M.; Mäenpää, T.; Viertola, J.; Kyllönen, J.; Huovinen, S. Outex—New Framework for Empirical Evaluation of Texture Analysis Algorithms. In Proceedings of the 16th International Conference on Pattern Recognition (ICPR’02), Quebec, QC, Canada, 11–15 August 2002; Volume 1, pp. 701–706. [Google Scholar]
- Jantzen, J.; Noras, J.; Dounias, G.; Bjerregaard, B. Pap-smear Benchmark Data For Pattern Classification. In Nature Inspired Smart Information Systems (NiSIS 2005); NiSIS: Albufeira, Portugal, 2005. [Google Scholar]
- Casanova, D.; de Mesquita Sá Junior, J.J.; Bruno, O.M. Plant leaf identification using Gabor wavelets. Int. J. Imaging Syst. Technol. 2009, 19, 236–243. [Google Scholar] [CrossRef]
- Cusano, C.; Napoletano, P.; Schettini, R. Evaluating color texture descriptors under large variations of controlled lighting conditions. J. Opt. Soc. Am. A 2016, 33, 17–30. [Google Scholar] [CrossRef] [PubMed]
- RawFooT DB: Raw Food Texture Database. 2015. Available online: http:projects.ivl.disco.unimib.it/rawfoot/ (accessed on 22 September 2016).
- Kandaswamy, U.; Schuckers, S.A.; Adjeroh, D. Comparison of Texture Analysis Schemes Under Nonideal Conditions. IEEE Trans. Image Process. 2011, 20, 2260–2275. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zhao, L.; Long, Y.; Kuang, G.; Fieguth, P.W. Extended local binary patterns for texture classification. Image Vis. Comput. 2012, 30, 86–99. [Google Scholar] [CrossRef]
- Fernández, A.; Lima, D.; Bianconi, F.; Smeraldi, F. Compact Color Texture Descriptor Based on Rank Transform and Product Ordering in the RGB Color Space. In Proceedings of the IEEE International Conference on Computer Vision Workshops, ICCVW 2017, Venice, Italy, 22–29 October 2017; Institute of Electrical and Electronics Engineers Inc.: Venice, Italy, 2017; pp. 1032–1040. [Google Scholar]
- Drimbarean, A.; Whelan, P.F. Experiments in colour texture analysis. Pattern Recognit. Lett. 2001, 22, 1161–1167. [Google Scholar] [CrossRef]
- Mäenpää, T.; Pietikäinen, M. Classification with color and texture: Jointly or separately? Pattern Recognit. 2004, 37, 1629–1640. [Google Scholar] [CrossRef]
- Bianconi, F.; Harvey, R.; Southam, P.; Fernández, A. Theoretical and experimental comparison of different approaches for color texture classification. J. Electron. Imaging 2011, 20, 043006. [Google Scholar] [CrossRef]
- Abdollahyan, M.; Cascianelli, S.; Bellocchio, E.; Costante, G.; Ciarfuglia, T.A.; Bianconi, F.; Smeraldi, F.; Fravolini, M.L. Visual Localization in the Presence of Appearance Changes Using the Partial Order Kernel. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Roma, Italy, 3–7 September 2018; pp. 697–701. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).