Abstract
The natural vibration behavior of axially functionally graded (AFG) double nanobeams is studied based on the Euler–Bernoulli beam and Eringen’s non-local elasticity theory. The double nanobeams are continuously connected by a layer of linear springs. The oscillatory differential equation of motion is established using the Hamilton’s principle and the constitutive relations. The Chebyshev spectral collocation method (CSCM) is used to transform the coupled governing differential equations of motion into algebraic equations. The discretized boundary conditions are used to modify the Chebyshev differentiation matrices, and the system of equations is put in the matrix-vector form. Then, the dimensionless transverse frequencies and the mode shapes are obtained by solving the standard eigenvalue problem. The effects of the coupling springs, Winkler stiffness, the shear stiffness parameter, the breadth and taper ratios, the small-scale parameter, and the boundary conditions on the natural transverse frequencies are carried out. Several numerical examples were conducted, and the authors believe that the results may be interesting in designing and analyzing double and multiple one-dimensional nano structures.
1. Introduction
Micro and nano electromechanical systems (MEMS and NEMS) have aroused great research interest due to their unique properties and features. These systems have widespread applications in many engineering and modern technology fields such as composites and electronics. During the manufacturing process, producing, assembling, and packaging, some micro and nano-structures may have geometrical irregularities, as variations in the height and the width that may have significant effect on the characteristics and the performance of these structures.
For more damage tolerance and vibration control, and for the sake of providing weight reduction, structures with non-uniform cross sections (tapered) are used in several industrial applications. Therefore, it is worthwhile to create reliable models for these non-uniform micro and nano structures in order to predict their dynamical response and characteristics. Additionally, for the sake of increasing the strength with respect to the weight of a structure, functionally graded (FG) materials are found in numerous civil and aerospace structures [1]. Moreover, carbon nanomaterials such as carbon nanotubes and graphene are heterogeneous and non-uniform because of the effect of grid distance or particle size on their characteristics and properties.
Double-beam structures are commonly utilized in numerous applications due to their high specific strength, high rigidity, and vibration isolation. However, investigating the vibrations of axially functionally graded (AFG) non-uniform double beams has not been well addressed in the literature. Therefore, the motivation of this research is to fill the gap in modeling and analyzing the vibration characteristics of double AFG nanobeams lying on elastic medium.
Experimental statistical investigations and simulations are able to display the effect of the scale parameter on the response of structures at the micro and nano scales; however, these approaches are costly, time consuming, and limited. As the continuum approach for elastic structures at the regular macro scales are not capable of showing the influence of the scale parameter on the behavior of different nano structures; therefore, the local continuum approach is insufficient to expect the dynamical response of these systems [2]. In order to use the continuum theories to study different characteristics of nanostructures, the scale parameter must be taken into consideration. Thus, different theories were proposed, such as the strain gradient theory, the modified coupled stress theory, and the nonlocal elasticity theory [3] that will be applied in this research to carry out the vibrations of axially functionally graded double beams lying on elastic medium.
Many researchers applied Eringen’s non-local theory to analyze the vibration and buckling behavior of micro and nano structures. For example, Challamel et al. [4] examined the natural vibration and the buckling analyses of micro-structured plates utilizing Eringen’s nonlocal elasticity model with three different plate theories. Analytical solutions for frequencies and critical loads of these structures were obtained, and it was found that the buckling load and the geometry of the plate have remarkable influence on the small-scale parameter. Liu et al. [5] used the nonlocal theory along with the Kelvin model to study the flexural oscillations of double-viscoelastic-Functionally Graded (FG) nanoplate system resting on a visco-elastic Pasternak medium, and subjected to in-plane loads. It was observed that the frequencies and the buckling loads depend on the structural damping, loading ratio, Pasternak foundation, and the small-scale effect. Shahidi et al. [6] used Eringen’s theory to study the vibrations of orthotropic Kirchhoff nano-plates. The effects of several factors including the scale parameter on the frequencies were conducted.
Moreover, Namin and Pilafkan [7] used Eringen’s nonlocal theory to examine the natural vibration of defective graphene sheets. Moreover, Reddy [8] applied the nonlocal elasticity theory to analyze the bending, buckling, and vibration of various beams including the Euler–Bernoulli, Timoshenko, Reddy, and Linenson beam. Analytical solutions were obtained, and the effect of the small-scale parameter was shown. Li and Hu [9] reported on the torsional vibration of tubes made of a bi-directional FG material. It was shown that the frequencies decline as the nonlocal scale effect rises. Demir and Civalek [10] presented the vibrations of nanobeams subjected to thermal loads and resting on an elastic foundation. A new finite element technique was used to obtain the frequencies, and it was concluded that the modulus of the foundation, the scale effect, and the thermal loads have a remarkable influence on the frequencies. Besides, Murmu and Adhikari [11] applied Eringen’s nonlocal theory to study the vibrations of a double-nanoplate-system connected by a continuous linear springs. The frequencies of the system were found analytically.
Mechab et al. [12] used Eringen’s nonlocal elasticity theory to investigate the natural vibrations of orthotropic composite nano beams. The Poisson effect was included in the study, and the effects of the thickness of the beams, the scale parameter, and the number of the layers on the natural frequencies were studied. Moreover, Zhang et al. [13] applied Eringen’s elasticity theory to present the scale parameter coefficients for the natural vibrations and buckling behavior of simply supported rectangular plates. Further studies about this topic were examined by other authors [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].
In this research, the natural transverse vibrations of AFG tapered double nanobeams embedded in elastic medium are investigated. Eringen’s nonlocal elasticity theory is utilized to account for the scale parameter. The equation of the transverse motion is obtained and the Chebyshev spectral collocation method (CSCM) is applied to find the dimensionless frequencies and the corresponding mode shapes.
2. Theory
2.1. Chebyshev Spectral Collocation Method
Obtaining exact solutions for the natural vibrations of nonlocal AFG tapered double micro/nano Euler–Bernoulli beams is challenging. Thus, CSCM is applied for numerical solutions. The Chebyshev collocation points are given in the range of [–1, 1] as [32]:
The differentiation matrix, [D]N, is an (N + 1) (N + 1) square matrix. The entries of this matrix are expressed as:
In the current research, the axial direction x is adjusted to be in the interval [0, 1]; hence, the entries of the [D]N matrix will have different values than those given in Equation (2) as these entries are functions of the Chebyshev points. Due to its stability, rapid convergence, and accuracy, the CSCM has been successfully utilized to perform the natural vibrations and buckling characteristics of different continuous systems [33,34,35]. When using this method to discretize ordinary and partial differential equations, the nth derivative of an unknown function (the transverse displacement in the current study) is expressed as Dn = (DN)n.
2.2. Nonlocal Theory
Eringen’s nonlocal elasticity theory [3] assumes that the stress field at any point in an elastic domain depends on the strains at all points of the body, unlike the stress field at the regular macro scale, which is a function of the strain at the same specific point only. Thus, the non-local stress is given as:
where is a kernel function that represents the non-local modulus, is the local stress at the macro scale, α is a material constant that depends on the internal and external characteristics lengths, and is the distance between the points x and in Euclidean form.
For simplicity, Eringen [3] suggested a differential form, which is equivalent to Equation (3) as:
where is a constant that depends on the material properties, l represents the internal characteristic length, and is the Laplace operator given as
As the differential form is mathematically simpler than the integral form, Equation (4) has been repeatedly utilized in applying Eringen’s nonlocal theory to investigate the vibrations (natural and forced) and the buckling behaviors of different dynamical systems at the nano scale.
3. Problem Formulation
3.1. Mathematical Model
Figure 1 shows a tapered AFG double nano beam lying on an elastic foundation. According to Euler–Bernoulli theorem, the normal strain , the bending strain , and the bending moment are given as:
where is the transverse deflection, x is the longitudinal axis of the beam, z is the transverse axis taken from the mid-plane of the beam along its thickness, and E(x) is the modulus of elasticity, is the normal stress, and A(x) is the beam’s cross sectional area. The kinetic energy T may be written as:
where L is the length of the beam, is the density, and is the time. The potential energy is given as:
where and are the Winkler stiffness and the shear stiffness of the surrounding foundation, respectively. Hamilton’s principle is applied to obtain the governing equation of motion as:
where is the variation operator. From Equation (9), the variation of the kinetic energy is given as:
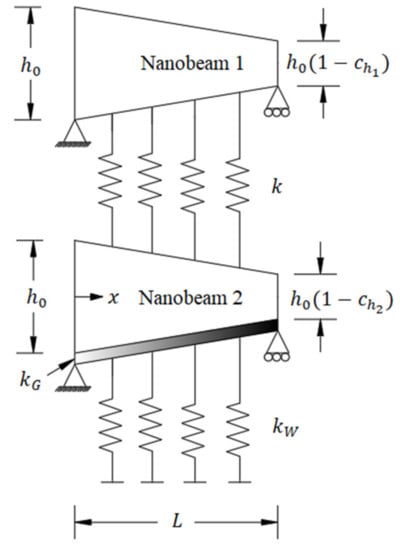
Figure 1.
The tapered nonlocal axially functionally graded (AFG) Euler–Bernoulli double nanobeam resting on elastic foundation.
Based on Equation (10), the variation of the potential energy is expressed as:
Using Equations (11)–(13), and after some manipulation and simplification, one obtains
Then, integrating by parts and since δ is arbitrary, we get the following governing equation of motion as:
In light of Equation (4), the normal stress for the Euler–Bernoulli nano beam is defined as:
Multiplying Equation (16) by zdA and integrating over the area of the beam, we get
Using Equations (15) and (17), the bending moment in nonlocal form is defined as
In light of Equations (15) and (18), and after some manipulation and rearranging, one obtains
Using Equation (19), the governing coupled equations for nonlocal AFG double nanobeam are given as
where , , Ij, and Aj (j = 1, 2) are the stiffness of the elastic layer between beams, the transverse displacement, the area moment of inertia, and the cross sectional area for nanobeam-j, respectively. It is assumed that both nanobeams have the same length L, modulus of elasticity , density , , and , which are the area moment of inertia, and the cross sectional area at x = 0, respectively. In the present research, and are given as [36]:
where and are the modulus of elasticity and the density at x = 0, respectively, and and are the breadth and the height taper ratios of nanobeam-j, respectively.
For harmonic natural vibration, the transverse displacements are given as:
where ω is the transverse natural frequency in rad/s. For convenience, we introduced the following dimensionless variables as
Substituting Equations (23) and (24) into Equations (20) and (21) yields:
The dimensionless natural transverse frequencies are calculated by solving the eigenvalue problem resulted from the discretization of Equations (25) and (26).
3.2. Solution Procedure
The CSCM is employed to transform the governing differential equations of transverse motion and boundary conditions into algebraic equations. For thin structures modeled such as Euler–Bernoulli beams, two boundary conditions are imposed at each edge, and as there is only one equation for each beam; hence, the CSCM will be used for one of the boundary conditions only. To resolve this issue, these conditions are satisfied by expressing the transverse deflections at the boundaries and their adjacent points in terms of the transverse deflections of other points along the beam’s span. For example, if the ends of nano beam 1 are clamped, the boundary conditions are given as:
Using the Chebyshev collocation method, these conditions are discretized as:
From Equation (27), the deflections and are expressed in terms of the deflections at all other points in the domain as:
where Det is given by
Consequently, the Chebyshev collocation differentiation matrices are modified as:
for
In case beam-2 has simply supported edges, the boundary conditions are expressed as:
The boundary conditions given in Equation (32) are discretized using the CSCM as in Equation (28), except that each differentiation matrix is substituted with the differentiation matrix . Using the proposed method, Equations (25) and (26) are given as:
where
i = 1, 2, …, M − 4, j = 1, 2, and M = N + 1. I is a (M − 4)X (M − 4) identity matrix, , , , , , and are diagonal (M − 4)X (M − 4) matrices, and are the modified Chebyshev collocation differentiation matrices of order n for beam 1 and beam 2, respectively.
4. Results and Discussion
For the purpose of examining the validity of the suggested model of the AFG Euler–Bernoulli nanobeams, a comparison study was conducted. Initially, the frequencies of AFG local single beam (by neglecting the nonlocal scale parameter) were compared to those reported by Shahba and Rajasekaran [36]. Then, the frequencies of a double isotropic nano beam were compared with those obtained by Murmu and Adhikari [37]. In Table 1, the first two dimensionless frequencies for AFG Euler–Bernoulli beams with clamped edges (C-C) are presented. Moreover, in Table 2, the first four dimensionless frequencies of the suggested model for nonlocal Euler–Bernoulli simply supported double beams were compared with those obtained by Murmu and Adhikari [37]. As observed from these tables, the proposed method could be used to obtain accurate results.

Table 1.
The dimensionless natural transverse frequencies for an AFG C-C tapered single beam.

Table 2.
The dimensionless natural transverse frequencies for an isotropic simply supported uniform double nanobeam.
Figure 2 shows the influence of the nonlocal scale parameter on the first three dimensionless transverse frequencies of AFG nano CC-CC and SS-SS double beams with and . The notations CC-CC and SS-SS denote that the two nanobeams were clamped and simply supported at both boundaries, respectively. The nonlocal scale parameter was assumed to be in the interval [0, 1]. It is clear that the frequencies of the CC-CC AFG double nanobeams were greater than that for the SS-SS double beams. Moreover, the results indicate that as the nonlocal scale parameter rises, the dimensionless transverse frequencies decrease and the reduction is more significant for the higher modes. In Figure 2a, of CC-CC double beam decreased by 55.2%, by 56.48%, and by 75.3% as the nonlocal scale parameter µ varied from the range 0 to 1. In Figure 2b, of SS-SS double nanobeam decreased by 35.49%, by 48.09%, and by 67.38%. It is observed that the veering phenomenon took place as the scale parameter grew. The veering occurred when two consecutive frequencies came near each other and then veered apart as a parameter was changed (the nonlocal scale parameter in Figure 2a,b). For example, at µ = 0.32, veering occurred between and for the CC-CC and SS-SS AFG double nanobeams.

Figure 2.
Variations of , , and as a function of the non-local scale parameter of an AFG Euler–Bernoulli double nanobeam (a) CC-CC and (b) SS-SS.
Figure 3a,b displays the impact of the shear modulus parameter on , , and of AFG CC-CC and SS-SS double nanobeams with and . These figures show that the dimensionless natural transverse frequencies grow as increased, and the dimensionless frequencies for the CC-CC double beam were higher than that for the SS-SS double beam for the same value of . However, the rate at which these frequencies increase with was higher for the SS-SS double nanobeam. For example, of a SS-SS double nanobeam increased by 7.5%, by 10.56%, and by 1.83% as the parameter increased from 0 to 10. On the other hand, of a CC-CC double nanobeam increased by 2.17%, by 8.48%, and by 0.97% or the same range of .
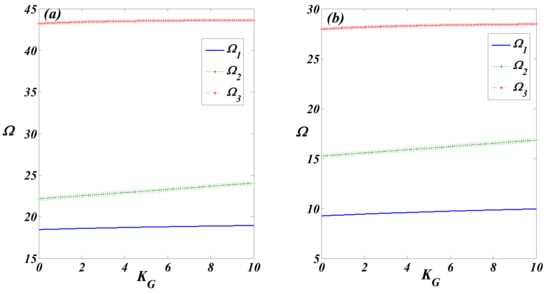
Figure 3.
Variations of , , and as function of of a nonlocal AFG Euler–Bernoulli double nanobeam (a) CC-CC and (b) SS-SS.
Figure 4a,b displays the effect of the Winkler modulus stiffness on the first three dimensionless natural transverse frequencies of AFG CC-CC and SS-SS double nanobeams with , and . As predicted, it was revealed that rising had a hardening effect on the frequencies. For the CC-CC and SS-SS double nanobeams, was more affected by increasing the Winkler modulus parameter than and . For example, of a CC-CC double nanobeam increased by 23.11% as rose from 0 to 400. The first and third dimensionless frequencies increased by 2.71% and 0.19%, respectively. It is noticed from Figure 4b that of a SS-SS double nanobeam increased nonlinearly with the parameter , unlike the second and third dimensionless frequencies that increased linearly.

Figure 4.
The first three dimensionless natural transverse frequencies as function of Winkler modulus stiffness of a nonlocal AFG Euler–Bernoulli double nanobeam (a) CC-CC and (b) SS-SS.
Figure 5 shows the influence of the stiffness of the coupling elastic springs K on the dimensionless natural frequencies of AFG CC-CC and SS-SS double nanobeams with , and , and the parameter K was taken in the range of 0–1000. The figures revealed that the first dimensionless frequencies increased nonlinearly with the parameter K for the CC-CC and SS-SS doubled nanobeams. For the CC-CC double nanobeam, the second dimensionless frequency increased linearly by a rate of 54.55% as the parameter K grew from 0 to 652, whereas it increased by 1.74% in the range of 625 and 1000. From this figure, it is noted that the rate at which the frequencies rose depended on the range of the parameter K. Furthermore, the veering phenomena takes place between and at K = 625 and K = 348 for the CC-CC and SS-SS double nanobeams, respectively.
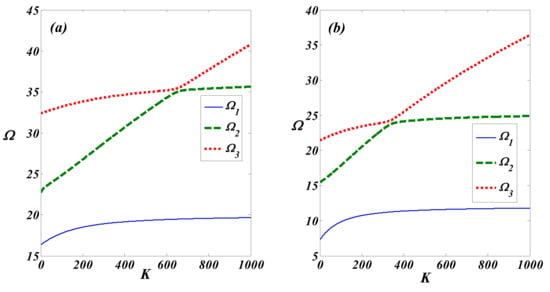
Figure 5.
The first three dimensionless natural transverse frequencies as function of the coupling elastic springs parameter K of a nonlocal AFG Euler–Bernoulli double nanobeam (a) CC-CC and (b) SS-SS.
The first three dimensionless natural transverse frequencies as function of the breadth taper ratio of nanobeam-1 for CC-CC and SS-SS double nanobeams with , and are presented in Figure 6a,b. The breadth taper ratio was assumed in the range of 0–0.8. The figure revealed that as the value of gets larger, the dimensionless natural frequencies increase. It was also noticed that and were less sensitive to the rise of than . As an illustration, and for a CC-CC double nanobeam increase by 21% and 18%, respectively, whereas increased by 21.11% as was varied from 0 to 0.8. The influence of the height taper ratio of nanobeam-2 on the first three dimensionless natural transverse frequencies of CC-CC and SS-SS double nanobeams with
, and are shown in Figure 7a,b. It is clear that the relation between these frequencies and was non-monotonic. For example, as displayed in Figure 7a, of a CC-CC double AFG nano beam got smaller as varied from 0 to 0.448. In contrary, of a SS-SS double AFG nano beam increased as varied from 0 to 0.8 as presented in Figure 7b.

Figure 6.
The effect of the breadth taper ratio of nanobeam-1 on the first three dimensionless natural transverse frequencies of a nonlocal AFG Euler–Bernoulli double nanobeam (a) CC-CC and (b) SS-SS.

Figure 7.
The first three dimensionless natural transverse frequencies as function of height taper ratio of nanobeam-2 of a nonlocal AFG Euler–Bernoulli double nanobeam (a) CC-CC and (b) SS-SS.
In Figure 8, the fundamental dimensionless frequency of a double CS-CS nano beam with
and was plotted versus the nonlocal scale parameter and the stiffness of the coupling elastic springs K. The notation CS-CS denotes that both nanobeams were clamped at x = 0, and simply supported at x = 1. The figure revealed that as K grew, the percentage of the decrease in with the nonlocal scale parameter got smaller. For instance, at K = 10, the dimensionless natural frequency of the CS-CS AFG double nano-beam declined by 66.95% as µ increased from 0 to 1. However, at K = 100, of the CS-CS double nanobeam decreased by 44.62% as µ varied from 0 to 1. Additionally, the results show that at higher values of µ, the rate at which the fundamental dimensionless natural frequency rises with K got larger. For example, for µ = 0.1 and 0.9, the dimensionless natural frequency rose by 24.59% and 80.86%, respectively, as K increased from 50 to 400. Figure 9 shows the influence of the breadth taper ratio and the height taper ratio of nanobeam-1 on the fundamental frequency of a CC-CC AFG double nano beam with, and . It is noticed that grows as the parameter rises. Moreover, as shown in the figure, the frequencies were reduced as rose to a certain value, and then they tended to augment as increased.

Figure 8.
The fundamental dimensionless transverse frequency of CS-CS double AFG nanobeam as function of the stiffness of the elastic layer and the nonlocal scale coefficient .

Figure 9.
The fundamental dimensionless natural transverse frequency of CC-CC AFG double beam as function of the breadth taper ratio and the height taper ratio of nanobeam-1 ( and ).
Figure 10, Figure 11 and Figure 12 present the influence of the boundary conditions on the fundamental dimensionless natural transverse frequencies of AFG double nanobeams with and. These figures revealed that the fundamental dimensionless frequencies of the AFG CC-CC double nanobeams were larger compared to those of the AFG CS-CS and SS-SS double nanobeams. In Figure 10, the fundamental dimensionless frequencies of the CC-CC double nanobeams decreased by 38.7%, the CS-CS by 31.86%, whereas the SS-SS by 20.95% as µ varied from 0 to 1. Figure 11 shows that of the CC-CC double nanobeams rose by 23.6%, the CS-CS by 42.9%, and the SS-SS by 78.7% as K grew over the range 0 to 500. From Figure 12, it is depicted that of the CC-CC double nanobeams grew by 11%, the CS-CS by 21.5%, and the SS-SS by 41% as the Winkler modulus parameter varied over the range 0–400.

Figure 10.
The fundamental dimensionless natural transverse frequency as function of the nonlocal scale coefficient of AFG Euler–Bernoulli double nanobeam with different boundary conditions .

Figure 11.
The fundamental dimensionless natural transverse frequency versus the stiffness of the coupling elastic layer K of a nonlocal AFG Euler–Bernoulli double nanobeam at different boundary conditions .

Figure 12.
The fundamental dimensionless natural transverse frequency versus the Winkler modulus parameter of a nonlocal AFG Euler–Bernoulli double nanobeam at different boundary conditions .
The mode shapes of AFG SS-SS double nanobeams are displayed in Figure 13a–d and Figure 14a–d. These figures indicate that the mode shapes were sensitive to the change in the nonlocal scale coefficient . For instance, it is clearly seen in Figure 13b–d, that the mode shapes of nanobeam-1 (in blue) looked different at several values of . Furthermore, Figure 14b shows that the mode shapes of nanobeam-2 (in green) were sensitive to the change in the value of the stiffness parameter K. Similar observations could be obtained from Figure 14c,d.

Figure 13.
The first four mode shapes of a SS-SS AFG nonlocal Euler–Bernoulli double nanobeam (Blue: beam 1 and green: beam 2) at different values of the nonlocal parameter (solid: µ = 0, dashed: µ = 0.2, and dotted: µ = 0.8) (a) First mode shape, (b) second mode shape, (c) third mode shape, and (d) fourth mode shape.

Figure 14.
The first four mode shapes of a SS-SS AFG nonlocal Euler–Bernoulli double nanobeam (Blue: beam 1 and green: beam 2) at different values of the stiffness parameter (solid: K = 10, dashed: K = 100, and dotted: K = 1000) (a) First mode shape, (b) second mode shape, (c) third mode shape, and (d) fourth mode shape.
5. Conclusions
The natural transverse vibration behavior of nonlocal AFG double nanobeams was examined. The double beams were modeled using the Euler–Bernoulli beam theory, and it was assumed that they were joined by a continuous layer of linear springs. The Chebyshev spectral collocation method was applied, and the partial differential equations of transverse motion were transformed into algebraic equations. Then, the boundary conditions were imposed, and the coupled equations were put in the matrix vector form, and the standard eigenvalue problem was formulated and solved to obtain the dimensionless natural transverse frequencies and the corresponding mode shapes. The influence of the coupling springs, Winkler and the shear moduli parameters, the breadth and height taper ratios, the nonlocal scale parameter, and the boundary conditions on the natural transverse frequencies were examined. The authors believe that the findings may be useful for researchers and engineers in manufacturing and analyzing axially functionally graded double micro/nano beams.
Author Contributions
Conceptualization, M.S.S. and W.G.A.-K.; methodology, M.S.S., and A.M.A.; validation, M.S.S.; formal analysis, M.S.S., A.M.A. and W.G.A.-K.; investigation, M.S.S.; resources, A.M.A. and W.G.A.-K.; writing—original draft preparation, M.S.S.; writing—review and editing, M.S.S., A.M.A. and W.G.A.-K.; supervision, M.S.S. and W.G.A.-K.; project administration, M.S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Natarajan, S.; Ferreira, A.J.M.; Bordas, S.; Carrera, E.; Cinefra, M.; Zenkour, A.M. Analysis of Functionally Graded Material Plates Using Triangular Elements with Cell-Based Smoothed Discrete Shear Gap Method. Math. Probl. Eng. 2014, 2014, 247932. [Google Scholar] [CrossRef]
- Wang, C.M.; Zhang, Y.Y.; He, X.Q. Vibration of nonlocal Timoshenko beams. Nanotechnology 2007, 18, 105401. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Challamel, N.; Hache, F.; Elishakoff, I.; Wang, C.M. Buckling and vibrations of microstructured rectangular plates considering phenomenological and lattice-based nonlocal continuum models. Compos. Struct. 2016, 149, 145–156. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Fan, L. Nonlocal vibration and biaxial buckling of double-viscoelastic-FGM-nanoplate system with viscoelastic Pasternak medium in between. Phys. Lett. A 2017, 381, 1228–1235. [Google Scholar] [CrossRef]
- Shahidi, A.R.; Anjomshoa, A.; Shahidi, S.H.; Kamrani, M. Fundamental size dependent natural frequencies of non-uniform orthotropic nano scaled plates using nonlocal variational principle and finite element method. Appl. Math. Model. 2013, 37, 7047–7061. [Google Scholar] [CrossRef]
- Namin, S.F.A.; Pilafkan, R. Vibration analysis of defective graphene sheets using nonlocal elasticity theory. Phys. E Low Dimens. Syst. Nanostruct. 2017. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Torsional vibration of bi-directional functionally graded nanotubes based on nonlocal elasticity theory. Compos. Struct. 2017, 172, 242–250. [Google Scholar] [CrossRef]
- Demir, Ç.; Civalek, Ö. A new nonlocal FEM via Hermitian cubic shape functions for thermal vibration of nano beams surrounded by an elastic matrix. Compos. Struct. 2017, 168, 872–884. [Google Scholar] [CrossRef]
- Murmu, T.; Adhikari, S. Nonlocal vibration of bonded double-nanoplate-systems. Compos. Part B Eng. 2011, 42, 1901–1911. [Google Scholar] [CrossRef]
- Mechab, I.; El Meiche, N.; Bernard, F. Free vibration analysis of higher-order shear elasticity nanocomposite beams with consideration of nonlocal elasticity and Poisson effect. J. Eng. Mech. 2016, 6, 04016006. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.M.; Challamel, N. Eringen’s length-scale coefficients for vibration and buckling of nonlocal rectangular plates with simply supported edges. J. Eng. Mech. 2015, 141, 04014117. [Google Scholar] [CrossRef]
- Challamel, N.; Wang, C.M.; Zhang, H.; Kitipornchai, S. Exact and Nonlocal Solutions for Vibration of Axial Lattice with Direct and Indirect Neighboring Interactions. J. Eng. Mech. 2018, 144, 04018025. [Google Scholar] [CrossRef]
- Zorica, D.; Atanackovi, T.M.; Vrcelj, Z.; Novakovic, B. Dynamic stability of axially loaded nonlocal rod on generalized Pasternak foundation. J. Eng. Mech. 2017, 143, D4016003. [Google Scholar] [CrossRef]
- Mehar, K.; Mahapatra, T.R.; Panda, S.K.; Katariya, P.V.; Tompe, U.K. Finite-Element Solution to Nonlocal Elasticity and Scale Effect on Frequency Behavior of Shear Deformable Nanoplate Structure. J. Eng. Mech. 2018, 144, 04018094. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; de Sciarra, F.M. Free vibrations of elastic beams by modified nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R. Vibrations of Bernoulli-Euler beams using the two-phase nonlocal elasticity theory. Int. J. Eng. Sci. 2017, 119, 232–248. [Google Scholar] [CrossRef]
- Rezaee, M.; Lotfan, S. Non-linear nonlocal vibration and stability analysis of axially moving nanoscale beams with time-dependent velocity. Int. J. Mech. Sci. 2015, 96, 3–46. [Google Scholar] [CrossRef]
- Wu, C.P.; Lai, W.W. Free vibration of an embedded single-walled carbon nanotube with various boundary conditions using the RMVT-based nonlocal Timoshenko beam theory and DQ method. Phys. E Low Dimens. Syst. Nanostruct. 2015, 68, 8–21. [Google Scholar] [CrossRef]
- Nazemnezhad, R. Nonlocal Timoshenko beam model for considering shear effect of van der Waals interactions on free vibration of multilayer graphene nanoribbons. Compos. Struct. 2015, 133, 522–528. [Google Scholar] [CrossRef]
- Glabisz, W.; Jarczewska, K.; Hołubowski, R. Stability of Timoshenko beams with frequency and initial stress dependent nonlocal parameters. Arch. Civ. Mech. Eng. 2019, 19, 1116–1126. [Google Scholar] [CrossRef]
- Niknam, H.; Aghdam, M.M. A semi analytical approach for large amplitude free vibration and buckling of nonlocal FG beams resting on elastic foundation. Compos. Struct. 2015, 119, 452–462. [Google Scholar] [CrossRef]
- Lal, R.; Dangi, C. Thermomechanical vibration of bi-directional functionally graded non-uniform timoshenko nanobeam using nonlocal elasticity theory. Compos. Part B Eng. 2019, 172, 724–742. [Google Scholar] [CrossRef]
- Fuschi, P.; Pisano, A.A.; Polizzotto, C. Size effects of small-scale beams in bending addressed with a strain-difference based nonlocal elasticity theory. Int. J. Mech. Sci. 2019, 151, 661–671. [Google Scholar] [CrossRef]
- Loghmani, M.; Yazdi, M.R.H. An analytical method for free vibration of multi cracked and stepped nonlocal nanobeams based on wave approach. Results Phys. 2018, 11, 166–181. [Google Scholar] [CrossRef]
- Emam, S.A.; Eltaher, M.A.; Khater, M.E.; Abdalla, W.S. Postbuckling and Free Vibration of Multilayer Imperfect Nanobeams under a Pre-Stress Load. Appl. Sci. 2018, 8, 2238. [Google Scholar] [CrossRef]
- Naghinejad, M.; Ovesy, H.R. Viscoelastic free vibration behavior of nano-scaled beams via finite element nonlocal integral elasticity approach. J. Vib. Control 2018, 25, 445–459. [Google Scholar] [CrossRef]
- Karličić, D.Z.; Ayed, S.; Flaieh, E. Nonlocal axial vibration of the multiple Bishop nanorod system. Math. Mech. Solids 2018, 24, 1668–1691. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, S.; Dai, L.; Hu, H. Analysis of a micro piezoelectric vibration energy harvester by nonlocal elasticity theory. Adv. Mech. Eng. 2016, 8, 1–10. [Google Scholar] [CrossRef]
- Waksmanski, N.; Pan, E. An analytical three-dimensional solution for free vibration of a magneto-electro-elastic plate considering the nonlocal effect. J. Intell. Mater. Syst. Struct. 2016, 28, 1501–1513. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB, Software, Enviroments, and Tools; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Sari, M.S. Free Vibration Analysis of Annular Sector Mindlin Plates Using the Nonlocal Continuum Theory. Int. J. Mech. Sci. 2015, 96, 25–35. [Google Scholar] [CrossRef]
- Sari, M.S.; Al-Kouz, W.G. Vibration analysis of non-uniform orthotropic Kirchhoff plates resting on elastic foundation based on nonlocal elasticity theory. Int. J. Mech. Sci. 2016, 114, 1–11. [Google Scholar] [CrossRef]
- Sari, M.; Shaat, M.; Abdelkefi, A. Frequency and mode veering phenomena of axially functionally graded non-uniform beams with nonlocal residuals. Compos. Struct. 2017, 163, 280–292. [Google Scholar] [CrossRef]
- Shahba, A.; Rajasekaran, S. Free vibration and stability of tapered Euler–Bernoulli beams made of axially functionally graded materials. Appl. Math. Model. 2012, 36, 3094–3111. [Google Scholar] [CrossRef]
- Murmu, T.; Adhikari, S. Nonlocal transverse vibration of double-nanobeam-systems. J. Appl. Phys. 2010, 108, 083514. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).