Abstract
In this paper, rectangular multi-Gaussian Schell-model (MGSM) array beams, which consists N×D beams in rectangular symmetry, are first introduced. The analytical expressions of MGSM array beams propagating through free space and non-Kolmogorov turbulence are derived. The propagation properties, such as normalized average intensity and effective beam sizes of MGSM array beams are investigated and analyzed. It is found that the propagation properties of MGSM array beams depend on the parameters of the MGSM source and turbulence. It can also be seen that the beam size of Gaussian beams translated by MGSM array beams will become larger as the total number of terms, M, increases or coherence length, , decreases, and the beam in stronger non-Kolmogorov turbulence (larger and , or smaller ) will also have a larger beam size.
1. Introduction
In past years, the topic of beams propagating in atmospheric turbulence has been explored, and different models, such as Kolmogorov and non-Kolmogorov turbulences, were given to describe the atmosphere. The propagation properties of beams, such as average intensity, polarization, scintillation index, and degree of coherence, were widely investigated in Kolmogorov turbulent atmosphere [1,2,3,4,5,6,7,8,9,10,11] and non-Kolmogorov turbulence [12,13,14,15,16,17,18,19,20,21,22].
However, the array beams were widely studied because they can provide higher power output than single beam. The Talbot effect, which describes the periodic beam propagating in studies of self-imaging, was investigated [23,24], and array beams with orbital angular momentum can also be generated based on Talbot effect [25,26]. In free space communication, the properties of coherent array beams propagating in free space and turbulent atmosphere have been widely investigated [27,28,29,30]. According to previous work, the partially coherent beams can reduce the effects of turbulent atmosphere [31], thus the evolutions of partially coherent array beams in turbulence, such as Gaussian Schell-model array beams [3,32,33,34], radial phase-locked array beams [35,36,37,38,39,40], and optical coherence vortex lattices [41], were also investigated. The multi-Gaussian Schell-model (MGSM) beams will evolve into flat-topped beams, thus the beams generated by a MGSM source have attracted much attention [42,43,44,45,46,47,48]. Considering the special properties of MGSM beams, it will thus be very interesting to investigate the array beams generated by a MGSM source. In this paper, we first introduce the model of a rectangular MGSM array beam, and then investigate the evolutions of MGSM array beams propagating through free space and non-Kolmogorov turbulence.
2. Propagation Analysis of MGSM Array Beams
2.1. Analytical Expressions of MGSM Array Beams
Recalling the descriptions of MGSM beams, the spectral degree of coherence of the MGSM source takes the form as follows [49]:
with
where represents normalization coefficient, is the initial correlation coherence length, is total number of terms of MGSM source, and is the position vector.
Considering the diagram of a array beam in rectangular symmetry, the cross-spectral density (CSD) of a rectangular MGSM array beam generated by a MGSM source is described by the following:
where and are odd numbers and represent the orders of individual off-axis MGSM beams along the x- and y-axes, and denote separations distances along the x- and y-axes, and represents the beam waist. The contour graphs of MGSM array beams in source plane z = 0 are plotted in Figure 1, which shows that the distance between the different beamlets will increase as the off-axis parameters and increase.
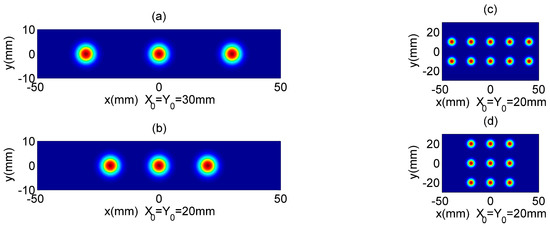
Figure 1.
The contour graphs of MGSM array beam at the plane z = 0. (a) , (b) , (c) , and (d) .
2.2. Propagation Theory
Considering the extended Huygens–Fresnel integral, the CSD of MGSM array beams in non-Kolmogorov turbulent atmosphere at the plane z is written as follows [15,16,17,18,19,20]:
where is the wave number with as the wavelength. The definitions of can be found in reference [19], and as follows:
where , is the magnitude of spatial frequency, and is the power law exponent. The non-Kolmogorov power spectrum can be described by the following [15,16,17]:
where is the turbulent structure constant with units ; , where is the outer scale; and , where is the inner scale; and
where denotes the Gamma function. Substituting Equations (6)–(8) into the definition of , we can obtain the following:
where represents the incomplete Gamma function.
Thus, the propagation CSD of MGSM array beams in non-Kolmogorov turbulent atmosphere are derived as follows:
where and are given as follows:
with
where or in all locations of equations. When , the symbols and represent and in all equations, respectively. When , the symbols and represent and in all equations, respectively.
The intensity [50] and effective beam widths [51] along the x- and y-axes of MGSM array beams propagating through non-Kolmogorov turbulent atmosphere can be written as follows:
Substituting Equations (10)–(14) into Equation (16), the effective beam widths of a MGSM array beam propagating through non-Kolmogorov turbulent atmosphere can be obtained as follows:
where
with
Due to the symmetrical characteristics, the effective beam size and will have similar properties. Thus, only the effective beam size is investigated in the following numerical analysis.
3. Numerical Examples
In this section, we numerically investigate the evolutions of MGSM array beams propagating through free space and non-Kolmogorov turbulent atmosphere by applying the derived formulae. In the numerical simulation, unless other values are given, the following parameters are used: , , , , , , , , , and .
The normalized intensity of MGSM array beams propagating through free space () and non-Kolmogorov turbulent atmosphere are illustrated in Figure 2 and Figure 3, respectively. According to Figure 2, we can see that the MGSM array beams in free space will maintain the rectangular distribution of beamlets in the short propagation distance. As z increases, the individual beamlets will gradually translate into a flat-topped beam caused by the influence of the MGSM sources. As z further increases, the individual flat-topped beams will overlap with each other. Eventually, the MGSM array beam will translate a solid beam; at last, the MGSM array beams will involve into a beam with flat-topped profile. While MGSM array beams propagating through non-Kolmogorov turbulent atmosphere will have similar evolution properties with array beams in free space, the individual beamlets in non-Kolmogorov turbulent atmosphere will overlap with each other more rapidly than the array beams in free space at the same distance, m (Figure 2b and Figure 3a). As z further increases, the array beams in non-Kolmogorov turbulent atmosphere will evolve into a Gaussian beam. The phenomenon in Figure 2 and Figure 3 can be explained as the general beams propagation in atmosphere can translate into Gaussian beams [52]. To view the effects of non-Kolmogorov turbulent atmosphere, the cross sections of MGSM array beams with through non-Kolmogorov turbulent atmosphere for the different are shown in Figure 4. It can be seen that the MGSM array beams propagating through non-Kolmogorov turbulent atmosphere with a larger will translate into a larger Gaussian-like beam spot more rapidly than in free space () at the same distance z.
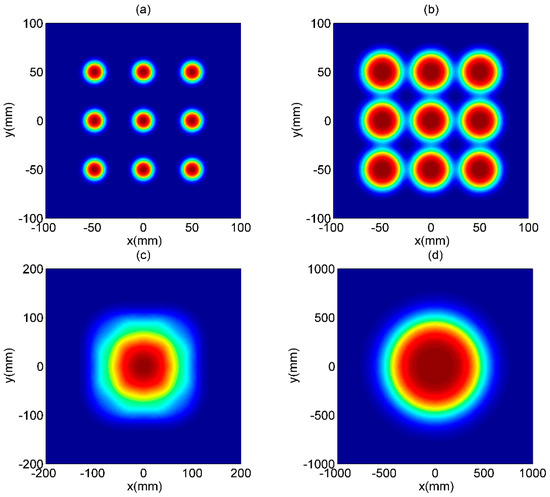
Figure 2.
The contour graphs of
MGSM array beams propagating through free space with . (a) , (b) , (c) , and (d) .
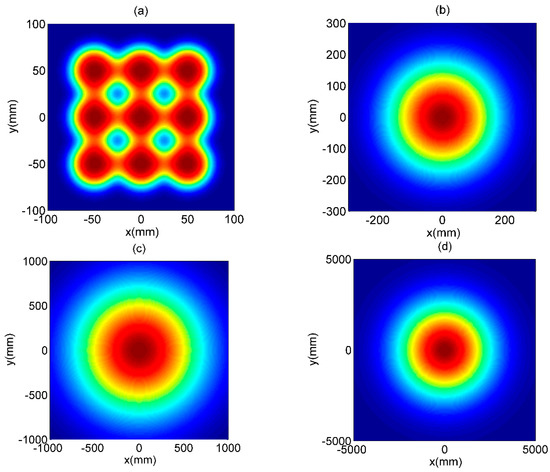
Figure 3.
The contour graphs of
MGSM array beams propagating through non- Kolmogorov turbulent atmosphere with . (a) , (b) , (c) , and (d) .
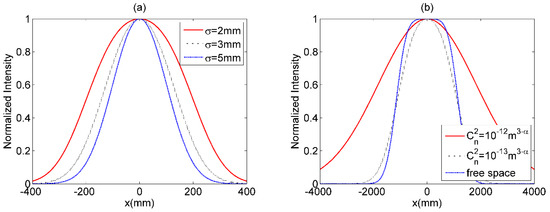
Figure 4.
The cross sections of
MGSM array beams with propagating through non-Kolmogorov turbulent atmosphere for . (a) and (b) .
The effects of coherence length, , on MGSM array beams with propagating through non-Kolmogorov turbulent atmosphere are illustrated in Figure 5. As can be found, the MGSM array beams with smaller will evolve into a Gaussian beam more rapidly with increasing propagation distance z, and will have a larger spot. To investigate the effective beam size of a Gaussian beam translated by the MGSM array beam, Figure 6 gives the effective beam size of the Gaussian beam for different and . One can see that of a Gaussian beam obtained by a MGSM array beam will increase with the increase of or the decrease of .
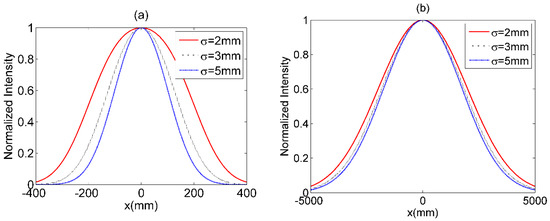
Figure 5.
The cross sections of
MGSM array beam with , propagating through non- Kolmogorov turbulent atmosphere for . (a) and (b) .
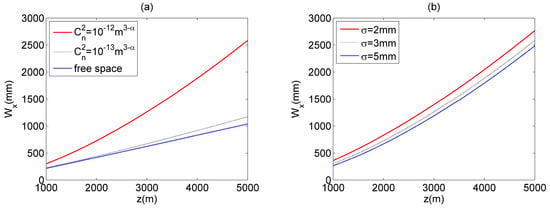
Figure 6.
The
of MGSM array beams with propagating through non- Kolmogorov turbulent atmosphere. (a) different and (b) different .
By changing the parameters and , the effective beam size for MGSM array beams propagating through non- Kolmogorov turbulent atmosphere is shown in Figure 7. As can be found, when the propagation distance z remains the same, the Gaussian beam translated by the MGSM array beams with larger can have a larger effective beam size. When , the MGSM array beam will reduce into a GSM array beam, which will have the smallest effective beam size. While, in the influence of , we can find that as z increases, the effects of on the effective beam size of the Gaussian beam will disappear. These results mean that the MGSM array beams with different will have almost the same effective beam size. Thus, the larger the , the higher the power the Gaussian beam will have. This phenomenon is beneficial for free space optical communications using MGSM array beams.
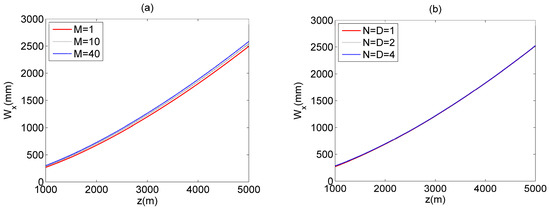
Figure 7.
The
of MGSM array beams propagating through non-Kolmogorov turbulent atmosphere. (a) different , (b) different .
The influences of non-Kolmogorov turbulent atmosphere parameters , , and on are shown in Figure 8. When z increases to , the MGSM array beams will become the Gaussian beam, the effective beam size, , of the Gaussian-like beam translated by the MGSM array beams will increase with , and a decrease of or an increase of . The phenomenon can be explained as follows: The strength of non-Kolmogorov turbulent atmosphere depends on , , and .
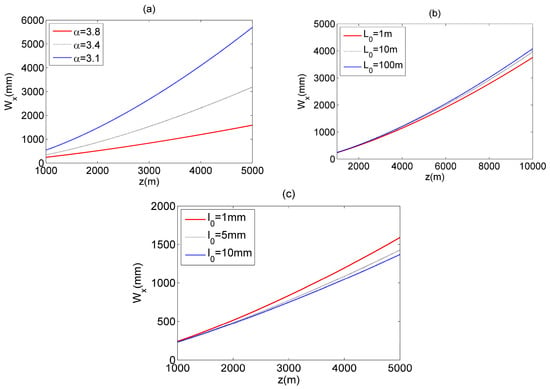
Figure 8.
The
of MGSM array beams propagating through non-Kolmogorov turbulent atmosphere. (a) different , (b) different , and (c) different .
4. Conclusions
In conclusion, the rectangular MGSM array beams composed by MGSM beams in rectangular symmetry are given, and the intensity and effective beam size of MGSM array beams in free space and in non-Kolmogorov turbulent atmosphere were investigated. Based on the derived equations, the results show that the MGSM array beams propagating through non-Kolmogorov turbulent atmosphere will become a Gaussian beam caused by the non-Kolmogorov turbulent atmosphere, while array beams propagating through free space will translate into flat-topped beams. With an increase in and , or and decrease of and , the Gaussian-like beam will have a larger beam size. With M increases or decreases, the array beams will also evolve into beams with a larger spot. The obtained results may be beneficial for free space optical communication.
Author Contributions
X.M. (Data curation, Writing—original draft preparation); Y.W. (software, Validation); H.Y. (formal analysis); H.Z. (software); D.L. (Supervision, Writing—Review, Editing, and Validation); G.W. (Supervision, Writing—Review, Editing, and Validation). All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by National Natural Science Foundation of China [11604038, 11404048, 11875096], and the Fundamental Research Funds for the Central Universities [3132019182, 3132019184].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eyyuboglu, H.T.; Baykal, Y. Average intensity and spreading of cosh-Gaussian laser beams in the turbulent atmosphere. Appl. Opt. 2005, 44, 976–983. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.J.; Lin, Q.; Baykal, Y.; Eyyuboglu, H.T. Off-axis Gaussian Schell-model beam and partially coherent laser array beam in a turbulent atmosphere. Opt. Commun. 2007, 278, 157–167. [Google Scholar] [CrossRef]
- Zhu, Y.B.; Zhao, D.M.; Du, X.Y. Propagation of stochastic Gaussian-Schell model array beams in turbulent atmosphere. Opt. Express 2008, 16, 18437–18442. [Google Scholar] [CrossRef]
- Zhou, G. Average intensity and spreading of super Lorentz-Gauss modes in turbulent atmosphere. Appl. Phys. B 2010, 101, 371–379. [Google Scholar] [CrossRef]
- Wang, D.; Wang, F.; Cai, Y.; Chen, J. Evolution properties of the complex degree of coherence of a partially coherent Laguerre–Gaussian beam in turbulent atmosphere. J. Mod. Opt. 2012, 59, 372–380. [Google Scholar] [CrossRef]
- Zhang, L.C.; Yin, X.; Zhu, Y. Polarization fluctuations of partially coherent Hermite-Gaussian beams in a slant turbulent channel. Opt. Int. J. Light Electron Opt. 2014, 125, 3272–3276. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Wang, G.; Yin, H. Propagation Properties of a Partially Coherent Flat-Topped Vortex Hollow Beam in Turbulent Atmosphere. J. Opt. Soc. Korea 2016, 20, 1–7. [Google Scholar] [CrossRef]
- Liu, D.; Luo, X.; Wang, G.; Wang, Y. Spectral and Coherence Properties of Spectrally Partially Coherent Gaussian Schell-model Pulsed Beams Propagating in Turbulent Atmosphere. Curr. Opt. Photonics 2017, 1, 271–277. [Google Scholar]
- Liu, Y.; Zhang, K.; Chen, Z.; Pu, J. Scintillation index of double vortex beams in turbulent atmosphere. Opt. Int. J. Light Electron Opt. 2019, 181, 571–574. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, X.; Yuan, X. Performance analysis of sinh-Gaussian vortex beams propagation in turbulent atmosphere. Opt. Commun. 2019, 440, 100–105. [Google Scholar] [CrossRef]
- Malik, M.; O’Sullivan, M.; Rodenburg, B.; Mirhosseini, M.; Leach, J.; Lavery, M.P.J.; Padgett, M.J.; Boyd, R.W. Influence of atmospheric turbulence on optical communications using orbital angular momentum for encoding. Opt. Express 2012, 20, 13195–13200. [Google Scholar] [CrossRef]
- Toselli, I.; Andrews, L.C.; Phillips, R.L.; Ferrero, V. Free-space optical system performance for laser beam propagation through non-Kolmogorov turbulence. Opt. Eng. 2008, 47, 026003. [Google Scholar]
- Shchepakina, E.; Korotkova, O. Second-order statistics of stochastic electromagnetic beams propagating through non-Kolmogorov turbulence. Opt. Express 2010, 18, 10650–10658. [Google Scholar] [CrossRef]
- Tang, H.; Ou, B. Average spreading of a linear Gaussian-Schell model beam array in non-Kolmogorov turbulence. Appl. Phys. B 2011, 104, 1007–1012. [Google Scholar] [CrossRef]
- Jiang, Y.S.; Wang, S.H.; Zhang, J.H.; Ou, J.; Tang, H. Spiral spectrum of Laguerre-Gaussian beam propagation in non-Kolmogorov turbulence. Opt. Commun. 2013, 303, 38–41. [Google Scholar] [CrossRef]
- Xu, H.F.; Zhang, Z.; Qu, J.; Huang, W. Propagation factors of cosine-Gaussian-correlated Schell-model beams in non-Kolmogorov turbulence. Opt. Express 2014, 22, 22479–22489. [Google Scholar] [CrossRef]
- Wang, X.; Yao, M.; Yi, X.; Qiu, Z.; Liu, Z. Spreading and evolution behavior of coherent vortices of multi-Gaussian Schell-model vortex beams propagating through non-Kolmogorov turbulence. Opt. Laser Technol. 2017, 87, 99–107. [Google Scholar] [CrossRef]
- Song, Z.-Z.; Liu, Z.-J.; Zhou, K.-Y.; Sun, Q.-G.; Liu, S.-T. Propagation factor of electromagnetic concentric rings Schell-model beams in non-Kolmogorov turbulence. Chin. Phys. B 2017, 26, 024201. [Google Scholar] [CrossRef]
- Zhi, D.; Tao, R.M.; Zhou, P.; Ma, Y.X.; Wu, W.M.; Wang, X.L.; Si, L. Propagation of ring Airy Gaussian beams with optical vortices through anisotropic non-Kolmogorov turbulence. Opt. Commun. 2017, 387, 157–165. [Google Scholar] [CrossRef]
- Tang, L.; Wang, H.; Zhang, X.; Zhu, S. Propagation properties of partially coherent Lommel beams in non-Kolmogorov turbulence. Opt. Commun. 2018, 427, 79–84. [Google Scholar] [CrossRef]
- Huang, Y.; Zeng, A. Effect of anisotropic non-Kolmogorov turbulence on the evolution behavior of Gaussian Schell-model vortex beams. Opt. Commun. 2019, 436, 63–68. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Y.X. Beam spreading and wander of partially coherent Lommel-Gaussian beam in turbulent biological tissue. J. Quant. Spectrosc. Radiat. Transf. 2018, 217, 315–320. [Google Scholar] [CrossRef]
- Song, X.; Wang, H.; Xiong, J.; Wang, K.; Zhang, X.; Luo, K.; Wu, L. Experimental observation of quantum Talbot effect. Phys. Rev. Lett. 2011, 107, 033902. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, J.; Zhu, S.; Xiao, M. Nonlinear Talbot effect. Phys. Rev. Lett. 2010, 104, 183901. [Google Scholar] [CrossRef]
- Wei, G.-X.; Lu, L.-L.; Guo, C.-S. Generation of optical vortex array based on the fractional Talbot effect. Opt. Commun. 2009, 282, 2665–2669. [Google Scholar] [CrossRef]
- Sarenac, D.; Cory, D.G.; Nsofini, J.; Hincks, I.; Miguel, P.; Arif, M.; Clark, C.W.; Huber, M.G.; Pushin, D.A. Generation of a Lattice of Spin-Orbit Beams via Coherent Averaging. Phys. Rev. Lett. 2018, 121, 183602. [Google Scholar] [CrossRef]
- Eyyuboğlu, H.T.; Baykal, Y.; Cai, Y. Scintillations of laser array beams. Appl. Phys. B 2008, 91, 265–271. [Google Scholar] [CrossRef]
- Lu, L.; Ji, X.L.; Deng, J.P.; Li, X.Q. A further study on the spreading and directionality of Gaussian array beams in non-Kolmogorov turbulence. Chin. Phys. B 2014, 23, 064209. [Google Scholar] [CrossRef]
- Zhou, G.Q. Propagation of a radial phased-locked Lorentz beam array in turbulent atmosphere. Opt. Express 2011, 19, 24699–24711. [Google Scholar] [CrossRef]
- Lu, L.; Wang, Z.Q.; Zhang, J.H.; Zhang, P.F.; Qiao, C.H.; Fan, C.Y.; Ji, X.L. Average intensity of M x N Gaussian array beams in oceanic turbulence. Appl. Opt. 2015, 54, 7500–7507. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.L.; Cai, Y.J. Propagation of Partially Coherent Beam in Turbulent Atmosphere: A Review. Prog. Electromagn. Res. 2015, 150, 123–143. [Google Scholar] [CrossRef]
- Mao, Y.H.; Mei, Z.R.; Gu, J.G. Propagation of Gaussian Schell-model Array beams in free space and atmospheric turbulence. Opt. Laser Technol. 2016, 86, 14–20. [Google Scholar] [CrossRef]
- Huang, Y.P.; Zeng, A.P.; Gao, Z.H.; Zhang, B. Beam wander of partially coherent array beams through non-Kolmogorov turbulence. Opt. Lett. 2015, 40, 1619–1622. [Google Scholar] [CrossRef]
- Song, Z.Z.; Liu, Z.J.; Zhou, K.Y.; Sun, Q.G.; Liu, S.T. Propagation properties of Gaussian Schell-model array beams in non-Kolmogorov turbulence. J. Opt. 2016, 18, 105601. [Google Scholar] [CrossRef]
- Razzaghi, D.; Hajiesmaeilbaigi, F.; Alavinejad, M. Spectrum changes of phase-locked partially coherent flat topped laser beam array propagating in turbulent atmosphere. Opt. Int. J. Light Electron Opt. 2013, 124, 2135–2139. [Google Scholar] [CrossRef]
- Liu, H.L.; Lu, Y.F.; Xia, J.; Chen, D.; He, W.; Pu, X.Y. Radial phased-locked partially coherent flat-topped vortex beam array in non-Kolmogorov medium. Opt. Express 2016, 24, 19695–19712. [Google Scholar] [CrossRef]
- Kashani, F.D.; Yousefi, M. Analyzing the propagation behavior of coherence and polarization degrees of a phase-locked partially coherent radial flat-topped array laser beam in underwater turbulence. Appl. Opt. 2016, 55, 6311–6320. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Zhong, H. Average intensity of radial phased-locked partially coherent standard Hermite-Gaussian beam in oceanic turbulence. Opt. Laser Technol. 2018, 106, 495–505. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y. Evolution properties of a radial phased-locked partially coherent Lorentz-Gauss array beam in oceanic turbulence. Opt. Laser Technol. 2018, 103, 33–41. [Google Scholar] [CrossRef]
- Liu, D.; Zhong, H.; Wang, G.; Yin, H.; Wang, Y. Propagation of a radial phase-locked partially coherent elegant Laguerre–Gaussian beam array in non-Kolmogorov medium. Appl. Phys. B 2019, 125, 52. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, Y.S.; Liu, X.L.; Zeng, J.; Wang, F.; Yu, J.Y.; Liu, L.; Cai, Y.J. Propagation of Optical Coherence Vortex Lattices in Turbulent Atmosphere. Appl. Sci. 2018, 8, 2476. [Google Scholar] [CrossRef]
- Mei, Z.R.; Korotkova, O.; Shchepakina, E. Electromagnetic multi-Gaussian Schell-model beams. J. Opt. 2013, 15, 025705. [Google Scholar] [CrossRef]
- Cang, J.; Fang, X.; Liu, X. Propagation properties of multi-Gaussian Schell-model beams through ABCD optical systems and in atmospheric turbulence. Opt. Laser Technol. 2013, 50, 65–70. [Google Scholar] [CrossRef]
- Zhang, H.; Fu, W. Polarization properties of Square Multi-Gaussian Schell-Model beam propagating through non-Kolmogorov turbulence. Opt. Int. J. Light Electron Opt. 2017, 134, 161–169. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Zhao, D.M. Propagation properties of a twisted rectangular multi-Gaussian Schell-model beam in free space and oceanic turbulence. Appl. Opt. 2018, 57, 8978–8983. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y. Properties of a random electromagnetic multi-Gaussian Schell-model vortex beam in oceanic turbulence. Appl. Phys. B 2018, 124, 176. [Google Scholar] [CrossRef]
- Korotkova, O.; Shchepakina, E. Rectangular Multi-Gaussian Schell-Model beams in atmospheric turbulence. J. Opt. 2014, 16, 045704. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Ding, C.L.; Pan, L.Z.; Cai, Y.J. Laser arrays of partially coherent beams with multi-Gaussian correlation function. J. Quant. Spectrosc. Radiat. Transf. 2018, 218, 1–11. [Google Scholar] [CrossRef]
- Korotkova, O.; Sahin, S.; Shchepakina, E. Multi-Gaussian Schell-model beams. J. Opt. Soc. Am. A 2012, 29, 2159–2164. [Google Scholar] [CrossRef]
- Wolf, E. Unified theory of coherence and polarization of random electromagnetic beams. Phys. Lett. A 2003, 312, 263–267. [Google Scholar] [CrossRef]
- Carter, W. Spot size and divergence for Hermite Gaussian beams of any order. Appl. Opt. 1980, 19, 1027–1029. [Google Scholar] [CrossRef]
- Eyyuboglu, H.T.; Baykal, Y.; Sermutlu, E. Convergence of general beams into Gaussian-intensity profiles after propagation in turbulent atmosphere. Opt. Commun. 2006, 265, 399–405. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).