1. Introduction
As the “skeleton” and “muscle” of the aircraft structure, the flight control actuation system plays an irreplaceable role in its structure [
1,
2,
3]. At present, most civil and military aircraft use a central hydraulic oil source for centralized fluid supply, adopt engine-driven pumps to provide high pressure, and employ servo valves to implement servo control of the rudder surface and landing gear through the throttle principle [
2,
3,
4]. This method has mature technology and good dynamic performance, but low efficiency and complex pipeline layout problems have become the main factors restricting the further improvement of aircraft performance [
5]. In modern battlefields, it is increasingly demanding for fighter jets maneuverability, energy efficiency, fuselage layout, survivability, etc., and this raises a higher challenge requirement for flight control actuator system as one of the key components of airborne electromechanical systems and flight control systems [
6]. With the exploded appearance and swift advancement of more/all-electric-aircraft (MEA/AEA), a power-by-wire actuation system has become main steam behind aviation progression, which exterminates the desideratum for the aircraft’s classical hydraulic system and only requires a variety of energy procreation (electric power) resulting in simplifying secondary energy systems, so it brings about more advanced reliability and lowers design and maintenance costs [
7,
8,
9].
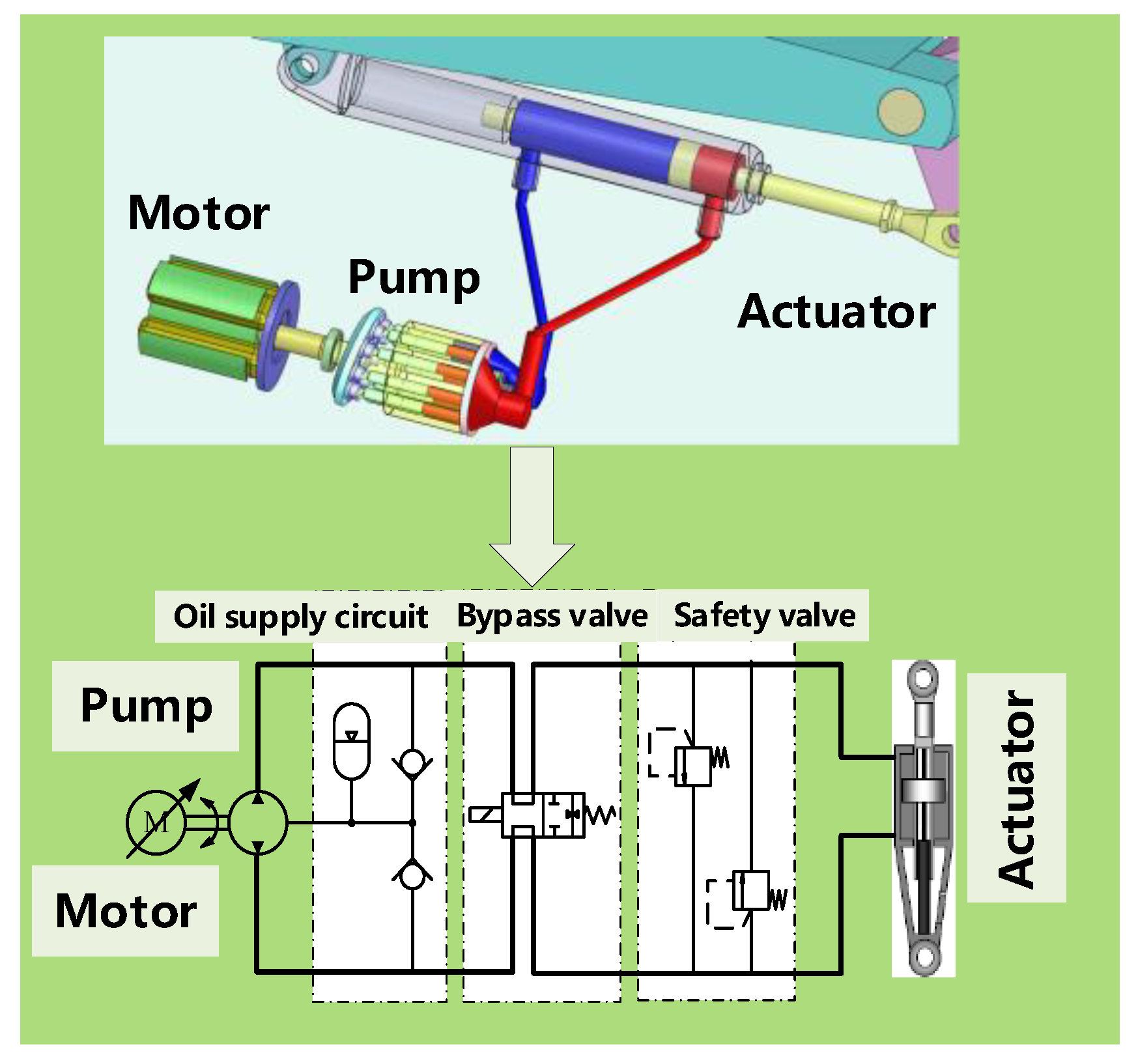
EHA is an attractive category of power by wire, and it utilizes a hydraulic pump as a transmission reducer to transform the motor’s rotational motion into the linear motion of the actuator’s output with other components, such as oil supply circuit, bypass valve and safety valve, as shown in
Figure 1. Hydraulic coupling allows greater flexibility in integrated design of EHA components. The installing position and direction of the motor and pump relative to the actuator can be flexibly adjusted to satisfy the demand for integrated volume size. This is a superiority of EHA compared to another candidate power-by-wire electromechanical actuator (EMA). The installing position and direction of motor and gear of EMA do not allow to be dexterously shifted [
10]. EHA can regulate the transmission ratio by controlling the pump displacement. Adjustable transmission ratio can increase the actuator stiffness, reduce integration volume, and decrease system heating. In the flight control system, using EHAs instead of the currently used relatively mature electro-hydraulic valve-controlled actuators, there are three prevailing concerns, namely heating, size, and stiffness [
11]. So far, the average efficiency of the EHA applied in the aviation field is about 35%, and the bandwidth is generally about 7Hz [
12].
EHA heating is an imperative dilemma. In a central hydraulic pump system, heat loss is transferred from the actuator to the central heat exchanger via hydraulic fluid, however EHA has no fluid exchange, so a separate heat exchanger mounted on the EHA or a fluid radiator added to the aircraft is required for cooling, which will greatly increase the difficulty for the confined space to package the actuator neighboring the control surface. An important source of heat loss is the nature of the aerodynamic load. The operating conditions of EHA include forward load and reverse load. When EHA operates under aiding load condition, the aerodynamic load works on the actuator, reversely driving the pump to rotate the motor as generator. The aiding-load energy is converted into electric energy which moves in the form of a current in the system. Another vital reason for EHA heating is the low efficiency of the system components. The most remarkable one is the motor copper loss. The motor torque is proportional to its current. The torque required to balance the load is proportional to the pump displacement which necessarily matches the motor speed and the actuator piston area to meet the actuator speed. In short, motor is the main heat source of EHA, e.g., an experimental result shown in
Figure 2. Under the condition of 4t with load and continuous working for seven minutes, the surface temperature of the motor rises from 29.5 °C to 51.6 °C, and the hydraulic-part temperature remained essentially unchanged. The problem of motor heating is the main reason affecting the EHA widespread application [
13]. The energy loss of the motor is mostly dissipated through heat generation in the form of copper and iron losses. Meanwhile, the dynamic performance of the system at high temperatures will be affected to some extent. If the motor heating can be reduced, it is of great significance for EHA to improve the efficiency, dynamics and reliability, as well as increase continuous the working time and lifetime [
14].
The idea of solving the problem of motor heating- is to popularly use high-speed motor and high-pressure system for the EHA-FPVM. For example, the EHA system designed by SAFRAN in France and UTC-Goodrich in the United States uses 20,000 rmp motors and 35MPa hydraulic systems. The system achieved a level of 16,000 rpm and a peak pressure of 35 MPa. The method of high pressure and high speed can expand the speed regulation range of the motor and enable the motor to work in the high efficiency area [
15]. This method is currently very popular because of its simple structure and control, but this fixed displacement architecture cannot achieve the optimal power matching of motor and pump, where the power of the selected motor is the larger, which is disadvantageous for high power density requirements. The EHA with variable pump displacement and variable motor speed (EHA-VPVM) has become a popular concern, because its two control variables can well achieve the motor-pump power matching and reduce the motor heating, as well as improve the EHA stiffness [
16]. The general variable displacement mechanism requires an open valve-controlled cylinder with additional oil supply pressure to alter the pump displacement through varying the tilt angle of the swash plate [
17]. The principle structure has fast response but increases the cost and complexity of the system. Reference [
18] proposed a new type of electric variable mechanism composed of a direct current (DC) servo motor and related transmissions (gearbox + sector gear). The purpose is to simplify the structure of the variable mechanism, reduce hydraulic faults and improve maintainability. The meshing between gears inevitably has problems such as tooth-side clearance, inter-tooth lubrication media, and various transmission errors (including various manufacturing errors, installation errors, thermal deformation, wear, etc.). These coupling effects have a certain degree of influence on the performance of the electric variable mechanism. Chao etc. designed a load-sensing pump based on a variable displacement architecture to reduce EHA heat generation in [
19]. Jiao advanced the principle of direct load-sensitive EHA (DLS-EHA) based on load-sensing pumps [
20]. The DLS-EHA automatically adjusts the pump displacement through the load pressure without the need for an additional power source, which can decrease the motor heating and achieve the motor-pump power matching to a certain extent. However, the back pressure spring of the variable mechanism must be selected according to the maximum load pressure to ensure that the variable mechanism is sufficiently rigid to stabilize the system. A large back pressure spring stiffness results in a low rate of change in displacement with load pressure. DLS-EHA does not give consideration to the dynamics and the efficiency of the system, and the variable characteristic is a constant value making it difficult to achieve optimal matching.
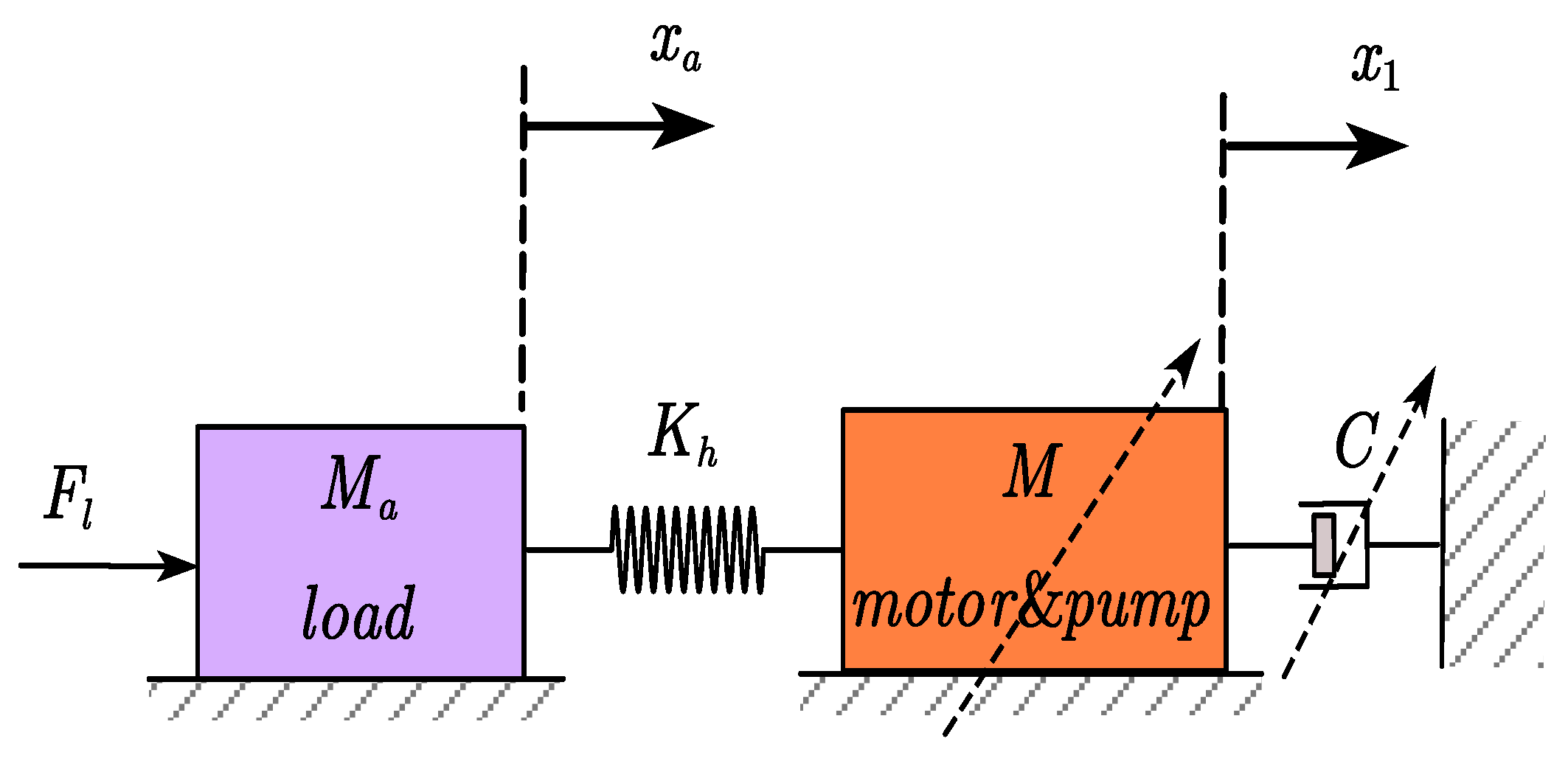
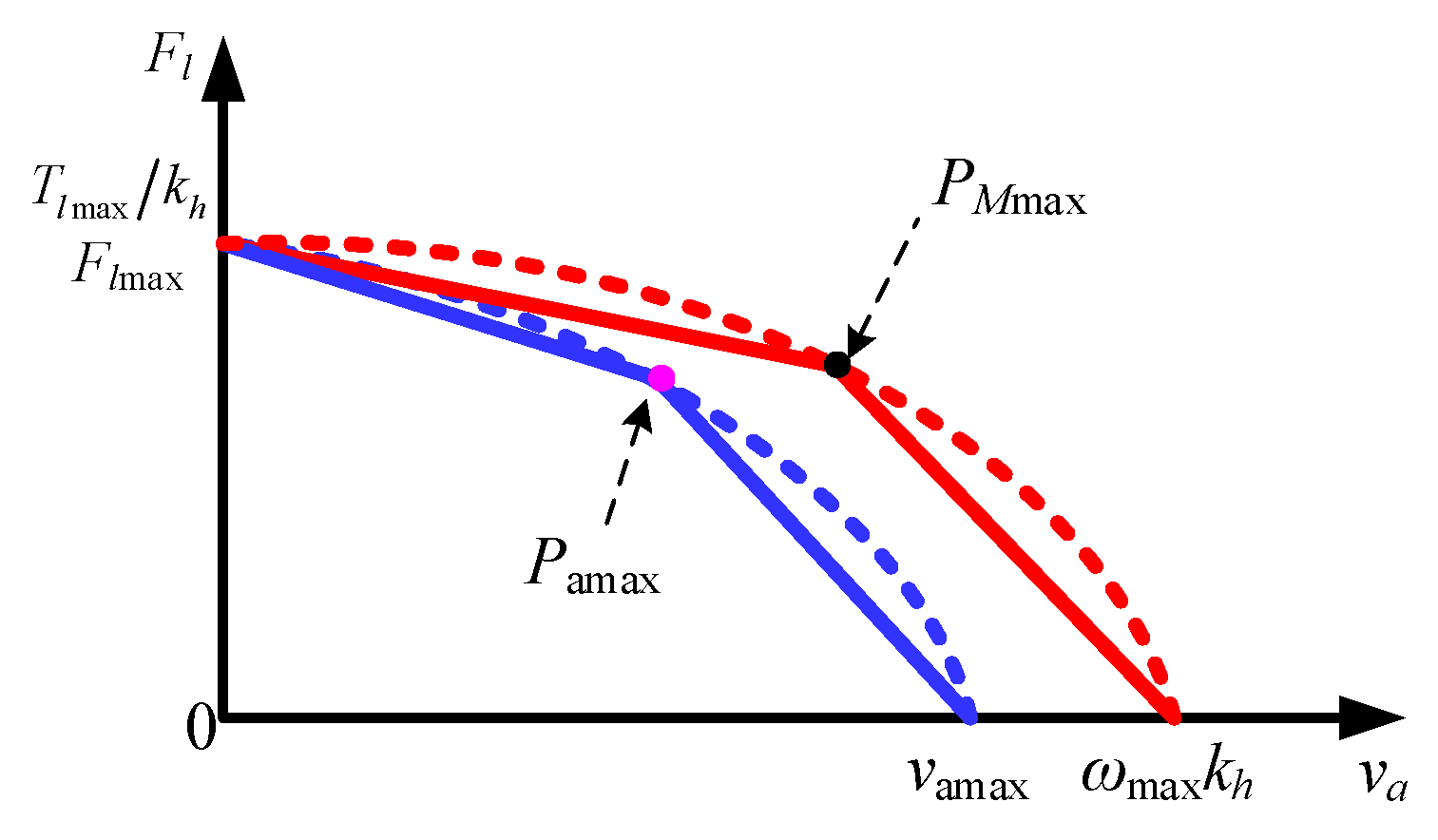
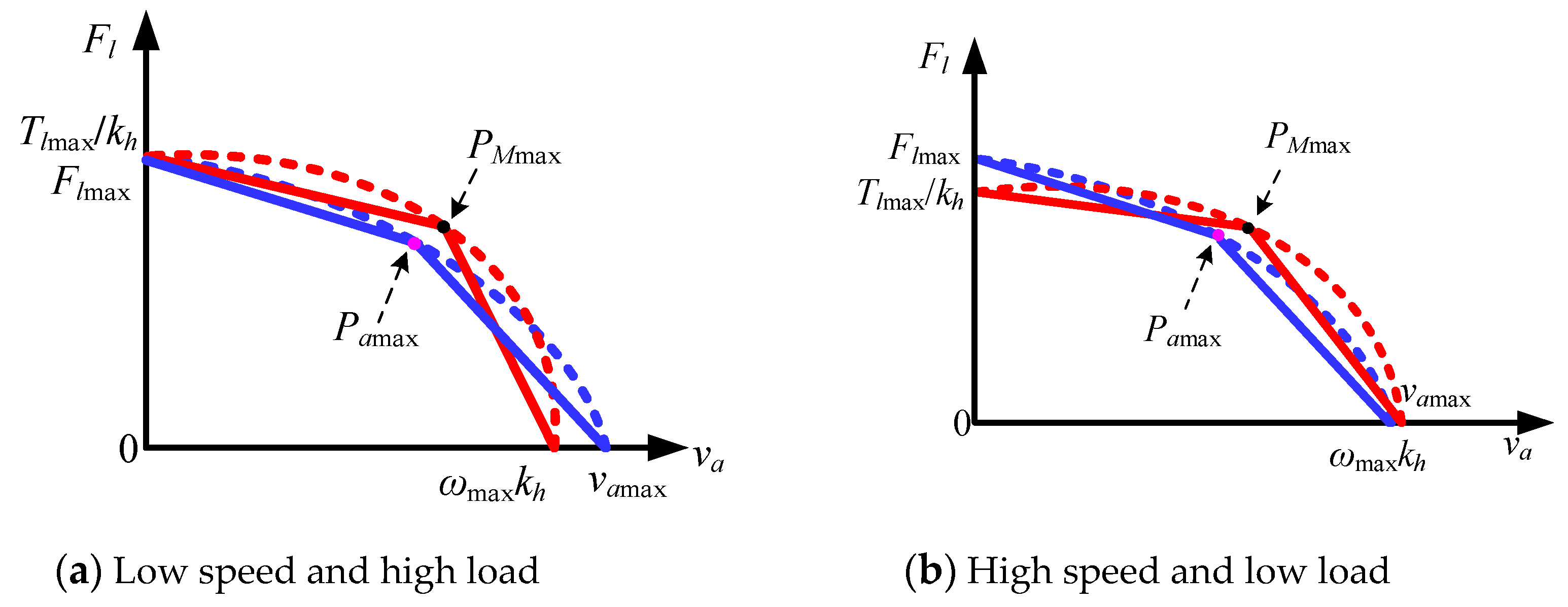
Stiffness is an index to measure the effect on the system output when the load force changes. Dynamic stiffness describes the changing law of stiffness in the dynamic process. The stiffness characteristics of the flight control actuation system can be divided into three parts according to frequency: (1) Within the bandwidth of the closed control system, the stiffness can be controlled due to the controller’ function that can guarantee the actuator output track the input. (2) At the reversal point of the frequency, the controller’s adjustment effect is positive feedback to cause the actuator output to alter greatly, so the system stiffness is the lowest. (3) Since it is too late for the actuator to respond to the disturbance at high frequencies, its stiffness is related to the passive components of the system. EHA is developed as a potential substitute for the valve-control actuation system in the flight control actuation system, its stiffness is also a major consideration [
21,
22,
23]. The stiffness characteristics of EHA and the valve-controlled actuator are distinct, especially at direct current and low frequencies. Regarding the stiffness of the valve-controlled actuator, the valve opening is not affected by the load pressure perturbance that keeps closed and its two chambers hold blocked. The impedance of the valve-controlled actuator is governed by the hydraulic stiffness of the two choked chambers of the actuator, where the enclosed oil has ability to counteract the load. If it is a double-rod actuator (the pressure goes up on one side of the piston and lowers on the other when the actuator is loaded), the impedance at the middle of the actuator stroke is
(where
is elastic modulus of oil, while
and
represent the area and stroke of the cylinder respectively), however, the stiffness of the single active side actuator is half of the former’s. Thus, stiffness is related to piston displacement. When the dynamic side has the shortest liquid column length, the stiffness is the largest, and when the high pressure side has the longest liquid column length, the stiffness is the smallest at the other end of the cylinder. The minimum stiffness of the single-rod actuator is a quarter of the one of the double-rod actuators. Compared with the valve-controlled actuator, in fact, the EHA has no real impedance, since EHA is a combination of electric and hydraulic and its two chambers cannot be obstructed, considering the increasing load pressure can drive the motor rotation back. Therefore, the stiffness of EHA depends on the hydraulic stiffness of the actuator and the electrical stiffness of the motor. Load disturbance will drive the motor to rotate and cause the actuator output displacement to vary, so it is necessary to improve the electrical stiffness. The displacement of EHA-FPVM cannot be adjusted, so the disturbance torque of the motor cannot be regulated, so its electrical stiffness is constant. For the new configuration of ALS-EHA mentioned in this paper, the displacement can be actively shifted, so the disturbance torque to the motor can also be lowered, and the stiffness of the new configuration can also be enhanced.
The structure for the whole paper is arranged as follows:
Section 2 mainly presents the research on the principle analysis and mathematical modeling of ALS-EHA based on DLS-EHA configuration.
Section 3 mainly studies the dynamic stiffness of ALS-EHA and the relationship between the stiffness at low frequencies and the hydraulic transmission ratio.
Section 4 mainly compares the power matching of ALS-EHA with that of EHA-FPVM, and then further analyzes the former matching rule. In
Section 5, the experiments of EHA-FPVM and ALS-EHA are compared to verify the performance of the latter, and final conclusions are presented.
2. The Principle Analysis and Modeling for ALS-EHA
In order to solve the heating problem of the motor, our research group proposed a novel EHA configuration based on load-sensing technology. In this part, the principle of load sensitivity is first analyzed. Based the simple structure of DLS-EHA, the ALS-EHA which is mainly studied in this paper is derived and the load sensitive characteristics are studied by means of mathematical modeling.
2.1. The Load Sensing Principle Description
Load-sensitive EHA includes two types: DLS-EHA and ALS-EHA.
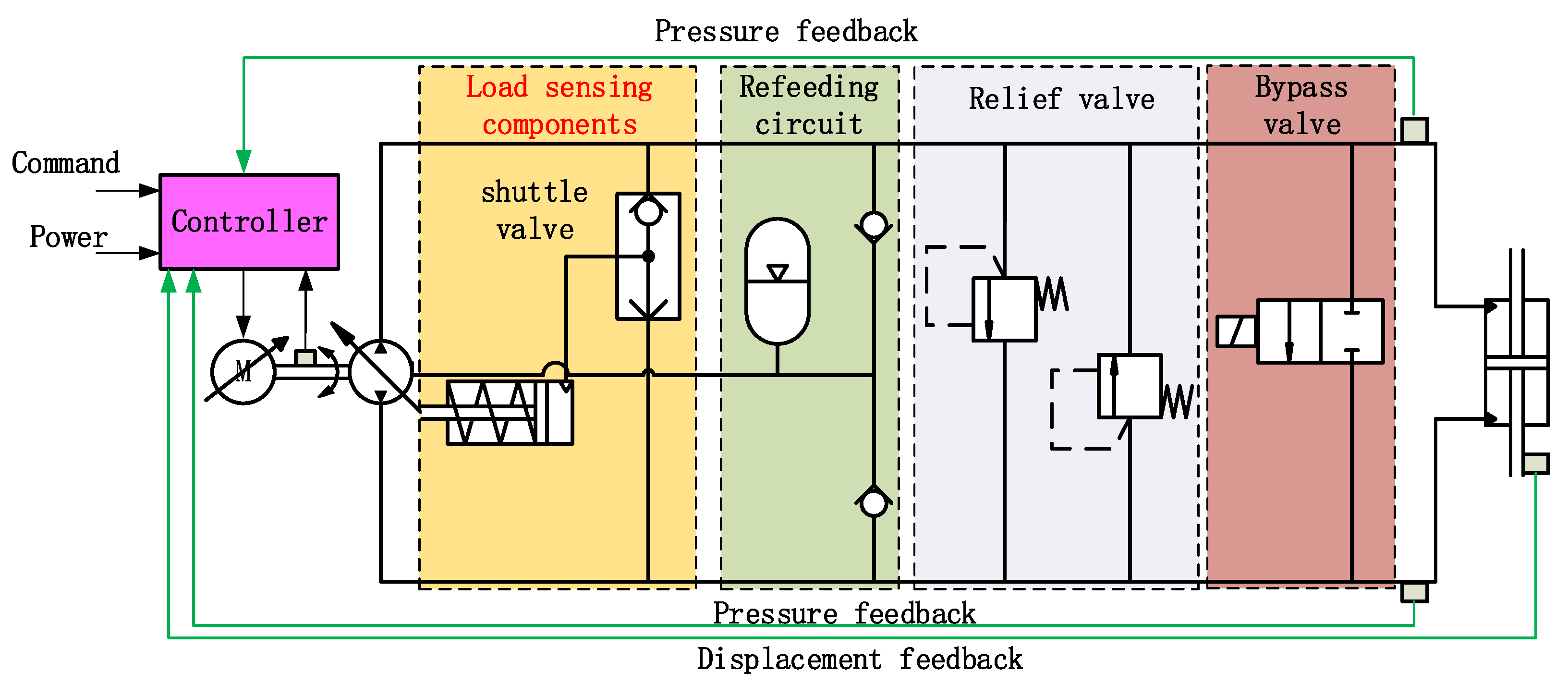
The DLS-EHA schematic is displayed in
Figure 3. The load-sensitive servo mechanism uses a shuttle valve to guide the pressure of the high-pressure chamber of the EHA to the swash plate mechanism of the variable pump. Thus, the function of passively regulating the displacement with the load is realized. Adding a damping hole between the valve port and the variable mechanism can effectively alleviate the fluctuation of system performance caused by load shock.
According to the principle of direct load sensitivity, it can be known that, when the external load is large, the pressure introduced into the pump variable mechanism increases, so the displacement of the pump decreases.
According to the analysis in
Section 2.2, it can be known that the motor current can be effectually alleviated in the stalled condition; in the non-stalled condition, the motor current can be validly subsided within a certain adjustment range. Therefore, the DLS-EHA can effectively reduce the copper loss of the motor within a certain operating range. However, because the pump displacement is passively adjusted with the load, the system stiffness is reduced, resulting in a significant reduction in system dynamic performance under heavy load conditions. The existing improvement method is to appropriately increase the spring stiffness of the variable displacement mechanism of the plunger pump, thereby which is in favor of increasing the system stiffness and reducing the gradient of displacement with load pressure, but will increase the loss of the motor at the same time. In addition, the view that the smaller the pump displacement is regulated, the less the heat is generated by the motor is still to be further verified: According to the analysis in
Section 2.2, it can be known that the conclusion that the smaller the displacement is, the less heat the motor generates is a one-sided and inaccurate conclusion. Under medium/high speed and heavy load conditions, it may be happened that within the displacement adjustment range, the motor heat generation will first fall and then rise as the pump displacement drops. Under these conditions, the use of DLS-EHA may even outweigh the benefits.
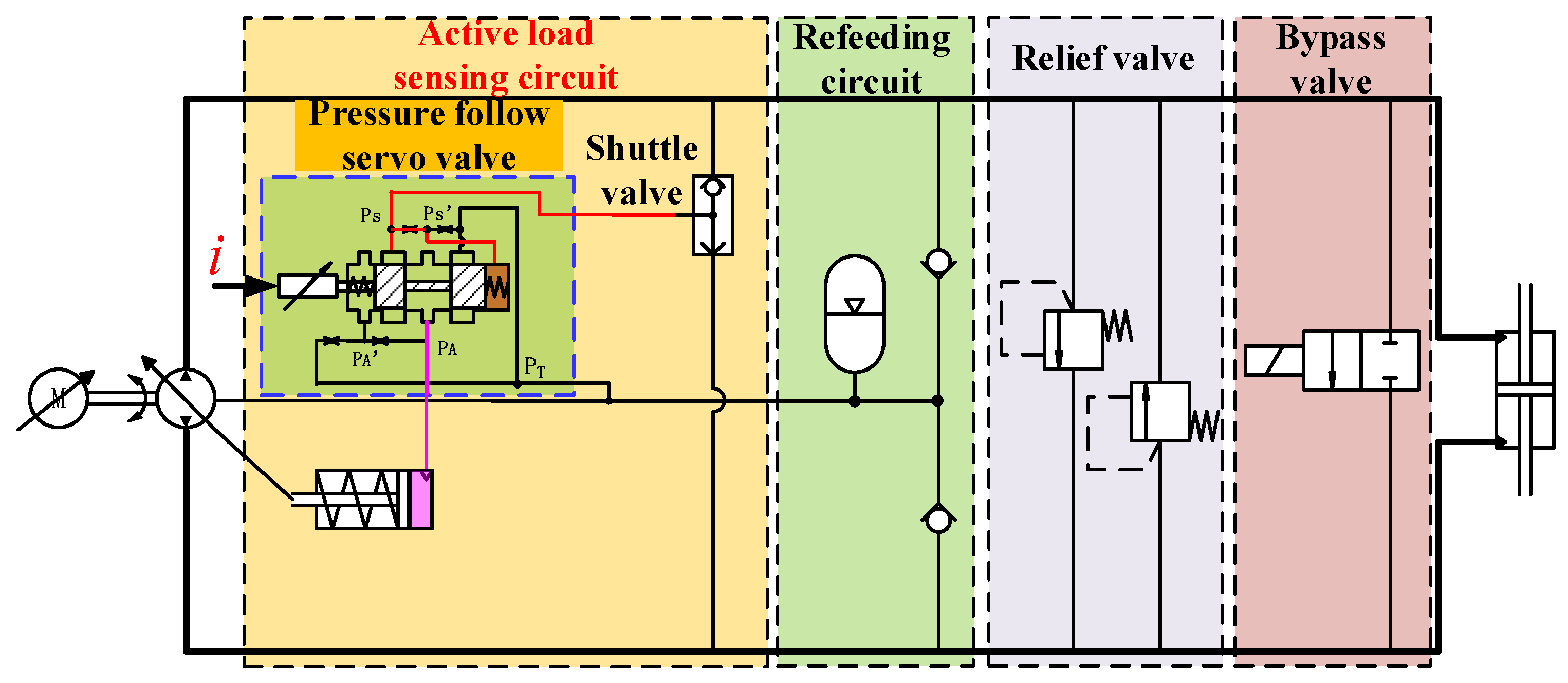
So as to deal with the direct discrepancy between dynamic performance and efficiency in DLS-EHA, a novel active load sensitive technology is proposed. The ALS-EHA is based on the DLS-EHA, and a pressure follow valve (PFV) that can actively adjust the pressure enforcing the variable pump swash plate is added. The schematic of the ALS-EHA is shown in
Figure 4.
The principle of the ALS-EHA is that the load pressure is imported to the PFV through the shuttle valve and then the valve outlet pressure can be controlled at range of 0 to the maximum load pressure by the external control signals, which is connected to the swashplate variable mechanism of the pump. It can be known that by controlling the PFV input current, the pump swashplate angle can be adjusted between the maximum and the value corresponding to the load pressure.
Since the pump displacement can be actively controlled in the ALS-EHA, by designing a desirable control law, it can effectively avoid the problem that the decrement in displacement leads to the increment in motor heating and the decrease in dynamic. Meanwhile, the system needs better tracking performance and the external load is relatively large, the motor efficiency can be sacrificed to ensure the dynamic performance. Therefore, under the trade-off, the ALS-EHA is relatively superior in performance.
Compared with the conventional EHA-VPVM, the ALS-EHA need not have a separate power source, and can realize the active adaptive control on displacement through a PFV, which has the advantages of small size, light weight, and simple structure.
2.2. Modeling Investigation
2.2.1. Motor Pump Main Loop
For a brushless DC motor, the torque dynamics balance equation is:
where
is the motor torque constant;
is the total inertia moment and damping coefficient equivalent to the motor shaft, respectively;
is the motor output torque (pump input torque), which drives the pump to rotate;
,
,
represent motor current, electromagnetic torque, and rotational speed, respectively.
Without considering leakage, the system flow equation is shown as follow:
where
is load flow of the system;
represent the piston area and speed of the cylinder, respectively;
is pump displacement. The equation of pump input torque is obtained from load pressure and displacement:
where
is load pressure of the system.
(1) In the stalling condition, combining formulas (1) and (3), the follow equation can be gotten
At this time, the motor current is proportional to the pump displacement, that is, the larger the displacement, the more heat the motor generates in the stall condition.
(2) In non-stalling mode, for purpose of simplifying the calculation, it is assumed that the angular acceleration of the motor is known. Equation (5) can be obtained by combining formulas (1) and (3).
where
is actuator displacement. Observing formula (5), the part in parentheses shows a logarithmic function relationship. It can be seen that, in a certain range under this operating condition, the motor current and the pump displacement are approximately a logarithmic function relationship, i.e., the current gradually decreases to minimum first and then increases as the displacement goes down.
The pump in EHA is equivalent to a reducer without considering pump loss, and the hydraulic reduction ratio is defined as
. Under the law of conservation of power,
, combined
with
, we get
which is the ratio of the pump displacement to the actuator area. Formula (5) can be changed as follows:
where
is the output force (load force) of the actuator. Formula (6) shows that the hydraulic reduction ratio can be controlled by adjusting pump displacement to minimize motor current.
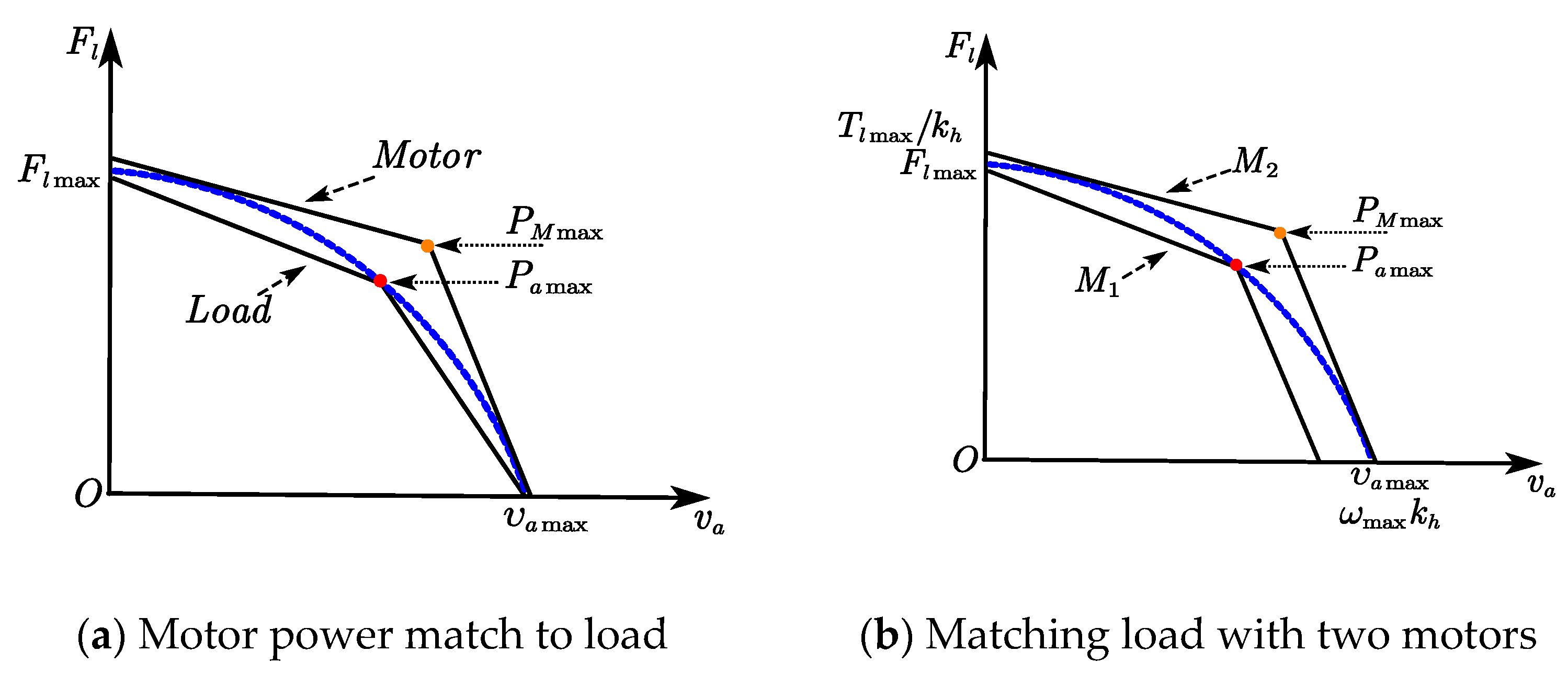
In addition, if the iron loss of the motor and various efficiency losses of the pump are comprehensively considered, the relationship between the total heat generation of the motor and the displacement of the pump is complicated, and further modeling research is needed. For two control variable ALS-EHA, motor velocity and pump displacement can be actively controlled. Therefore, by designing a reasonable control law, e.g., the fuzzy neural control method of lifting system dynamics as proposed in Ref. [
24], it is possible to effectively reduce the motor current and lower the motor heating. This is the basic idea of power matching design.
2.2.2. Load-Sensitive Loop
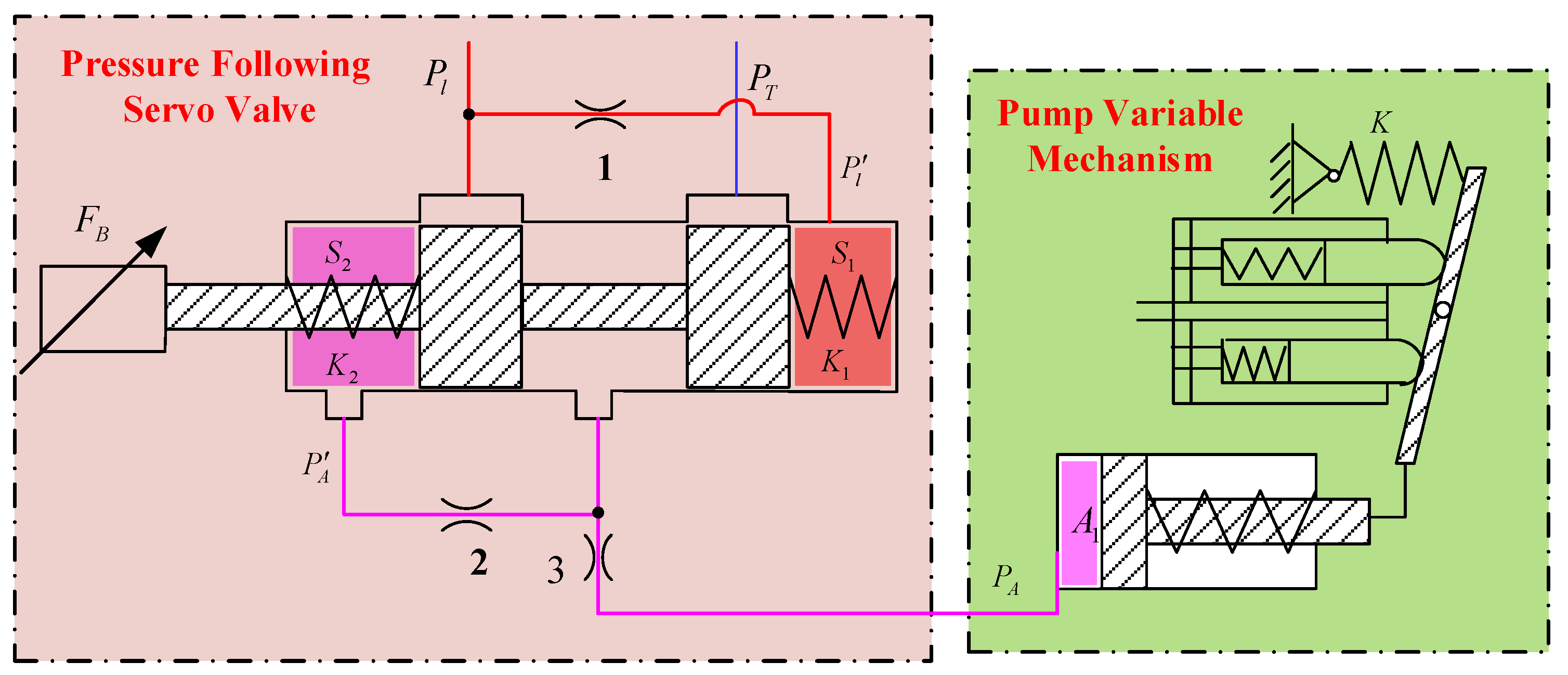
Load-sensitive loop consists of pump variable mechanism and PFV, of which output pressure and flow act on the variable hydraulic cylinder to move its piston to push the swash plate to adjust its inclination as shown in
Figure 5. The loads acting on the swash plate mainly include the spring pre-tightening force, the hydraulic load, and the inertia force.
1. The force balance equation of the variable piston is as follows:
where
mvt indicates the total mass of the piston and load,
Bvc represents viscous damping coefficient,
K is load spring stiffness,
is spring preload,
Fv is variable piston force acting on the swash plate,
is output pressure of valve,
,
denote the velocity and the area of the piston, respectively.
2. Moment balance equation of swash plate:
where
Lf denotes the arm of the variable piston force acting on swash plate,
Js denotes moment of inertia of swash plate,
Bs denotes viscous damping coefficient,
MT,
M0 denote the torque generated by the hydraulic load and spring preload acting on the swash plate.
γ denotes swash plate inclination.
Remark 1. The average value of the resultant moment of the force acting on the swash plate at high speed is basically 0, so it can be assumedduring analysis.
So, formula (8) can be simplified as:
The relationship between the inclination angle of the variable pump swash plate and the displacement of the variable piston is as follows:
Since
is generally small in practice, assuming that it can be approximated as
The following formula can be derived from Equations (8) to (12)
where
,
are the total equivalent inertia and damping of load sensitive loop, respectively.
According to the relationship between the tilt angle of the swash plate and the displacement, the displacement can be expressed as follows
where
,
represent the swash plate inclination maximum and displacement maximum, respectively;
is pump displacement gain. Combining formulas (11) to (13) gives:
where
is equal to
. Formula (14) shows that the load sensitive loop is a spring mass damping system. Since the inertia of load sensitive loop is very small, it can be simplified as elastic link to analyze the load sensitive characteristic.
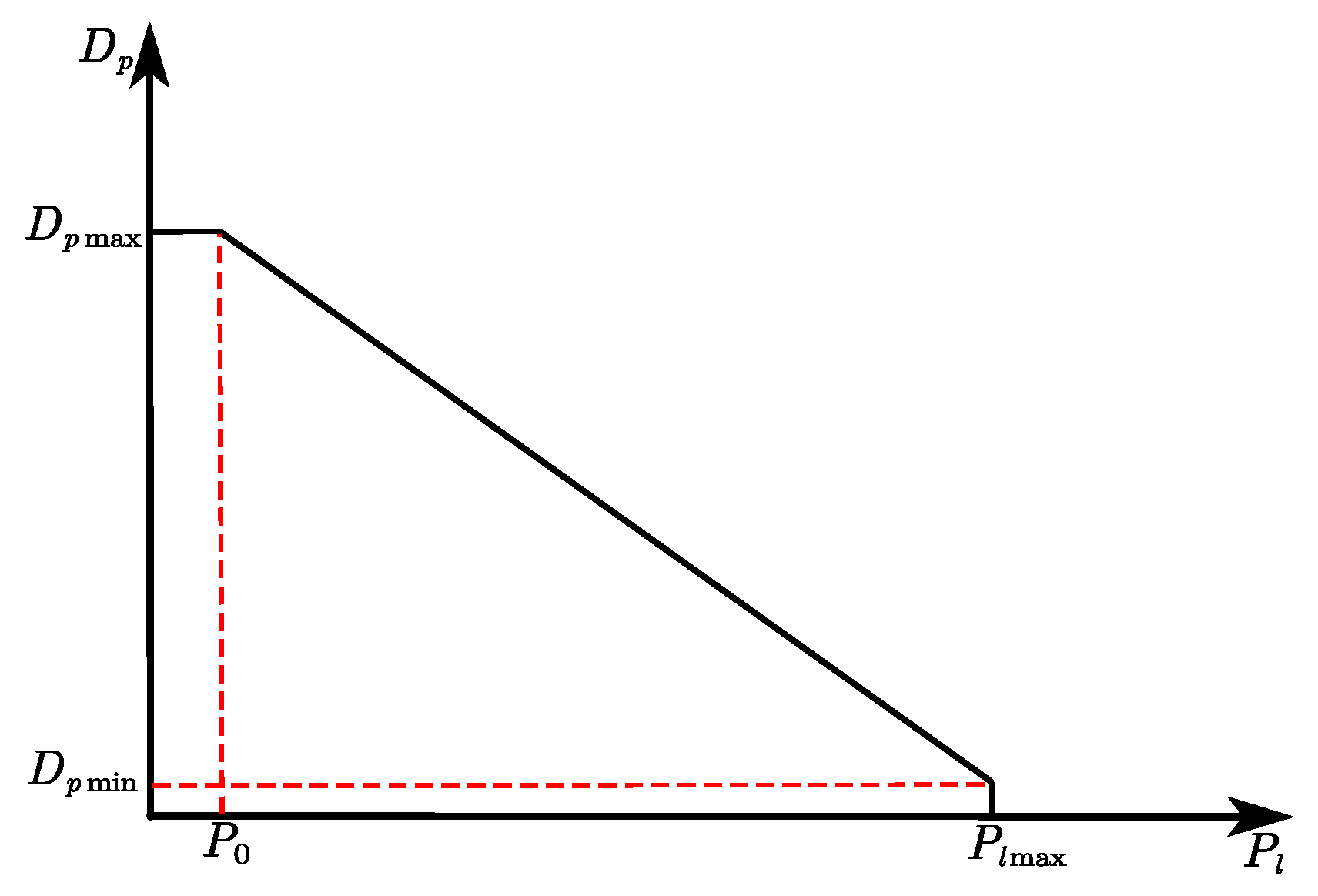
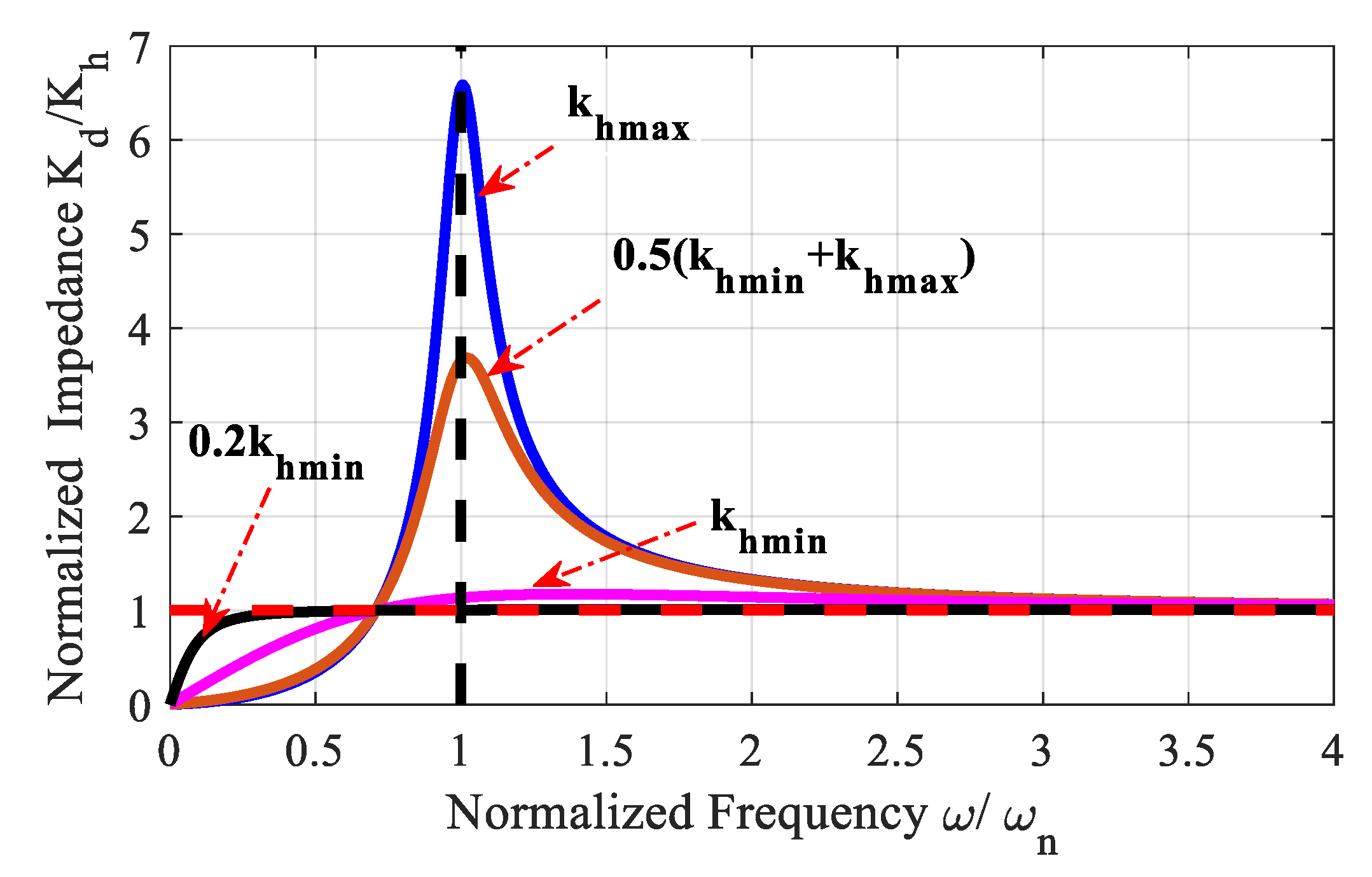
The DLS characteristics derived from formula (14) after simplification are shown in the
Figure 6 below [
19].
where
,
represent the maximum and minimum displacement of pump,
,
are the maximum load pressure and the swash plate pre-tightening pressure.
According to the [
21], the formula for calculating the stiffness of the back pressure spring of the variable mechanism is shown below:
where
. By combining formulas (15) and (16), the following equation can be derived.
As shown in Equation (16), the stiffness of the compressed spring of the variable mechanism for DLS-EHA must be selected according to the maximum load pressure, therefore, K should be selected large enough to ensure the stability of the system. According to
Figure 6 and Equation (17), it can be concluded that the gradient of displacement to load pressure is a constant and cannot be adjusted which cannot guarantee that under all load conditions, the system performance such as efficiency and dynamics are optimal. The load-sensitive circuit has passive attribute.
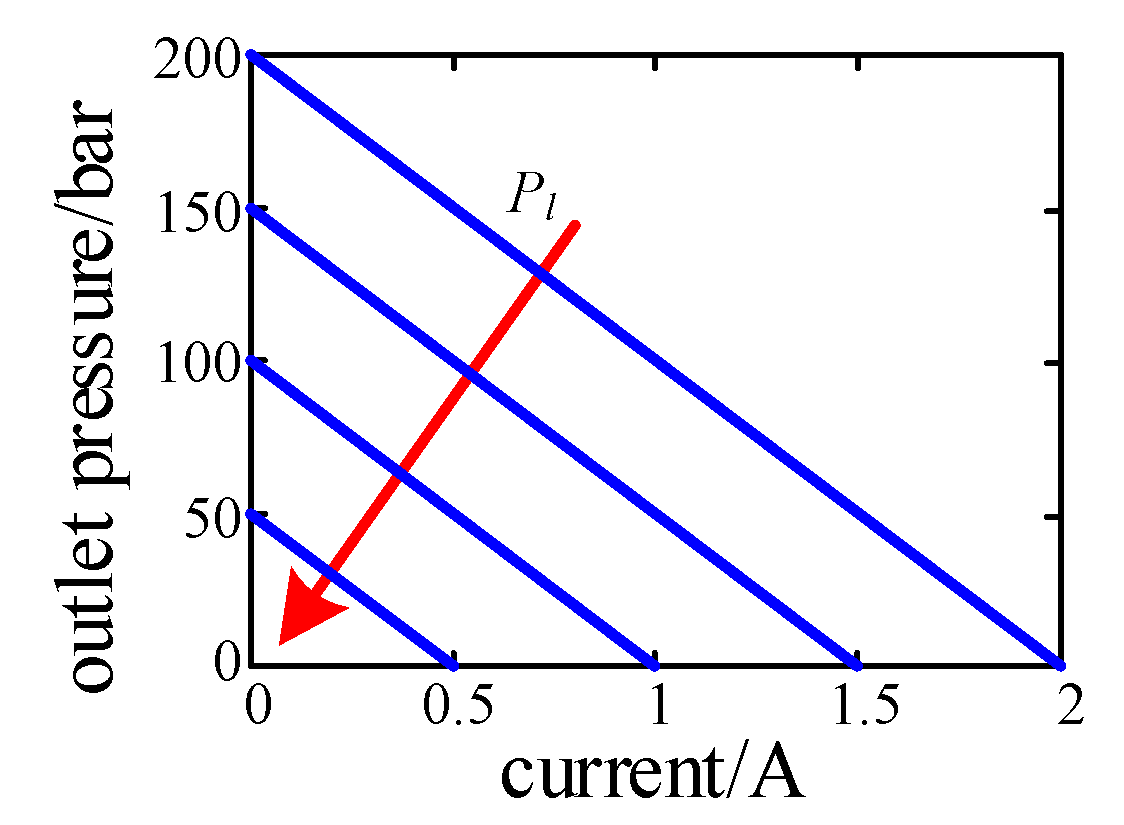
PFV has the same principle as the proportional pressure reducing valve, of which output pressure can be linearly controlled by actively controlling valve input current. The PFV characteristics are shown below
Figure 7. So, it can be modeled as follows
where
,
are pressure gain and input current of the valve, respectively.
Load sensitivity is expressed below:
Let be equal to .
Equation (14) can be written as:
Remark 2. When the input pressure Pl is constant, the output pressure is a linear function of the input current. As the input current grows, the output pressure declines. Pl affects the gradient value of the output.
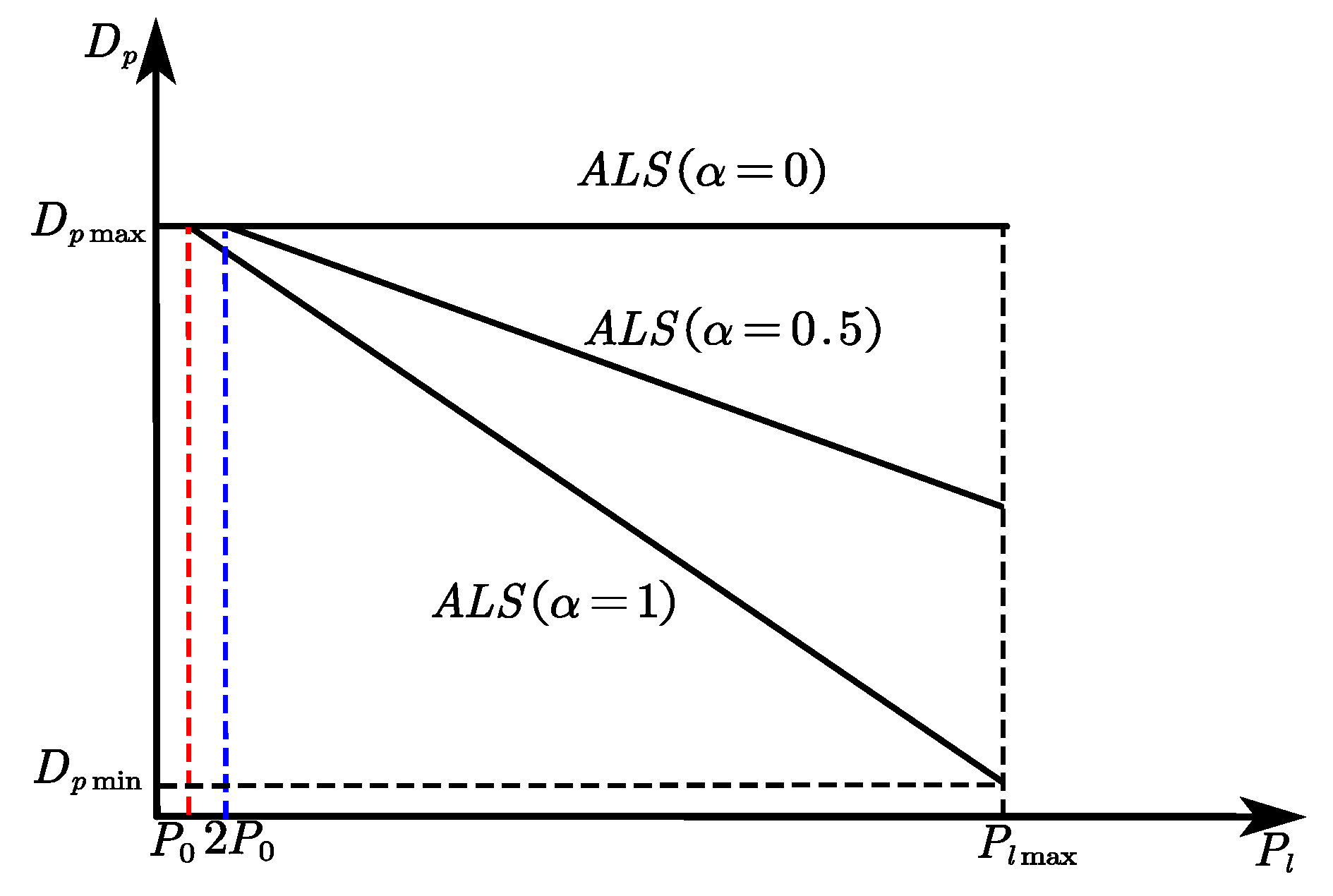
Based on the ALS principle combined with the characteristics of the DLS variables, we can draw the relationship of the characteristics of the ALS variables as shown follows:
As shown in
Figure 8, a PFV capable of active control is added to the original DLS loop. The stiffness of the spring is still selected according to the DLS. It can be concluded that the gradient of displacement to load pressure varies with the load sensitive, that is, it can be actively adjusted. The greater the load sensitivity is, the greater the gradient is. We can also see that the EHA-FPVM and the DLS-EHA are two boundaries of active load sensitivity. The former has a load sensitivity of 0 and the latter is 1.
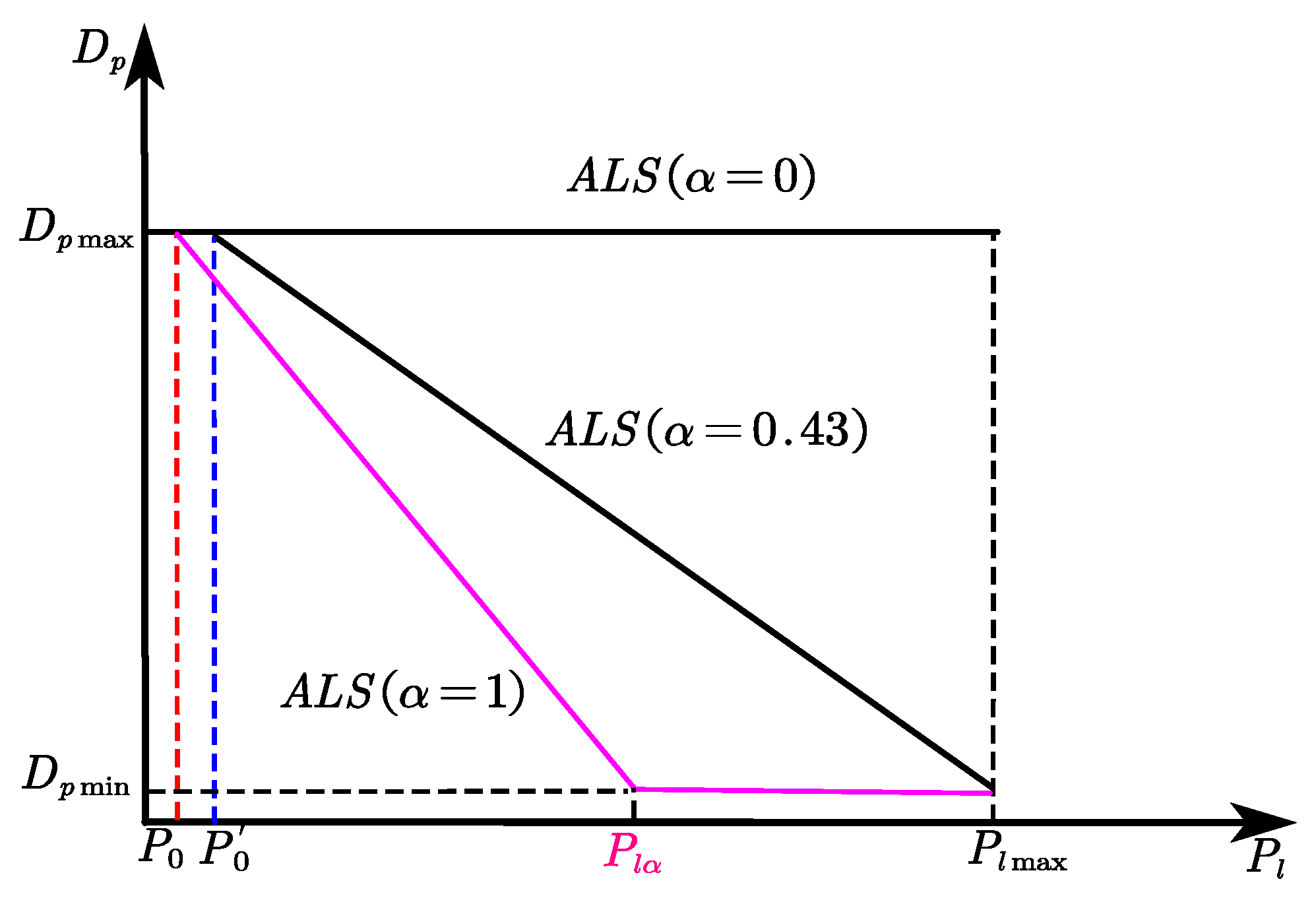
In the ALS loop, we choose the stiffness of the back pressure spring according to the following formula (22).
It can be known from the formula 22 that the spring stiffness for ALS-EHA can be less than that for DLS-EHA which is conducive to increasing the adjustment range and is beneficial to the improvement of system performance and the flexibility of control. After the compressed spring stiffness is corrected, the characteristic curve for ALS-EHA is shown in
Figure 9 below.
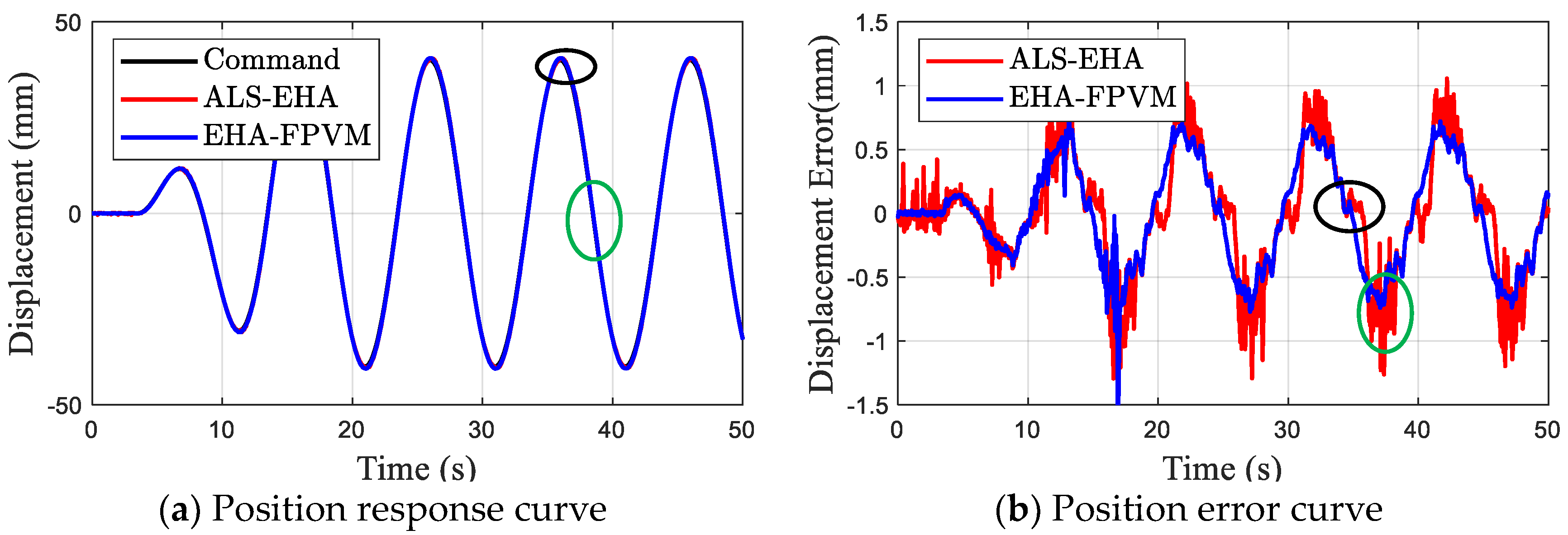
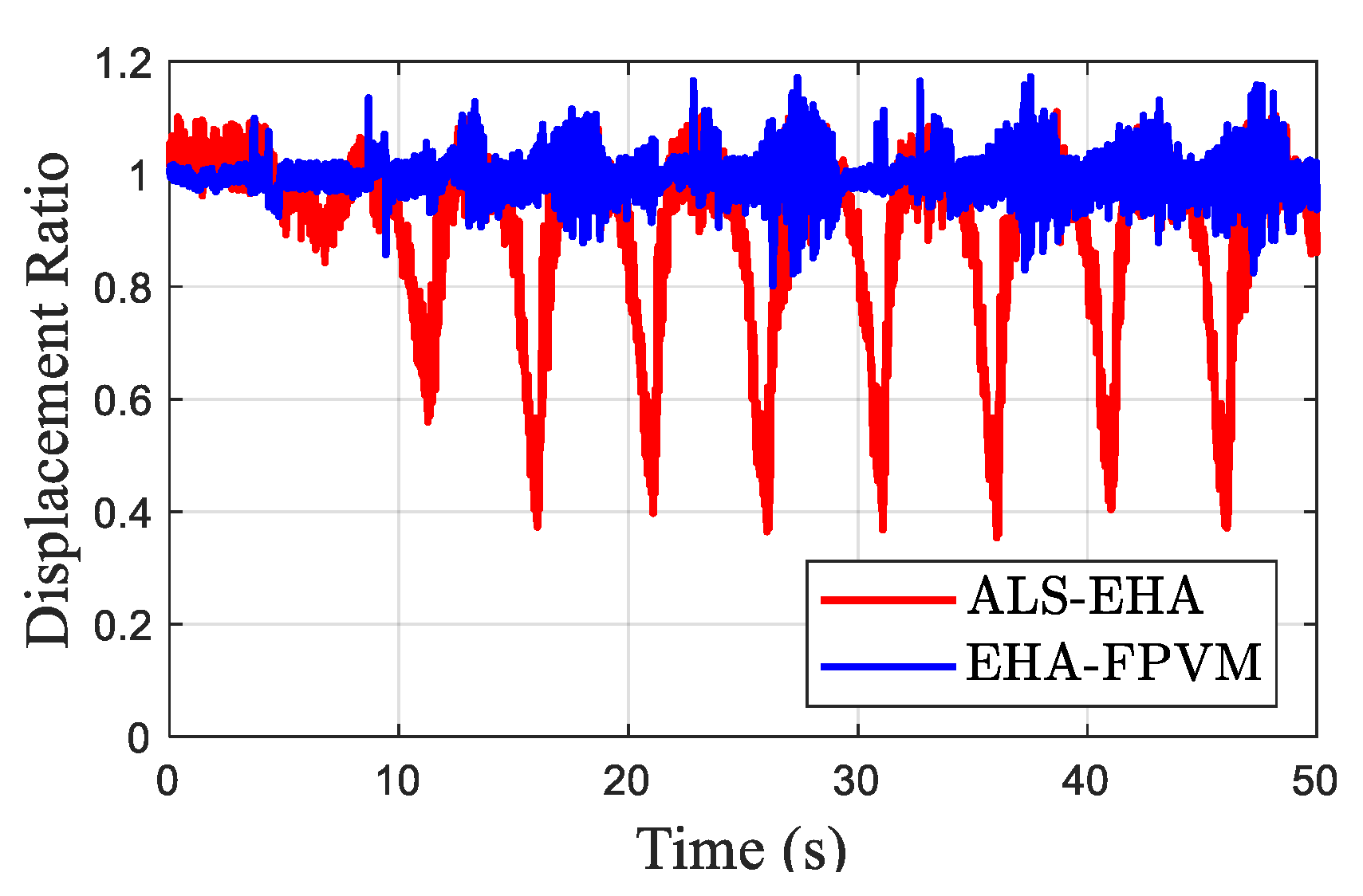
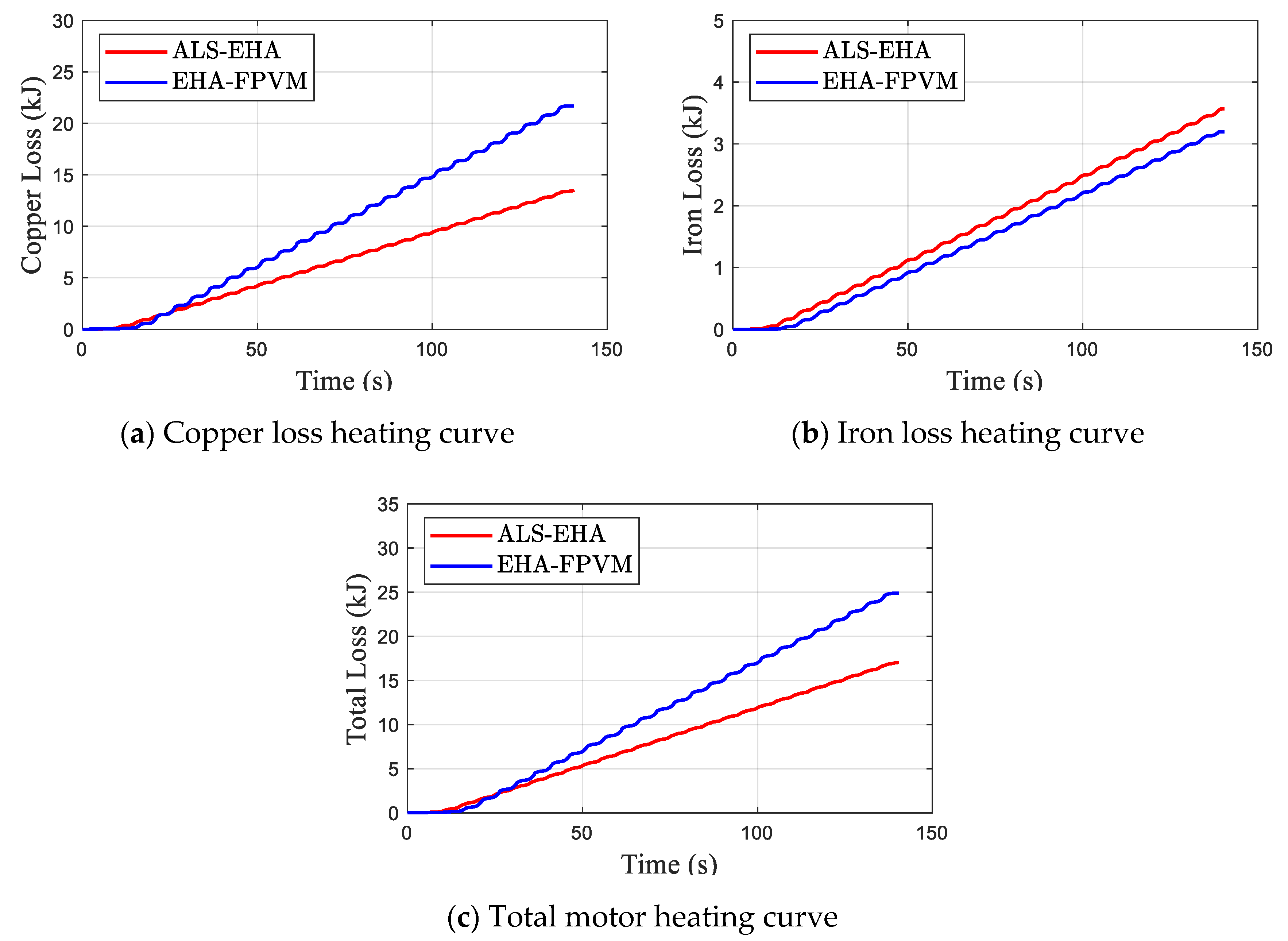
6. Conclusions
EHA fever is a headache problem, especially as its main heat source is a motor of which heating is an urgent need to solve. So, we developed a novel configuration of ALS-EHA based on this case, which inherits the passivity of the DLS-EHA and the advantage of less system heating. The load sensitive characteristics is analyzed for ALS-EHA to clear up the obstacle of DLS-EHA. In order to ensure the stability and dynamics of DLS-EHA, the stiffness of the back pressure spring is selected to be very large (according to the maximum load pressure), and the displacement adjustment range of pump is smaller with only linear regulation. However, ALS-EHA decreases the need for sufficiently large stiffness of the variable mechanism back pressure spring, and thereby increases the load-sensitive adjustment range, which is beneficial to the improvement of system performance, such as dynamics and efficiency with nonlinear adjustment. It can be inferred from the experimental results that the tracking error must also be the largest at the maximum DLS-EHA velocity point. The ALS-EHA mathematical model is established, and the correlation is obtained between the motor current and the hydraulic reduction ratio. For low-speed and high-load conditions, the relationship is approximately linear, that is, the greater the hydraulic reduction ratio is, the larger the displacement, the higher the motor current, and the greater the motor copper loss and motor heating. The experiment verifies this conclusion. Since the active load sensitive loop can reduce the pump displacement under large load conditions, the investigated ALS-EHA generates less calories than EHA-FPVM so that it perfectly achieves motor power matching for EHA design and operation, and its displacement tracking error is smaller at the speed of near zero due to its high impedance, but the maximum tracking error is larger on account of pump displacement variation. According to the above experimental results and the analysis, it is verified that the ALS-EHA is correct in principle, improving upon the performance of EHA-FPVM and DLS-EHA.