Alignment Method of an Axis Based on Camera Calibration in a Rotating Optical Measurement System
Abstract
1. Introduction
2. Principle
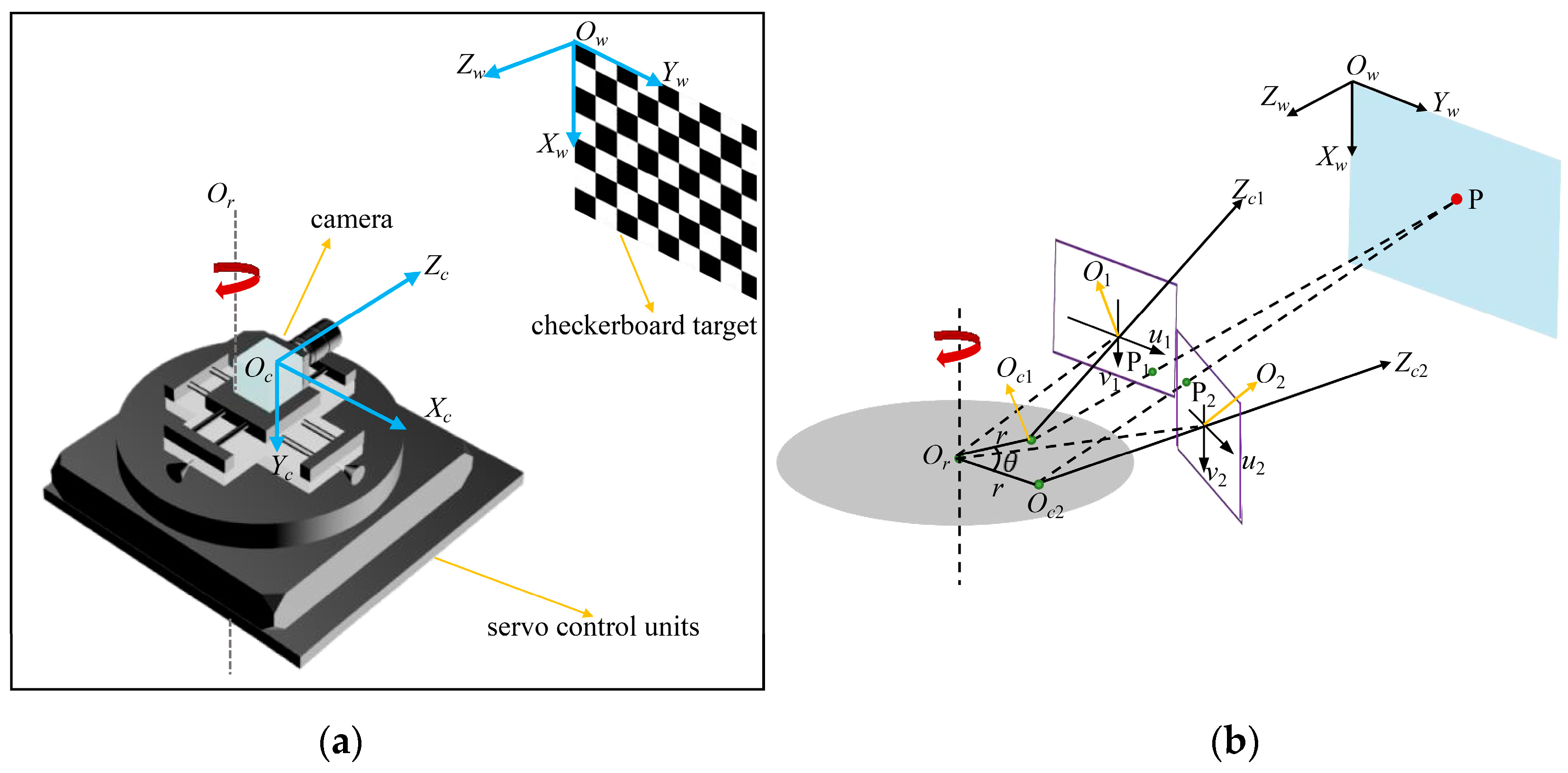
2.1. The Composition of the Rotating Optical Measurement System
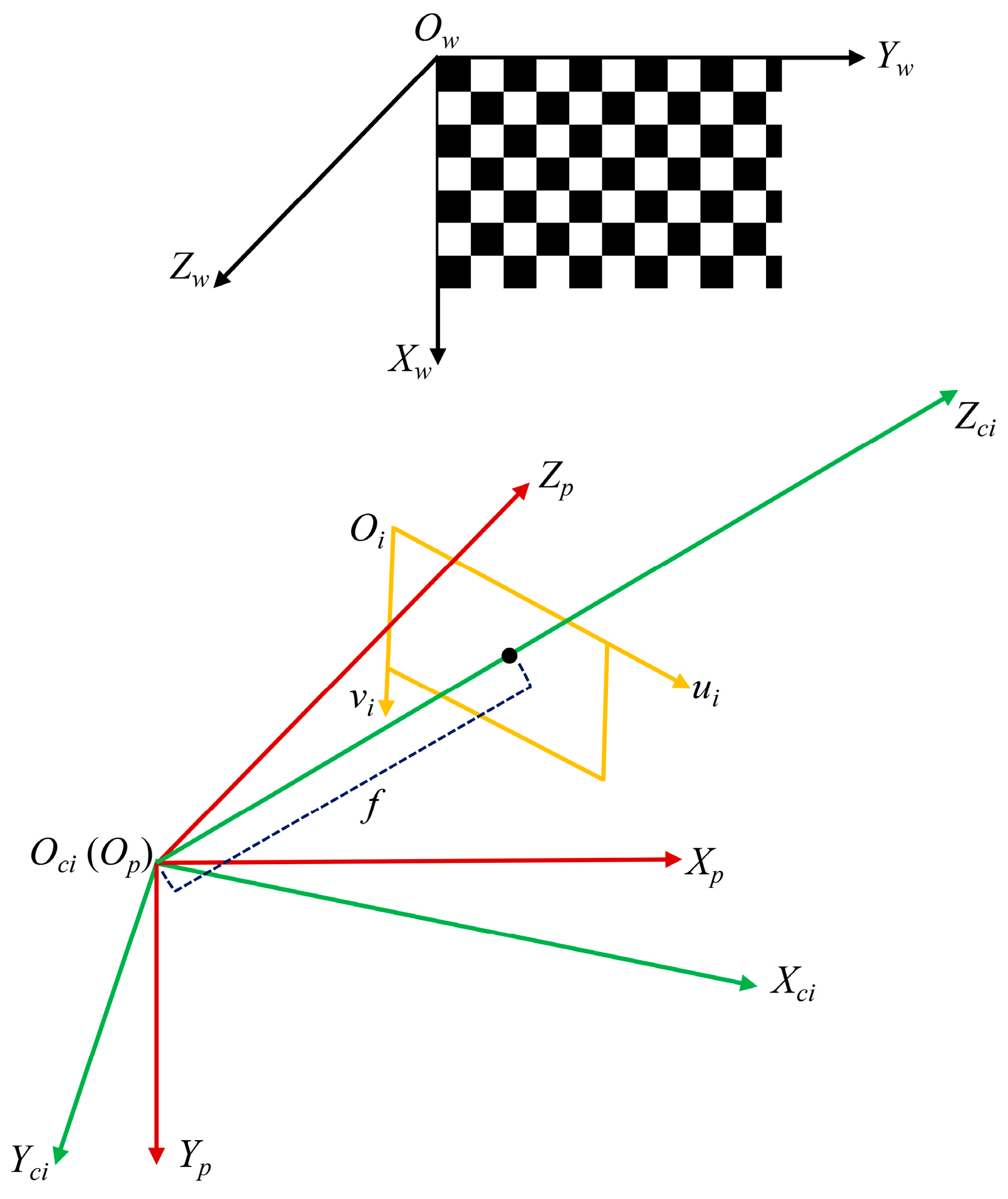
2.2. Imaging Model
- World Coordinate System Ow-XwYwZw is a right-handed (Xw-Yw-Zw), orthogonal, three-dimensional coordinate system, whose original point Ow is established on the upper left corner of the fixed checkerboard plane; that is, Zw = 0 for points on the fixed checkerboard plane. The world coordinate system is selected as reference coordinate system during calibration.
- Image Coordinate System Oi-uivi is an orthogonal coordinate system fixed in the image plane of the camera, where the ui and vi axes are parallel to the upper and side edges of the sensor array, respectively, and the origin Oi is located at the upper left corner of the array.
- Camera Coordinate System Oci-XciYciZci is a right-handed (Xci-Yci-Zci), orthogonal coordinate system. The origin Oci is located at the camera’s optical center, and the Zci axis is perpendicular to the image plane and coincides with the optical axis of the camera. The Xci and Yci axes are parallel to the ui and vi axes of the Oi-uivi, respectively. The plane where Zci = f is the image plane, where f is the principal distance between the optical center and the image plane.
- Auxiliary Coordinate System Op-XpYpZp is a right-handed (Xp-Yp-Zp), orthogonal coordinate system. Its origin Op is located at the optical center. The plane XpOpZp is a virtual plane, whose axis of Xp and Yp are parallel to that of Yw and Xw in the same direction, respectively, and the axis of Zp is parallel to that of Zw in the opposite direction.
2.3. Steps to Determine the Rotation Center of the Rotating Optical Measurement System
2.3.1. Calculate the Optical Center of the Camera
2.3.2. Method for Coincidence of the Optical Center and the Rotation Center
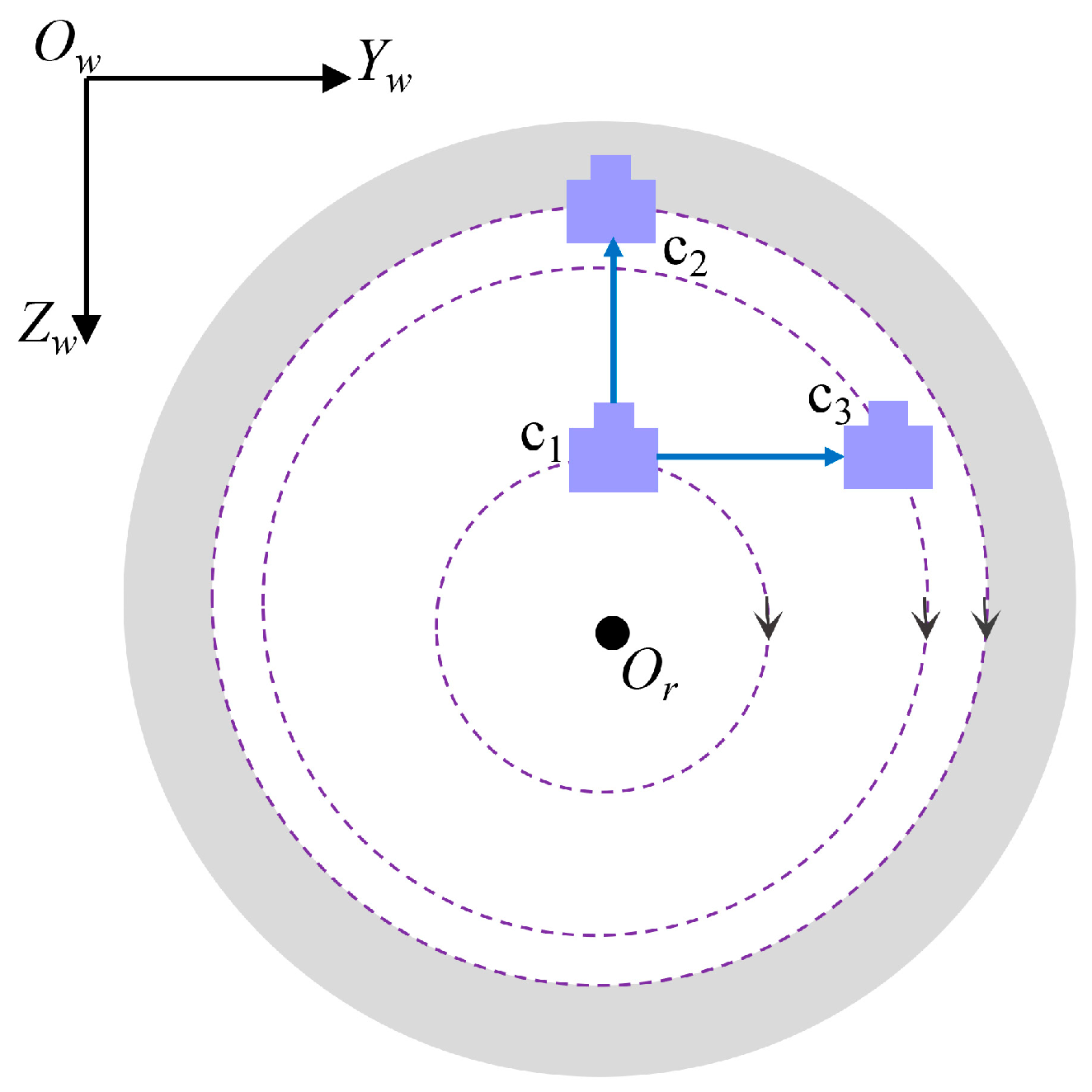
3. Computer Simulation
4. Experiment
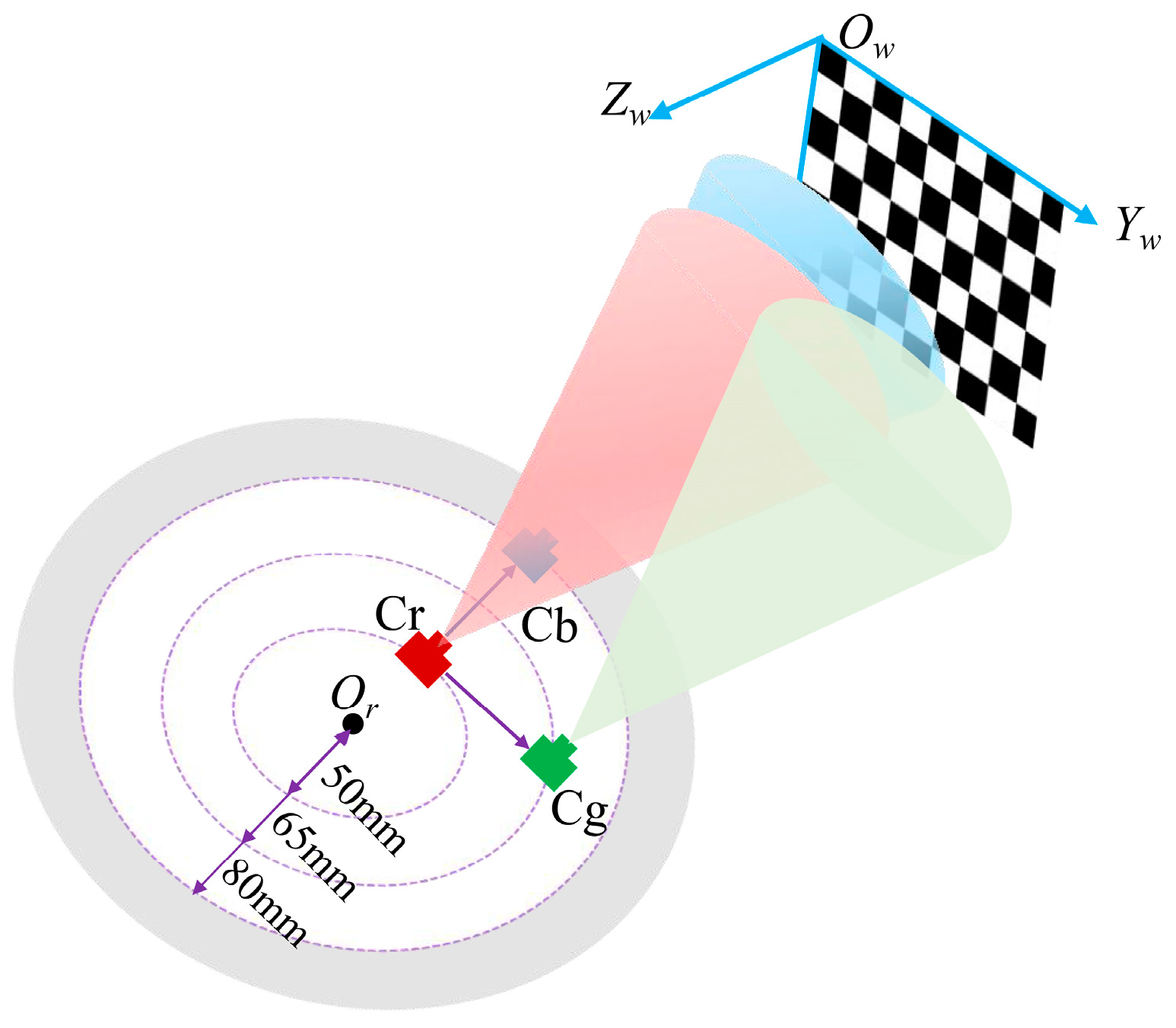
4.1. Experimental Setting
4.2. Determination of the Rotation Center
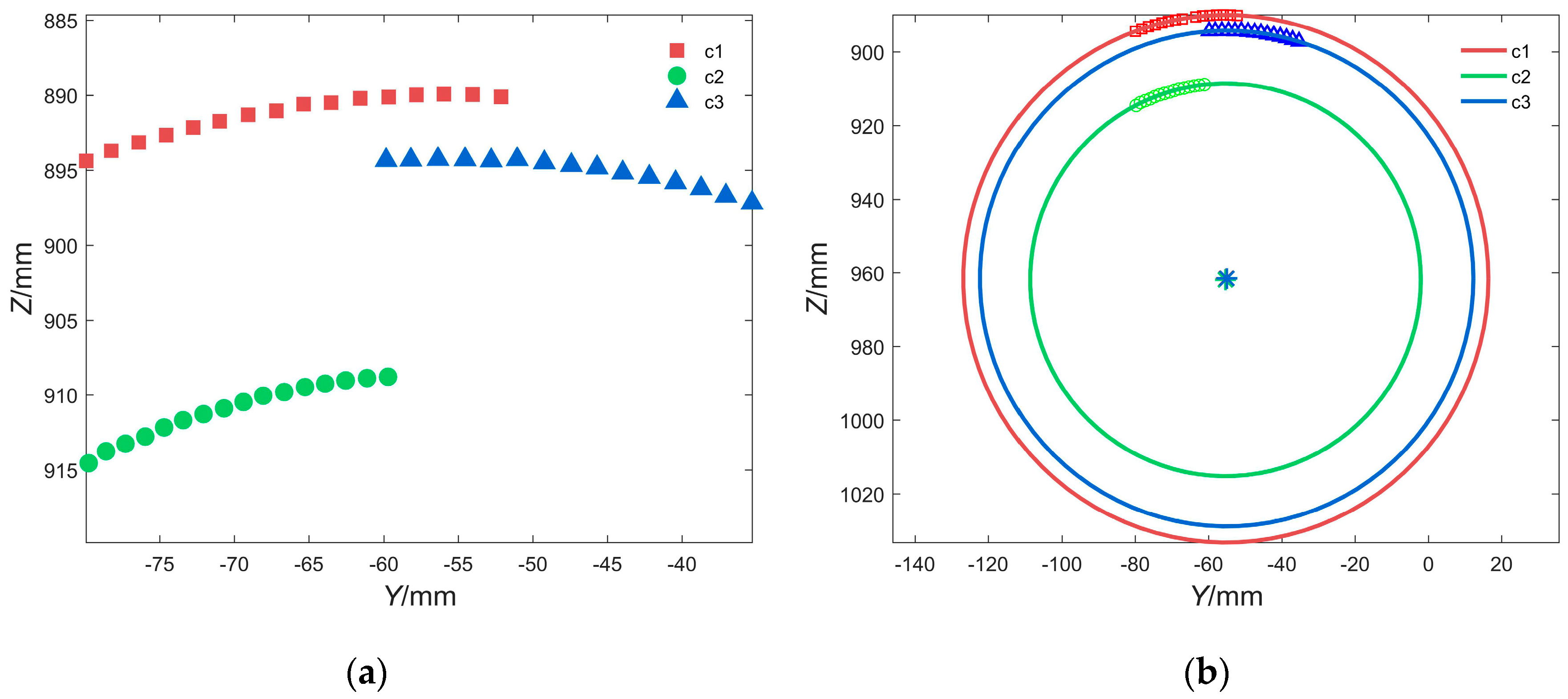
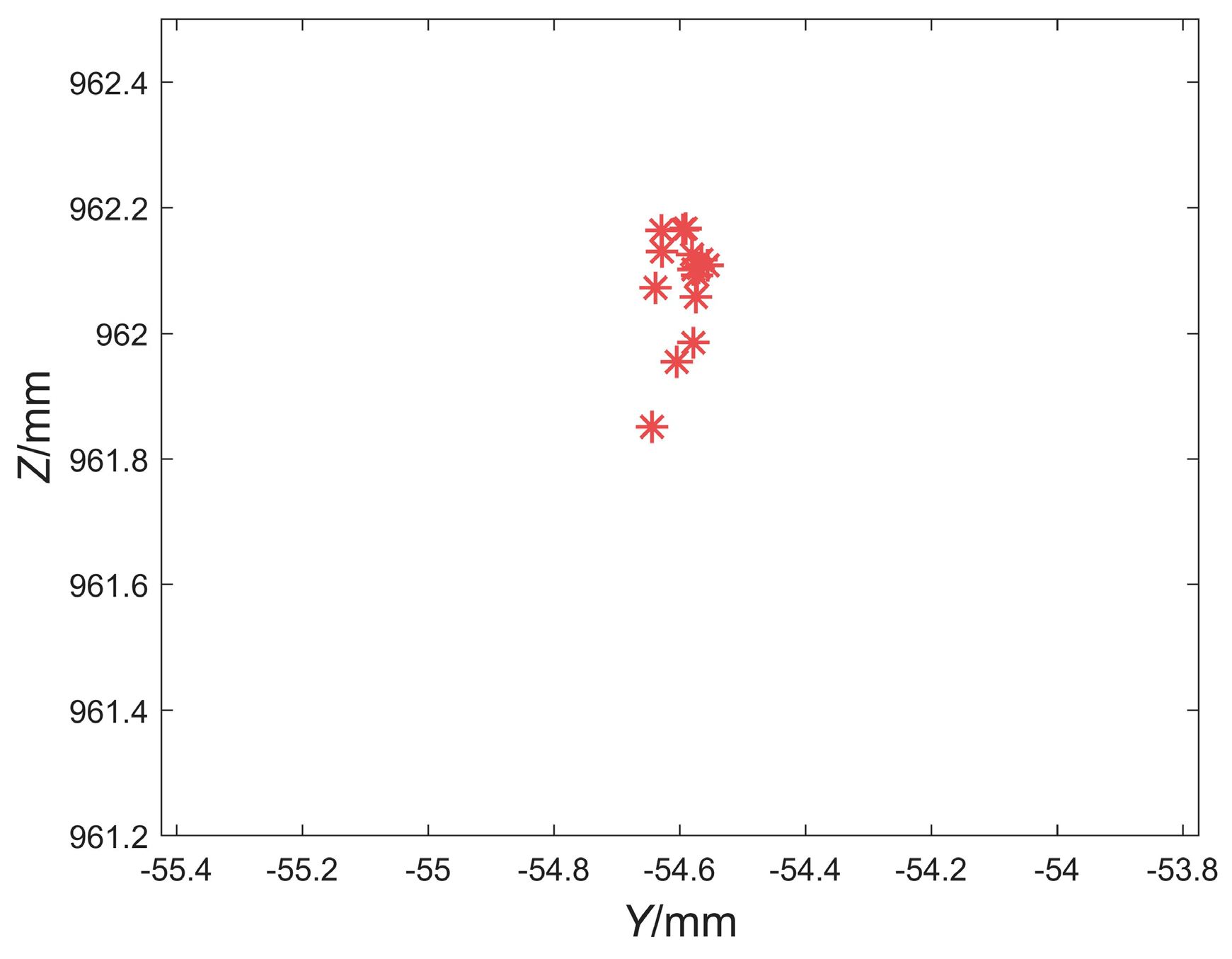
4.3. Verification
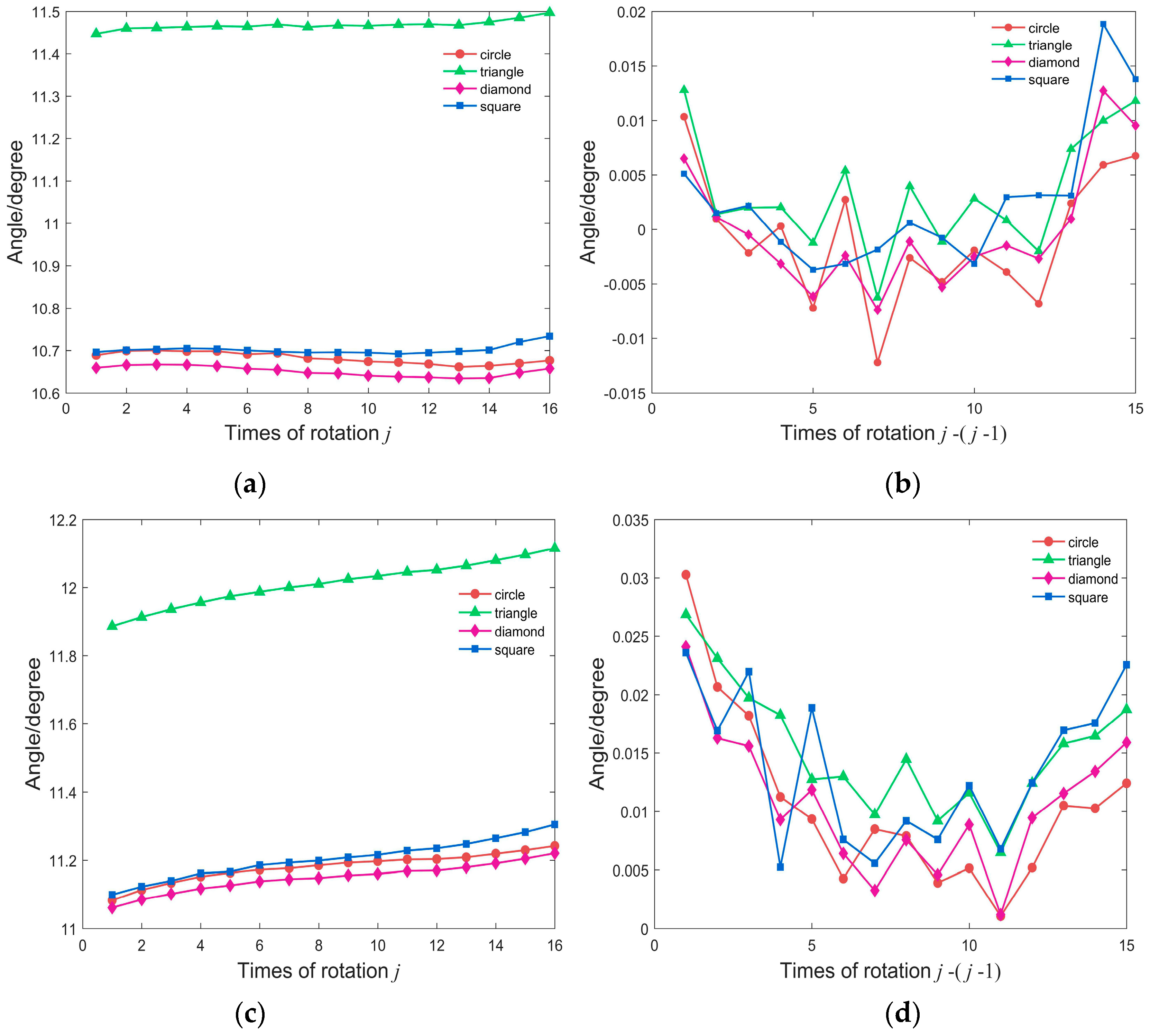
4.3.1. Calculating the Angle Formed by the Two Space Points M1, M2 and the Optical Center
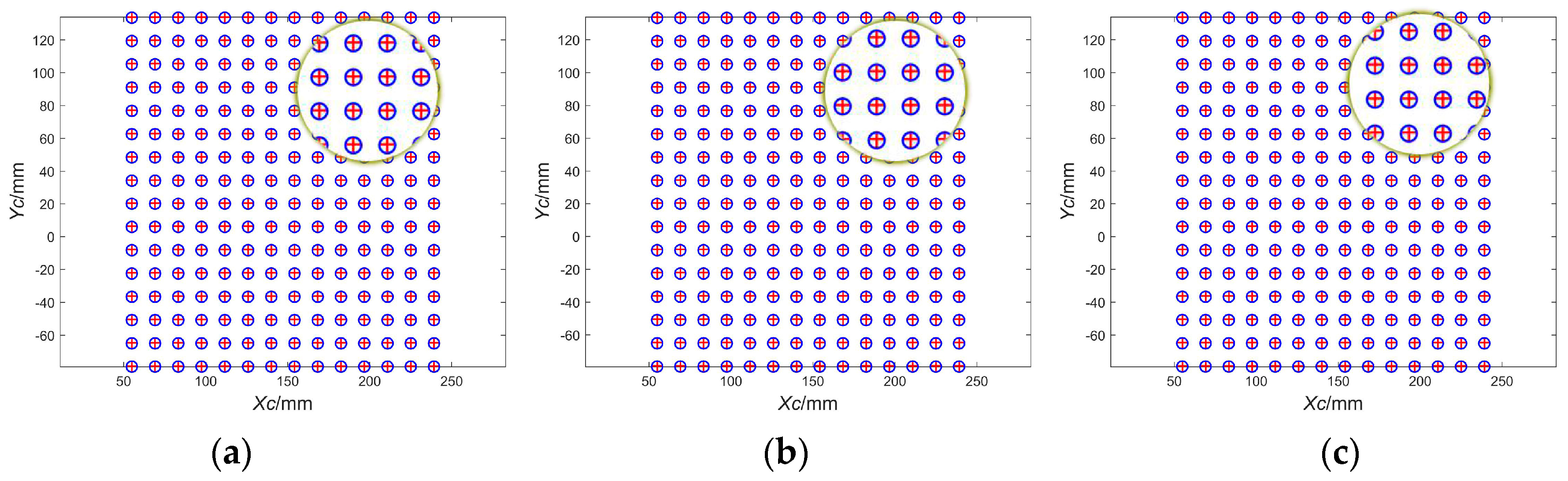
4.3.2. Camera Coordinates Registration of the Same Spatial Points Before and After Camera Rotation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging. Photogramm. Eng. Remote Sens. 2015, 81, 273–274. [Google Scholar]
- Sun, T.; Xing, F.; You, Z. Optical system error analysis and calibration method of high-accuracy star trackers. Sensors (Basel) 2013, 13, 4598–4623. [Google Scholar] [CrossRef] [PubMed]
- Luhmann, T. Close range photogrammetry for industrial applications. ISPRS J. Photogramm. Remote Sens. 2010, 65, 558–569. [Google Scholar] [CrossRef]
- Robert, S.; Holger, B.; Armin, K.; Richard, K. Measurement of three-dimensional deformation vectors with digital holography and stereo photogrammetry. Opt. Lett. 2012, 37, 1943–1945. [Google Scholar]
- Li, J.; Liu, Z. Efficient camera self-calibration method for remote sensing photogrammetry. Opt. Express 2018, 26, 14213–14231. [Google Scholar] [CrossRef]
- Zhang, S. Three-dimensional range data compression using computer graphics rendering pipeline. Appl. Opt. 2012, 51, 4058–4064. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Ma, L.; Shi, Y. Three-dimensional imaging and display of real-existing scene using fringe. In Proceedings of the Volume 8769, International Conference on Optics in Precision Engineering and Nanotechnology (icOPEN2013), Singapore, 22 June 2013; Quan, C., Qian, K., Asundi, A., Eds.; p. 87691I1-9. [Google Scholar]
- Sun, P.; Lu, N.; Dong, M. Modelling and calibration of depth-dependent distortion for large depth visual measurement cameras. Opt. Express 2017, 25, 9834–9847. [Google Scholar] [CrossRef]
- Xiao, Y.; Su, X.; Chen, W.; Liu, Y. Three-dimensional shape measurement of aspheric mirrors with fringe reflection photogrammetry. Appl. Opt. 2012, 51, 457–464. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, Z.; Ke, T.; Tang, M.; Xu, X. Scanning Photogrammetry for Measuring Large Targets in Close Range. Remote Sens. 2015, 7, 10042–10077. [Google Scholar] [CrossRef]
- Tomasi, C.; Zhang, J. How to rotate a camera. In Proceedings of the 10th International Conference on Image Analysis and Processing, Venice, Italy, 27–29 September 1999; pp. 606–611. [Google Scholar]
- Gledhill, D.; Tian, G.; Taylor, D.; Clarke, D. Panoramic imaging—A review. Comput. Graph. 2003, 27, 435–445. [Google Scholar] [CrossRef]
- Luhmann, T. A historical review on panorama photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 34, 8. [Google Scholar]
- Kukko, A. A new method for perspective centre alignment for spherical panoramic imaging. Photogramm. J. Finl. 2004, 19, 37–46. [Google Scholar]
- Kauhanen, H.; Rönnholm, P.; Lehtola, V.V. Motorized panoramic camera mount-calibration and image capture. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 89–96. [Google Scholar] [CrossRef]
- Huang, Y. 3-D measuring systems based on theodolite-CCD cameras. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 1993, 29, 541. [Google Scholar]
- Huang, Y. Calibration of the Wild P32 camera using the camera-on-theodolite method. Photogrammetric Rec. 1998, 16, 97–104. [Google Scholar] [CrossRef]
- Andreas, W. A new approach for geo-monitoring using modern total stations and RGB + D images. Measurement 2016, 82, 64–74. [Google Scholar]
- Zhang, Z.; Zheng, S.; Zhan, Z. Digital terrestrial photogrammetry with photo total station. Int. Arch. Photogramm. Remote Sens. Istanb. Turk. 2004, 232–236. [Google Scholar]
- Zhang, Z.; Zhan, Z.; Zheng, S. Photo total station systemthe integration of digital photogrammetry and total station. Bull. Surv. Mapp. 2005, 11, 1–5. [Google Scholar]
- Zhang, X.; Zhu, Z.; Yuan, Y.; Li, L.; Sun, X.; Yu, Q.; Ou, J. A universal and flexible theodolite-camera system for making accurate measurements over large volumes. Opt. Lasers Eng. 2012, 50, 1611–1620. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, Q.; Asundi, A. Flexible camera calibration using not-measured imperfect target. Appl. Opt. 2013, 52, 6278–6286. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, Q.; Asundi, A. Camera calibration with active phase target: Improvement on feature detection and optimization. Opt. Lett. 2013, 38, 1446–1448. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, Y.; Liu, L.; Chen, X. Defocused camera calibration with a conventional periodic target based on Fourier transform. Opt. Lett. 2019, 44, 3254–3257. [Google Scholar] [CrossRef] [PubMed]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Gao, X.; Hou, X.; Tang, J.; Cheng, H. Complete solution classification for the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 930–943. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Gander, W.; Golub, G.H.; Strebel, R. Least-squares fitting of circles and ellipses. BIT 1994, 34, 558–578. [Google Scholar] [CrossRef]

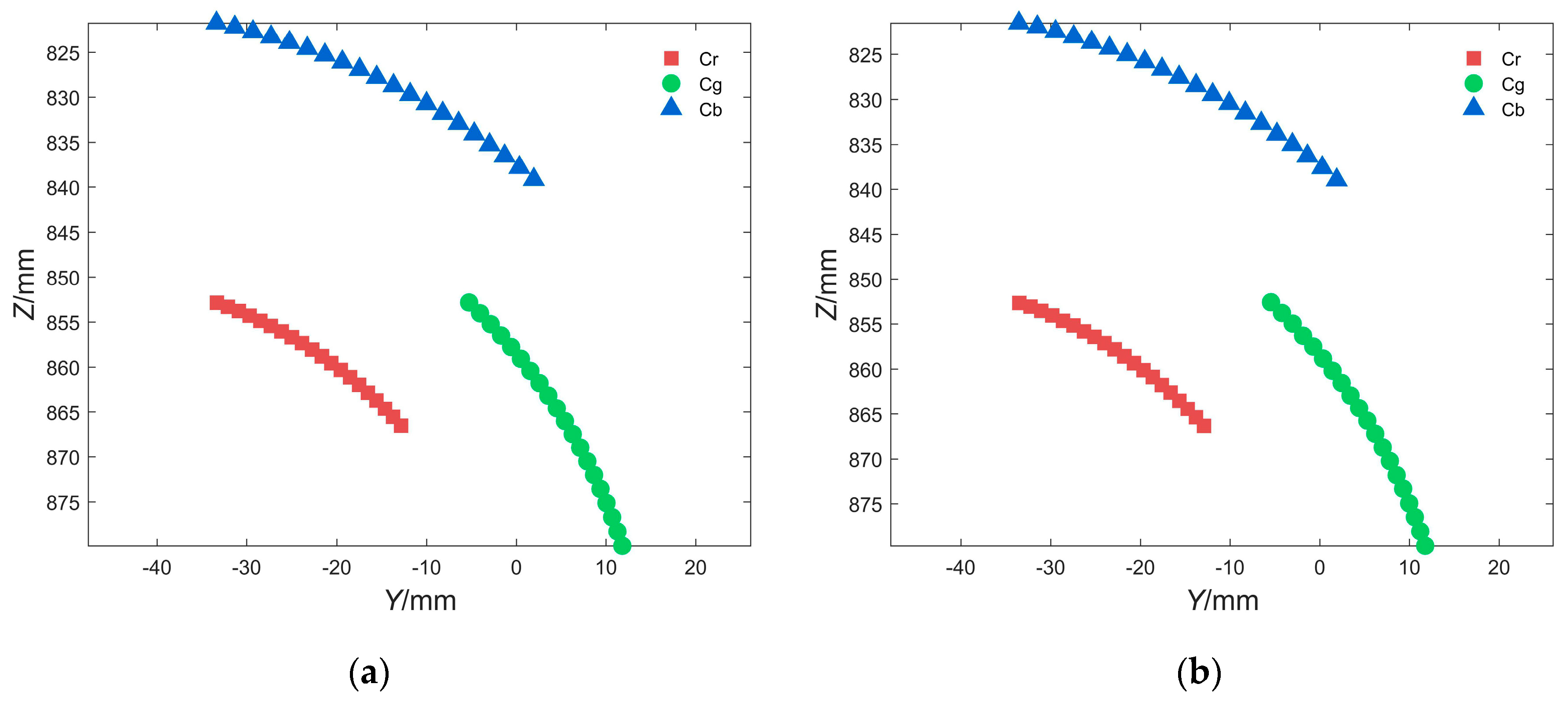
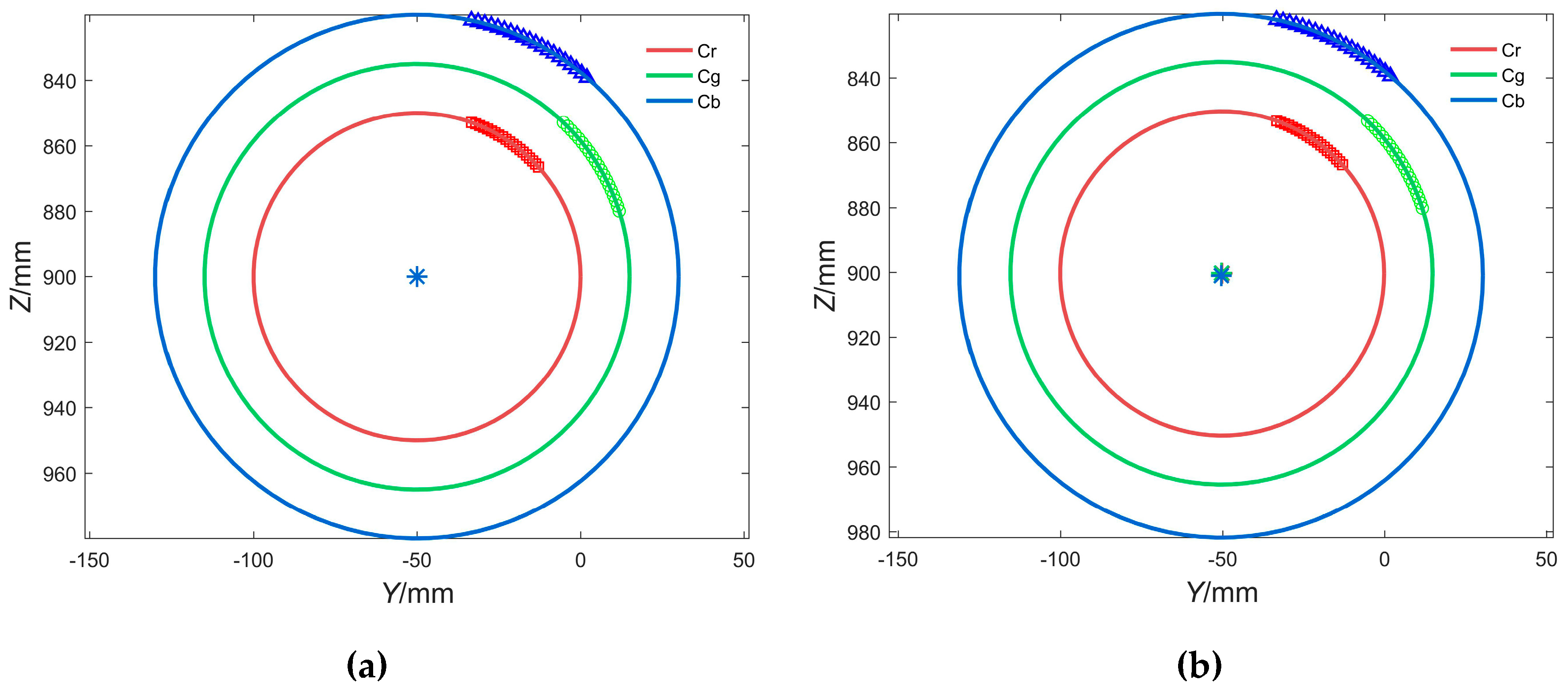

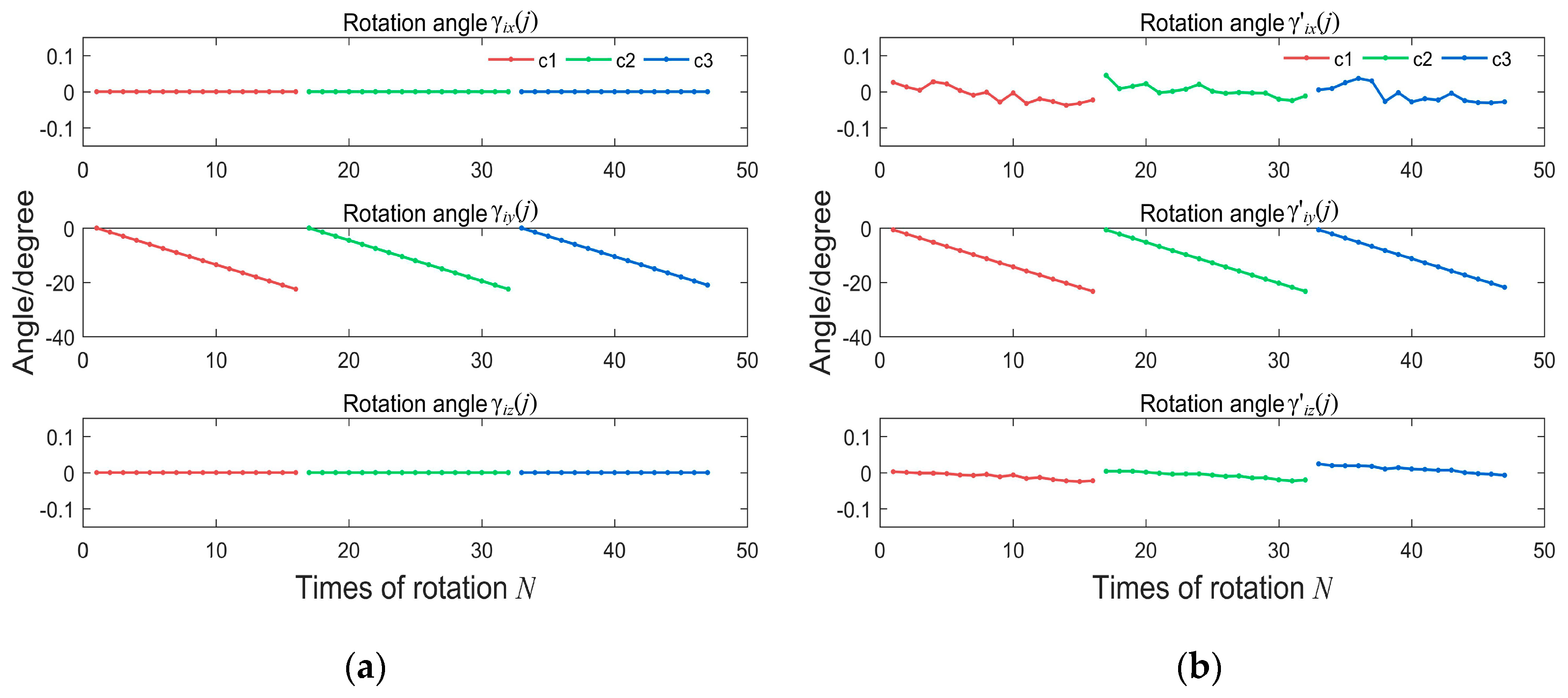
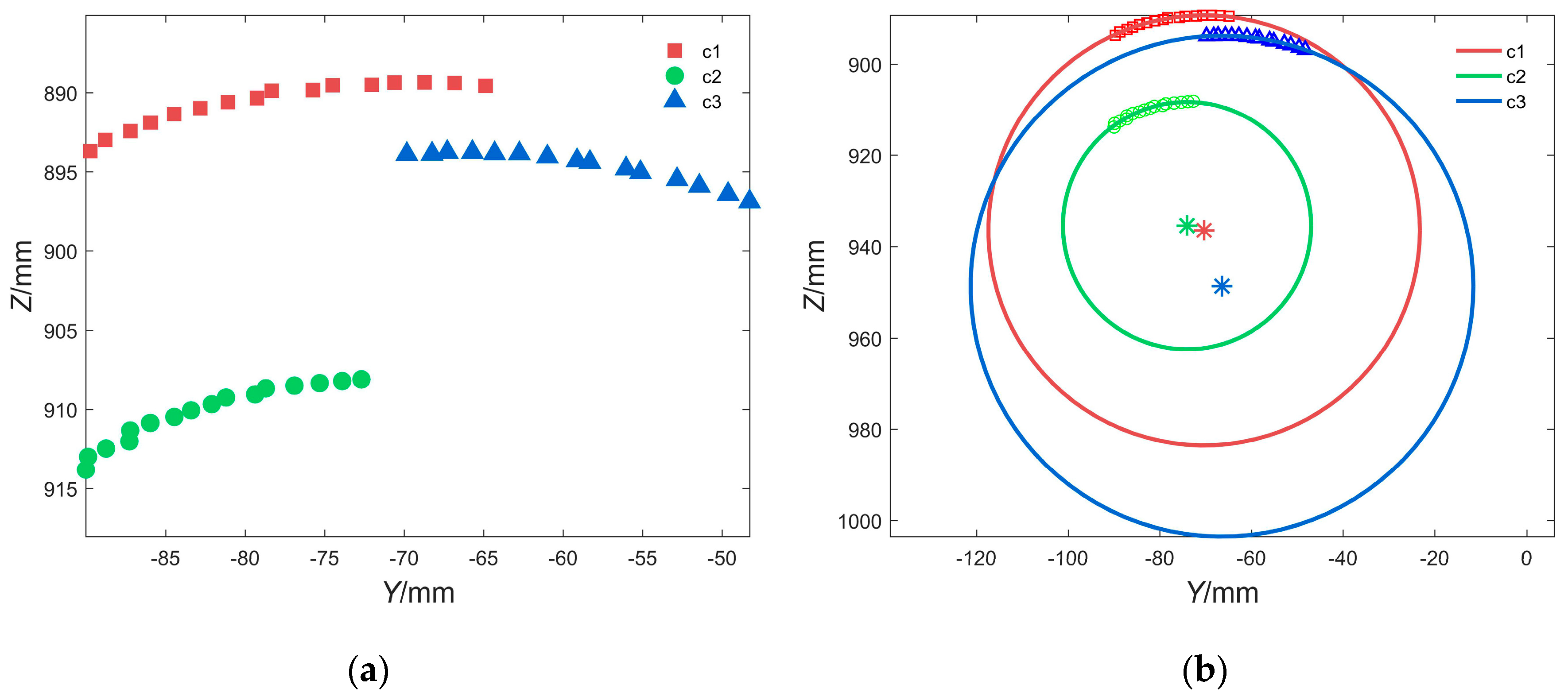




| Parameter | fx/Pixels | fy/Pixels | u0/Pixels | v0/Pixels | α | Pixel Error/Pixels |
|---|---|---|---|---|---|---|
| Without noise | 1700.00 | 1700.00 | 600.00 | 500.00 | 0 | 0 |
| 3.5% Gaussian noise | 1698.84 | 1698.78 | 599.77 | 500.05 | 0 | 0.035 |
| Fitted Center/mm | Fitted Radius/mm | |
|---|---|---|
| Without noise | Or = (−50.00, 900.00) | r = 50.00 |
| Og = (−50.00, 900.00) | r = 65.00 | |
| Ob = (−50.00, 900.00) | r = 80.00 | |
| 3.5% random noise | Or = (−49.96, 900.04) | r = 49.96 |
| Og = (−50.01, 900.03) | r = 65.19 | |
| Ob = (−49.96, 900.01) | r = 79.99 |
| The Initial Position of the Camera | Fitted Center/mm | Fitted Radius/mm | RMSE/mm |
|---|---|---|---|
| c1 | Or1 = (−55.23, 961.58) | r1 = 71.62 | 0.042 |
| c2 | Or2 = (−55.38, 961.88) | r2 = 53.32 | 0.054 |
| c3 | Or3 = (−55.00, 961.53) | r3 = 67.29 | 0.042 |
| Standard Deviation/mm | Yw | Zw |
|---|---|---|
| O’rj relative to Or | 0.029 | 0.141 |
| O’’rj relative to Or | 0.022 | 0.117 |
| Standard Deviation/Degree | Red Circle | Green Triangle | Pink Diamond | Blue Square |
|---|---|---|---|---|
| Alignment | 0.013 | 0.011 | 0.011 | 0.011 |
| Misalignment | 0.043 | 0.066 | 0.043 | 0.057 |
| Direction | STD/mm 6° | STD/mm 9° | STD/mm 12° | |
|---|---|---|---|---|
| Alignment | Xc | 0.010 | 0.048 | 0.065 |
| Yc | 0.015 | 0.037 | 0.063 | |
| Misalignment | Xc | 7.221 | 10.910 | 14.641 |
| Yc | 0.314 | 0.358 | 0.424 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Y.; Su, X.; Chen, W. Alignment Method of an Axis Based on Camera Calibration in a Rotating Optical Measurement System. Appl. Sci. 2020, 10, 6962. https://doi.org/10.3390/app10196962
Hou Y, Su X, Chen W. Alignment Method of an Axis Based on Camera Calibration in a Rotating Optical Measurement System. Applied Sciences. 2020; 10(19):6962. https://doi.org/10.3390/app10196962
Chicago/Turabian StyleHou, Yanli, Xianyu Su, and Wenjing Chen. 2020. "Alignment Method of an Axis Based on Camera Calibration in a Rotating Optical Measurement System" Applied Sciences 10, no. 19: 6962. https://doi.org/10.3390/app10196962
APA StyleHou, Y., Su, X., & Chen, W. (2020). Alignment Method of an Axis Based on Camera Calibration in a Rotating Optical Measurement System. Applied Sciences, 10(19), 6962. https://doi.org/10.3390/app10196962




